Self-Consistent Soundscape Ranking Index: The Case of an Urban Park
Abstract
:1. Introduction
2. Materials and Methods
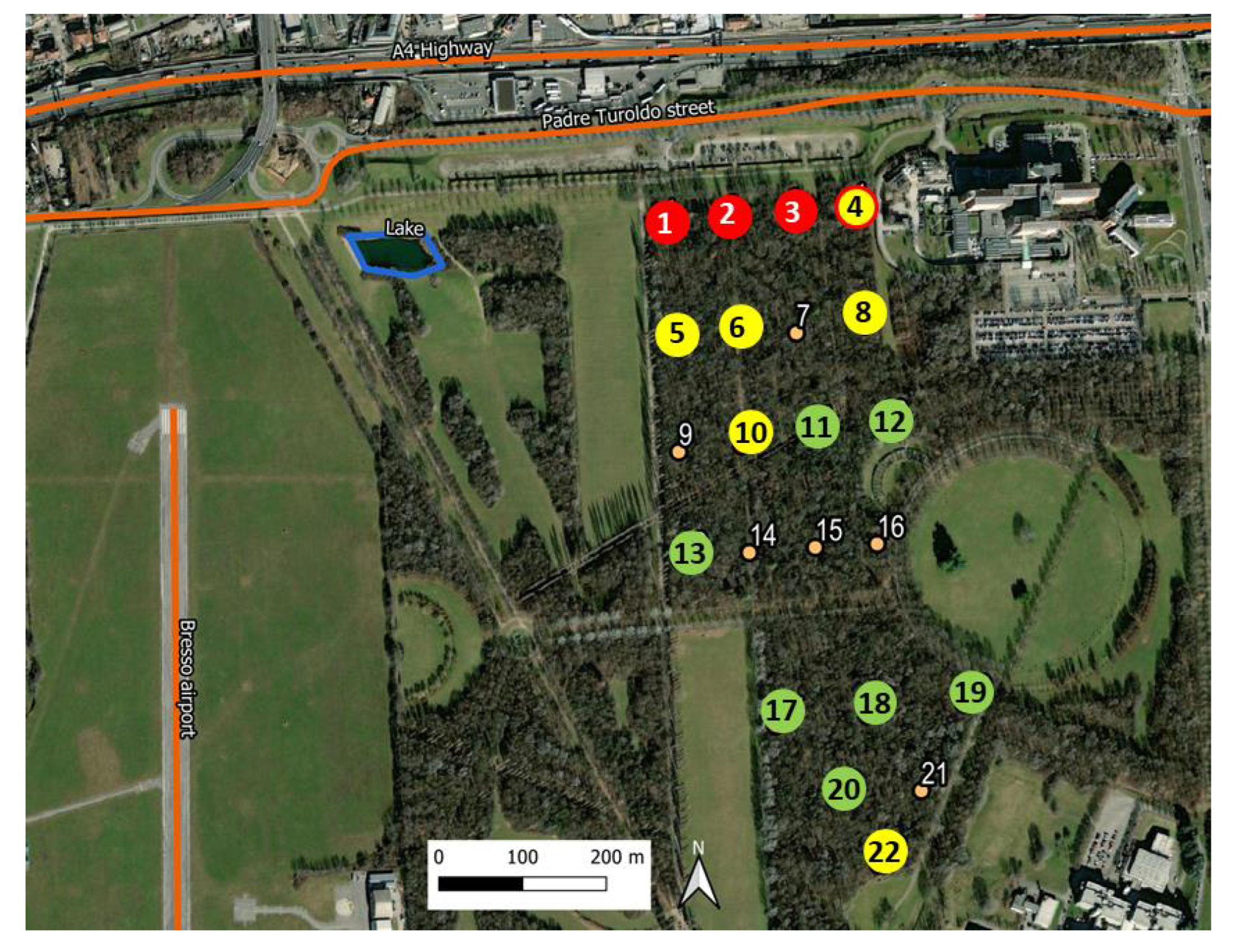
2.1. Area of the Study
2.2. Audio Recorders
- Computation of the acoustic complexity index (ACI, see [27]) for a white noise source.
- Behavior of each VLCR at different frequencies.
2.3. Measurement Scheme
2.4. Aural Survey
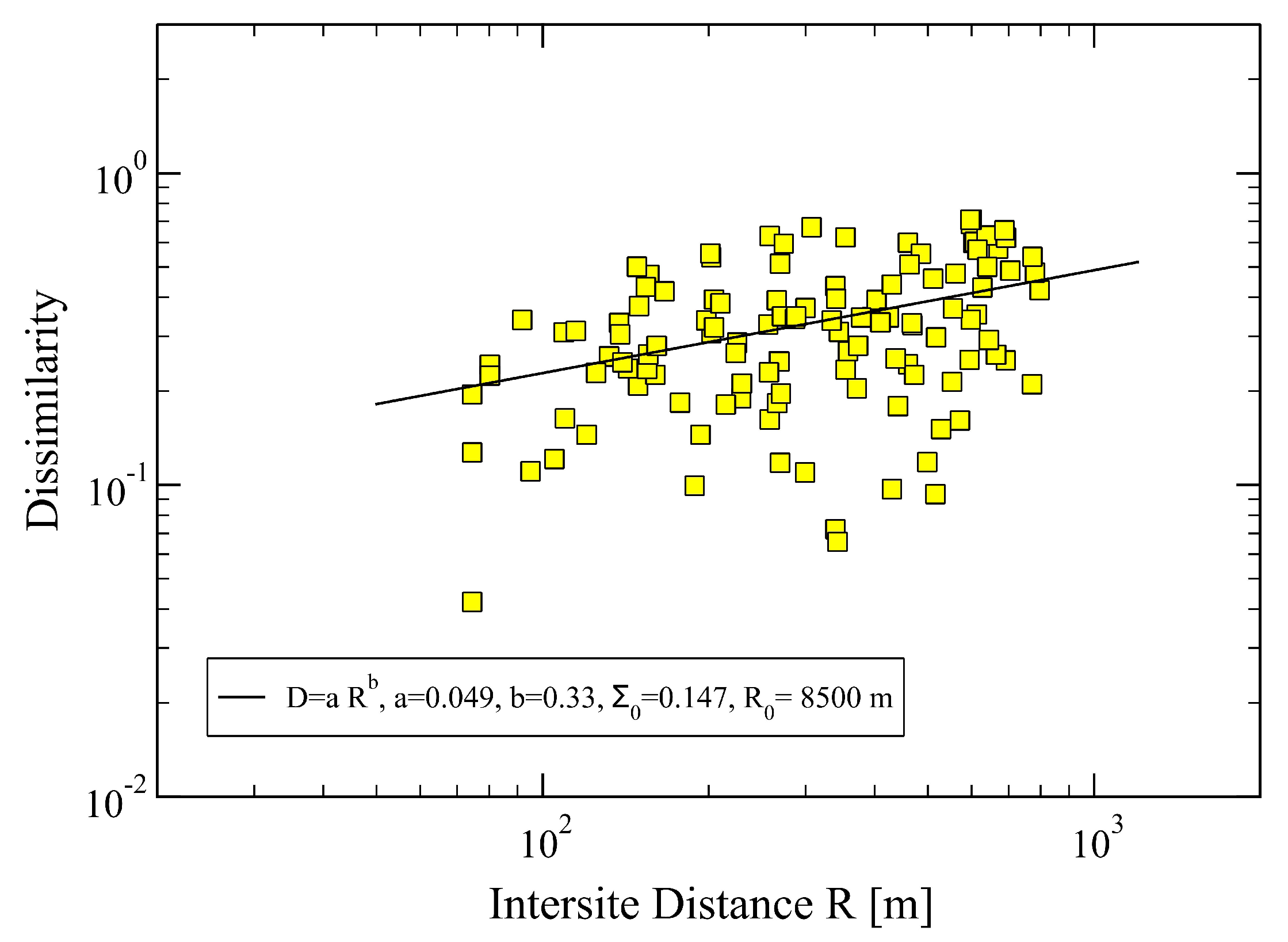
2.5. The Soundscape Ranking Index
2.6. Optimization Procedure for
3. Results
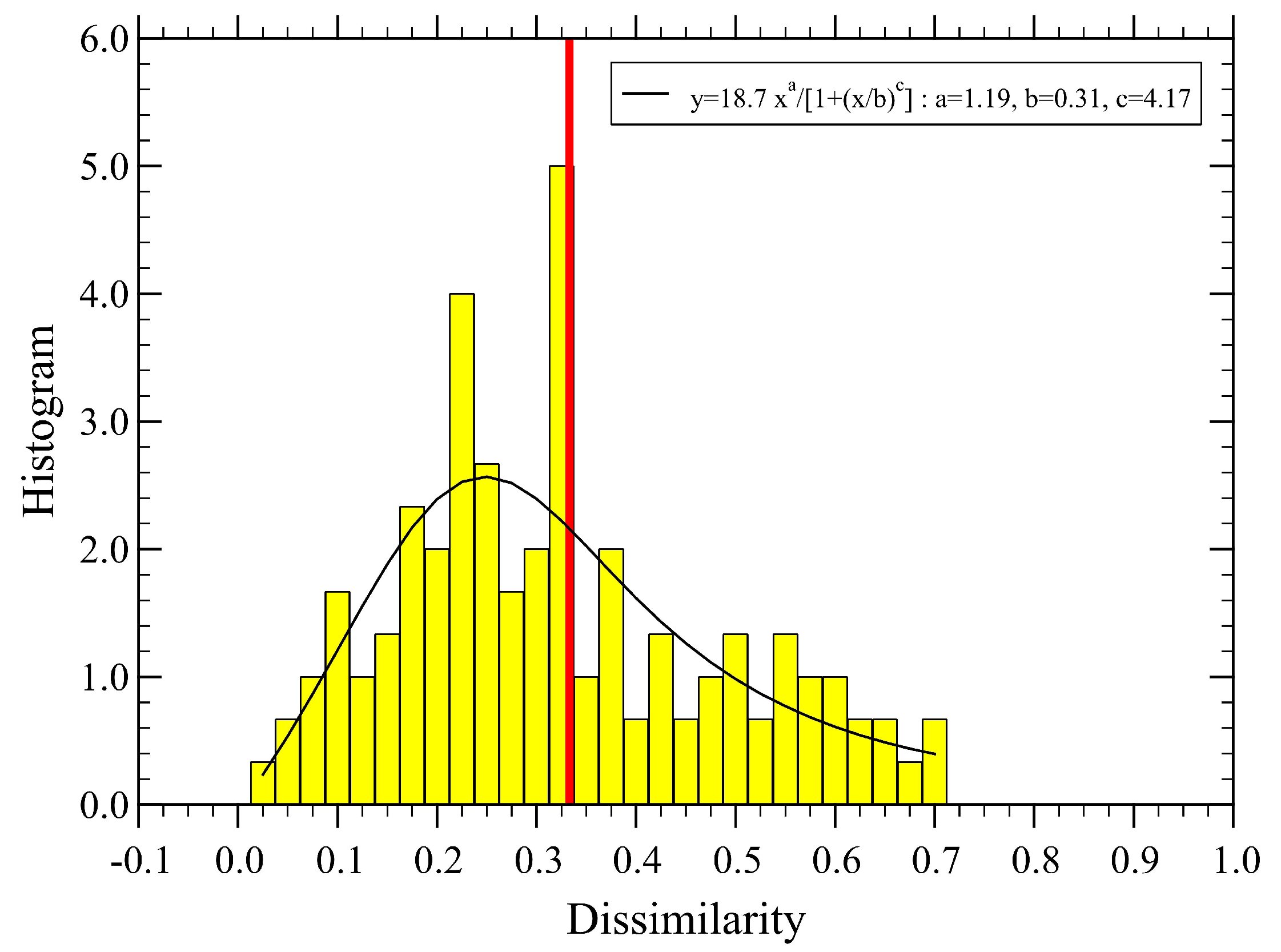
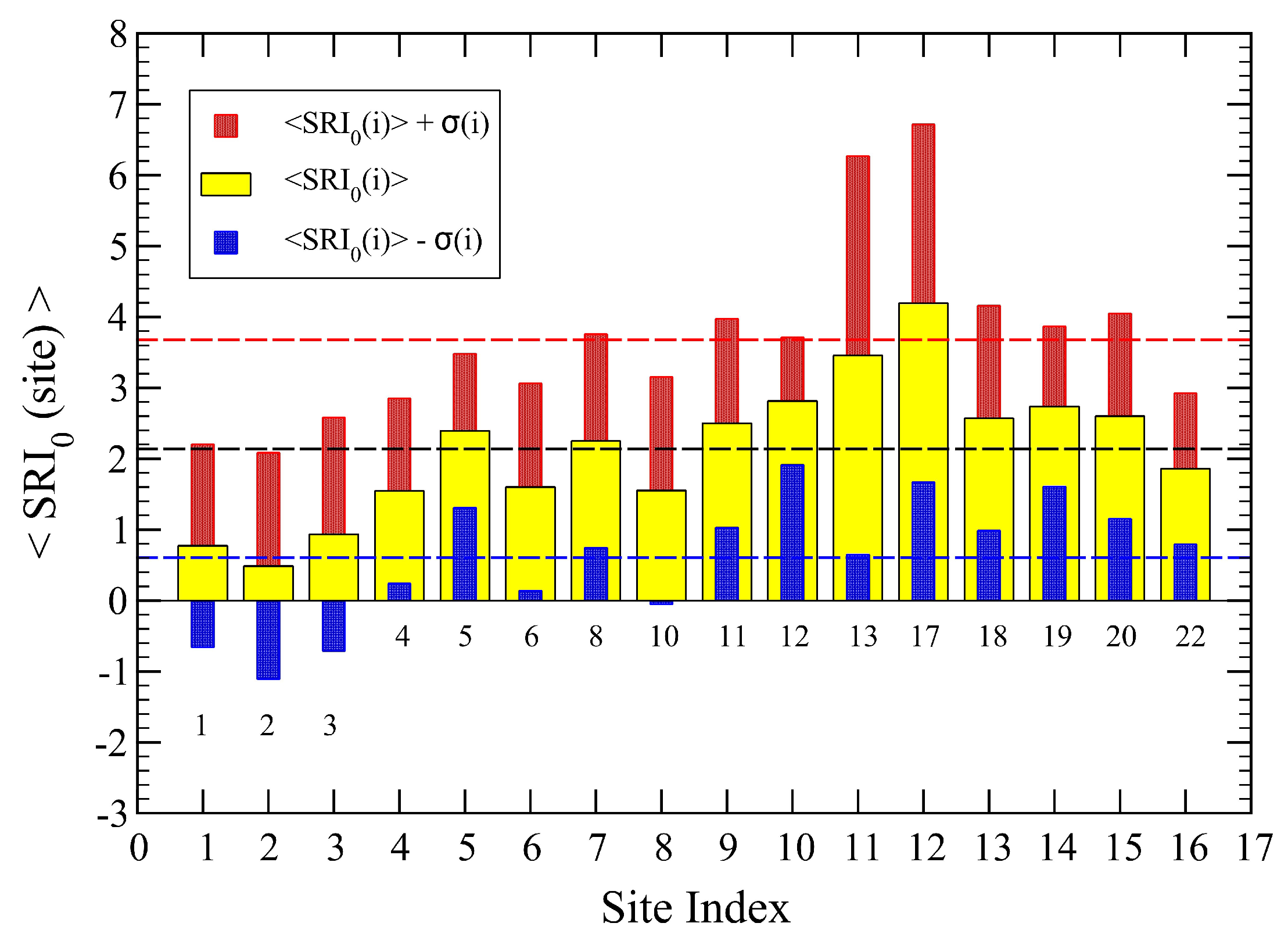
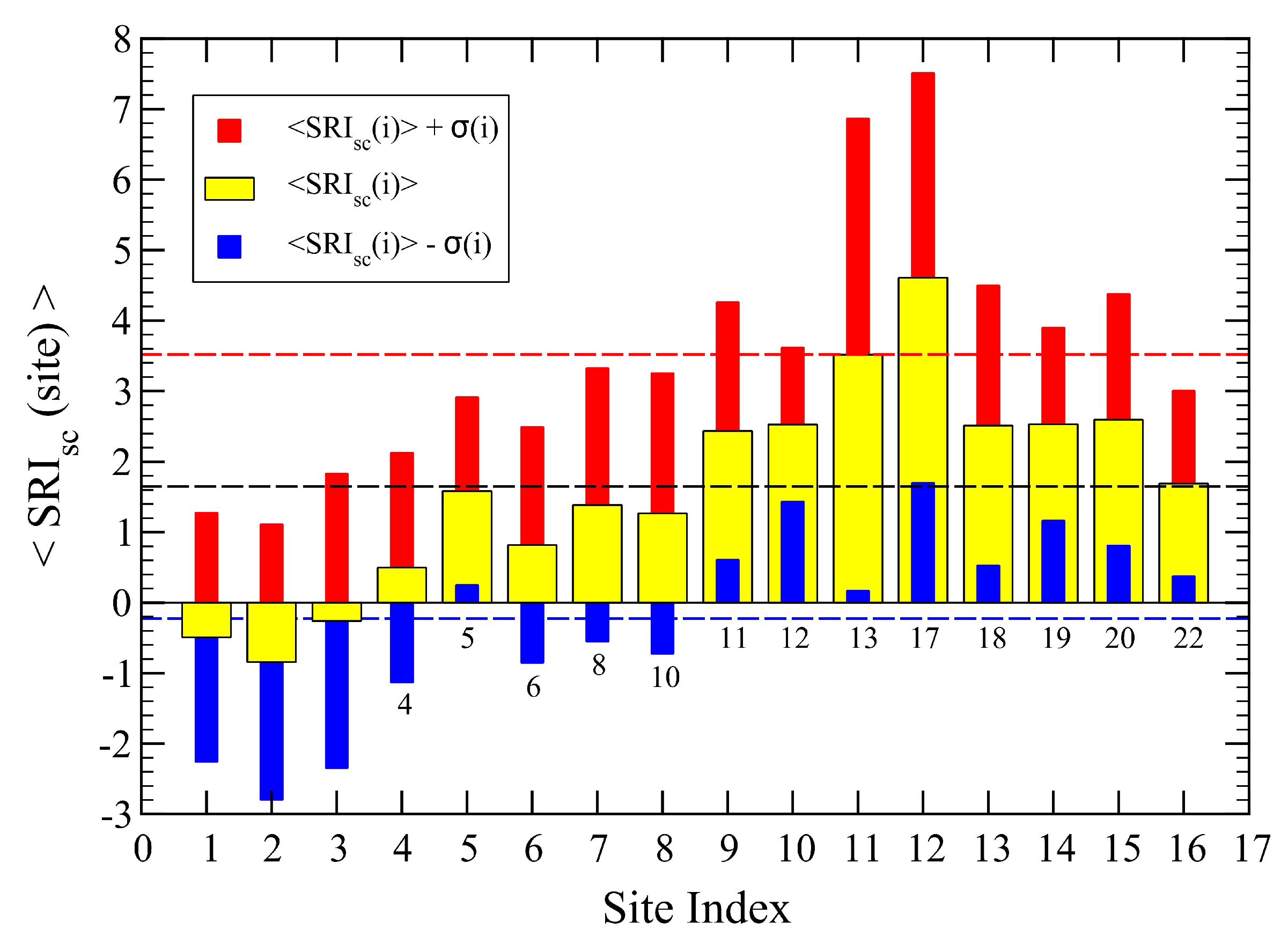
3.1. Initial Values
3.2. Optimized Values
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schafer, R.M. The Soundscape: Our Sonic Environment and the Tuning of the World; Simon and Schuster: New York, NY, USA, 1993. [Google Scholar]
- Dumyahn, S.L.; Pijanowski, B.C. Soundscape conservation. Landsc. Ecol. 2011, 26, 1327–1344. [Google Scholar] [CrossRef]
- Barber, J.R.; Crooks, K.R.; Fristrup, K.M. The costs of chronic noise exposure for terrestrial organisms. Trends Ecol. Evol. 2010, 25, 180–189. [Google Scholar] [CrossRef]
- Lawson, G.M. Networks cities and ecological habitats. In Networks Cities; Qun, F., Brearley, J., Eds.; China Architecture and Building Press: Beijing, China, 2011; pp. 250–253. Available online: https://eprints.qut.edu.au/40229/ (accessed on 15 March 2023).
- Francis, C.D.; Newman, P.; Taff, B.D.; White, C.; Monz, C.A.; Levenhagen, M.; Petrelli, A.R.; Abbott, L.C.; Newton, J.; Burson, S.; et al. Acoustic environments matter: Synergistic benefits to humans and ecological communities. J. Environ. Manag. 2017, 203, 245–254. [Google Scholar] [CrossRef]
- Doser, J.W.; Hannam, K.M.; Finley, A.O. Characterizing functional relationships between technophony and biophony: A western New York soundscape case study. Landsc. Ecol. 2020, 35, 689–707. [Google Scholar] [CrossRef] [Green Version]
- Sayuri Moreira, S.L.; Freire, S.T.S.; Wagner, R.J., Jr.; Diego, L. Terrestrial Passive Acoustic Monitoring: Review and Perspectives. BioScience 2019, 69, 15–25. [Google Scholar] [CrossRef]
- Mellinger, D.K.; Stafford, K.M.; Moore, S.E.; Dziak, R.P.; Matsumoto, H. An overview of fixed passive acoustic observation methods for cetaceans. Oceanography 2007, 20, 36–45. Available online: https://www.jstor.org/stable/24860138 (accessed on 15 March 2023). [CrossRef] [Green Version]
- Ribeiro, J.W.; Sugai, L.S.M.; Campos-Cerqueira, M. Passive acoustic monitoring as a complementary strategy to assess biodiversity in the Brazilian Amazonia. Biodivers. Conserv. 2017, 26, 2999–3002. [Google Scholar] [CrossRef] [Green Version]
- Browning, E.; Gibb, R.; Glover-Kapfer, P.; Jones, K.E. Passive Acoustic Monitoring in Ecology and Conservation; WWF: Woking, UK, 2017; p. 76. Available online: https://repository.oceanbestpractices.org/handle/11329/1370 (accessed on 15 March 2023).
- Sueur, J.; Farina, A.; Gasc, A.; Pieretti, N.; Pavoine, S. Acoustic indices for biodiversity assessment and landscape investigation. Acta Acust. United Acust. 2014, 100, 772–781. [Google Scholar] [CrossRef] [Green Version]
- Krause, B. The Loss of Natural Soundscapes. Earth Isl. J. 2002, 17, 27–29. Available online: www.earthisland.org/journal/index.php/magazine/archive (accessed on 15 March 2023).
- Pijanowski, B.C.; Farina, A.; Gage, S.H.; Dumyahn, S.L.; Krause, B.L. What is soundscape ecology? An introduction and overview of an emerging new science. Landsc. Ecol. 2011, 26, 1213–1232. [Google Scholar] [CrossRef]
- Yang, W.; Kang, J. Soundscape and sound preferences in urban squares: A case study in Sheffield. J. Urban Des. 2005, 10, 61–80. [Google Scholar] [CrossRef]
- Pavan, G. Fundamentals of Soundscape Conservation. In Ecoacoustics: The Ecological Role of Sounds; Farina, A., Gage, S.H., Eds.; Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 235–258. [Google Scholar] [CrossRef]
- Sethi, S.S.; Jones, N.S.; Fulcher, B.D.; Picinali, L.; Clink, D.J.; Klinck, H.; Orme, C.D.L.; Wrege, P.H.; Ewers, R.M. Characterizing soundscapes across diverse ecosystems using a universal acoustic feature set. Proc. Natl. Acad. Sci. USA 2020, 117, 17049–17055. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Kang, J.; Luo, T.; Behm, H. Landscape effects on soundscape experience in city parks. Sci. Total. Environ. 2013, 454–455, 474–481. [Google Scholar] [CrossRef]
- Raimbault, M.; Lavier, C.; Bérengier, M. Ambient sound assessment of urban environments: Field studies in two French cities. Appl. Acoust. 2003, 64, 1241–1256. [Google Scholar] [CrossRef]
- Uebel, K.; Rhodes, J.R.; Wilson, K.; Dean, A.J. Urban park soundscapes: Spatial and social factors influencing bird and traffic sound experiences. People Nat. 2022, 4, 1616–1628. [Google Scholar] [CrossRef]
- Brambilla, G.; Gallo, V.; Asdrubali, F.; D’Alessro, F. The perceived quality of soundscape in three urban parks in Rome. J. Acoust. Soc. Am. 2013, 134, 832–839. [Google Scholar] [CrossRef]
- Szeremeta, B.; Zannin, P.H.T. Analysis and evaluation of soundscapes in public parks through interviews and measurement of noise. Sci. Total. Environ. 2009, 407, 6143–6149. [Google Scholar] [CrossRef]
- Uebel, K.; Marselle, M.; Dean, A.J.; Rhodes, J.R.; Bonn, A. Urban green space soundscapes and their perceived restorativeness. People Nat. 2021, 3, 756–769. [Google Scholar] [CrossRef]
- Lellouch, L.; Pavoine, S.; Jiguet, F.; Glotin, H.; Sueur, J. Monitoring temporal change of bird communities with dissimilarity acoustic indices. Methods Ecol. Evol. 2014, 5, 495–505. [Google Scholar] [CrossRef]
- Kasten, E.P.; Gage, S.H.; Fox, J.; Joo, W. The remote environmental assessment laboratory’s acoustic library: An archive for studying soundscape ecology. Ecol. Inform. 2012, 12, 50–67. [Google Scholar] [CrossRef]
- Boelman, N.T.; Asner, G.P.; Hart, P.J.; Martin, R.E. Multitrophic invasion resistance in hawaii: Bioacoustics, field surveys, and airborne remote sensing. Ecol. Appl. 2007, 17, 2137–2144. [Google Scholar] [CrossRef] [PubMed]
- Sueur, J.; Pavoine, S.; Hamerlynck, O.; Duvail, S. Rapid acoustic survey for biodiversity appraisal. PLoS ONE 2008, 3, e4065. [Google Scholar] [CrossRef] [Green Version]
- Pieretti, N.; Farina, A.; Morri, D. A new methodology to infer the singing activity of an avian community: The Acoustic Complexity Index (ACI). Ecol. Indic. 2011, 11, 868–873. [Google Scholar] [CrossRef]
- Eldridge, A.; Guyot, P.; Moscoso, P.; Johnston, A.; Eyre-Walker, Y.; Peck, M. Sounding out ecoacoustic metrics: Avian species richness is predicted by acoustic indices in temperate but not tropical habitats. Ecol. Indic. 2018, 95, 939–952. [Google Scholar] [CrossRef] [Green Version]
- Benocci, R.; Brambilla, G.; Bisceglie, A.; Zambon, G. Eco-Acoustic Indices to Evaluate Soundscape Degradation Due to Human Intrusion. Sustainability 2020, 12, 10455. [Google Scholar] [CrossRef]
- Bertucci, F.; Parmentier, E.; Berten, L.; Brooker, R.M.; Lecchini, D. Temporal and spatial comparisons of underwater sound signatures of different reef habitats in Moorea Island, French Polynesia. PLoS ONE 2015, 10, e0135733. [Google Scholar] [CrossRef]
- Harris, S.A.; Shears, N.T.; Radford, C.A. Ecoacoustic indices as proxies for biodiversity on temperate reefs. Methods Ecol. Evol. 2016, 7, 713–724. [Google Scholar] [CrossRef] [Green Version]
- Shonfield, J.; Bayne, E.M. Autonomous recording units in avian ecological research: Current use and future applications. Avian Conserv. Ecol. 2017, 12, 14. [Google Scholar] [CrossRef]
- Pérez-Granados, C.; Traba, J. Estimating bird density using passive acoustic monitoring: A review of methods and suggestions for further research. Ibis 2021, 163, 765–783. [Google Scholar] [CrossRef]
- Benocci, R.; Roman, H.E.; Bisceglie, A.; Angelini, F.; Brambilla, G.; Zambon, G. Eco-acoustic assessment of an urban park by statistical analysis. Sustainability 2021, 13, 7857. [Google Scholar] [CrossRef]
- Benocci, R.; Potenza, A.; Bisceglie, A.; Roman, H.E.; Zambon, G. Mapping of the Acoustic Environment at an Urban Park in the City Area of Milan, Italy, Using Very Low-Cost Sensors. Sensors 2022, 22, 3528. [Google Scholar] [CrossRef]
- Truax, B. Handbook for Acoustic Ecology; A.R.C. Publications: Vancouver, BC, Canada, 1978. [Google Scholar]
- Pijanowski, B.C.; Villanueva-Rivera, L.J.; Dumyahn, S.L.; Farina, A.; Krause, B.L.; Napoletano, B.M.; Gage, S.H.; Pieretti, N. Soundscape ecology: The science of sound in the landscape. Bioscience 2011, 61, 203–216. [Google Scholar] [CrossRef] [Green Version]
- Benocci, R.; Roman, H.E.; Bisceglie, A.; Angelini, F.; Brambilla, G.; Zambon, G. Auto-correlations and long time memory of environment sound: The case of an Urban Park in the city of Milan (Italy). Ecol. Indic. 2022, 134, 108492. [Google Scholar] [CrossRef]
- Roman, H.E.; Albergante, M.; Colombo, M.; Croccolo, F.; Marini, F.; Riccardi, C. Modeling cross correlations within a many-assets market. Phys. Rev. E 2006, 73, 036129. [Google Scholar] [CrossRef]
- Gage, S.H.; Farina, A. Ecoacoustics: The Ecological Role of Sounds; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Sueur, J.; Farina, A. Ecoacoustics: The ecological investigation and interpretation of environment sound. Biosemiotics 2015, 8, 493–502. [Google Scholar] [CrossRef]
- Farina, A. Soundscape Ecology; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Krause, B.; Farina, A. Using ecoacoustic methods to survey the impacts of climate change on biodiversity. Biol. Conserv. 2016, 195, 245–254. [Google Scholar] [CrossRef]




| Sound Source | Quantity | Parameters | Identification |
|---|---|---|---|
| Many | 1 | Many birds | |
| Birds number | Few | 2 | Few birds, no traffic |
| None | 3 | No birds, no other sources | |
| >1 | 1 | Many species | |
| Birds species | 1 | 2 | One species, no traffic |
| None | 3 | No birds, no other sources | |
| 100% | 1 | 60 s | |
| Birds | 75% | 1 | 45 s |
| sound | 50% | 1 | 30 s |
| duration | 25% | 1 | 15 s |
| 0% | 1 | 0 s | |
| None | 2 | Few birds, no traffic | |
| Traffic level | Low | 4 | Continuous/low traffic |
| High | 5 | Intermittent/high traffic | |
| None | 2 | No traffic | |
| Traffic type | Continuous | 4 | Continuous/low traffic |
| Intermittent | 5 | Intermittent/high traffic | |
| Trains | Present | 5 | Trains |
| Airplanes | Present | 5 | Airplanes, other sources |
| n | P(n) | Identification |
|---|---|---|
| 1 | 2 | Many birds/species |
| 2 | 1 | Few birds/no traffic |
| 3 | 0 | No birds/no other sources |
| 4 | −1 | Continuous/low traffic |
| 5 | −2 | Intermittent/high traffic/other sources |
| Poor Quality | Medium Quality | Good Quality |
|---|---|---|
| SRI < 0 | 0 ≤ SRI ≤ 2 | SRI > 2 |
| Initial Parameters | Optimized Parameters | |
|---|---|---|
| 1/3 | 1/2 | |
| P(1) | 2.0 | 2.290 |
| P(2) | 1.0 | 0.766 |
| P(3) | 0.0 | 0.000 |
| P(4) | −1.0 | −1.528 |
| P(5) | −2.0 | −2.262 |
| 〈SRI〉 | 2.14 | 1.65 |
| 1.54 | 1.88 | |
| 0.333 | 0.375 | |
| 8500 m | 2270 m | |
| 0.147 | 0.139 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benocci, R.; Afify, A.; Potenza, A.; Roman, H.E.; Zambon, G. Self-Consistent Soundscape Ranking Index: The Case of an Urban Park. Sensors 2023, 23, 3401. https://doi.org/10.3390/s23073401
Benocci R, Afify A, Potenza A, Roman HE, Zambon G. Self-Consistent Soundscape Ranking Index: The Case of an Urban Park. Sensors. 2023; 23(7):3401. https://doi.org/10.3390/s23073401
Chicago/Turabian StyleBenocci, Roberto, Andrea Afify, Andrea Potenza, H. Eduardo Roman, and Giovanni Zambon. 2023. "Self-Consistent Soundscape Ranking Index: The Case of an Urban Park" Sensors 23, no. 7: 3401. https://doi.org/10.3390/s23073401
APA StyleBenocci, R., Afify, A., Potenza, A., Roman, H. E., & Zambon, G. (2023). Self-Consistent Soundscape Ranking Index: The Case of an Urban Park. Sensors, 23(7), 3401. https://doi.org/10.3390/s23073401










