Deconvolved Fractional Fourier Domain Beamforming for Linear Frequency Modulation Signals
Abstract
1. Introduction
2. The Fractional Fourier Domain Array Signal Model
3. Deconvolved Beamforming in the Fractional Fourier Domain
3.1. Fractional Fourier Domain Delay-and-Sum Beamforming
3.2. Deconvolution of the Beamforming Complex Output
| Algorithm 1: MFISTA algorithm. |
| Input: FrFB complex output , complex beam pattern , regularization coefficient , iteration times , and initial value ; |
| Output: the estimation of source signal distribution ; |
| 1. set ; |
| 2. for to |
| 3. ; |
| 4. ; |
| 5. ; |
| 6. ; |
| 7. end |
4. Simulation Results
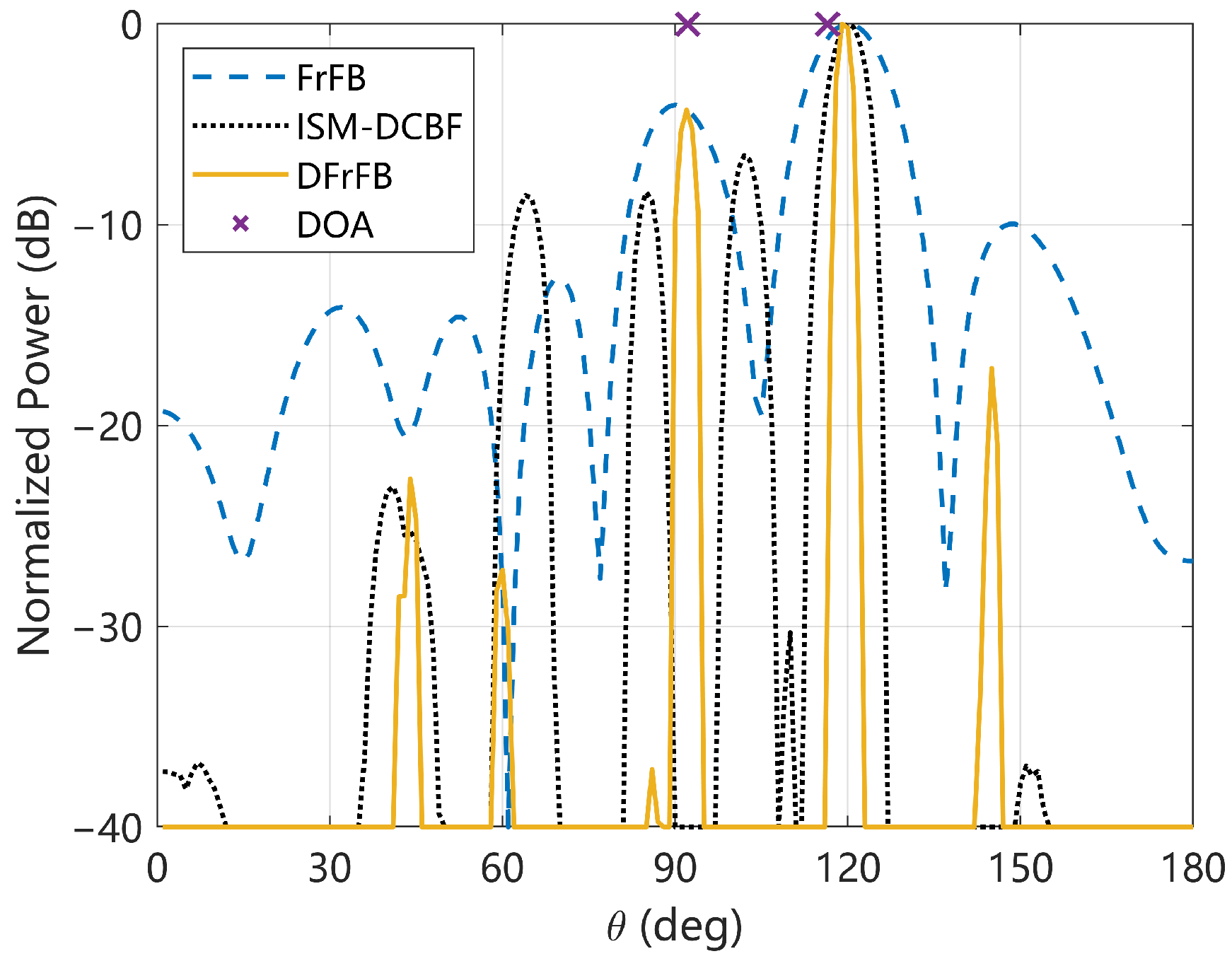
4.1. Spatial Spectrum
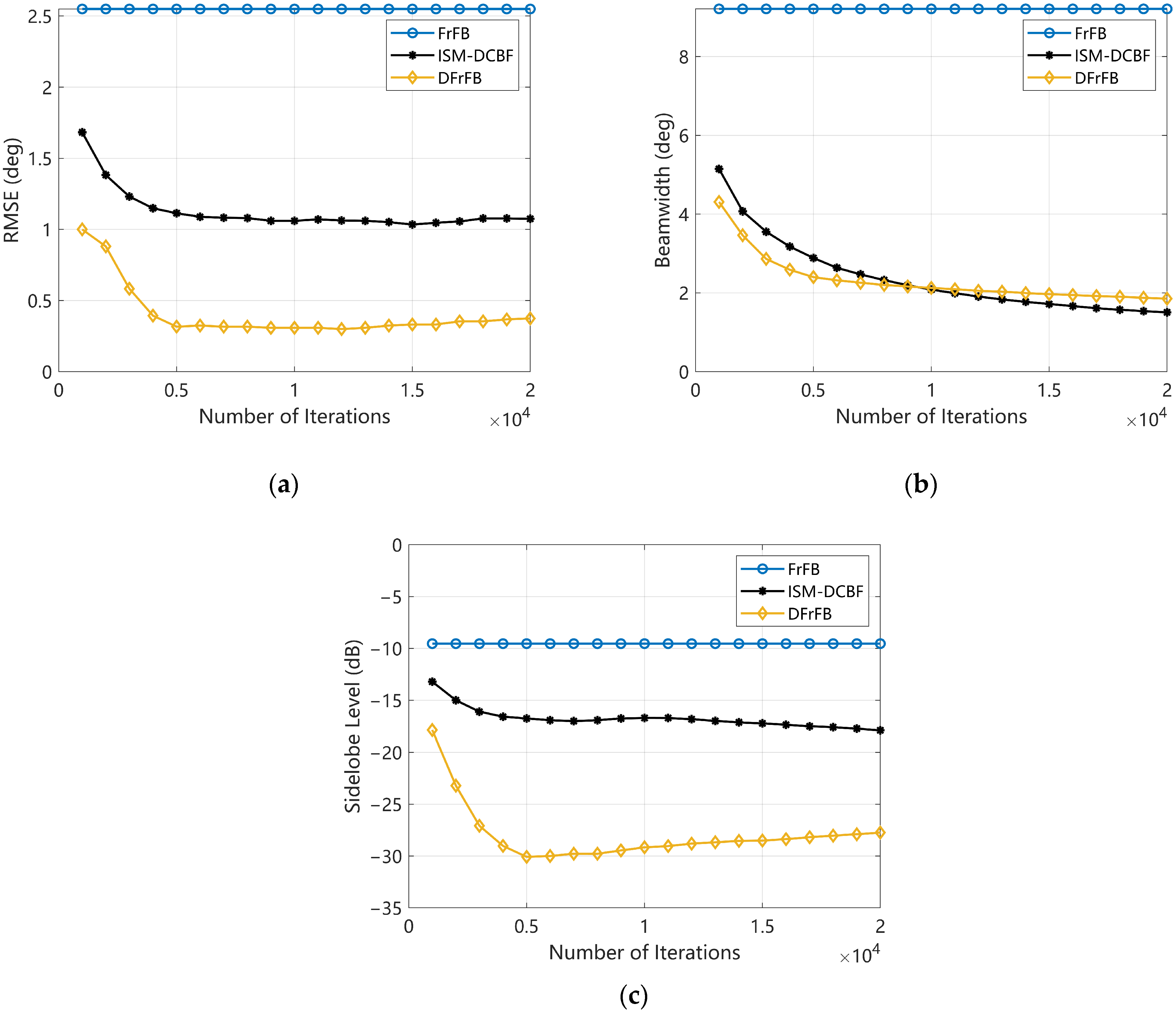
4.2. The Number of Deconvolution Iterations
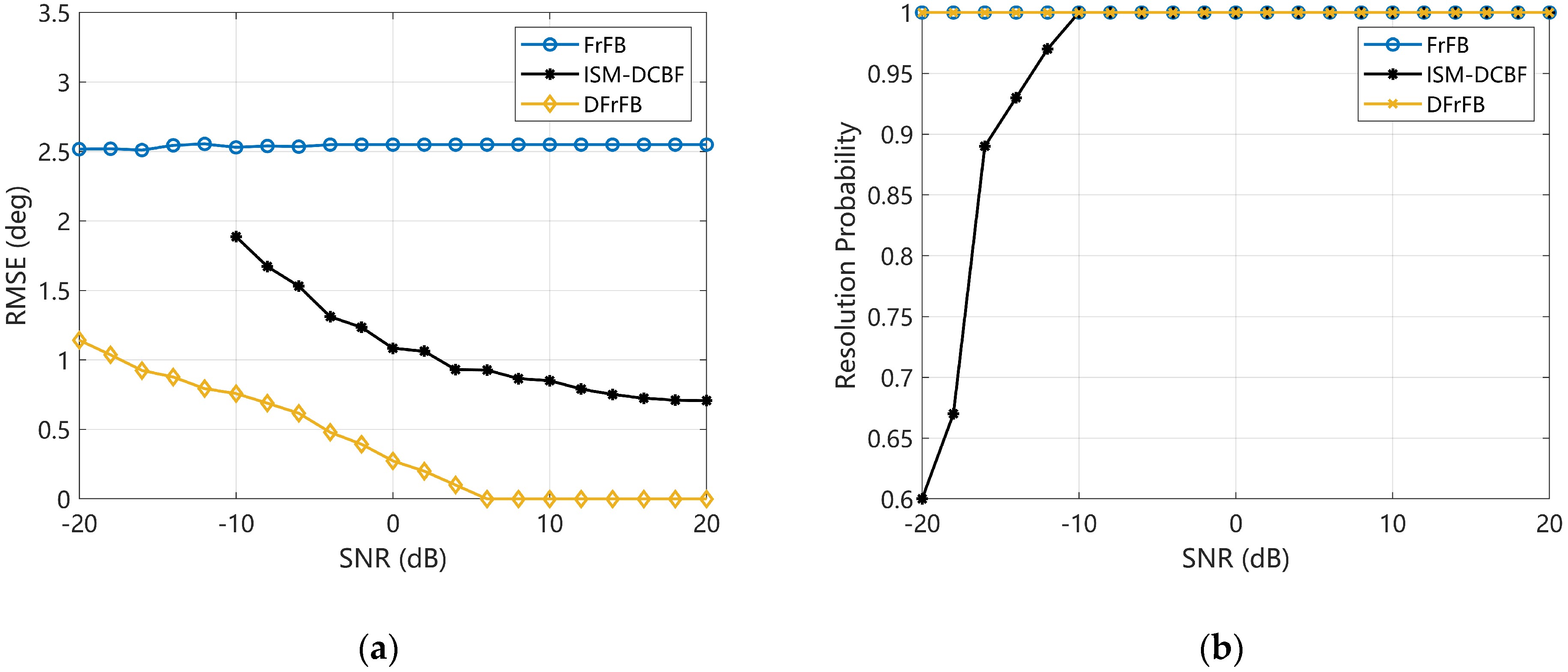
4.3. SNR
4.4. The Number of Hydrophones
4.5. Angular Interval
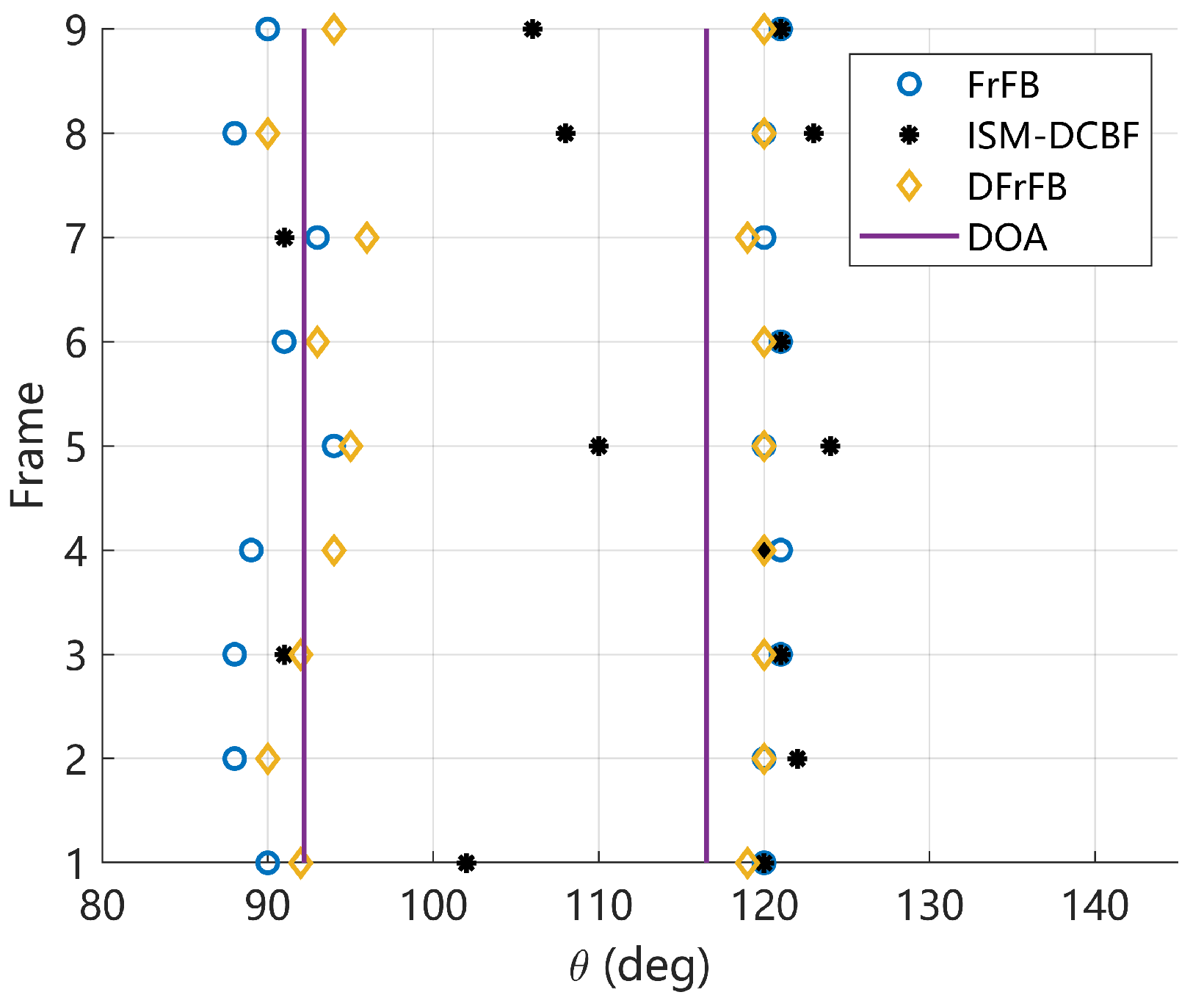
5. Experimental Results
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, D.-H.; Shin, J.-W.; Do, D.-W.; Choi, S.-M.; Kim, H.-N. Robust LFM target detection in wideband sonar systems. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2399–2412. [Google Scholar] [CrossRef]
- Liu, D.L.; Qu, H.R.; Wang, W.; Deng, J.J. Multiple targets detection of linear frequency-modulated continuous wave active sonar using fractional Fourier transform. Integr. Ferroelectr. 2020, 209, 1–10. [Google Scholar] [CrossRef]
- Bartlett, M.S. Smoothing periodograms from time-series with continuous spectra. Nature 1948, 161, 686–687. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Chiariotti, P.; Martarelli, M.; Castellini, P. Acoustic beamforming for noise source localization—Reviews, methodology and applications. Mech. Syst. Signal Process. 2019, 120, 422–448. [Google Scholar] [CrossRef]
- Ahmad, Z.; Song, Y.L.; Du, Q. Wideband DOA estimation based on incoherent signal subspace method. Compel-Int. J. Comp. Math. Electr. Electron. Eng. 2018, 37, 1271–1289. [Google Scholar] [CrossRef]
- Wang, H.; Kaveh, M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 823–831. [Google Scholar] [CrossRef]
- Yin, J.W.; Guo, K.; Han, X.; Yu, G. Fractional Fourier transform based underwater multi-targets direction-of-arrival estimation using wideband linear chirps. Appl. Acoust. 2020, 169, 7. [Google Scholar] [CrossRef]
- Khodja, M.; Belouchrani, A.; Abed-Meraim, K. Performance analysis for time-frequency MUSIC algorithm in presence of both additive noise and array calibration errors. EURASIP J. Adv. Signal Process. 2012, 11, 94. [Google Scholar] [CrossRef]
- Ghofrani, S. Matching pursuit for direction of arrival estimation in the presence of Gaussian noise and impulsive noise. IET Signal Process. 2014, 8, 540–551. [Google Scholar] [CrossRef]
- Cui, K.B.; Wu, W.W.; Huang, J.J.; Chen, X.; Yuan, N.C. DOA estimation of LFM signals based on STFT and multiple invariance ESPRIT. AEU-Int. J. Electron. Commun. 2017, 77, 10–17. [Google Scholar] [CrossRef]
- Han, X.Y.; Liu, M.Q.; Zhang, S.N.; Zheng, R.H.; Lan, J. A passive DOA estimation algorithm of underwater multipath signals via spatial time-frequency distributions. IEEE Trans. Veh. Technol. 2021, 70, 3439–3455. [Google Scholar] [CrossRef]
- Shi, J.; Yang, D.S.; Shi, S.G.; Zhu, Z.R.; Hu, B. Spatial time-frequency DOA estimation based on joint diagonalization using Jacobi rotation. Appl. Acoust. 2017, 116, 24–32. [Google Scholar] [CrossRef]
- Salin, B.M.; Salin, M.B. Methods for measuring bistatic characteristics of sound scattering by the ocean bottom and surface. Acoust. Phys. 2016, 62, 575–582. [Google Scholar] [CrossRef]
- Kim, M.; Lee, S.H.; Choi, I.O.; Kim, K.T. Direction finding for multiple wideband chirp signal sources using blind signal separation and matched filtering. Signal Process. 2022, 200, 15. [Google Scholar] [CrossRef]
- Ozaktas, H.M.; Arikan, O.; Kutay, M.A.; Bozdagt, G. Digital computation of the fractional Fourier transform. IEEE Trans. Signal Process. 1996, 44, 2141–2150. [Google Scholar] [CrossRef]
- Bultheel, A.; Martínez Sulbaran, H.E. Computation of the fractional Fourier transform. Appl. Comput. Harmon. Anal. 2004, 16, 182–202. [Google Scholar] [CrossRef]
- Tao, R.; Deng, B.; Wang, Y. Research progress of the fractional Fourier transform in signal processing. Sci. China Ser. F 2006, 49, 1–25. [Google Scholar] [CrossRef]
- Sejdic, E.; Djurovic, I.; Stankovic, L. Fractional Fourier transform as a signal processing tool: An overview of recent developments. Signal Process. 2011, 91, 1351–1369. [Google Scholar] [CrossRef]
- Coetmellec, S.; Brunel, M.; Lebrun, D.; Lecourt, J.B. Fractional-order Fourier series expansion for the analysis of chirped pulses. Opt. Commun. 2005, 249, 145–152. [Google Scholar] [CrossRef]
- Zhu, Y.C.; Yang, K.D.; Li, H.; Wu, F.Y.; Yang, Q.L.; Xue, R.Z. Research on DOA estimation of nonstationary signal based on fractional Fourier transform. In Proceedings of the OCEANS—MTS/IEEE Kobe Techno-Oceans Conference (OTO), Kobe, Japan, 28–31 May 2018. [Google Scholar]
- Wang, X.H.; Li, B.; Yang, H.J.; Lu, W.D. Off-grid DOA estimation for wideband LFM signals in FRFT domain using the sensor arrays. IEEE Access 2019, 7, 18500–18509. [Google Scholar] [CrossRef]
- Sreekumar, G.; Mary, L.; Unnikrishnan, A. Performance analysis of fractional Fourier domain beam-forming methods for sensor arrays. Smart Sci. 2019, 7, 28–38. [Google Scholar] [CrossRef]
- Zhang, H.-x.; Liu, H.-d.; Chen, S.; Zhang, Y.; Wang, X.-y. Parameter estimation of chirp signals based on fractional Fourier transform. J. China Univ. Posts Telecommun. 2013, 20, 95–100. [Google Scholar] [CrossRef]
- Levonen, M.; McLaughlin, S. Fractional Fourier transform techniques applied to active sonar. In Proceedings of the MTS/IEEE Conference on Celebrating the Past—Teaming Toward the Future, San Diego, CA, USA, 22–26 September 2003; pp. 1894–1899. [Google Scholar]
- Yang, T.C. Deconvolved conventional beamforming for a horizontal line array. IEEE J. Ocean. Eng. 2018, 43, 160–172. [Google Scholar] [CrossRef]
- Khan, M.K.; Morigi, S.; Reichel, L.; Sgallari, F. Iterative methods of Richardson-Lucy-Type for image deblurring. Numer. Math.-Theory Methods Appl. 2013, 6, 262–275. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, T.C.; Pan, X. Deconvolved conventional beamforming for a planar array and Cramer Rao bound. J. Acoust. Soc. Am. 2018, 144, 1971. [Google Scholar] [CrossRef]
- Sun, D.; Ma, C.; Mei, J.; Shi, W.; Gao, L. The deconvolved conventional beamforming for non-uniform line arrays. In Proceedings of the 2018 OCEANS—MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–4. [Google Scholar]
- Huang, J.; Zhou, T.; Du, W.; Shen, J.; Zhang, W. Smart ocean: A new fast deconvolved beamforming algorithm for multibeam sonar. Sensors 2018, 18, 4013. [Google Scholar] [CrossRef]
- Yang, T.C. Performance analysis of superdirectivity of circular arrays and implications for sonar systems. IEEE J. Ocean. Eng. 2019, 44, 156–166. [Google Scholar] [CrossRef]
- Yang, T. Superdirective beamforming applied to SWellEx96 horizontal arrays data for source localization. J. Acoust. Soc. Am. 2019, 145, EL179–EL184. [Google Scholar] [CrossRef]
- Ye, Z.; Yang, T.C. Deconvolved conventional beamforming for a coprime array. In Proceedings of the Oceans 2019—MARSEILLE, Marseille, France, 17–20 June 2019. [Google Scholar]
- Sun, D.; Ma, C.; Yang, T.C.; Mei, J.; Shi, W. Improving the performance of a vector sensor line array by deconvolution. IEEE J. Ocean. Eng. 2020, 45, 1063–1077. [Google Scholar] [CrossRef]
- Ma, S.H.; Yang, T.C. The effect of elevation angle on bearing estimation for array beamforming in shallow water. In Proceedings of the Global Oceans 2020: Singapore—U.S. Gulf Coast, Biloxi, MS, USA, 5–30 October 2020. [Google Scholar]
- Yang, T.C. Deconvolution of decomposed conventional beamforming. J. Acoust. Soc. Am. 2020, 148, EL195–EL201. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Huang, J.; Du, W.; Shen, J.; Yuan, W. 2-D deconvolved conventional beamforming for a planar array. Circuits Syst. Signal Process. 2021, 40, 5572–5593. [Google Scholar] [CrossRef]
- Wang, F.; Tian, X.; Liu, X.; Gu, B.; Zhou, F.; Chen, Y. Combination complex-valued bayesian compressive sensing method for sparsity constrained deconvolution beamforming. IEEE Trans. Instrum. Meas. 2022, 71, 9506013. [Google Scholar] [CrossRef]
- Wang, S.H.; Lu, M.Y.; Mei, J.D.; Cui, W.T. Deconvolved beamforming using the chebyshev weighting method. J. Mar. Sci. Appl. 2022, 21, 228–235. [Google Scholar] [CrossRef]
- Xie, L.; Sun, C.; Tian, J. Deconvolved frequency-difference beamforming for a linear array. J. Acoust. Soc. Am. 2020, 148, EL440–EL446. [Google Scholar] [CrossRef] [PubMed]
- Prasad, S. Statistical-information-based performance criteria for Richardson-Lucy image deblurring. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 2002, 19, 1286–1296. [Google Scholar] [CrossRef] [PubMed]
- Zibetti, M.V.W.; Helou, E.S.; Regatte, R.R.; Herman, G.T. Monotone FISTA with variable acceleration for compressed sensing magnetic resonance imaging. IEEE Trans. Comput. Imaging 2019, 5, 109–119. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Wang, J.F. Wideband LFM interference suppression based on fractional Fourier transform and projection techniques. Circuits Syst. Signal Process. 2014, 33, 613–627. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, J.F.; Sun, H.X.; Jiang, H.; Yang, K.; Zhang, J.F. Gridless underdetermined DOA estimation of wideband LFM signals with unknown amplitude distortion based on fractional Fourier transform. IEEE Internet Things J. 2020, 7, 11612–11625. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| beamwidth | 1 kHz |
| center frequency | 7.5 kHz |
| frequency modulation rate | 20 kHz |
| time duration | 0.05 s |
| sampling rate | 62.5 kHz |
| Indicators | FrFB | ISM-DCBF | DFrFB |
|---|---|---|---|
| DOA (deg) | 72, 87 | 74, 86 | 75, 85 |
| beamwidth (deg) | 9.3 | 3.6 | 2.3 |
| sidelobe level (deg) | −9.6 | −13.9 | −27.3 |
| Indicators | FrFB | ISM-DCBF | DFrFB |
|---|---|---|---|
| RMSE (deg) | 3.5 | 15.1 | 2.8 |
| beamwidth (deg) | 14.5 | 5.7 | 3.3 |
| sidelobe level (dB) | −10.1 | −7.3 | −16.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Tao, Q.; Sun, W.; Fu, X. Deconvolved Fractional Fourier Domain Beamforming for Linear Frequency Modulation Signals. Sensors 2023, 23, 3511. https://doi.org/10.3390/s23073511
Liu Z, Tao Q, Sun W, Fu X. Deconvolved Fractional Fourier Domain Beamforming for Linear Frequency Modulation Signals. Sensors. 2023; 23(7):3511. https://doi.org/10.3390/s23073511
Chicago/Turabian StyleLiu, Zhuoran, Quan Tao, Wanzhong Sun, and Xiaomei Fu. 2023. "Deconvolved Fractional Fourier Domain Beamforming for Linear Frequency Modulation Signals" Sensors 23, no. 7: 3511. https://doi.org/10.3390/s23073511
APA StyleLiu, Z., Tao, Q., Sun, W., & Fu, X. (2023). Deconvolved Fractional Fourier Domain Beamforming for Linear Frequency Modulation Signals. Sensors, 23(7), 3511. https://doi.org/10.3390/s23073511







