DV-Hop Algorithm Based on Multi-Objective Salp Swarm Algorithm Optimization
Abstract
:1. Introduction
Related Work
2. Methods
2.1. DV-Hop
2.2. Multi-Objective Salp Swarm Algorithm
2.2.1. Single-Objective Salp Swarm Algorithm
2.2.2. Multi-Objective Salp Swarm Algorithm
- (1)
- If a salp is superior in the repository, then that salp should be put into the repository, and the original solution should be taken out. If a salp is superior to a group of solutions in the repository, then that group of solutions should be removed from the repository, and the salp should be added to the repository.
- (2)
- If there is at least one original solution in the repository that is superior to that salp, then that salp should be discarded and not added to the repository.
- (3)
- If the salp is not superior to all repository residents, the salp is the optimal solution and must be added to the repository.
- (4)
- If the repository is full and salp is not superior to the repository’s original solution, a distance d for calculating the neighboring solution numbers is introduced at this time. As shown in Equation (22). The number of neighboring solutions is calculated, and the roulette wheel selection strategy is used to select the solution with a high number of neighboring solutions for deletion.where and are the minimum and maximum fitness values in the population, respectively; and repository size is the number of current repositories.
3. Our Proposed IMSSA-DV-Hop Scheme
3.1. Error Analysis
3.2. Subdivision Hop Count
3.3. Beacon Node Average Hop Distance Correction
3.4. Multi-Objective Model
3.5. Improved Multi-Objective Salp Swarm Algorithm
3.5.1. Initialization
3.5.2. Fuzzy Selection
3.5.3. Leader Position Updates Strategy
- (1)
- Parameter adjustment
- (2)
- Adaptive weight
- (3)
- Levy flight strategy
- (4)
- Follower location update strategy
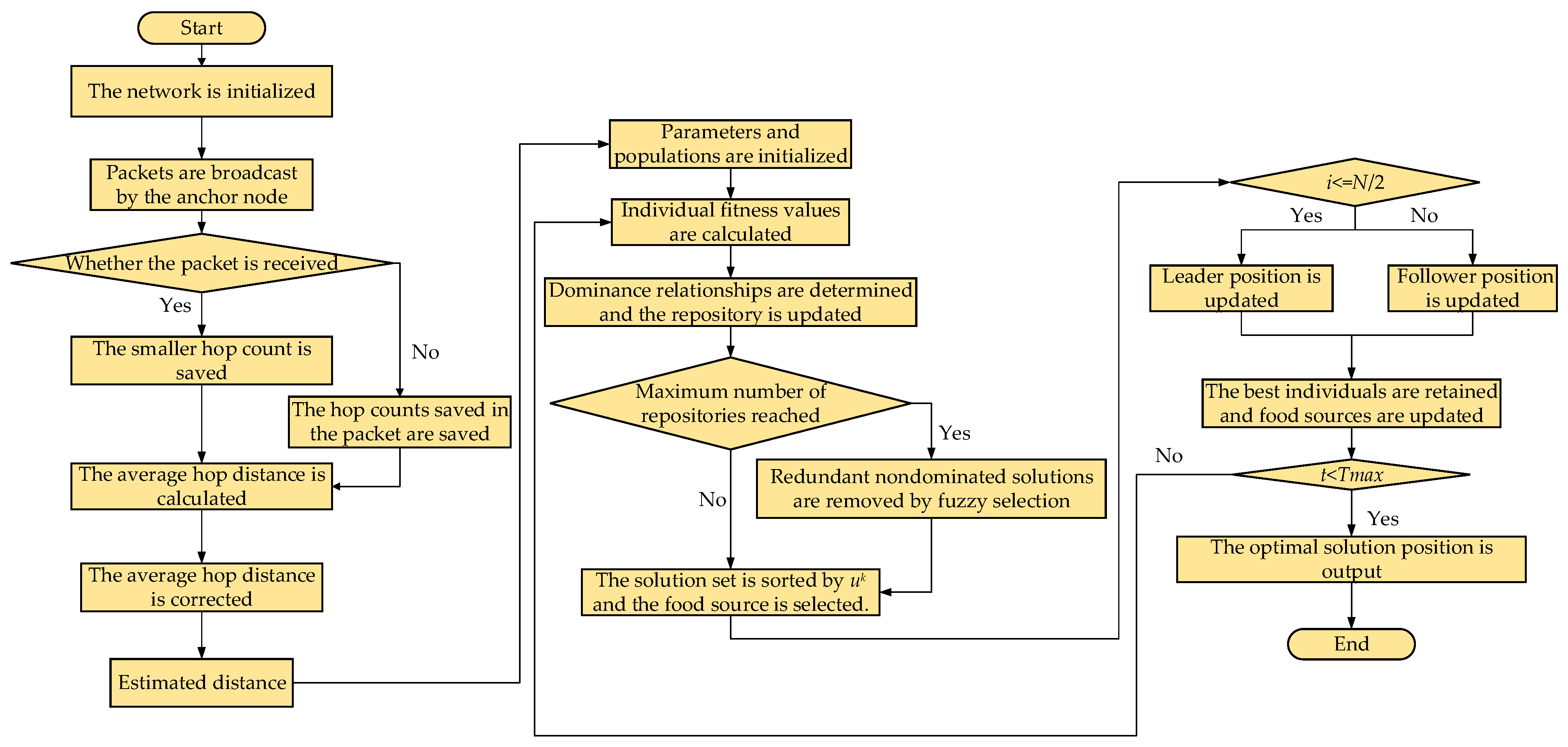
3.6. IMSSA-DV-Hop Algorithm Flow Chart
4. Experimental Results and Analysis
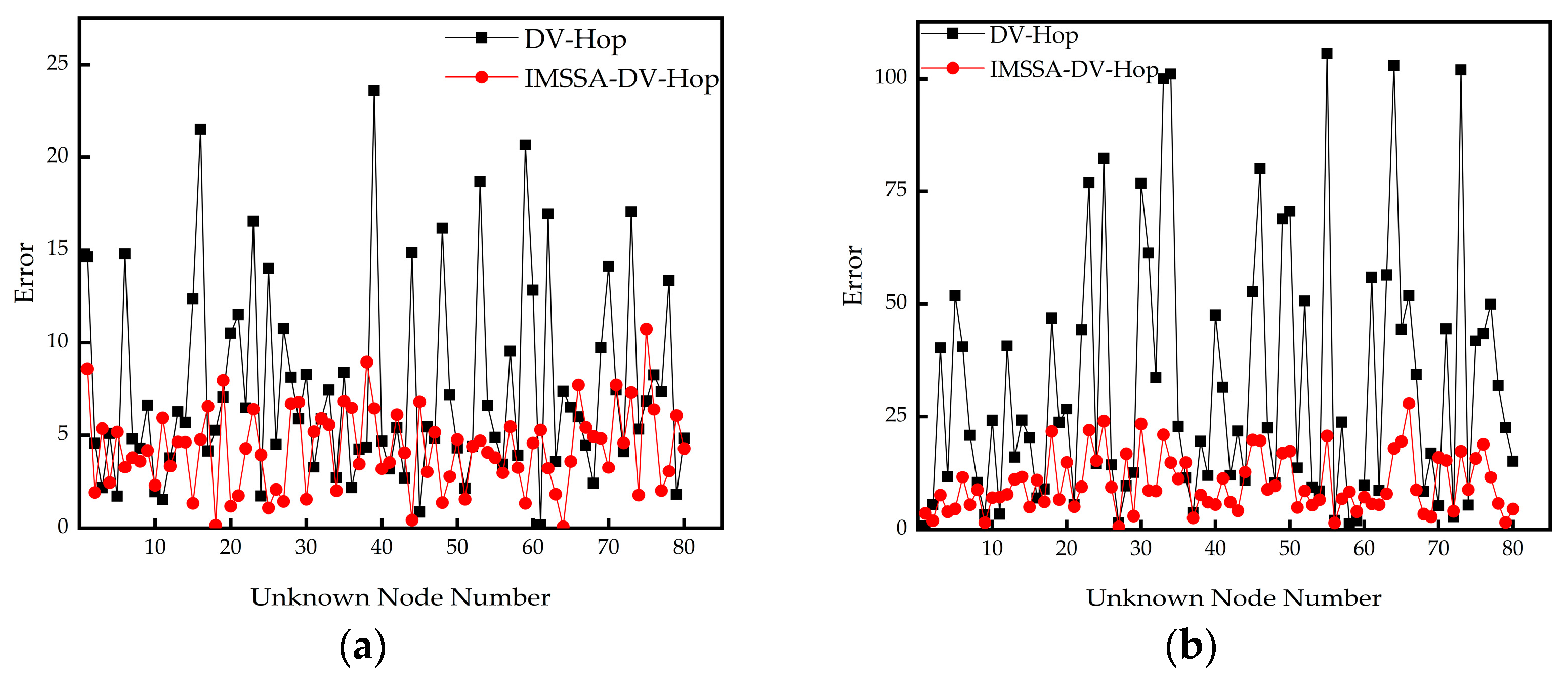
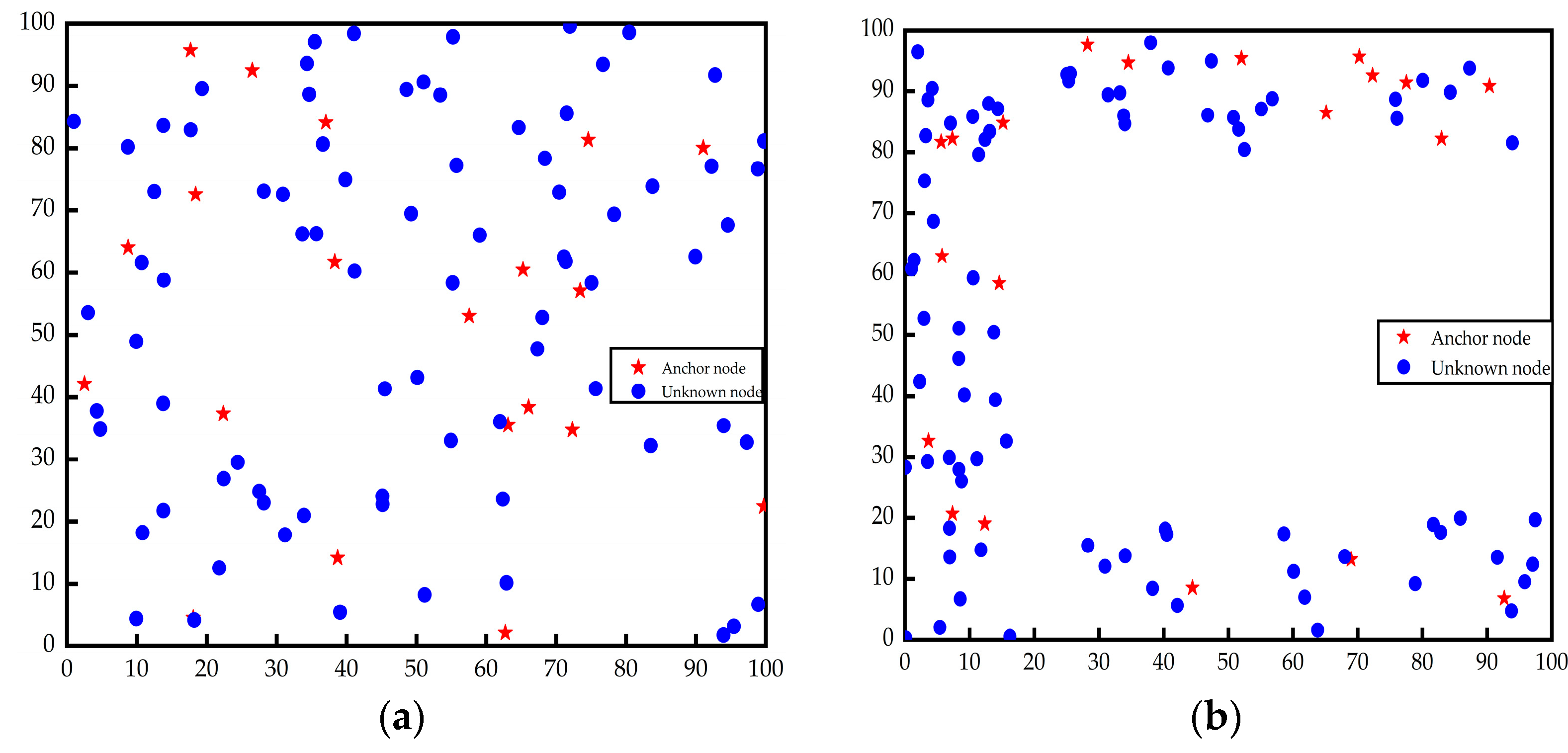
4.1. Experimental Environment and Evaluation Criteria
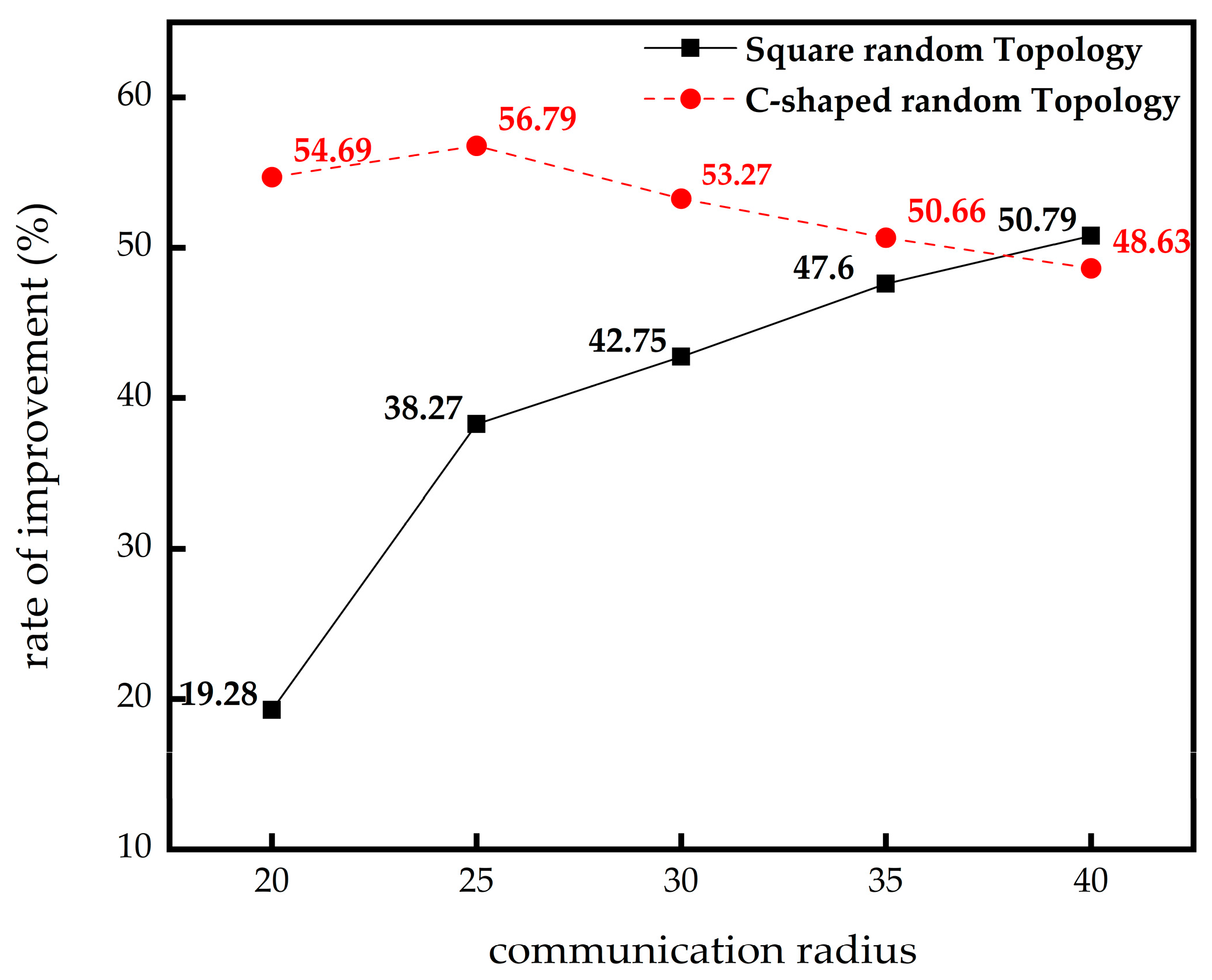
4.2. The Influence of Communication Radius on Localization Error
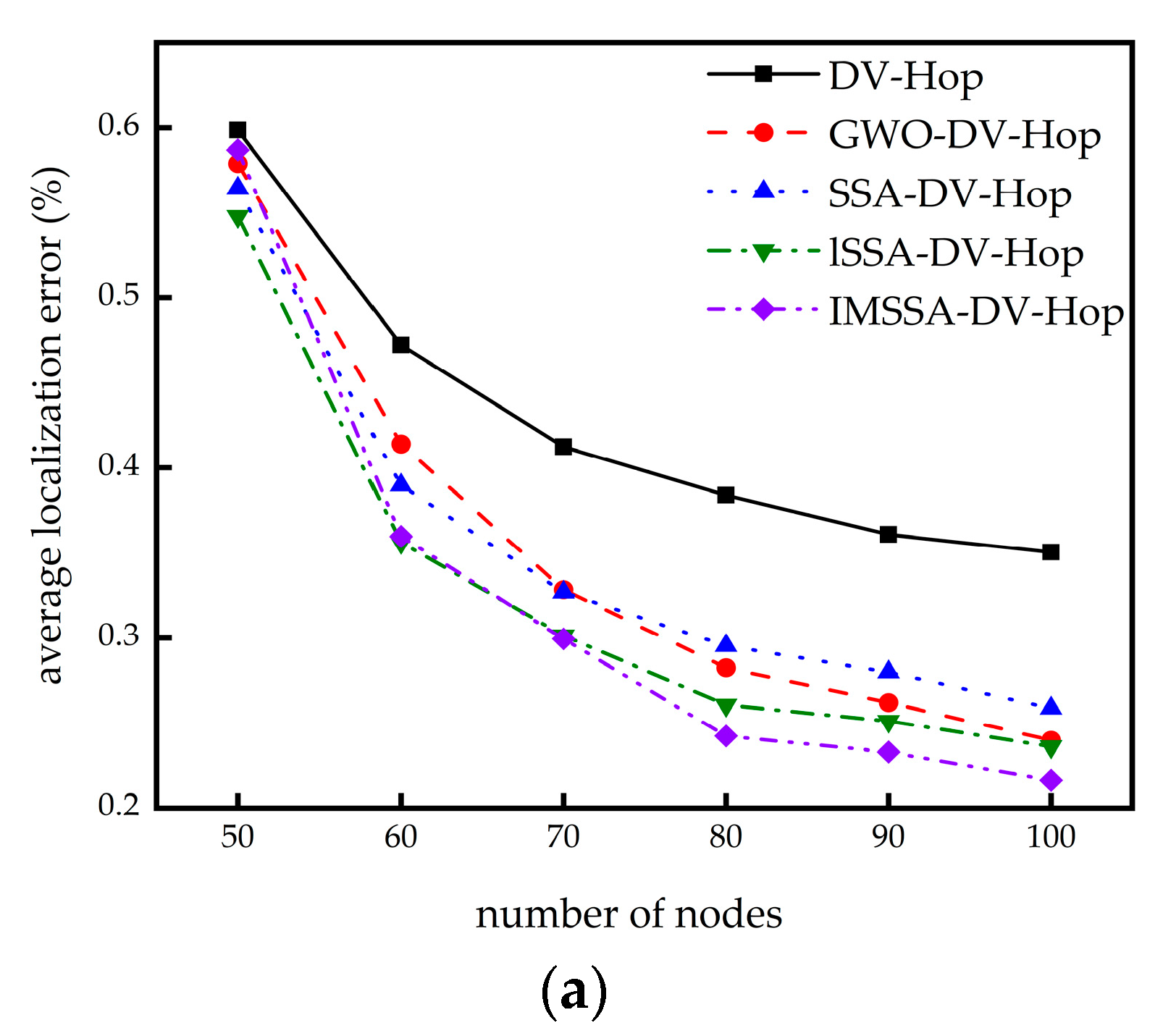
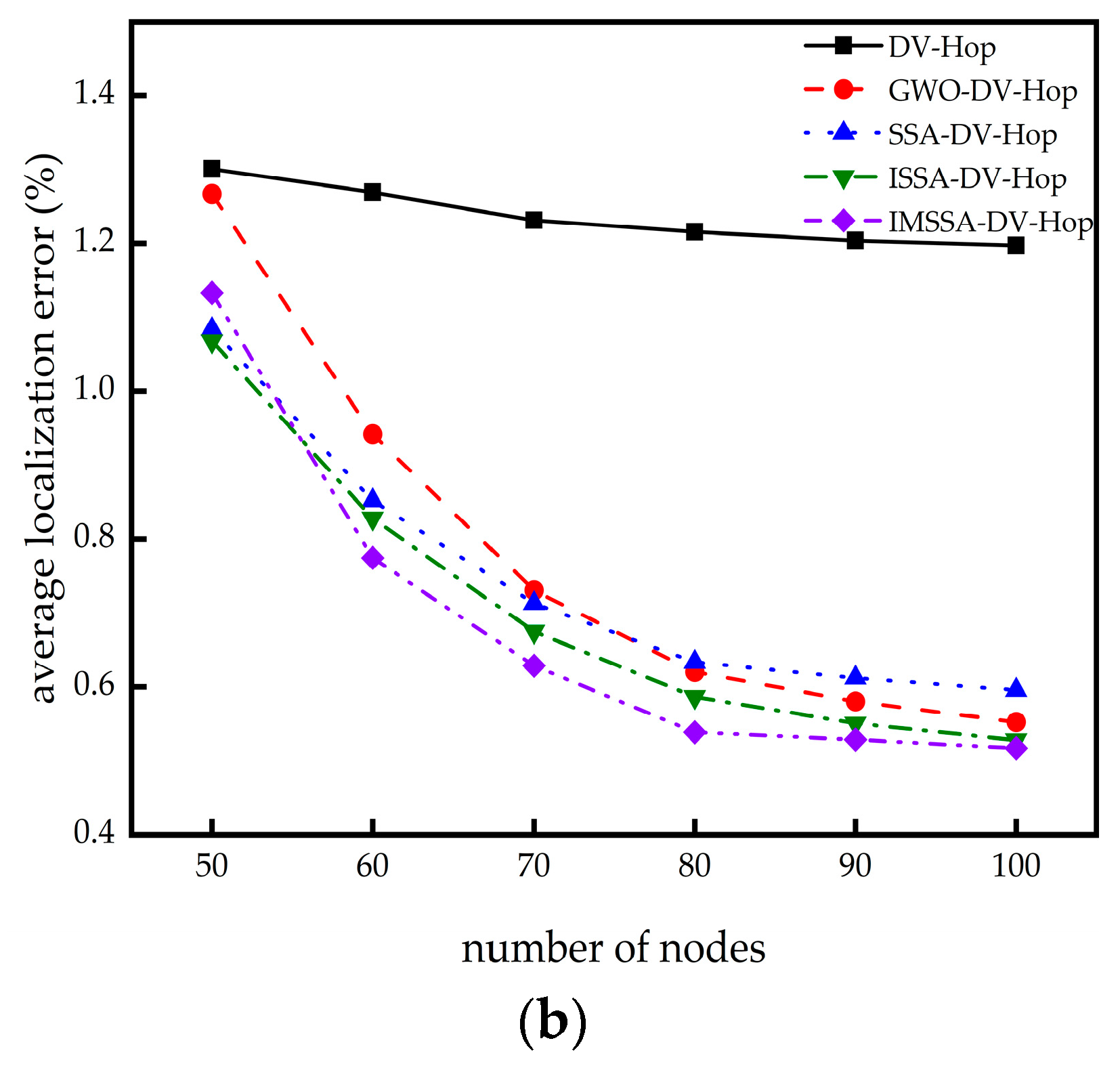
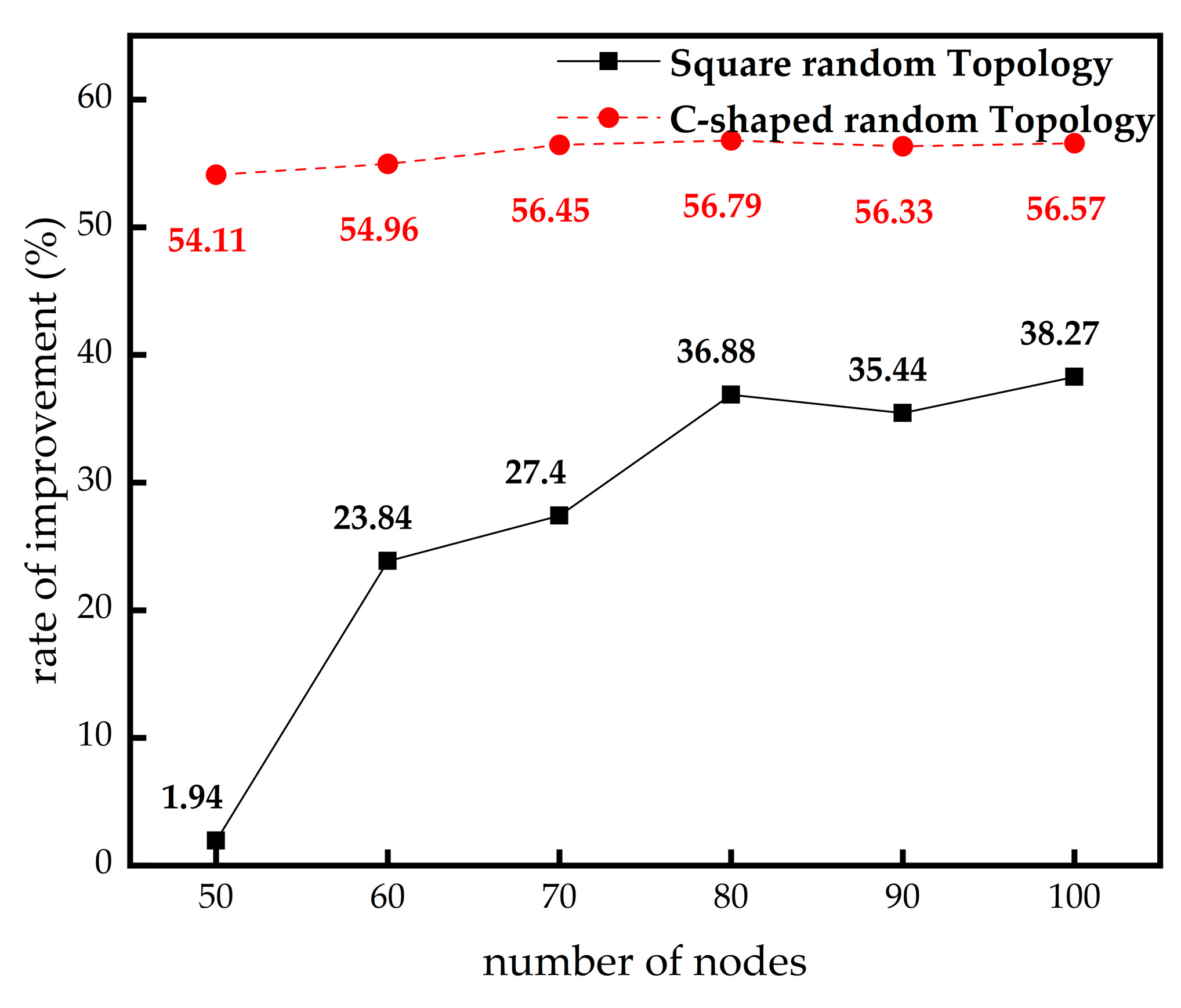
4.3. The Influence of Node Numbers on Localization Error
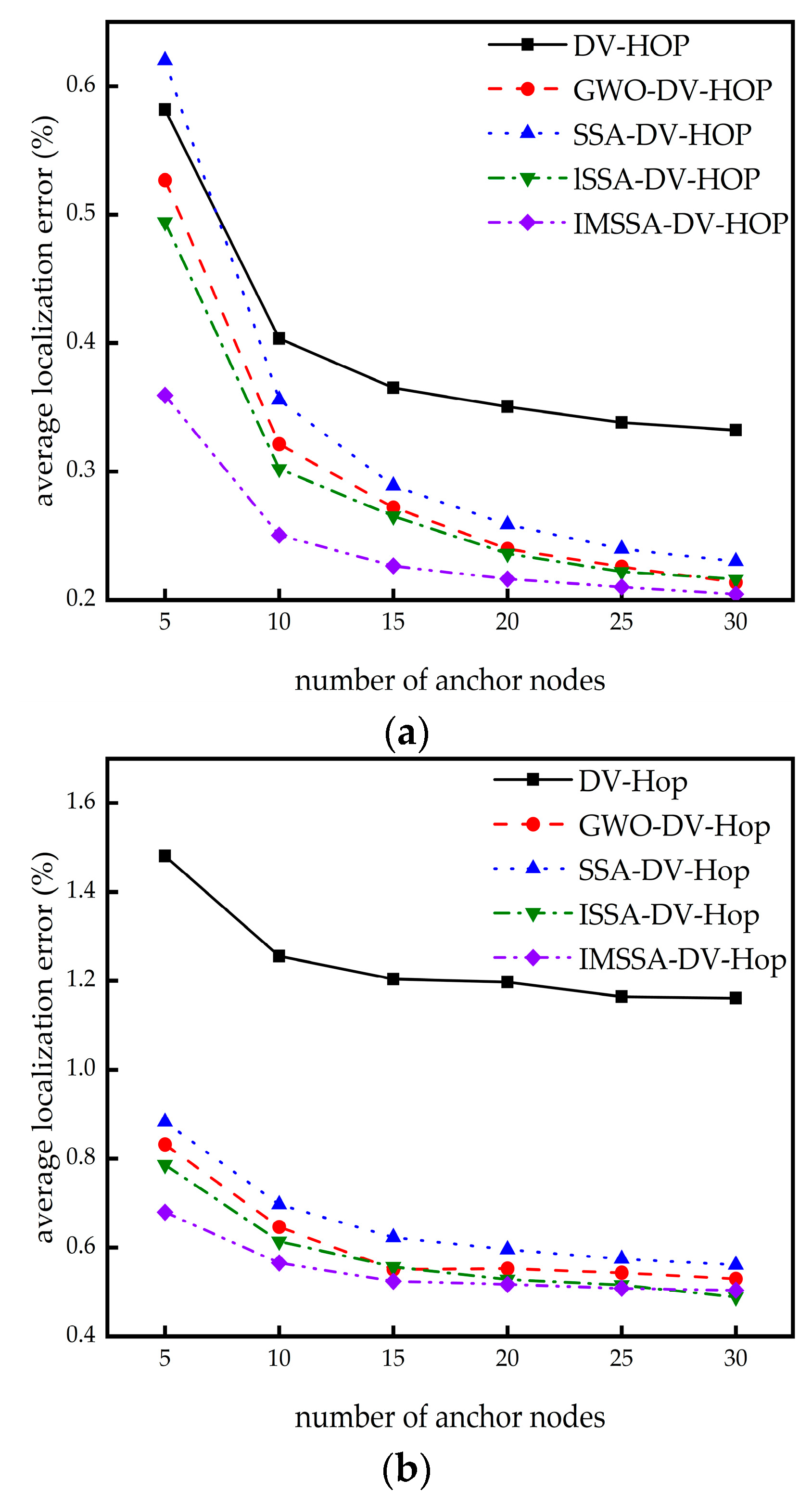
4.4. The Influence of Beacon Node Numbers on Localization Error
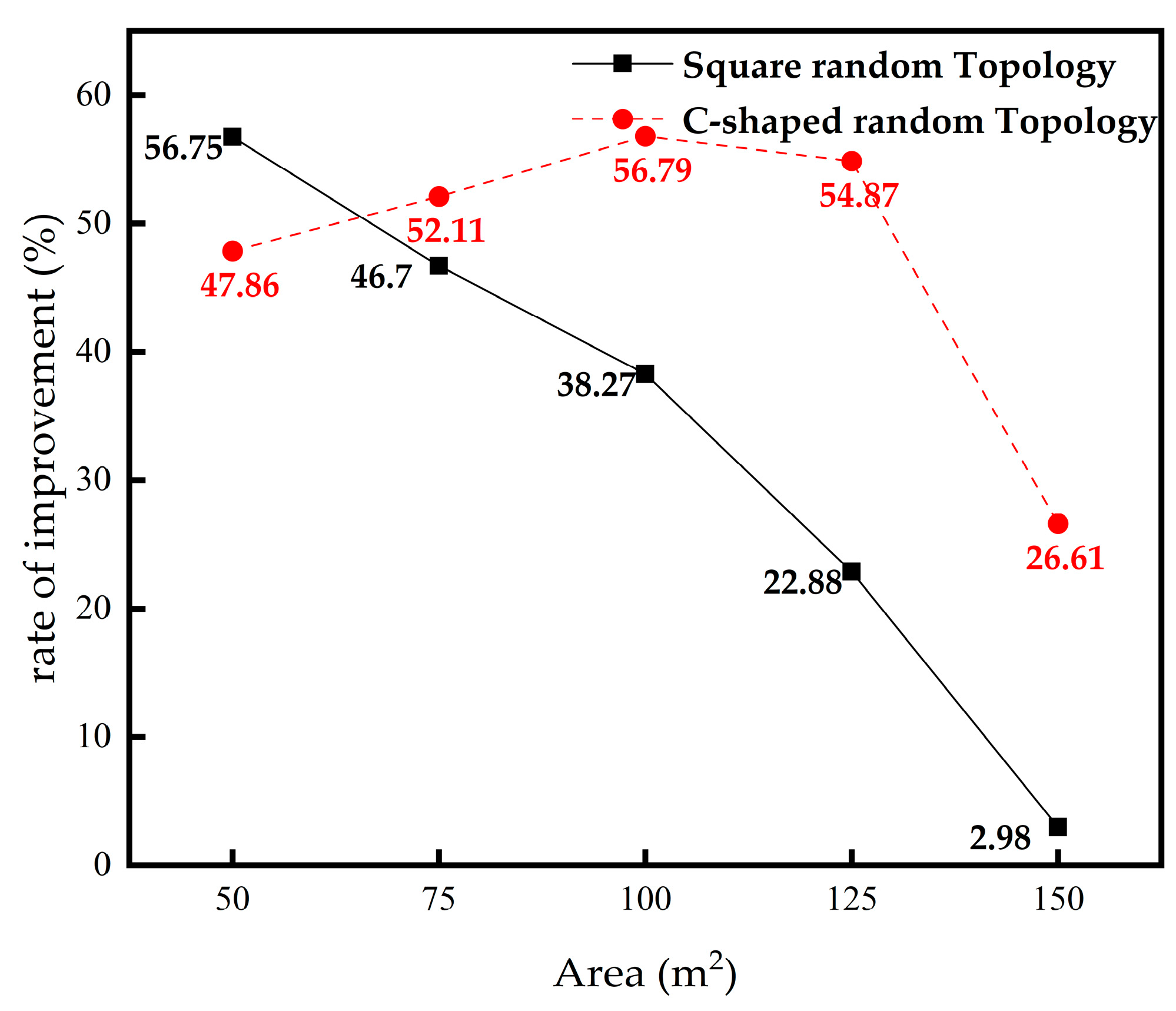
4.5. The Influence of Area on Localization Error
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kanwar, V.; Kumar, A. DV-Hop-based range-free localization algorithm for wireless sensor network using runner-root optimization. J. Supercomput. 2020, 77, 3044–3061. [Google Scholar] [CrossRef]
- Rawat, P.; Singh, K.D.; Chaouchi, H.; Bonnin, J.M. Wireless sensor networks: A survey on recent developments and potential synergies. J. Supercomput. 2013, 68, 1–48. [Google Scholar] [CrossRef]
- Elhabyan, R.; Shi, W.; St-Hilaire, M. Coverage Protocols for Wireless Sensor Networks: Review and Future Directions. J. Commun. Netw. 2019, 21, 45–60. [Google Scholar] [CrossRef] [Green Version]
- Ullah, I.; Shen, Y.; Su, X.; Esposito, C.; Choi, C. A Localization Based on Unscented Kalman Filter and Particle Filter Localization Algorithms. IEEE Access 2020, 8, 2233–2246. [Google Scholar] [CrossRef]
- Wan, X.W.; Lu, J.C. Improved DV-Hop Localization Algorithm Based on Weighted Least Squares Cycle Optimization in Anisotropic Networks. Wirel. Pers. Commun. 2022, 126, 895–909. [Google Scholar] [CrossRef]
- Messous, S.; Liouane, H. Online Sequential DV-Hop Localization Algorithm for Wireless Sensor Networks. Mob. Inf. Syst. 2020, 2020, 8195309. [Google Scholar] [CrossRef]
- Ahmad, T.; Li, X.J.; Seet, B.C.; Cano, J.C. Social Network Analysis Based Localization Technique with Clustered Closeness Centrality for 3D Wireless Sensor Networks. Electronics 2020, 9, 738. [Google Scholar] [CrossRef]
- Chen, T.F.; Hou, S.X.; Sun, L.J.; Sun, K.K. An Enhanced DV-Hop Localization Scheme Based on Weighted Iteration and Optimal Beacon Set. Electronics 2022, 11, 1774. [Google Scholar] [CrossRef]
- Zhang, L.Z. Improved DV-Hop Algorithm Based on Swarm Intelligence for AI and IoT-Federated Applications in Industry 4.0. Math. Probl. Eng. 2022, 2022, 1194752. [Google Scholar] [CrossRef]
- Sun, L.J.; Chen, T.F. Difference DV_Distance Localization Algorithm Using Correction Coefficients of Unknown Nodes. Sensors 2018, 18, 2860. [Google Scholar] [CrossRef] [Green Version]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent Advances in Indoor Localization: A Survey on Theoretical Approaches and Applications. IEEE Commun. Surv. Tutor. 2017, 19, 1327–1346. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, X.D.; Wang, D.M.; Agrawal, D.P. Range-Free Localization Using Expected Hop Progress in Wireless Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 1540–1552. [Google Scholar] [CrossRef]
- Chowdhury, T.J.S.; Elkin, C.; Devabhaktuni, V.; Rawat, D.B.; Oluoch, J. Advances on localization techniques for wireless sensor networks: A survey. Comput. Netw. 2016, 110, 284–305. [Google Scholar] [CrossRef]
- Gui, L.; Zhang, X.; Ding, Q.; Shu, F.; Wei, A. Reference Anchor Selection and Global Optimized Solution for DV-Hop Localization in Wireless Sensor Networks. Wirel. Pers. Commun. 2017, 96, 5995–6005. [Google Scholar] [CrossRef]
- Elnahrawy, E.; Xiaoyan, L.; Martin, R.P. The limits of localization using signal strength: A comparative study. In Proceedings of the First Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks, Santa Clara, CA, USA, 4–7 October 2004; pp. 406–414. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Mittal, N.; Salgotra, R. Comparison of range-based versus range-free WSNs localization using adaptive SSA algorithm. Wirel. Netw. 2022, 28, 1625–1647. [Google Scholar] [CrossRef]
- Chen, T.F.; Hou, S.X.; Sun, L.J. An Enhanced DV-Hop Positioning Scheme Based on Spring Model and Reliable Beacon Node Set. Comput. Netw. 2022, 209, 108926. [Google Scholar] [CrossRef]
- Chen, H.Y.; Liu, B.; Huang, P.; Liang, J.L.; Gu, Y. Mobility-Assisted Node Localization Based on TOA Measurements Without Time Synchronization in Wireless Sensor Networks. Mob. Netw. Appl. 2012, 17, 90–99. [Google Scholar] [CrossRef]
- Luomala, J.; Hakala, I. Analysis and evaluation of adaptive RSSI-based ranging in outdoor wireless sensor networks. Ad Hoc Netw. 2019, 87, 100–112. [Google Scholar] [CrossRef]
- Mao, G.Q.; Fidan, B.; Anderson, B.D.O. Wireless sensor network localization techniques. Comput. Netw. 2007, 51, 2529–2553. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Xu, H.; Duong, T.Q.; Jiang, J.; Hara, T. Localization algorithms of Wireless Sensor Networks: A survey. Telecommun. Syst. 2011, 52, 2419–2436. [Google Scholar] [CrossRef]
- Liu, J.P.; Liu, M.; Du, X.J.; Stanimirovi, P.S.; Jin, L. An improved DV-Hop algorithm for wireless sensor networks based on neural dynamics. Neurocomputing 2022, 491, 172–185. [Google Scholar] [CrossRef]
- Jiang, R.; Yang, Z. An improved centroid localization algorithm based on iterative computation for wireless sensor network. Acta Phys. Sin. 2016, 65, 030101. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Yao, M.; Qiu, Z. VN-APIT: Virtual nodes-based range-free APIT localization scheme for WSN. Wirel. Netw. 2015, 22, 867–878. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Y. An improved distance vector-Hop localization algorithm based on coordinate correction. Int. J. Distrib. Sens. Netw. 2017, 13. [Google Scholar] [CrossRef] [Green Version]
- Niculescu, D.; Nath, B. DV based positioning in ad hoc networks. Telecommun. Syst. 2003, 22, 267–280. [Google Scholar] [CrossRef]
- Cui, L.; Xu, C.; Li, G.; Ming, Z.; Feng, Y.; Lu, N. A high accurate localization algorithm with DV-Hop and differential evolution for wireless sensor network. Appl. Soft Comput. 2018, 68, 39–52. [Google Scholar] [CrossRef]
- Messous, S.; Liouane, H.; Cheikhrouhou, O.; Hamam, H. Improved Recursive DV-Hop Localization Algorithm with RSSI Measurement for Wireless Sensor Networks. Sensors 2021, 21, 4152. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Gou, X.; Li, Y.-P.; Shan-shan, H. DV-Hop Based Self-Adaptive Positioning in Wireless Sensor Networks. In Proceedings of the 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24–26 September 2009. [Google Scholar] [CrossRef]
- Shoufeng, H.; Xiaojia, Z.; Xinxin, L. A novel DV-Hop localization algorithm for asymmetry distributed wireless sensor networks. In Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010; Volume 4, p. 248. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Hou, A.; Tu, Y.; Yu, H. An Improved DV-Hop Localization Algorithm Based on Selected Anchors. Comput. Mater. Contin. 2020, 65, 977–991. [Google Scholar] [CrossRef]
- Chen, T.; Sun, L.; Wang, Z.; Wang, Y.; Zhao, Z.; Zhao, P. An enhanced nonlinear iterative localization algorithm for DV_Hop with uniform calculation criterion. Ad Hoc Netw. 2021, 111. [Google Scholar] [CrossRef]
- Gui, L.; Val, T.; Wei, A.; Dalce, R. Improvement of range-free localization technology by a novel DV-hop protocol in wireless sensor networks. Ad Hoc Netw. 2015, 24, 55–73. [Google Scholar] [CrossRef] [Green Version]
- Peng, B.; Li, L. An improved localization algorithm based on genetic algorithm in wireless sensor networks. Cogn. Neurodyn. 2015, 9, 249–256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singh, S.P.; Sharma, S.C. A PSO Based Improved Localization Algorithm for Wireless Sensor Network. Wirel. Pers. Commun. 2017, 98, 487–503. [Google Scholar] [CrossRef]
- Kaur, A.; Kumar, P.; Gupta, G.P. Nature Inspired Algorithm-Based Improved Variants of DV-Hop Algorithm for Randomly Deployed 2D and 3D Wireless Sensor Networks. Wirel. Pers. Commun. 2018, 101, 567–582. [Google Scholar] [CrossRef]
- Chai, Q.-W.; Chu, S.-C.; Pan, J.-S.; Hu, P.; Zheng, W.-M. A parallel WOA with two communication strategies applied in DV-Hop localization method. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 50. [Google Scholar] [CrossRef]
- Li, J.; Gao, M.; Pan, J.-S.; Chu, S.-C. A parallel compact cat swarm optimization and its application in DV-Hop node localization for wireless sensor network. Wirel. Netw. 2021, 27, 2081–2101. [Google Scholar] [CrossRef]
- Sabahat, E.; Eslaminejad, M.; Ashoormahani, E. A new localization method in internet of things by improving beetle antenna search algorithm. Wirel. Netw. 2022, 28, 1067–1078. [Google Scholar] [CrossRef]
- Wang, P.; Xue, F.; Li, H.; Cui, Z.; Chen, J. A Multi-Objective DV-Hop Localization Algorithm Based on NSGA-II in Internet of Things. Mathematics 2019, 7, 184. [Google Scholar] [CrossRef] [Green Version]
- Kanwar, V.; Kumar, A. Range Free Localization for Three Dimensional Wireless Sensor Networks Using Multi Objective Particle Swarm Optimization. Wirel. Pers. Commun. 2020, 117, 901–921. [Google Scholar] [CrossRef]
- Huang, X.; Han, D.; Weng, T.-H.; Wu, Z.; Han, B.; Wang, J.; Cui, M.; Li, K.-C. A localization algorithm for DV-Hop wireless sensor networks based on manhattan distance. Telecommun. Syst. 2022, 81, 207–224. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- He, G.; Lu, X.L. Good point set and double attractors based-QPSO and application in portfolio with transaction fee and financing cost. Expert Syst. Appl. 2022, 209, 118339. [Google Scholar] [CrossRef]
- Deepa, R.; Venkataraman, R. Enhancing Whale Optimization Algorithm with Levy Flight for coverage optimization in wireless sensor networks. Comput. Electr. Eng. 2021, 94, 107359. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Communication radius (R) | 25 m |
| Nodes | 100 |
| Beacon nodes | 20 |
| Area | 100 × 100 m |
| Communication Radius | 20 | 25 | 30 | 35 | 40 | |
|---|---|---|---|---|---|---|
| Square random topology | DV-Hop | 0.4793 | 0.3504 | 0.3097 | 0.2958 | 0.2849 |
| GWO-DV-Hop | 0.3921 | 0.2397 | 0.2116 | 0.2105 | 0.2051 | |
| SSA-DV-Hop | 0.3673 | 0.2587 | 0.2304 | 0.2417 | 0.2162 | |
| ISSA-DV-Hop | 0.3651 | 0.2360 | 0.2109 | 0.2048 | 0.2024 | |
| IMSSA-DV-Hop | 0.3869 | 0.2163 | 0.1773 | 0.1550 | 0.1402 | |
| Communication Radius | 20 | 25 | 30 | 35 | 40 | |
|---|---|---|---|---|---|---|
| C-shaped random topology | DV-Hop | 1.5847 | 1.1970 | 0.9225 | 0.7766 | 0.6467 |
| GWO-DV-Hop | 0.8149 | 0.5525 | 0.4484 | 0.4340 | 0.3692 | |
| SSA-DV-Hop | 0.8335 | 0.5957 | 0.4966 | 0.4423 | 0.3981 | |
| ISSA-DV-Hop | 0.7438 | 0.5283 | 0.4402 | 0.3963 | 0.3589 | |
| IMSSA-DV-Hop | 0.7181 | 0.5172 | 0.4311 | 0.3832 | 0.3322 | |
| Number of Nodes | 50 | 60 | 70 | 80 | 90 | 100 | |
|---|---|---|---|---|---|---|---|
| Square random Topology | DV-Hop | 0.5986 | 0.4723 | 0.4124 | 0.3839 | 0.3608 | 0.3504 |
| GWO-DV-Hop | 0.5789 | 0.4141 | 0.3284 | 0.2824 | 0.2620 | 0.2397 | |
| SSA-DV-Hop | 0.5644 | 0.3897 | 0.3268 | 0.2954 | 0.2798 | 0.2587 | |
| ISSA-DV-Hop | 0.5479 | 0.3562 | 0.3014 | 0.2606 | 0.2511 | 0.2360 | |
| IMSSA-DV-Hop | 0.5870 | 0.3597 | 0.2994 | 0.2423 | 0.2329 | 0.2163 | |
| Number of Nodes | 50 | 60 | 70 | 80 | 90 | 100 | |
|---|---|---|---|---|---|---|---|
| C-shaped random Topology | DV-Hop | 1.3009 | 1.2689 | 1.2315 | 1.2156 | 1.2036 | 1.1970 |
| GWO-DV-Hop | 1.2668 | 0.9418 | 0.7309 | 0.6203 | 0.5806 | 0.5525 | |
| SSA-DV-Hop | 1.0839 | 0.8523 | 0.7131 | 0.6338 | 0.6122 | 0.5957 | |
| ISSA-DV-Hop | 1.0680 | 0.8284 | 0.6751 | 0.5868 | 0.5509 | 0.5283 | |
| IMSSA-DV-Hop | 1.1330 | 0.7749 | 0.6289 | 0.5389 | 0.5288 | 0.5172 | |
| Number of Beacon Nodes | 5 | 10 | 15 | 20 | 25 | 30 | |
|---|---|---|---|---|---|---|---|
| Square random Topology | DV-Hop | 0.5817 | 0.4035 | 0.3652 | 0.3504 | 0.3382 | 0.3322 |
| GWO-DV-Hop | 0.5269 | 0.3213 | 0.2721 | 0.2397 | 0.2258 | 0.2136 | |
| SSA-DV-Hop | 0.6200 | 0.3559 | 0.2889 | 0.2587 | 0.2397 | 0.2301 | |
| ISSA-DV-Hop | 0.4943 | 0.3021 | 0.2652 | 0.2360 | 0.2220 | 0.2162 | |
| IMSSA-DV-Hop | 0.3593 | 0.2504 | 0.2265 | 0.2163 | 0.2101 | 0.2045 | |
| Number of Beacon Nodes | 5 | 10 | 15 | 20 | 25 | 30 | |
|---|---|---|---|---|---|---|---|
| C-shaped random Topology | DV-Hop | 1.4806 | 1.2556 | 1.2038 | 1.1970 | 1.1643 | 1.1610 |
| GWO-DV-Hop | 0.8321 | 0.6464 | 0.5507 | 0.5525 | 0.5433 | 0.5298 | |
| SSA-DV-Hop | 0.8828 | 0.6969 | 0.6229 | 0.5957 | 0.5742 | 0.5611 | |
| ISSA-DV-Hop | 0.7864 | 0.6142 | 0.5568 | 0.5283 | 0.5160 | 0.4888 | |
| IMSSA-DV-Hop | 0.6795 | 0.5655 | 0.5242 | 0.5172 | 0.5085 | 0.5042 | |
| Area | 50 | 75 | 100 | 125 | 150 | |
|---|---|---|---|---|---|---|
| square random Topology | DV-Hop | 0.2833 | 0.3026 | 0.3504 | 0.4813 | 0.8404 |
| GWO-DV-Hop | 0.2172 | 0.2139 | 0.2397 | 0.3717 | 1.2178 | |
| SSA-DV-Hop | 0.2214 | 0.2227 | 0.2587 | 0.4085 | 0.9347 | |
| ISSA-DV-Hop | 0.1854 | 0.1730 | 0.2360 | 0.3589 | 0.9519 | |
| IMSSA-DV-Hop | 0.1225 | 0.1613 | 0.2163 | 0.3947 | 1.1674 | |
| Area | 50 | 75 | 100 | 125 | 150 | |
|---|---|---|---|---|---|---|
| C-shaped random Topology | DV-Hop | 0.5102 | 0.8216 | 1.1970 | 1.5913 | 1.9785 |
| GWO-DV-Hop | 0.3378 | 0.4127 | 0.5525 | 0.8108 | 1.4908 | |
| SSA-DV-Hop | 0.3569 | 0.4494 | 0.5957 | 0.8523 | 1.4290 | |
| ISSA-DV-Hop | 0.3353 | 0.4045 | 0.5283 | 0.7418 | 1.4082 | |
| IMSSA-DV-Hop | 0.2660 | 0.3935 | 0.5172 | 0.7181 | 1.4520 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Li, J.; Zheng, A.; Zheng, Z.; Jiang, X.; Zhang, S. DV-Hop Algorithm Based on Multi-Objective Salp Swarm Algorithm Optimization. Sensors 2023, 23, 3698. https://doi.org/10.3390/s23073698
Liu W, Li J, Zheng A, Zheng Z, Jiang X, Zhang S. DV-Hop Algorithm Based on Multi-Objective Salp Swarm Algorithm Optimization. Sensors. 2023; 23(7):3698. https://doi.org/10.3390/s23073698
Chicago/Turabian StyleLiu, Weimin, Jinhang Li, Aiyun Zheng, Zhi Zheng, Xinyu Jiang, and Shaoning Zhang. 2023. "DV-Hop Algorithm Based on Multi-Objective Salp Swarm Algorithm Optimization" Sensors 23, no. 7: 3698. https://doi.org/10.3390/s23073698
APA StyleLiu, W., Li, J., Zheng, A., Zheng, Z., Jiang, X., & Zhang, S. (2023). DV-Hop Algorithm Based on Multi-Objective Salp Swarm Algorithm Optimization. Sensors, 23(7), 3698. https://doi.org/10.3390/s23073698





