Dynamic Speed of Sound Adaptive Transmission–Reflection Ultrasound Computed Tomography
Abstract
:1. Introduction
2. Methods
3. Simulation and Results
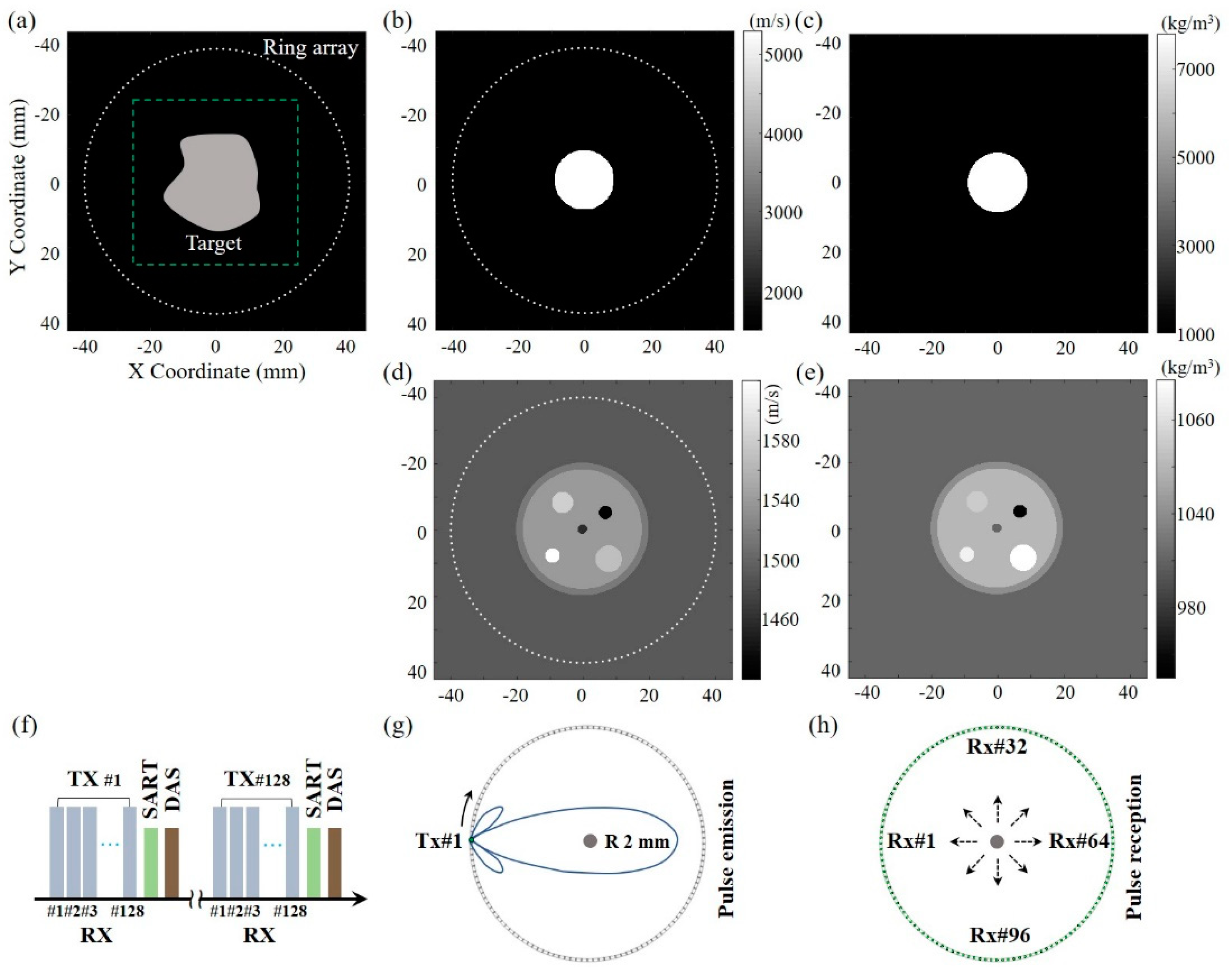
3.1. Simulation Models
3.2. Simulation Results
4. Experiments and Results
4.1. Experiment Setup
4.2. Phantom Experimental Results
4.3. In Vivo Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Sloun, R.; Pandharipande, A.; Mischi, M.; Demi, L. Compressed Sensing for Ultrasound Computed Tomography. IEEE Trans. Biomed. Eng. 2015, 62, 1660–1664. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, Y.; Yuan, Z. Dual-Modality Imaging of the Human Finger Joint Systems by Using Combined Multispectral Photoacoustic Computed Tomography and Ultrasound Computed Tomography. BioMed Res. Int. 2016, 2016, 1453272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haynes, M.; Moghaddam, M. Large-Domain, Low-Contrast Acoustic Inverse Scattering for Ultrasound Breast Imaging. IEEE Trans. Biomed. Eng. 2010, 57, 2712–2722. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.E.; Kim, K.W. Contrast-enhanced ultrasonography: Advance and current status in abdominal imaging. Ultrasonography 2014, 34, 3–18. [Google Scholar] [CrossRef] [PubMed]
- Hua, S.; Ding, M.; Yuchi, M. Sparse-View Ultrasound Diffraction Tomography Using Compressed Sensing with Nonuniform FFT. Comput. Math. Methods Med. 2014, 2014, 329350. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wienbeck, S.; Fischer, U.; Luftner-Nagel, S.; Lotz, J.; Uhlig, J. Contrast-enhanced cone-beam breast-CT (CBBCT): Clinical performance compared to mam-mography and MRI. Eur. Radiol. 2018, 28, 3731–3741. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, J.; White, D.L.; Genant, H.K. Micro CT and Micro MR imaging of 3D architecture of animal skeleton. J. Musculoskelet. Neuronal Interact. 2000, 1, 45–51. [Google Scholar]
- Klibanov, A.L.; Hossack, J.A. Ultrasound in radiology: From anatomic, functional, molecular imaging to drug delivery and image-guided therapy. Invest. Radiol. 2015, 50, 657–670. [Google Scholar] [CrossRef] [Green Version]
- Duric, N. WE-G-210-02: Ultrasound Tomography: A Breast Imaging Modality Whose Time Has Come. Med. Phys. 2015, 42, 3699. [Google Scholar] [CrossRef]
- Carson, P.L.; Oughton, T.V.; Hendee, W.R.; Ahuja, A.S. Imaging soft tissue through bone with ultrasound transmission tomography by reconstruction. Med. Phys. 1977, 4, 302–309. [Google Scholar] [CrossRef]
- Mercep, E.; Herraiz, J.L.; Deán-Ben, X.L.; Razansky, D. Transmission–reflection optoacoustic ultrasound (TROPUS) computed tomography of small animals. Light. Sci. Appl. 2019, 8, 18. [Google Scholar] [CrossRef] [Green Version]
- Koulountzios, P.; Rymarczyk, T.; Soleimani, M. A triple-modality ultrasound computed tomography based on full-waveform data for in-dustrial processes. IEEE Sens. J. 2021, 21, 20896–20909. [Google Scholar] [CrossRef]
- Norton, S.J.; Linzer, M. Ultrasonic Reflectivity Tomography: Reconstruction with Circular Transducer Arrays. Ultrason. Imaging 1979, 1, 154–184. [Google Scholar] [CrossRef] [PubMed]
- Forte, S.; Dellas, S.; Stieltjes, B.; Bongartz, B. Multimodal ultrasound tomography for breast imaging: A prospective study of clinical feasibility. Eur. Radiol. Exp. 2017, 1, 27. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, F.; Villa, U.; Park, S.; Anastasio, M.A. 3-D Stochastic Numerical Breast Phantoms for Enabling Virtual Imaging Trials of Ultrasound Computed Tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 135–146. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; Ding, M.; Yuchi, M. Deep Learning Ultrasound Computed Tomography with Sparse Transmissions. In Proceedings of the IEEE International Ultrasonics Symposium, Xi’an, China, 11–16 September 2021; p. 21434924. [Google Scholar]
- Liu, X.; Mohamed, A. Ultrasound computed tomography using physical-informed neural network. In Proceedings of the IEEE International Ultrasonics Symposium, Xi’an, China, 11–16 September 2021; p. 21298935. [Google Scholar]
- Andersen, A. A ray tracing approach to restoration and resolution enhancement in experimental ultrasound tomography. Ultrason. Imaging 1990, 12, 268–291. [Google Scholar] [CrossRef]
- Li, S.; Jackowski, M.; Dione, D.P.; Varslot, T.; Staib, L.H.; Mueller, K. Refraction corrected transmission ultrasound computed tomography for application in breast im-aging. Med. Phys. 2010, 37, 2233–2246. [Google Scholar] [CrossRef] [Green Version]
- Roberts, B.A.; Kak, A.C. Reflection mode diffraction tomography. Ultrason. Imaging 1985, 7, 300–320. [Google Scholar] [CrossRef]
- Horbelt, S.; Liebling, M.; Unser, M. Discretization of the radon transform and of its inverse by spline convolutions. IEEE Trans. Med. Imaging 2002, 21, 363–376. [Google Scholar] [CrossRef] [PubMed]
- Devaney, A. A Fast Filtered Backpropagation Algorithm for Ultrasound Tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 330–340. [Google Scholar] [CrossRef] [PubMed]
- Intrator, M.; Lin, Y.; Chen, T.; Shin, J.; Huang, L. Ultrasound bent-ray tomography with a modified total-variation regularization scheme. In Proceedings of the SPIE Medical Imaging, Orlando, FL, USA, 21–26 February 2015; p. 9419. [Google Scholar] [CrossRef]
- Andersen, A.H.; Kak, A.C. Simultaneous Algebraic Reconstruction Technique (SART): A Superior Implementation of the ART Algorithm. Ultrason. Imaging 1984, 6, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Goss, S.A.; Johnston, R.L.; Dunn, F. Comprehensive compilation of empirical ultrasonic properties of mammalian tissues. J. Acoust. Soc. Am. 1978, 64, 423–457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, T.; Jing, Y. Transcranial ultrasound imaging with speed of sound-based phase correction: A numerical study. Phys. Med. Biol. 2013, 58, 6663–6681. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Sun, M.; Liu, Y.; Shen, Z.; Shen, Y.; Feng, N. Variable speed of sound compensation in the linear-array photoacoustic tomography using a multi-stencils fast marching method. Biomed. Signal Process. 2018, 44, 67–74. [Google Scholar] [CrossRef]
- Ali, R.; Dahl, J.J. Distributed Phase Aberration Correction Techniques Based on Local Sound Speed Estimates. In Proceedings of the IEEE International Ultrasonics Symposium, Kobe, Japan, 22–25 October 2018; p. 18326663. [Google Scholar] [CrossRef]
- Qu, X.; Azuma, T.; Lin, H.; Imoto, H.; Tamano, S.; Takagi, S.; Umemura, S.-I.; Sakuma, I.; Matsumoto, Y. Phase aberration correction by multi-stencils fast marching method using sound speed image in ultrasound computed tomography. In Proceedings of the SPIE Medical Imaging, San Diego, CA, USA, 27 February–3 March 2016; p. 979018. [Google Scholar] [CrossRef]
- Stotzka, R.; Widmann, H.; Mueller, T.O.; Schlote-Holubek, K.; Gemmeke, H.; Ruiter, N.V.; Goebel, G. Prototype of a new 3D ultrasound computer tomography system: Transducer design and data recording. In Proceedings of the SPIE—Medical Imaging 2004: Ultrasonic Imaging and Signal Processing, San Diego, CA, USA, 17–19 February 2004; pp. 70–79. [Google Scholar] [CrossRef]
- Li, C.; Huang, L.; Duric, N.; Zhang, H.; Rowe, C. An improved automatic time-of-flight picker for medical ultrasound tomography. Ultrasonics 2009, 49, 61–72. [Google Scholar] [CrossRef] [Green Version]
- Cobbold, R. Foundations of Biomedical Ultrasound; Oxford University Press: Oxford, UK, 2007; pp. 135–163. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Shi, H.; Fu, Z.; Lin, H.; Chen, S.; Chen, X.; Chen, M. Dynamic Speed of Sound Adaptive Transmission–Reflection Ultrasound Computed Tomography. Sensors 2023, 23, 3701. https://doi.org/10.3390/s23073701
Lin X, Shi H, Fu Z, Lin H, Chen S, Chen X, Chen M. Dynamic Speed of Sound Adaptive Transmission–Reflection Ultrasound Computed Tomography. Sensors. 2023; 23(7):3701. https://doi.org/10.3390/s23073701
Chicago/Turabian StyleLin, Xiangwei, Hongji Shi, Zhenyu Fu, Haoming Lin, Siping Chen, Xin Chen, and Mian Chen. 2023. "Dynamic Speed of Sound Adaptive Transmission–Reflection Ultrasound Computed Tomography" Sensors 23, no. 7: 3701. https://doi.org/10.3390/s23073701
APA StyleLin, X., Shi, H., Fu, Z., Lin, H., Chen, S., Chen, X., & Chen, M. (2023). Dynamic Speed of Sound Adaptive Transmission–Reflection Ultrasound Computed Tomography. Sensors, 23(7), 3701. https://doi.org/10.3390/s23073701





