Wind Preview-Based Model Predictive Control of Multi-Rotor UAVs Using LiDAR
Abstract
:1. Introduction
2. Methods and Systems
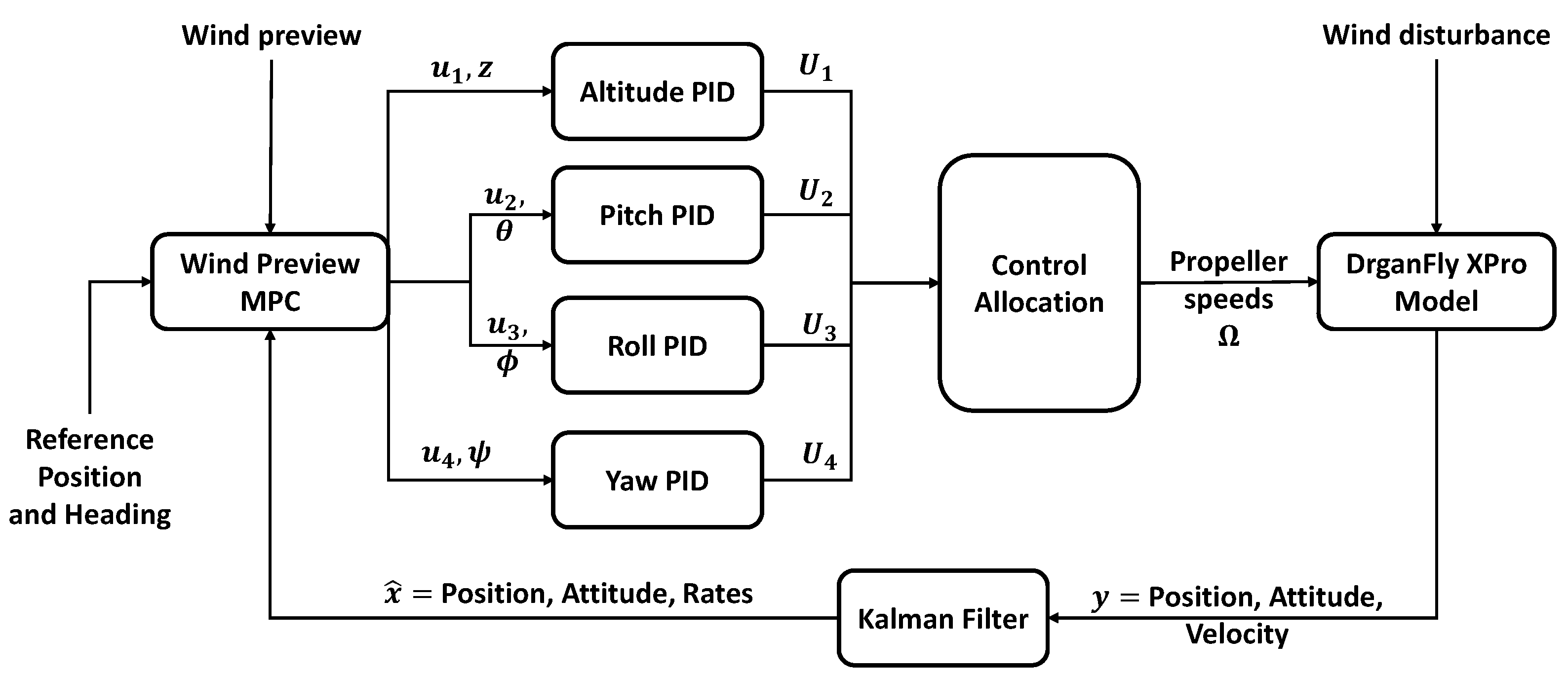
2.1. Control Architecture
- To impart modularity in the overall system and to allow the outer-loop control to be kept off-board the aircraft. This removes any weight constraints for the gust rejection controller and hence makes computational expensive controllers more feasible.
- To keep the inner-loop of the quadrotor unmodified and hence minimise the effect the outer-loop controller has on the stability characteristics of the aircraft. This can be further ensured by bounding the output attitude demands of the outer-loop controller.
- The identification of the aircraft model required for MPC design becomes easier. The placement of the controller on the outer-loop eliminates the need to identify/model the inner-loop dynamics of the aircraft which tend to be more non-linear. This also adds to the modularity of the gust rejection system as the model identification required for different UAVs becomes quicker.
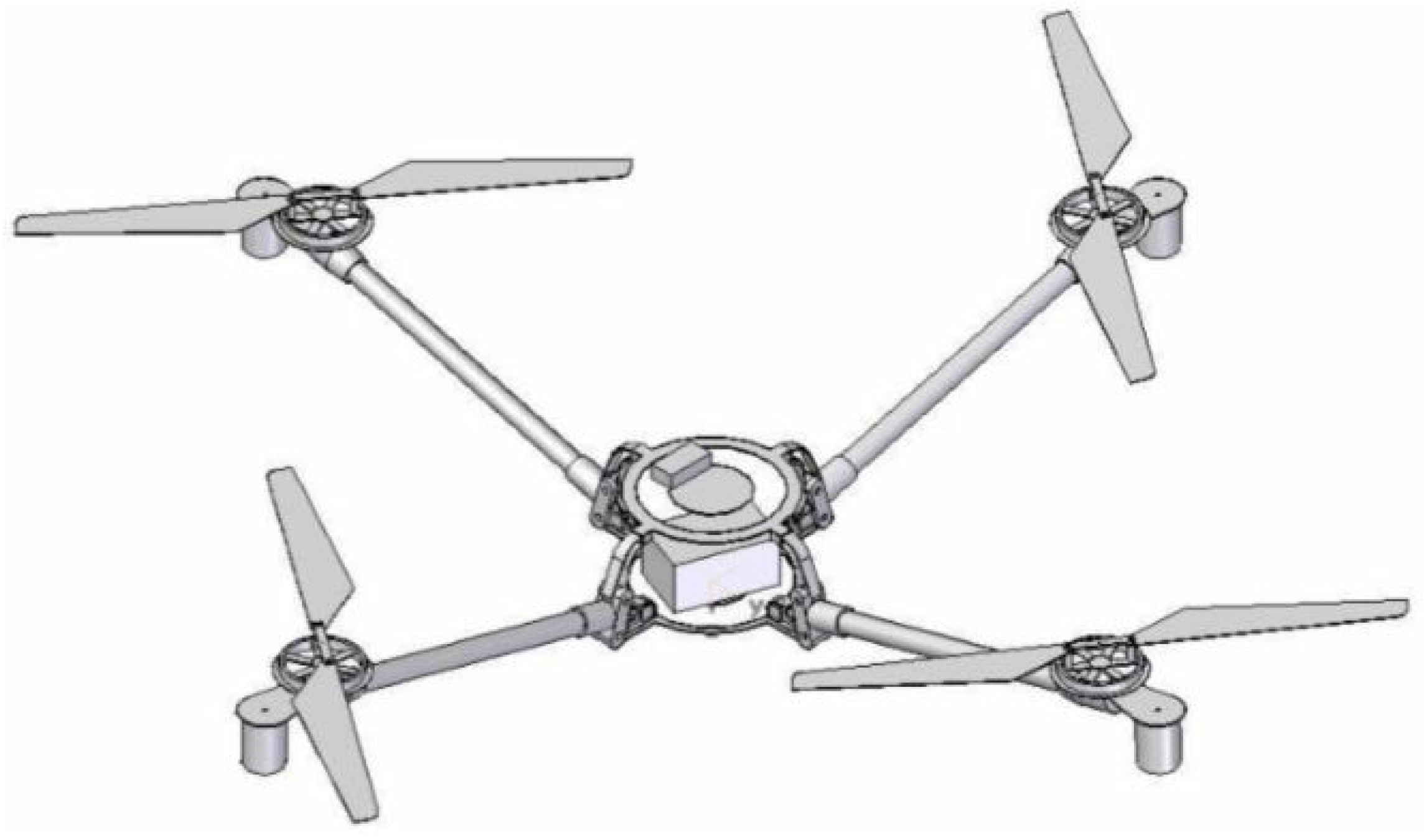
2.2. Quadrotor Simulation Model
Linear Model for MPC Design
2.3. MPC with Wind Disturbance Preview
Constraint Handling for Real-Time Implementation
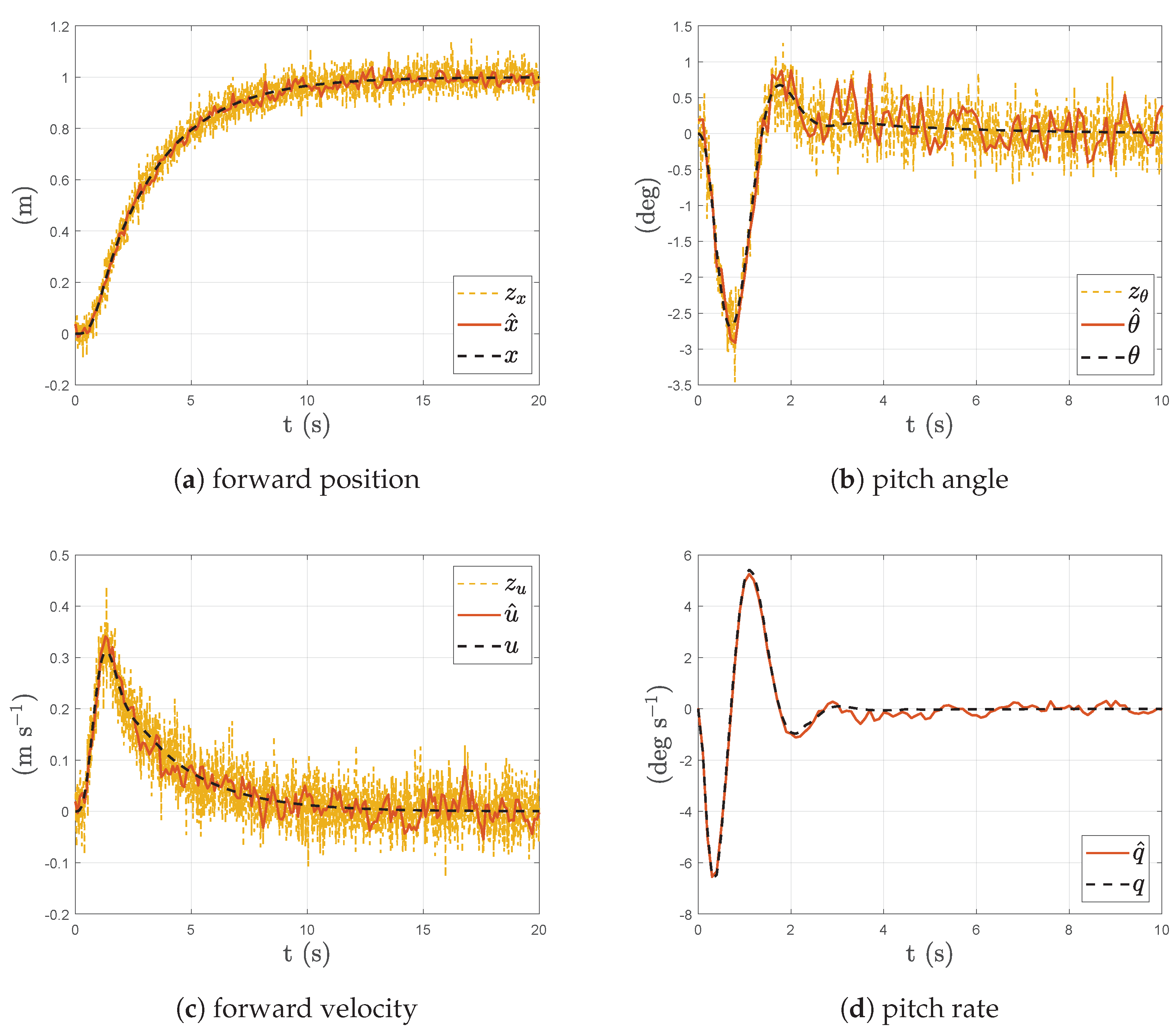
2.4. KF for State Estimation
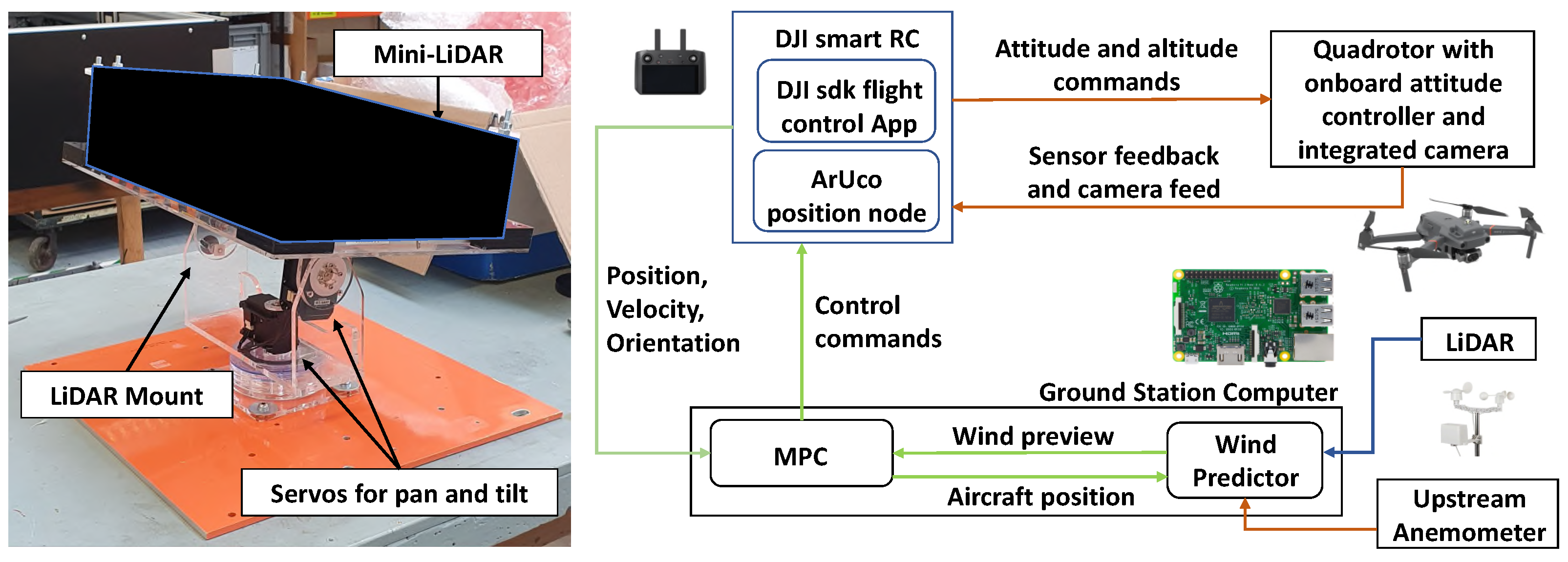
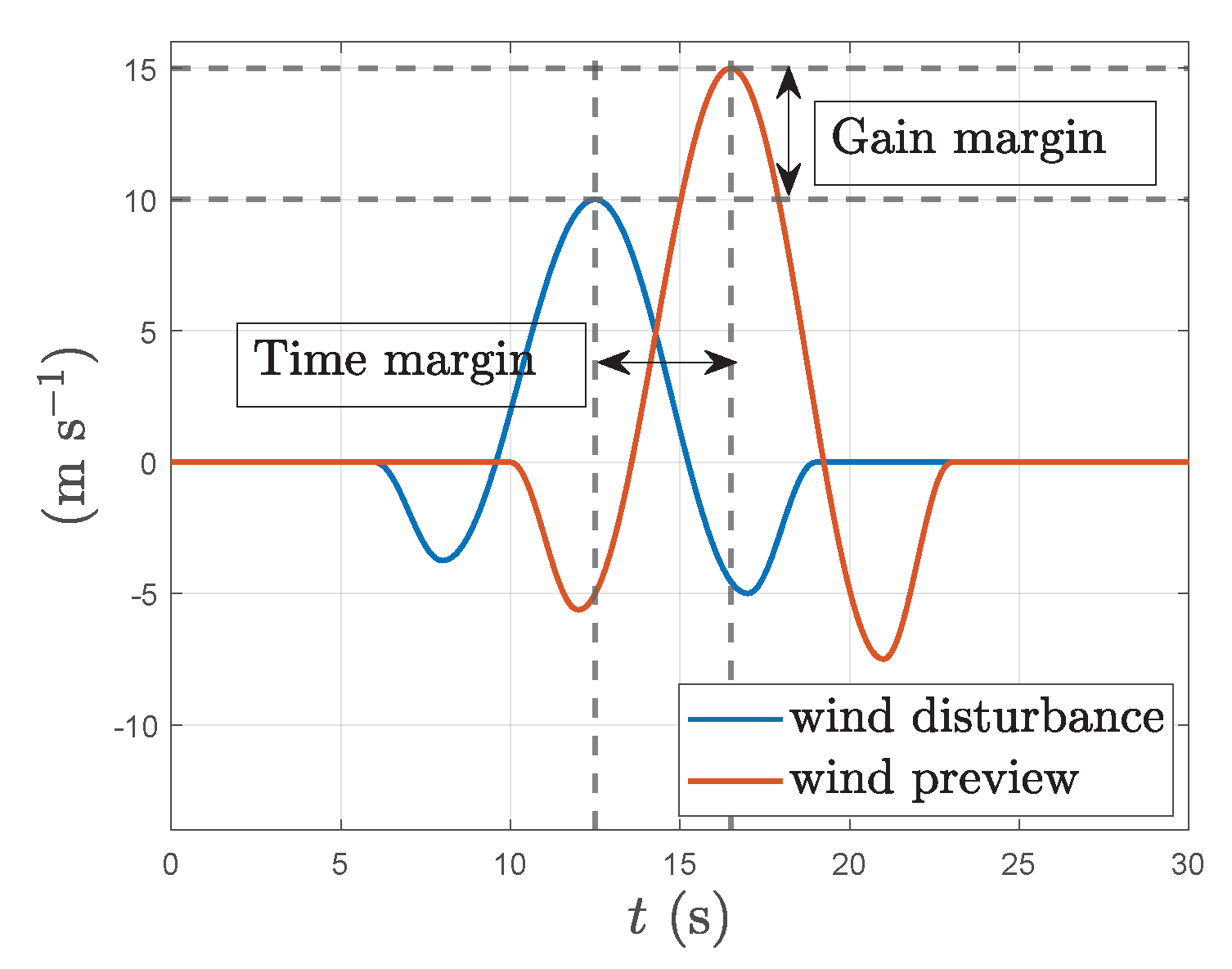
2.5. LiDAR for Wind Preview
3. Results and Discussion
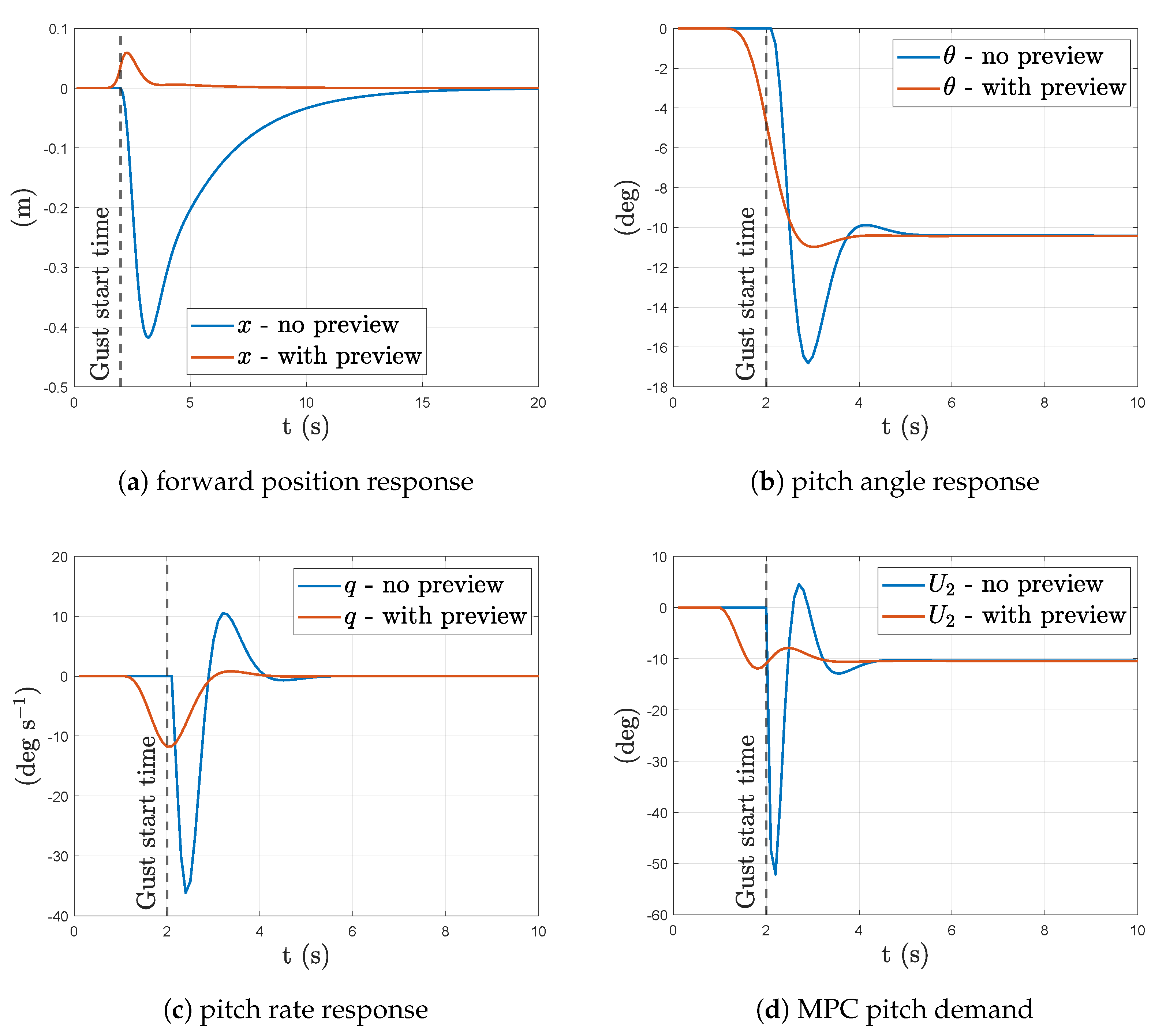
3.1. Linear Model Simulations–MPC with Wind Preview
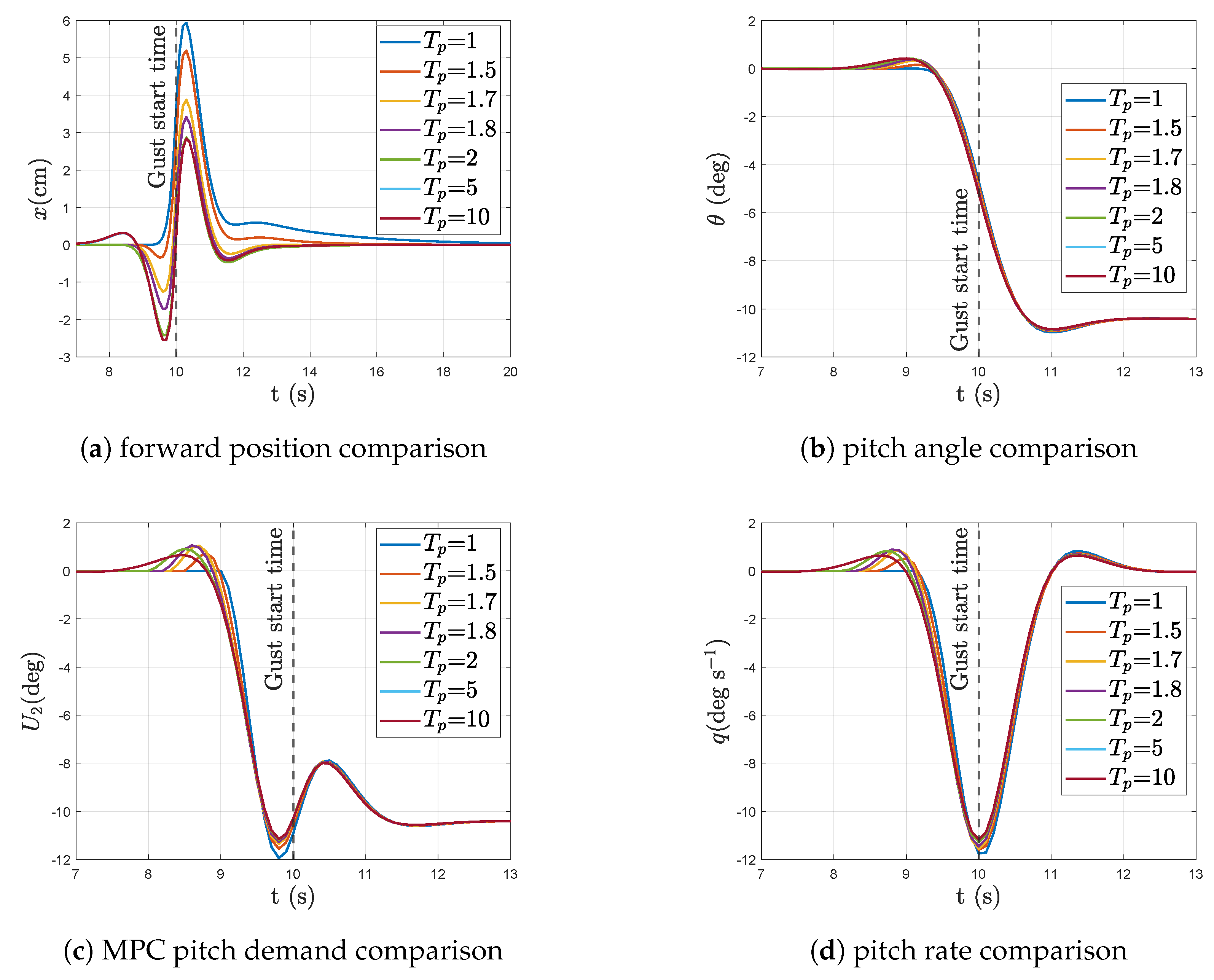
3.2. Linear Simulations–Prediction Horizon Length
3.3. Non-Linear Model Simulations
3.4. Non-Linear Simulations–MPC with LiDAR Data
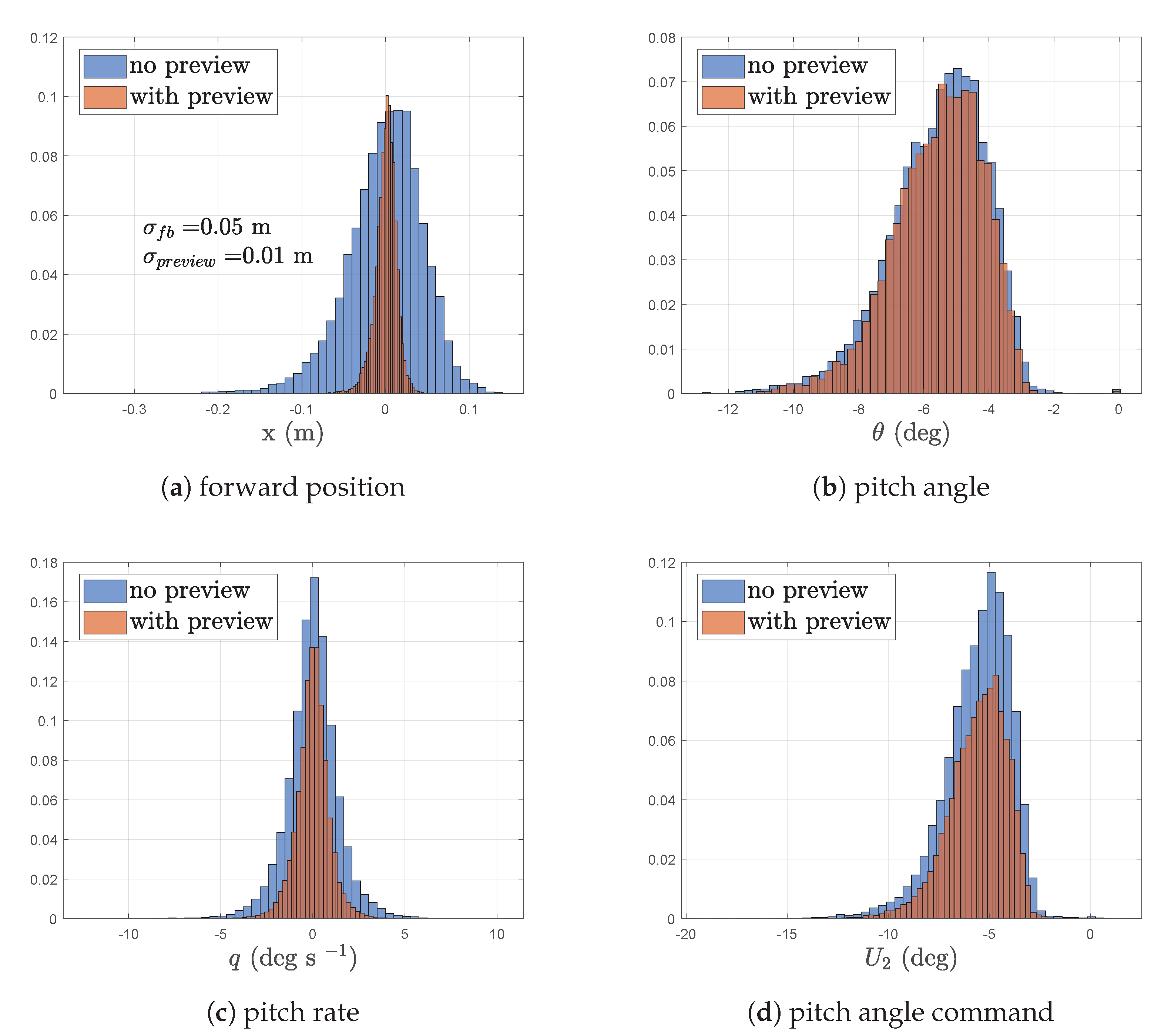
3.5. Robustness Analysis
4. Summary and Conclusions
Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MPC | Model Predictive Control |
| UAV | Unmanned Aerial Vehicle |
| LiDAR | Light Detection and Ranging |
| KF | Kalman Filter |
| rms | Root-Mean-Square |
| VTOL | Vertical Takeoff and Landing |
| PID | Proportional-Integral-Derivative |
References
- Shi, D.; Wu, Z.; Chou, W. Generalized extended state observer based high precision attitude control of quadrotor vehicles subject to wind disturbance. IEEE Access 2018, 6, 32349–32359. [Google Scholar] [CrossRef]
- Waslander, S.; Wang, C. Wind disturbance estimation and rejection for quadrotor position control. In Proceedings of the AIAA Infotech@ Aerospace Conference, Seattle, WA, USA, 6–9 April 2009; p. 1983. [Google Scholar] [CrossRef]
- Pappu, V.S.R.; Liu, Y.; Horn, J.F.; Cooper, J. Wind gust estimation on a small VTOL UAV. In Proceedings of the 7th AHS Technical Meeting on VTOL Unmanned Aircraft Systems and Autonomy, Mesa, AZ, USA, 24–26 January 2017; pp. 24–26. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Yang, H.; Cheng, L.; Xia, Y.; Yuan, Y. Active disturbance rejection attitude control for a dual closed-loop quadrotor under gust wind. IEEE Trans. Control Syst. Technol. 2017, 26, 1400–1405. [Google Scholar] [CrossRef]
- Orozco Soto, S.M.; Cacace, J.; Ruggiero, F.; Lippiello, V. Active Disturbance Rejection Control for the Robust Flight of a Passively Tilted Hexarotor. Drones 2022, 6, 258. [Google Scholar] [CrossRef]
- Ma, D.; Xia, Y.; Li, T.; Chang, K. Active disturbance rejection and predictive control strategy for a quadrotor helicopter. IET Control Theory Appl. 2016, 10, 2213–2222. [Google Scholar] [CrossRef]
- Garcia, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Singh, L.; Fuller, J. Trajectory generation for a UAV in urban terrain, using nonlinear MPC. In Proceedings of the 2001 American Control Conference (Cat. No. 01CH37148), Arlington, AV, USA, 25–27 June 2001; pp. 2301–2308. [Google Scholar] [CrossRef]
- Neunert, M.; De Crousaz, C.; Furrer, F.; Kamel, M.; Farshidian, F.; Siegwart, R.; Buchli, J. Fast nonlinear model predictive control for unified trajectory optimization and tracking. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1398–1404. [Google Scholar] [CrossRef]
- Bangura, M.; Mahony, R. Real-time model predictive control for quadrotors. In Proceedings of the 19th World Congress the International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014; pp. 11773–11780. [Google Scholar] [CrossRef]
- Owis, M.; El-Bouhy, S.; El-Badawy, A. Quadrotor trajectory tracking control using non-linear model predictive control with ros implementation. In Proceedings of the 2019 7th International Conference on Control, Mechatronics and Automation (ICCMA), Delft, The Netherlands, 6–8 November 2019; pp. 243–247. [Google Scholar] [CrossRef]
- Falanga, D.; Foehn, P.; Lu, P.; Scaramuzza, D. PAMPC: Perception-aware model predictive control for quadrotors. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Penin, B.; Spica, R.; Giordano, P.R.; Chaumette, F. PAMPC: Vision-based minimum-time trajectory generation for a quadrotor UAV. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6199–6206. [Google Scholar] [CrossRef] [Green Version]
- Kamel, M.; Burri, M.; Siegwart, R. Linear vs nonlinear mpc for trajectory tracking applied to rotary wing micro aerial vehicles. IFAC-PapersOnLine 2017, 50, 3463–3469. [Google Scholar] [CrossRef]
- Muske, K.R.; Badgwell, T.A. Disturbance modeling for offset-free linear model predictive control. J. Process Control 2002, 12, 617–632. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.; Liu, S.; Deng, X. Tracking control of multiple unmanned aerial vehicles incorporating disturbance observer and model predictive approach. Trans. Inst. Meas. Control 2020, 42, 951–964. [Google Scholar] [CrossRef]
- Li, B.; Zhou, W.; Sun, J.; Wen, C.; Chen, C. Development of model predictive controller for a Tail-Sitter VTOL UAV in hover flight. Sensors 2018, 18, 2859. [Google Scholar] [CrossRef] [Green Version]
- Wenjie, W.; Zhen, H.; Rui, C.; Feiteng, J.; Huiming, S. Trajectory Tracking Control Design for UAV Based on MPC and Active Disturbance Rejection. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; Akiyama, K.; Nonaka, K.; Sekiguchi, K. Experimental verification of the model predictive control with disturbance rejection for quadrotors. In Proceedings of the 54th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hangzhou, China, 28–30 July 2015; pp. 778–783. [Google Scholar] [CrossRef]
- Harris, M.; Hand, M.; Wright, A. Lidar for Turbine Control, Technical Report; NREL/TP-500-39154; National Renewable Energy Laboratory: Golden, CO, USA, 2006. Available online: https://www.nrel.gov/docs/fy06osti/39154.pdf (accessed on 30 March 2023).
- Dunne, F.; Simley, E.; Pao, L.Y. LIDAR Wind Speed Measurement Analysis and Feed-Forward Blade Pitch Control for Load Mitigation in Wind Turbines, Subcontract Report; NREL/SR-5000-52098; National Renewable Energy Laboratory: Golden, CO, USA, 2011. Available online: https://www.nrel.gov/docs/fy12osti/52098.pdf (accessed on 30 March 2023).
- Mirzaei, M.; Hansen, M.H. A LIDAR-assisted model predictive controller added on a traditional wind turbine controller. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1381–1386. [Google Scholar] [CrossRef]
- Schlipf, D.; Pao, L.Y.; Cheng, P.W. Comparison of feedforward and model predictive control of wind turbines using LIDAR. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3050–3055. [Google Scholar] [CrossRef] [Green Version]
- Harris, M.; Bryce, D.J.; Coffey, A.S.; Smith, D.A.; Birkemeyer, J.; Knopf, U. Advance measurement of gusts by laser anemometry. J. Wind Eng. Ind. Aerodyn. 2007, 95, 1637–1647. [Google Scholar] [CrossRef]
- Schlipf, D.; Schlipf, D.J.; Kühn, M. Nonlinear model predictive control of wind turbines using LIDAR. Wind Energy 2013, 16, 1107–1129. [Google Scholar] [CrossRef]
- De Wekker, S.F.J.; Godwin, K.S.; Emmitt, G.D.; Greco, S. Airborne Doppler lidar measurements of valley flows in complex coastal terrain. J. Appl. Meteorol. Climatol. 2012, 51, 1558–1574. [Google Scholar] [CrossRef] [Green Version]
- Godwin, K.S.; De Wekker, S.F.J.; Emmitt, G.D. Retrieving winds in the surface layer over land using an airborne Doppler lidar. J. Atmos. Ocean. Technol. 2012, 29, 487–499. [Google Scholar] [CrossRef] [Green Version]
- Soleimanzadeh, M.; Wisniewski, R.; Brand, A. State-space representation of the wind flow model in wind farms. Wind Energy 2014, 17, 627–639. [Google Scholar] [CrossRef]
- Towers, P.; Jones, B.L. Real-time wind field reconstruction from LiDAR measurements using a dynamic wind model and state estimation. Wind Energy 2016, 19, 133–150. [Google Scholar] [CrossRef] [Green Version]
- Bogue, R.K.; Ehernberger, L.J.; Soreide, D.; Bagley, H. Coherent Lidar Turbulence Measurement for Gust Load Alleviation. NASA Tech. Memo. 1996, 104318. Available online: https://www.nasa.gov/centers/dryden/pdf/88432main_H-2117.pdf (accessed on 30 March 2023).
- Khalil, A.; Fezans, N. Gust load alleviation for flexible aircraft using discrete-time preview control. Aeronaut. J. 2021, 125, 341–364. [Google Scholar] [CrossRef]
- Fezans, N.; Schwithal, J.; Fischenberg, D. In-flight remote sensing and identification of gusts, turbulence, and wake vortices using a Doppler LIDAR. CEAS Aeronaut. J. 2017, 8, 313–333. [Google Scholar] [CrossRef] [Green Version]
- Vasiljević, N.; Harris, M.; Tegtmeier Pedersen, A.; Rolighed Thorsen, G.; Pitter, M.; Harris, J.; Bajpai, K.; Courtney, M. Wind sensing with drone-mounted wind lidars: Proof of concept. Atmos. Meas. Tech. 2020, 13, 521–536. [Google Scholar] [CrossRef] [Green Version]
- Qi, P.; Zhao, X.; Palacios, R. Autonomous landing control of highly flexible aircraft based on lidar preview in the presence of wind turbulence. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2543–2555. [Google Scholar] [CrossRef] [Green Version]
- Mendez, A.P.; Whidborne, J.F.; Chen, L. Experimental verification of an LiDAR based Gust Rejection System for a Quadrotor UAV. In Proceedings of the 2022 IEEE International Conference on Unmanned Aircraft Systems, Dubrovnik, Croatia, 21–25 June 2022; pp. 1455–1464. [Google Scholar] [CrossRef]
- Mendez, A.P. A Study into the Effects of Rotor Tilt on the Gust Rejection Properties of a Quadrotor. Master’s Thesis, Cranfield University, Bedford, UK, 2019. [Google Scholar]
- Whidborne, J.F.; Cooke, A.K. Gust rejection properties of VTOL multirotor aircraft. IFAC-PapersOnLine 2017, 50, 175–180. [Google Scholar] [CrossRef]
- Whidborne, J.F.; Mendez, A.P.; Cooke, A.K. Effect of Rotor Tilt on the Gust Rejection Properties of Multirotor Aircraft. Drones 2022, 6, 305. [Google Scholar] [CrossRef]
- McCormick, B.W. Aerodynamics, Aeronautics, and Flight Mechanics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1994; pp. 162–232. [Google Scholar]
- Martinez, V. Modelling of the Flight Dynamics of a Quadrotor Helicopter. Master’s Thesis, Cranfield University, Bedford, UK, 2007. [Google Scholar]
- Maciejowski, J.M.; Huzmezan, M. Predictive Control, 1st ed.; Springer: Berlin, Germany, 2007; pp. 125–134. [Google Scholar]
- Rossiter, J.A. Model-Based Predictive Control: A Practical Approach, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB®, 1st ed.; Springer Science & Business Media: Berlin, Germany, 2009; pp. 27–110. [Google Scholar]
- Hildreth, C. A quadratic programming procedure. Nav. Res. Logist. Q. 1957, 4, 79–85. [Google Scholar] [CrossRef]



| Property | Value |
|---|---|
| Mass (kg) | 2.36 |
| Inertia matrix (kg m2) | |
| Surface areas (m2) | |
| Airframe drag coeff. () | 1.05 |
| Propeller arm length (m) | 0.45 |
| Number of blades per propeller | 2 |
| Blade chord (m) | 0.04 |
| Blade lift-curve-slope | 5.5 |
| Blade pitch (rad) | 0.3025 |
| Blade zero-lift drag coeff. | 0.05 |
| Blade drag coeff. due to angle of attack | 0.7 |
| Aerodynamic/Control Derivative | Value |
|---|---|
| Forward force due to forward airpseed— (N s m−1) | −0.1785 |
| lateral force due to lateral airpseed— (N s m−1) | −0.1785 |
| Vertical force due to vertical airpseed— (N s m−1) | −1.2495 |
| Vertical force due to altitude— (N m−1) | −0.8169 |
| Rolling moment due to roll angle— (N m rad−1) | −3.6594 |
| Pitching moment due to pitch angle— (N m rad−1) | −3.6376 |
| Yawing moment due to yaw angle— (N m rad−1) | −0.0785 |
| Rolling moment due to roll rate— (N m s rad−1) | −1.7815 |
| Pitching moment due to pitch rate— (N m s rad−1) | −1.7709 |
| Yawing moment due to yaw rate— (N m s rad−1) | −0.2868 |
| Vertical force due to control input — (N) | −0.8160 |
| Pitching moment due to control input — (N m) | 3.6376 |
| Rolling moment due to control input — (N m) | 3.6594 |
| Yawing moment due to control input — (N m) | 0.0785 |
| Control Channel | Proportional Gain | Integral Gain | Derivative Gain |
|---|---|---|---|
| Altitude | 5.89 | 0.80 | 8.72 |
| Pitch/roll | 5.89 | 0.13 | 1.62 |
| Yaw | 2.44 | 0.08 | 6.56 |
| Wind Preview Length (s) | (cm) | (deg) | (deg) | (deg s−1) |
|---|---|---|---|---|
| No preview | 14.57 | 10.58 | 8.71 | 5.9 |
| = 1.0 | 1.25 (−91%) | 8.66 (−18%) | 8.44 (−3%) | 2.51 (−57%) |
| = 1.5 | 1.04 (−16%) | 8.66 (0%) | 8.44 (0%) | 2.51 (0%) |
| = 1.7 | 0.76 (−28%) | 8.66 (0%) | 8.45 (0%) | 2.52 (0%) |
| = 1.8 | 0.70 (−8%) | 8.65 (0%) | 8.45 (0%) | 2.51 (0%) |
| = 2.0 | 0.68 (−2%) | 8.65 (0%) | 8.45 (0%) | 2.49 (−1%) |
| = 5.0 | 0.70 (+2%) | 8.65 (0%) | 8.45 (0%) | 2.47 (−1%) |
| = 10 | 0.70 (0%) | 8.65 (0%) | 8.45 (0%) | 2.47 (0%) |
| Uncertainty | (cm) | (deg) | (deg) | (deg s−1) |
|---|---|---|---|---|
| Baseline | 14.89 | 4.20 | 4.26 | 2.99 |
| s | 4.84 | 3.98 | 4.06 | 2.84 |
| s | 9.56 | 4.09 | 4.12 | 3.05 |
| s | 13.94 | 4.18 | 4.26 | 3.17 |
| s | 15.93 | 4.22 | 4.31 | 3.19 |
| s | 17.68 | 4.25 | 4.34 | 3.18 |
| % | 5.73 | 3.75 | 3.83 | 2.44 |
| % | 12.55 | 3.63 | 3.68 | 2.31 |
| % | 15.30 | 3.59 | 3.62 | 2.26 |
| % | 19.35 | 3.52 | 3.53 | 2.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendez, A.P.; Whidborne, J.F.; Chen, L. Wind Preview-Based Model Predictive Control of Multi-Rotor UAVs Using LiDAR. Sensors 2023, 23, 3711. https://doi.org/10.3390/s23073711
Mendez AP, Whidborne JF, Chen L. Wind Preview-Based Model Predictive Control of Multi-Rotor UAVs Using LiDAR. Sensors. 2023; 23(7):3711. https://doi.org/10.3390/s23073711
Chicago/Turabian StyleMendez, Arthur P., James F. Whidborne, and Lejun Chen. 2023. "Wind Preview-Based Model Predictive Control of Multi-Rotor UAVs Using LiDAR" Sensors 23, no. 7: 3711. https://doi.org/10.3390/s23073711
APA StyleMendez, A. P., Whidborne, J. F., & Chen, L. (2023). Wind Preview-Based Model Predictive Control of Multi-Rotor UAVs Using LiDAR. Sensors, 23(7), 3711. https://doi.org/10.3390/s23073711





