Axial Load Measurement of Bolts with Different Clamping Lengths Based on High-Frequency Ultrasonic ZnO Film Sensor
Abstract
:1. Introduction
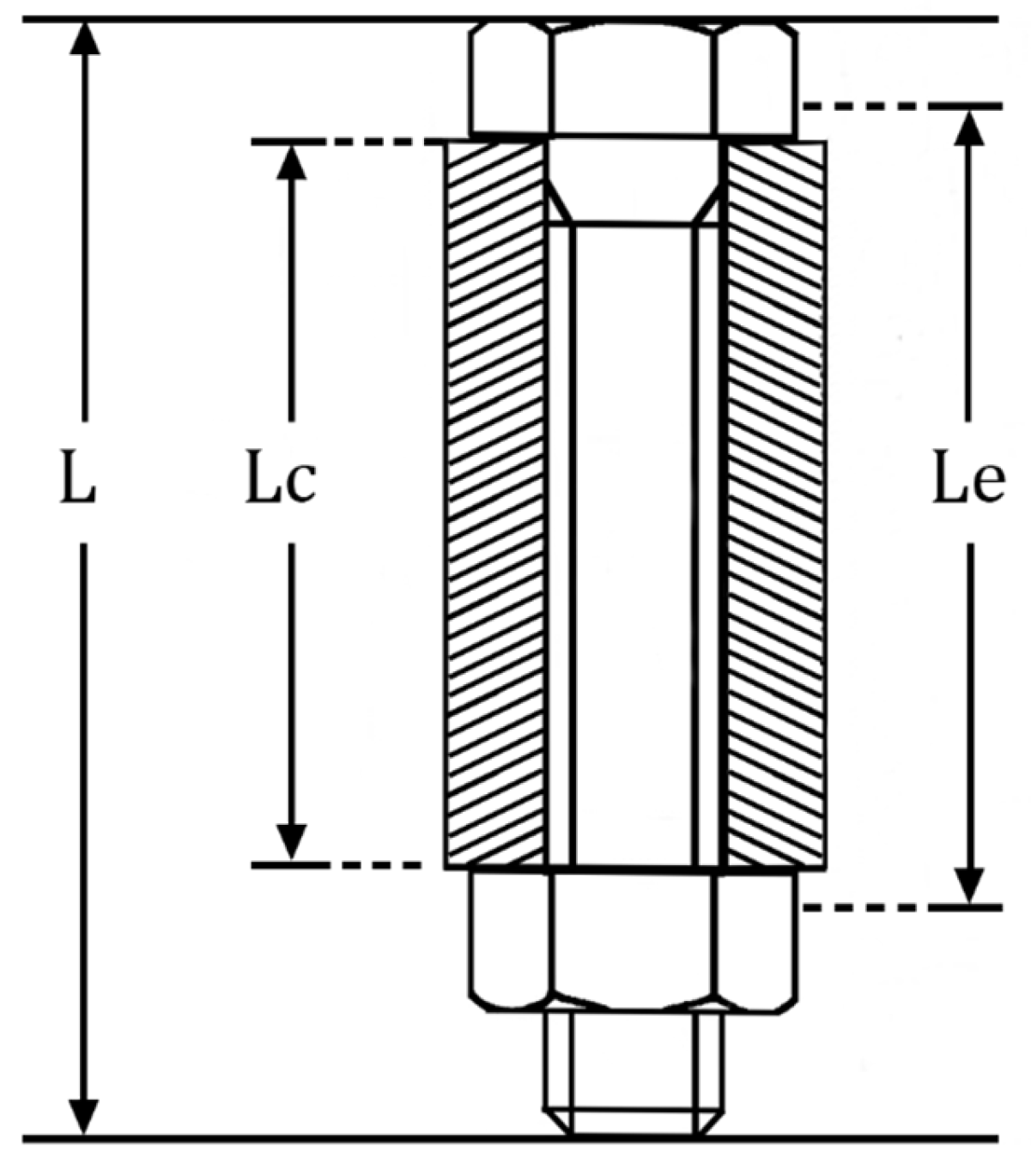
2. Clamping Length Correction Method
3. Experiment
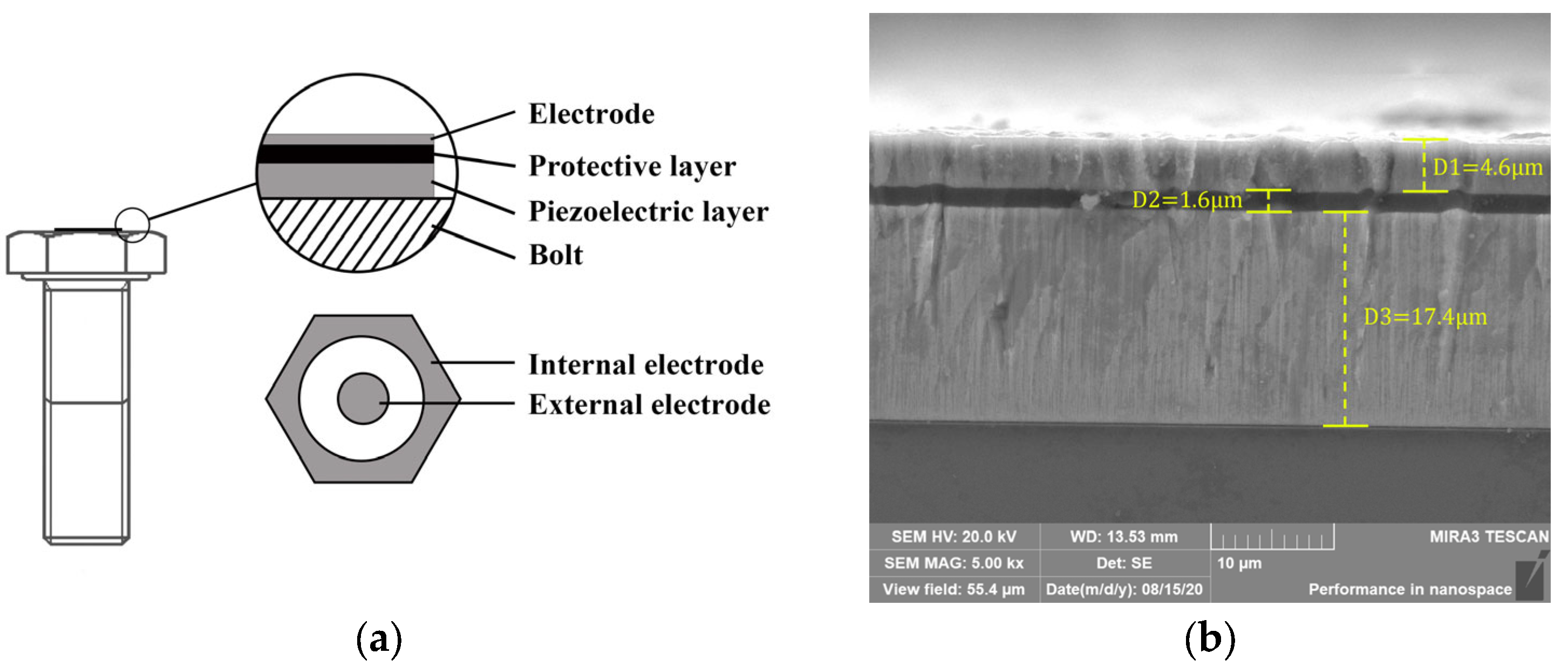
3.1. Piezoelectric Film Sensor
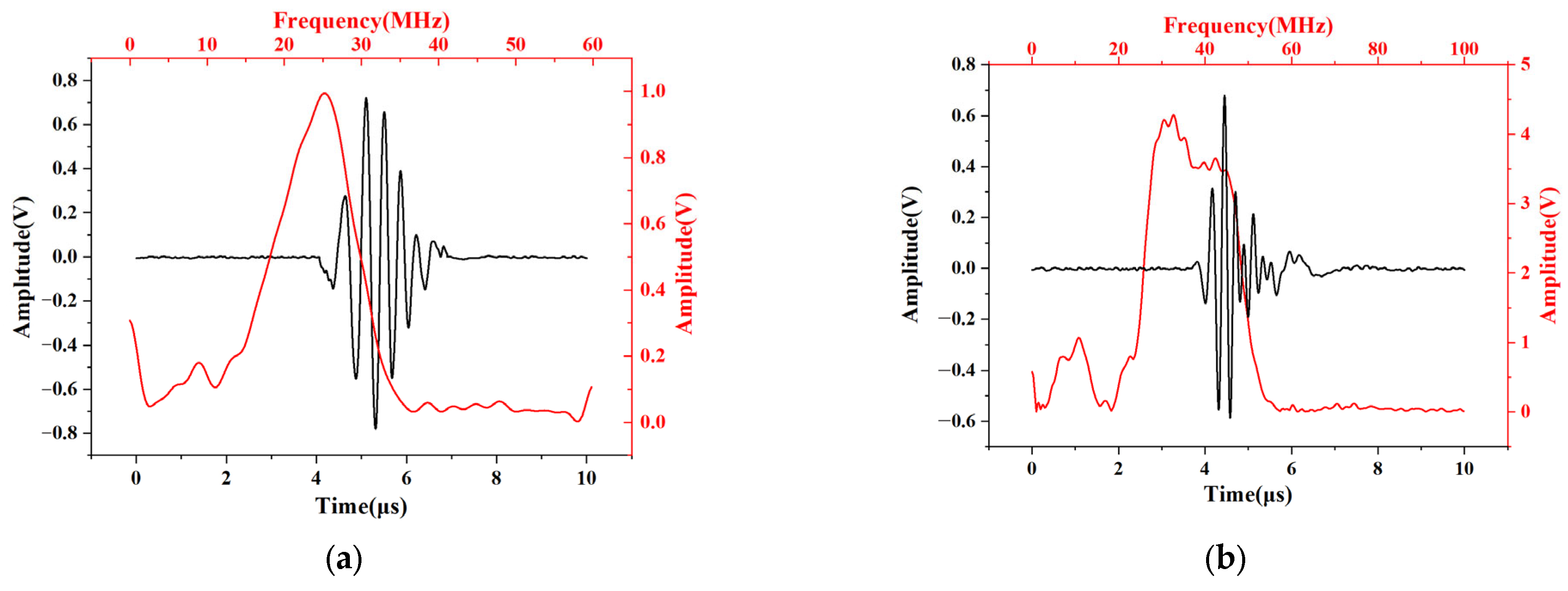
3.2. Ultrasonic Test Experiment
4. Results and Discussion
4.1. Characterization Results of Piezoelectric Film Sensor
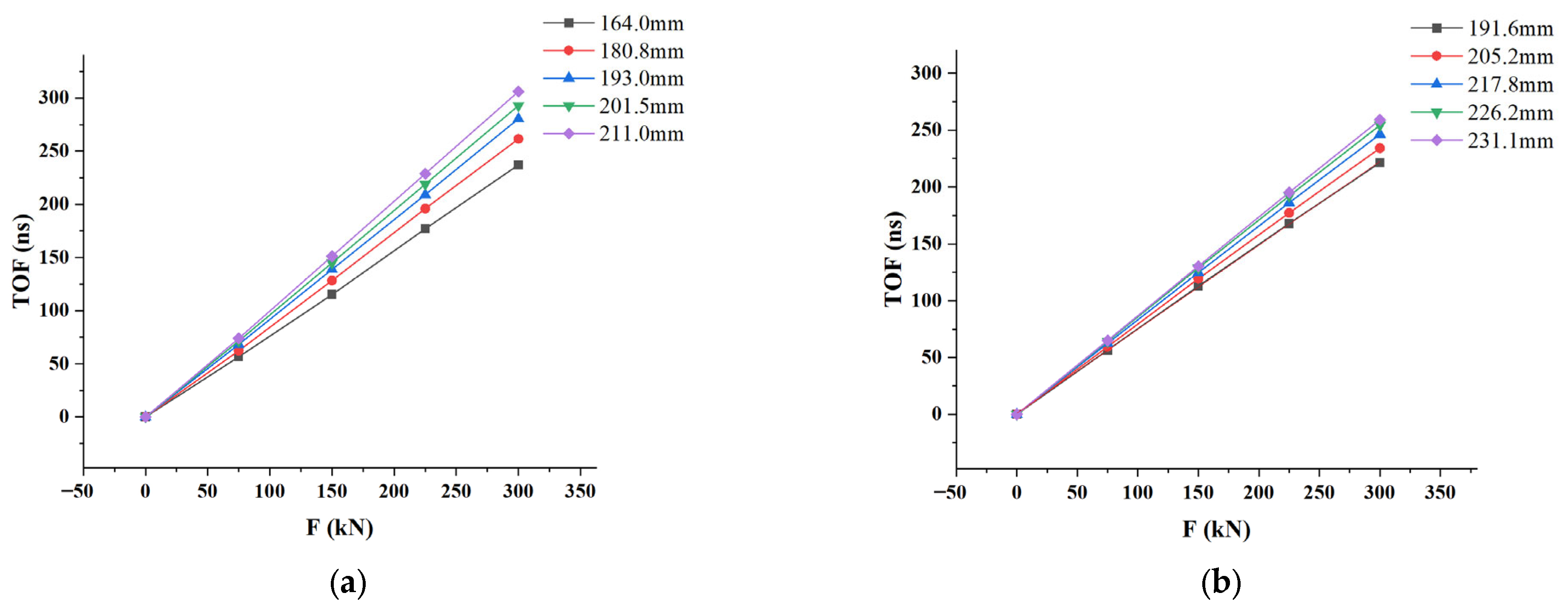
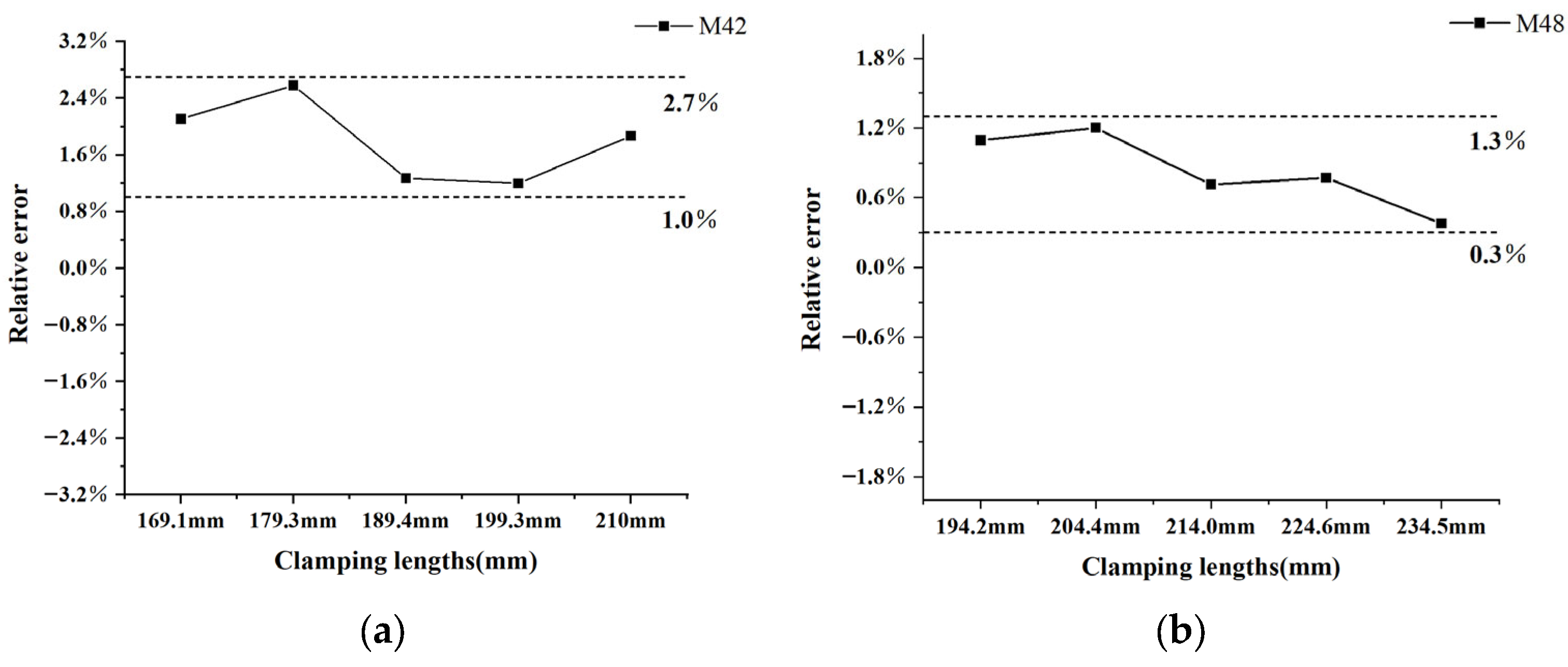
4.2. Influence of Clamping Length on Axial Load Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bickford, J.H. Introduction to the Design and Behavior of Bolted Joints: Non-Gasketed Joints; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Fukuoka, T.; Takaki, T. Evaluations of the Tightening Process of Bolted Joint With Elastic Angle Control Method. In Proceedings of the ASME Pressure Vessels and Piping Conference, San Diego, CA, USA, 25–29 July 2004; pp. 11–18. [Google Scholar] [CrossRef]
- Nazarko, P.; Ziemianski, L. Force identification in bolts of flange connections for structural health monitoring and failure prevention. Procedia Struct. Integr. 2017, 5, 460–467. [Google Scholar] [CrossRef]
- Khomenko, A.; Koricho, E.G.; Haq, M.; Cloud, G.L. Bolt tension monitoring with reusable fiber Bragg-grating sensors. J. Strain Anal. Eng. Des. 2016, 51, 101–108. [Google Scholar] [CrossRef]
- Chen, D.; Huo, L.; Li, H.; Song, G. A Fiber Bragg Grating (FBG)-Enabled Smart Washer for Bolt Pre-Load Measurement: Design, Analysis, Calibration, and Experimental Validation. Sensors 2018, 18, 2586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horstman, R.; Peters, K.; Meltzer, R.; Vieth, M.B.; Heyman, J.; Chern, E. Ultrasonic Measurement of Axial Stress. J. Test. Eval. 1982, 10, 202. [Google Scholar] [CrossRef]
- Wolfenden, A.; Johnson, G.; Holt, A.; Cunningham, B. An Ultrasonic Method for Determining Axial Stress in Bolts. J. Test. Eval. 1986, 14, 253. [Google Scholar] [CrossRef]
- Crecraft, D. Ultrasonic measurement of stresses. Ultrasonics 1968, 6, 117–121. [Google Scholar] [CrossRef]
- Hughes, D.S.; Kelly, J.L. Second-Order Elastic Deformation of Solids. Phys. Rev. 1953, 92, 1145–1149. [Google Scholar] [CrossRef]
- Joshi, S.; Pathare, R. Ultrasonic instrument for measuring bolt stress. Ultrasonics 1984, 22, 261–269. [Google Scholar] [CrossRef]
- Froggat, M.; Allison, S. Interrupted ultrasonic bolt load measurements using the pulsed phase-locked loop system. IEEE Trans. Instrum. Meas. 1996, 45, 112–116. [Google Scholar] [CrossRef]
- Jhang, K.-Y.; Quan, H.-H.; Ha, J.; Kim, N.-Y. Estimation of clamping force in high-tension bolts through ultrasonic velocity measurement. Ultrasonics 2006, 44, e1339–e1342. [Google Scholar] [CrossRef] [PubMed]
- Yasui, H.; Tanaka, H.; Fujii, I.; Kawashima, K. Ultrasonic Measurement of Axial Stress in Short Bolts with Consideration of Nonlinear Deformation. JSME Int. J. Ser. A Solid Mech. Mater. Eng. 1999, 42, 111–118. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Yuan, B.; Mu, X.; Sun, W. Bolt preload measurement based on the acoustoelastic effect using smart piezoelectric bolt. Smart Mater. Struct. 2019, 28, 10. [Google Scholar] [CrossRef]
- Chaki, S.; Corneloup, G.; Lillamand, I.; Walaszek, H. Combination of Longitudinal and Transverse Ultrasonic Waves for In Situ Control of the Tightening of Bolts. J. Press. Vessel. Technol. 2006, 129, 383–390. [Google Scholar] [CrossRef]
- Ding, X.; Wu, X.; Wang, Y. Bolt axial stress measurement based on a mode-converted ultrasound method using an electromagnetic acoustic transducer. Ultrasonics 2014, 54, 914–920. [Google Scholar] [CrossRef] [PubMed]
- Ogi, H.; Hirao, M.; Fukuoka, H. Noncontacting ultrasonic measurement of bolt axial stress with electromagnetic acoustic transducer. In Proceedings of the First US-Japan Symposium on Advances in NDT, Kahuku, HI, USA, 24–28 June 1996; pp. 37–42. [Google Scholar]
- Kim, N.; Hong, M. Measurement of axial stress using mode-converted ultrasound. NDT E Int. 2009, 42, 164–169. [Google Scholar] [CrossRef]
- Dahmani, H.; Zaaroura, I.; Salhab, A.; Campistron, P.; Carlier, J.; Toubal, M.; Harmand, S.; Thomy, V.; Neyens, M.; Nongaillard, B. Fabrication and Optimization of High Frequency ZnO Transducers for Both Longitudinal and Shear Emission: Application of Viscosity Measurement using Ultrasound. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 1428–1435. [Google Scholar] [CrossRef]
- Koshti, A.M. Estimation of accuracy in ultrasonic preload measurements. In Proceedings of the Advanced Nondestructive Evaluation for Structural and Biological Health Monitoring, Newport Beach, CA, USA, 24 July 2001; pp. 300–311. [Google Scholar]
- Al-Khawaja, S.; Abdallah, B.; Shaker, S.A.; Kakhia, M. Thickness effect on stress, structural, electrical and sensing properties of (0 0 2) preferentially oriented undoped ZnO thin films. Compos. Interfaces 2015, 22, 221–231. [Google Scholar] [CrossRef]
- Dang, W.; Fu, Y.; Luo, J.; Flewitt, A.; Milne, W. Deposition and characterization of sputtered ZnO films. Superlattices Microstruct. 2007, 42, 89–93. [Google Scholar] [CrossRef]
- Barakat, M.A.Y.; El-Wakil, A.A.A. Preparation and characterization of EVA/ZnO composites as piezoelectric elements for ultrasonic transducers. Mater. Res. Express 2021, 8, 14. [Google Scholar] [CrossRef]



| Bolt Type | Total Length/(mm) | Thread Area/(mm) | Material | Sensor Size |
|---|---|---|---|---|
| M42 | 268 | 160–268 | 40CrNiMo | 16 |
| M48 | 303 | 182–303 | 40CrNiMo | 16 |
| M42 | 164 mm | 180.8 mm | 193.0 mm | 201.5 mm | 211.0 mm | Average |
|---|---|---|---|---|---|---|
| — | 7.86 | 7.84 | 6.13 | 7.41 | 7.31 | |
| 4.671 | 4.673 | 4.673 | 4.675 | 4.673 | 4.673 | |
| M48 | 191.6 mm | 205.2 mm | 217.8 mm | 226.2 mm | 231.1 mm | Average |
| — | 44.43 | 37.21 | 40.31 | 38.18 | 40.03 | |
| 3.191 | 3.189 | 3.188 | 3.189 | 3.191 | 3.190 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, X.; Dai, H.; Xu, W.; Zhao, Y.; Zhang, J.; Yang, B. Axial Load Measurement of Bolts with Different Clamping Lengths Based on High-Frequency Ultrasonic ZnO Film Sensor. Sensors 2023, 23, 3712. https://doi.org/10.3390/s23073712
Jing X, Dai H, Xu W, Zhao Y, Zhang J, Yang B. Axial Load Measurement of Bolts with Different Clamping Lengths Based on High-Frequency Ultrasonic ZnO Film Sensor. Sensors. 2023; 23(7):3712. https://doi.org/10.3390/s23073712
Chicago/Turabian StyleJing, Xuechao, Hongwei Dai, Wanli Xu, Yue Zhao, Jun Zhang, and Bing Yang. 2023. "Axial Load Measurement of Bolts with Different Clamping Lengths Based on High-Frequency Ultrasonic ZnO Film Sensor" Sensors 23, no. 7: 3712. https://doi.org/10.3390/s23073712
APA StyleJing, X., Dai, H., Xu, W., Zhao, Y., Zhang, J., & Yang, B. (2023). Axial Load Measurement of Bolts with Different Clamping Lengths Based on High-Frequency Ultrasonic ZnO Film Sensor. Sensors, 23(7), 3712. https://doi.org/10.3390/s23073712






