Two-Step Matching Approach to Obtain More Control Points for SIFT-like Very-High-Resolution SAR Image Registration
Abstract
:1. Introduction
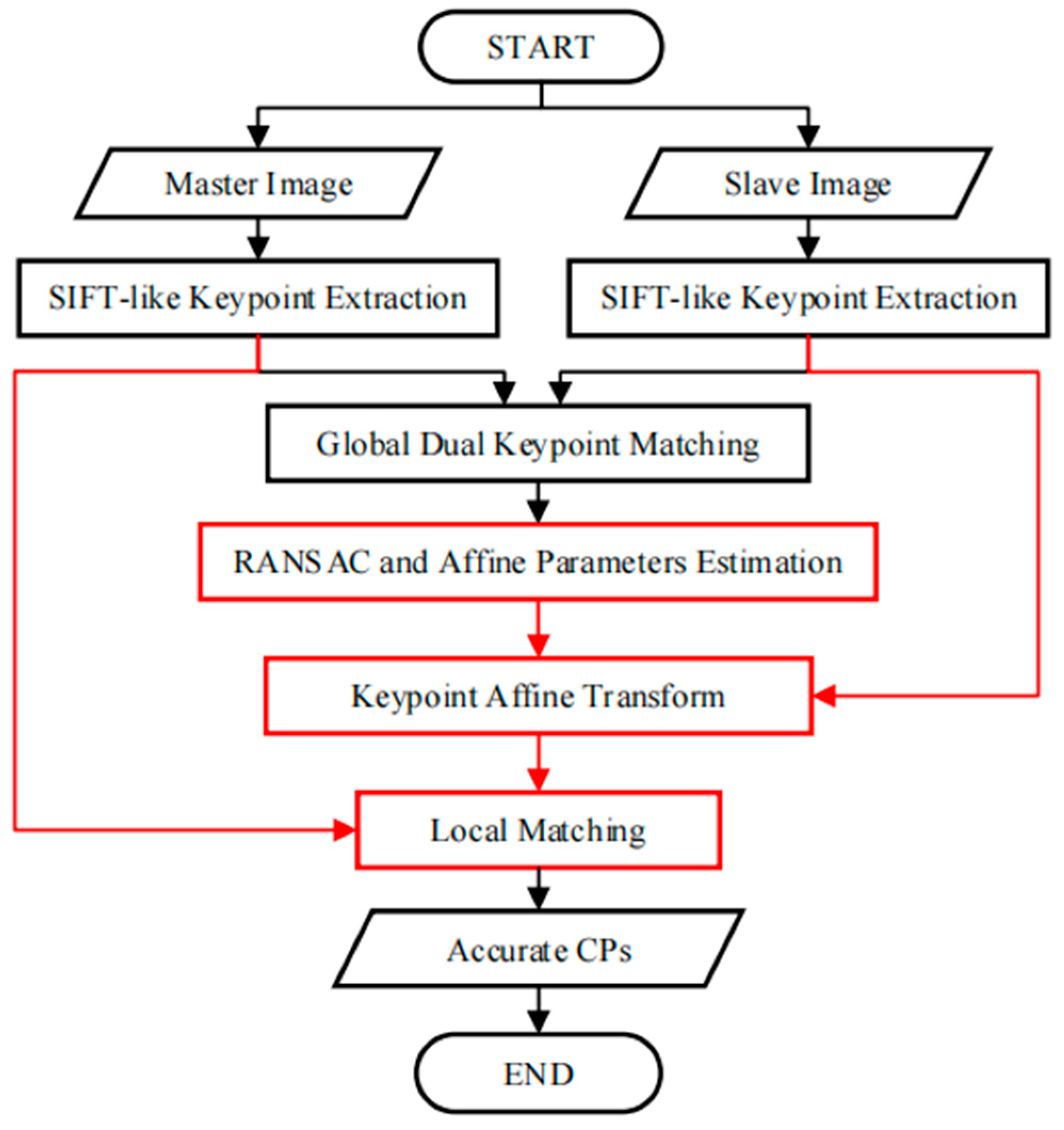
2. Two-Step Matching
2.1. Registration Model
2.2. Motivation for Two Steps
2.3. Two-Step CP Extraction Scheme
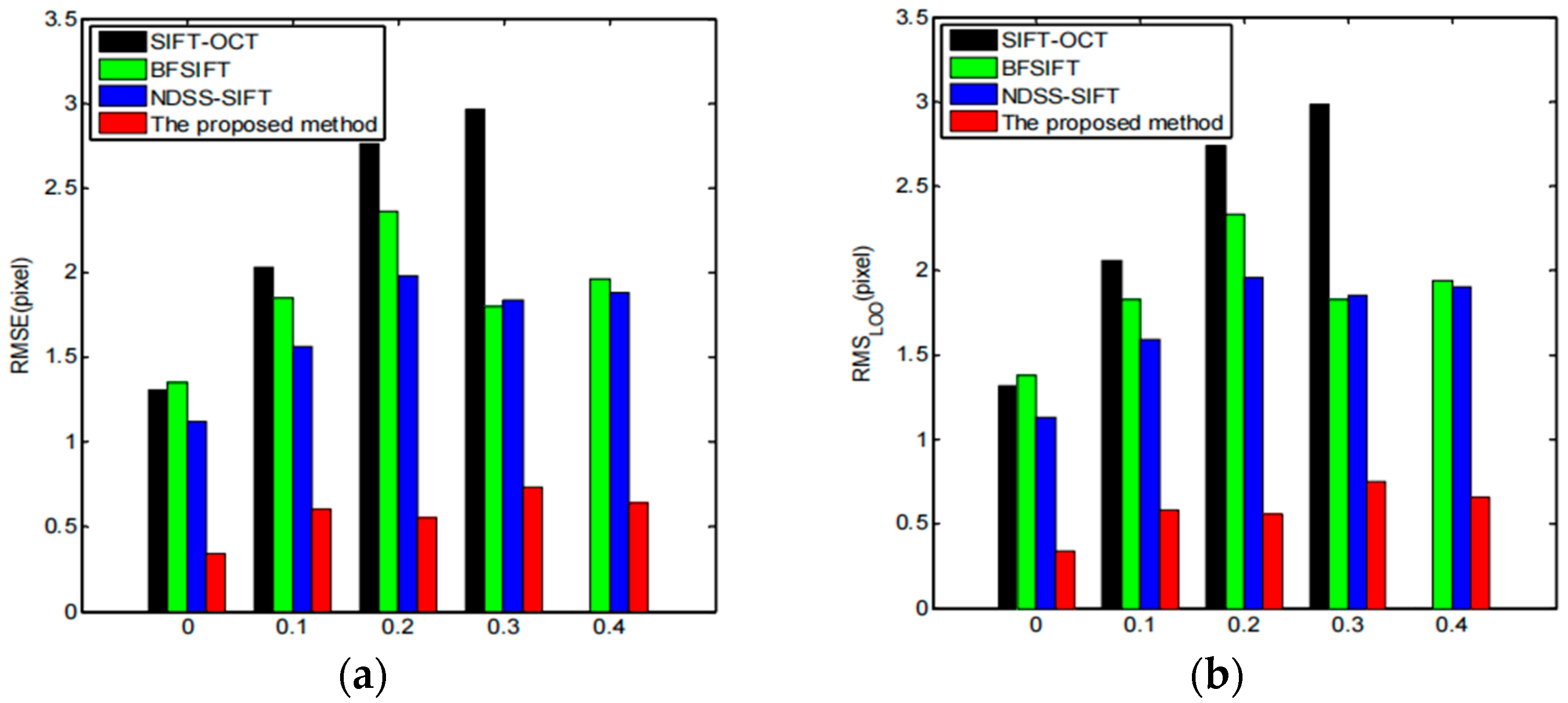
3. Experimental Results and Analysis
3.1. Dataset
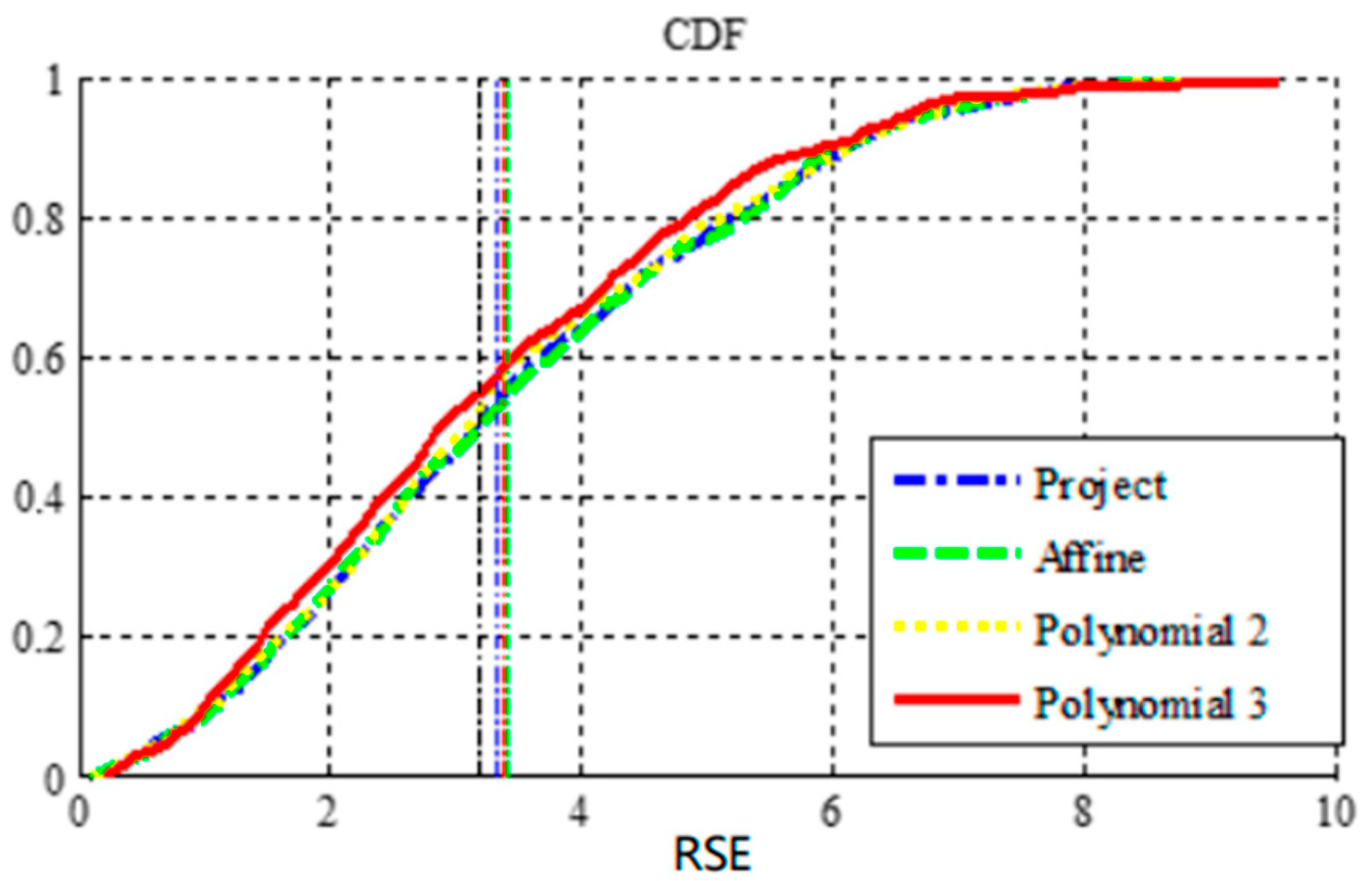
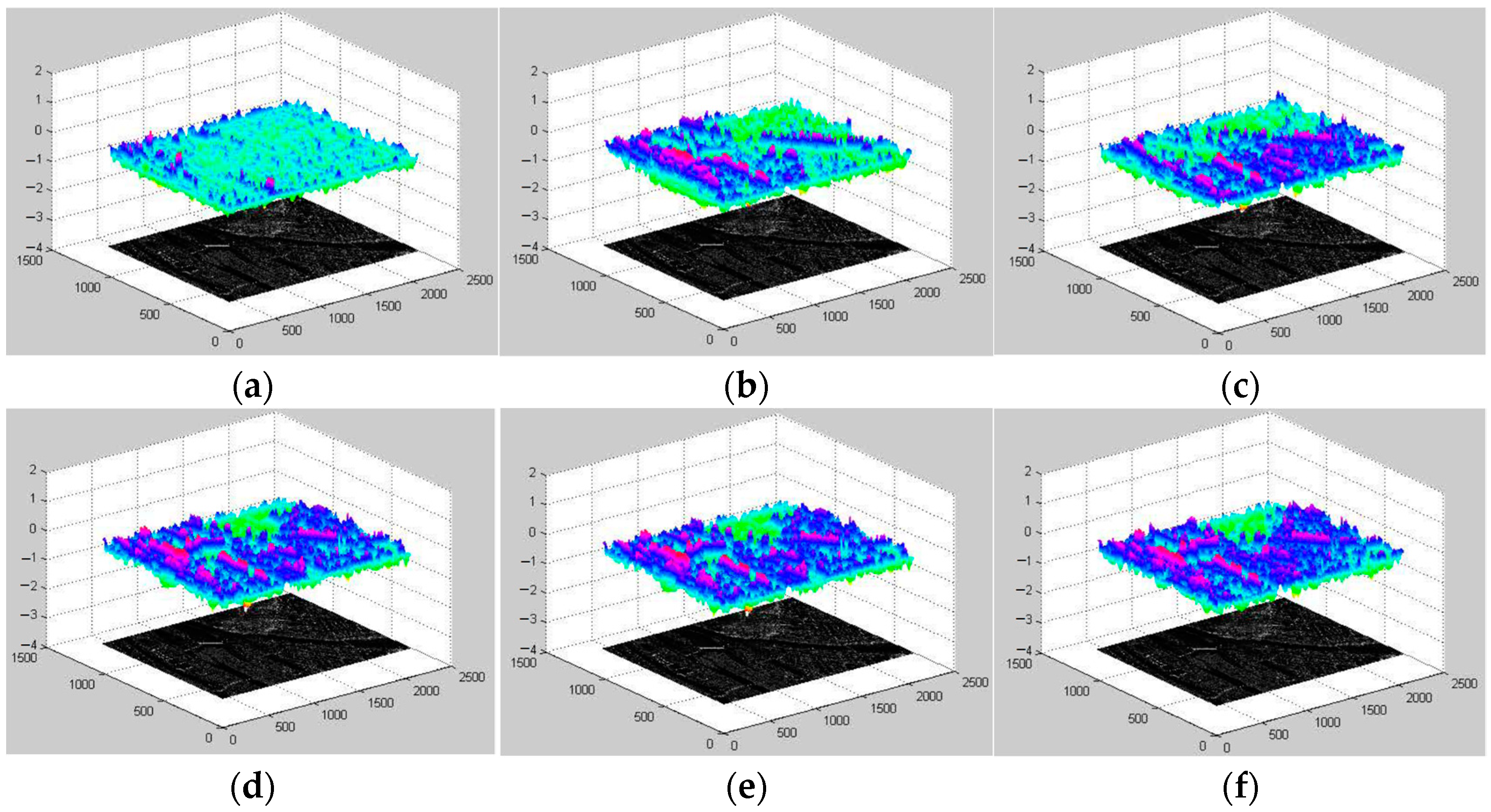
3.2. Analysis
3.3. Registration Result
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Singha, S.; Ressel, R.; Lehner, S. Multi-frequency and multi-polarization analysis of oil slicks using TerraSAR-X and RADARSAT-2 data. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Cui, Z.; Wang, X.; Liu, N.; Cao, Z.; Yang, J. Ship detection in large-scale SAR images via spatial shuffle-group enhance attention. IEEE Trans. Geosci. Remote Sens. 2020, 59, 379–391. [Google Scholar] [CrossRef]
- Qiang, L.; Jingfa, Z. Gaofeng-3 satellite fully polarized SAR image Jiuzhaigou earthquake landslide survey. J. Remote Sens. 2019, 23, 883–891. [Google Scholar]
- Kang, S.; Liu, C.; Zhu, L.; Ji, L. Study the source mechanism of M_S6.4 earthquake in 2020 based on lifting rail Sentinel-1 SAR data. Earthquake 2021, 41, 80–91. [Google Scholar]
- Elegant, X.; Xiufeng, H. Research on deformation monitoring of InSAR Dam. J. Wuhan Univ. (Inf. Sci. Ed.) 2019, 44, 1334–1341. [Google Scholar]
- Zhu, M.; Shen, T.; Lu, F.; Ge, C.; Bai, S.; Jia, Z.; Wang, D. In SAR deformation data decomposition and information extraction of Jiaozhou Bay Bridge in Qingdao. J. Remote Sens. 2020, 24, 883–893. [Google Scholar]
- Li, X.; Su, J.; Yang, L. Building detection in sar images based on bi-dimensional empirical mode decomposition algorithm. IEEE Geosci. Remote Sens. Lett. 2019, 17, 641–645. [Google Scholar] [CrossRef]
- Meng, F. High Resolution SAR Urban Building Target Detection Algorithm; Xidian University: Xi’an, China, 2020. [Google Scholar]
- Zhang, L.; Jia, H.; Lu, Z.; Liang, H.; Ding, X.; Li, X. Minimizing height effects in MTInSAR for deformation detection over built areas. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9167–9176. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, Y.; Dong, X.; Zhai, W.; Yang, S.; Xu, X. Measurement of Yangtze River’s Water Level by Tiangong-2 Interferometric Imaging Radar Altimeter. In Proceedings of the 2019 PhotonIcs & Electromagnetics Research Symposium-Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019. [Google Scholar]
- Zhu, P.; Huang, S.; Yang, Y.; Ma, J.; Sun, Y.; Gao, S. High-frequency Monitoring of Inland Lakes Water Extent Using Time-Series Sentinel-1 SAR Data. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019. [Google Scholar]
- Fei, M. Study on InSAR Monitoring and Prediction Method of Mine Settlement; Changan University: Xi’an, China, 2020. [Google Scholar]
- Ertao, G. Study on Deformation along High-Speed Railway Based on High-Resolution SAR Image Monitoring; Southwest Jiaotong University: Xi’an, China, 2017. [Google Scholar]
- Dongdong, G. Research on Object Classification Techniques for High-Resolution SAR Images. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2019. [Google Scholar]
- Lin, S.-Y.; Lin, C.-W.; Van Gasselt, S. Towards Monitoring of Mountain Mass Wasting Using Object Based Image Analysis Using SAR Intensity Images. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021. [Google Scholar]
- Zhiping, F. Research and System Realization of GB-InSAR Landslide Disasters; Chongqing University: Chongqing, China, 2018. [Google Scholar]
- Lvsouras, E.; Gasteratos, A. A new method to combine detection and tracking algorithms for fast and accurate human localization in UAV-based SAR operations. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020. [Google Scholar]
- Yang, Z.; Dan, T.; Yang, Y.J. Multi-temporal remote sensing image registration using deep convolutional features. IEEE Access 2018, 6, 38544–38555. [Google Scholar] [CrossRef]
- Moravec, H.P. Obstacle Avoidance and Navigation in the Real World by a Seeing Robot Rover; Stanford University CA Dept of Computer Science: Stanford, CA, USA, 1980. [Google Scholar]
- Harris, C.G.; Stephens, M. A combined corner and edge detector. Alvey Vis. Conf. 1988, 15, 10-5244. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Zhenhuan, Z.; Ming, Z. Based on the invariant moment scene matching algorithm. Comput. Eng. 2007, 22, 203–205+222. [Google Scholar]
- Zhaohui, Y.; Ying, C.; Yongshe, S.; Shaoming, Z. A scene matching method based on SIFT features. Comput. Appl. 2008, 9, 2404–2406. [Google Scholar]
- Zhi, X.; Fang, C.; Dan, W.; Jianye, L. SAR/INS, a robust scene matching algorithm based on SURF in combined navigation. J. Nanjing Univ. Aeronaut. Astronaut. 2017, 43, 49–54. [Google Scholar]
- Jiang, D.; Jianhua, Y.; Jing, S. Mismatch elimination method in scene matching positioning guidance. J. Navig. Position. 2019, 5, 5–8+18. [Google Scholar]
- Rui, L. Research on Aerial Image Localization Based on Image Matching; Dalian University of Technology: Dalian, China, 2019. [Google Scholar]
- Wang, Y.; Yu, Q.; Yu, W. An improved Normalized Cross Correlation algorithm for SAR image registration. In Proceedings of the 2022 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2022; pp. 2086–2089. [Google Scholar]
- Pallotta, L.; Giunta, G.; Clemente, C. Subpixel SAR image registration through parabolic interpolation of the 2D cross-correlation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4132–4144. [Google Scholar] [CrossRef] [Green Version]
- Schwind, P.; Suri, S.; Reinartz, P.; Siebert, A. Applicability of the SIFT operator to geometric SAR image registration. Int. J. Remote Sens. 2010, 31, 1959–1980. [Google Scholar] [CrossRef]
- Wang, S.; You, H.; Fu, K. BFSIFT: A novel method to find feature matches for SAR image registration. IEEE Geosci. Remote Sens. Lett. 2012, 9, 649–653. [Google Scholar] [CrossRef]
- Wang, F.; You, H.; Fu, X. Adapted anisotropic Gaussian sift matching strategy for SAR registration. IEEE Geosci. Remote Sens. Lett. 2015, 12, 160–164. [Google Scholar] [CrossRef]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-like algorithm for SAR images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Zhang, J.; Lu, L.; Huang, G.; Zhao, Z. A uniform SIFT-like algorithm for SAR image registration. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1426–1430. [Google Scholar] [CrossRef]
- Yan, K.; Sukthankar, R. PCA-SIFT: A more distinctive representation for local image descriptors. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004, CVPR 2004, Washington, DC, USA, 27 June–2 July 2004; Volume 2II–506. [Google Scholar]
- Jean-Michel, M.; Yu, G. ASIFT: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar]
- Qiaoliang, L.; Wang, G.; Liu, J.; Chen, S. Robust Scale-Invariant Feature Matching for Remote Sensing Image Registration. IEEE Geosci. Remote Sens. Lett. 2009, 6, 287–291. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform robust scaleinvariant feature matching for optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. SURF: Speeded up robust features. Lect. Notes Comput. Sci. 2006, 3951, 404–417. [Google Scholar]
- Moreno, P.; Bernardino, A.; Santos-Victor, J. Improving the SIFT descriptor with smooth derivative fifilters. Pattern Recognit. Lett. 2009, 30, 18–26. [Google Scholar] [CrossRef] [Green Version]
- Suri, S.; Schwind, P.; Uhl, J.; Reinartz, P. Modifications in the sift operator for effective SAR image matching. Int. J. Image Data Fusion 2010, 1, 243–256. [Google Scholar] [CrossRef] [Green Version]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef] [Green Version]
- Chureesampant, K.; Susaki, J. Automatic GCP Extraction of Fully Polarimetric SAR Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 137–148. [Google Scholar] [CrossRef]
- Ma, W.; Wu, Y.; Zheng, Y.; Wen, Z.; Liu, L. Remote sensing image registration based on multifeature and region division. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1680–1684. [Google Scholar] [CrossRef]
- Paul, S.; Pati, U.C. SAR image registration using an improved SAR-SIFT algorithm and Delaunay-triangulation-based local matching. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 2958–2966. [Google Scholar] [CrossRef]
- Liu, F.; Bi, F.; Chen, L.; Wei, H.; Tie, W. An optimization algorithm based on Bi-SIFT for SAR image registration. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Yu, Q.; Pang, B.; Wu, P.; Zhang, Y. Automatic coarse-to-precise subpixel multiband SAR images co-registration based affine SIFT and radial base function (RBF). In Proceedings of the 2015 IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 1–4 September 2015; pp. 684–687. [Google Scholar]
- Zhou, D.; Zeng, L.; Liang, J.; Zhang, K. Improved method for SAR image registration based on scale invariant feature transform. IET Radar Sonar Navig. 2016, 11, 579–585. [Google Scholar] [CrossRef]
- Divya, S.; Paul, S.; Pati, U.C. Structure tensor-based SIFT algorithm for SAR image registration. ET Image Process. 2020, 14, 929–938. [Google Scholar]
- Zhu, H.; Ma, W.; Hou, B.; Jiao, L. SAR image registration based on multifeature detection and arborescence network matching. IEEE Geosci. Remote Sens. Lett. 2016, 13, 706–710. [Google Scholar] [CrossRef]
- Fan, J.; Wu, Y.; Wang, F.; Zhang, Q.; Liao, G.; Li, M. SAR image registration using phase congruency and nonlinear diffusion-based SIFT. IEEE Geosci. Remote Sens. Lett. 2015, 12, 562–566. [Google Scholar]
- Kovesi, P. Image features from phase congruency. Videre J. Comput. Vis. Res. 1999, 1, 1–26. [Google Scholar]
- Fan, J.; Wu, Y.; Li, M.; Liang, W.; Zhang, Q. SAR image registration using multiscale image patch features with sparse representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1483–1493. [Google Scholar] [CrossRef]
- Paul, S.; Pati, U.C. SAR image registration using an improved anisotropic Gaussian-sift algorithm. In Proceedings of the 2017 14th IEEE India Council International Conference (INDICON), Roorkee, India, 15–17 December 2017; pp. 1–5. [Google Scholar]
- Bookstein, F.L. Principal warps: Thin-plate splines and the decomposition of deformations. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 567–585. [Google Scholar] [CrossRef] [Green Version]
- Aurenhammer, F. Voronoi diagrams–a survey of a fundamental geometric data structure. ACM Comput. Surv. (CSUR) 1991, 23, 345–405. [Google Scholar] [CrossRef]
- Zongying, Z. Study of SAR Image Registration Method; Shandong University of Science and Technology: Qingdao, China, 2010. [Google Scholar]
- Wang, D. A Study on Registration of Multi-Modal and Huge-Size Images. Ph.D. Thesis, Chines Academy of Sciences, Beijing, China, 2002. [Google Scholar]
- Bentoutou, Y.; Taleb, N.; Kpalma, K.; Ronsin, J. An Automatic Image Registration for Applications in Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2127–2137. [Google Scholar] [CrossRef]
- Casu, F.; Manconi, A.; Pepe, A.; Lanari, R. Deformation Time-Series Generation in Areas Characterized by Large Displacement Dynamics: The SAR Amplitude Pixel-Offset SBAS Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2752–2763. [Google Scholar] [CrossRef]
- Suri, S.; Reinartz, P. Mutual-Information-Based Registration of TerraSAR-X and Ikonos Imagery in Urban Areas. IEEE Trans. Geosci. Remote Sens. 2010, 48, 939–949. [Google Scholar] [CrossRef]



















| Algorithm | One Step | Two Steps | ||||
|---|---|---|---|---|---|---|
| Matching Points | Correct Points | Correct Rate (%) | Matching Points | Correct Points | Correct Rate (%) | |
| SIFT | 21 | 9 | 42.9 | 437 | 388 | 88.8 |
| SIFT-OCT | 26 | 22 | 84.6 | 457 | 432 | 94.5 |
| SAR-SIFT | 192 | 159 | 82.8 | 4013 | 3809 | 94.9 |
| PCA-SIFT | 51 | 35 | 68.6 | 989 | 891 | 90.1 |
| BF-SIFT | 137 | 110 | 80.3 | 2815 | 2640 | 93.8 |
| AM | IM (10−5) | MCS (10−1) | MI | ||||||
|---|---|---|---|---|---|---|---|---|---|
| G | L | G | L | G | L | G | L | ||
| Max | SIFT | 53.9 | 75.4 | 79.5 | 111.7 | 8.1 | 9.1 | 4.5 | 5.3 |
| SIFT-OCT | 65.0 | 66.1 | 33.7 | 116.1 | 8.9 | 9.0 | 4.6 | 5.3 | |
| Min | SIFT | 1.3 | 0.8 | 0.3 | 0.3 | 2.0 | 0.5 | 0.5 | 0.2 |
| SIFT-OCT | 1.5 | 0.8 | 0.3 | 0.1 | 2.1 | 0.4 | 0.5 | 0.2 | |
| Mean | SIFT | 10.9 | 12.0 | 10.1 | 7.0 | 4.4 | 4.5 | 2.9 | 3.2 |
| SIFT-OCT | 10.4 | 11.0 | 10.0 | 7.4 | 4.9 | 4.4 | 2.7 | 3.1 | |
| Method | Matching Points | Correct Points | Correct Rate (%) |
|---|---|---|---|
| SIFT G | 21 | 15 | 71.4 |
| SIFT L | 437 | 338 | 72.8 |
| SIFT L (triangle network) | 437 | 372 | 85.1 |
| SIFT L (TPS) | 437 | 395 | 90.4 |
| SIFT L (proposed) | 437 | 407 | 93.1 |
| Region | Method | Matching Points | Correct Points | Correct Rate (%) |
|---|---|---|---|---|
| Region 1 | Triangle network | 23 | 19 | 82.6 |
| TPS | 23 | 20 | 87.0 | |
| Proposed | 23 | 22 | 95.7 | |
| Region 2 | triangle network | 27 | 23 | 85.2 |
| TPS | 27 | 24 | 88.9 | |
| proposed | 27 | 25 | 92.6 |
| Method | First Set of SAR Images | Second Set of SAR Images | ||
|---|---|---|---|---|
| Matching Points | RMSE | Matching Points | RMSE | |
| BFSIFT | 437 | 1.28 | 27 | 1.19 |
| SAR-SIFT | 573 | 1.13 | 34 | 0.93 |
| Proposed | 947 | 0.65 | 97 | 0.47 |
| SIFT | SIFT-OCT | SAR-SIFT | Proposed | |||
|---|---|---|---|---|---|---|
| First set of data | CPs | Master image | 214 | 267 | 349 | 503 |
| Slave image | 165 | 196 | 247 | 315 | ||
| Matching pairs | 81 | 20 | 40 | 32 | ||
| Correct matching pairs | * | 6 | 9 | 11 | ||
| Match time/s | 1.3425 | 1.683 | 1.945 | 2.094 | ||
| CMR | * | 0.300 | 0.225 | 0.344 | ||
| Second set of data | CPs | Master image | 1053 | 905 | 1204 | 1865 |
| Slave image | 907 | 490 | 661 | 1002 | ||
| Matching pairs | 809 | 253 | 401 | 318 | ||
| Correct matching pairs | * | 134 | 296 | 248 | ||
| Match time/s | 6.6936 | 5.802 | 7.099 | 8.2734 | ||
| CMR | * | 0.530 | 0.738 | 0.780 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Deng, Y. Two-Step Matching Approach to Obtain More Control Points for SIFT-like Very-High-Resolution SAR Image Registration. Sensors 2023, 23, 3739. https://doi.org/10.3390/s23073739
Deng Y, Deng Y. Two-Step Matching Approach to Obtain More Control Points for SIFT-like Very-High-Resolution SAR Image Registration. Sensors. 2023; 23(7):3739. https://doi.org/10.3390/s23073739
Chicago/Turabian StyleDeng, Yang, and Yunkai Deng. 2023. "Two-Step Matching Approach to Obtain More Control Points for SIFT-like Very-High-Resolution SAR Image Registration" Sensors 23, no. 7: 3739. https://doi.org/10.3390/s23073739
APA StyleDeng, Y., & Deng, Y. (2023). Two-Step Matching Approach to Obtain More Control Points for SIFT-like Very-High-Resolution SAR Image Registration. Sensors, 23(7), 3739. https://doi.org/10.3390/s23073739






