Comparison of Performance between Single- and Multiparameter Luminescence Thermometry Methods Based on the Mn5+ Near-Infrared Emission
Abstract
:1. Introduction
2. Materials and Methods
3. Results
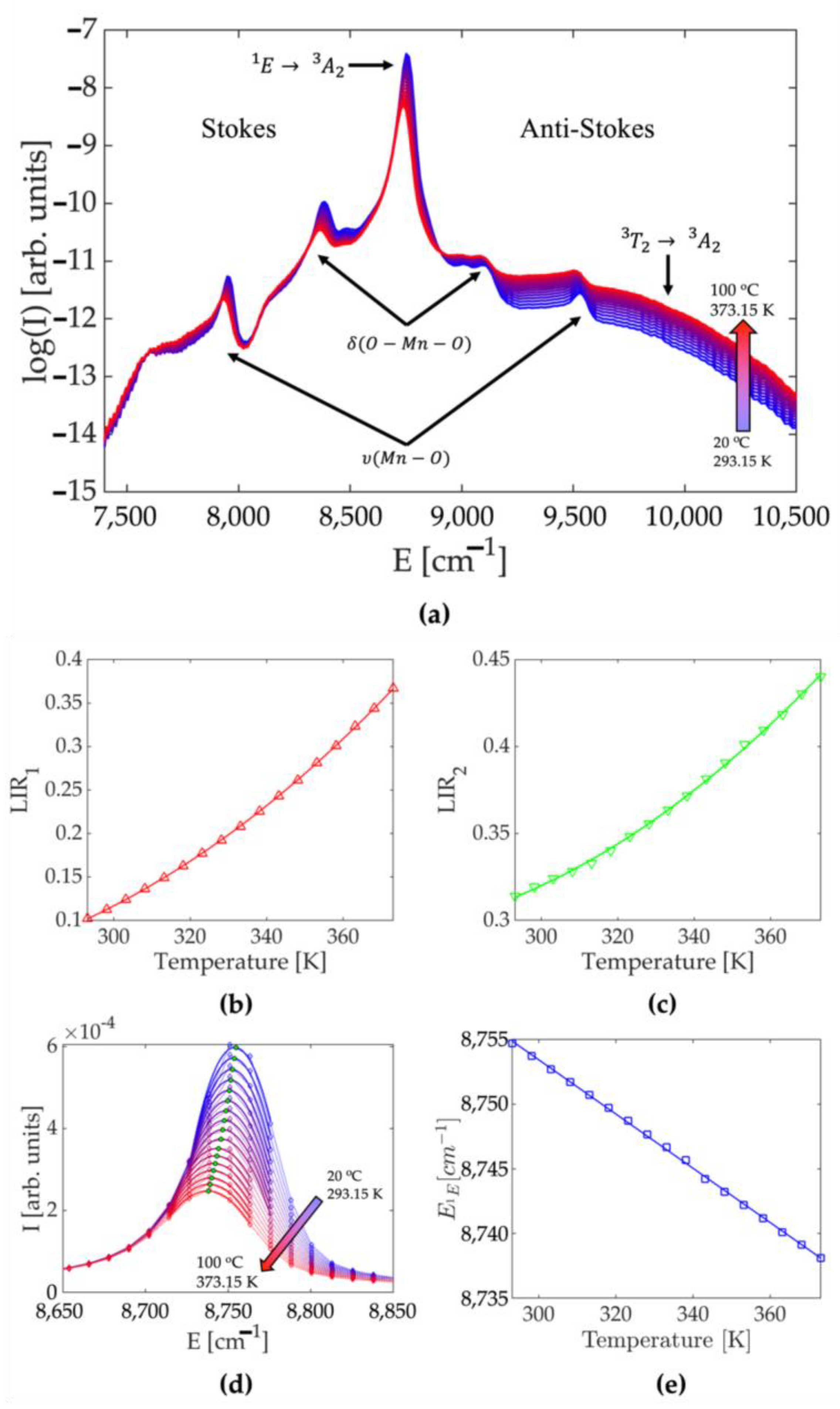
3.1. Photoluminescence and Single-Parameter Thermometry
3.2. Multiparametric Luminescence Thermometry
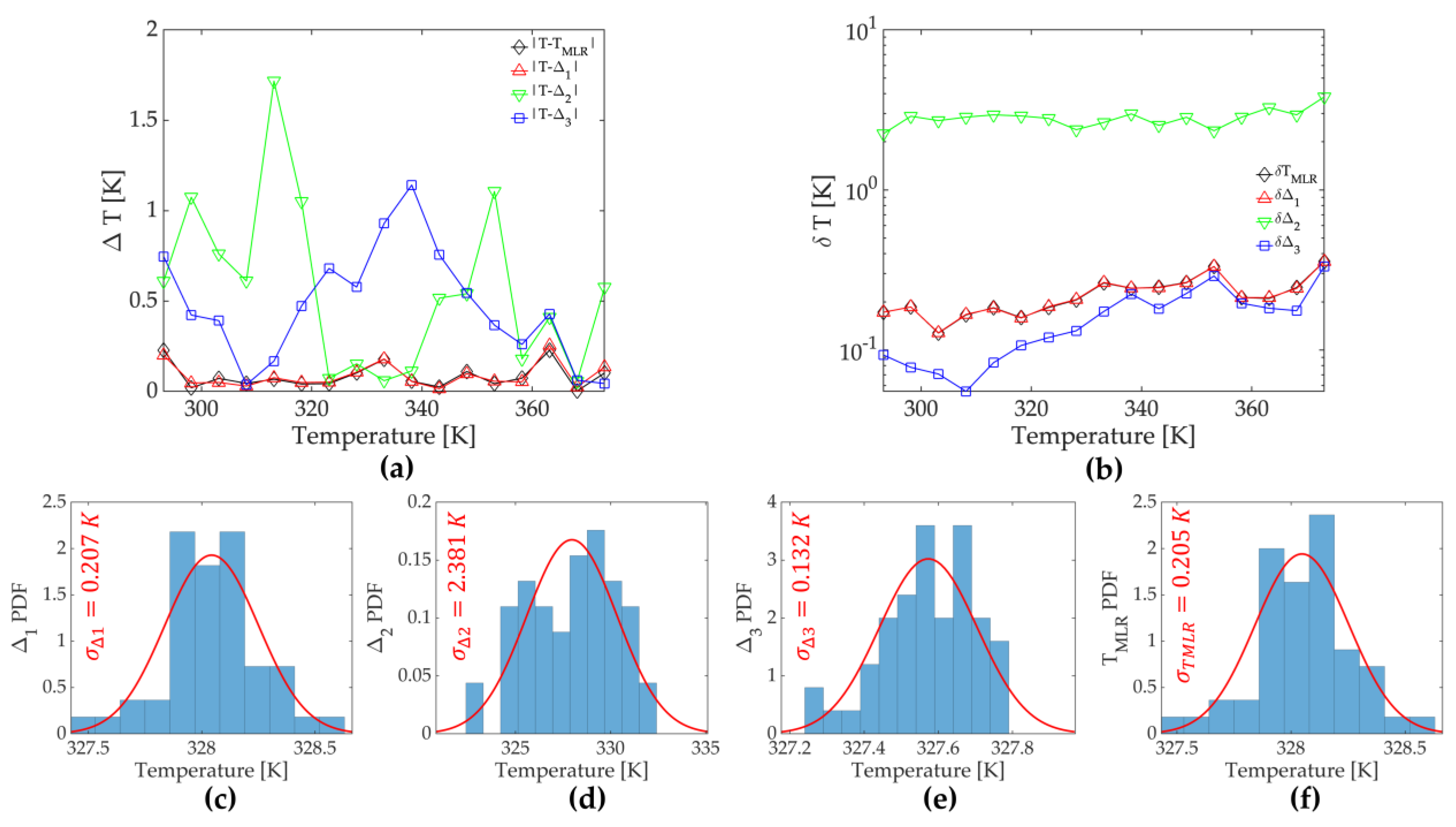
3.3. Performance Comparison of Multiparametric Luminescence Thermometry with Single-Parameter Thermometry
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Wolfbeis, O.S.; Meier, R.J. Luminescent Probes and Sensors for Temperature. Chem. Soc. Rev. 2013, 42, 7834–7869. [Google Scholar] [CrossRef]
- Dramićanin, M. Schemes for Temperature Read-Out from Luminescence. In Luminescence Thermometry; Elsevier: Amsterdam, The Netherlands, 2018; pp. 63–83. [Google Scholar]
- Jaque, D.; Vetrone, F. Luminescence Nanothermometry. Nanoscale 2012, 4, 4301–4326. [Google Scholar] [CrossRef]
- Marciniak, L.; Kniec, K.; Elżbieciak-Piecka, K.; Trejgis, K.; Stefanska, J.; Dramićanin, M. Luminescence Thermometry with Transition Metal Ions. A Review. Coord. Chem. Rev. 2022, 469, 214671. [Google Scholar] [CrossRef]
- Khalid, A.H.; Kontis, K. Thermographic Phosphors for High Temperature Measurements: Principles, Current State of the Art and Recent Applications. Sensors 2008, 8, 5673–5744. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Veltcheva, R.I.; Rusby, R.L.; Peters, D.M.; Watkins, R.E.J. Experiences in Calibrating Industrial Platinum Resistance Sensors Between −196 °C and 80 °C. Int. J. Thermophys. 2018, 39, 65. [Google Scholar] [CrossRef]
- Fernicola, V.C.; Iacomini, L. Approximating the ITS-90 Temperature Scale with Industrial Platinum Resistance Thermometers. Int. J. Thermophys. 2008, 29, 1817–1827. [Google Scholar] [CrossRef]
- Liu, C.; Tang, C.; Mu, H.; Huang, Z. A data fusion approach with high spatiotemporal resolution for wall temperature measurement upon jet impingement. Int. J. Heat Mass Transf. 2022, 183, 122084. [Google Scholar] [CrossRef]
- Zhang, X.; Choi, H.; Datta, A.; Li, X. Design, fabrication and characterization of metal embedded thin film thermocouples with various film thicknesses and junction sizes. J. Micromech. Microeng. 2006, 16, 900–905. [Google Scholar] [CrossRef]
- Liu, L.; Zhong, K.; Munro, T.; Alvarado, S.; Côte, R.; Creten, S.; Fron, E.; Ban, H.; Van der Auweraer, M.; Roozen, N.B.; et al. Wideband fluorescence-based thermometry by neural network recognition: Photothermal application with 10 ns time resolution. J. Appl. Phys. 2015, 118, 184906. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Qin, F.; Zhou, Y.; Zheng, Y.; Miao, J.; Zhang, Z. Three-energy-level-cascaded strategy for a more sensitive luminescence ratiometric thermometry. Sens. Actuators A Phys. 2020, 304, 111864. [Google Scholar] [CrossRef]
- Ćirić, A.; Periša, J.; Zeković, I.; Antić, Ž.; Dramićanin, M.D. Multilevel-cascade intensity ratio temperature read-out of Dy3+ luminescence thermometers. J. Lumin. 2022, 245, 118795. [Google Scholar] [CrossRef]
- Tian, X.; Wei, X.; Chen, Y.; Duan, C.; Yin, M. Temperature sensor based on ladder-level assisted thermal coupling and thermal-enhanced luminescence in NaYF4:Nd3+. Opt. Express 2014, 22, 30333. [Google Scholar] [CrossRef]
- Ćirić, A.; Aleksić, J.; Barudžija, T.; Antić, Ž.; Đorđević, V.; Medić, M.; Periša, J.; Zeković, I.; Mitrić, M.; Dramićanin, M.D. Comparison of three ratiometric temperature readings from the Er3+ upconversion emission. Nanomaterials 2020, 10, 627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, D.; Li, H.; Zhang, D.; Zhang, Q.; Meijerink, A.; Suta, M. One ion to catch them all: Targeted high-precision Boltzmann thermometry over a wide temperature range with Gd3+. Light Sci. Appl. 2021, 10, 236. [Google Scholar] [CrossRef] [PubMed]
- Souza, A.S.; Nunes, L.A.O.; Silva, I.G.N.; Oliveira, F.A.M.; da Luz, L.L.; Brito, H.F.; Felinto, M.C.F.C.; Ferreira, R.A.S.; Júnior, S.A.; Carlos, L.D.; et al. Highly-sensitive Eu3+ ratiometric thermometers based on excited state absorption with predictable calibration. Nanoscale 2016, 8, 5327–5333. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Zhou, Q.; Zhu, X.; Wu, Z.; Feng, W.; Li, L. Ratiometric upconversion nanothermometry with dual emission at the same wavelength decoded via a time-resolved technique. Nat. Commun. 2020, 11, 4. [Google Scholar] [CrossRef] [Green Version]
- Ćirić, A.; Marciniak, Ł.; Dramićanin, M.D. Luminescence intensity ratio squared—A new luminescence thermometry method for enhanced sensitivity. J. Appl. Phys. 2022, 131, 114501. [Google Scholar] [CrossRef]
- Mykhaylyk, V.; Kraus, H.; Zhydachevskyy, Y.; Tsiumra, V.; Luchechko, A.; Wagner, A.; Suchocki, A. Multimodal Non-Contact Luminescence Thermometry with Cr-Doped Oxides. Sensors 2020, 20, 5259. [Google Scholar] [CrossRef]
- Li, H.; Heydari, E.; Li, Y.; Xu, H.; Xu, S.; Chen, L.; Bai, G. Multi-Mode Lanthanide-Doped Ratiometric Luminescent Nanothermometer for Near-Infrared Imaging within Biological Windows. Nanomaterials 2023, 13, 219. [Google Scholar] [CrossRef]
- Savchuk, O.; Carvajal Marti, J.J.; Cascales, C.; Haro-Gonzalez, P.; Sanz-Rodríguez, F.; Aguilo, M.; Diaz, F. Bifunctional Tm3+,Yb3+:GdVO4@SiO2 Core-Shell Nanoparticles in HeLa Cells: Upconversion Luminescence Nanothermometry in the First Biological Window and Biolabelling in the Visible. Nanomaterials 2020, 10, 993. [Google Scholar] [CrossRef]
- Wang, J.; Lu, J.; Wu, Y.; Song, M. Luminescence of Mn4+ in a Zero-Dimensional Organic–Inorganic Hybrid Phosphor [N(CH3)4]2ZrF6 for Dual-Mode Temperature Sensing. Materials 2022, 15, 6543. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Y.; Chen, J.Q.; Li, L.J.; Zhang, W.N.; Chen, L.P.; Guo, H. A Four-Mode High-Sensitive Optical Thermometer Based on Ca3LiZnV3O12:Sm3+ Phosphors. Mater. Today Chem. 2023, 29, 101409. [Google Scholar] [CrossRef]
- Shen, Y.; Santos, H.D.A.; Ximendes, E.C.; Lifante, J.; Sanz-Portilla, A.; Monge, L.; Fernández, N.; Chaves-Coira, I.; Jacinto, C.; Brites, C.D.S.; et al. Ag2S Nanoheaters with Multiparameter Sensing for Reliable Thermal Feedback during In Vivo Tumor Therapy. Adv. Funct. Mater. 2020, 30, 2002730. [Google Scholar] [CrossRef]
- Maturi, F.E.; Brites, C.D.S.; Ximendes, E.C.; Mills, C.; Olsen, B.; Jaque, D.; Ribeiro, S.J.L.; Carlos, L.D. Going Above and Beyond: A Tenfold Gain in the Performance of Luminescence Thermometers Joining Multiparametric Sensing and Multiple Regression. Laser Photonics Rev. 2021, 15, 2100301. [Google Scholar] [CrossRef]
- Aseev, V.A.; Borisevich, D.A.; Khodasevich, M.A.; Kuz’menko, N.K.; Fedorov, Y.K. Calibration of Temperature by Normalized Up-Conversion Fluorescence Spectra of Germanate Glasses and Glass Ceramics Doped with Erbium and Ytterbium Ions. Opt. Spectrosc. 2021, 129, 297–302. [Google Scholar] [CrossRef]
- Borisov, E.V.; Kalinichev, A.A.; Kolesnikov, I.E. ZnTe Crystal Multimode Cryogenic Thermometry Using Raman and Luminescence Spectroscopy. Materials 2023, 16, 1311. [Google Scholar] [CrossRef]
- Lewis, C.; Erikson, J.W.; Sanchez, D.A.; McClure, C.E.; Nordin, G.P.; Munro, T.R.; Colton, J.S. Use of Machine Learning with Temporal Photoluminescence Signals from CdTe Quantum Dots for Temperature Measurement in Microfluidic Devices. ACS Appl. Nano Mater. 2020, 3, 4045–4053. [Google Scholar] [CrossRef]
- Cui, J.; Xu, W.; Yao, M.; Zheng, L.; Hu, C.; Zhang, Z.; Sun, Z. Convolutional neural networks open up horizons for luminescence thermometry. J. Lumin. 2023, 256, 119637. [Google Scholar] [CrossRef]
- Ximendes, E.; Marin, R.; Carlos, L.D.; Jaque, D. Less is more: Dimensionality reduction as a general strategy for more precise luminescence thermometry. Light Sci. Appl. 2022, 11, 237. [Google Scholar] [CrossRef]
- Bednarkiewicz, A.; Drabik, J.; Trejgis, K.; Jaque, D.; Ximendes, E.; Marciniak, L. Luminescence Based Temperature Bio-Imaging: Status, Challenges, and Perspectives. Appl. Phys. Rev. 2021, 8, 011317. [Google Scholar] [CrossRef]
- Dramićanin, M.D.; Marciniak, Ł.; Kuzman, S.; Piotrowski, W.; Ristić, Z.; Periša, J.; Evans, I.; Mitrić, J.; Đorđević, V.; Romčević, N.; et al. Mn5+-activated Ca6Ba(PO4)4O near-infrared phosphor and its application in luminescence thermometry. Light Sci. Appl. 2022, 11, 279–292. [Google Scholar] [CrossRef] [PubMed]
- Dramićanin, M.D. Trends in luminescence thermometry. J. Appl. Phys. 2020, 128, 40902. [Google Scholar] [CrossRef]
- Geitenbeek, R.G.; de Wijn, H.W.; Meijerink, A. Non-Boltzmann Luminescence in NaYF4:Eu3+: Implications for Luminescence Thermometry. Phys. Rev. Appl. 2018, 10, 64006. [Google Scholar] [CrossRef] [Green Version]
- Wade, S.A.; Collins, S.F.; Baxter, G.W. Fluorescence intensity ratio technique for optical fiber point temperature sensing. J. Appl. Phys. 2003, 94, 4743–4756. [Google Scholar] [CrossRef]
- Ćirić, A.; Ristić, Z.; Antić, Ž; Dramićanin, M.D. An approximate deconvolution method for the luminescence intensity ratio calculations from overlapping emissions. Phys. B Condens. Matter 2022, 624, 413454. [Google Scholar] [CrossRef]
- van Swieten, T.P.; Meijerink, A.; Rabouw, F.T. Impact of Noise and Background on Measurement Uncertainties in Luminescence Thermometry. ACS Photonics 2022, 9, 1366–1374. [Google Scholar] [CrossRef]

| Parameters from Fitting | B | ∆E [cm−1] | a [K−2] | b [K−1] | c | d [K−1cm−1] | h [cm−1] |
|---|---|---|---|---|---|---|---|
| 39.93 | 1216 | 8.667 × 10−6 | −4.174 × 10−3 | 7.921 × 10−1 | −2.098 × 10−1 | 8.816 × 103 |
| Method | LIR1 | LIR2 | E1E | MLR |
|---|---|---|---|---|
| ΔT [K] | 0.0868 | 0.5649 | 0.4720 | 0.0841 |
| δT [K] | 0.2213 | 2.8204 | 0.1601 | 0.2212 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrebdi, T.A.; Alodhayb, A.N.; Ristić, Z.; Dramićanin, M.D. Comparison of Performance between Single- and Multiparameter Luminescence Thermometry Methods Based on the Mn5+ Near-Infrared Emission. Sensors 2023, 23, 3839. https://doi.org/10.3390/s23083839
Alrebdi TA, Alodhayb AN, Ristić Z, Dramićanin MD. Comparison of Performance between Single- and Multiparameter Luminescence Thermometry Methods Based on the Mn5+ Near-Infrared Emission. Sensors. 2023; 23(8):3839. https://doi.org/10.3390/s23083839
Chicago/Turabian StyleAlrebdi, Tahani A., Abdullah N. Alodhayb, Zoran Ristić, and Miroslav D. Dramićanin. 2023. "Comparison of Performance between Single- and Multiparameter Luminescence Thermometry Methods Based on the Mn5+ Near-Infrared Emission" Sensors 23, no. 8: 3839. https://doi.org/10.3390/s23083839
APA StyleAlrebdi, T. A., Alodhayb, A. N., Ristić, Z., & Dramićanin, M. D. (2023). Comparison of Performance between Single- and Multiparameter Luminescence Thermometry Methods Based on the Mn5+ Near-Infrared Emission. Sensors, 23(8), 3839. https://doi.org/10.3390/s23083839







