Self-Calibration Sensor for Contactless Voltage Measurement Based on Dynamic Capacitance
Abstract
1. Introduction
2. Principle of Voltage Measurement
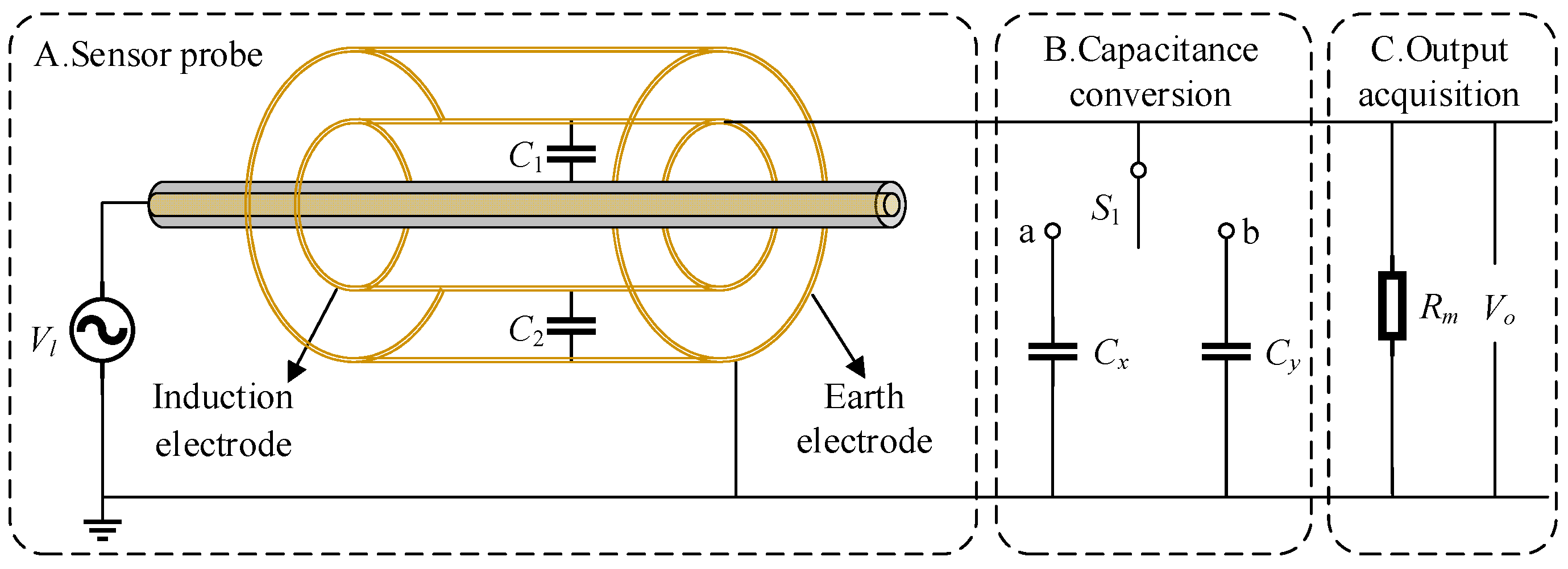
2.1. Noncontact Voltage Measurement Based on Electric Field Coupling
2.2. A Method Based on Dynamic Capacitance Self-Calibration
2.3. Error Analysis and Model Optimization
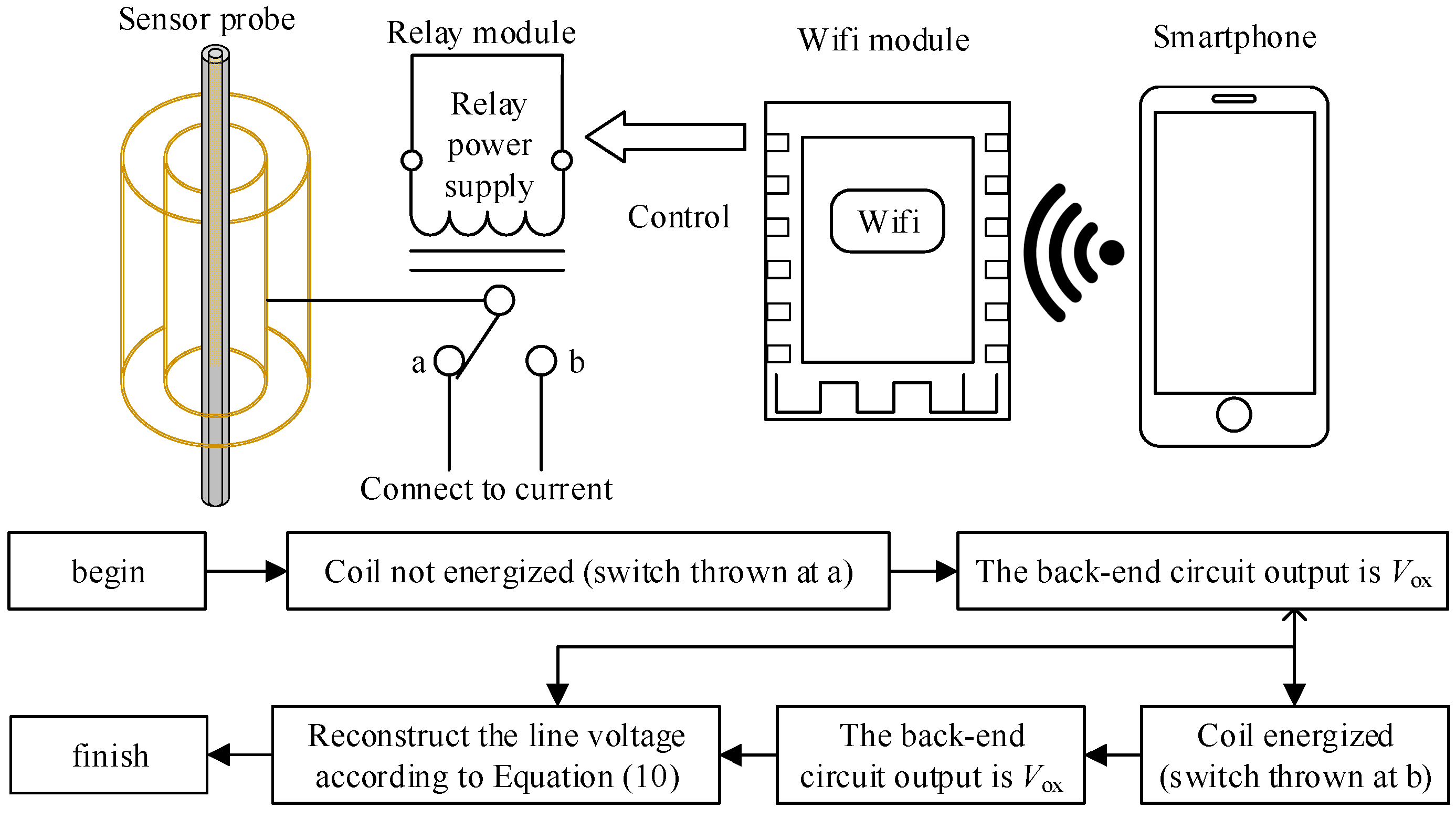
3. Design and Application of Self-Calibrating Voltage Sensor
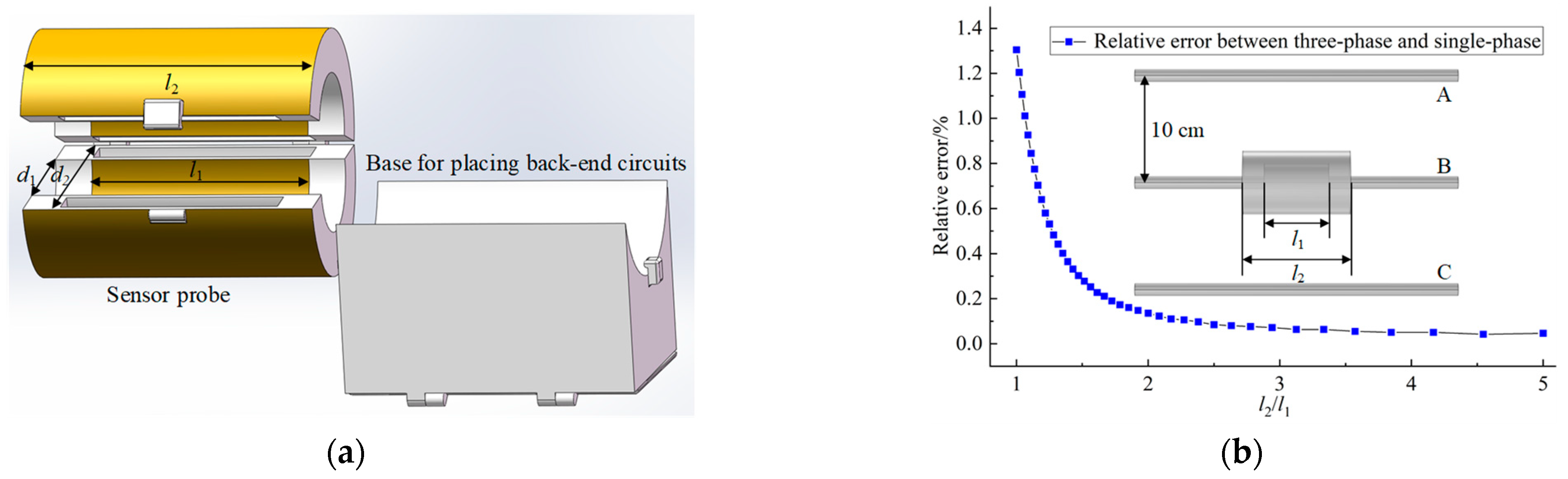
3.1. Design and Parameter Selection of Sensor Probe
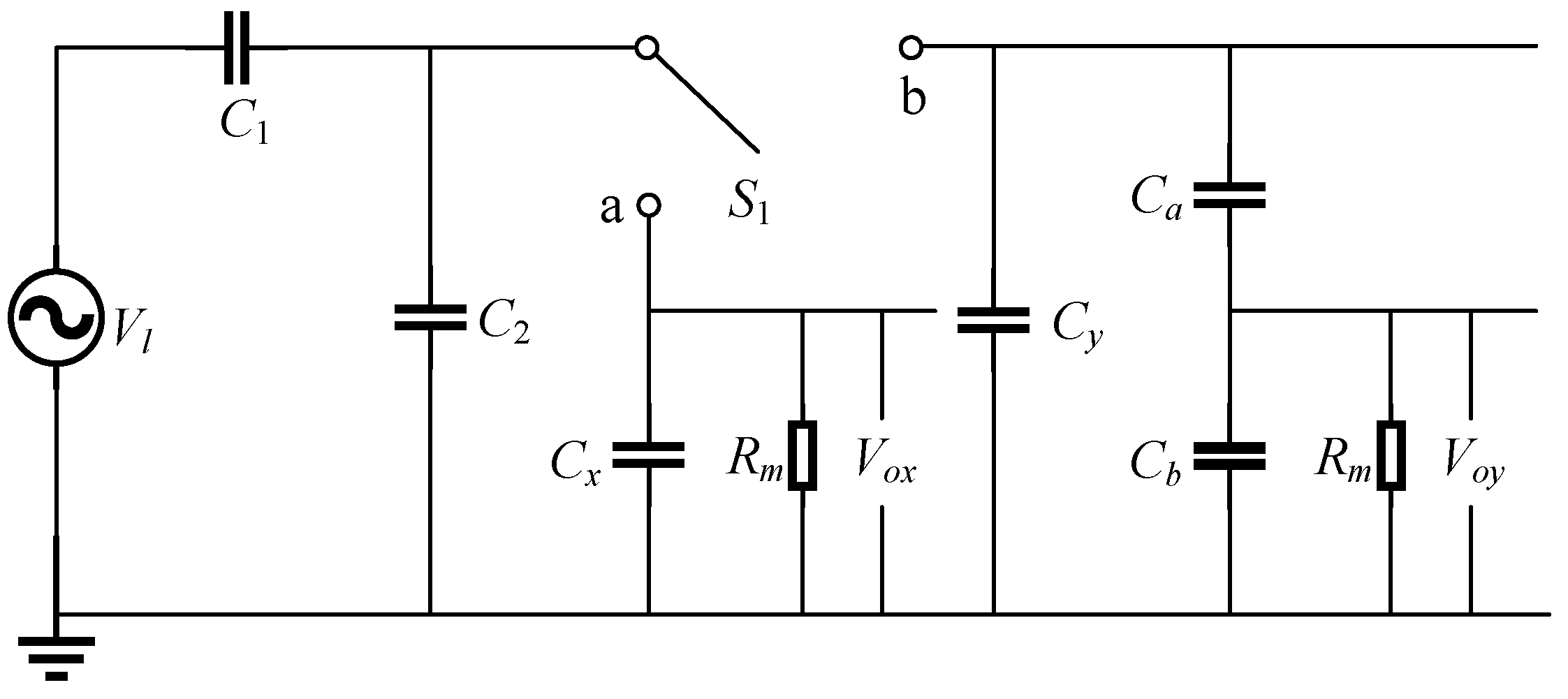
3.2. Circuit Topology Parameter Selection
3.3. Switch Control and Voltage Calibration Steps
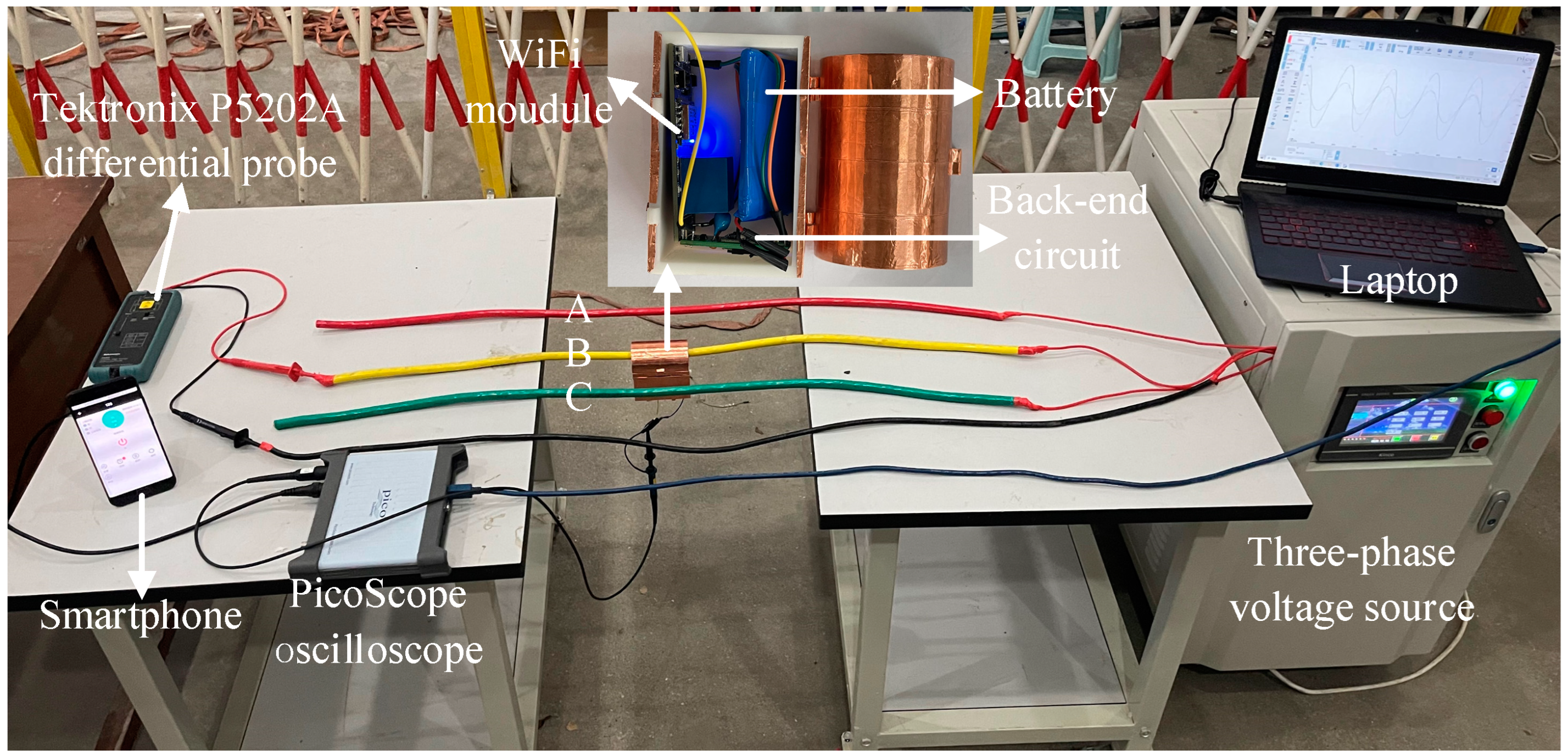
4. Experimental Testing and Result Analysis
4.1. Establishment of Experimental Platform
4.2. Amplitude and Phase Accuracy Test
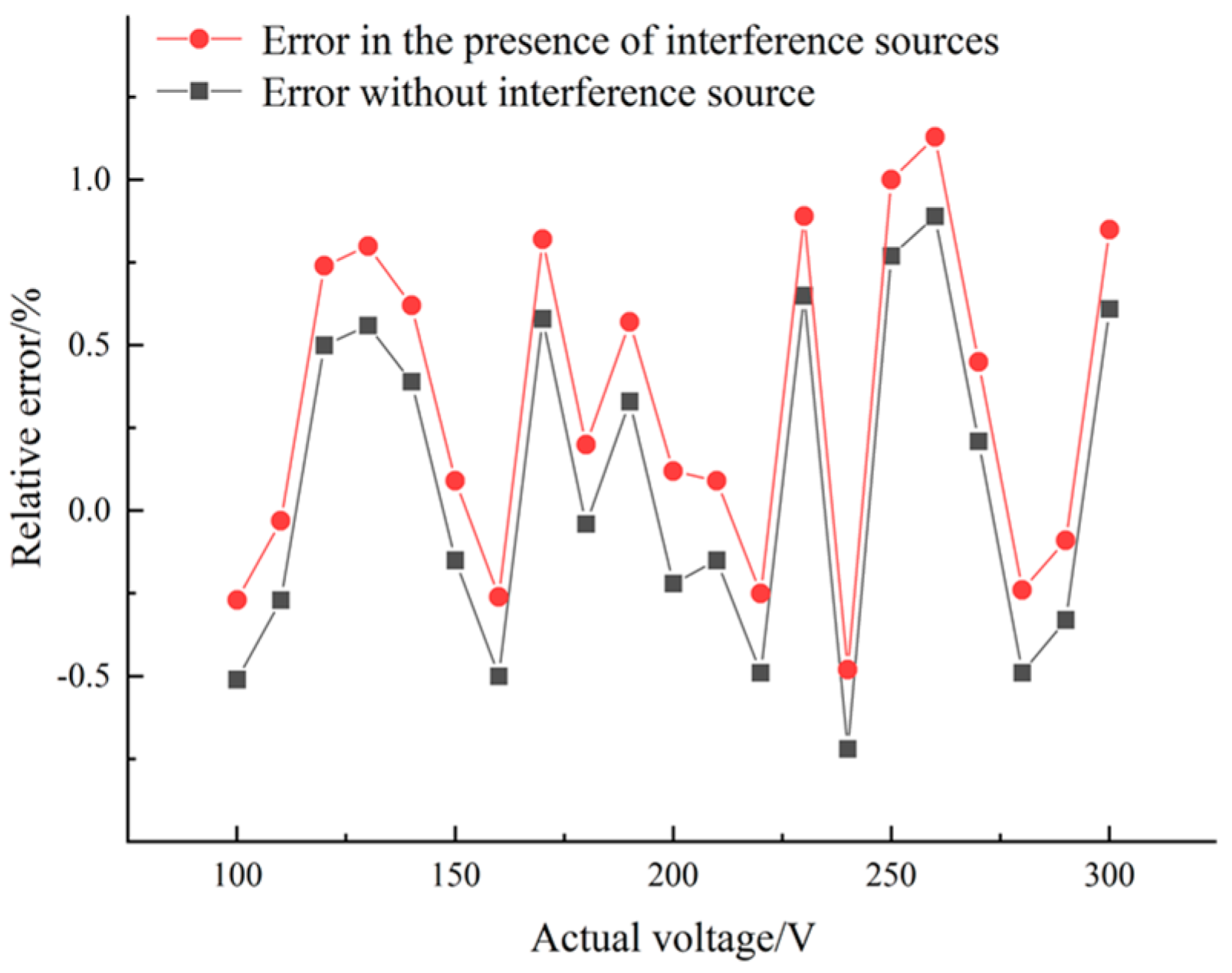
4.3. Anti-Interference Ability Test
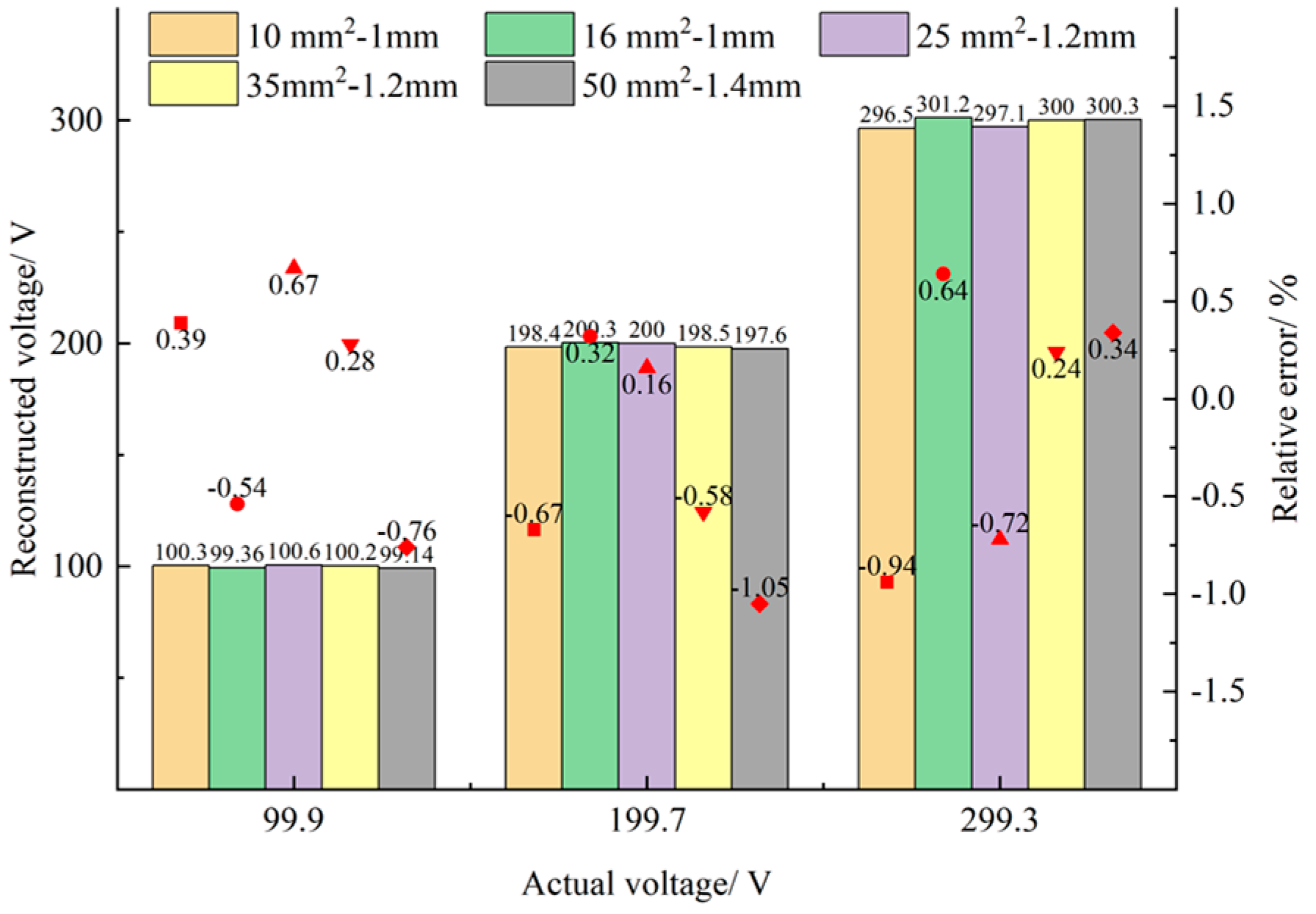
4.4. Conductor Adaptability Test
5. Conclusions
- (1)
- Aiming at the difficulty in determining the sensor gain in practical measurement of traditional capacitive coupled noncontact voltage sensors, a dynamic capacitive noncontact voltage measurement self-calibration method is proposed to achieve self-calibration of the sensor gain in practical measurement.
- (2)
- Theoretical research and transfer function analysis were conducted on the proposed method. Through error analysis and simulation research, the model and parameter optimization design of the dynamic capacitor conversion system were carried out. Based on this, a prototype of anti-interference sensor probe and remote dynamic capacitance control unit were developed.
- (3)
- The calibration accuracy test was conducted using a sensor prototype at a power frequency voltage of 100 Vrms to 300 Vrms. The results showed that the maximum amplitude error was 0.89%, and the phase error was 1.57%. Subsequently, an anti-interference capability test was conducted, and compared to the error of the reconstructed voltage without interference sources, the overall error offset with interference sources was 0.25%. Finally, adaptability tests were conducted on different types of circuits. The test results show that the maximum relative error is 1.01%, and the measurement line has a small impact on the calibration accuracy.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chu, S.Y.; Cui, X.; Zan, X. Transfer-power measurement using a non-contact method for fair and accurate metering of wireless power transfer in electric vehicles. IEEE Trans. Power Electron. 2022, 37, 1244–1271. [Google Scholar] [CrossRef]
- Li, C.; Qian, Z.; Shen, W.; Yao, S.; Shi, X.; Yu, X.; Bian, S. A condition based maintenance system for important auxiliary equipment of thermal power unit. J. Phys. Conf. Ser. 2021, 2076, 012114. [Google Scholar] [CrossRef]
- Kumar, R.; Saxena, A.; Kumar, R.; Marwaha, S.; Singh, J.; Singh, G.K. A comprehensive overview on modified versions of stockwell transform for power quality monitoring. IEEE Access 2022, 10, 1. [Google Scholar] [CrossRef]
- Tan, X.; Li, W.; Qian, G.; Ao, G.; Xu, X.; Wei, R.; Ke, Y.; Zhang, W. Design of a fluxgate weak current sensor with anti-low frequency interference ability. Energies 2022, 15, 8489. [Google Scholar] [CrossRef]
- Ranasingh, S.; Pradhan, T.; Raju, D.K.; Singh, A.R.; Piantini, A. An approach to wire-wound hall-effect based current sensor for offset reduction. IEEE Sens. J. 2021, 22, 2006–2015. [Google Scholar] [CrossRef]
- Orlando, M.; Estebsari, A.; Pons, E.; Pau, M.; Quer, S.; Poncino, M.; Bottaccioli, L.; Patti, E. A smart meter infrastructure for smart grid iot applications. IEEE Internet Things J. 2021, 9, 12529–12541. [Google Scholar] [CrossRef]
- Liu, X.; Kang, L.; Shang, Y.; Sun, L.; Li, Z.; Wu, Q.; Zhang, M.; Wang, H. In Research on fault diagnosis optimization of intelligent acquisition terminal. E3S Web Conf. 2019, 136, 01034. [Google Scholar] [CrossRef]
- Sun, W.; Wang, H.; Liu, Y. In Research on an invasive low frequency power consumption data acquisition method. J. Phys. Conf. Ser. 2022, 2078, 012059. [Google Scholar] [CrossRef]
- Portelli, A.; Nasuto, S. Design and development of non-contact bio-potential electrodes for pervasive health monitoring applications. Biosensors 2017, 7, 2. [Google Scholar] [CrossRef]
- Xiao, Z.; Xing, Y.; Yang, C.; Li, J.; Liu, C. Non-contact electrocardiograms acquisition method based on capacitive coupling. IEEE Instrum. Meas. Mag. 2022, 25, 53–61. [Google Scholar] [CrossRef]
- Wenxia, S.; Huangjing, Z.; Ming, Y.; Hui, W.; Jianwei, X.; Yuhang, H. Statistical analysis of the amplitude and waveform characteristics of intrusive lightning overvoltages measured from the 10 kv system of a substation. High Volt. Eng. 2021, 47, 214–222. [Google Scholar]
- Han, R.; Yang, Q.; Sima, W.; Zhang, Y.; Sun, S.; Liu, T.; Chen, S. Non-contact measurement of lightning and switching transient overvoltage based on capacitive coupling and pockels effects. Electr. Power Syst. Res. 2016, 139, 93–100. [Google Scholar] [CrossRef]
- Yan, X.; Wang, J.; Shen, Z.; Zhao, P.; Li, X.; Wang, H. A self-decoupling contactless overvoltage measurement method based on optimization of measuring point. IEEE Trans. Instrum. Meas. 2022, 71, 1002711. [Google Scholar] [CrossRef]
- Walczak, K.; Sikorski, W. Non-contact high voltage measurement in the online partial discharge monitoring system. Energies 2021, 14, 5777. [Google Scholar] [CrossRef]
- Zhang, X.; Pang, B.; Liu, Y.; Liu, S.; Xu, P.; Li, Y.; Liu, Y.; Qi, L.; Xie, Q. Review on detection and analysis of partial discharge along power cables. Energies 2021, 14, 7692. [Google Scholar] [CrossRef]
- Xiaolei, X.; Yadong, L.; Peng, S.; Gehao, S.; Xiuchen, J. Smart voltage sensor of distribution lines based on the capacitive voltage divider. Chin. J. Sci. Instrum. 2016, 37, 10. [Google Scholar]
- Yang, P.; Wen, X.; Chu, Z.; Ni, X.; Peng, C. Non-intrusive dc voltage measurement based on resonant electric field microsensors. J. Micromechanics Microengineering 2021, 31, 064001. [Google Scholar] [CrossRef]
- Lawrence, D.; Donnal, J.S.; Leeb, S.; He, Y. Non-contact measurement of line voltage. IEEE Sens. J. 2016, 16, 8990–8997. [Google Scholar] [CrossRef]
- Yeqian, C.; Guangmin, W.; Wenbin, Z.; Xiangyu, T.; Ke, W. Measurement of VFTO based on electric field sensor. Chin. J. Sens. Actuators 2016, 30, 385–390. [Google Scholar]
- Wang, L.; Zhang, W.; Tan, X.; Chen, W.; Liang, S.; Suo, C. Research and experiments on an external miniaturized vfto measurement system. Sensors 2019, 20, 244. [Google Scholar] [CrossRef]
- Haberman, M.A.; Spinelli, E.M. A noncontact voltage measurement system for power-line voltage waveforms. IEEE Trans. Instrum. Meas. 2019, 69, 2790–2797. [Google Scholar] [CrossRef]
- Shenil, P.; George, B. Nonintrusive ac voltage measurement unit utilizing the capacitive coupling to the power system ground. IEEE Trans. Instrum. Meas. 2020, 70, 3507708. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, Y.; Li, W.; Zeng, X.; Tang, J.; Wang, Y.; Deng, X. Research on transmission line voltage measurement method of d-dot sensor based on gaussian integral. Sensors 2018, 18, 2455. [Google Scholar] [CrossRef]
- Wang, J.; Yan, X.; Li, X.; Liao, J.; Tao, Y. Method and experimental study of transmission line voltage measurement based on a gauss-type integral algorithm. Trans. China Electrotech. Soc. 2021, 36, 9. [Google Scholar]
- Chen, S.; Wang, H.; Du, L.; Li, J. Research on a new type of overvoltages monitoring sensor and decoupling technology. IEEE Trans. Appl. Supercond. 2014, 24, 9501304. [Google Scholar]
- IEC 60227-4; Polyvinyl Chloride Insulated Cables with Rated Voltages up to and Including 450/750 v—Part 4: Sheathed Cables for Fixed Wiring. International Electrotechnical Commission: Geneva, Switzerland, 1997.
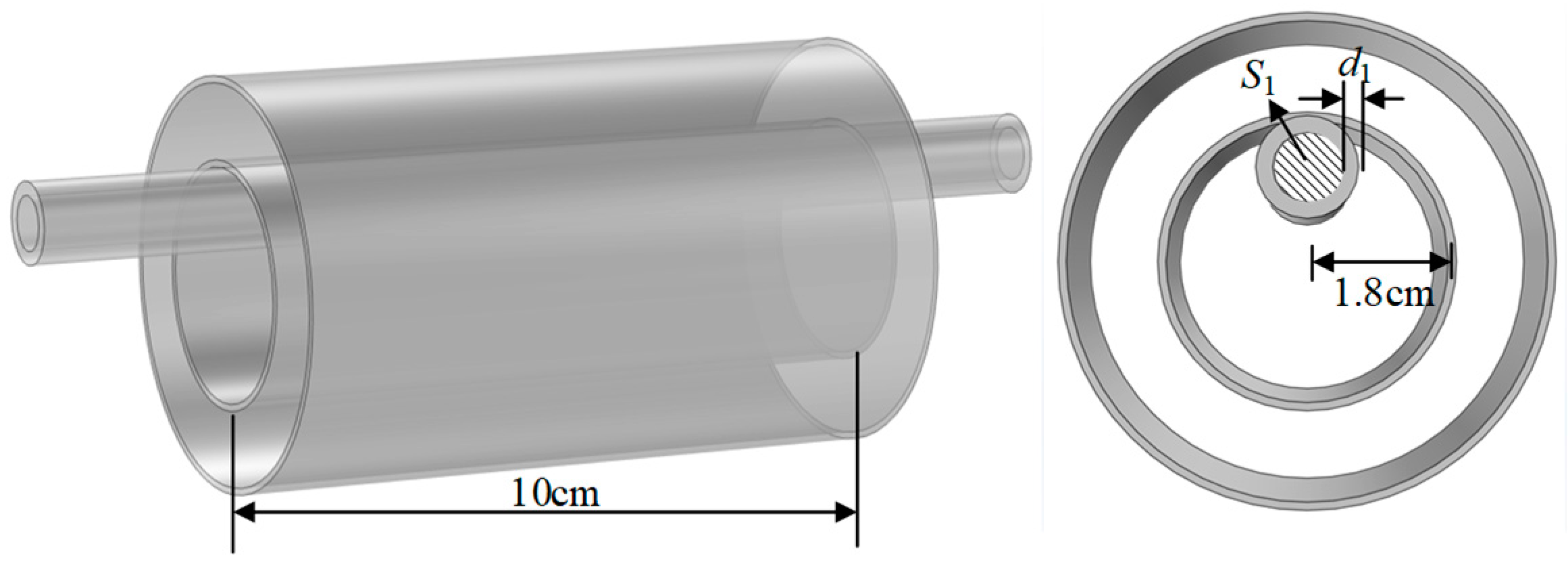


| S1/mm2 | d1/mm | C1/pF | Change Rate/% |
|---|---|---|---|
| 10 | 1 | 9.122 | / |
| 16 | 1 | 10.69 | 14.7 |
| 25 | 1.2 | 11.22 | 18.7 |
| 35 | 1.2 | 12.53 | 27.2 |
| 50 | 1.4 | 13.07 | 30.2 |
| 70 | 1.4 | 14.66 | 37.8 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| l1/cm | 4 | l2/cm | 8 |
| d1/cm | 3 | d2/cm | 5.4 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| /pF | 6.46 | /nF | 2.07 |
| /pF | 5.08 | /pF | 31.1 |
| /nF | 1.96 | /MΩ | 20 |
| Vox/mV | Voy/mV | Vr/V | Va/V | Vox/mV | Voy/mV | Vr/V | Va/V |
|---|---|---|---|---|---|---|---|
| 263.6 | 179.8 | 99.4 | 99.9 | 553.4 | 377.6 | 209.3 | 209.6 |
| 289.9 | 197.8 | 109.6 | 109.9 | 579.7 | 395.4 | 218.5 | 219.6 |
| 316.3 | 216 | 120.5 | 119.9 | 606.2 | 414 | 231.1 | 229.6 |
| 342.5 | 233.9 | 130.5 | 129.8 | 632.7 | 431.4 | 237.8 | 239.5 |
| 369.1 | 252 | 140.3 | 139.8 | 659 | 450.1 | 251.4 | 249.5 |
| 395.4 | 269.8 | 149.6 | 149.8 | 685.4 | 468.2 | 261.8 | 259.5 |
| 421.8 | 287.7 | 159 | 159.8 | 711.7 | 485.8 | 270.1 | 269.5 |
| 448.1 | 306 | 170.7 | 169.7 | 738.1 | 503.4 | 278 | 279.4 |
| 474.5 | 323.8 | 179.6 | 179.7 | 764.5 | 521.5 | 288.4 | 289.4 |
| 500.8 | 341.9 | 190.3 | 189.7 | 789.8 | 539.4 | 301.1 | 299.3 |
| 527.3 | 359.8 | 199.3 | 199.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suo, C.; Huang, R.; Zhou, G.; Zhang, W.; Wang, Y.; He, M. Self-Calibration Sensor for Contactless Voltage Measurement Based on Dynamic Capacitance. Sensors 2023, 23, 3851. https://doi.org/10.3390/s23083851
Suo C, Huang R, Zhou G, Zhang W, Wang Y, He M. Self-Calibration Sensor for Contactless Voltage Measurement Based on Dynamic Capacitance. Sensors. 2023; 23(8):3851. https://doi.org/10.3390/s23083851
Chicago/Turabian StyleSuo, Chunguang, Rujin Huang, Guoqiong Zhou, Wenbin Zhang, Yanyun Wang, and Mingxing He. 2023. "Self-Calibration Sensor for Contactless Voltage Measurement Based on Dynamic Capacitance" Sensors 23, no. 8: 3851. https://doi.org/10.3390/s23083851
APA StyleSuo, C., Huang, R., Zhou, G., Zhang, W., Wang, Y., & He, M. (2023). Self-Calibration Sensor for Contactless Voltage Measurement Based on Dynamic Capacitance. Sensors, 23(8), 3851. https://doi.org/10.3390/s23083851





