A Novel Fiber-Optic Ice Sensor to Identify Ice Types Based on Total Reflection
Abstract
1. Introduction
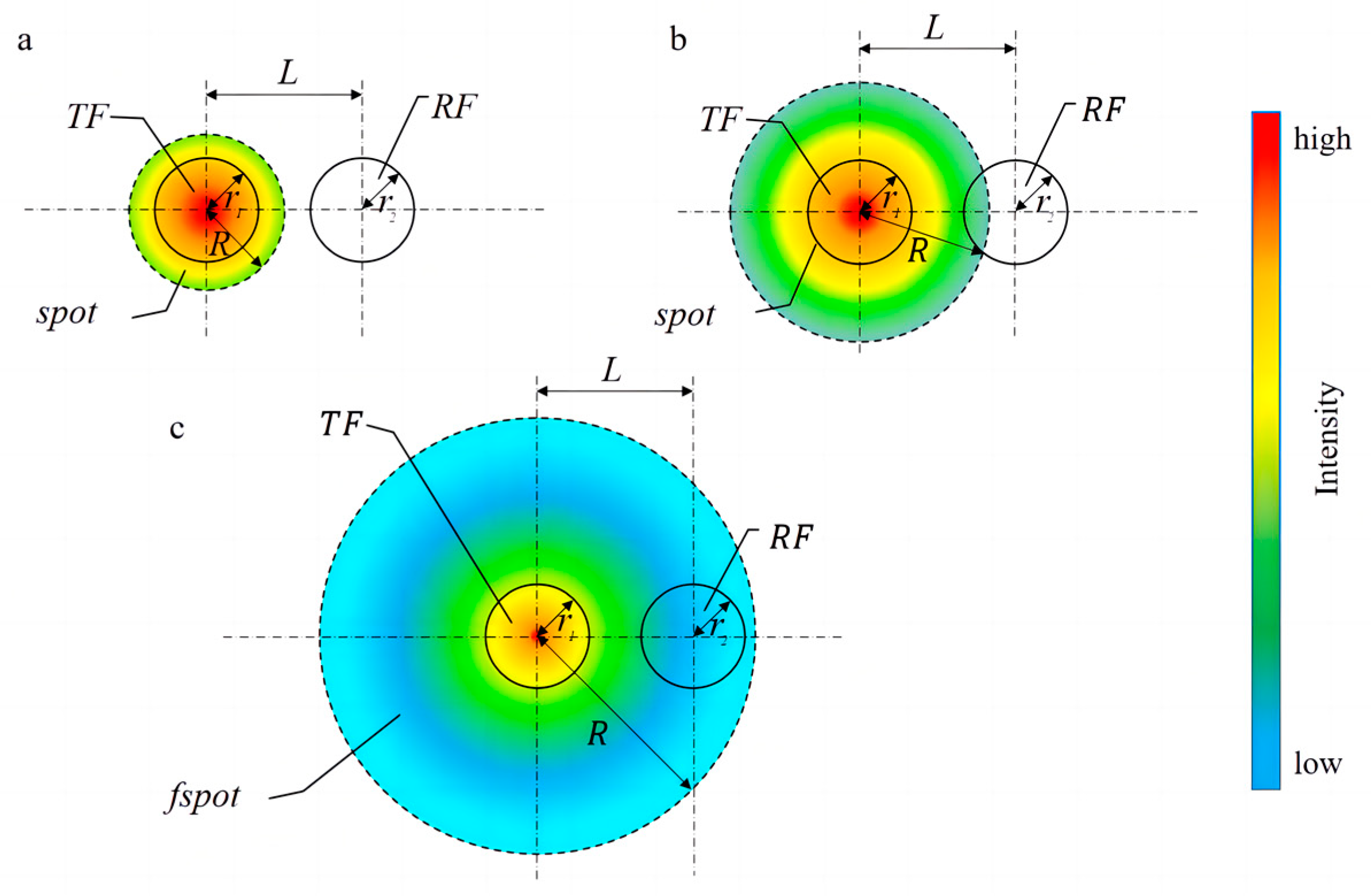
2. Mathematical Modeling of Fiber-Optic Ice Sensors
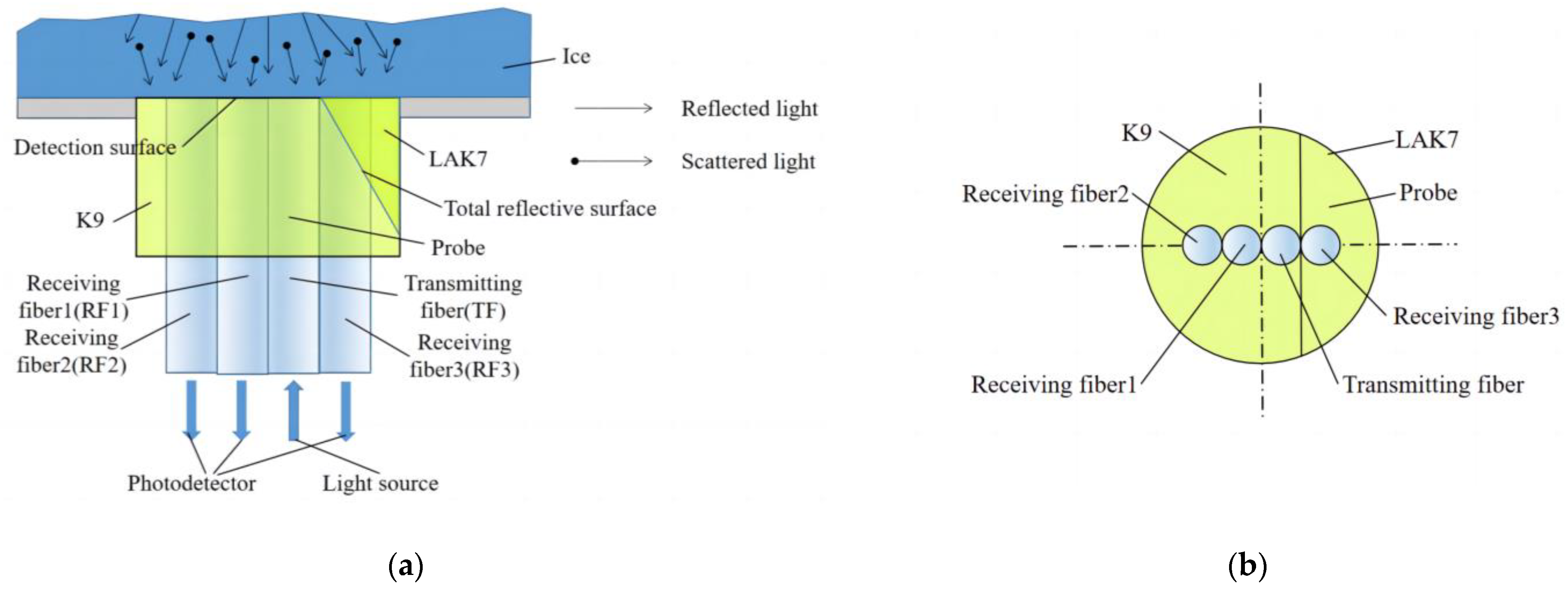
3. Design of Fiber-Optic Ice Sensor
3.1. Structure Design
3.2. Circuit Design
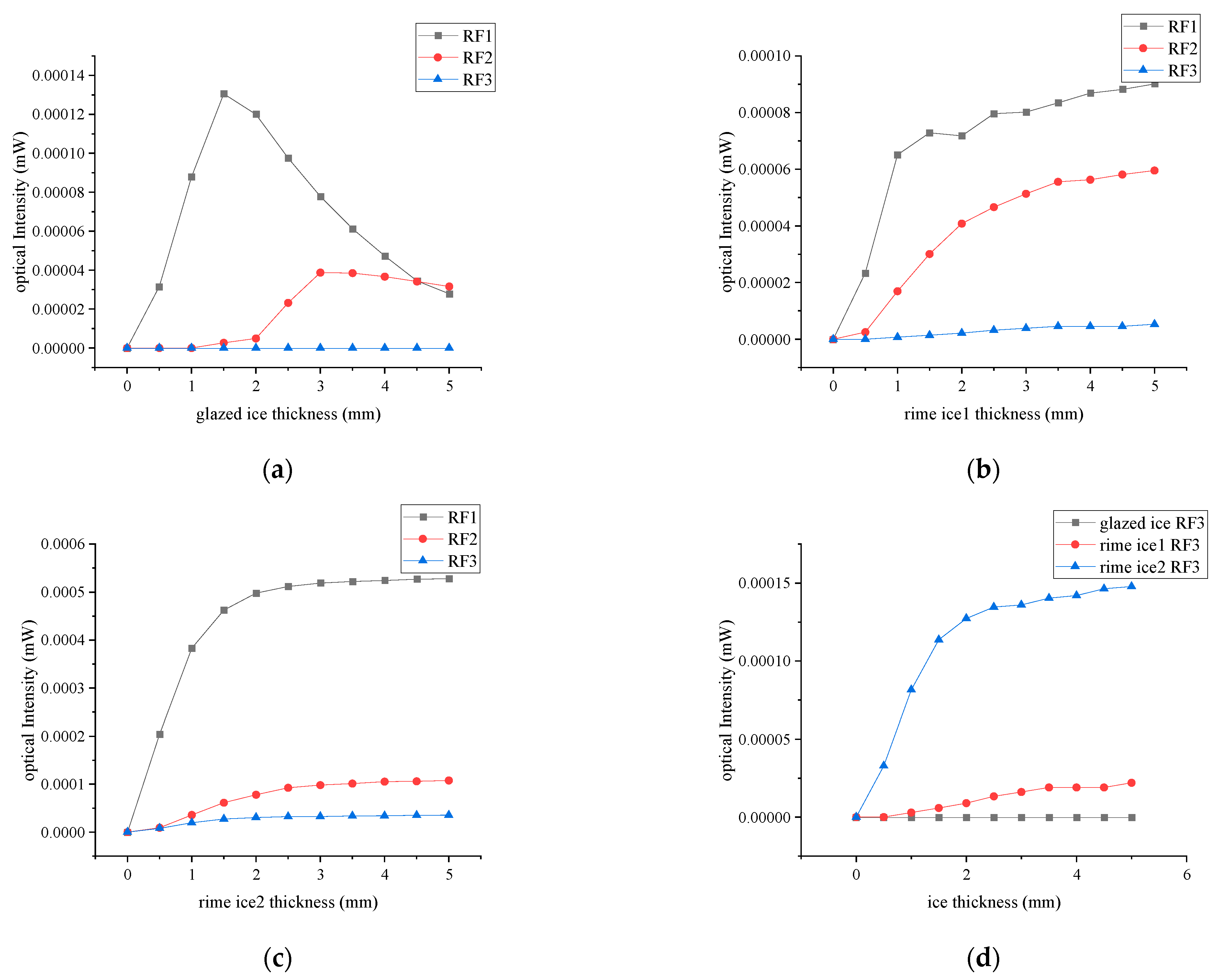
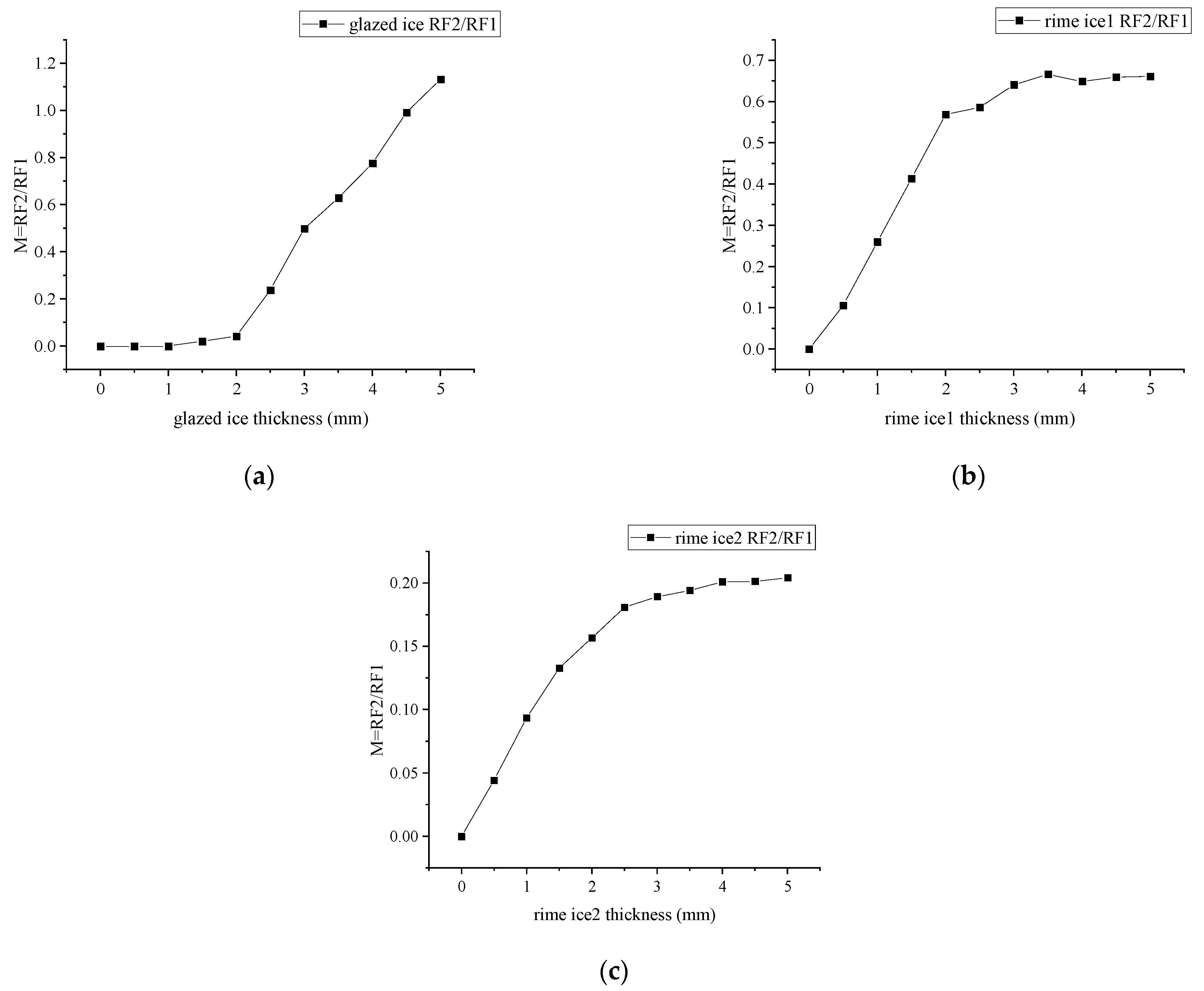
4. Simulation Results
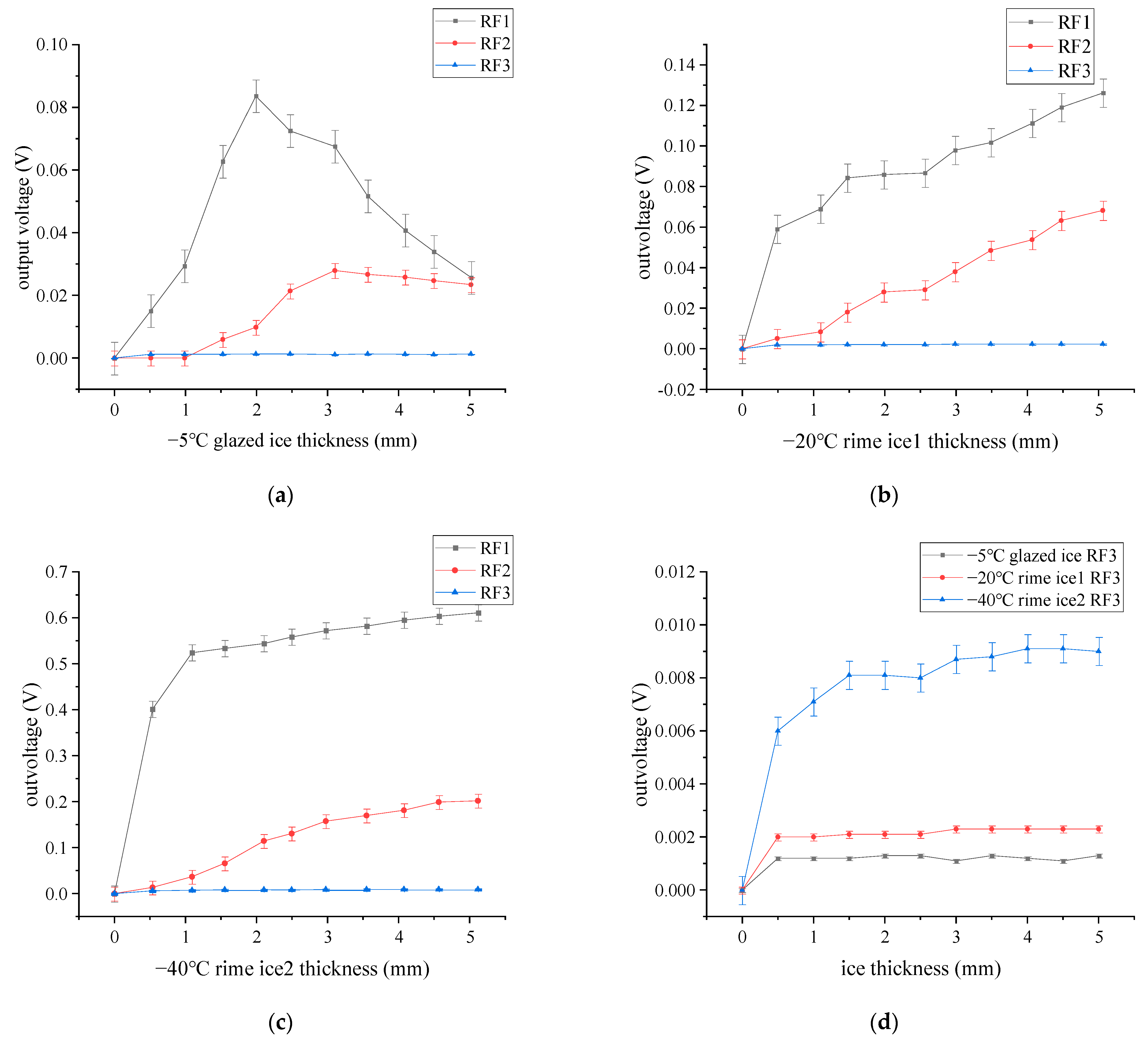
5. Experimental Detection
6. Conclusions
- (1)
- The ice type can be achieved by using the output voltage from RF3. Then, we can detect the ice thickness by using the light intensity modulation function in each ice type case.
- (2)
- The ice sensor can measure the glazed ice thicknesses from 1 to 5 mm. For the rime ice, the measuring range of ice thickness is from 0.5 to 5 mm.
- (3)
- The maximum and minimum ice thickness measurement errors are 0.283 mm and 0.087 mm, respectively, for the measuring range of 0.5 to 5 mm at −5 °C, −20 °C, and −40 °C.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Sensor Source | Maximum Ice Thickness | Error |
|---|---|---|
| [17] | 10 mm | 0.5 mm |
| [24] | 2.5 mm | −0.2–0.2 mm |
| This paper reported | 5 mm | 0.283 mm |
References
- Heinrich, A.; Ross, R.; Zumwalt, G.; Provorse, J.; Padmanabhan, V. Aircraft Icing Handbook; FAA Technical Center Publication: Atlantic City, NJ, USA, 1991. [Google Scholar]
- Reehorst, A.; Chung, J.; Potapczuk, M.; Choo, Y. Study of icing effects on performance and controllability of an accident aircraft. J. Aircr. 2000, 37, 253–259. [Google Scholar] [CrossRef]
- Green, S.D. A study of U.S. inflight icing accidents and incidents, 1978 to 2002. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Awad, H.; Gül, M.; Salim, K.E.; Yu, H. Predicting the energy production by solar photovoltaic systems in cold-climate regions. Int. J. Sustain. Energy 2017, 37, 1–21. [Google Scholar] [CrossRef]
- Tautz-Weinert, J.; Yürüsen, N.Y.; Melero, J.J.; Watson, S.J. Sensitivity study of a wind farm maintenance decision-a performance and revenue analysis. Renew. Energy 2019, 132, 93–105. [Google Scholar] [CrossRef]
- Zeng, J.; Song, B. Research on experiment and numerical simulation of ultrasonic de-icing for wind turbine blades. Renew. Energy 2017, 113, 706–712. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O. Wind energy resource, wind energy conversion system modeling and integration: A survey. Int. J. Sol. Energy 2013, 34, 657–671. [Google Scholar]
- Gnatowska, R.; Moryn-Kucharczyk, E. Current status of wind energy policy in Poland. Renew. Energy 2019, 135, 232–237. [Google Scholar] [CrossRef]
- Marjaniemi, M.; Peltola, E. Blade Heating Element Design and Practical Experiences. In Proceedings of the Boreas IV Conference, Enontekiö, Finland, 31 March–2 April 1998; pp. 197–209. [Google Scholar]
- Botta, G.; Cavaliere, M.; Holttinen, H. Ice Accretion at Acqua Spruzza and its Effects on Wind Turbine Operation and Loss of Energy Production. In Proceedings of the Boreas IV Conference, Enontekiö, Finland, 31 March–2 April 1998; pp. 77–86. [Google Scholar]
- Muñoz, C.Q.G.; Márquez, F.P.G.; Tomás, J.M.S. Ice detection using thermal infrared radiometry on wind turbine blades. Measurement 2016, 93, 157–163. [Google Scholar] [CrossRef]
- Xu, B.; Guo, X.; Chen, H. Active icing monitoring for wind turbine blade models with PZT technology. Piezoelectrics Acoustooptics 2017, 39, 72–76. [Google Scholar]
- Xu, B.; Lu, F.; Dyke, S.J.; Guo, X. Icing Monitoring for a Wind Turbine Model Blade with Active PZT Technology. Earth Space 2014, 2014, 703–710. [Google Scholar] [CrossRef]
- Deanna, R. Ice Detection Sensor. U.S. Patent 5,886,256, 23 March 1999. [Google Scholar]
- Carlsson, V. Measuring Routines of Ice Accretion for Wind Turbine Applications: The Correlation of Production Losses and Detection of Ice. Bachelor’s Thesis, Umeå University, Umeå, Sweden, 2010. [Google Scholar]
- Ikiades, A.A.; Armstrong, D.J.; Howard, G. Optical diffusion and polarization characteristics of ice accreting in dynamic conditions using a backscattering fiber optic technique. Sens. Actuators A Phys. 2007, 140, 43–50. [Google Scholar] [CrossRef]
- Ikiades, A. Fiber Optic Ice Sensor for Measuring Ice Thickness, Type, and the Freezing Fraction on Aircraft Wings. Aerospace 2022, 10, 31. [Google Scholar] [CrossRef]
- Ge, J.; Lin, Y.; Zou, J. A novel fiber-optic ice sensor capable of identifying ice type accurately. Sens. Actuators A Phys. 2012, 175, 35–42. [Google Scholar] [CrossRef]
- Gang, H.; Frank, W.; Cuomo, A. Light intensity function suitable for multimode fiber optic sensors. J. Light. Technol. 1991, 9, 545–551. [Google Scholar]
- Sagrario, D.; Mead, P. Axial and angular displacement fiber-optic sensor. Appl. Opt. 1998, 37, 6748–6754. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Li, P.; Wang, C.; Pu, Z. A novel fiber-optic sensor used for small internal curved surface measurement. Sens. Actuators 2000, A86, 211–215. [Google Scholar] [CrossRef]
- Petrov, D.V.; Zhuzhulina, E.A.; Kiselev, N.N. Influence of the Spectral Dependence of Refractive Index on the Polarimetric Properties of Ice Particles. Sol. Syst. Res. 2020, 54, 70–83. [Google Scholar] [CrossRef]
- Wang, J.; Ge, J.; Wei, M.; Yu, W. Influence of scattering properties due to complex refractive index of ice. In Proceedings of the IEEE Third International Conference on Information Science and Technology (ICIST), Yangzhou, China, 23–25 March 2013; pp. 997–999. [Google Scholar] [CrossRef]
- Zheng, D.; Li, Z.; Du, Z.; Ma, Y.; Zhang, L.; Du, C.; Deng, X. Design of Capacitance and Impedance Dual-Parameters Planar Electrode Sensor for Thin Ice Detection of Aircraft Wings. IEEE Sens. J. 2022, 22, 11006–11015. [Google Scholar] [CrossRef]




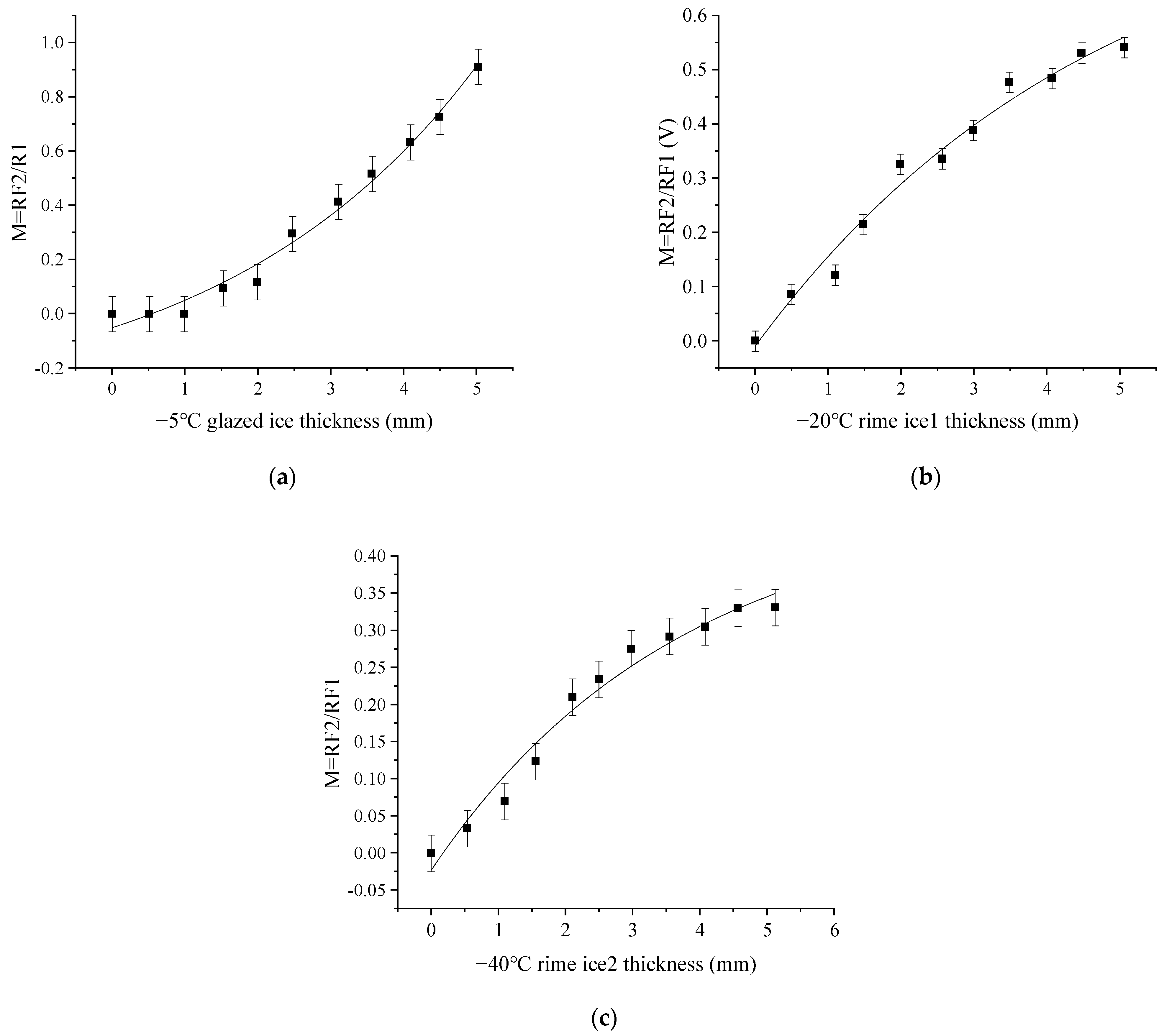
| Parameter | Numerical |
|---|---|
| Light-emitting angle | Arctan (0.5/1) |
| (nm) | 980 |
| Power (W) | 0.24 |
| Fiber-Optic Name | Fiber-Optic Length | Core Radius | Cladding Thickness |
|---|---|---|---|
| RF1 | 1000 mm | 0.5 mm | 0.05 mm |
| RF2 | 1000 mm | 0.5 mm | 0.05 mm |
| RF3 | 1000 mm | 0.5 mm | 0.05 mm |
| Structure Name | Refractive Index | Transmittance (1/m) |
|---|---|---|
| Core | 1.48 | 0.9899 |
| Cladding | 1.38 | 0.9200 |
| Title 1 | Rime Ice 1 | Rime Ice 2 |
|---|---|---|
| SPS (mm) | 10, 15, 20, 25, 30 | 7, 8, 9, 10, 11 |
| SPND (1/mm3) | 1.0851 × 104 | 1.5733 × 105 |
| M | Out Voltage (RF3) (V) | Detected Ice Type | Realistic Ice Type | |||
|---|---|---|---|---|---|---|
| 0.1159 | 1.534 | 1.621 | 0.087 | 0.0015 | Glazed ice | Glazed ice |
| 0.0015 | 3.425 | 3.624 | 0.199 | 0.0015 | Glazed ice | Glazed ice |
| 0.0014 | 5.006 | 5.284 | 0.278 | 0.0014 | Glazed ice | Glazed ice |
| 0.1664 | 1.078 | 1.263 | 0.185 | 0.0023 | Rime ice 1 | Rime ice 1 |
| 0.3998 | 3.026 | 2.921 | 0.105 | 0.0025 | Rime ice 1 | Rime ice 1 |
| 0.5538 | 4.965 | 5.248 | 0.283 | 0.0025 | Rime ice 1 | Rime ice 1 |
| 0.0878 | 0.937 | 1.098 | 0.161 | 0.0081 | Rime ice 2 | Rime ice 2 |
| 0.2234 | 2.539 | 2.316 | 0.223 | 0.0091 | Rime ice 2 | Rime ice 2 |
| 0.3481 | 5.097 | 4.896 | 0.201 | 0.0089 | Rime ice 2 | Rime ice 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Xiao, C.; Li, S.; Guo, X.; Wang, Q.; He, Y.; Lv, H.; Yan, H.; Liu, D. A Novel Fiber-Optic Ice Sensor to Identify Ice Types Based on Total Reflection. Sensors 2023, 23, 3996. https://doi.org/10.3390/s23083996
Zhang C, Xiao C, Li S, Guo X, Wang Q, He Y, Lv H, Yan H, Liu D. A Novel Fiber-Optic Ice Sensor to Identify Ice Types Based on Total Reflection. Sensors. 2023; 23(8):3996. https://doi.org/10.3390/s23083996
Chicago/Turabian StyleZhang, Chi, Chunhua Xiao, Shaorong Li, Xiaowei Guo, Qi Wang, Yizhou He, Huiyan Lv, Hongkai Yan, and Dongan Liu. 2023. "A Novel Fiber-Optic Ice Sensor to Identify Ice Types Based on Total Reflection" Sensors 23, no. 8: 3996. https://doi.org/10.3390/s23083996
APA StyleZhang, C., Xiao, C., Li, S., Guo, X., Wang, Q., He, Y., Lv, H., Yan, H., & Liu, D. (2023). A Novel Fiber-Optic Ice Sensor to Identify Ice Types Based on Total Reflection. Sensors, 23(8), 3996. https://doi.org/10.3390/s23083996








