Regression-Based Camera Pose Estimation through Multi-Level Local Features and Global Features
Abstract
:1. Introduction
1.1. Background and Introduction
- We propose a novel end-to-end camera pose estimation framework that uses image pairs as input and leverages epipolar geometry to generate image pixel pairs for estimating the camera pose. The framework also includes the automatic fine-tuning of hyperparameters during the training process, resulting in improved accuracy and adaptability.
- We adopt a multi-level deformable convolution approach that simultaneously detects and describes the network to extract local features. This addresses the issue of sensitivity to shape information (such as scale, orientation, etc.) and inaccurate keypoint positioning, leading to more robust and accurate camera pose estimation;
- We propose a novel loss that integrates the detection and description loss based on local features with the relative pose loss function based on global features. This novel loss function enhances the accuracy of camera pose estimation by jointly optimizing local and global feature representations, leading to improved performance compared to existing methods;
- The proposed method is evaluated on benchmark datasets, including HPatches and 7Scenes. The HPatches dataset provides diverse image patches for illumination, viewpoint, and scale evaluation, while the 7Scenes dataset offers realistic indoor sequences for accuracy and stability testing. The experimental results verify the effectiveness of the proposed method for image-matching tasks and camera pose estimation tasks, and demonstrate its superiority compared to state-of-the-art methods.
1.2. Organization
2. Related Work
2.1. Localization with Sparse Local Feature Matching
2.2. Camera Localization with Global Feature Regression
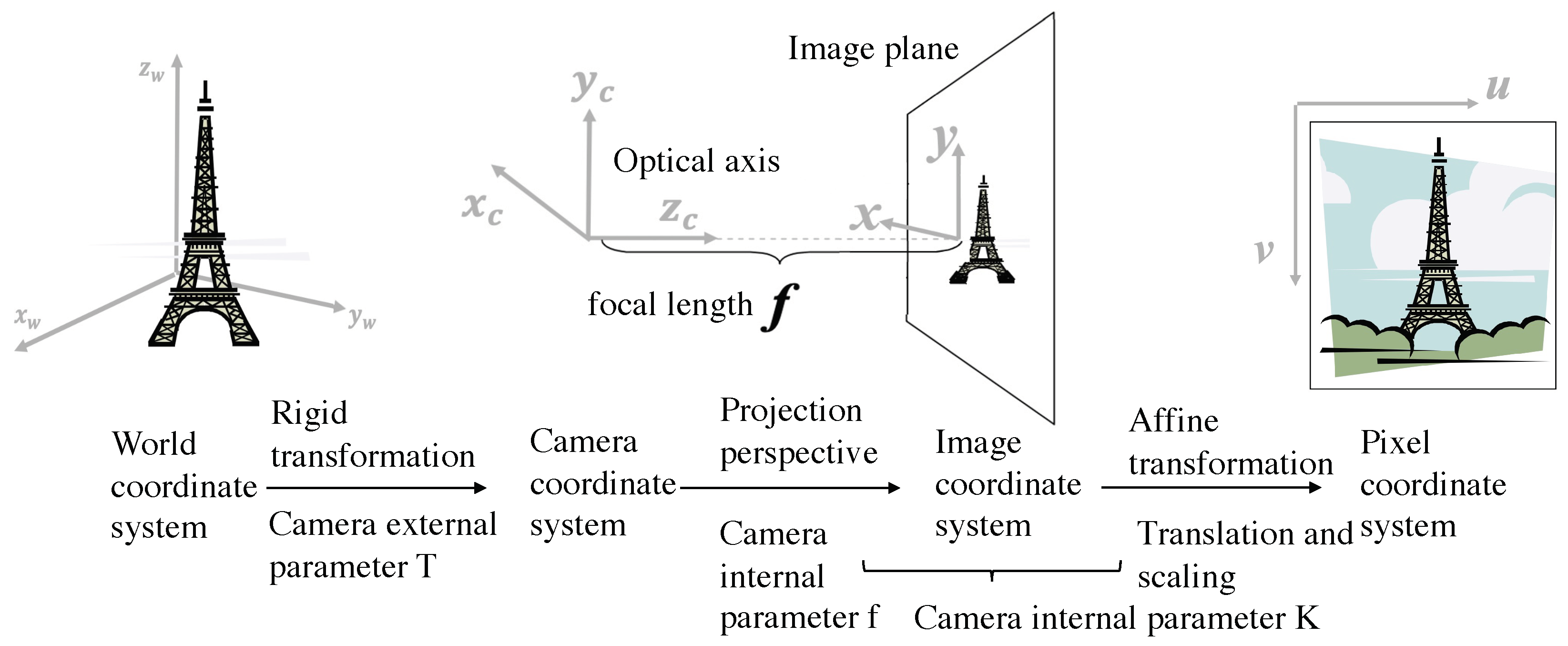
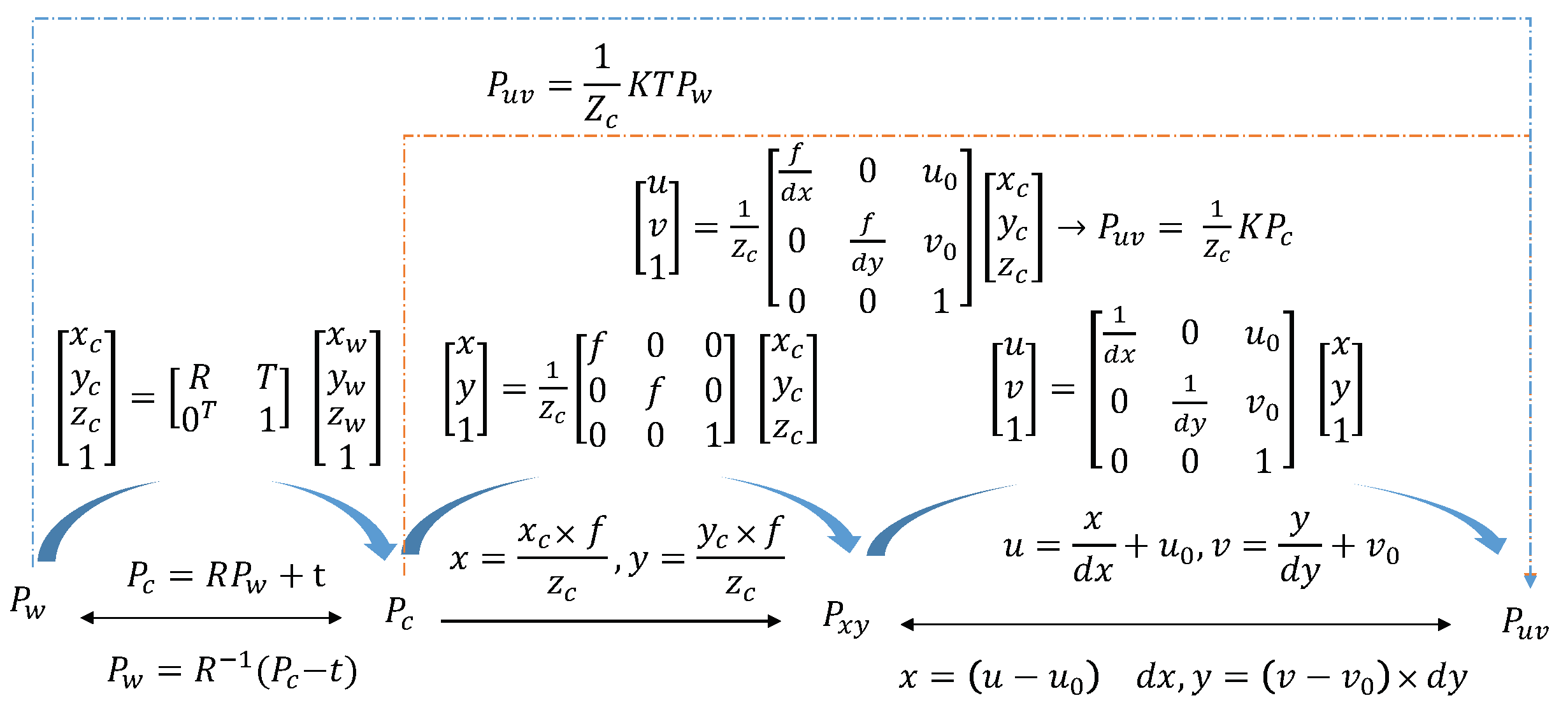
3. Dataset Preprocessing and Epipolar Geometry
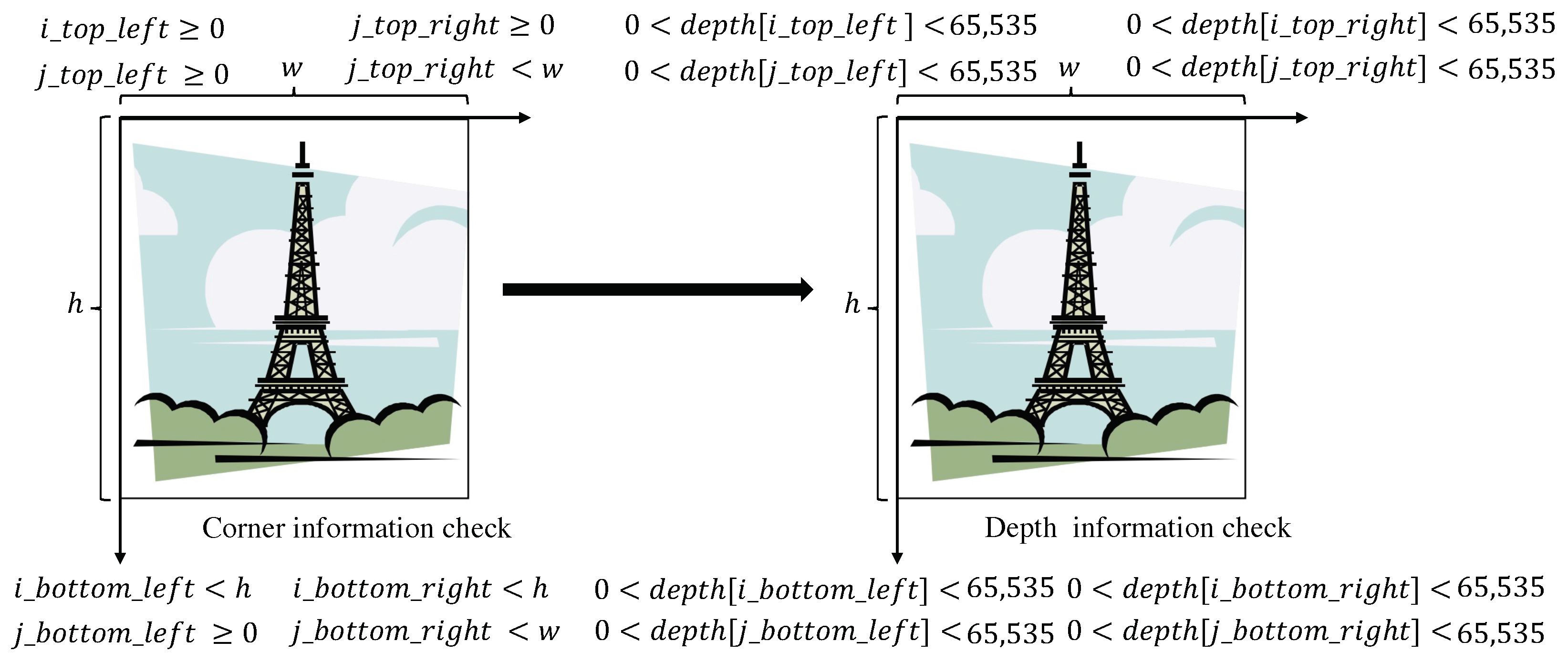
3.1. Update Depth Image Using Position Grid
3.2. Associate Pixels of the Color Image and Depth Image
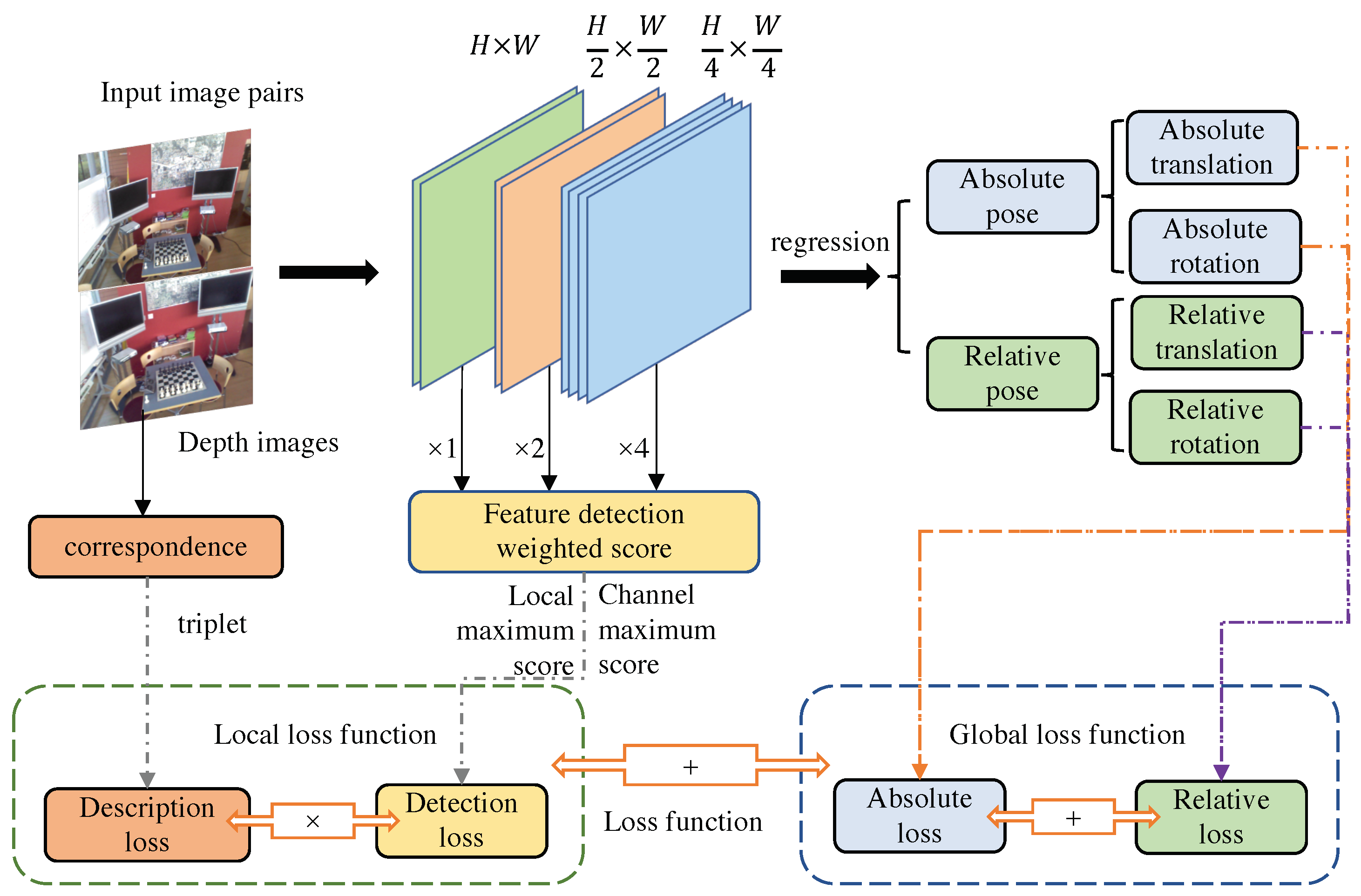
4. Method
4.1. Multi-Level Deformable Network
4.1.1. Deformable Convolutional Network
4.1.2. Multi-Level Feature Detection Network
4.2. Local Feature Extraction Based on Pixel Matching
4.2.1. Loss of Feature Descriptor
4.2.2. Feature Detection Sub-Loss
4.2.3. Loss Function Based on the Image Sequence for Global Features
5. Experiment and Discussion
5.1. Experimental Settings
5.1.1. Datasets
5.1.2. Implementation Details
- Batch size of 4. This choice balances computational efficiency and memory usage;
- Number of matching correspondences of 128. This value is commonly used in related literature for keypoint matching tasks [33];
- Training iterations of 1000. This value was determined based on empirical experimentation to achieve optimal convergence and performance;
- Balancing factors between detection loss and description loss, absolute loss and relative loss, and local loss and global loss, all set to 1. These values were chosen to give equal importance to different components of the loss function, which could also achieve better performance according to the experiments;
- Initial learning rate of for the first 100 iterations, divided by 5 for every 100 iterations thereafter. This learning rate scheduling was determined based on empirical experimentation to achieve optimal training progress and convergence.
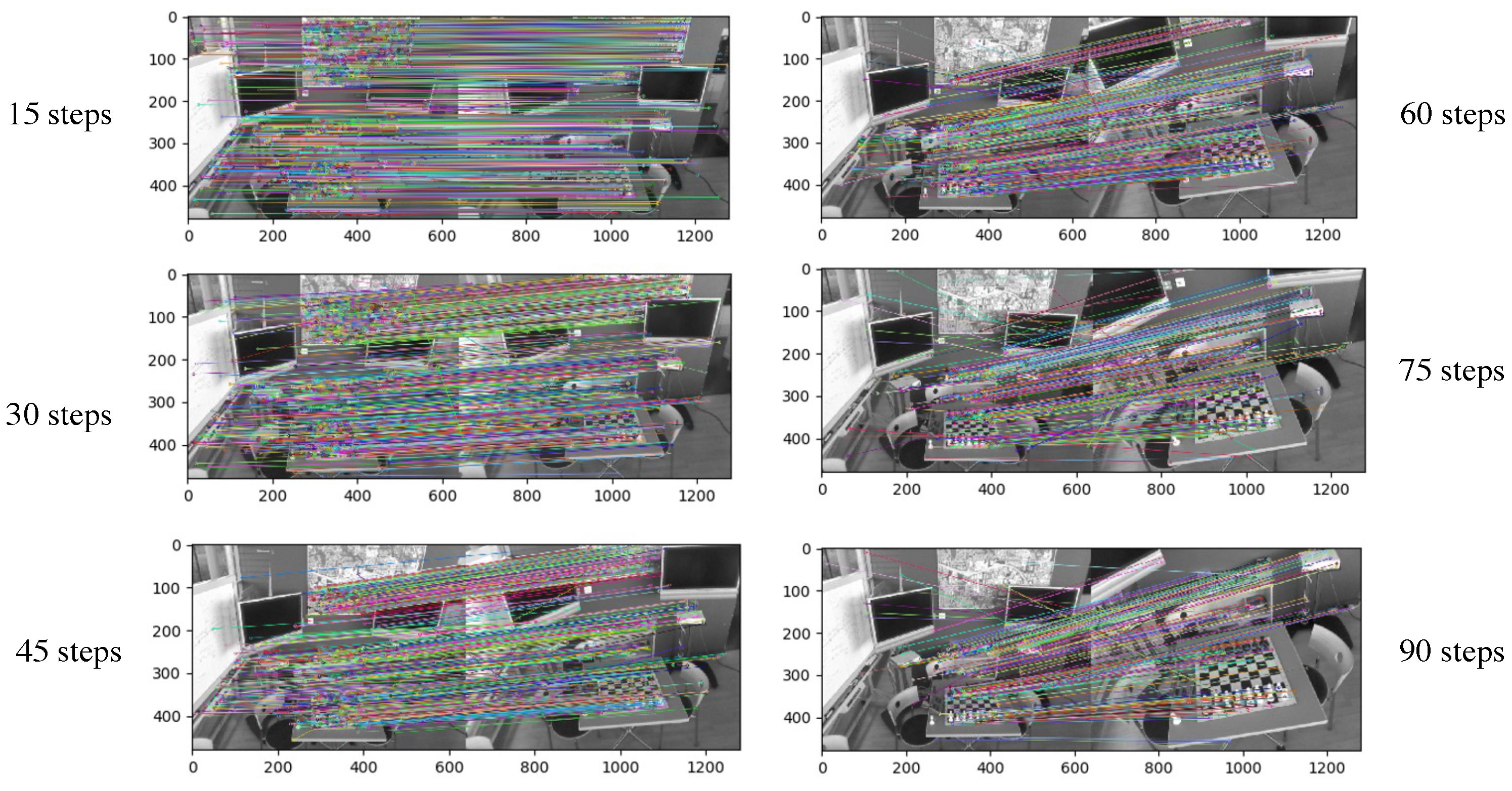
5.2. Multi-Step Image Pixel Reprojection
5.3. Image-Matching Experiment on HPatches Dataset
5.4. Pose Estimation Experiment on 7Scenes Dataset
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| I | image |
| h | height of the image |
| w | width of the image |
| i | index value of the image height |
| j | index value of the image width |
| the point coordinates in the world coordinate system | |
| the point coordinates in the camera coordinate system | |
| the point coordinates in the image coordinate system | |
| the point coordinates in the pixel coordinate system | |
| f | the focal length in the pinhole model |
| T | camera external parameter matrix |
| K | camera internal parameter matrix |
| x | feature map |
| R | regular grid |
| the enumeration of the location in R | |
| the learnable offset | |
| the module scale factor of the position | |
| the weight factor in different convolutional layers | |
| the expansion rate of searching for neighboring pixels | |
| F | the tensor obtained through the multi-level deformable convolutional network |
| n | number of channels |
| d | descriptor vector |
| N | negative sample points in the image I |
| D | two-dimensional response |
| resolution |
References
- Garcia, P.P.; Santos, T.G.; Machado, M.A.; Mendes, N. Deep Learning Framework for Controlling Work Sequence in Collaborative Human–Robot Assembly Processes. Sensors 2023, 23, 553. [Google Scholar] [CrossRef]
- Mundt, M.; Born, Z.; Goldacre, M.; Alderson, J. Estimating Ground Reaction Forces from Two-Dimensional Pose Data: A Biomechanics-Based Comparison of AlphaPose, BlazePose, and OpenPose. Sensors 2023, 23, 78. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wang, Y.; Xu, B.; Zhang, J.; Ren, J.; Poslad, S.; Xu, P. A critical analysis of image-based camera pose estimation techniques. arXiv 2022, arXiv:2201.05816. [Google Scholar]
- Zhang, Z.; Xu, M.; Zhou, W.; Peng, T.; Li, L.; Poslad, S. BEV-Locator: An End-to-end Visual Semantic Localization Network Using Multi-View Images. arXiv 2022, arXiv:2211.14927. [Google Scholar]
- Yan, G.; Luo, Z.; Liu, Z.; Li, Y. SensorX2car: Sensors-to-car calibration for autonomous driving in road scenarios. arXiv 2023, arXiv:2301.07279. [Google Scholar]
- Wei, X.; Xiao, C. MVAD: Monocular vision-based autonomous driving distance perception system. In Proceedings of the Third International Conference on Computer Vision and Data Mining (ICCVDM 2022), Hulun Buir, China, 19–21 August 2023; Volume 12511, pp. 258–263. [Google Scholar]
- Xu, M.; Wang, L.; Ren, J.; Poslad, S. Use of LSTM Regression and Rotation Classification to Improve Camera Pose Localization Estimation. In Proceedings of the 2020 IEEE 14th International Conference on Anti-Counterfeiting, Security, and Identification (ASID), Xiamen, China, 30 October–1 November 2020; pp. 6–10. [Google Scholar]
- Xu, M.; Shen, C.; Zhang, J.; Wang, Z.; Ruan, Z.; Poslad, S.; Xu, P. A Stricter Constraint Produces Outstanding Matching: Learning Reliable Image Matching with a Quadratic Hinge Triplet Loss Network. In Graphics Interface. 2021. Available online: https://graphicsinterface.org/wp-content/uploads/gi2021-23.pdf (accessed on 19 March 2023).
- Yi, K.M.; Trulls, E.; Lepetit, V.; Fua, P. Lift: Learned invariant feature transform. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 467–483. [Google Scholar]
- Tian, Y.; Fan, B.; Wu, F. L2-net: Deep learning of discriminative patch descriptor in euclidean space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 661–669. [Google Scholar]
- Kendall, A.; Grimes, M.; Cipolla, R. Posenet: A convolutional network for real-time 6-dof camera relocalization. In Proceedings of the IEEE International Conference on Computer Vision; 2015; pp. 2938–2946. Available online: https://openaccess.thecvf.com/content_iccv_2015/papers/Kendall_PoseNet_A_Convolutional_ICCV_2015_paper.pdf (accessed on 19 March 2023).
- Brahmbhatt, S.; Gu, J.; Kim, K.; Hays, J.; Kautz, J. Geometry-aware learning of maps for camera localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2018; pp. 2616–2625. Available online: https://openaccess.thecvf.com/content_cvpr_2018/papers/Brahmbhatt_Geometry-Aware_Learning_of_CVPR_2018_paper.pdf (accessed on 19 March 2023).
- Huang, Z.; Xu, Y.; Shi, J.; Zhou, X.; Bao, H.; Zhang, G. Prior guided dropout for robust visual localization in dynamic environments. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2791–2800. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Zhu, X.; Hu, H.; Lin, S.; Dai, J. Deformable convnets v2: More deformable, better results. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9308–9316. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Smith, S.M.; Brady, J.M. SUSAN—a new approach to low level image processing. Int. J. Comput. Vis. 1997, 23, 45–78. [Google Scholar] [CrossRef]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 430–443. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2548–2555. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Verdie, Y.; Yi, K.; Fua, P.; Lepetit, V. Tilde: A temporally invariant learned detector. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5279–5288. [Google Scholar]
- Lenc, K.; Vedaldi, A. Learning covariant feature detectors. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 100–117. [Google Scholar]
- Zhang, X.; Yu, F.X.; Karaman, S.; Chang, S.F. Learning discriminative and transformation covariant local feature detectors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6818–6826. [Google Scholar]
- Savinov, N.; Seki, A.; Ladicky, L.; Sattler, T.; Pollefeys, M. Quad-networks: Unsupervised learning to rank for interest point detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1822–1830. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Toward geometric deep slam. arXiv 2017, arXiv:1707.07410. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Han, X.; Leung, T.; Jia, Y.; Sukthankar, R.; Berg, A.C. Matchnet: Unifying feature and metric learning for patch-based matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3279–3286. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Learning to compare image patches via convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4353–4361. [Google Scholar]
- Tian, Y.; Yu, X.; Fan, B.; Wu, F.; Heijnen, H.; Balntas, V. Sosnet: Second order similarity regularization for local descriptor learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11016–11025. [Google Scholar]
- Ono, Y.; Trulls, E.; Fua, P.; Yi, K.M. LF-Net: Learning local features from images. arXiv 2018, arXiv:1805.09662. [Google Scholar]
- Revaud, J.; Weinzaepfel, P.; De Souza, C.; Pion, N.; Csurka, G.; Cabon, Y.; Humenberger, M. R2D2: Repeatable and reliable detector and descriptor. arXiv 2019, arXiv:1906.06195. [Google Scholar]
- Luo, Z.; Zhou, L.; Bai, X.; Chen, H.; Zhang, J.; Yao, Y.; Li, S.; Fang, T.; Quan, L. Aslfeat: Learning local features of accurate shape and localization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6589–6598. [Google Scholar]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-net: A trainable cnn for joint detection and description of local features. arXiv 2019, arXiv:1905.03561. [Google Scholar]
- Du, J.; Wang, R.; Cremers, D. Dh3d: Deep hierarchical 3d descriptors for robust large-scale 6dof relocalization. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 744–762. [Google Scholar]
- Benbihi, A.; Geist, M.; Pradalier, C. Elf: Embedded localisation of features in pre-trained cnn. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October 2019–2 November 2019; pp. 7940–7949. [Google Scholar]
- Kendall, A.; Cipolla, R. Modelling uncertainty in deep learning for camera relocalization. In Proceedings of the 2016 IEEE international conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4762–4769. [Google Scholar]
- Walch, F.; Hazirbas, C.; Leal-Taixe, L.; Sattler, T.; Hilsenbeck, S.; Cremers, D. Image-based localization using lstms for structured feature correlation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 627–637. [Google Scholar]
- Wang, B.; Chen, C.; Lu, C.X.; Zhao, P.; Trigoni, N.; Markham, A. Atloc: Attention guided camera localization. Proc. AAAI Conf. Artif. Intell. 2020, 34, 10393–10401. [Google Scholar] [CrossRef]
- Naseer, T.; Burgard, W. Deep regression for monocular camera-based 6-dof global localization in outdoor environments. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1525–1530. [Google Scholar]
- Kendall, A.; Cipolla, R. Geometric loss functions for camera pose regression with deep learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5974–5983. [Google Scholar]
- Chidlovskii, B.; Sadek, A. Adversarial Transfer of Pose Estimation Regression. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 646–661. [Google Scholar]
- Lin, Y.; Liu, Z.; Huang, J.; Wang, C.; Du, G.; Bai, J.; Lian, S. Deep global-relative networks for end-to-end 6-dof visual localization and odometry. In Pacific Rim International Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; pp. 454–467. [Google Scholar]
- Oh, J. Novel Approach to Epipolar Resampling of HRSI and Satellite Stereo Imagery-Based Georeferencing of Aerial Images. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2011. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. Refinenet: Multi-path refinement networks for high-resolution semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1925–1934. [Google Scholar]
- Tolias, G.; Sicre, R.; Jégou, H. Particular object retrieval with integral max-pooling of CNN activations. arXiv 2015, arXiv:1511.05879. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; Volume 15, pp. 10–5244. [Google Scholar]
- Shotton, J.; Glocker, B.; Zach, C.; Izadi, S.; Criminisi, A.; Fitzgibbon, A. Scene coordinate regression forests for camera relocalization in RGB-D images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2930–2937. [Google Scholar]
- Balntas, V.; Lenc, K.; Vedaldi, A.; Mikolajczyk, K. HPatches: A benchmark and evaluation of handcrafted and learned local descriptors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5173–5182. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017) Workshop on Autodiff, Long Beach, CA, USA, 4–9 December 2017; 2017. [Google Scholar]
- NVIDIA; Vingelmann, P.; Fitzek, F.H. CUDA, Release: 10.2.89; NVIDIA: Santa Clara, CA, USA, 2020. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Clark, R.; Wang, S.; Markham, A.; Trigoni, N.; Wen, H. Vidloc: A deep spatio-temporal model for 6-dof video-clip relocalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6856–6864. [Google Scholar]
- Xue, F.; Wang, X.; Yan, Z.; Wang, Q.; Wang, J.; Zha, H. Local supports global: Deep camera relocalization with sequence enhancement. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2841–2850. [Google Scholar]
- Melekhov, I.; Ylioinas, J.; Kannala, J.; Rahtu, E. Image-based localization using hourglass networks. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 879–886. [Google Scholar]
- Wu, J.; Ma, L.; Hu, X. Delving deeper into convolutional neural networks for camera relocalization. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5644–5651. [Google Scholar]
- Bui, M.; Baur, C.; Navab, N.; Ilic, S.; Albarqouni, S. Adversarial networks for camera pose regression and refinement. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar]
- Cai, M.; Shen, C.; Reid, I. A hybrid Probabilistic Model for Camera Relocalization; BMVC Press: London, UK, 2019. [Google Scholar]


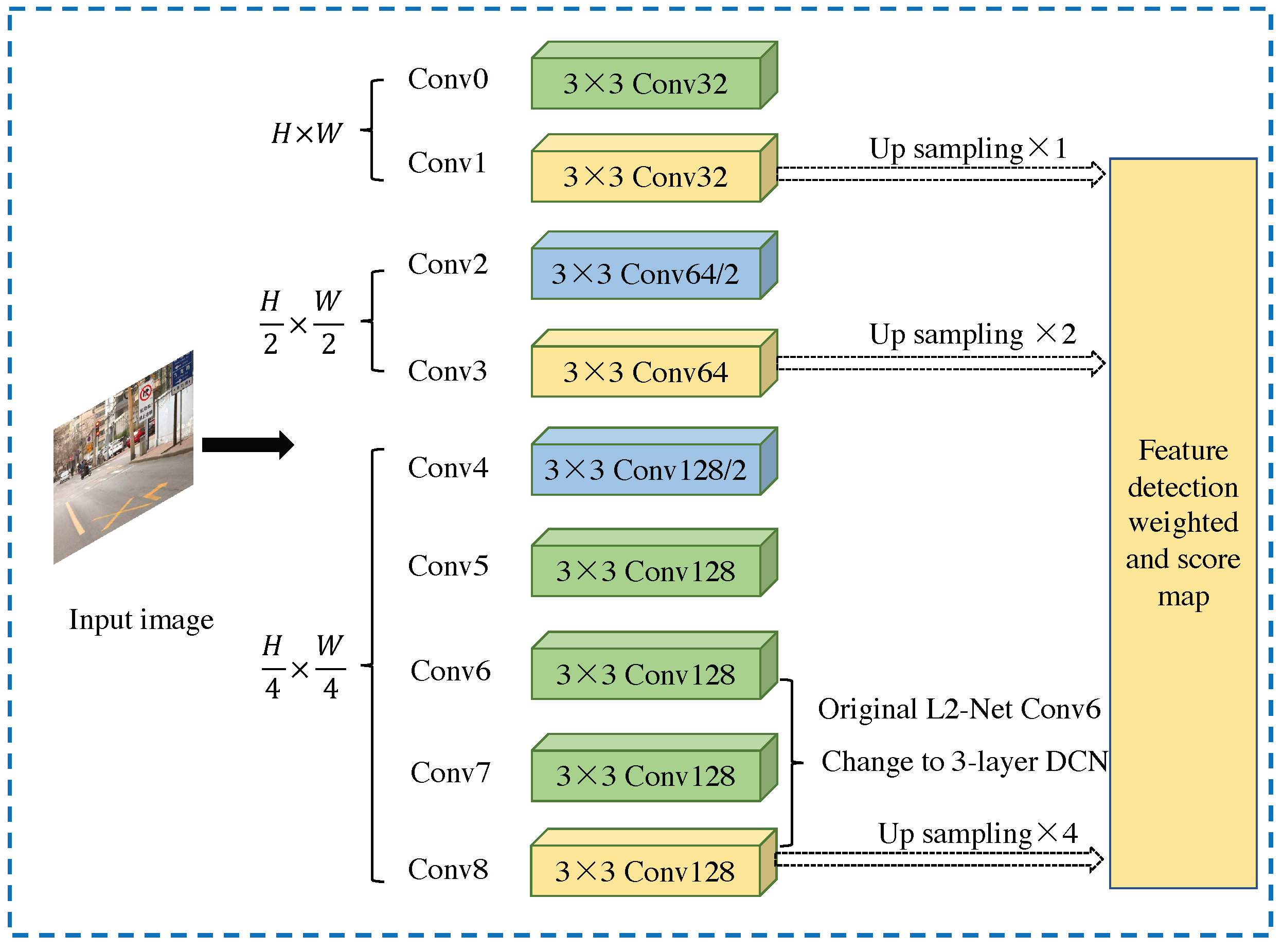
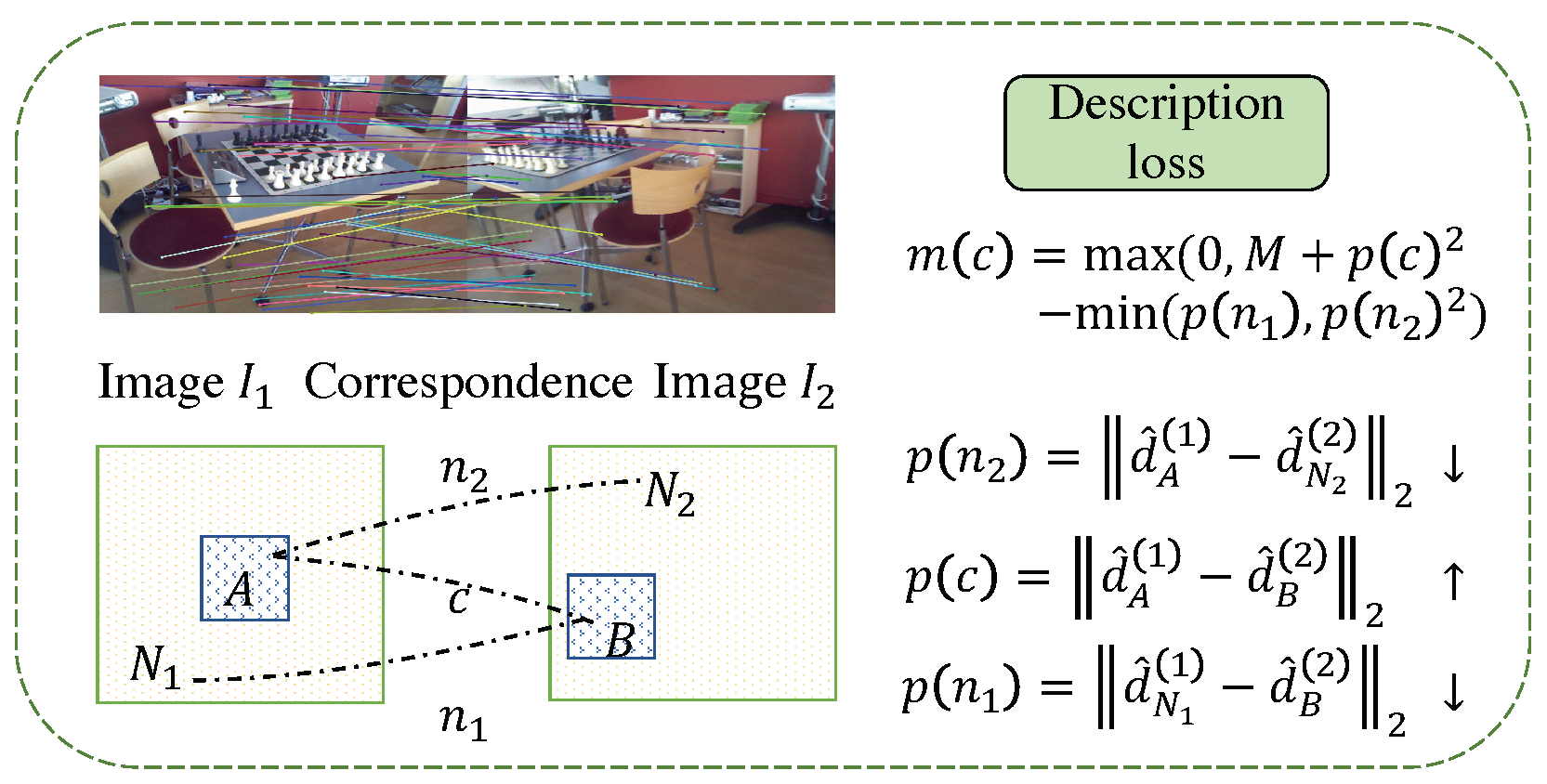
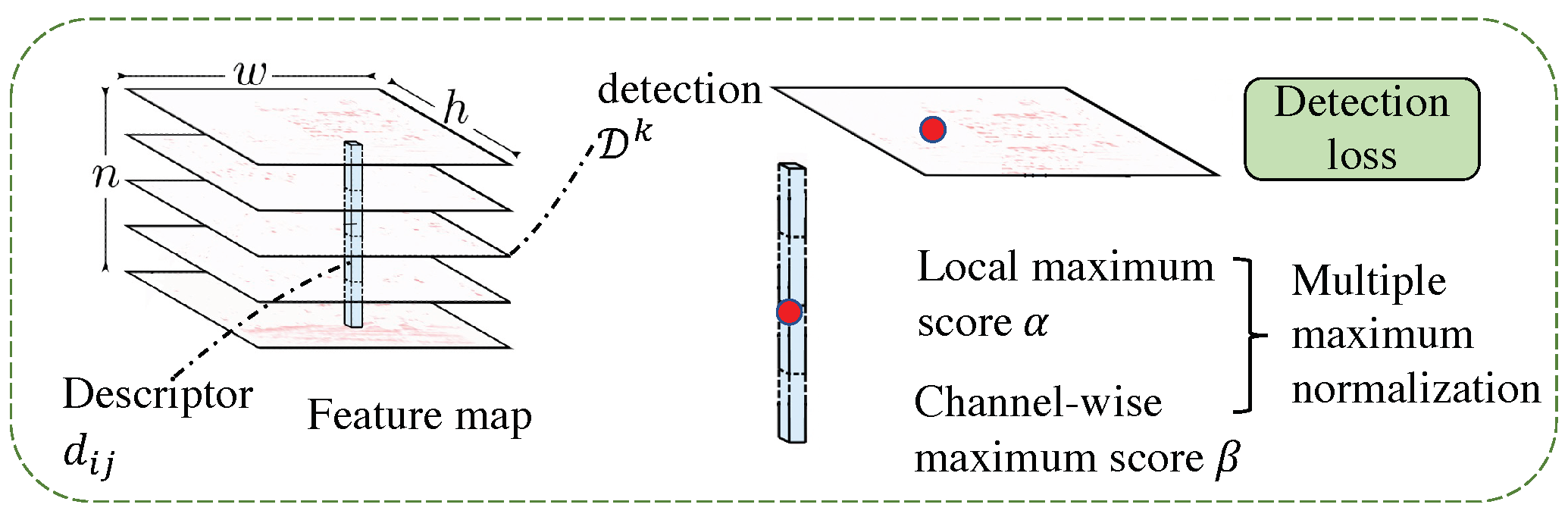

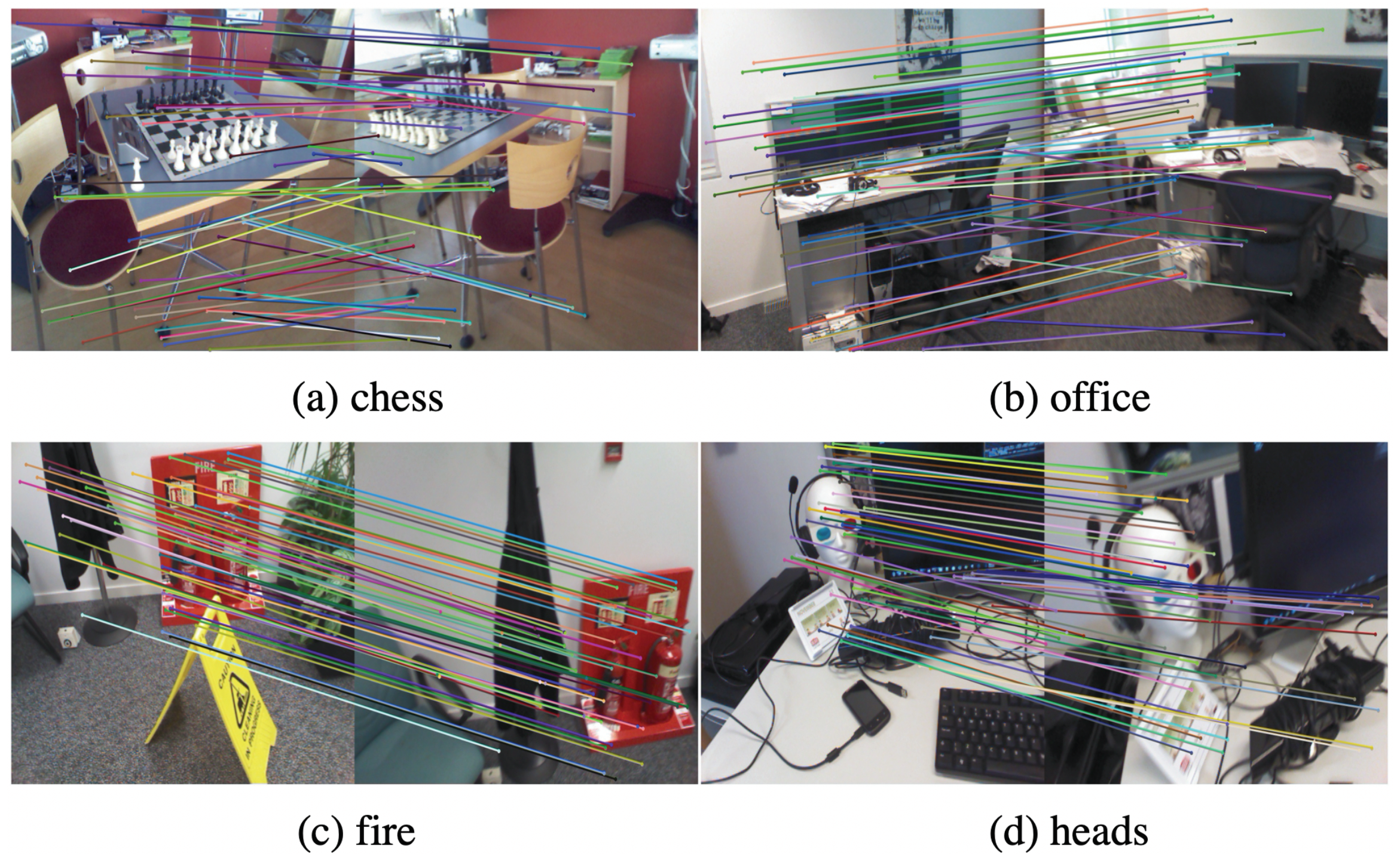
| Layer | Input Channel | Output Channel | Kernel Size | Stride | Resolution | BN Layer | ReLU Layer | Padding | Dilation |
|---|---|---|---|---|---|---|---|---|---|
| Input | 3 | ||||||||
| Conv0 | 3 | 32 | 3 | 1 | ✔ | ✔ | 1 | 1 | |
| Conv1 | 32 | 32 | 3 | 1 | ✔ | ✔ | 1 | 1 | |
| Conv2 | 32 | 64 | 3 | 2 | ✔ | ✔ | 1 | 1 | |
| Conv3 | 64 | 64 | 3 | 1 | ✔ | ✔ | 1 | 1 | |
| Conv4 | 64 | 128 | 3 | 2 | ✔ | ✔ | 1 | 1 | |
| Conv5 | 128 | 128 | 3 | 1 | ✔ | ✔ | 1 | 1 | |
| Conv6 | 128 | 128 | 3 | 1 | ✔ | ✔ | 1 | 1 | |
| Conv7 | 128 | 128 | 3 | 1 | ✔ | ✔ | 1 | 1 | |
| Conv8 | 128 | 128 | 3 | 1 | 1 | 1 |
| SuperPoint [26] | 45.80 | 31.23 | 39.82 |
| D2-Net [33] | 47.86 | 23.58 | 43.00 |
| This method | 72.33 | 42.58 | 68.31 |
| Sparse Matching | Dense Matching | ||
|---|---|---|---|
| Detect-then-Describe | Detect-and-Describe | Detect | |
| Process | Detect the keypoints of the image; extract the descriptors from the image patches around the keypoint; output the compact representation of the image patch | Extract descriptors and keypoints on the feature map; detect the high-dimensional keypoints with locally unique descriptors. | Perform the description stage densely on the entire image. |
| Advantages | High matching and storage efficiency, keypoints are sensitive to low-dimensional information, and high positioning accuracy. | Robust to challenging environments, efficient storage and matching. | Robust dense descriptors for environmental changes. |
| Disadvantages | Poor performance in challenging environments (weak textures, etc.), poor repeatability in keypoint detection. | Dense descriptors lead to low computational efficiency, and the accuracy of key points obtained by detectors based on high-dimensional information is not high. | High matching time consumption and memory. |
| Methods | Chess | Fire | Heads | Office | Pumpkin | Kitchen | Stairs |
|---|---|---|---|---|---|---|---|
| PoseNet [11] | 0.32 m, 8.12 | 0.47 m, 14.4 | 0.29 m, 12.0 | 0.48 m, 7.68 | 0.47 m, 8.42 | 0.59 m, 8.64 | 0.47 m, 13.8 |
| Dense PoseNet [11] | 0.32 m, 6.60 | 0.47 m, 14.0 | 0.30 m, 12.2 | 0.48 m, 7.24 | 0.49 m, 8.12 | 0.58 m, 8.34 | 0.48 m, 13.1 |
| Bayesian PoseNet [36] | 0.37 m, 7.24 | 0.43 m, 13.7 | 0.31 m, 12.0 | 0.48 m, 8.04 | 0.61 m, 7.08 | 0.58 m, 7.54 | 0.48 m, 13.1 |
| LSTM PoseNet [56] | 0.24 m, 5.77 | 0.34 m, 11.9 | 0.21 m, 13.7 | 0.30 m, 8.08 | 0.33 m, 7.00 | 0.37 m, 8.83 | 0.40 m, 13.7 |
| Hourglass PoseNet [56] | 0.15 m, 6.17 | 0.27 m, 10.84 | 0.19 m, 11.63 | 0.21 m, 8.48 | 0.25 m, 7.01 | 0.27 m, 10.15 | 0.29 m, 12.46 |
| BranchNet [57] | 0.18 m, 5.17 | 0.34 m, 8.99 | 0.20 m, 14.15 | 0.30 m, 7.05 | 0.27 m, 5.10 | 0.33 m, 7.40 | 0.38 m, 10.26 |
| Geo.PoseNet [40] | 0.14 m, 4.50 | 0.27 m, 11.8 | 0.18 m, 12.1 | 0.20 m, 5.77 | 0.25 m, 4.82 | 0.24 m, 5.52 | 0.37 m, 10.6 |
| AdPR [58] | 0.12 m, 4.8 | 0.27 m, 11.6 | 0.16 m, 12.4 | 0.19 m, 6.8 | 0.21 m, 5.2 | 0.25 m, 6.0 | 0.28 m, 8.4 |
| APANet [41] | N/A, N/A | 0.21 m, 9.72 | 0.15 m, 9.35 | 0.15 m, 6.69 | 0.19 m, 5.87 | 0.16 m, 5.13 | 0.16 m, 11.77 |
| Geo.PoseNet (reprojection) [40] | 0.13 m, 4.48 | 0.27 m, 11.3 | 0.17 m, 13.0 | 0.19 m, 5.55 | 0.26 m, 4.75 | 0.23 m, 5.35 | 0.35 m, 12.4 |
| GPoseNet [59] | 0.20 m, 7.11 | 0.38 m, 12.3 | 0.21 m, 13.8 | 0.28 m, 8.83 | 0.37 m, 6.94 | 0.35 m, 8.15 | 0.37 m, 12.5 |
| MapNet [12] | 0.08 m, 3.25 | 0.27 m, 11.7 | 0.18 m, 13.3 | 0.17 m, 5.15 | 0.22 m, 4.02 | 0.23 m, 4.93 | 0.30 m, 12.1 |
| LSG [55] | 0.09 m, 3.28 | 0.26 m, 10.92 | 0.17 m, 12.70 | 0.18 m, 5.45 | 0.20 m, 3.69 | 0.23 m, 4.92 | 0.23 m, 11.3 |
| VidLoc [54] | 0.18 m, N/A | 0.26 m, N/A | 0.14 m, N/A | 0.26 m, N/A | 0.36 m, N/A | 0.31 m, N/A | 0.26 m, N/A |
| This method | 0.08 m, 3.19 | 0.25 m, 10.89 | 0.14 m, 12.5 | 0.16 m, 5.15 | 0.20 m, 4.01 | 0.21 m, 4.91 | 0.25 m, 11.2 |
| Methods | Input | Robustness | Graphics Card | Pixel Values | Time (ms) |
|---|---|---|---|---|---|
| VidLoc [54] | Video | Temporal smooth | Titan X | 18∼43 | |
| MapNet [12] | Image pair, video | Locally smooth drift-free | / | 9.4 | |
| LSG [55] | Image pair | Posture uncertainty caused by content enhancement | Nvidia 1080Ti | unknown | |
| This method | Image pair, depth image | Time smooth, motion blur, no drift | Nvidia Titan X GPU | 10.2 |
| Networks | Modules | 7Scenes Dataset | |||
|---|---|---|---|---|---|
| ResNet34 | Multi-Level Deformation Network | Global Loss | Local Loss | Local Loss Weight | Heads Scenes |
| ✔ | ✔ | m, | |||
| ✔ | ✔ | m, | |||
| ✔ | ✔ | ✔ | 1.0 | m, | |
| ✔ | ✔ | ✔ | 2.0 | m, | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Zhang, Z.; Gong, Y.; Poslad, S. Regression-Based Camera Pose Estimation through Multi-Level Local Features and Global Features. Sensors 2023, 23, 4063. https://doi.org/10.3390/s23084063
Xu M, Zhang Z, Gong Y, Poslad S. Regression-Based Camera Pose Estimation through Multi-Level Local Features and Global Features. Sensors. 2023; 23(8):4063. https://doi.org/10.3390/s23084063
Chicago/Turabian StyleXu, Meng, Zhihuang Zhang, Yuanhao Gong, and Stefan Poslad. 2023. "Regression-Based Camera Pose Estimation through Multi-Level Local Features and Global Features" Sensors 23, no. 8: 4063. https://doi.org/10.3390/s23084063
APA StyleXu, M., Zhang, Z., Gong, Y., & Poslad, S. (2023). Regression-Based Camera Pose Estimation through Multi-Level Local Features and Global Features. Sensors, 23(8), 4063. https://doi.org/10.3390/s23084063







