Binary Chimp Optimization Algorithm with ML Based Intrusion Detection for Secure IoT-Assisted Wireless Sensor Networks
Abstract
1. Introduction
2. Related Works
3. The Proposed Intrusion Detection Model
3.1. Data Normalization
3.2. Feature Selection Using BCOA
3.3. Intrusion Detection Using Optimal CCR-ELM Model
- The motion direction;
- The movement place;
- Emphasizing or de-emphasizing the target effect;
- Swapping amongst the sine and cosine elements.
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ramana, K.; Revathi, A.; Gayathri, A.; Jhaveri, R.H.; Narayana, C.L.; Kumar, B.N. WOGRU-IDS—An intelligent intrusion detection system for IoT-assisted Wireless Sensor Networks. Comput. Commun. 2022, 196, 195–206. [Google Scholar] [CrossRef]
- Rajan, D.A.J.; Naganathan, E.R. Trust-based anonymous intrusion detection for cloud-assisted WSN-IOT. Glob. Transit. Proc. 2022, 3, 104–108. [Google Scholar] [CrossRef]
- Ramana, T.V.; Thirunavukkarasan, M.; Mohammed, A.S.; Devarajan, G.G.; Nagarajan, S.M. Ambient intelligence approach: IoT-based decision performance analysis for intrusion detection. Comput. Commun. 2022, 195, 315–322. [Google Scholar] [CrossRef]
- RM, B.; K Mewada, H.; BR, R. Hybrid machine learning approach based intrusion detection in the cloud: A metaheuristic assisted model. Multiagent Grid Syst. 2022, 18, 21–43. [Google Scholar]
- Mohan, P.; Subramani, N.; Alotaibi, Y.; Alghamdi, S.; Khalaf, O.I.; Ulaganathan, S. Improved metaheuristics-based clustering with multihop routing protocol for underwater wireless sensor networks. Sensors 2022, 22, 1618. [Google Scholar] [CrossRef] [PubMed]
- Abuqaddom, I.; Mahafzah, B.; Faris, H. Oriented stochastic loss descent algorithm to train very deep multi-layer neural networks without vanishing gradients. Knowl. Based Syst. 2021, 230, 107391. [Google Scholar] [CrossRef]
- Al-Shaikh, A.; Mahafzah, B.; Alshraideh, M. Hybrid harmony search algorithm for social network contact tracing of COVID-19. Soft Comput. 2021, 27, 3343–3365. [Google Scholar] [CrossRef]
- Quincozes, S.E.; Passos, D.; Albuquerque, C.; Mossé, D.; Ochi, L.S. An extended assessment of metaheuristics-based feature selection for intrusion detection in CPS perception layer. Ann. Telecommun. 2022, 77, 457–471. [Google Scholar] [CrossRef]
- Tabash, M.; Abd Allah, M.; Tawfik, B. Intrusion detection model using naive bayes and deep learning technique. Int. Arab J. Inf. Technol. 2020, 17, 215–224. [Google Scholar] [CrossRef]
- Fatani, A.; Abd Elaziz, M.; Dahou, A.; Al-Qaness, M.A.; Lu, S. IoT intrusion detection system using deep learning and enhanced transient search optimization. IEEE Access 2021, 9, 123448–123464. [Google Scholar] [CrossRef]
- Qaiwmchi, N.A.H.; Amintoosi, H.; Mohajerzadeh, A. Intrusion detection system based on gradient-corrected online sequential extreme learning machine. IEEE Access 2020, 9, 4983–4999. [Google Scholar] [CrossRef]
- Pandey, J.K.; Kumar, S.; Lamin, M.; Gupta, S.; Dubey, R.K.; Sammy, F. A Metaheuristic Autoencoder Deep Learning Model for Intrusion Detector System. Math. Probl. Eng. 2022, 2022, 3859155. [Google Scholar] [CrossRef]
- Almomani, O. A hybrid model using bio-inspired metaheuristic algorithms for network intrusion detection system. Comput. Mater. Contin 2021, 68, 409–429. [Google Scholar] [CrossRef]
- Kagade, R.B.; Jayagopalan, S. Optimization-assisted DL-based intrusion detection system in a wireless sensor network with two-tier trust evaluation. Int. J. Netw. Manag. 2022, 32, e2196. [Google Scholar] [CrossRef]
- Krishnan, R.; Krishnan, R.S.; Robinson, Y.H.; Julie, E.G.; Long, H.V.; Sangeetha, A.; Subramanian, M.; Kumar, R. An intrusion detection and prevention protocol for internet of things based wireless sensor networks. Wirel. Pers. Commun. 2022, 124, 3461–3483. [Google Scholar] [CrossRef]
- Yadav, N.; Pande, S.; Khamparia, A.; Gupta, D. Intrusion detection system on IoT with 5G network using deep learning. Wirel. Commun. Mob. Comput. 2022, 2022, 9304689. [Google Scholar] [CrossRef]
- Zhiqiang, L.; Mohiuddin, G.; Jiangbin, Z.; Asim, M.; Sifei, W. Intrusion detection in wireless sensor network using enhanced empirical-based component analysis. Future Gener. Comput. Syst. 2022, 135, 181–193. [Google Scholar] [CrossRef]
- Muruganandam, S.; Joshi, R.; Suresh, P.; Balakrishna, N.; Kishore, K.H.; Manikanthan, S.V. A deep learning-based feed-forward artificial neural network to predict the K-barriers for intrusion detection using a wireless sensor network. Meas. Sens. 2022, 25, 100613. [Google Scholar] [CrossRef]
- Subramani, S.; Selvi, M. Multi-objective PSO-based feature selection for intrusion detection in IoT-based wireless sensor networks. Optik 2023, 273, 170419. [Google Scholar] [CrossRef]
- Saba, T.; Rehman, A.; Sadad, T.; Kolivand, H.; Bahaj, S.A. Anomaly-based intrusion detection system for IoT networks through deep learning model. Comput. Electr. Eng. 2022, 99, 107810. [Google Scholar] [CrossRef]
- Sadeghi, F.; Larijani, A.; Rostami, O.; Martín, D.; Hajirahimi, P. A Novel Multi-Objective Binary Chimp Optimization Algorithm for Optimal Feature Selection: Application of Deep-Learning-Based Approaches for SAR Image Classification. Sensors 2023, 23, 1180. [Google Scholar] [CrossRef]
- Henry, A.; Gautam, S.; Khanna, S.; Rabie, K.; Shongwe, T.; Bhattacharya, P.; Sharma, B.; Chowdhury, S. Composition of Hybrid Deep Learning Model and Feature Optimization for Intrusion Detection System. Sensors 2023, 23, 890. [Google Scholar] [CrossRef] [PubMed]
- Balla, A.; Habaebi, M.H.; Elsheikh, E.A.A.; Islam, M.R.; Suliman, F.M. The Effect of Dataset Imbalance on the Performance of SCADA Intrusion Detection Systems. Sensors 2023, 23, 758. [Google Scholar] [CrossRef] [PubMed]
- Abosata, N.; Al-Rubaye, S.; Inalhan, G. Customised Intrusion Detection for an Industrial IoT Heterogeneous Network Based on Machine Learning Algorithms Called FTL-CID. Sensors 2023, 23, 321. [Google Scholar] [CrossRef] [PubMed]
- Salman, E.H.; Taher, M.A.; Hammadi, Y.I.; Mahmood, O.A.; Muthanna, A.; Koucheryavy, A. An Anomaly Intrusion Detection for High-Density Internet of Things Wireless Communication Network Based Deep Learning Algorithms. Sensors 2023, 23, 206. [Google Scholar] [CrossRef]
- Hafeez, G.; Khan, I.; Jan, S.; Shah, I.A.; Khan, F.A.; Derhab, A. A novel hybrid load forecasting framework with intelligent feature engineering and optimization algorithm in smart grid. Appl. Energy 2021, 299, 117178. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, J.; Guo, Y.N.; Cheng, S.; Yang, L.; Zhang, P. Adaptive CCR-ELM with variable-length brainstorm optimization algorithm for class-imbalance learning. Nat. Comput. 2021, 20, 11–22. [Google Scholar] [CrossRef]
- Abdelhamid, A.A.; El-Kenawy, E.S.M.; Khodadadi, N.; Mirjalili, S.; Khafaga, D.S.; Alharbi, A.H.; Ibrahim, A.; Eid, M.M.; Saber, M. Classification of monkeypox images based on transfer learning and the Al-Biruni Earth Radius Optimization algorithm. Mathematics 2022, 10, 3614. [Google Scholar] [CrossRef]
- Almomani, I.; Al-Kasasbeh, B.; Al-Akhras, M. WSN-DS: A Dataset for Intrusion Detection Systems in Wireless Sensor Networks. J. Sens. 2016, 2016, 4731953. [Google Scholar] [CrossRef]
- Alqahtani, M.; Gumaei, A.; Mathkour, H.; Maher Ben Ismail, M. A genetic-based extreme gradient boosting model for detecting intrusions in wireless sensor networks. Sensors 2019, 19, 4383. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, H.; Fan, F.; Liu, G.; Xu, Q.; Nazir, S. An enhanced intrusion detection model based on improved kNN in WSNs. Sensors 2022, 22, 1407. [Google Scholar] [CrossRef] [PubMed]







| Class | No. of Samples |
|---|---|
| Normal | 340,066 |
| Blackhole | 10,049 |
| Grayhole | 14,596 |
| Flooding | 3312 |
| Scheduling Attacks | 6638 |
| Total Number of Samples | 374,661 |
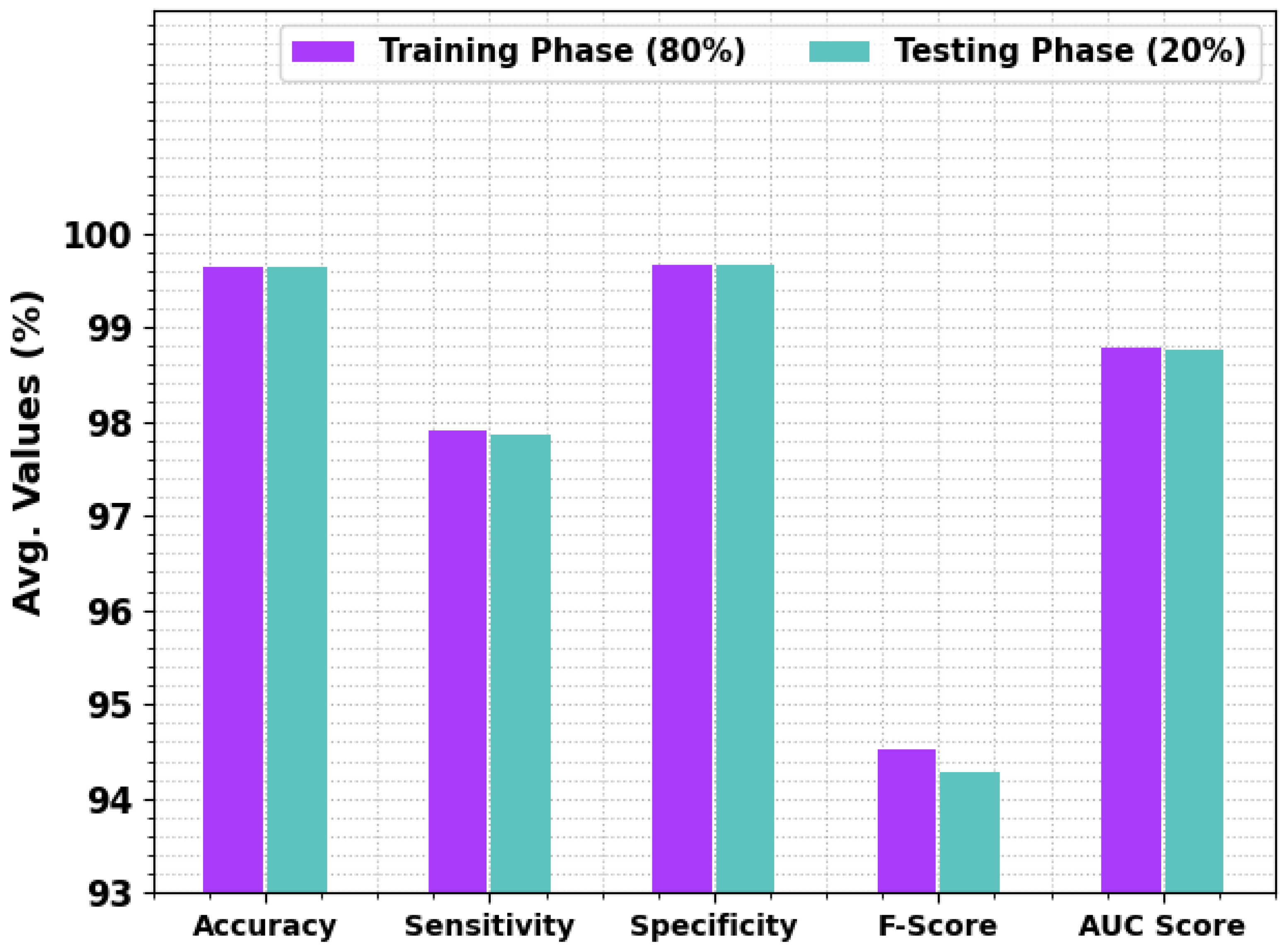
| Class Labels | Accuy | Sensy | Specy | Fscore | AUCscore |
|---|---|---|---|---|---|
| Training Phase (80%) | |||||
| Normal | 99.19 | 99.19 | 99.21 | 99.55 | 99.20 |
| Blackhole | 99.75 | 98.44 | 99.79 | 95.46 | 99.11 |
| Grayhole | 99.71 | 98.45 | 99.76 | 96.38 | 99.11 |
| Flooding | 99.77 | 95.64 | 99.80 | 87.84 | 97.72 |
| Scheduling Attacks | 99.75 | 97.84 | 99.79 | 93.39 | 98.81 |
| Average | 99.63 | 97.91 | 99.67 | 94.52 | 98.79 |
| Testing Phase (20%) | |||||
| Normal | 99.17 | 99.17 | 99.16 | 99.54 | 99.16 |
| Blackhole | 99.77 | 98.72 | 99.80 | 95.87 | 99.26 |
| Grayhole | 99.73 | 98.45 | 99.78 | 96.53 | 99.11 |
| Flooding | 99.73 | 94.79 | 99.78 | 86.43 | 97.28 |
| Scheduling Attacks | 99.75 | 98.18 | 99.78 | 93.03 | 98.98 |
| Average | 99.63 | 97.86 | 99.66 | 94.28 | 98.76 |
| Class Labels | Accuy | Sensy | Specy | Fscore | AUCscore |
|---|---|---|---|---|---|
| Training Phase (70%) | |||||
| Normal | 98.63 | 98.90 | 95.99 | 99.25 | 97.45 |
| Blackhole | 99.39 | 94.15 | 99.53 | 89.19 | 96.84 |
| Grayhole | 99.28 | 87.97 | 99.74 | 90.46 | 93.85 |
| Flooding | 99.45 | 82.38 | 99.60 | 72.83 | 90.99 |
| Scheduling Attacks | 99.21 | 86.39 | 99.44 | 79.43 | 92.92 |
| Average | 99.19 | 89.96 | 98.86 | 86.23 | 94.41 |
| Testing Phase (30%) | |||||
| Normal | 98.63 | 98.92 | 95.76 | 99.24 | 97.34 |
| Blackhole | 99.39 | 94.27 | 99.53 | 89.29 | 96.90 |
| Grayhole | 99.25 | 87.55 | 99.74 | 90.27 | 93.64 |
| Flooding | 99.43 | 81.72 | 99.58 | 70.90 | 90.65 |
| Scheduling Attacks | 99.19 | 84.57 | 99.45 | 78.82 | 92.01 |
| Average | 99.18 | 89.41 | 98.81 | 85.70 | 94.11 |
| Methods | Accuy | Sensy | Specy | Fscore |
|---|---|---|---|---|
| BCOA-MLID | 99.63 | 97.91 | 99.67 | 94.52 |
| AdaBoost | 95.69 | 95.77 | 95.00 | 90.31 |
| GB Model | 94.58 | 95.25 | 94.09 | 93.31 |
| XGBoost | 96.83 | 96.10 | 94.43 | 91.52 |
| KNN-AOA | 97.20 | 96.49 | 96.34 | 90.23 |
| KNN-PSO | 92.89 | 95.63 | 95.08 | 92.99 |
| Methods | Computational Time (s) |
|---|---|
| BCOA-MLID | 7.26 |
| AdaBoost | 15.65 |
| GB Model | 12.75 |
| XGBoost | 13.67 |
| KNN | 15.01 |
| KNN-PSO | 14.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljebreen, M.; Alohali, M.A.; Saeed, M.K.; Mohsen, H.; Al Duhayyim, M.; Abdelmageed, A.A.; Drar, S.; Abdelbagi, S. Binary Chimp Optimization Algorithm with ML Based Intrusion Detection for Secure IoT-Assisted Wireless Sensor Networks. Sensors 2023, 23, 4073. https://doi.org/10.3390/s23084073
Aljebreen M, Alohali MA, Saeed MK, Mohsen H, Al Duhayyim M, Abdelmageed AA, Drar S, Abdelbagi S. Binary Chimp Optimization Algorithm with ML Based Intrusion Detection for Secure IoT-Assisted Wireless Sensor Networks. Sensors. 2023; 23(8):4073. https://doi.org/10.3390/s23084073
Chicago/Turabian StyleAljebreen, Mohammed, Manal Abdullah Alohali, Muhammad Kashif Saeed, Heba Mohsen, Mesfer Al Duhayyim, Amgad Atta Abdelmageed, Suhanda Drar, and Sitelbanat Abdelbagi. 2023. "Binary Chimp Optimization Algorithm with ML Based Intrusion Detection for Secure IoT-Assisted Wireless Sensor Networks" Sensors 23, no. 8: 4073. https://doi.org/10.3390/s23084073
APA StyleAljebreen, M., Alohali, M. A., Saeed, M. K., Mohsen, H., Al Duhayyim, M., Abdelmageed, A. A., Drar, S., & Abdelbagi, S. (2023). Binary Chimp Optimization Algorithm with ML Based Intrusion Detection for Secure IoT-Assisted Wireless Sensor Networks. Sensors, 23(8), 4073. https://doi.org/10.3390/s23084073







