Dynamic Path Planning of AGV Based on Kinematical Constraint A* Algorithm and Following DWA Fusion Algorithms
Abstract
:1. Introduction
- (1)
- Improve the child node selection method and heuristic function of A* algorithm. This can improve the search efficiency of the algorithm. Reduce computing burden. Make the generated path more realistic;
- (2)
- For secondary redundant node removal, use B spline curve for smoothness constraint. This reduces the number of redundant points in the path. The generated path conforms to the dynamic constraints;
- (3)
- Intercept the key node information and apply improved DWA algorithm to make the local path planning follow the global path contour, so as to make the path smoother and achieve avoidance of local dynamic obstacle. It can prevent DWA algorithm from falling into local optimal. It allows the mobile robot to avoid moving obstacles.
2. Improved A* Algorithm
2.1. Node Optimization
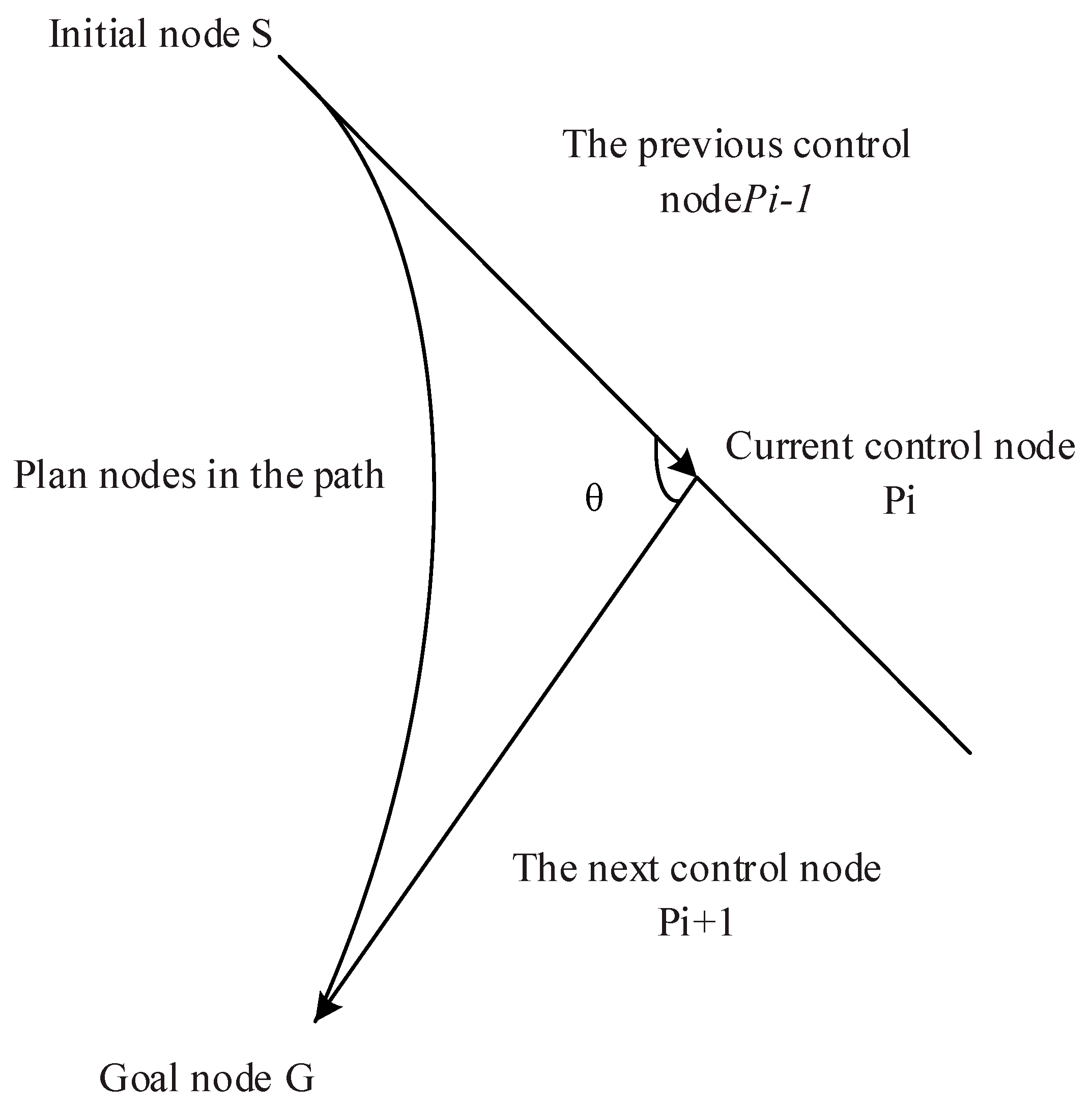
2.2. Improved Heuristic Function
2.3. Redundancy Removal
2.4. B Spline Curve Smoothing Constraints
3. Improved DWA Algorithm
3.1. Motion Model of Mobile Robot
3.2. Speed Sampling for Mobile Robots
3.3. Optimization of Evaluation Function
3.4. Algorithm Fusion
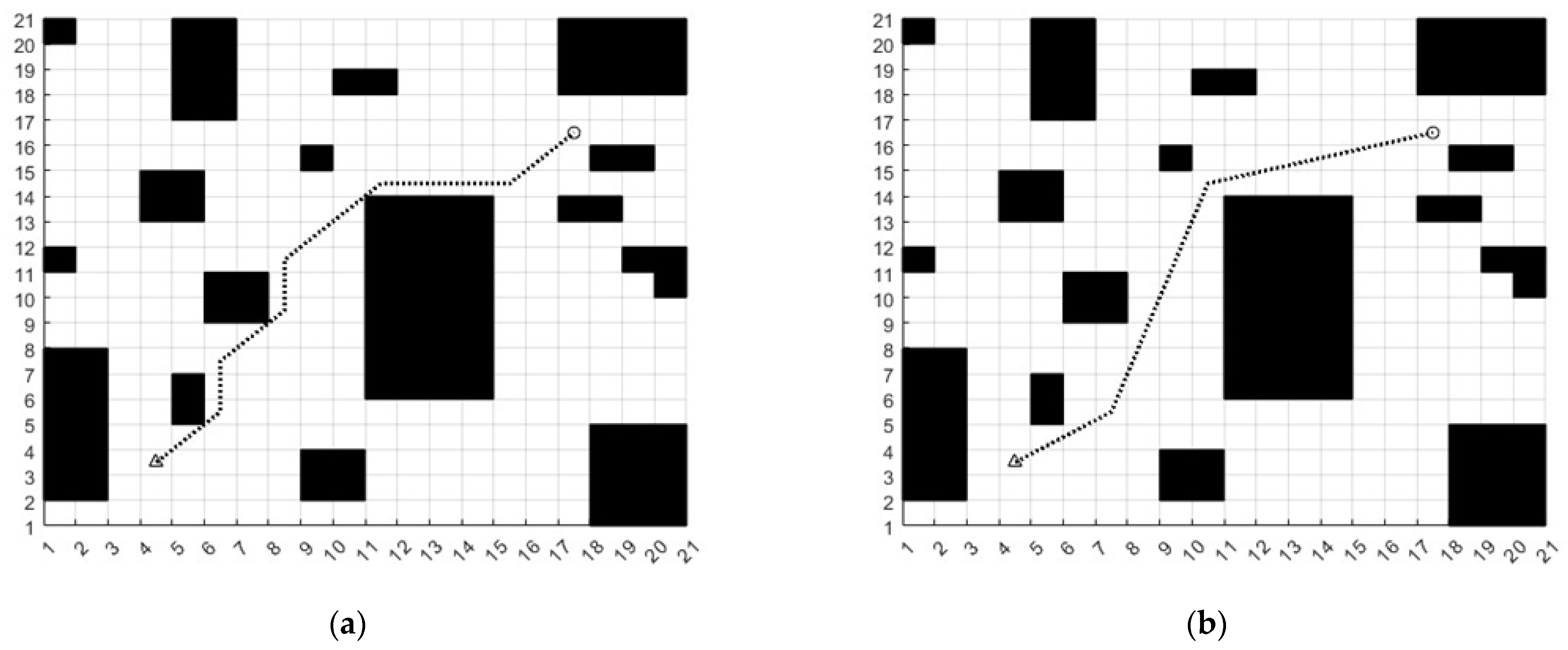
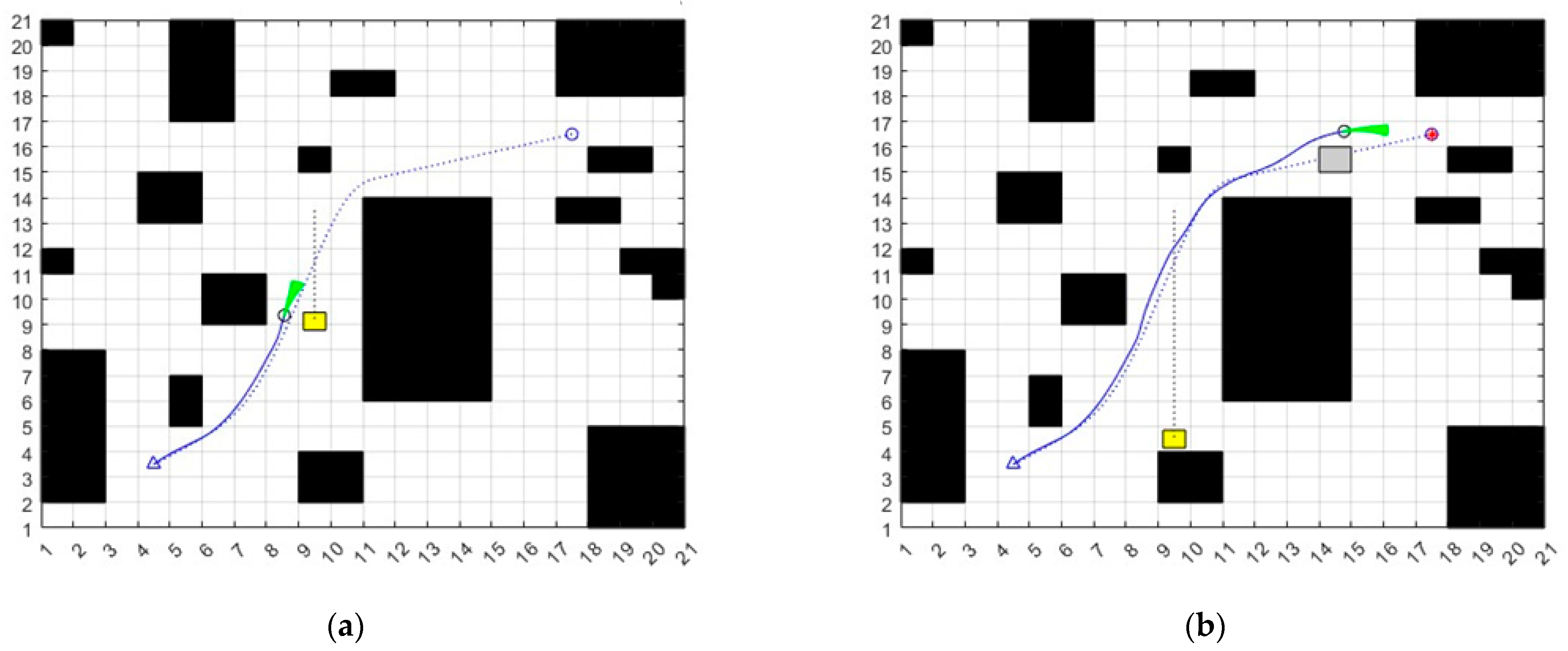
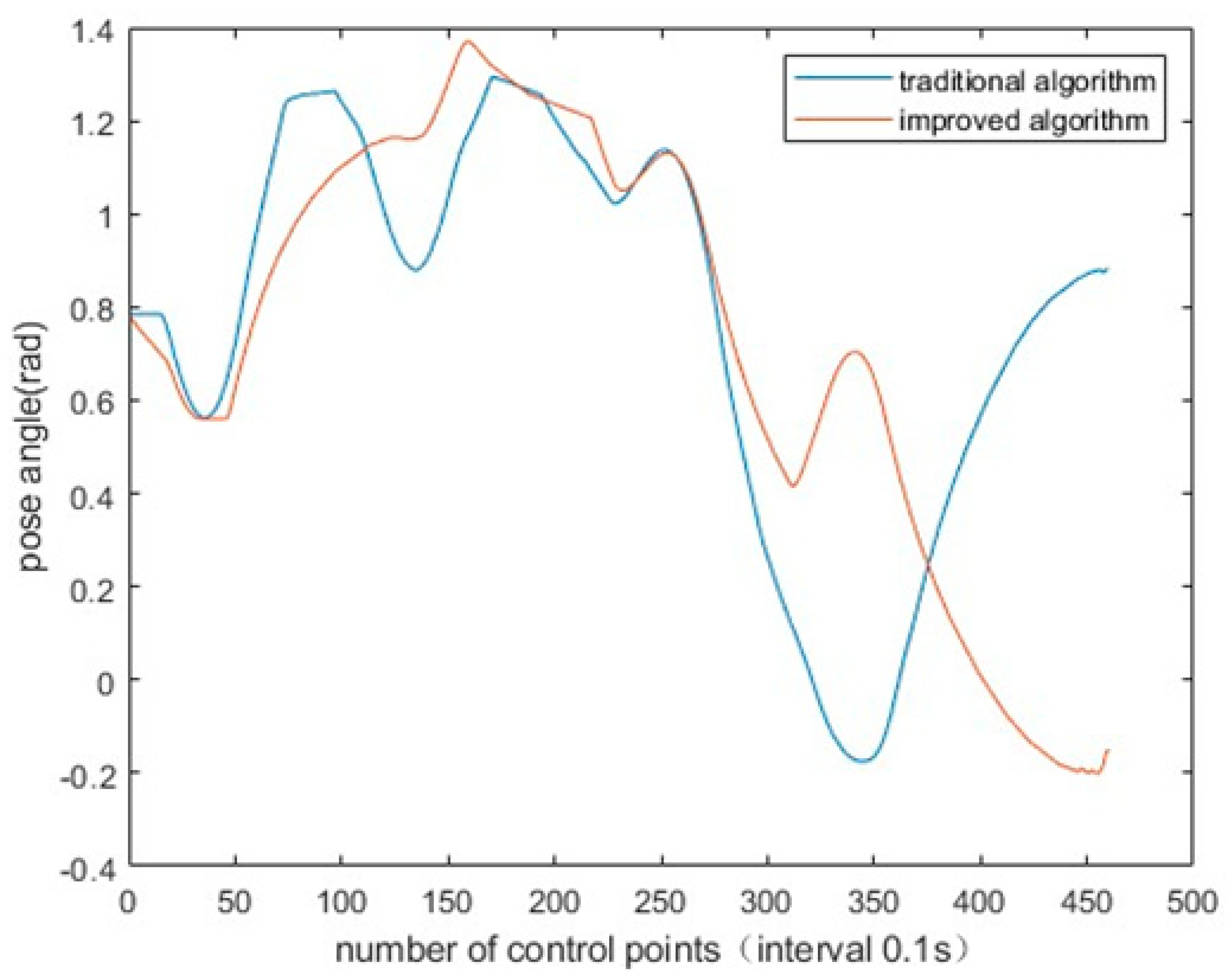
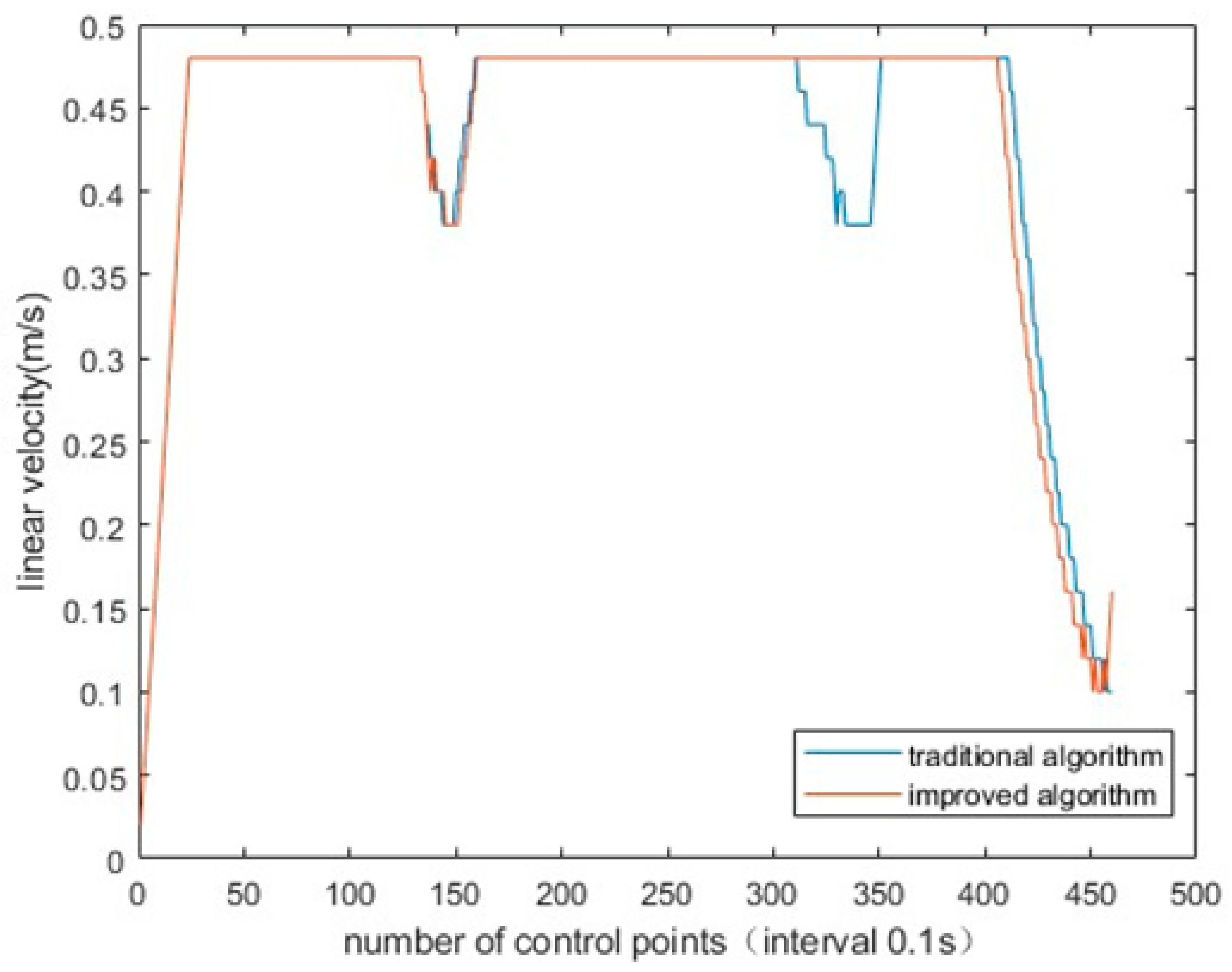
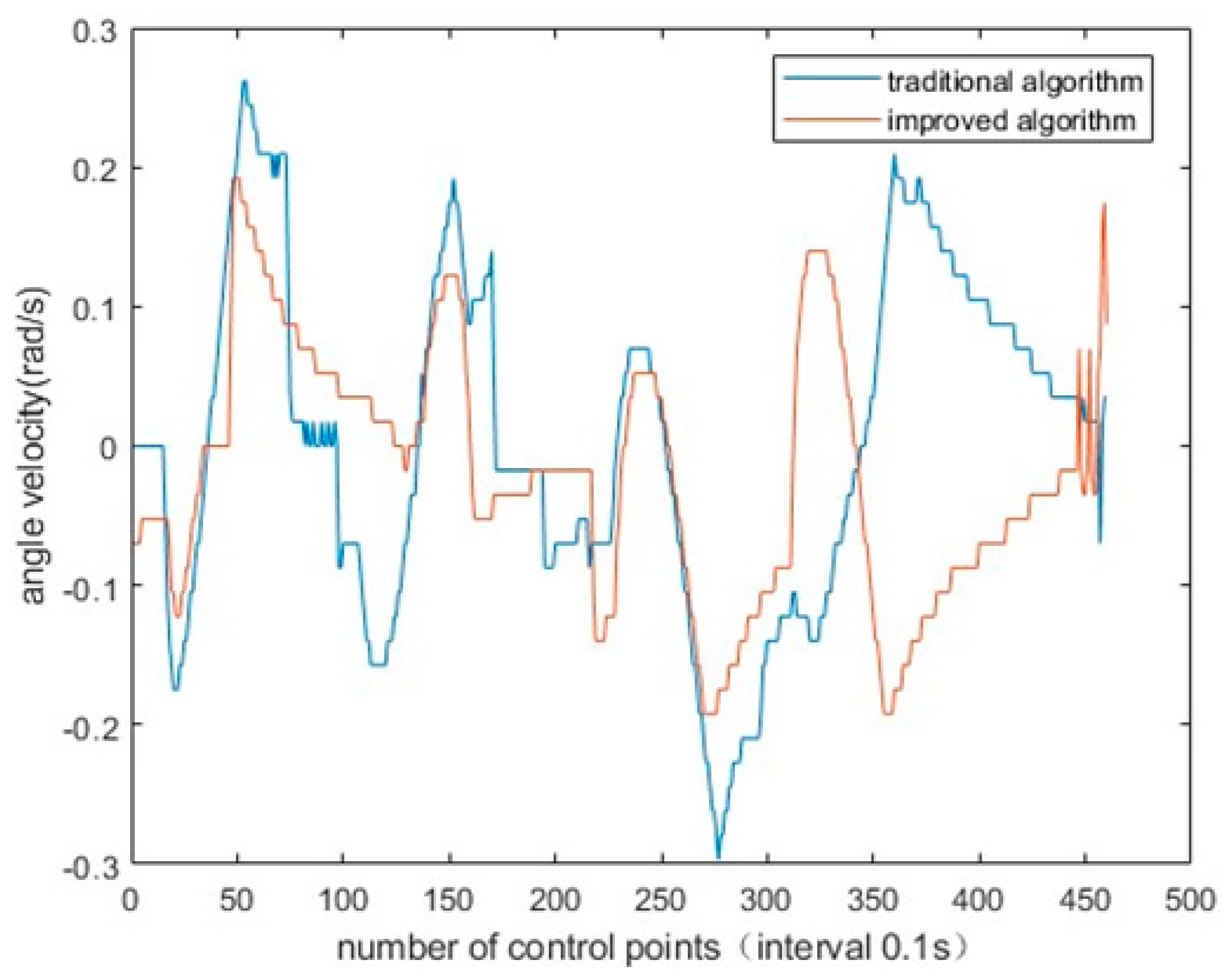
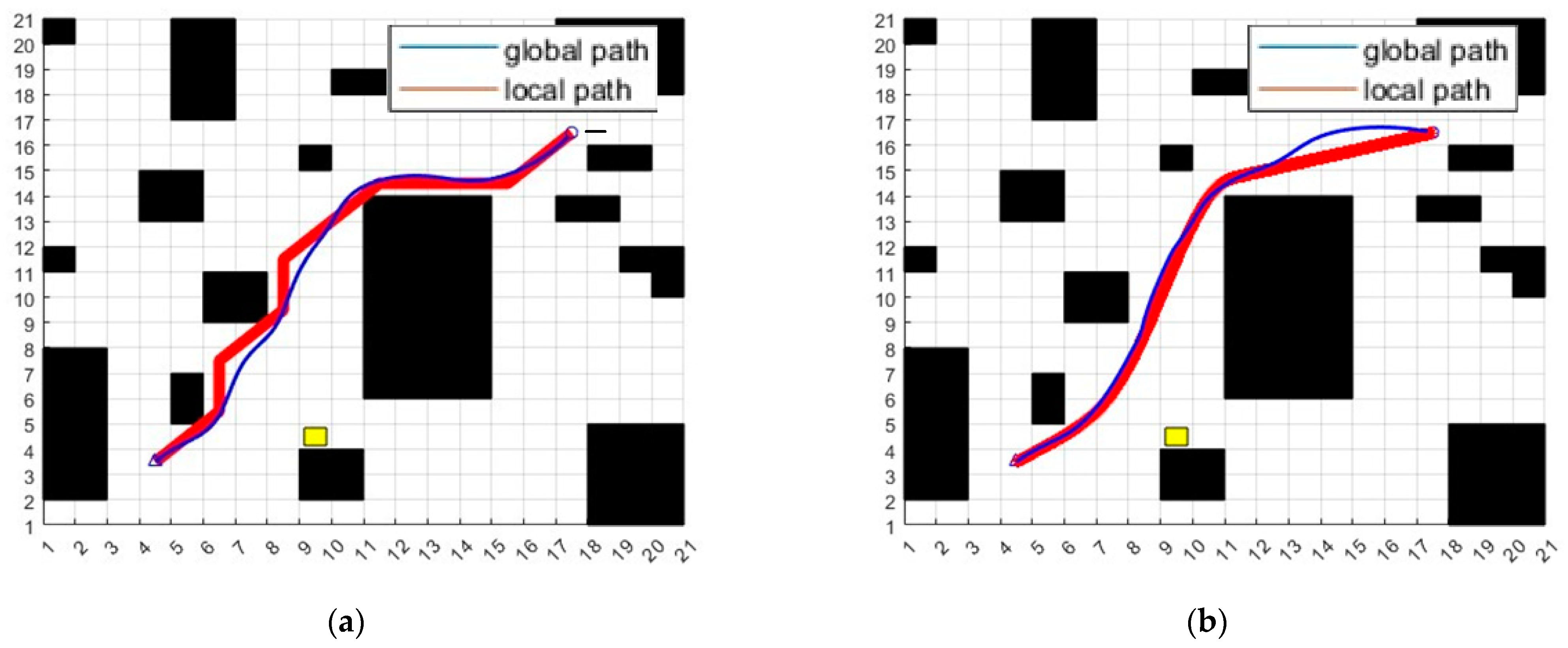
4. Experimental and Results
5. Conclusions
- (1)
- In fusion algorithm, the kinematic characteristics of the mobile robot are considered. The energy efficiency of the mobile robot is not considered. This may not save energy on mobile robots;
- (2)
- The fusion algorithm in this paper does not integrate environmental awareness. It only carries out path planning on the established map. There is a need to integrate efficient perception methods.
- (1)
- The fusion algorithm is applied to a real mobile robot. Verify the feasibility of fusion algorithm in a real mobile robot. The fusion algorithm is tested on different mobile robots. Verify the compatibility of the fusion algorithm. Test the fusion algorithm in different environments. Some coefficients in the fusion algorithm are adjusted for different environments;
- (2)
- Coordinate and control robot clusters to prevent conflicts. Multi-machine collaboration can expand the working radius of the mobile robots. Autonomously assign multiple tasks. Multi-task assignment can make the mobile robots work more efficiently. Research is a hot topic.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wu, B.; Chi, X.; Zhao, C.; Zhang, W.; Lu, Y.; Jiang, D. Dynamic Path Planning for Forklift AGV Based on Smoothing A* and Improved DWA Hybrid Algorithm. Sensors 2022, 22, 7079. [Google Scholar] [CrossRef] [PubMed]
- Shivgan, R.; Dong, Z. Energy-efficient drone coverage path planning using genetic algorithm. In Proceedings of the 2020 IEEE 21st International Conference on High Performance Switching and Routing (HPSR), Newark, NJ, USA, 11–14 May 2020; pp. 1–6. [Google Scholar]
- Xiang, D.; Lin, H.; Ouyang, J.; Huang, D. Combined improved A* and greedy algorithm for path planning of multi-objective mobile robot. Sci. Rep. 2022, 12, 13273. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Jiang, H.; Cui, J.; Lu, K.; Chen, P.; Zhang, M. UAV Path Planning Based on Improved A* and DWA Algorithms. Int. J. Aerosp. Eng. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Zhou, S.; Cheng, G.; Meng, Q.; Lin, H.; Du, Z.; Wang, F. Development of multi-sensor information fusion and AGV navigation system. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; Volume 1, pp. 2043–2046. [Google Scholar]
- Chang, X.; Ren, P.; Xu, P.; Li, Z.; Chen, X.; Hauptmann, A. A comprehensive survey of scene graphs: Generation and application. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 45, 1–26. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, Y.; Guan, Y. Research on hybrid-load AGV dispatching problem for mixed-model automobile assembly line. Procedia CIRP 2019, 81, 1059–1064. [Google Scholar] [CrossRef]
- Zhang, L.; Chang, X.; Liu, J.; Luo, M.; Li, Z.; Yao, L.; Hauptmann, A. TN-ZSTAD: Transferable Network for Zero-Shot Temporal Activity Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 3848–3861. [Google Scholar] [CrossRef]
- Manikandan, S.; Kaliyaperumal, G.; Hakak, S.; Gadekallu, T.R. Curve-Aware Model Predictive Control (C-MPC) Trajectory Tracking for Automated Guided Vehicle (AGV) over On-Road, In-Door, and Agricultural-Land. Sustainability 2022, 14, 12021. [Google Scholar] [CrossRef]
- Li, M.; Huang, P.Y.; Chang, X.; Hu, J.; Yang, Y.; Hauptmann, A. Video pivoting unsupervised multi-modal machine translation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 3918–3932. [Google Scholar] [CrossRef]
- Yan, C.; Chang, X.; Li, Z.; Guan, W.; Ge, Z.; Zhu, L.; Zheng, Q. Zeronas: Differentiable generative adversarial networks search for zero-shot learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 9733–9740. [Google Scholar] [CrossRef]
- Luo, Q.; Wang, H.; Zheng, Y.; He, J. Research on path planning of mobile robot based on improved ant colony algorithm. Neural Comput. Appl. 2020, 32, 1555–1566. [Google Scholar] [CrossRef]
- Sang, H.; You, Y.; Sun, X.; Zhou, Y.; Liu, F. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations. Ocean Eng. 2021, 223, 108709. [Google Scholar] [CrossRef]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A* algorithm: An improved A* algorithm for AGV path planning in a port environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Wang, H.; Lou, S.; Jing, J.; Wang, Y.; Liu, W.; Liu, T. The EBS-A* algorithm: An improved A* algorithm for path planning. PLoS ONE 2022, 17, e0263841. [Google Scholar] [CrossRef] [PubMed]
- Bayerlein, H.; Theile, M.; Caccamo, M.; Gesbert, D. Multi-UAV path planning for wireless data harvesting with deep reinforcement learning. IEEE Open J. Commun. Soc. 2021, 2, 1171–1187. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, J.; Zhao, Y.; Zhu, Z.; Hao, G. Based on kalman filter to improve the compression algorithm of vehicle tracking perception. J. Hunan Univ. (Nat. Sci. Ed.) 2023, 50, 11–21. [Google Scholar]
- Li, F.F.; Du, Y.; Jia, K.J. Path planning and smoothing of mobile robot based on improved artificial fish swarm algorithm. Sci. Rep. 2022, 12, 659. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, D.; Tao, B.; Jiang, G.; Sun, Y.; Kong, J.; Tong, X.; Zhao, G.; Chen, B. Genetic algorithm-based trajectory optimization for digital twin robots. Front. Bioeng. Biotechnol. 2022, 9, 1433. [Google Scholar] [CrossRef]
- Yuan, C.; Liu, G.; Zhang, W.; Pan, X. An efficient RRT cache method in dynamic environments for path planning. Robot. Auton. Syst. 2020, 131, 103595. [Google Scholar] [CrossRef]
- Sharma, K.; Swarup, C.; Pandey, S.K.; Kumar, A.; Doriya, R.; Singh, K.U.; Singh, T. Early Detection of Obstacle to Optimize the Robot Path Planning. Drones 2022, 6, 265. [Google Scholar] [CrossRef]
- Szczepanski, R.; Tarczewski, T.; Erwinski, K. Energy efficient local path planning algorithm based on predictive artificial potential field. IEEE Access 2022, 10, 39729–39742. [Google Scholar] [CrossRef]
- Alireza, M.; Vincent, D.; Tony, W. Experimental study of path planning problem using EMCOA for a holonomic mobile robot. J. Syst. Eng. Electron. 2021, 32, 1450–1462. [Google Scholar] [CrossRef]
- Li, Y.; Wei, W.; Gao, Y.; Wang, D.; Fan, Z. PQ-RRT*: An improved path planning algorithm for mobile robots. Expert Syst. Appl. 2020, 152, 113425. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Li, Y. Mobile robot path planning based on improved localized particle swarm optimization. IEEE Sens. J. 2020, 21, 6962–6972. [Google Scholar] [CrossRef]
- XiangRong, T.; Yukun, Z.; XinXin, J. Improved A* algorithm for robot path planning in static environment. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1792, p. 012067. [Google Scholar]
- Fu, B.; Chen, L.; Zhou, Y.; Zheng, D.; Wei, Z.; Dai, J.; Pan, H. An improved A* algorithm for the industrial robot path planning with high success rate and short length. Robot. Auton. Syst. 2018, 106, 26–37. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Wang, P.; Yang, J.; Zhang, Y.; Wang, Q.; Sun, B.; Guo, D. Obstacle-Avoidance Path-Planning Algorithm for Autonomous Vehicles Based on B-Spline Algorithm. World Electr. Veh. J. 2022, 13, 233. [Google Scholar] [CrossRef]
- Li, H.; Luo, Y.; Wu, J. Collision-free path planning for intelligent vehicles based on Bézier curve. IEEE Access 2019, 7, 123334–123340. [Google Scholar] [CrossRef]
- Sun, C.; Li, Q.; Li, L. A gridmap-path reshaping algorithm for path planning. IEEE Access 2019, 7, 183150–183161. [Google Scholar] [CrossRef]






| Θ | Keep 5 Directions | Abandon Direction |
|---|---|---|
| [337.5°, 360°) ∪ [0°, 22.5°) | 000T, 045T, 090T, 270T, 315T | 135T, 180T, 225T |
| [22.5°, 67.5°) | 000T, 045T, 090T, 135T, 315T | 180T, 225T, 270T |
| [67.5°, 112.5°) | 000T, 045T, 090T, 135T, 180T | 225T, 270T, 315T |
| [112.5°, 157.5°) | 045T, 090T, 135T, 180T, 225T | 270T, 315T, 000T |
| [157.5°, 202.5°) | 090T, 135T, 180T, 225T, 270T | 000T, 045T, 315T |
| [202.5°, 247.5°) | 135T, 180T, 225T, 270T, 315T | 000T, 045T, 090T |
| [247.5°, 292.5°) | 180T, 225T, 270T, 315T, 000T | 045T, 090T, 135T |
| [292.5°, 337.5°) | 225T, 270T, 315T, 000T, 045T | 090T, 135T, 180T |
| Map/m2 | Algorithm | Path Length (m) | Number of Turns | Path Time (s) |
|---|---|---|---|---|
| 21 × 21 | Traditional A* + DWA | 35.39 | 13 | 125 |
| Improved A* + DWA | 31.68 | 11 | 120 | |
| Traditional A* + Traditional DWA | 20.72 | 4 | 64.5 | |
| Improved A* + Improved DWA | 19.98 | 3 | 60.2 |
| Map/m2 | Obstacles | Path Length (m) | Number of Turns | Path Time (s) |
|---|---|---|---|---|
| 21 × 21 | dynamic obstacle | 19.93 | 3 | 59.6 |
| mixed obstacles | 20.2 | 4 | 60.2 |
| Algorithm | Global Optimality | Smooth Path | Local Optimality | Deceleration Obstacle Avoidance | Dynamic Obstacle Avoidance |
|---|---|---|---|---|---|
| Tradition A* | T | F | F | F | F |
| Improved A* | T | T | F | F | F |
| Hybrid Algorithm | T | T | T | T | T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.; Cai, P.; Zhao, K.; Zhang, Y.; Zhou, Q.; Yao, D. Dynamic Path Planning of AGV Based on Kinematical Constraint A* Algorithm and Following DWA Fusion Algorithms. Sensors 2023, 23, 4102. https://doi.org/10.3390/s23084102
Yin X, Cai P, Zhao K, Zhang Y, Zhou Q, Yao D. Dynamic Path Planning of AGV Based on Kinematical Constraint A* Algorithm and Following DWA Fusion Algorithms. Sensors. 2023; 23(8):4102. https://doi.org/10.3390/s23084102
Chicago/Turabian StyleYin, Xiong, Ping Cai, Kangwen Zhao, Yu Zhang, Qian Zhou, and Daojin Yao. 2023. "Dynamic Path Planning of AGV Based on Kinematical Constraint A* Algorithm and Following DWA Fusion Algorithms" Sensors 23, no. 8: 4102. https://doi.org/10.3390/s23084102
APA StyleYin, X., Cai, P., Zhao, K., Zhang, Y., Zhou, Q., & Yao, D. (2023). Dynamic Path Planning of AGV Based on Kinematical Constraint A* Algorithm and Following DWA Fusion Algorithms. Sensors, 23(8), 4102. https://doi.org/10.3390/s23084102





