Silicon Fresnel Zone Plate Metalens with Subwavelength Gratings
Abstract
:1. Introduction
2. Materials and Methods
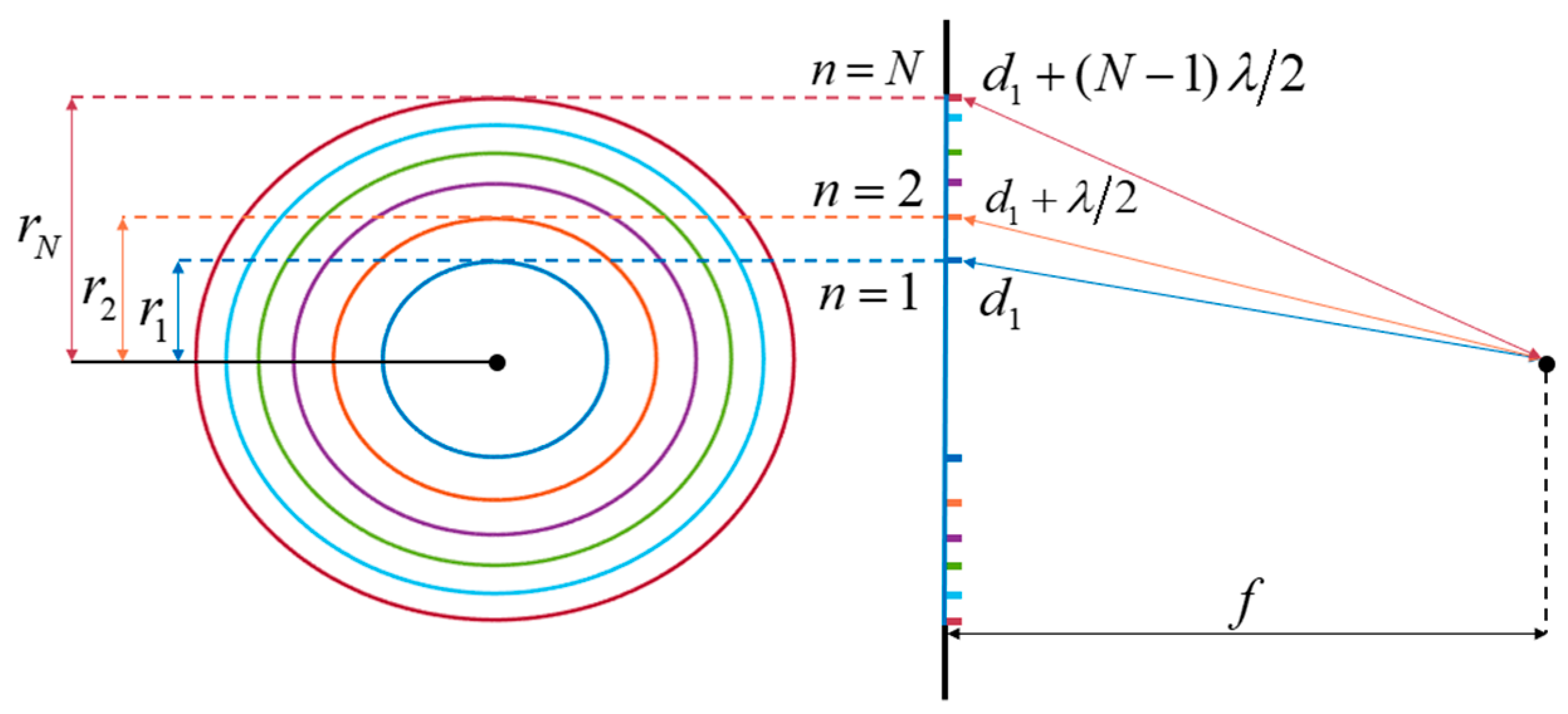
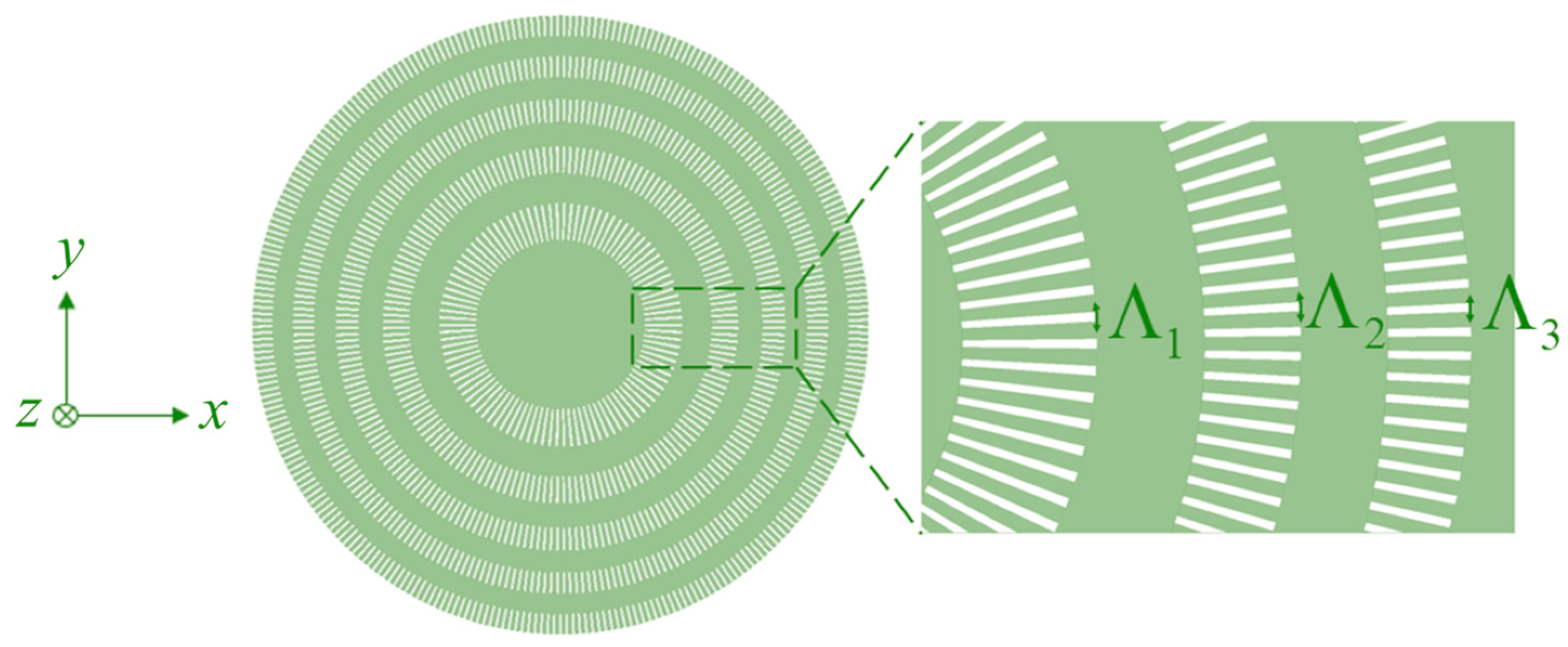
2.1. Polarization-Independent Binary Phase Fresnel Zone Plate
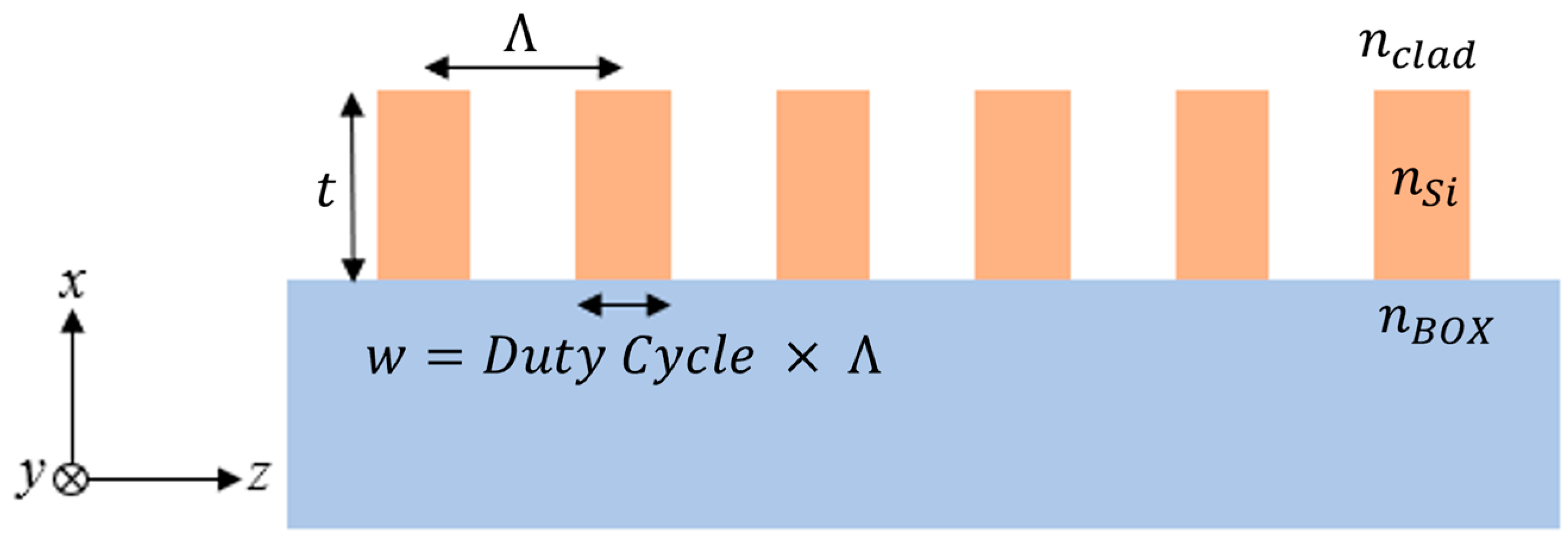
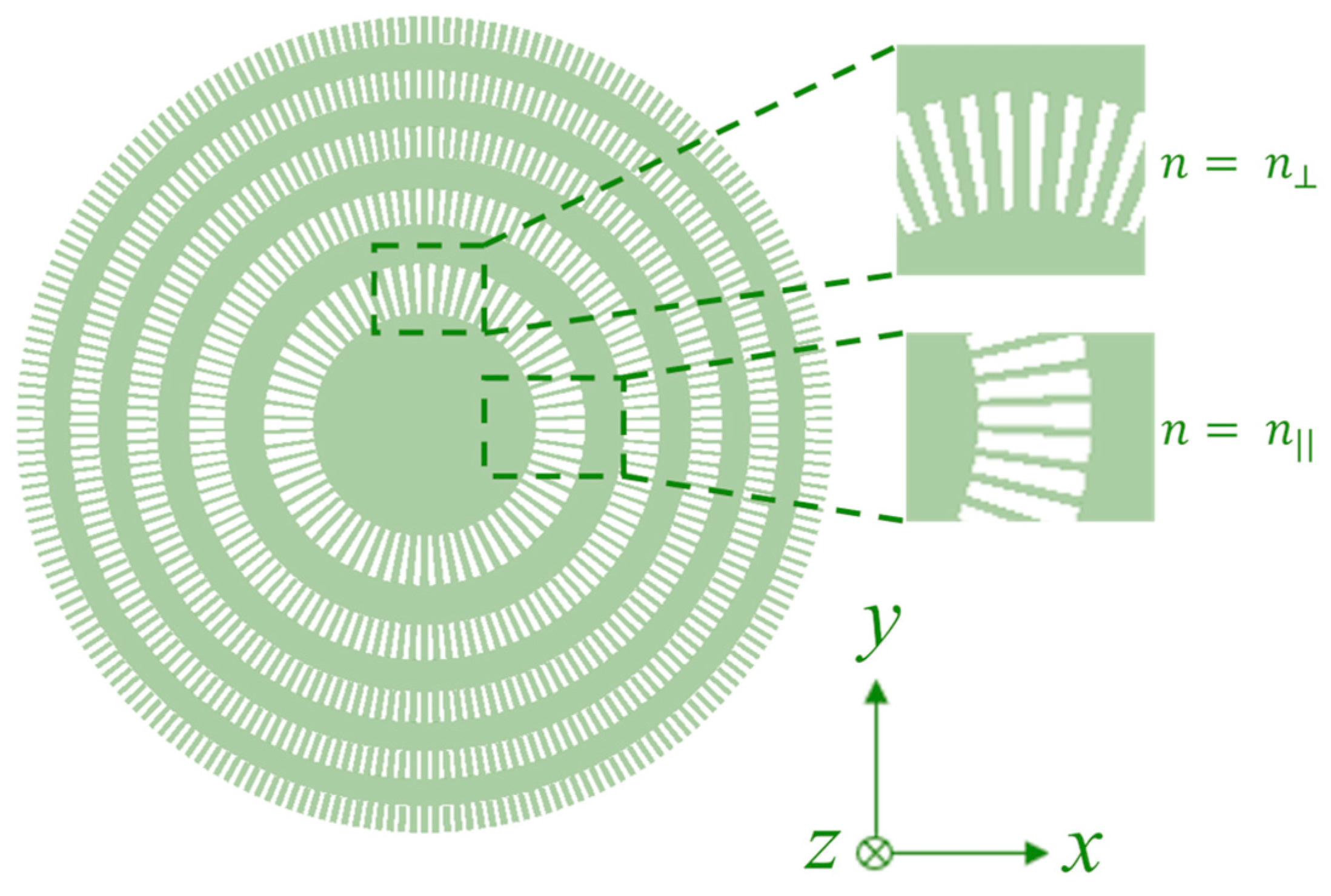
2.2. Polarization-Specific Binary Phase Fresnel Zone Plate
3. Results
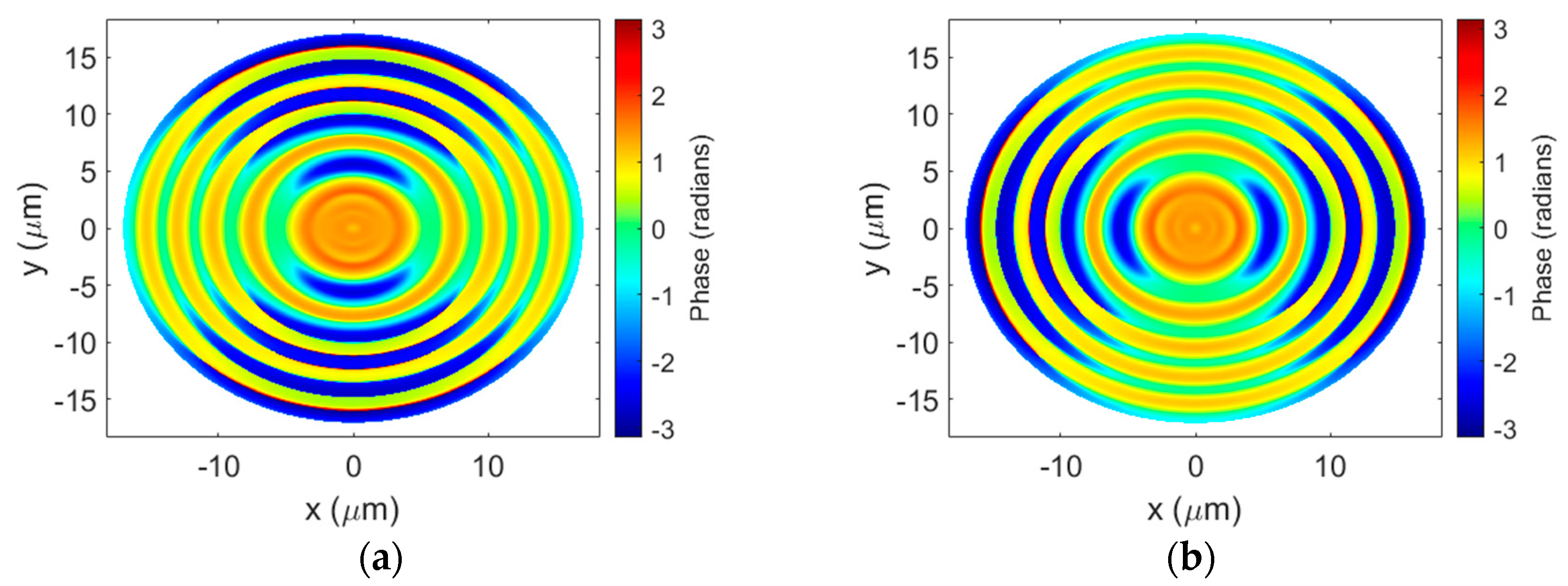
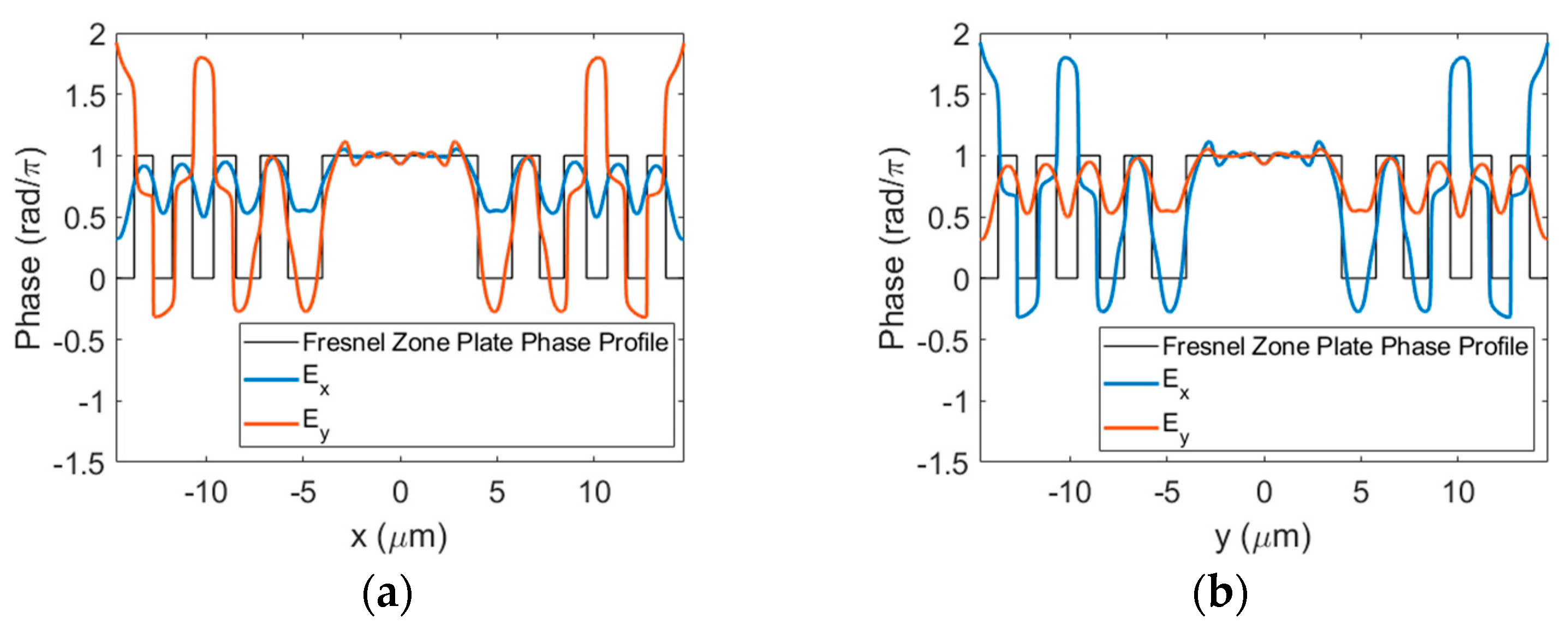
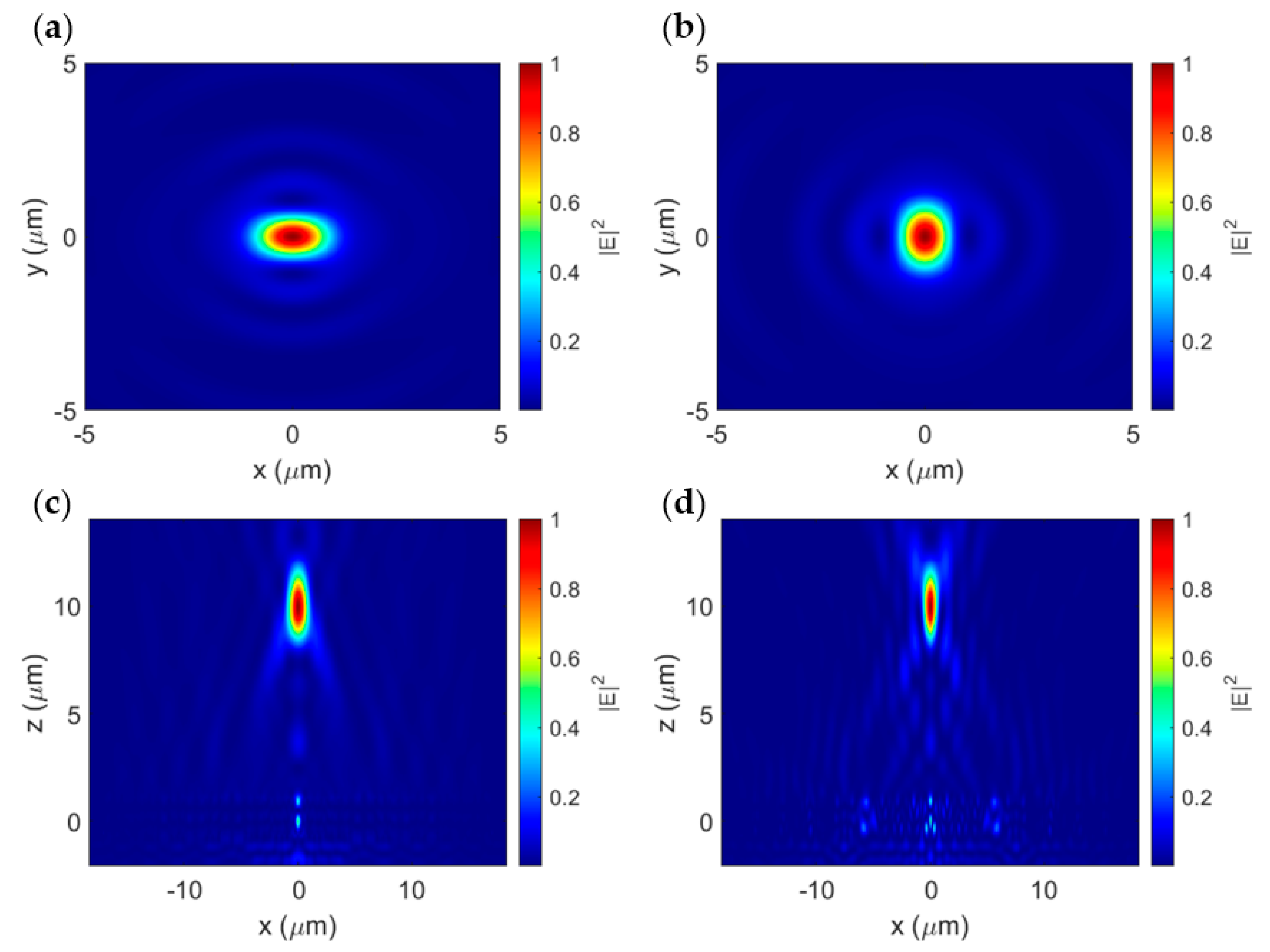
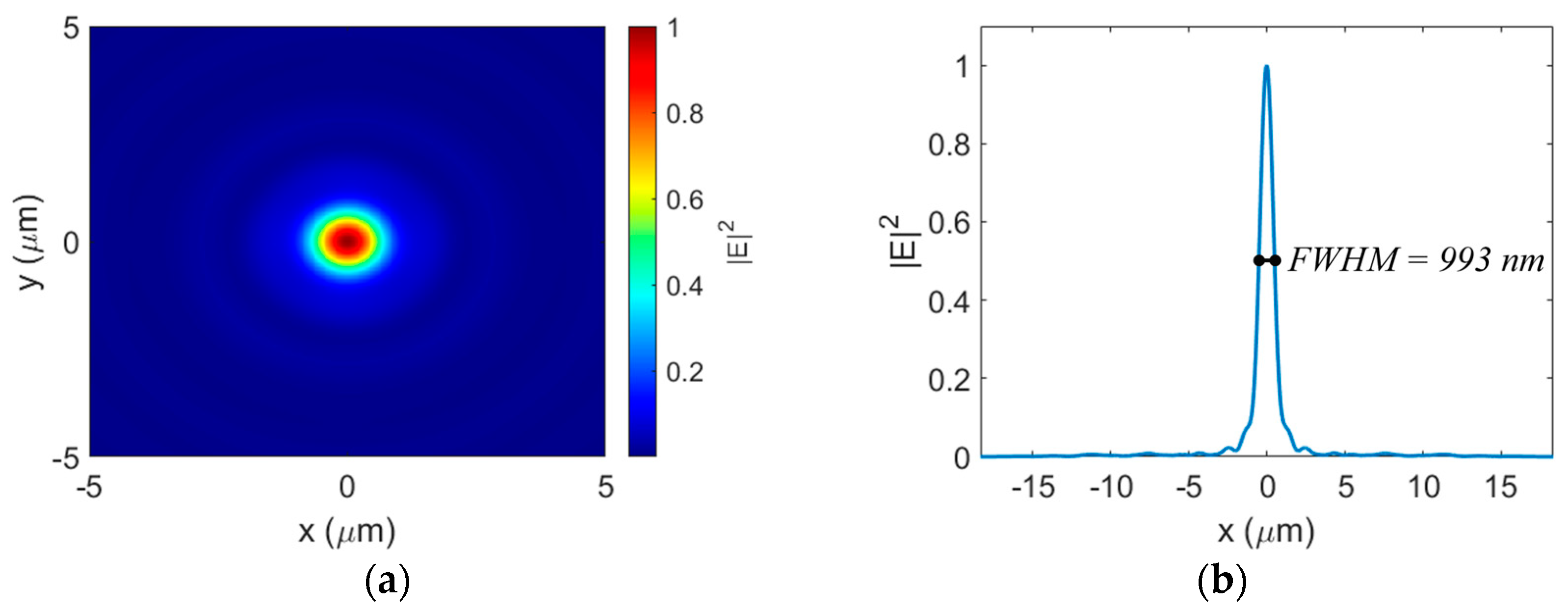
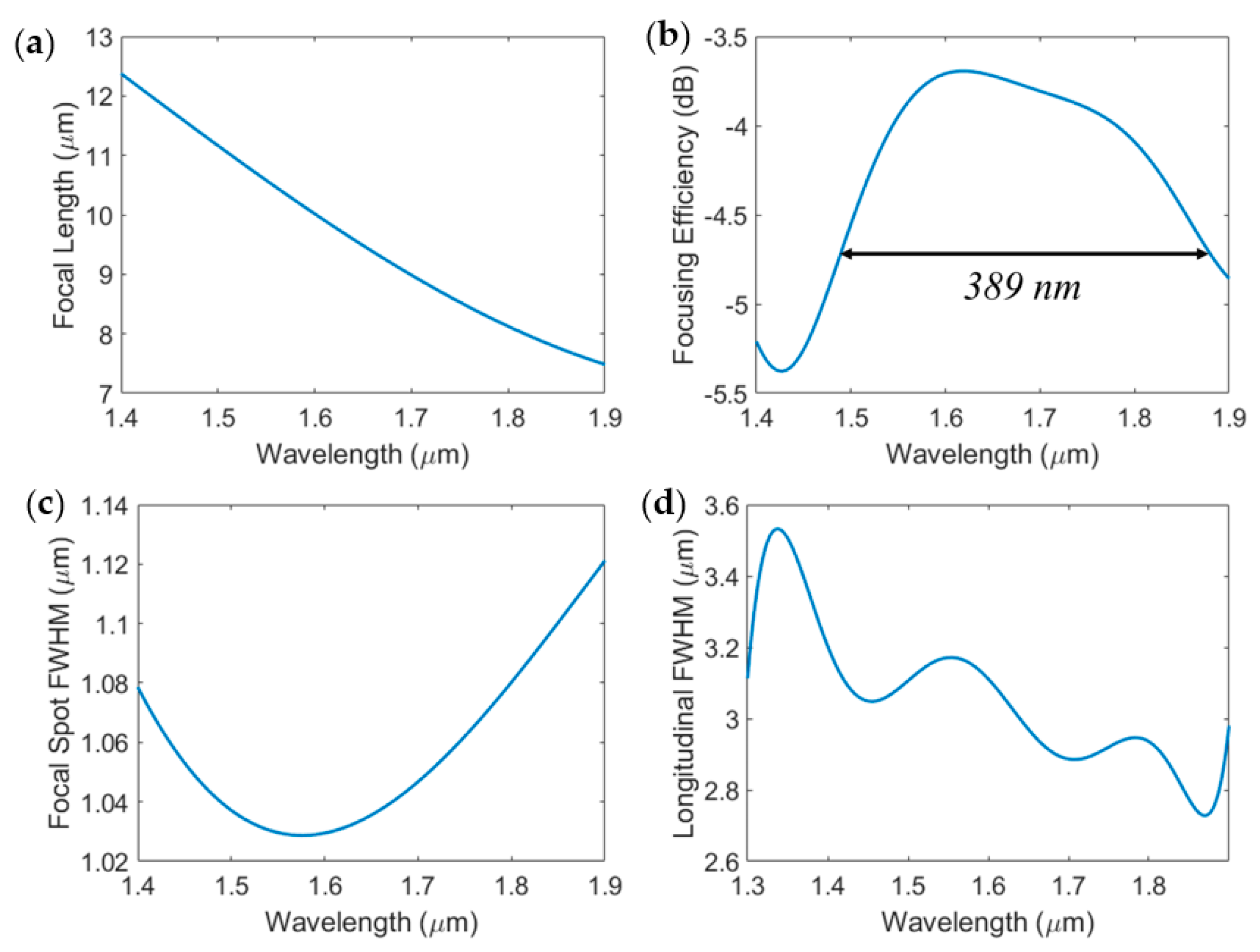
3.1. Polarization-Independent BPFZP Design
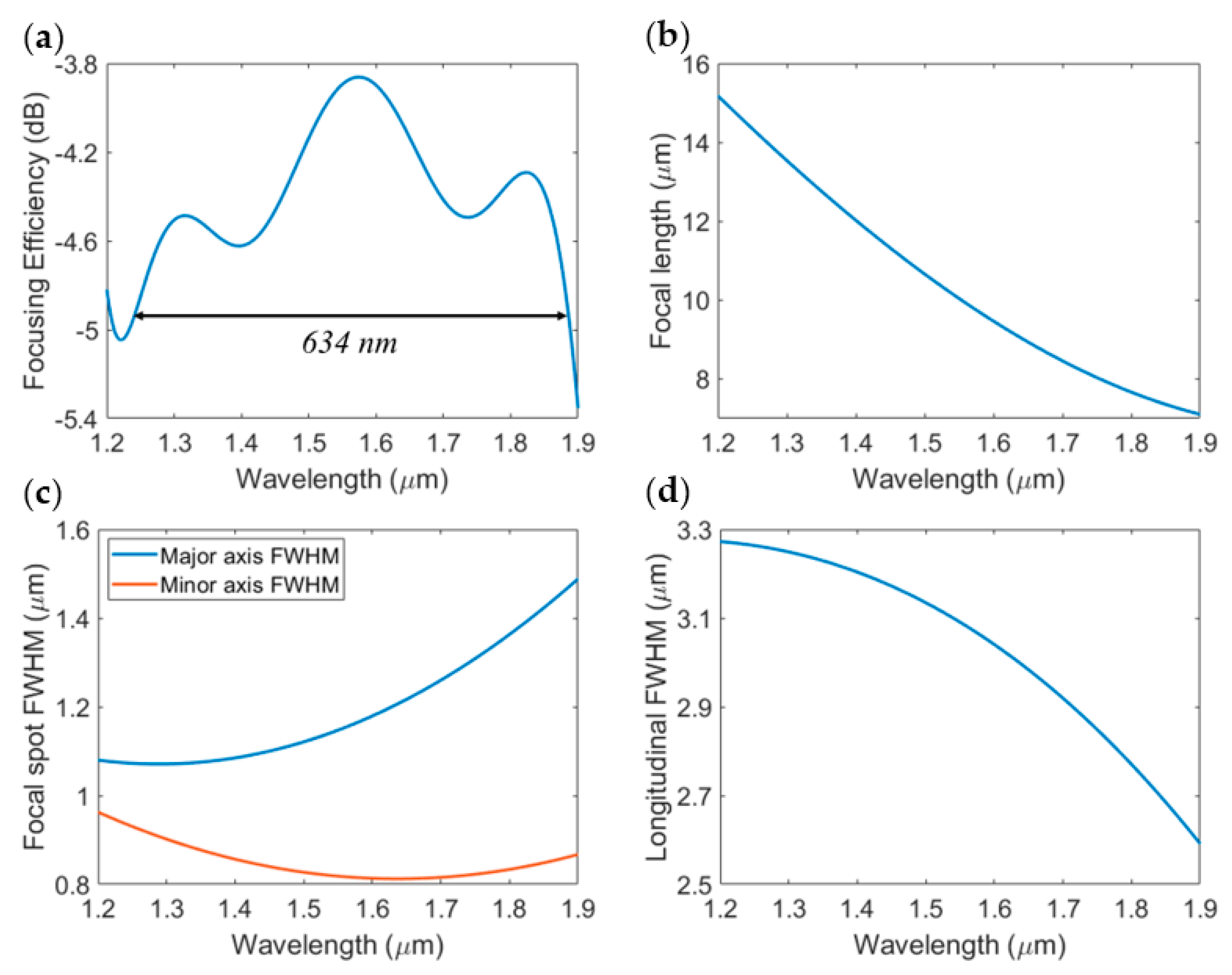
3.2. Polarization-Specific BPFZP Design
3.3. Fabrication Tolerance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-T.; Taylor, A.J.; Yu, N. A review of metasurfaces: physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Capasso, F. Metalenses: Versatile multifunctional photonic components. Science 2017, 358, eaam8100. [Google Scholar] [CrossRef]
- Engelberg, J.; Levy, U. The advantages of metalenses over diffractive lenses. Nat. Commun. 2020, 11, 1991. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, H.-H.; Chu, C.H.; Tsai, D.P. Fundamentals and Applications of Metasurfaces. Small Methods 2017, 1, 1600064. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Ball, A.J.; Bagheri, M.; Faraon, A. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nat. Commun. 2015, 6, 7069. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef]
- Liang, H.; Lin, Q.; Xie, X.; Sun, Q.; Wang, Y.; Zhou, L.; Liu, L.; Yu, X.; Zhou, J.; Krauss, T.F.; et al. Ultrahigh Numerical Aperture Metalens at Visible Wavelengths. Nano Lett. 2018, 18, 4460–4466. [Google Scholar] [CrossRef]
- Aieta, F.; Kats, M.A.; Genevet, P.; Capasso, F. Multiwavelength achromatic metasurfaces by dispersive phase compensation. Science 2015, 347, 1342–1345. [Google Scholar] [CrossRef]
- Colburn, S.; Zhan, A.; Majumdar, A. Metasurface optics for full-color computational imaging. Sci. Adv. 2018, 4, eaar2114. [Google Scholar] [CrossRef]
- Chung, H.; Miller, O.D. High-NA achromatic metalenses by inverse design. Opt. Express 2020, 28, 6945–6965. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Yang, W.; Ji, Z.; Jin, L.; Ma, X.; Song, Q.; Boltasseva, A.; Han, J.; Shalaev, V.M.; et al. High-efficiency broadband achromatic metalens for near-IR biological imaging window. Nat. Commun. 2021, 12, 1–7. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, M.; Dong, F.; Feng, L.; Chu, W. Broadband achromatic polarization insensitive metalens over 950 nm bandwidth in the visible and near-infrared. Chin. Opt. Lett. 2022, 20, 013601. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Shin, M.C.; Phare, C.T.; Miller, S.A.; Shim, E.; Lipson, M. 2D beam steerer based on metalens on silicon photonics. Opt. Express 2021, 29, 854–864. [Google Scholar] [CrossRef]
- Pahlevaninezhad, H.; Khorasaninejad, M.; Huang, Y.-W.; Shi, Z.; Hariri, L.P.; Adams, D.C.; Ding, V.; Zhu, A.; Qiu, C.-W.; Capasso, F.; et al. Nano-optic endoscope for high-resolution optical coherence tomography in vivo. Nat. Photon 2018, 12, 540–547. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Yan, F. A high numerical aperture terahertz all-silicon metalens with sub-diffraction focus and long depth of focus. J. Phys. D Appl. Phys. 2020, 54, 085103. [Google Scholar] [CrossRef]
- West, P.R.; Stewart, J.L.; Kildishev, A.V.; Shalaev, V.M.; Shkunov, V.V.; Strohkendl, F.; Zakharenkov, Y.A.; Dodds, R.K.; Byren, R. All-dielectric subwavelength metasurface focusing lens. Opt. Express 2014, 22, 26212–26221. [Google Scholar] [CrossRef]
- Fattal, D.; Li, J.; Peng, Z.; Fiorentino, M.; Beausoleil, R.G. Flat dielectric grating reflectors with focusing abilities. Nat. Photon 2010, 4, 466–470. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Crozier, K.B. Silicon nanofin grating as a miniature chirality-distinguishing beam-splitter. Nat. Commun. 2014, 5, 5386. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Chen, M.K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.-T.; Wang, J.-H.; et al. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef]
- Cai, H.; Czaplewski, D.; Ogando, K.; Martinson, A.; Gosztola, D.; Stan, L.; López, D. Ultrathin transmissive metasurfaces for multi-wavelength optics in the visible. Appl. Phys. Lett. 2019, 114, 071106. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhou, J.; Zhang, F.; Lippens, D. Mie resonance-based dielectric metamaterials. Mater. Today 2009, 12, 60–69. [Google Scholar] [CrossRef]
- Decker, M.; Staude, I.; Falkner, M.; Dominguez, J.; Neshev, D.N.; Brener, I.; Pertsch, T.; Kivshar, Y.S. High-Efficiency Dielectric Huygens’ Surfaces. Adv. Opt. Mater. 2015, 3, 813–820. [Google Scholar] [CrossRef]
- Geints, Y.E.; Panina, E.K.; Minin, I.V.; Minin, O.V. Study of focusing parameters of wavelength-scale binary phase Fresnel zone plate. J. Opt. 2021. [Google Scholar] [CrossRef]
- Zhuang, Z.-P.; Chen, R.; Fan, Z.-B.; Pang, X.-N.; Dong, J.-W. High focusing efficiency in subdiffraction focusing metalens. Nanophotonics 2019, 8, 1279–1289. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Kang, G. Achromatic focusing effect of metasurface-based binary phase Fresnel zone plate. Phys. Lett. A 2021, 407, 127463. [Google Scholar] [CrossRef]
- Kodate, K.; Tamura, H.; Okabe, Y.; Kamiya, T. Deep Ultraviolet Lithography Masks Using Amorphous Silicon Films. Jpn. J. Appl. Phys. 1984, 23, 382–383. [Google Scholar] [CrossRef]
- Rastani, K.; Marrakchi, A.; Habiby, S.F.; Hubbard, W.M.; Gilchrist, H.; Nahory, R.E. Binary phase Fresnel lenses for generation of two-dimensional beam arrays. Appl. Opt. 1991, 30, 1347–1354. [Google Scholar] [CrossRef]
- Lin, L.; Pister, K.; Lee, S.; Wu, M. Three-dimensional micro-Fresnel optical elements fabricated by micromachining technique. Electron. Lett. 1994, 30, 448–449. [Google Scholar] [CrossRef]
- David, C.; Nöhammer, B.; Ziegler, E. Wet etching of linear Fresnel zone plates for hard X-rays. Microelectron. Eng. 2002, 61–62, 987–992. [Google Scholar] [CrossRef]
- Schonbrun, E.; Ye, W.N.; Crozier, K.B. Scanning microscopy using a short-focal-length Fresnel zone plate. Opt. Lett. 2009, 34, 2228–2230. [Google Scholar] [CrossRef]
- Snigireva, I.; Snigirev, A.; Kohn, V.; Yunkin, V.; Grigoriev, M.; Kuznetsov, S.; Vaughan, G.; Di Michiel, M. Focusing high energy X-rays with stacked Fresnel zone plates. Phys. Status Solidi 2007, 204, 2817–2823. [Google Scholar] [CrossRef]
- Jokubauskis, D.; Minkevičius, L.; Karaliūnas, M.; Indrišiūnas, S.; Kašalynas, I.; Raciukaitis, G.; Valušis, G. Fibonacci terahertz imaging by silicon diffractive optics. Opt. Lett. 2018, 43, 2795–2798. [Google Scholar] [CrossRef]
- Zhou, F.; Sun, X.; Zhong, H.; Duan, L.; Hu, Y.; Duan, J.; Li, M. Optimization of the focusing characteristics of Fresnel zone plates fabricated with a femtosecond laser. J. Mod. Opt. 2021, 68, 100–107. [Google Scholar] [CrossRef]
- Guenther, B.D. Fresnel Diffraction. In Modern Optics, 2nd ed.; Oxford University Press: Oxford, UK, 2015; pp. 459–495. [Google Scholar]
- Pedrotti, F.L.; Pedrotti, L.S.; Pedrotti, L.M. Fresnel Diffraction. In Introduction to Optics, 3rd ed.; Pearson Prentice-Hall: Hoboken, NJ, USA, 2007; pp. 308–332. [Google Scholar]
- Stafeev, S.S.; Nalimov, A.G.; Kotlyar, M.V.; Gibson, D.; Song, S.; Hu, C.; O’Faolain, L.; Kotlyar, V.V. Focusing zone plate based on subwavelength grating. In Proceedings of the 19th International Conference on Transparent Optical Networks (ICTON), Girona, Spain, 2–6 July 2017. [Google Scholar]
- Cheben, P.; Halir, R.; Schmid, J.H.; Atwater, H.A.; Smith, D.R. Subwavelength integrated photonics. Nature 2018, 560, 565–572. [Google Scholar] [CrossRef]
- Halir, R.; Bock, P.J.; Cheben, P.; Ortega-Moñux, A.; Alonso-Ramos, C.; Schmid, J.H.; Lapointe, J.; Xu, D.; Wangüemert-Pérez, J.G.; Molina-Fernández, Í.; et al. Waveguide sub-wavelength structures: a review of principles and applications. Laser Photon-Rev. 2014, 9, 25–49. [Google Scholar] [CrossRef]
- Rytov, S. Electromagnetic properties of a finely stratified medium. Sov. Phys. JETP 1956, 2, 466–475. [Google Scholar]
- Chen, X.; Tsang, H.K. Polarization-independent grating couplers for silicon-on-insulator nanophotonic waveguides. Opt. Lett. 2011, 36, 796–798. [Google Scholar] [CrossRef]
- Arabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraon, A. Multiwavelength metasurfaces through spatial multiplexing. Sci. Rep. 2016, 6, 32803. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Liu, Y.; O’faolain, L.; Kovalev, A.A. Analysis of the shape of a subwavelength focal spot for the linearly polarized light. Appl. Opt. 2013, 52, 330–339. [Google Scholar] [CrossRef]
- Li, X.; Tang, J.; Baine, J. Polarization-Independent Metasurface Lens Based on Binary Phase Fresnel Zone Plate. Nanomaterials 2020, 10, 1467. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Yu, N. Broadband achromatic dielectric metalenses. Light. Sci. Appl. 2018, 7, 85. [Google Scholar] [CrossRef] [PubMed]


| Reference | Numerical Aperture | Focusing Efficiency | Bandwidth |
|---|---|---|---|
| This work | 0.83 | 39.2% | 1486–1874 nm |
| [9] | 0.05 | 9.8%, 10.3%, 12.6% | 1300 nm, 1550 nm, 1800 nm |
| [12] | 0.1–0.24 | 77.1–88.5% | 650–1000 nm |
| [15] | 0.28 | - | 1250–1370 nm |
| [26] | 0.2 | 26% | 532 nm |
| [26] | 0.97 | 13% | 532 nm |
| [26] | 0.97 | 4% | 473 nm, 532 nm, 633 nm |
| [44] | 0.59 | 4.1% | 633 nm |
| [45] | 0.24 | ≤60% | 1300–1650 nm |
| [45] | 0.24 | ≤50% | 1200–1650 nm |
| [45] | 0.13 | ≤55% | 1200–1650 nm |
| [45] | 0.88 | - | 1200–1400 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fraser, W.; Ye, W.N. Silicon Fresnel Zone Plate Metalens with Subwavelength Gratings. Sensors 2023, 23, 4137. https://doi.org/10.3390/s23084137
Fraser W, Ye WN. Silicon Fresnel Zone Plate Metalens with Subwavelength Gratings. Sensors. 2023; 23(8):4137. https://doi.org/10.3390/s23084137
Chicago/Turabian StyleFraser, William, and Winnie N. Ye. 2023. "Silicon Fresnel Zone Plate Metalens with Subwavelength Gratings" Sensors 23, no. 8: 4137. https://doi.org/10.3390/s23084137
APA StyleFraser, W., & Ye, W. N. (2023). Silicon Fresnel Zone Plate Metalens with Subwavelength Gratings. Sensors, 23(8), 4137. https://doi.org/10.3390/s23084137






