Design of the Bimodal Grating Sensor with a Built-In Mode Demultiplexer
Abstract
:1. Introduction
2. Materials and Methods
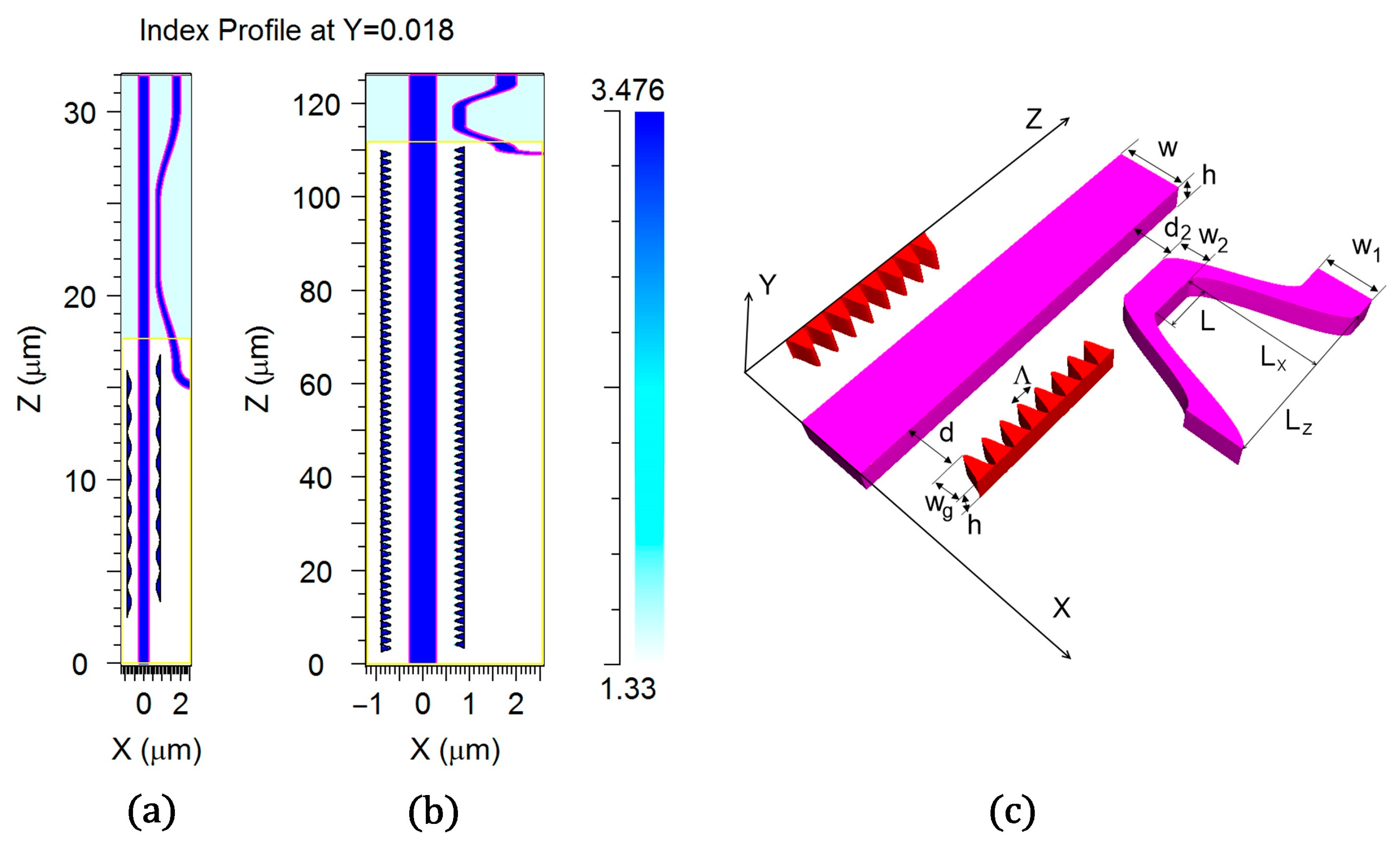
2.1. Sensor Design
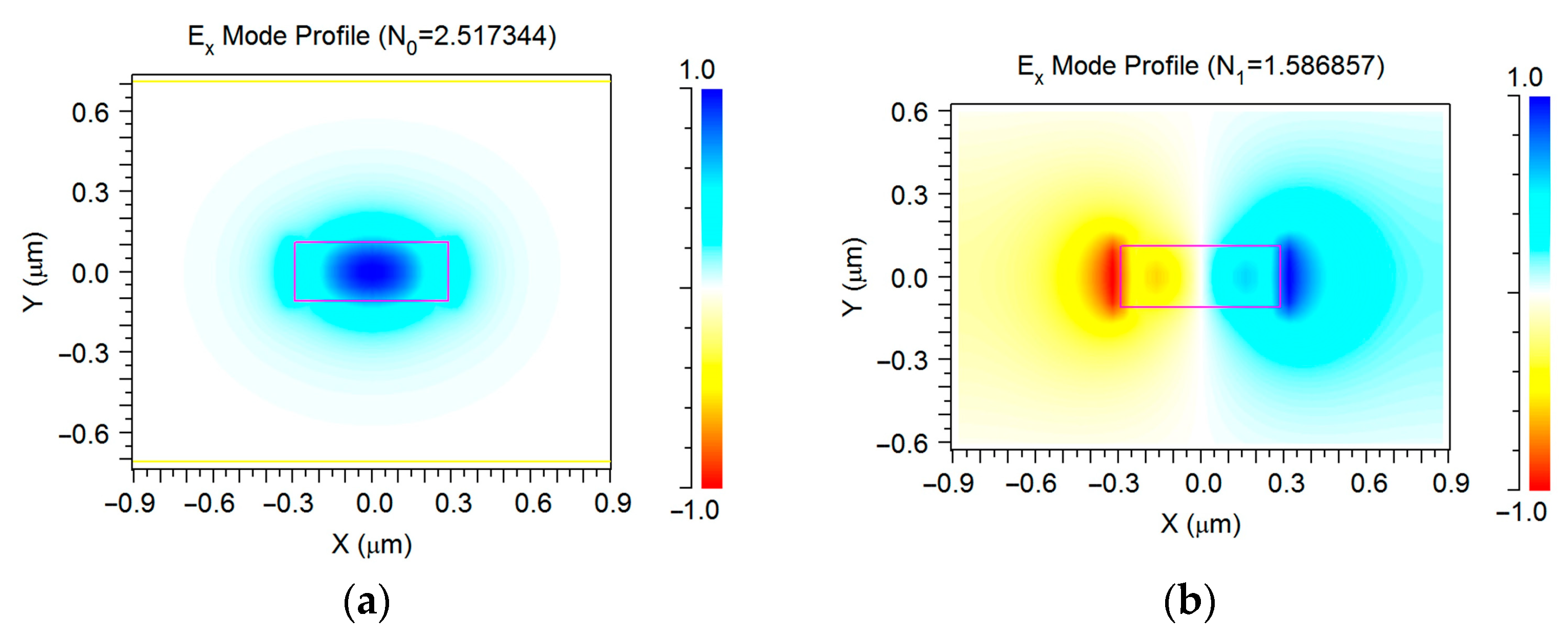
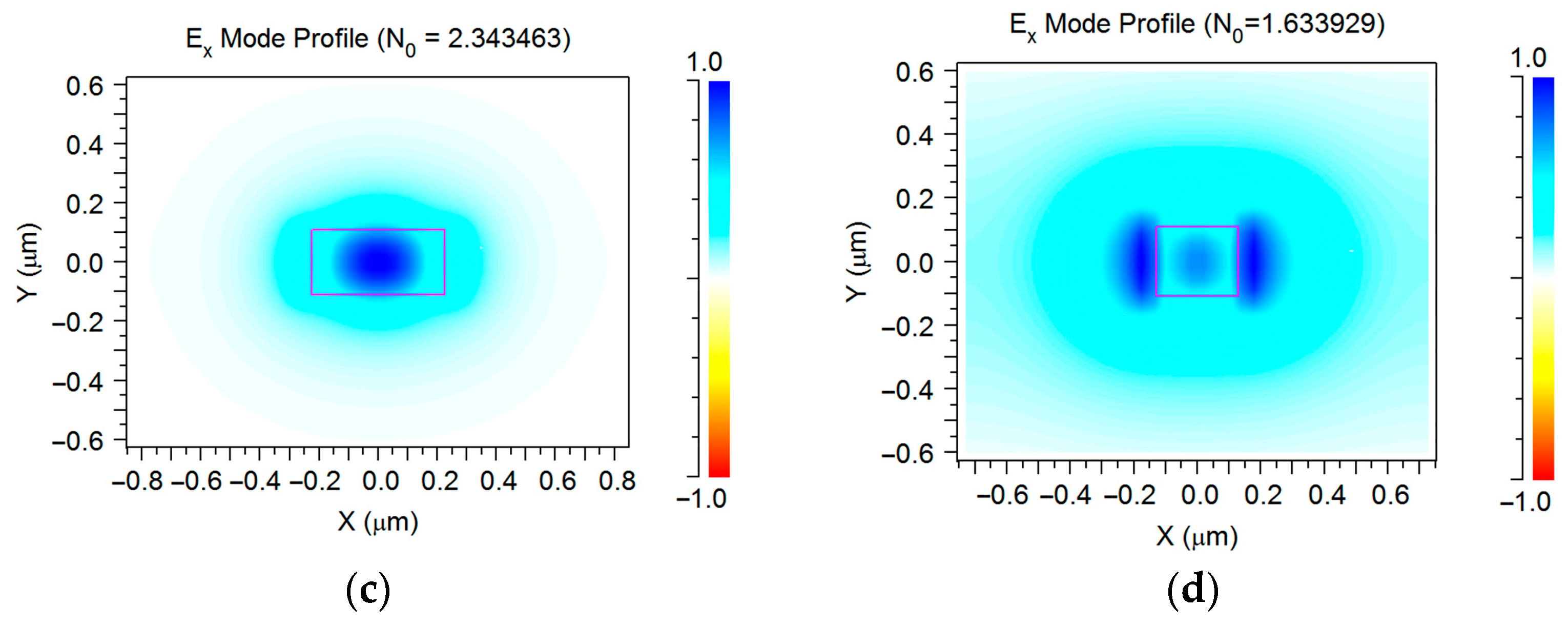
2.2. Grating Sensor Element
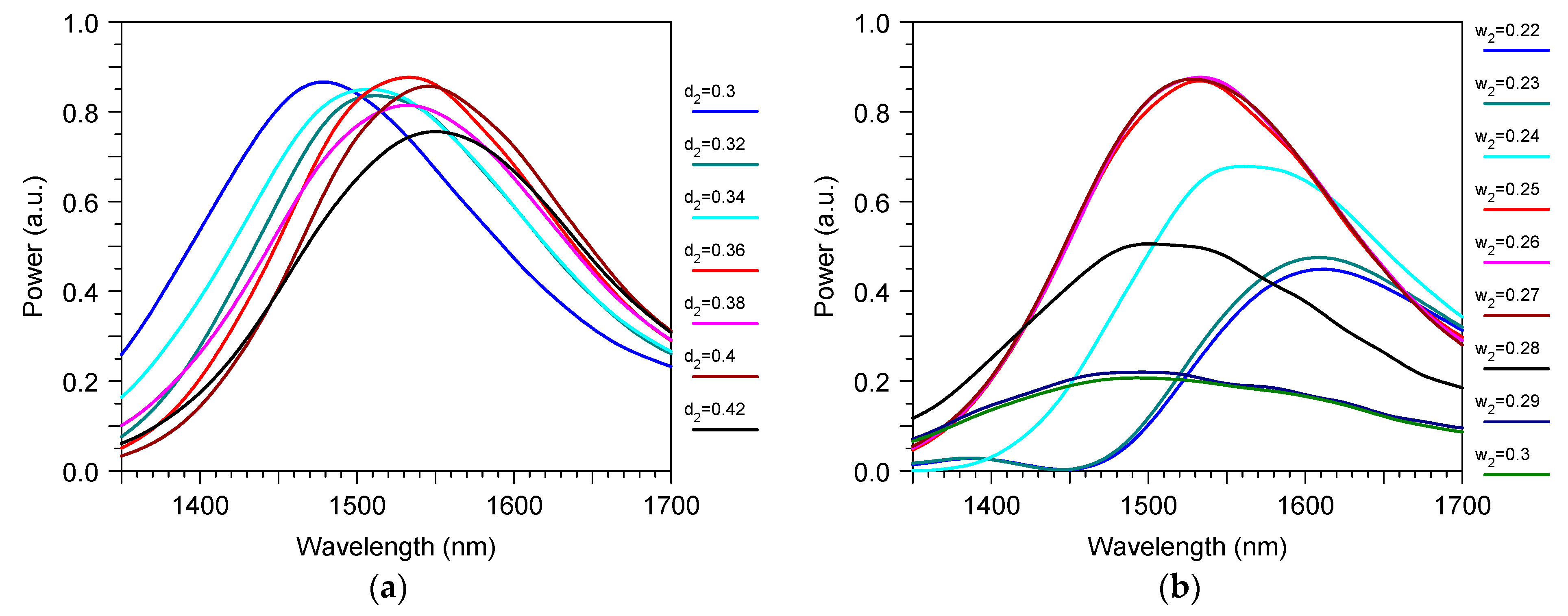
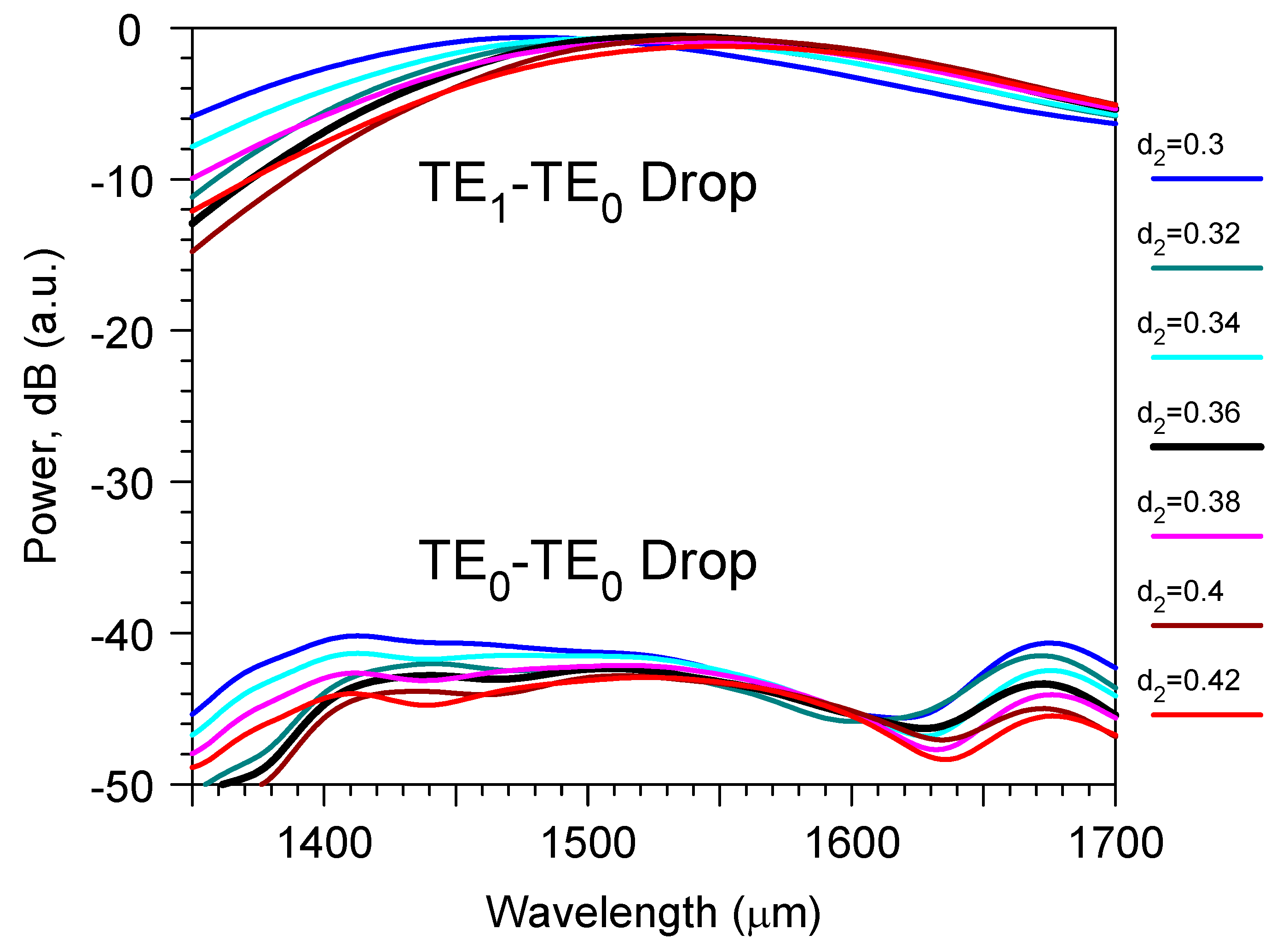
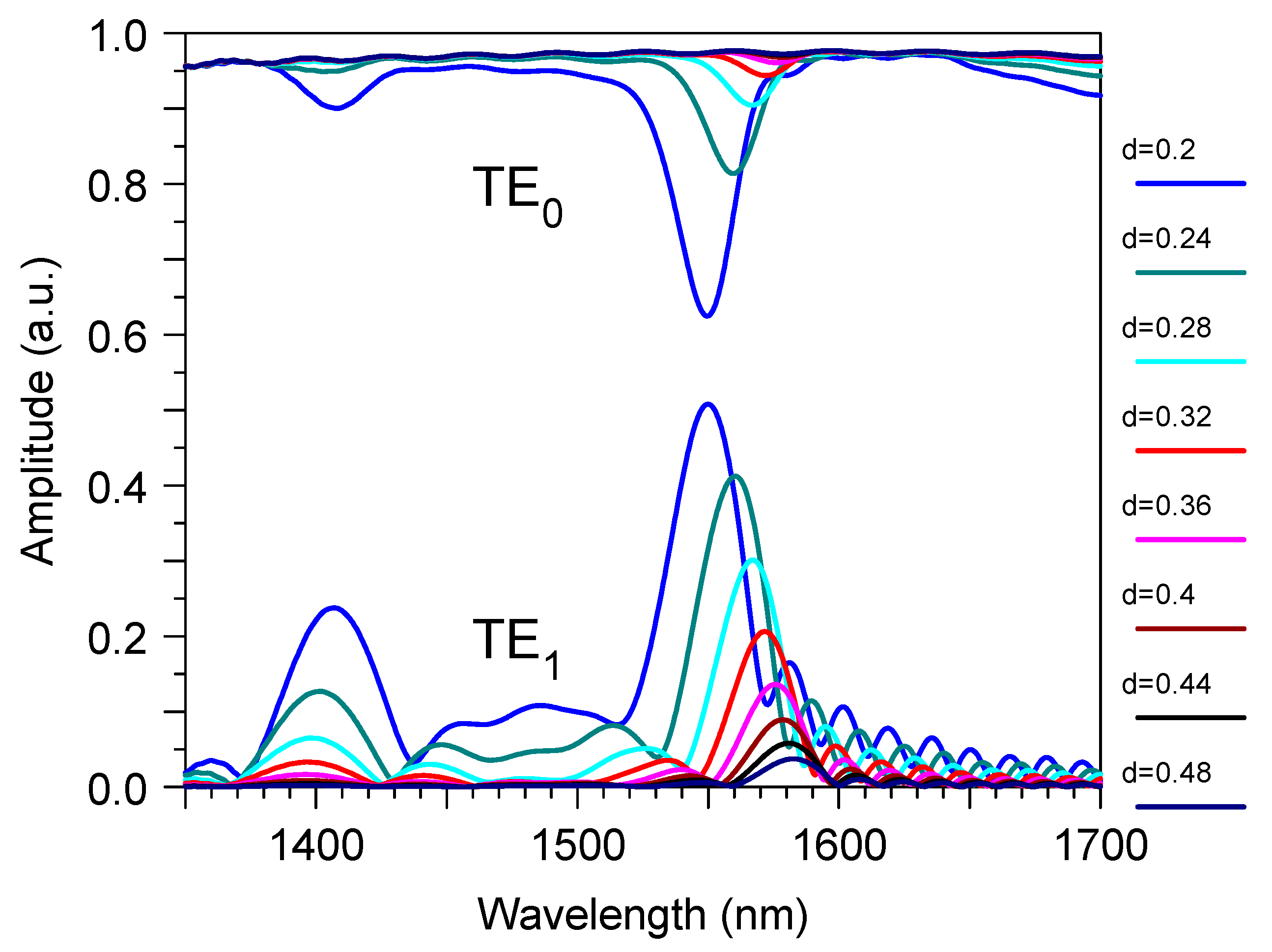
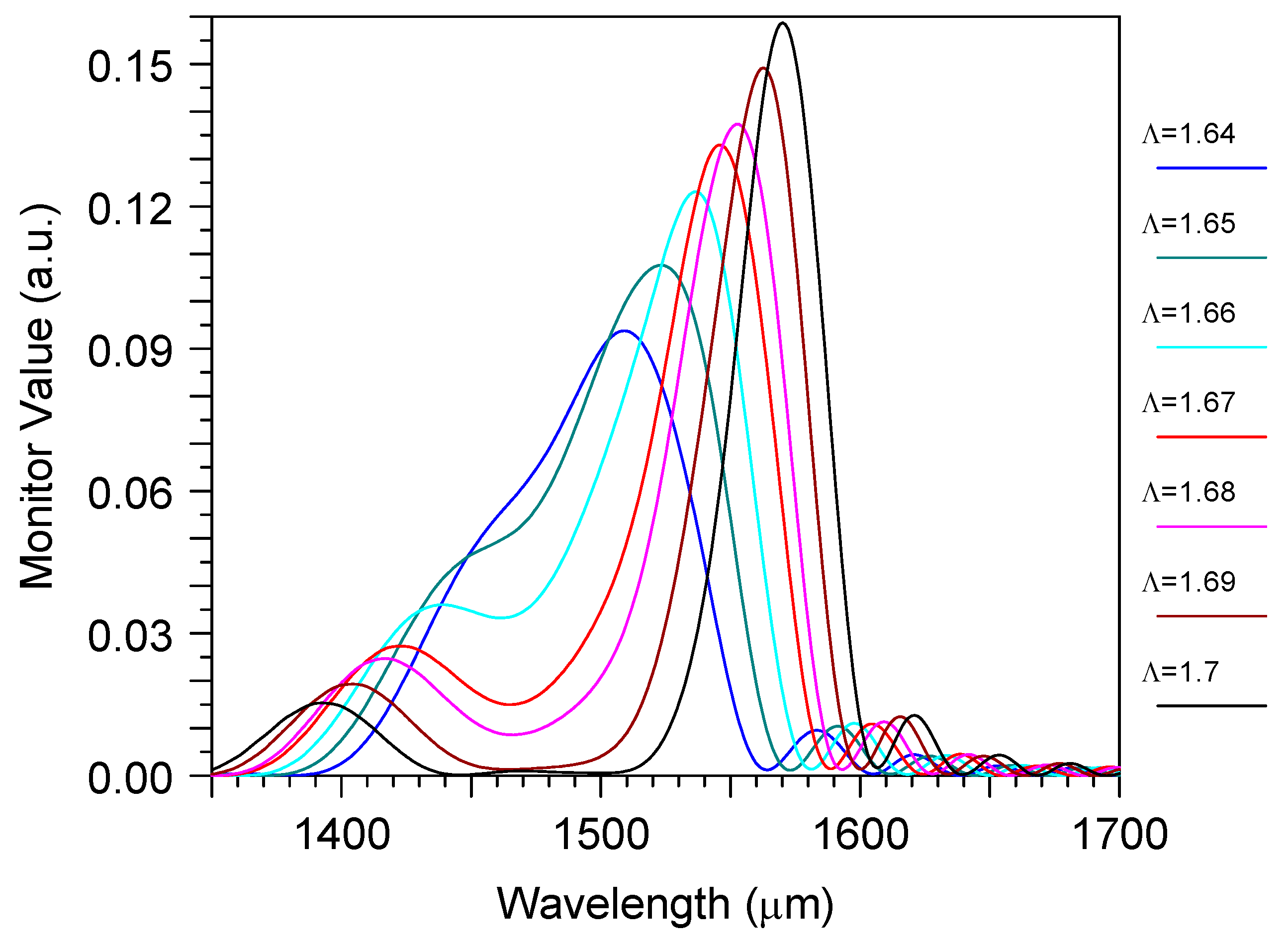
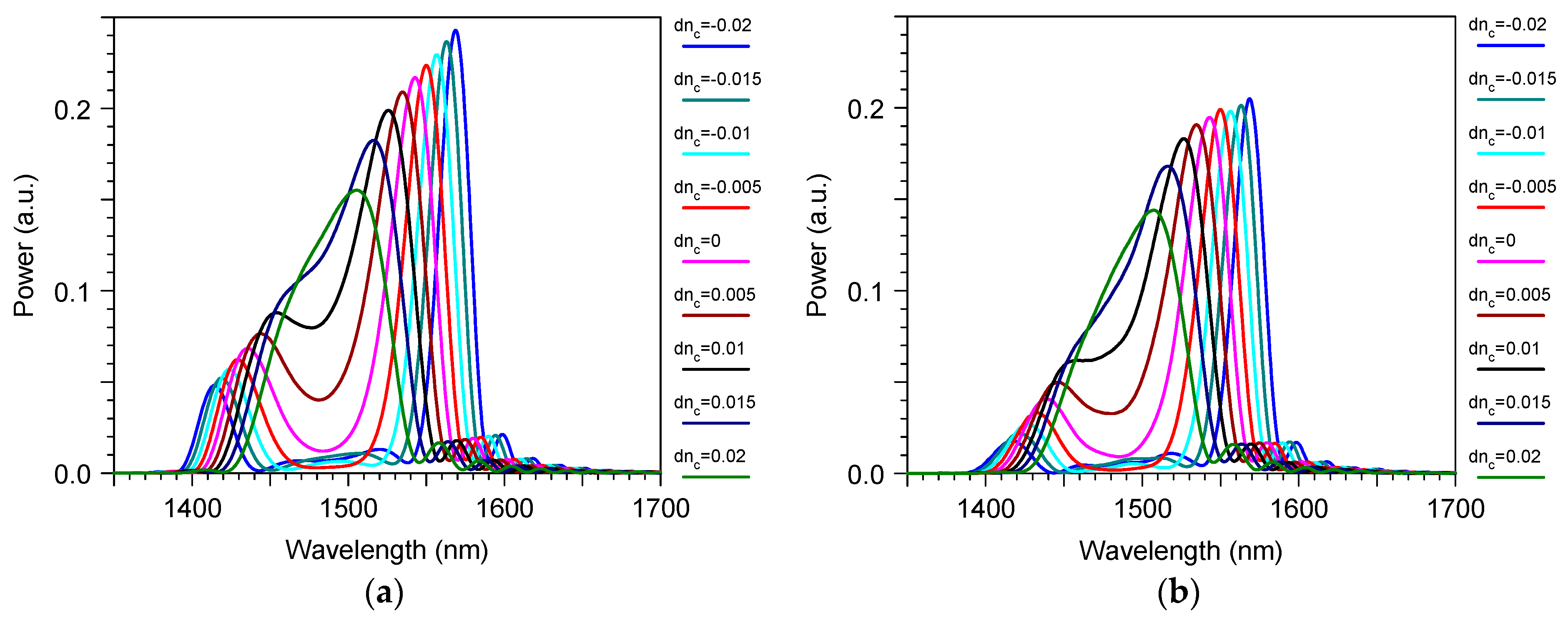
3. Results
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernández Gavela, A.; Grajales García, D.; Ramirez, J.C.; Lechuga, L.M. Last advances in silicon-based optical biosensors. Sensors 2016, 16, 285. [Google Scholar] [CrossRef] [PubMed]
- Steglich, P.; Hülsemann, M.; Dietzel, B.; Mai, A. Optical Biosensors Based on Silicon-On-Insulator Ring Resonators: A Review. Molecules 2019, 24, 519. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Hu, X.; Kundu, S.; Nag, A.; Afsarimanesh, N.; Sapra, S.; Mukhopadhyay, S.C.; Han, T. Silicon-Based Sensors for Biomedical Applications: A Review. Sensors 2019, 19, 2908. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Dar, T.; Viphavakit, C.; Pan, C.; Kejalakshmy, N.; Rahman, B.M.A. Compact Photonic SOI Sensors. In Computational Photonic Sensors; Hameed, M., Obayya, S., Eds.; Springer: Cham, Switzerland, 2019; pp. 343–383. [Google Scholar]
- Chen, Y.; Liu, J.; Yang, Z.; Wilkinson, J.S.; Zhou, X. Optical biosensors based on refractometric sensing schemes: A review. Biosens. Bioelectron. 2019, 144, 111693. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. [Google Scholar] [CrossRef]
- Tsarev, A. Overview of integrated optical sensors based on silicon—Forecasts and results of the decade. (Invited paper). Optoelectron. Instrum. Data Process. 2020, 56, 412–430. [Google Scholar] [CrossRef]
- Esposito, F.; Srivastava, A.; Sansone, L.; Giordano, M.; Campopiano, S.; Iadicicco, A. Label-free biosensors based on long period fiber gratings: A review. IEEE Sens. J. 2020, 21, 12692–12705. [Google Scholar] [CrossRef]
- Ramirez, J.C.; Grajales García, D.; Maldonado, J.; Fernández-Gavela, A. Current Trends in Photonic Biosensors: Advances towards Multiplexed Integration. Chemosensors 2022, 10, 398. [Google Scholar] [CrossRef]
- Dhote, C.; Singh, A.; Kumar, S. Silicon Photonics Sensors for Biophotonic Applications—A Review. IEEE Sens. J. 2022, 22, 18228–18239. [Google Scholar] [CrossRef]
- Sajan, S.C.; Singh, A.; Sharma, P.K.; Kumar, S. Silicon Photonics Biosensors for Cancer Cells Detection—A Review. IEEE Sens. J. 2023, 23, 3366–3377. [Google Scholar] [CrossRef]
- Kaur, B.; Kumar, S.; Kaushik, B.K. Novel Wearable Optical Sensors for Vital Health Monitoring Systems—A Review. Biosensors 2023, 13, 181. [Google Scholar] [CrossRef] [PubMed]
- Torrijos-Morán, L.; Lisboa, B.D.; Soler, M.; Lechuga, L.M.; García-Rupérez, J. Integrated optical bimodal waveguide biosensors: Principles and applications. Results Opt. 2022, 9, 100285. [Google Scholar] [CrossRef]
- Levy, R.; Ruschin, S. Critical sensitivity in hetero-modal interferometric sensor using spectral interrogation. Opt. Express 2008, 16, 20516–20521. [Google Scholar] [CrossRef] [PubMed]
- Levy, R.; Ruschin, S.; Goldring, D. Critical sensitivity effect in an interferometer sensor. Opt. Lett. 2009, 34, 3023–3025. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Kee, J.S.; Park, M.K. A refractive index sensor design based on grating-assisted coupling between a strip waveguide and a slot waveguide. Opt. Express 2013, 21, 5897–5909. [Google Scholar] [CrossRef]
- Liu, Q.; Gu, Z.; Park, M.K.; Chung, J. Experimental demonstration of highly sensitive optical sensor based on grating-assisted light coupling between strip and slot waveg, uides. Opt. Express 2016, 24, 12549–12556. [Google Scholar] [CrossRef]
- Kaur, P.; Shenoy, M.R. Highly Sensitive Refractive Index Sensor Based on Silicon Nitride Strip Waveguide Directional Coupler. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Zinoviev, K.; González-Guerrero, A.; Domínguez, C.; Lechuga, M. Integrated Bimodal Waveguide Interferometric Biosensor for Label-Free Analysis. J. Light. Technol. 2011, 29, 1926–1930. [Google Scholar] [CrossRef]
- González Guerrero, A.B.; Maldonado, J.; Dante, S.; Grajales, D.; Lechuga, L.M. Direct and label-free detection of the human growth hormone in urine by an ultrasensitive bimodal waveguide biosensor. J. Biophoton. 2017, 10, 61–67. [Google Scholar] [CrossRef]
- Bruck, R.; Hainberger, R. Sensitivity and design of grating-assisted bimodal interferometers for integrated optical biosensing. Opt. Express 2014, 22, 32344–32352. [Google Scholar] [CrossRef]
- Hoppe, N.; Föhn, T.; Diersing, P.; Scheck, P.; Vogel, W.; Félix Rosa, M.; Kaschel, M.; Bach, M.; Berroth, M. Design of an Integrated Dual-Mode Interferometer on 250 nm Silicon-on-Insulator. IEEE J. Sel. Top. Quant. Electron. 2017, 23, 444–451. [Google Scholar] [CrossRef]
- Hoppe, N.; Scheck, P.; Sweidan, R.; Diersing, P.; Rathgeber, L.; Vogel, W.; Riegger, B.; Southan, A.; Berroth, M. Silicon Integrated Dual-Mode Interferometer with Differential Outputs. Biosensors 2017, 7, 37. [Google Scholar] [CrossRef] [PubMed]
- Torrijos-Morán, L.; Griol, A.; García-Rupérez, J. Experimental study of subwavelength grating bimodal waveguides as ultrasensitive interferometric sensors. Opt. Lett. 2019, 44, 4702–4705. [Google Scholar] [CrossRef] [PubMed]
- Torrijos-Morán, L.; García-Rupérez, J. Single-channel bimodal interferometric sensor using subwavelength structures. Opt. Express 2019, 27, 8168–8179. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, J.; He, J.-J. Temperature sensor with enhanced sensitivity based on silicon Mach-Zehnder interferometer with waveguide group index engineering. Opt. Express 2018, 26, 26057–26064. [Google Scholar] [CrossRef]
- Tsarev, A. Effect of Dispersion-Enhanced Sensitivity in a Two-Mode Optical Waveguide with an Asymmetric Diffraction Grating. Sensors 2021, 21, 5492. [Google Scholar] [CrossRef]
- Zhang, G.; Huang, T.; Wu, Z.; Tu, X.; Zhang, X.; Luo, D.; Lei, R.; Xu, G.; Zhang, W. Design of an on-chip sensor operating near the dispersion turning point with ultrahigh sensitivity. J. Opt. Soc. Am. 2021, B38, 2786–2791. [Google Scholar] [CrossRef]
- Dwivedi, R.; Kumar, A.; Tripathi, S.M. Ultra High Sensitive Refractive Index Sensor Using a Metal Under-Clad Ridge Waveguide Modal Interferometer Near the Dispersion Turning Point. IEEE Sens. J. 2021, 21, 4674–4681. [Google Scholar] [CrossRef]
- Høvik, J.; Yadav, M.; Noh, J.W.; Aksnes, A. Waveguide asymmetric long-period grating couplers as refractive index sensors. Opt. Express 2020, 28, 23936–23949. [Google Scholar] [CrossRef]
- Schweikert, C.; Zhao, S.; Hoppe, N.; Vogel, W.; Berroth, M. Dual-Polarization Bimodal Waveguide Interferometer. In Proceedings of the 2022 IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 13–17 November 2022; pp. 1–2. [Google Scholar]
- Bassols-Cornudella, B.; Ramirez-Priego, P.; Soler, M.; Estévez, M.C.; Luis-Ravelo, H.J.D.; Cardenosa-Rubio, M.; Lechuga, L.M. Novel Sensing Algorithm for Linear Read-Out of Bimodal Waveguide Interferometric Biosensors. J. Light. Technol. 2022, 40, 237–244. [Google Scholar] [CrossRef]
- Huang, T.; Xu, G.; Tu, X.; Zhang, G.; Lei, R.; Wu, Y.; Pan, J.; Shao, L.; Shum, P.P. Design of highly sensitive interferometric sensors based on subwavelength grating waveguides operating at the dispersion turning point. JOSA B 2021, 38, 2680–2686. [Google Scholar] [CrossRef]
- Deleau, C.; Seat, H.C.; Bernal, O.; Surre, F. High-sensitivity integrated SiN rib-waveguide long period grating refractometer. Photonics Res. 2022, 10, 564–573. [Google Scholar] [CrossRef]
- Dandapat, K.; Saha, N.; Dwivedi, R.; Tripathi, S.M.; Kumar, A. A Long Period Waveguide Grating Sensor for Accurate Simultaneous Detection of Dual Analytes. IEEE Sens. J. 2023, 23, 7059–7067. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Dai, D. Multimode silicon photonics. Nanophotonics 2019, 8, 227–247. [Google Scholar] [CrossRef]
- Li, H.; Wang, P.; Yang, T.; Dai, T.; Wang, G.; Li, S.; Chen, W.; Yang, J. Experimental demonstration of a broadband two-mode multi/demultiplexer based on asymmetric Y-junctions. Opt. Laser Technol. 2018, 100, 7–11. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, C.; Cheng, B.; Xue, C. Compact two-mode (de) multiplexer based on symmetric Y-junction and multimode interference waveguides. Opt. Express 2014, 22, 5781–5786. [Google Scholar] [CrossRef]
- Uematsu, T.; Ishizaka, Y.; Kawaguchi, Y.; Saitoh, K.; Koshiba, M. Design of a compact two-mode multi/demultiplexer consisting of multimode interference waveguides and a wavelength-insensitive phase shifter for mode-division multiplexing transmission. J. Light. Technol. 2012, 30, 2421–2426. [Google Scholar] [CrossRef]
- Chack, D.; Hassan, S.; Qasim, M. Broadband and low crosstalk silicon on-chip mode converter and demultiplexer for mode division multiplexing. Appl. Opt. 2020, 59, 3652–3659. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Xu, J.; Da Ros, F.; Huang, B.; Ou, H.; Peucheret, C. On-chip two-mode division multiplexing using tapered directional coupler-based mode multiplexer and demultiplexer. Opt. Express 2013, 21, 10376–10382. [Google Scholar] [CrossRef]
- Xing, J.; Li, Z.; Xiao, X.; Yu, J.; Yu, Y. Two-mode multiplexer and demultiplexer based on adiabatic couplers. Opt. Lett. 2013, 38, 3468–3470. [Google Scholar] [CrossRef]
- Paredes, B.; Mohammed, Z.; Villegas, J.; Rasras, M. Dual-band (O & C-bands) two-mode multiplexer on the SOI platform. IEEE Photonics J. 2021, 13, 1–9. [Google Scholar]
- Masnad, M.M.; Zhang, G.; Xu, D.X.; Grinberg, Y.; Liboiron-Ladouceur, O. Fabrication error tolerant broadband mode converters and their working principles. Opt. Express 2022, 30, 25817–25829. [Google Scholar] [CrossRef]
- Li, K.; Cao, X.; Wan, Y.; Wu, G.; Wang, J. Fundamental analyses of fabrication-tolerant high-performance silicon mode (de)multiplexer. Opt. Express 2022, 30, 22649–22660. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Rodriguez, D.; Corral, J.L.; Griol, A.; Llorente, R. Dimensional variation tolerant mode converter/multiplexer fabricated in SOI technology for two-mode transmission at 1550 nm. Opt. Lett. 2017, 42, 1221–1224. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Rodriguez, D.; Corral, J.L.; Griol, A.; Llorente, R. Bimodal grating coupler design on SOI technology for mode division multiplexing at 1550 nm. Opt. Express 2018, 26, 19445–19455. [Google Scholar] [CrossRef] [PubMed]
- Orcutt, J.S.; Ram, R.J. Photonic Device Layout Within the Foundry CMOS Design Environment. IEEE Photon. Technol. Lett. 2010, 22, 544–546. [Google Scholar] [CrossRef]
- Bogaerts, W.; Chrostowski, L. Silicon photonics circuit design: Methods, tools and challenges. Laser Photonics Rev. 2018, 12, 1700237. [Google Scholar] [CrossRef]
- Selvaraja, S.K. Subnanometer Linewidth Uniformity in Silicon Nanophotonic Waveguide Devices Using CMOS Fabrication Technology. IEEE J. Sel. Top. Quant. Elect. 2010, 16, 316–324. [Google Scholar] [CrossRef]
- Ikeda, K.; Suzuki, K.; Konoike, R.; Namiki, S.; Kawashima, H. Large-scale silicon photonics switch based on 45-nm CMOS technology. Opt. Commun. 2020, 466, 125677. [Google Scholar] [CrossRef]
- Cho, Y.-B.; Yang, B.-K.; Lee, J.-H.; Yoon, J.-B.; Shin, S.-Y. Silicon Photonic Wire Filter Using Asymmetric Sidewall Long-Period Waveguide Grating in a Two-Mode Waveguide. IEEE Photonics Technol. Lett. 2008, 20, 520–522. [Google Scholar] [CrossRef]
- Liu, Q.; Gu, Z.; Kee, J.S.; Park, M.K. Silicon waveguide filter based on cladding modulated anti-symmetric long-period grating. Opt. Express 2014, 22, 29954–29963. [Google Scholar] [CrossRef] [PubMed]
- Tsarev, A.V. New wide strip and grating loaded quasi-single-mode waveguide on SOI. Opt. Express 2009, 17, 13095–13101. [Google Scholar] [CrossRef] [PubMed]
- RSoft Photonic Device Tools. Version 2020-09-1. Available online: https://www.synopsys.com/photonic-solutions/rsoft-photonic-device-tools.html (accessed on 14 March 2023).
- Chrostowski, L.; Grist, S.; Flueckiger, J.; Shi, W.; Wang, X.; Ouellet, E.; Yun, H.; Webb, M.; Nie, B.; Liang, Z.; et al. Silicon photonic resonator sensors and devices. Proc. SPIE 2012, 8236, 823620. [Google Scholar]
- Pérez-Armenta, C.; Ortega-Moñux, A.; Čtyroký, J.; Cheben, P.; Schmid, J.H.; Halir, R.; Molina-Fernández, Í.; Wangüemert-Pérez, J.G. Narrowband Bragg filters based on subwavelength grating waveguides for silicon photonic sensing. Opt. Express 2020, 28, 37971–37985. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsarev, A. Design of the Bimodal Grating Sensor with a Built-In Mode Demultiplexer. Sensors 2023, 23, 4327. https://doi.org/10.3390/s23094327
Tsarev A. Design of the Bimodal Grating Sensor with a Built-In Mode Demultiplexer. Sensors. 2023; 23(9):4327. https://doi.org/10.3390/s23094327
Chicago/Turabian StyleTsarev, Andrei. 2023. "Design of the Bimodal Grating Sensor with a Built-In Mode Demultiplexer" Sensors 23, no. 9: 4327. https://doi.org/10.3390/s23094327
APA StyleTsarev, A. (2023). Design of the Bimodal Grating Sensor with a Built-In Mode Demultiplexer. Sensors, 23(9), 4327. https://doi.org/10.3390/s23094327





