Spatio-Trajectorial Optical Flow for Higher-Order Deformation Analysis in Solid Experimental Mechanics
Abstract
:1. Introduction
2. State-of-the-Art
3. Spatio-Trajectorial Optical Flow Model
3.1. Data Term
3.2. Spatial Regularisation
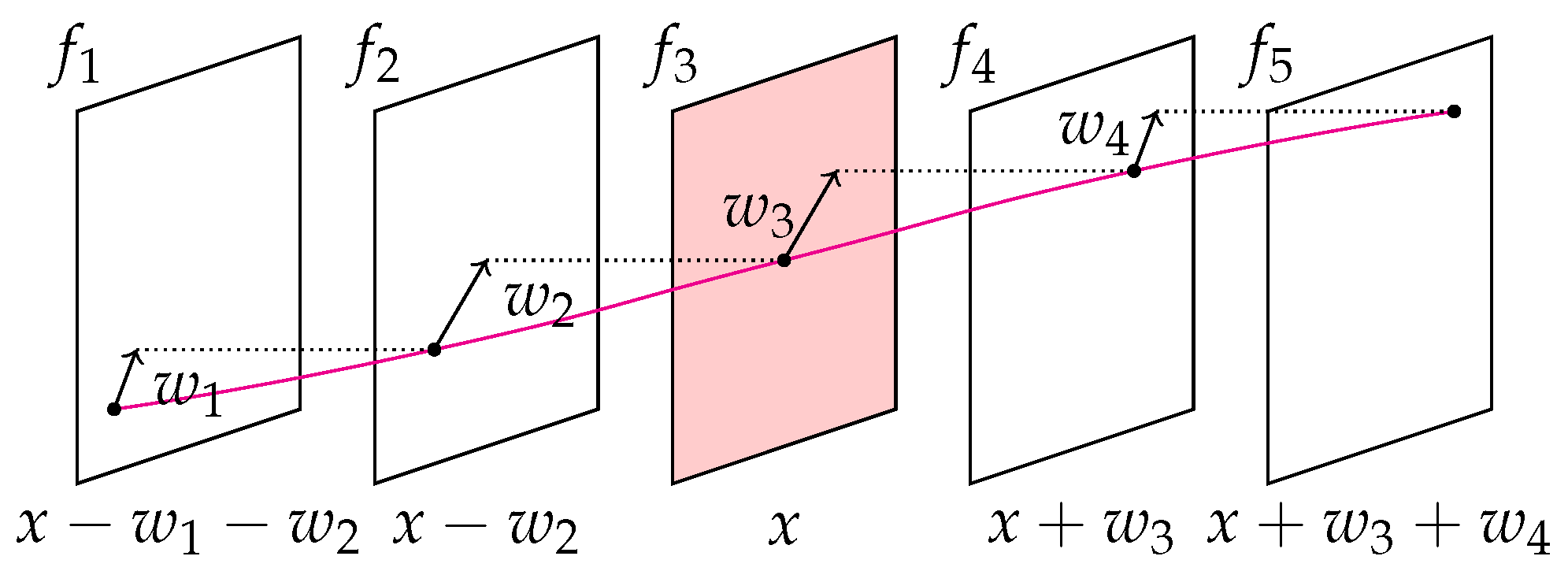
3.3. Trajectorial Regularisation
3.4. Optimisation
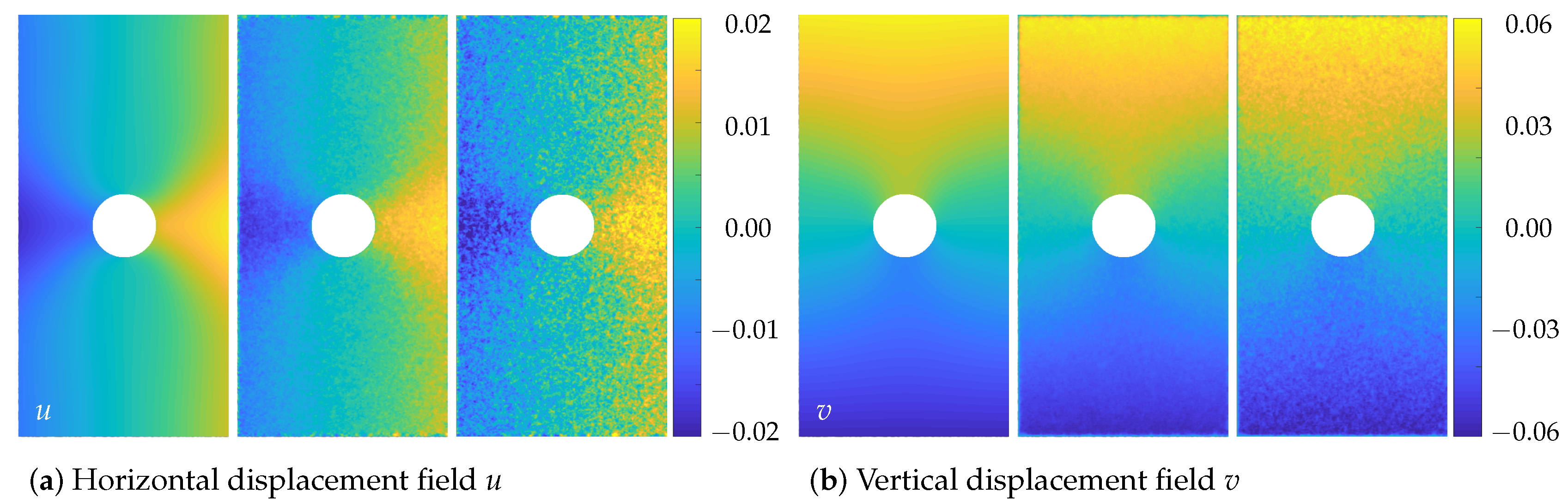
4. Validation
5. Experiments
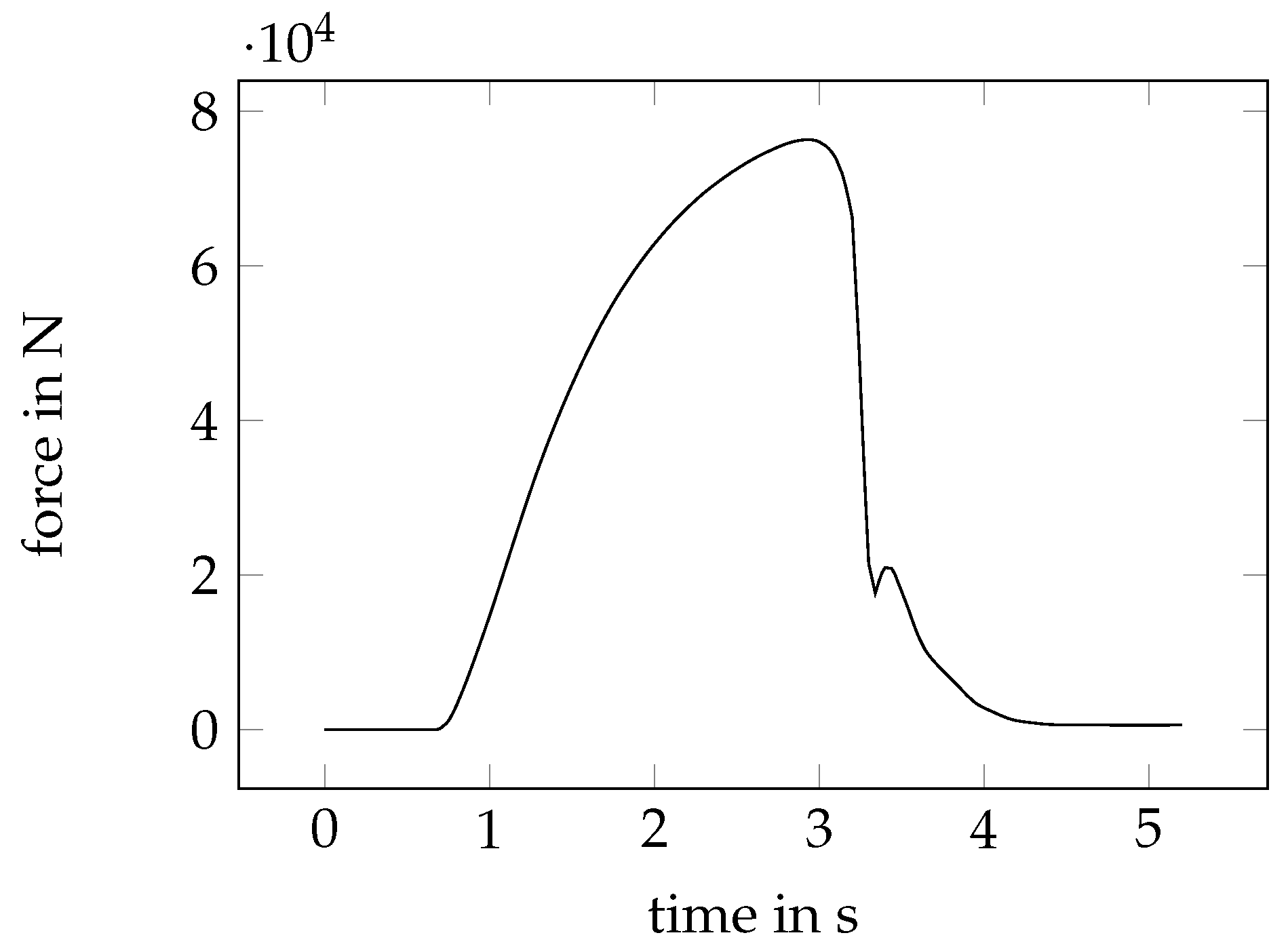
5.1. Experimental Setup
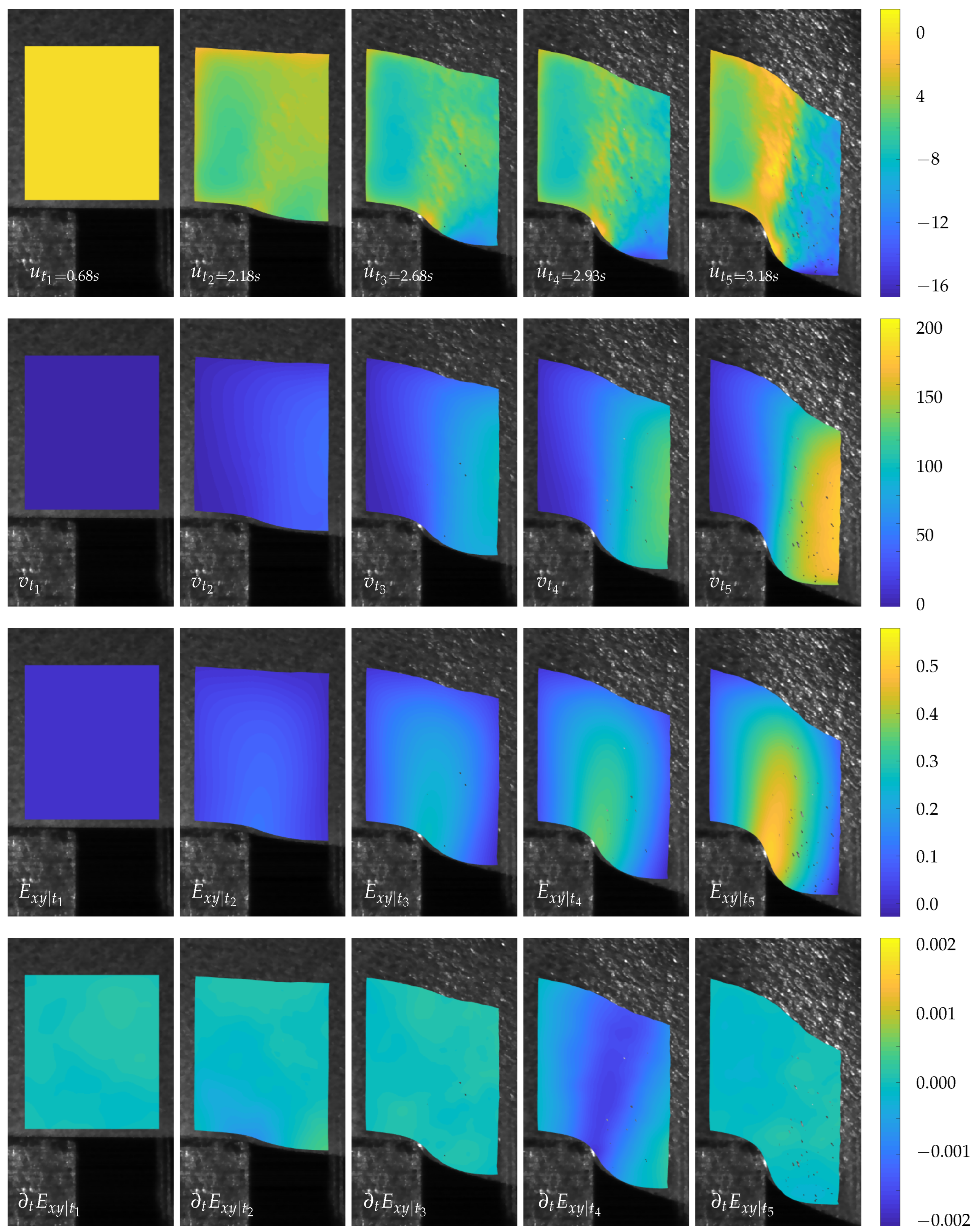
5.2. Experimental Results
6. Summary
7. Conclusions
8. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AE | Angular error |
| BCA | Brightness constancy assumption |
| DIC | Digital image correlation |
| GCA | Gradient constancy assumption |
| GT | Ground truth |
| OF | Optical flow |
| SOR | Successive over-relaxation |
| STOF | Spatio-trajectorial optical flow |
References
- Sharpe, W. Springer Handbook of Experimental Solid Mechanics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Hartmann, C.; Lechner, P.; Volk, W. In-situ measurement of higher-order strain derivatives for advanced analysis of forming processes using spatio-temporal optical flow. CIRP Ann. 2021, 70, 251–254. [Google Scholar] [CrossRef]
- Nie, G.Y.; Bodda, S.S.; Sandhu, H.K.; Han, K.; Gupta, A. Computer-Vision-Based Vibration Tracking Using a Digital Camera: A Sparse-Optical-Flow-Based Target Tracking Method. Sensors 2022, 22, 6869. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Liu, D.; Srivastava, G.; Połap, D.; Wozniak, M. Overview and methods of correlation filter algorithms in object tracking. Complex Intell. Syst. 2021, 7, 1895–1917. [Google Scholar] [CrossRef]
- Mekala, M.; Park, W.; Dhiman, G.; Park, J.; Jung, H.Y. Deep Learning Inspired Object Consolidation Approaches Using LiDAR Data for Autonomous Driving: A Review. Arch. Comput. Methods Eng. 2022, 29, 2579–2599. [Google Scholar] [CrossRef]
- Al-Qudah, S.; Yang, M. Large Displacement Detection Using Improved Lucas-Kanade Optical Flow. Sensors 2023, 23, 3152. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, C.; Weiss, H.A.; Lechner, P.; Volk, W.; Neumayer, S.; Fitschen, J.H.; Steidl, G. Measurement of strain, strain rate and crack evolution in shear cutting. J. Mater. Process. Technol. 2021, 288, 116872. [Google Scholar] [CrossRef]
- Horn, B.; Schunck, B. Determining Optical Flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef] [Green Version]
- Wedel, A.; Cremers, D. Stereo Scene Flow for 3D Motion Analysis, 1st ed.; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Corpetti, T.; Memin, E.; Santa Cruz, A.; Heitz, D.; Arroyo, G. Optical flow estimation in experimental fluid mechanics. In Proceedings of the Seventh International Symposium on Signal Processing and Its Applications, Paris, France, 4 July 2003; Volume 1, pp. 633–636. [Google Scholar]
- Alvarez, L.; Castaño, C.A.; García, M.; Krissian, K.; Mazorra, L.; Salgado, A.; Sánchez, J. Second order variational optic flow estimation. In Computer Aided Systems Theory—EUROCAST 2007; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4739. [Google Scholar]
- Hewer, A.; Weickert, J.; Seibert, H.; Scheffer, T.; Diebels, S. Lagrangian Strain Tensor Computation with Higher Order Variational Models. In Proceedings of the 24th British Machine Vision Conference, Bristol, UK, 9–13 Septamber 2013. [Google Scholar]
- Bredies, K.; Kunisch, K.; Pock, T. Total Generalized Variation. SIAM J. Img. Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef] [Green Version]
- Trobin, W.; Pock, T.; Cremers, D.; Bischof, H. An Unbiased Second-Order Prior for High-Accuracy Motion Estimation. In Proceedings of the DAGM 2008: Pattern Recognition, Munich, Germany, 10–13 June 2008; Rigoll, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 396–405. [Google Scholar]
- Volz, S.; Bruhn, A.; Valgaerts, L.; Zimmer, H. Modeling temporal coherence for optical flow. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 1116–1123. [Google Scholar]
- Fortun, D.; Bouthemy, P.; Kervrann, C. Optical Flow Modeling and Computation: A Survey. Comput. Vis. Image Underst. 2015, 134, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Ding, Z.; Zhao, R.; Zhang, J.; Gao, T.; Xiong, R.; Yu, Z.; Huang, T. Spatio-Temporal Recurrent Networks for Event-Based Optical Flow Estimation. In Proceedings of the AAAI Conference on Artificial Intelligence 2022, Online, 22 February–1 March 2022; Volume 36, pp. 525–533. [Google Scholar]
- Murray, D.; Buxton, B. Scene Segmentation from Visual Motion Using Global Optimization. IEEE Trans. Pattern Anal. Mach. Intell. 1987, PAMI-9, 220–228. [Google Scholar] [CrossRef] [PubMed]
- Nagel, H. Extending the ’Oriented Smoothness Constraint’ into the Temporal Domain and the Estimation of Derivatives of Optical Flow. In Proceedings of the ECCV, Antibes, France, 23–27 April 1990. [Google Scholar]
- Zimmer, H.; Bruhn, A.; Weickert, J. Optic Flow in Harmony. Int. J. Comput. Vis. 2011, 93, 368–388. [Google Scholar] [CrossRef]
- Weickert, J.; Schnörr, C. Variational Optic Flow Computation with a Spatio-Temporal Smoothness Constraint. J. Math. Imaging Vis. 2001, 14, 245–255. [Google Scholar] [CrossRef]
- Brox, T.; Bruhn, A.; Weickert, J. Variational motion segmentation with level sets. In Proceedings of the European Conference on Computer Vision (ECCV), Graz, Austria, 7–13 May 2016; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3951, pp. 471–483. [Google Scholar]
- Black, M.; Anandan, P. Robust dynamic motion estimation over time. In Proceedings of the 1991 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Maui, HI, USA, 3–6 June 1991; pp. 296–302. [Google Scholar]
- Salgado de la Nuez, A.; Sánchez Pérez, J. Temporal Constraints in Large Optical Flow Estimation. In Proceedings of the EUROCAST, Las Palmas de Gran Canaria, Spain, 12–16 February 2007. [Google Scholar]
- Hewer, A. A Generic Framework For Smoothness Terms Of Arbitrary Order; Saarland University: Saarbrücken, Germany, 2013. [Google Scholar]
- Hartmann, C.; Volk, W. Full-Field Strain Measurement in Multi-stage Shear Cutting: High-Speed Camera Setup and Variational Motion Estimation. In Forming the Future; Daehn, G., Cao, J., Kinsey, B., Tekkaya, E., Vivek, A., Yoshida, Y., Eds.; Springer: Cham, Switzerland, 2021; pp. 1605–1615. [Google Scholar]
- Werlberger, M.; Trobin, W.; Pock, T.; Wedel, A.; Cremers, D.; Bischof, H. Anisotropic Huber-L1 Optical Flow. In Proceedings of the BMVC, London, UK, 7–10 September 2009; British Machine Vision Association: Durham, UK, 2009. [Google Scholar]
- Brox, T.; Bruhn, A.; Papenberg, N.; Weickert, J. High Accuracy Optical Flow Estimation Based on a Theory for Warping. In Proceedings of the Computer Vision—ECCV 2004, Prague, Czech Republic, 11–14 May 2004; Pajdla, T., Matas, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 25–36. [Google Scholar]
- Papenberg, N.; Bruhn, A.; Brox, T.; Didas, S.; Weickert, J. Highly Accurate Optic Flow Computation with Theoretically Justified Warping. Int. J. Comput. Vis. 2006, 67, 141–158. [Google Scholar] [CrossRef] [Green Version]
- Morton, K.; Mayers, D. Numerical Solution of Partial Differential Equations: An Introduction, 2nd ed.; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Baker, S.; Scharstein, D.; Lewis, J.P.; Roth, S.; Black, M.J.; Szeliski, R. A Database and Evaluation Methodology for Optical Flow. Int. J. Comput. Vis. 2011, 92, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Hartmann, C.; Wang, J.; Opristescu, D.; Volk, W. Implementation and evaluation of optical flow methods for two-dimensional deformation measurement in comparison to digital image correlation. Opt. Lasers Eng. 2018, 107, 127–141. [Google Scholar] [CrossRef]
- Dunn, J.; Serrin, J. On the thermomechanics of interstitial working. Arch. Ration. Mech. Anal. 1985, 88, 95–133. [Google Scholar] [CrossRef]
- Capriz, G. Continua with latent microstructure. Arch. Ration. Mech. Anal. 1985, 90, 43–56. [Google Scholar] [CrossRef]
- Mariano, P.M. Second-neighbor interactions in classical field theories: Invariance of the relative power and covariance. Math. Methods Appl. Sci. 2017, 40, 1316–1332. [Google Scholar] [CrossRef]





| Parameter | Description |
|---|---|
| relative weight of the BCA and GCA of | |
| weight of spatial regulariser | |
| weight of trajectorial regulariser | |
| weight to reduce influence of constraints of larger temporal distance | |
| : robust penaliser () for , | |
| : Charbonnier penaliser () for | |
| SOR parameter |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bauer, A.; Hartmann, C. Spatio-Trajectorial Optical Flow for Higher-Order Deformation Analysis in Solid Experimental Mechanics. Sensors 2023, 23, 4408. https://doi.org/10.3390/s23094408
Bauer A, Hartmann C. Spatio-Trajectorial Optical Flow for Higher-Order Deformation Analysis in Solid Experimental Mechanics. Sensors. 2023; 23(9):4408. https://doi.org/10.3390/s23094408
Chicago/Turabian StyleBauer, Anna, and Christoph Hartmann. 2023. "Spatio-Trajectorial Optical Flow for Higher-Order Deformation Analysis in Solid Experimental Mechanics" Sensors 23, no. 9: 4408. https://doi.org/10.3390/s23094408





