High-Performance Adaptive Weak Fault Diagnosis Based on the Global Parameter Optimization Model of a Cascaded Stochastic Resonance System
Abstract
1. Introduction
2. Weak Signal Detection Approaches Based on Adaptive Cascaded SR Systems
2.1. Multi-Parameter-Adjusting SR
2.2. Models of Cascaded SR Systems
2.3. Optimization of the Cascaded SR System Based on the PSO Algorithm
3. Numerical Simulations
3.1. Weak Signal Detection Based on the FPO Model and the GPO Model
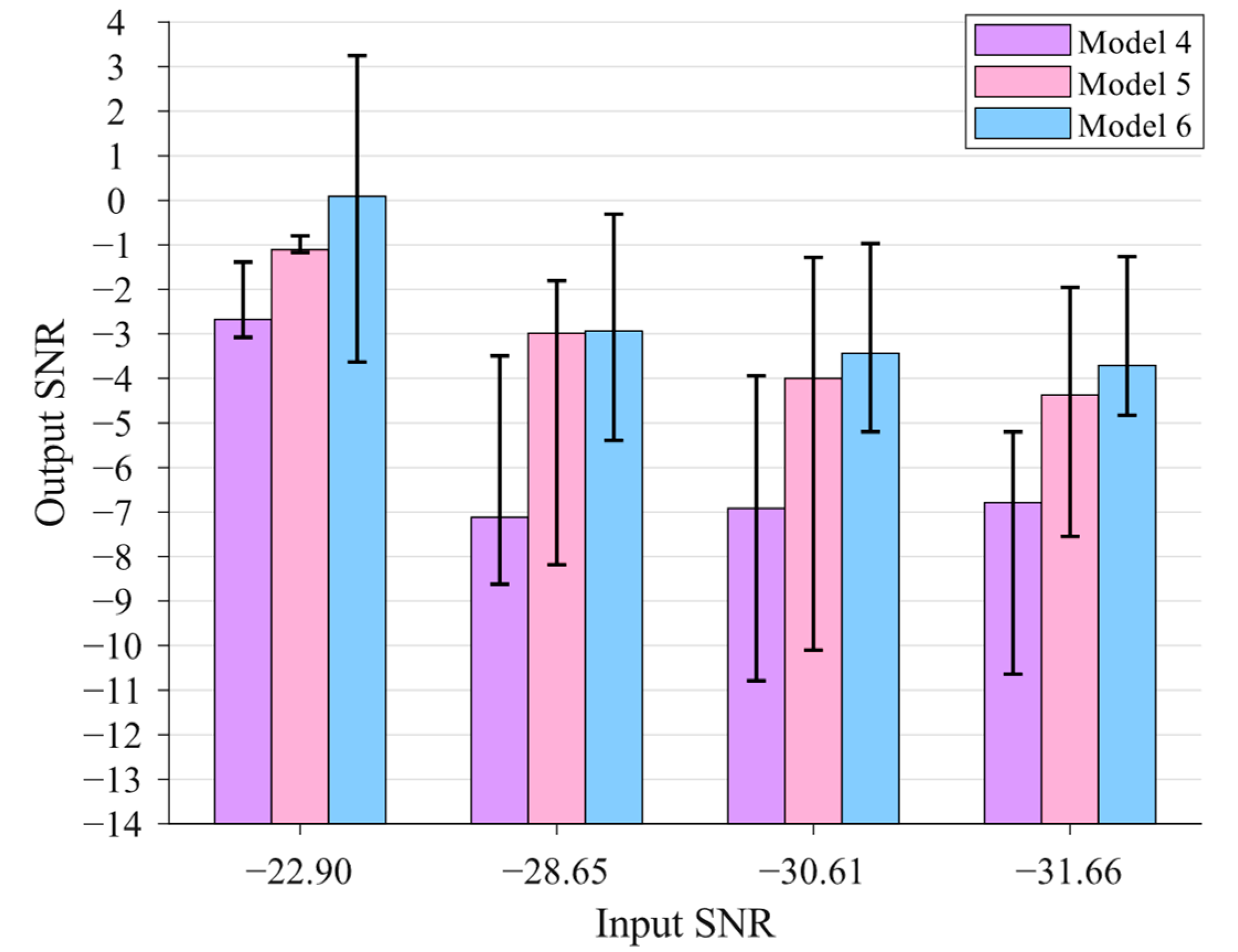
3.2. Statistical Analysis of the Weak Signal Detection Performances of Different Models
3.3. Influence of the Number of Subsystems
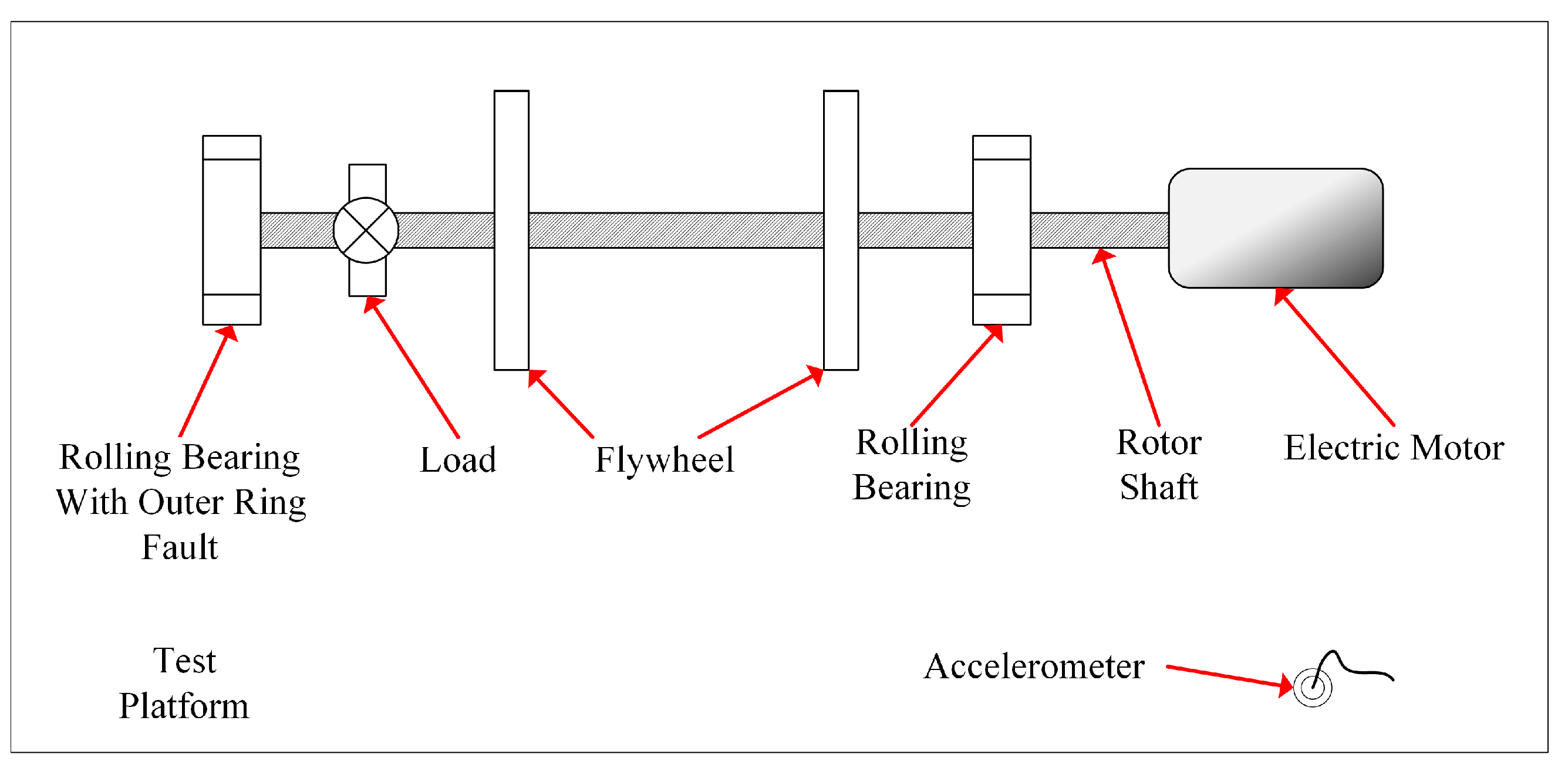
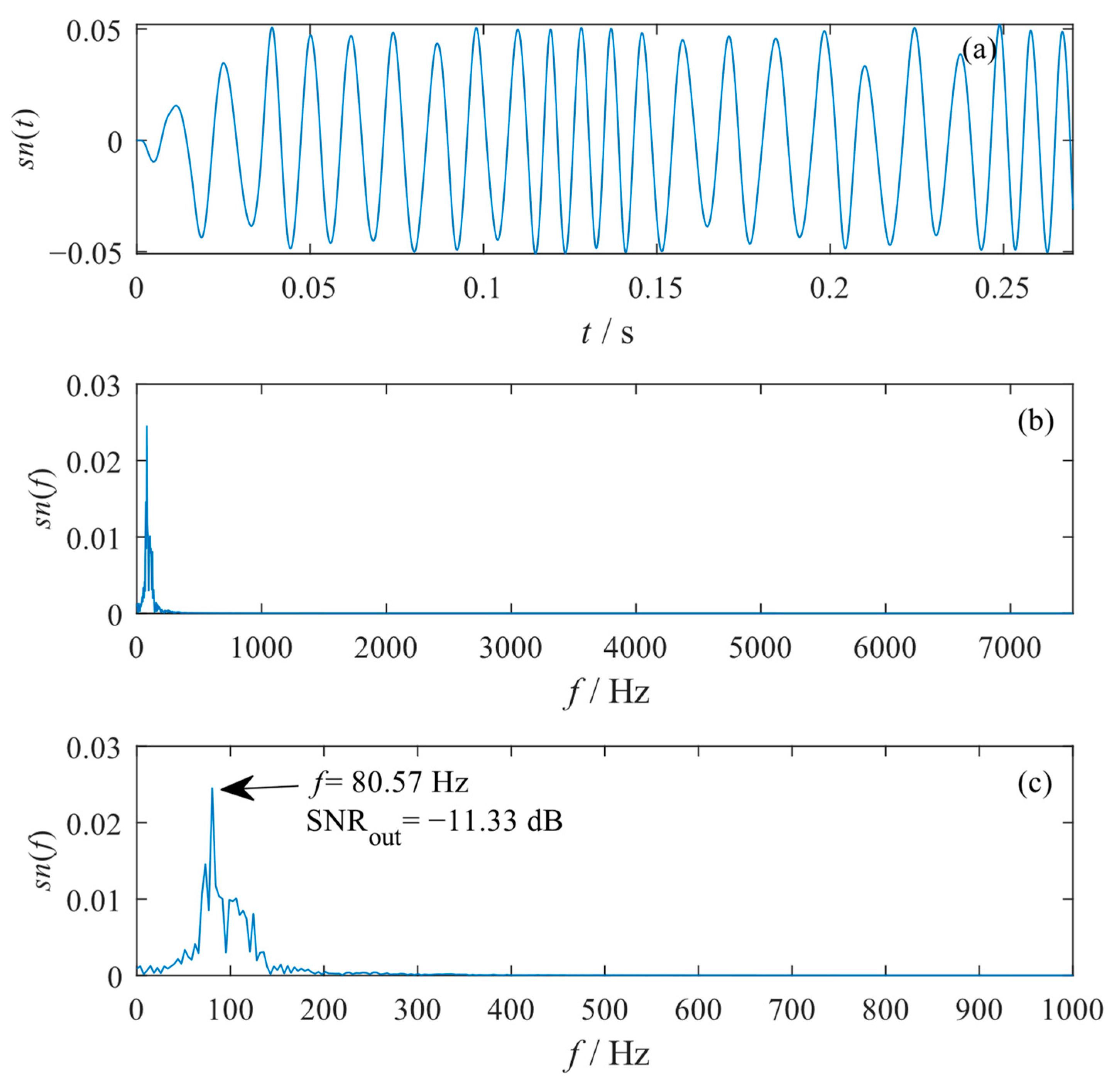
4. Experimental Verifications
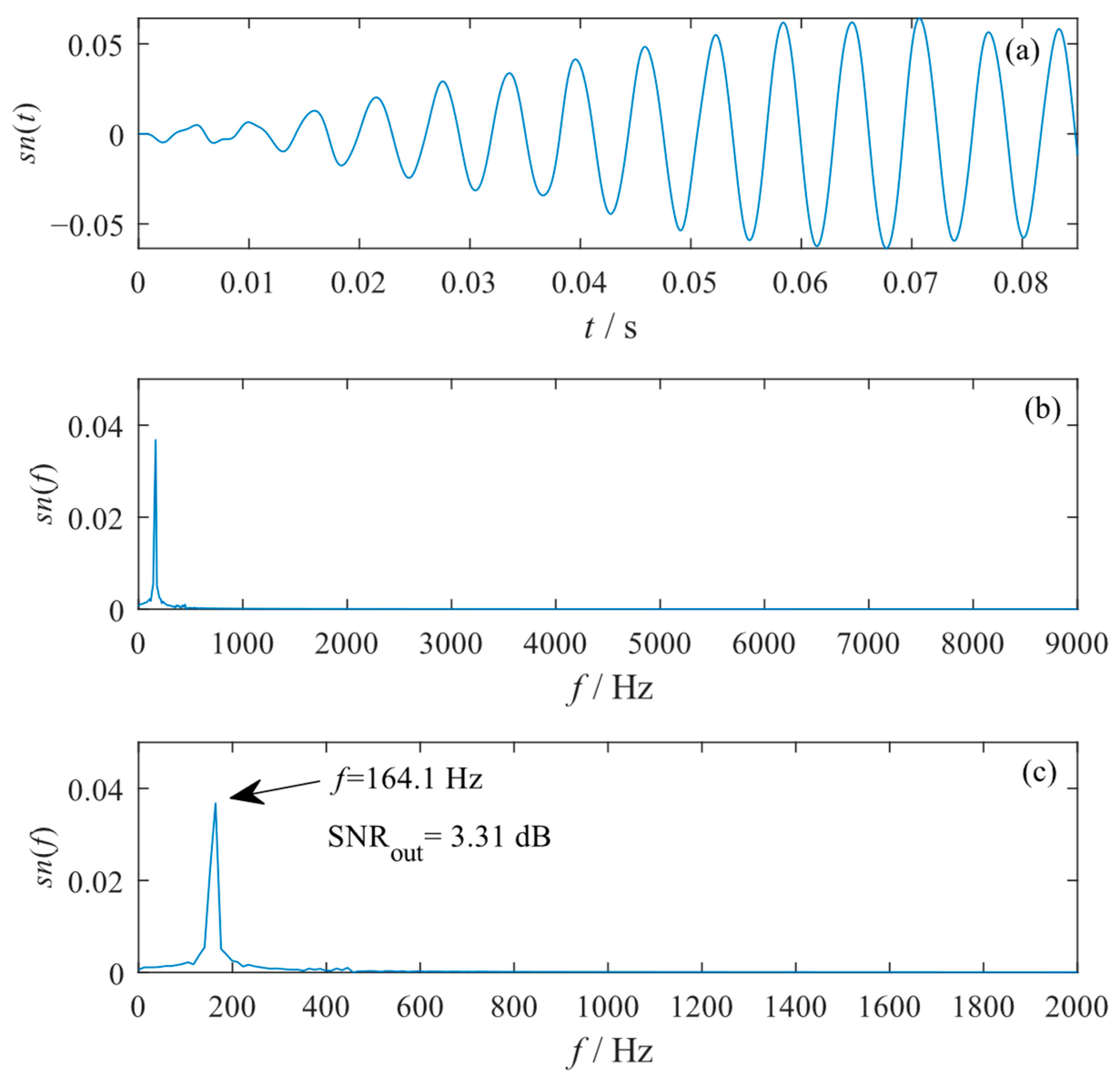
4.1. Case 1: Diagnosis of Rolling Bearing Inner Raceway Fault
4.2. Case 2: Diagnosis of Rolling Bearing Outer Raceway Fault
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CWRU | Case Western Reserve University |
| EDM | Electrical Discharge Machining |
| EMD | Empirical Mode Decomposition |
| FPO | Fixed-parameter Optimization |
| FRSR | Frequency Re-scaling Stochastic Resonance |
| FSRSR | Frequency-Shifted and Re-scaling Stochastic Resonance |
| GPO | Global parameter Optimization |
| MSR | Modulated Stochastic Resonance |
| PNSR | Parameter-Normalized Stochastic Resonance |
| PSO | Particle Swarm Optimization |
| QPSO | Quantum Particle Swarm Optimization |
| SK | Spectral Kurtosis |
| SNR | Signal-to-noise Ration |
| SR | Stochastic Resonance |
| WT | Wavelet Transform |
References
- Tang, J.; Shi, B.; Li, Z.; Li, Y. Weak fault feature extraction method based on compound tri-stable stochastic resonance. Chin. J. Phys. 2020, 66, 50–59. [Google Scholar] [CrossRef]
- Liu, J.; Shen, X.; Wang, J.; Jiang, L.; Zhang, H. An Intelligent Defect Detection Approach Based on Cascade Attention Network Under Complex Magnetic Flux Leakage Signals. IEEE Trans. Ind. Electron. 2023, 70, 7417–7427. [Google Scholar] [CrossRef]
- Kolbe, S.; Gelman, L.; Ball, A. Novel Prediction of Diagnosis Effectiveness for Adaptation of the Spectral Kurtosis Technology to Varying Operating Conditions. Sensors 2021, 21, 6913. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Han, S.; Zhang, S.; Liu, H.; Tang, C. Empirical mode decomposition of weak fault characteristic signal of rolling bearing under strong noise background. J. Vib. Eng. 2020, 33, 582–589. [Google Scholar]
- Zheng, J.D.; Su, M.X.; Ying, W.M.; Tong, J.Y.; Pan, Z.W. Improved uniform phase empirical mode decomposition and its application in machinery fault diagnosis. Measurement 2021, 179, 10. [Google Scholar] [CrossRef]
- Wang, L.M.; He, J.F.; Xiao, H.F.; Zeng, Q.; Ding, X.X.; Shao, Y.M. Joint suppression of normal gear mesh component and background noise for early local fault detection based on dynamic evolutionary digital filter. Measurement 2022, 201, 16. [Google Scholar] [CrossRef]
- Han, B.; Li, C.S.; Zhou, Y.Q.; Yu, G.; Wei, C.L. Second-Order Multisynchrosqueezing Wavelet Transform for Bearing Fault Detection. J. Vib. Eng. Technol. 2022, 10, 1541–1559. [Google Scholar] [CrossRef]
- Benzi, R.; Parisi, G.; Sutera, A.; Vulpiani, A. Stochastic resonance in climatic change. Tellus 1982, 34, 10–16. [Google Scholar] [CrossRef]
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A Math. Gen. 1981, 14, L453. [Google Scholar] [CrossRef]
- Shi, P.M.; Su, C.J.; Han, D.Y. Fault diagnosis of rotating machinery based on adaptive stochastic resonance and AMD-EEMD. Shock. Vib. 2016, 2016, 9278581. [Google Scholar] [CrossRef]
- Tang, J.C.; Shi, B.Q.; Bao, H.R.; Li, Z.X. A new method for weak fault feature extraction based on piecewise mixed stochastic resonance. Chin. J. Phys. 2020, 68, 87–99. [Google Scholar] [CrossRef]
- Lu, S.; He, Q.; Wang, J. A review of stochastic resonance in rotating machine fault detection. Mech. Syst. Signal Process. 2019, 116, 230–260. [Google Scholar] [CrossRef]
- Qiao, Z.J.; Elhattab, A.; Shu, X.D.; He, C.B. A second-order stochastic resonance method enhanced by fractional-order derivative for mechanical fault detection. Nonlinear Dyn. 2021, 106, 707–723. [Google Scholar] [CrossRef]
- Qiao, Z.; Shu, X. Coupled neurons with multi-objective optimization benefit incipient fault identification of machinery. Chaos Solitons Fractals 2021, 145, 110813. [Google Scholar] [CrossRef]
- Zhang, J.J.; Zhang, T. Parameter-induced stochastic resonance based on spectral entropy and its application to weak signal detection. Rev. Sci. Instrum. 2015, 86, 6. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, Y.L.; He, L.F. Research on fault detection of asymmetric piecewise well-posed stochastic resonance system. Rev. Sci. Instrum. 2021, 92, 11. [Google Scholar] [CrossRef]
- Qiao, Z.; Lei, Y.; Li, N. Applications of stochastic resonance to machinery fault detection: A review and tutorial. Mech. Syst. Signal Process. 2019, 122, 502–536. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.Q.; Zhou, F.X.; Ma, Y.J.; Yan, B.K. Weak fault feature extraction method based on improved stochastic resonance. Sensors 2022, 22, 6644. [Google Scholar] [CrossRef]
- Leng, Y.G.; Leng, Y.S.; Wang, T.Y.; Guo, Y. Numerical analysis and engineering application of large parameter stochastic resonance. J. Sound Vib. 2006, 292, 788–801. [Google Scholar] [CrossRef]
- Tan, J.; Chen, X.; Wang, J.; Chen, H.; Cao, H.; Zi, Y.; He, Z. Study of frequency-shifted and re-scaling stochastic resonance and its application to fault diagnosis. Mech. Syst. Signal Process. 2009, 23, 811–822. [Google Scholar] [CrossRef]
- Yang, D.X.; Hu, Z.; Yang, Y.M. The analysis of stochastic resonance of periodic signal with large parameters. Acta Phys. Sin. 2012, 61, 10. (In Chinese) [Google Scholar]
- Lin, M.; Huang, Y.M. Modulation and demodulation for detecting weak periodic signal of stochastic resonance. Acta Phys. Sin. 2006, 55, 3277–3282. (In Chinese) [Google Scholar] [CrossRef]
- Lai, Z.-H.; Leng, Y.-G. Weak-signal detection based on the stochastic resonance of bistable Duffing oscillator and its application in incipient fault diagnosis. Mech. Syst. Signal Process. 2016, 81, 60–74. [Google Scholar] [CrossRef]
- Xu, B.M.; Shi, J.C.; Zhong, M.; Zhang, J. Incipient fault diagnosis of planetary gearboxes based on an adaptive parameter-induced stochastic resonance method. Appl. Acoust. 2022, 188, 108587. [Google Scholar] [CrossRef]
- Hu, B.B.; Guo, C.; Wu, J.M.; Tang, J.H.; Zhang, J.L.; Wang, Y. An adaptive periodical stochastic resonance method based on the grey wolf optimizer algorithm and its application in rolling bearing fault diagnosis. J. Vib. Acoust. Trans. Asme 2019, 141, 9. [Google Scholar] [CrossRef]
- Cheng, W.; Xu, X.M.; Ding, Y.P.; Sun, K.H. Stochastic resonance in a single-well potential and its application in rolling bearing fault diagnosis. Rev. Sci. Instrum. 2020, 91, 16. [Google Scholar] [CrossRef]
- Tong, L.; Li, X.G.; Hu, J.H.; Ren, L.T. A PSO optimization scale-transformation stochastic-resonance algorithm with stability mutation operator. IEEE Access 2018, 6, 1167–1176. [Google Scholar] [CrossRef]
- Lai, Z.H.; Liu, J.S.; Zhang, H.T.; Zhang, C.L.; Zhang, J.W.; Duan, D.Z. Multi-parameter-adjusting stochastic resonance in a standard tri-stable system and its application in incipient fault diagnosis. Nonlinear Dyn. 2019, 96, 2069–2085. [Google Scholar] [CrossRef]
- Cui, H.J.; Guan, Y.; Chen, H.Y.; Deng, W. A novel advancing signal processing method based on coupled multi-stable stochastic resonance for fault detection. Appl. Sci. 2021, 11, 5385. [Google Scholar] [CrossRef]
- Qiao, Z.; Liu, J.; Ma, X.; Liu, J. Double stochastic resonance induced by varying potential-well depth and width. J. Frankl. Inst. 2021, 358, 2194–2211. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Li, Z.; Zhang, Y. Stochastic resonance in cascaded monostable systems with double feedback and its application in rolling bearing fault feature extraction. Nonlinear Dyn. 2021, 104, 971–988. [Google Scholar] [CrossRef]
- Gao, R.; Jiao, S.; Wang, Y.; Li, Y. Weak signal detection of composite multistable stochastic resonance with Woods-Saxon potential. Z. Fur Nat. Sect. A J. Phys. Sci. 2022, 77, 963–976. [Google Scholar] [CrossRef]
- Zhang, H.; He, Q.; Kong, F. Stochastic resonance in an underdamped system with pinning potential for weak signal detection. Sensors 2015, 15, 21169–21195. [Google Scholar] [CrossRef]
- Li, Z.X.; Liu, X.D.; Han, S.J.; Wang, J.G.; Ren, X.P. Fault diagnosis method and application based on unsaturated piecewise linear stochastic resonance. Rev. Sci. Instrum. 2019, 90, 10. [Google Scholar] [CrossRef]
- Li, J.M.; Zhang, Y.G.; Xie, P. A new adaptive cascaded stochastic resonance method for impact features extraction in gear fault diagnosis. Measurement 2016, 91, 499–508. [Google Scholar] [CrossRef]
- Guo, W.; Zhou, Z.; Chen, C.; Li, X. Multi-frequency weak signal detection based on multi-segment cascaded stochastic resonance for rolling bearings. Microelectron. Reliab. 2017, 75, 239–252. [Google Scholar] [CrossRef]
- Xu, D.; Ge, J.; Wang, Y.; Shao, J. Multi-Frequency Weak Signal Decomposition and Reconstruction of Rolling Bearing Based on Adaptive Cascaded Stochastic Resonance. Machines 2021, 9, 275. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Zhang, T.Q. Cascaded Nonlinear Mass Fluctuation Stochastic Resonance System and Its Application in Bearing Fault Diagnosis. Fluct. Noise Lett. 2021, 20, 2150045. [Google Scholar] [CrossRef]
- Li, J.M.; Zhang, J.F.; Li, M.; Zhang, Y.G. A novel adaptive stochastic resonance method based on coupled bistable systems and its application in rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2019, 114, 128–145. [Google Scholar] [CrossRef]
- Kim, J.; Harne, R.L.; Wang, K.W. Online signal denoising using adaptive stochastic resonance in parallel array and its application to acoustic emission signals. J. Vib. Acoust. Trans. Asme 2022, 144, 12. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Zhang, Q.; Xu, Y.; Liu, S.; Chen, Z.; Zhu, C.; Wang, Z.; Pan, M.; Hu, J.; et al. Magnetic Anomaly Signal Detection Using Parallel Monostable Stochastic Resonance System. IEEE Access 2020, 8, 162230–162237. [Google Scholar] [CrossRef]
- He, H.L.; Wang, T.Y.; Leng, Y.G.; Zhang, Y.; Li, Q. Study on non-linear filter characteristic and engineering application of cascaded bistable stochastic resonance system. Mech. Syst. Signal Process. 2007, 21, 2740–2749. [Google Scholar] [CrossRef]
- Hairan, R.; Jalimhan, E.; Dalabaev, S. Cascaded Bistable Stochastic Resonance Signal Detection under Dual-mode Non-Gaussian Noise Background. Telecommun. Eng. 2014, 54, 1260–1264. (In Chinese) [Google Scholar]
- Li, B.; Li, J.; He, Z. Fault feature enhancement of gearbox in combined machining center by using adaptive cascade stochastic resonance. Sci. China Technol. Sci. 2011, 54, 3203–3210. [Google Scholar] [CrossRef]
- Xiao, L.; Bajric, R.; Zhao, J.; Tang, J.; Zhang, X. An adaptive vibrational resonance method based on cascaded varying stable-state nonlinear systems and its application in rotating machine fault detection. Nonlinear Dyn. 2021, 103, 715–739. [Google Scholar] [CrossRef]
- Liu, H.; Han, S.; Yang, J.; Liu, S. Improving the weak feature extraction by adaptive stochastic resonance in cascaded piecewise-linear system and its application in bearing fault detection. J. Vibroeng. 2017, 19, 2506–2520. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, J.P.; Hong-Wei, L.I. Research on stochastic resonance characteristics of cascaded three-steady-state and its application. Comput. Sci. 2018, 45, 146–151. [Google Scholar]
- Lai, Z.H.; Leng, Y.G. Generalized parameter-adjusted stochastic resonance of Duffing oscillator and its application to weak-signal detection. Sensors 2015, 15, 21327–21349. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Z. Weak signal detection based on cascaded piecewise-linear stochastic resonance. China Mech. Eng. 2014, 25, 3343. (In Chinese) [Google Scholar]
- Lai, Z.H.; Leng, Y.G. Dynamic response and stochastic resonance of a tri-stable system. Acta Phys. Sin. 2015, 64, 12. (In Chinese) [Google Scholar]
- Zhang, G.; Yi, T.; Zhang, T.; Cao, L. A multiscale noise tuning stochastic resonance for fault diagnosis in rolling element bearings. Chin. J. Phys. 2018, 56, 145–157. [Google Scholar] [CrossRef]
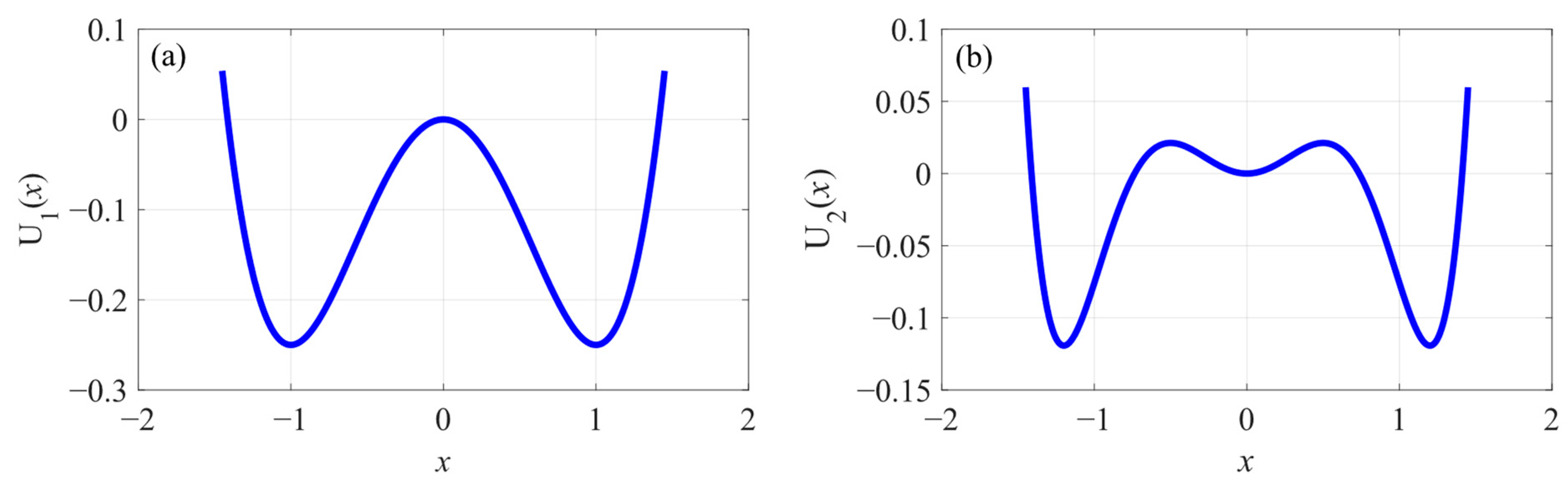








| Bistable Potential Field | Tri-Stable Potential Field | |
|---|---|---|
| Single SR system | Model 1 | Model 4 |
| FPO model of the cascaded SR system | Model 2 | Model 5 |
| GPO model of the cascaded SR system | Model 3 | Model 6 |
| Model of Bearing | Inside Diameter
(Inches) | Outside Diameter (Inches) | Thickness (Inches) | Ball Diameter (Inches) | No. of Rolling Elements Z | Contact Angle |
|---|---|---|---|---|---|---|
| SKF 6205-2RS JEM | 0.9843 | 2.0472 | 0.5906 | 0.3126 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Z.; Huang, Z.; Xu, M.; Wang, C.; Xu, J.; Zhang, C.; Zhu, R.; Qiao, Z. High-Performance Adaptive Weak Fault Diagnosis Based on the Global Parameter Optimization Model of a Cascaded Stochastic Resonance System. Sensors 2023, 23, 4429. https://doi.org/10.3390/s23094429
Lai Z, Huang Z, Xu M, Wang C, Xu J, Zhang C, Zhu R, Qiao Z. High-Performance Adaptive Weak Fault Diagnosis Based on the Global Parameter Optimization Model of a Cascaded Stochastic Resonance System. Sensors. 2023; 23(9):4429. https://doi.org/10.3390/s23094429
Chicago/Turabian StyleLai, Zhihui, Zhangjun Huang, Min Xu, Chen Wang, Junchen Xu, Cailiang Zhang, Ronghua Zhu, and Zijian Qiao. 2023. "High-Performance Adaptive Weak Fault Diagnosis Based on the Global Parameter Optimization Model of a Cascaded Stochastic Resonance System" Sensors 23, no. 9: 4429. https://doi.org/10.3390/s23094429
APA StyleLai, Z., Huang, Z., Xu, M., Wang, C., Xu, J., Zhang, C., Zhu, R., & Qiao, Z. (2023). High-Performance Adaptive Weak Fault Diagnosis Based on the Global Parameter Optimization Model of a Cascaded Stochastic Resonance System. Sensors, 23(9), 4429. https://doi.org/10.3390/s23094429





_Zhu.png)


