Modeling the Converse Magnetoelectric Effect in the Low-Frequency Range
Abstract
:1. Introduction
2. EMR Longitudinal Mode
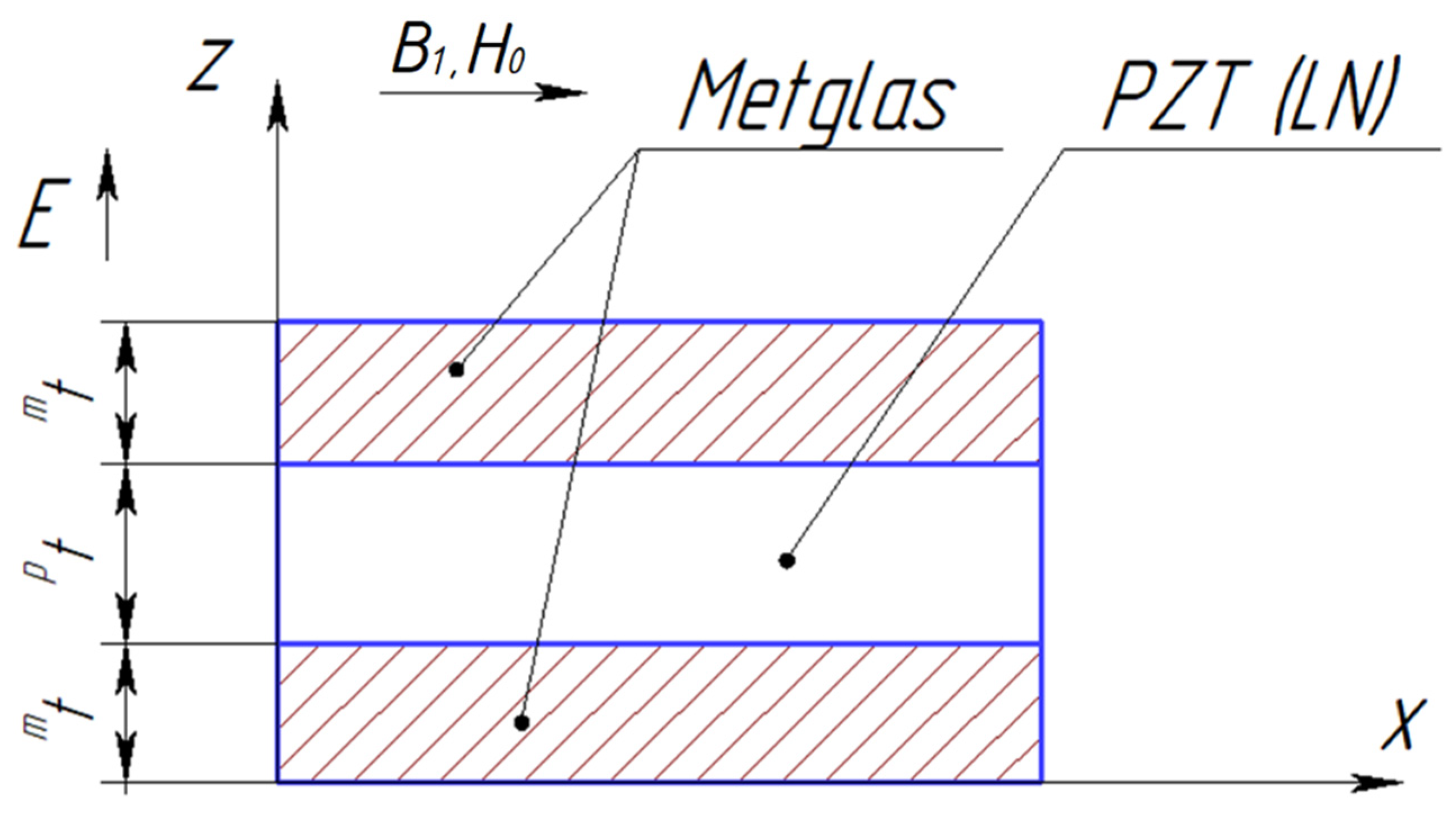
2.1. Symmetric Structure
2.1.1. Free Plate
2.1.2. Rigid End of the Plate
2.2. Asymmetric Structure
2.2.1. Free Plate
2.2.2. Rigid End of the Plate
3. EMR Bending Mode
3.1. Free Plate
3.2. Rigid End of the Plate
4. Quasi-Static Regime
4.1. Symmetric Structure
4.2. Asymmetric Structure
5. EMR Longitudinal Shear Mode
5.1. Symmetric Structure
5.2. Asymmetric Structure
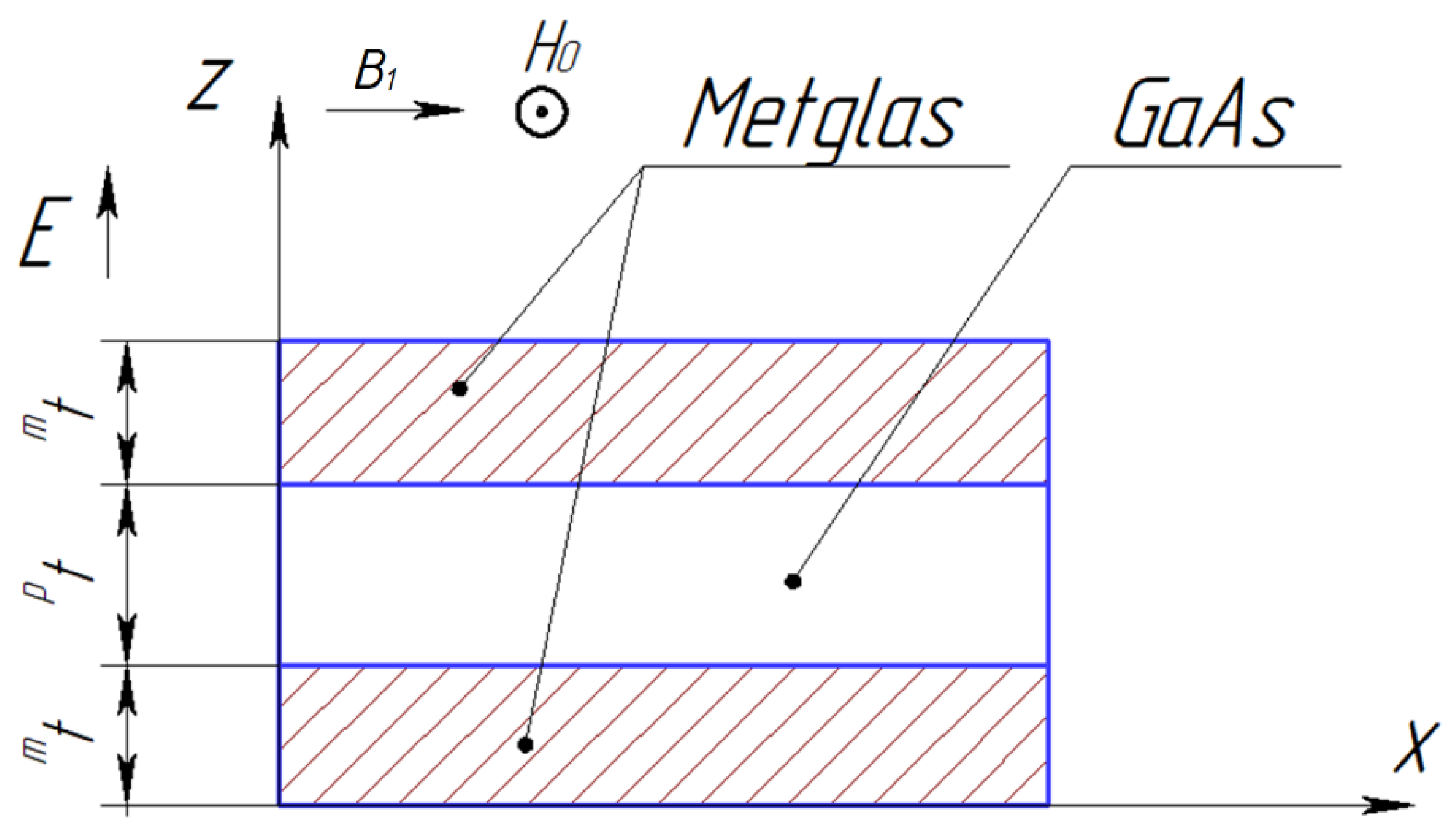
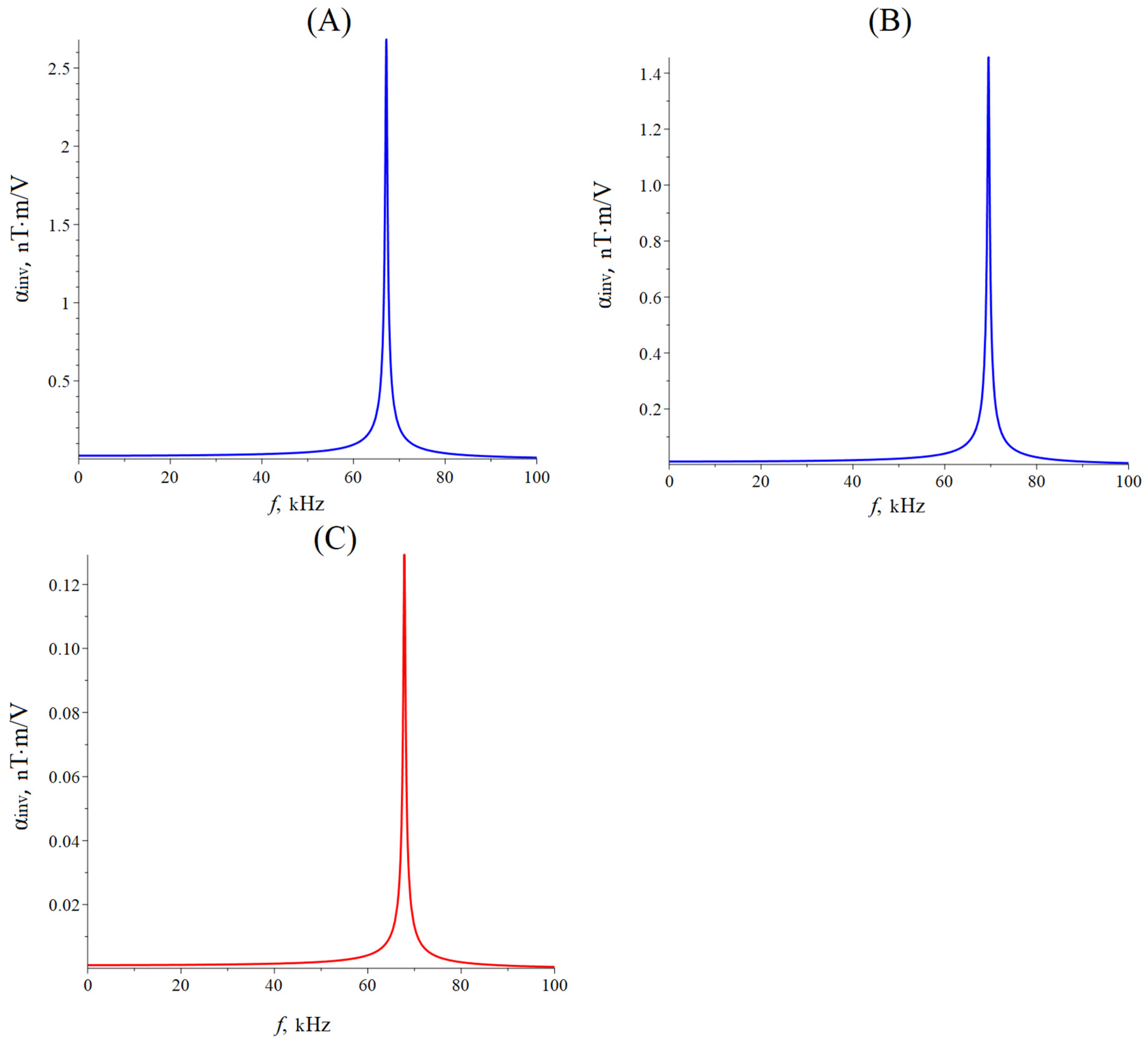
6. EMR Torsional Mode for ME Composite of Metglas/GaAs
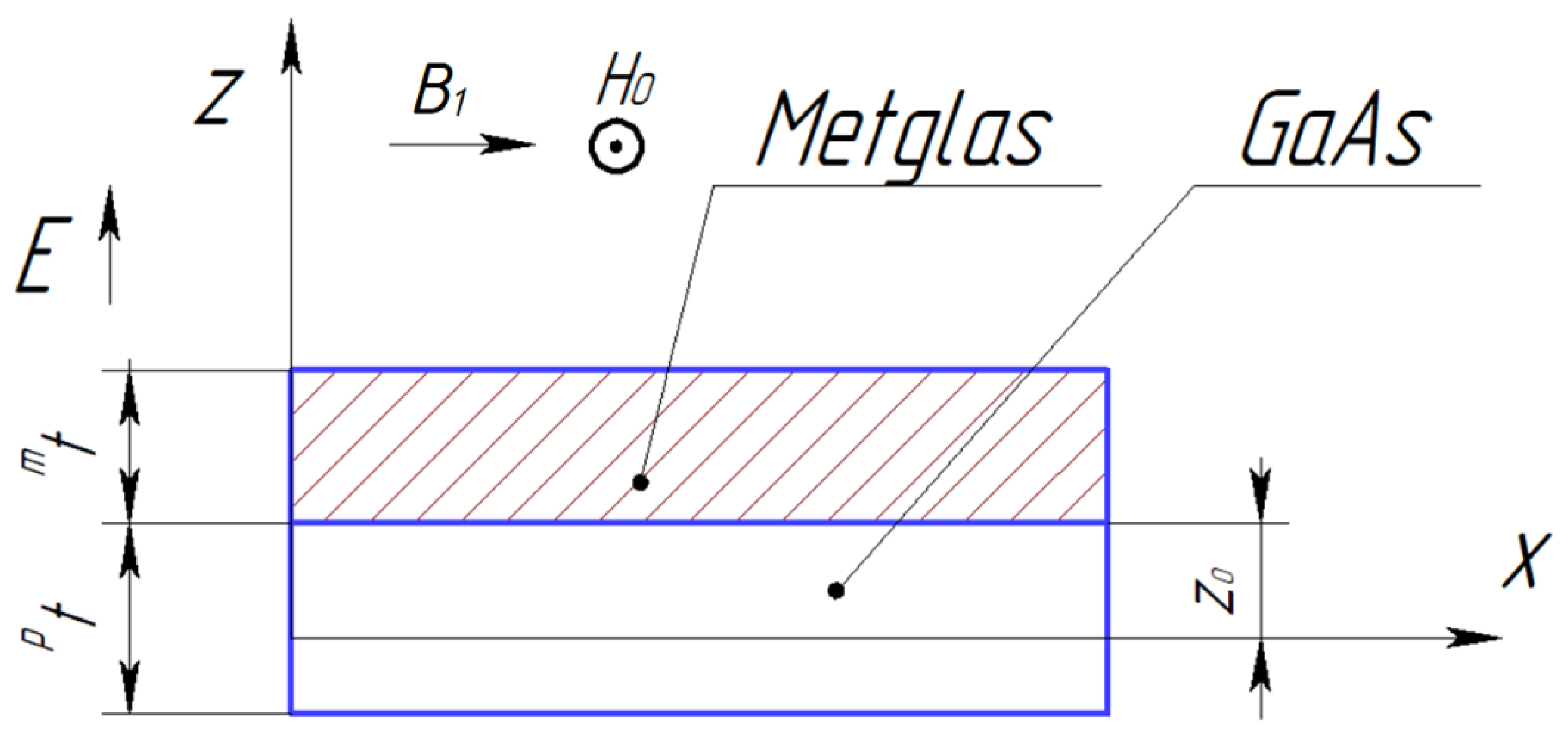
7. EMR Torsional Mode in a ME Composite Based on Bimorph LN
8. Quasi-Static Regime
8.1. ME Composite of Metglas/GaAs
8.1.1. Symmetric Structure
8.1.2. Asymmetric Structure
8.2. ME Composite Based on Bimorph LN
9. Discussion
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nan, C.-W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspectives, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Viehland, D. (Eds.) Magnetoelectricity in Composites; Pan Stanford Publishing Pte. Ltd.: Singapore, 2012; p. 273. [Google Scholar]
- Liang, X.; Chen, H.; Sun, N.X. Magnetoelectric materials and devices. APL Mater. 2021, 9, 041114. [Google Scholar] [CrossRef]
- Liang, X.; Matyushov, A.; Hayes, P.; Schell, V.; Dong, C.; Chen, H.; He, Y.; Will-Cole, A.; Quandt, E.; Martins, P.; et al. Roadmap on Magnetoelectric Materials and Devices. IEEE Trans. Magn. 2021, 57, 1. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Petrov, V.M.; Petrov, R.V.; Tatarenko, A.S. Magnetoelectric Composites; Pan Stanford Publishing Pte. Ltd.: Singapore, 2019; p. 280. [Google Scholar]
- Srinivasan, G.; Priya, S.; Sun, N.X. (Eds.) Composite Magnetoelectrics; Woodhead Publishing: Cambridge, UK, 2015; p. 381. [Google Scholar]
- Bichurin, M.; Petrov, R.; Sokolov, O.; Leontiev, V.; Kuts, V.; Kiselev, D.; Wang, Y. Magnetoelectric Magnetic Field Sensors: A Review. Sensors 2021, 21, 6232. [Google Scholar] [CrossRef] [PubMed]
- Viehland, D.; Wuttig, M.; McCord, J.; Quandt, E. Magnetoelectric magnetic field sensors. MRS Bull. 2018, 43, 834–840. [Google Scholar] [CrossRef]
- Bichurin, M.; Petrov, R.; Leontiev, V.; Semenov, G.; Sokolov, O. Magnetoelectric Current Sensors. Sensors 2017, 17, 1271. [Google Scholar] [CrossRef]
- Chu, Z.; Annapureddy, V.; PourhosseiniAsl, M.J.; Palneedi, H.; Ryu, J.; Dong, S. Dual-stimulus magnetoelectric energy harvesting. MRS Bull. 2018, 43, 199–205. [Google Scholar] [CrossRef]
- Bichurin, M.; Petrov, V. Magnetic resonance in layered ferrite-ferroelectric structures. Sov. Phys. JETP 1988, 58, 2277. [Google Scholar]
- Bichurin, M.; Kornev, I.; Petrov, V.; Lisnevskaya, I. Investigation of magnetoelectric interaction in composite. Ferroelectrics 1997, 204, 289–297. [Google Scholar] [CrossRef]
- Bichurin, M.; Petrov, R.; Kiliba, Y. Magnetoelectric microwave phase shifters. Ferroelectrics 1997, 204, 311–319. [Google Scholar] [CrossRef]
- Lou, J.; Liu, M.; Reed, D.; Ren, Y.; Sun, N.X. Giant Electric Field Tuning of Magnetism in Novel Multiferroic FeGaB/Lead Zinc Niobate–Lead Titanate (PZN-PT) Heterostructures. Adv. Mater. 2009, 21, 4711–4715. [Google Scholar] [CrossRef]
- Liu, M.; Obi, O.; Lou, J.; Chen, Y.; Cai, Z.; Stoute, S.; Espanol, M.; Lew, M.; Situ, X.; Ziemer, K.S.; et al. Giant Electric Field Tuning of Magnetic Properties in Multiferroic Ferrite/Ferroelectric Heterostructures. Adv. Funct. Mater. 2009, 19, 1826–1831. [Google Scholar] [CrossRef]
- Chu, Z.; Dong, C.; Tu, C.; Liang, X.; Chen, H.; Sun, C.; Yu, Z.; Dong, S.; Sun, N.-X. A low-power and high-sensitivity magnetic field sensor based on converse magnetoelectric effect. Appl. Phys. Lett. 2019, 115, 162901. [Google Scholar] [CrossRef]
- Yang, M.-T.; Sing, M.L.C.; Dolabdjian, C.; Staruch, M.; Finkel, P.; Zhuang, X.; Li, J.; Viehland, D. Phase Modulation Noise of a Magneto (Elasto) Electric Sensor Operating as a Magnetometer in the Non-Linear Regime–Theoretical and Experimental Studies. IEEE Sens. J. 2019, 10, 3647–3653. [Google Scholar] [CrossRef]
- Hayes, P.; Klug, M.J.; Toxværd, S.; Durdaut, P.; Schell, V.; Teplyuk, A.; Burdin, D.; Winkler, A.; Weser, R.; Fetisov, Y.; et al. Converse Magnetoelectric Composite Resonator for Sensing Small Magnetic Fields. Sci. Rep. 2019, 9, 16355. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, Y.E.; Keller, S.; Carman, G.P. Bulk acoustic wave-mediated multiferroic antennas: Architecture and performance bound. IEEE Trans. Antennas Propag. 2015, 63, 3335–3344. [Google Scholar] [CrossRef]
- Dong, C.Z.; He, Y.F.; Li, M.H.; Tu, C.; Chu, Z.; Liang, X.; Chen, H.; Wei, Y.; Zaeimbashi, M.; Wang, X.; et al. A Portable Very Low Frequency (VLF) Communication System Based on Acoustically Actuated Magnetoelectric Antennas. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 398–402. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Z.; Fu, G.; Wang, J.; Xi, Q.; Wang, Y.; Jia, Z.; Zi, G. A Low-Frequency MEMS Magnetoelectric Antenna Based on Mechanical Resonance. Micromachines 2022, 13, 864. [Google Scholar] [CrossRef]
- Lei, B.; Shi, Y.; You, Z. A two-dimensional multi-field coupling model for converse magnetoelectric effect in acoustically actuated an-tennas. Phys. Lett. A 2023, 471, 128802. [Google Scholar] [CrossRef]
- Zavaliche, F.; Zheng, H.; Mohaddes-Ardabili, L.; Yang, S.Y.; Zhan, Q.; Shafer, P.; Reilly, E.; Chopdekar, R.; Jia, Y.; Wright, P.; et al. Electric Field-Induced Magnetization Switching in Epitaxial Columnar Nanostructures. Nano Lett. 2005, 5, 1793–1796. [Google Scholar] [CrossRef]
- Hong, N.T.M.; Thang, P.D.; Tiep, N.H.; Cuong, L.V.; Duc, N.H. Voltage-controllable magnetic behavior in PZT/NiFe/CoFe nanocomposites. Adv. Nat. Sci. Nanosci. Nanotechnol. 2011, 2, 015015. [Google Scholar] [CrossRef]
- Chopdekar, V.; Buzzi, M.; Jenkins, C.; Arenholz, E.; Nolting, F.; Takamura, Y. Giant reversible anisotropy changes at room temperature in a (La,Sr)MnO3/Pb(Mg,Nb,Ti)O3 magneto-electric heterostructure. Sci. Rep. 2016, 6, 27501. [Google Scholar] [CrossRef] [PubMed]
- Spaldin, N.A.; Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 2019, 18, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Ghidini, M.; Maccherozzi, F.; Moya, X.; Phillips, L.C.; Yan, W.; Soussi, J.; Métallier, N.; Vickers, M.E.; Steinke, N.; Mansell, R.; et al. Perpendicular Local Magnetization Under Voltage Control in Ni Films on Ferroelectric BaTiO3 Substrates. Adv. Mater. 2015, 27, 1460–1465. [Google Scholar] [CrossRef] [PubMed]
- Ghidini, M.; Dhesi, S.; Mathur, N. Nanoscale magnetoelectric effects revealed by imaging. J. Magn. Magn. Mater. 2021, 520, 167016. [Google Scholar] [CrossRef]
- Eerenstein, W.; Wiora, M.; Pieto, J.L.; Scott, J.F.; Mathur, N.D. Giant sharp and persistent converse magnetoelectric effects in multiferroic epitaxial heterostructures. Nat. Mater. 2007, 6, 348–351. [Google Scholar] [CrossRef]
- Hu, J.-M.; Nan, C.W. Electric-field-induced magnetic easy-axis reorientation in ferromagnetic/ferroelectric layered heterostructures. Phys. Rev. B 2009, 80, 224416. [Google Scholar] [CrossRef]
- Wang, J.; Chen, A.; Li, P.; Zhang, S. Magnetoelectric Memory Based on Ferromagnetic/Ferroelectric Multiferroic Heterostructure. Materials 2021, 14, 4623. [Google Scholar] [CrossRef]
- Jia, Y.; Or, S.W.; Chan, H.L.W.; Zhao, X.; Luo, H. Converse magnetoelectric effect in laminated composites of PMN–PT single crystal and Terfenol-D alloy. Appl. Phys. Lett. 2006, 88, 242902. [Google Scholar] [CrossRef]
- Fetisov, Y.; Petrov, V.; Srinivasan, G. Inverse magnetoelectric effects in a ferromagnetic–piezoelectric layered structure. J. Mater. Res. 2007, 22, 2074–2080. [Google Scholar] [CrossRef]
- Chen, S.Y.; Wang, D.H.; Han, Z.D.; Zhang, C.L.; Du, Y.W.; Huang, Z.G. Converse magnetoelectric effect in ferromagnetic shape memory alloy/piezoelectric laminate. Appl. Phys. Lett. 2009, 95, 022501. [Google Scholar] [CrossRef]
- Gridnev, S.A.; Kalgin, A.V. Inverse Magnetoelectric Effect in Two Layer PbZr0.53Ti0.47O3–Mn0.4Zn0.6Fe2O4 Composite. Ferroelectrics 2010, 397, 128–134. [Google Scholar] [CrossRef]
- Filippov, D.A.; Galkina, T.A.; Srinivasan, G. Srinivasan. Inverse Magnetoelectric Effect in Ferrite–Piezoelectric Structures. Tech. Phys. Lett. 2010, 36, 984–986. [Google Scholar] [CrossRef]
- Xuan, H.C.; Wang, L.Y.; Ma, S.C.; Zheng, Y.X.; Cao, Q.Q.; Wang, D.H.; Du, Y.W. Large converse magnetoelectric effect in Metglas FeCoBSi and 0.7Pb(Mg1/3Nb2/3)O3-0.3PbTiO30.7Pb(Mg1/3Nb2/3)O3-0.3PbTiO3 laminated composite. Appl. Phys. Lett. 2011, 98, 052505. [Google Scholar] [CrossRef]
- Xuan, H.; Wang, D.; Du, Y. Electric-field-controlled magnetic responses in Metglas and lead zirconate titanate laminated composite. J. Alloys Compd. 2013, 550, 446–450. [Google Scholar] [CrossRef]
- Zhou, J.-P.; Wang, P.; Yang, J.; Liu, P.; Zhang, H.-W. Large converse magnetoelectric response in Rosen-type transformer and Terfenol-D laminated composite. J. Appl. Phys. 2012, 111, 033915. [Google Scholar] [CrossRef]
- Lou, J.; Pellegrini, G.N.; Liu, M.; Mathur, N.D.; Sun, N.X. Equivalence of direct and converse magnetoelectric coefficients in strain-coupled two-phase systems. Appl. Phys. Lett. 2012, 100, 102907. [Google Scholar] [CrossRef]
- Srinivas, A.; Krishnaiah, R.V.; Karthik, T.; Suresh, P.; Asthana, S.; Kamat, S.V. Observation of direct and indirect magnetoelectricity in lead free ferroelectric (Na0.5Bi0.5TiO3)–magnetostrictive (CoFe2O4) particulate composite. Appl. Phys. Lett. 2012, 101, 082902. [Google Scholar] [CrossRef]
- Bichurin, M.; Petrov, V.; Petrov, R. Direct and inverse magnetoelectric effect in layered composites in electromechanical resonance range: A review. J. Magn. Magn. Mater. 2012, 324, 3548–3550. [Google Scholar] [CrossRef]
- Kalgin, A.V.; Gridnev, S.A.; Gribe, Z.H. Specific features of the inverse magnetoelectric effect in two-layered Tb0.12Dy0.2Fe0.68-PbZr0.53Ti0.47O3 composites. Phys. Solid State 2014, 56, 1327–1333. [Google Scholar] [CrossRef]
- Ge, X.H.; Ji, H.; Li, Y.; Chen, J.K.; Wang, Y.G. Converse magnetoelectric effect in Ni(Terfenol-D)/Pb(Zr,Ti)O3 bilayer-laminated composite. Int. J. Mod. Phys. B 2018, 32, 1850175. [Google Scholar] [CrossRef]
- Timopheev, A.; Vidal, J.; Kholkin, A.; Sobolev, N. Direct and converse magnetoelectric effects in Metglas/LiNbO3/Metglas trilayers. J. Appl. Phys. 2013, 114, 044102. [Google Scholar] [CrossRef]
- Xue, F.; Hu, J.; Wang, S.X.; He, J. In-plane longitudinal converse magnetoelectric effect in laminated composites: Aiming at sensing wide range electric field. Appl. Phys. Lett. 2015, 106, 082901. [Google Scholar] [CrossRef]
- Bichurin, M.; Sokolov, O.; Ivanov, S.; Leontiev, V.; Petrov, D.; Semenov, G.; Lobekin, V. Physics of Composites for Low-Frequency Magnetoelectric Devices. Sensors 2022, 22, 4818. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Zhang, Q.; Wu, H.; You, H.; Jiao, J.; Luo, H.; Wang, Y.; Duan, C.; Gao, A. A very low frequency (VLF) antenna based on clamped bending-mode structure magnetoelectric laminates. J. Phys. Condens. Matter. 2022, 34, 414002. [Google Scholar] [CrossRef]
- Dong, S.; Li, J.F.; Viehland, D.; Cheng, J.; Cross, L.E. A strong magnetoelectric voltage gain effect in magnetostrictive-piezoelectric composite. Appl. Phys. Lett. 2004, 85, 3534–3536. [Google Scholar] [CrossRef]
- Xu, J.; Leung, C.M.; Zhuang, X.; Li, J.; Bhardwaj, S.; Volakis, J.; Viehland, D. A Low Frequency Mechanical Transmitter Based on Magnetoelectric Heterostructures Operated at Their Resonance Frequency. Sensors 2019, 19, 853. [Google Scholar] [CrossRef]
- Niu, Y.; Ren, H. A miniaturized low frequency (LF) magnetoelectric receiving antenna with an integrated DC magnetic bias. Appl. Phys. Lett. 2021, 118, 264104. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bichurin, M.; Sokolov, O.; Ivanov, S.; Leontiev, V.; Lobekin, V.; Semenov, G.; Wang, Y. Modeling the Converse Magnetoelectric Effect in the Low-Frequency Range. Sensors 2024, 24, 151. https://doi.org/10.3390/s24010151
Bichurin M, Sokolov O, Ivanov S, Leontiev V, Lobekin V, Semenov G, Wang Y. Modeling the Converse Magnetoelectric Effect in the Low-Frequency Range. Sensors. 2024; 24(1):151. https://doi.org/10.3390/s24010151
Chicago/Turabian StyleBichurin, Mirza, Oleg Sokolov, Sergey Ivanov, Viktor Leontiev, Vyacheslav Lobekin, Gennady Semenov, and Yaojin Wang. 2024. "Modeling the Converse Magnetoelectric Effect in the Low-Frequency Range" Sensors 24, no. 1: 151. https://doi.org/10.3390/s24010151




