FEM Modeling Strategies: Application to Mechanical and Dielectric Sensitivities of Love Wave Devices in Liquid Medium
Abstract
:1. Introduction
2. Context and State of the Art
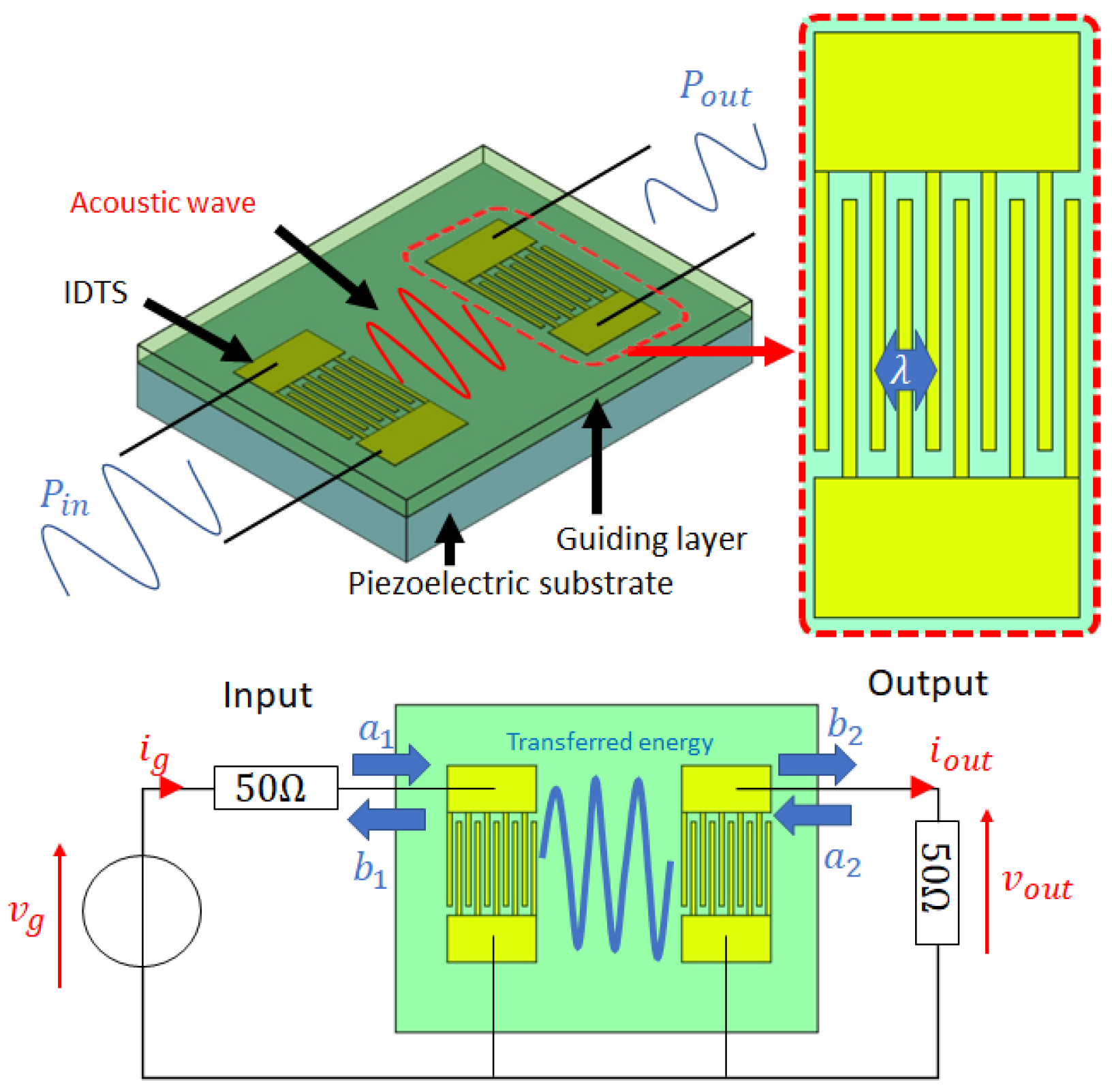
2.1. Love Wave Sensor in Liquid Medium—A Growing Complexity
2.2. A Brief History of FEM Modeling of Love Wave Sensor
3. Material and Methods
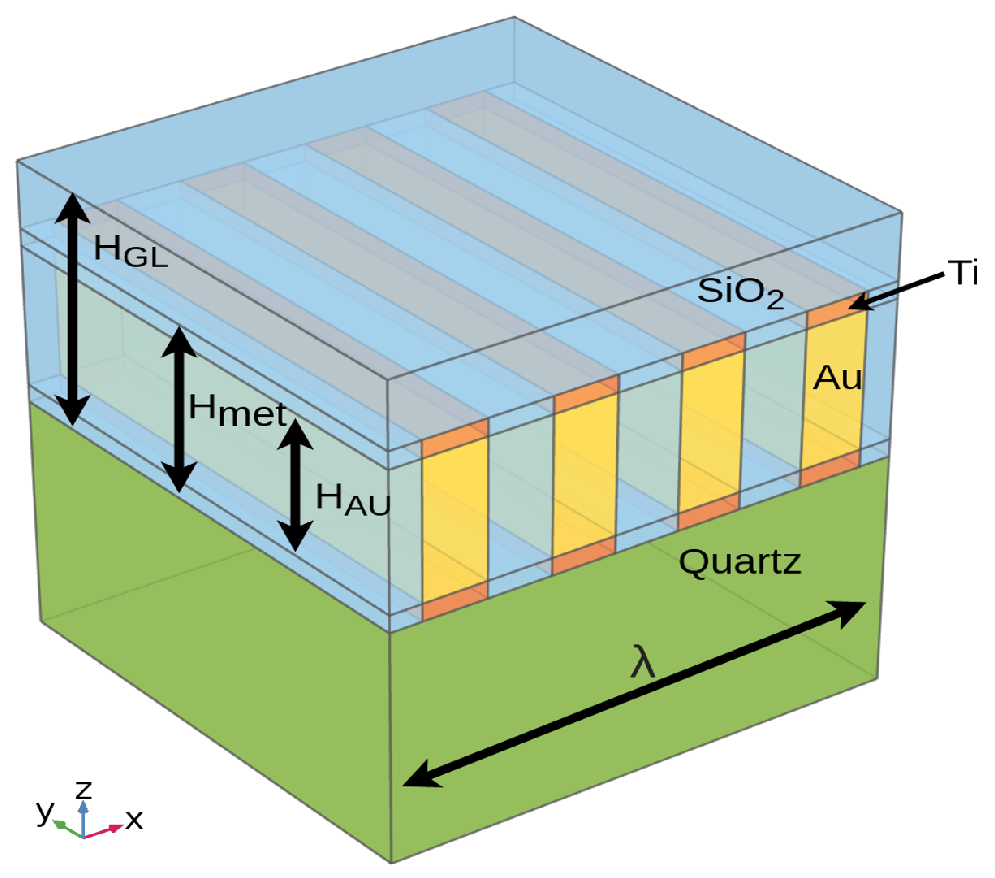
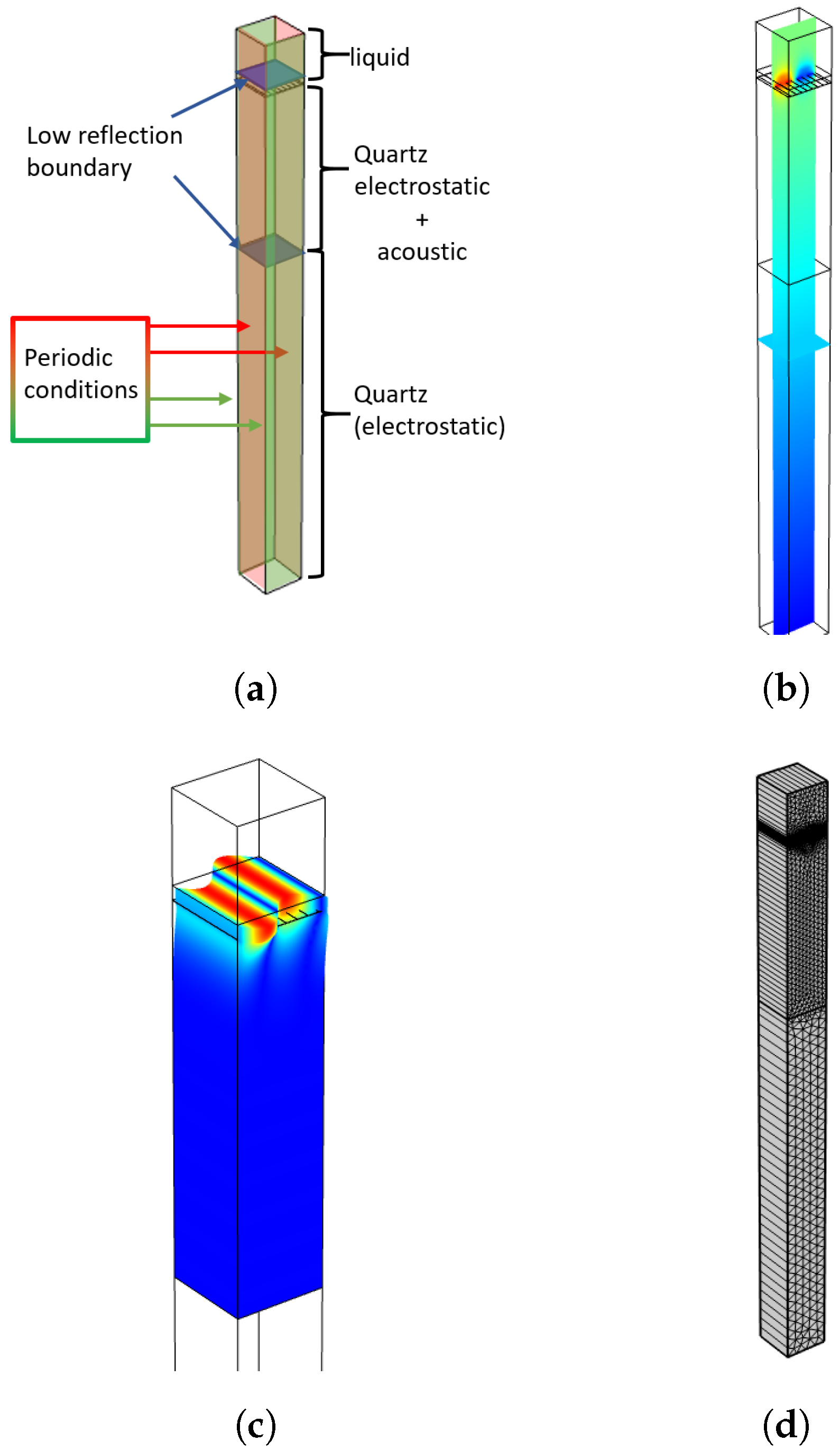
3.1. Representative Volume Element Model
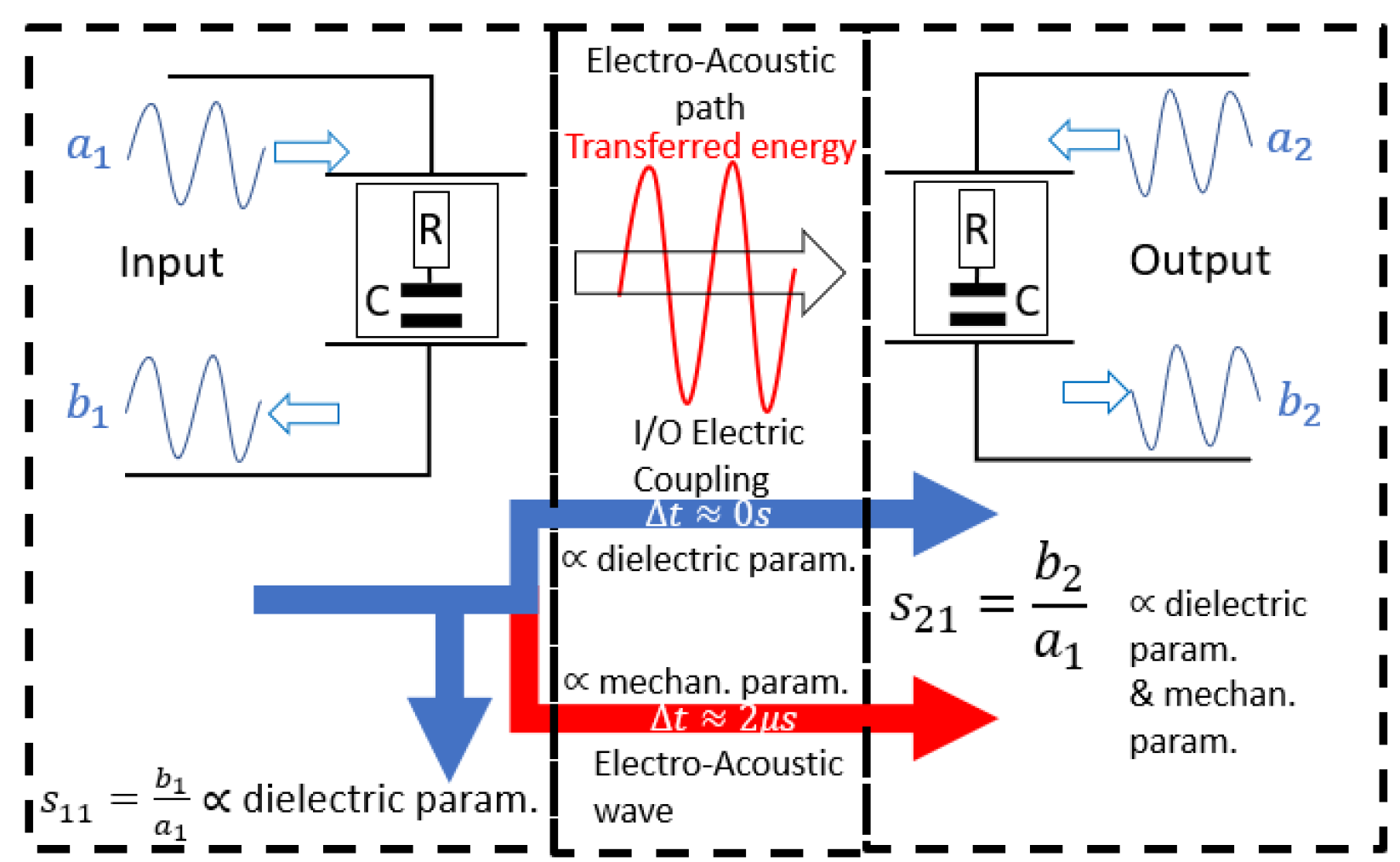
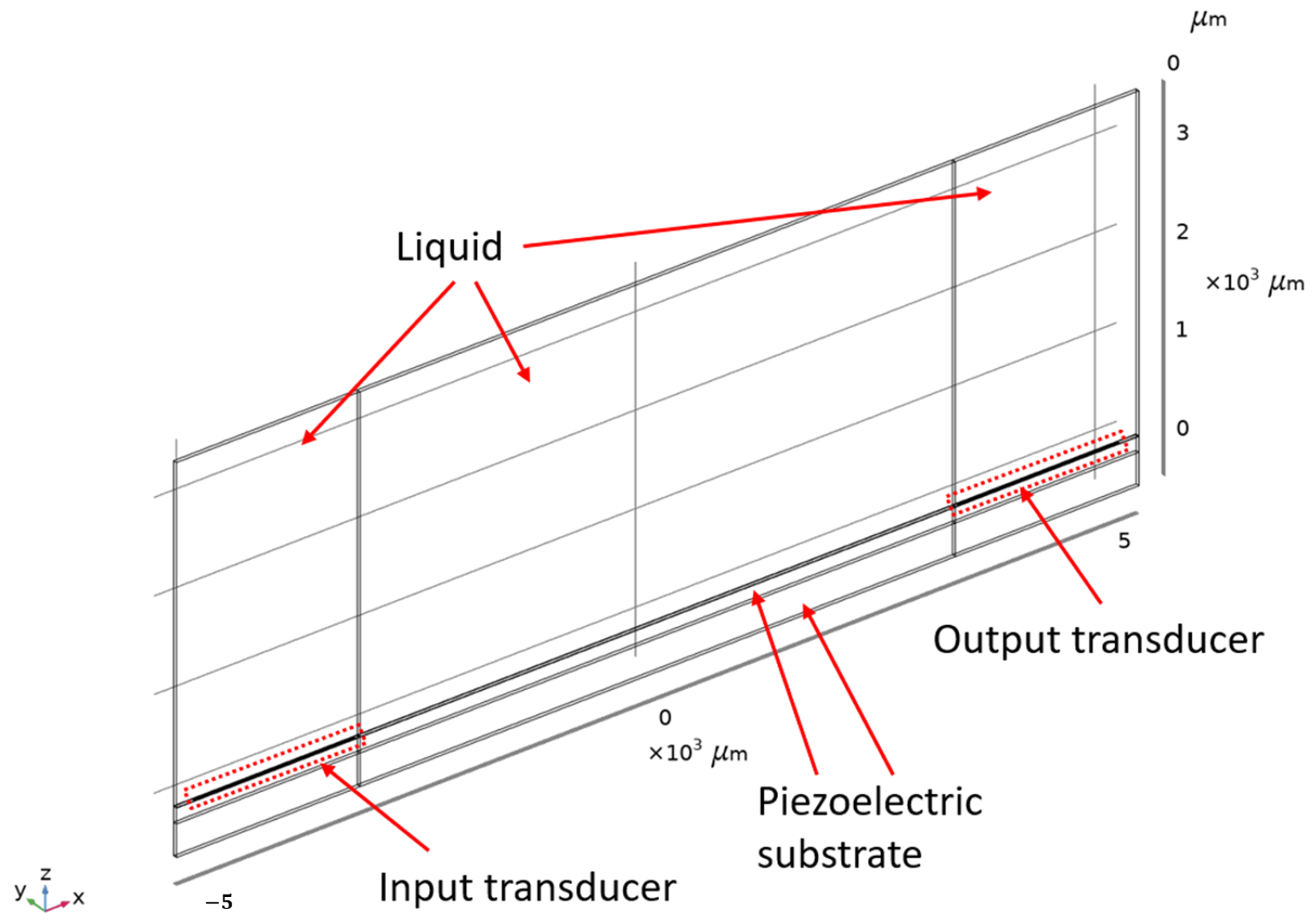
3.2. 2.5D Model
- : calculated input impedance;
- : calculated output impedance;
- : estimated impedance by the 2.5D model.
3.3. Used Love Wave Device and Liquid Samples
4. Results
4.1. RVE Simulation of Love Wave Device Electrical Responses
4.2. 2.5D Model: Estimation of Love Wave Device Electrical Responses
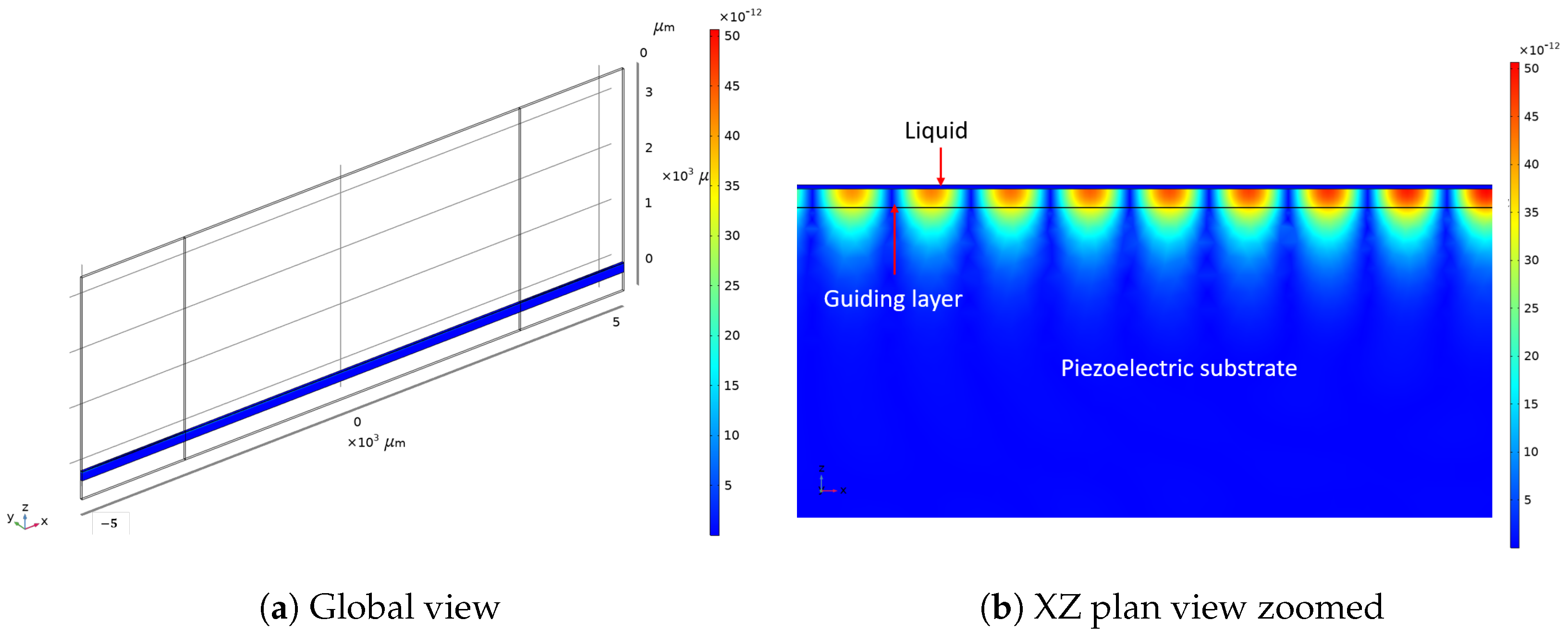
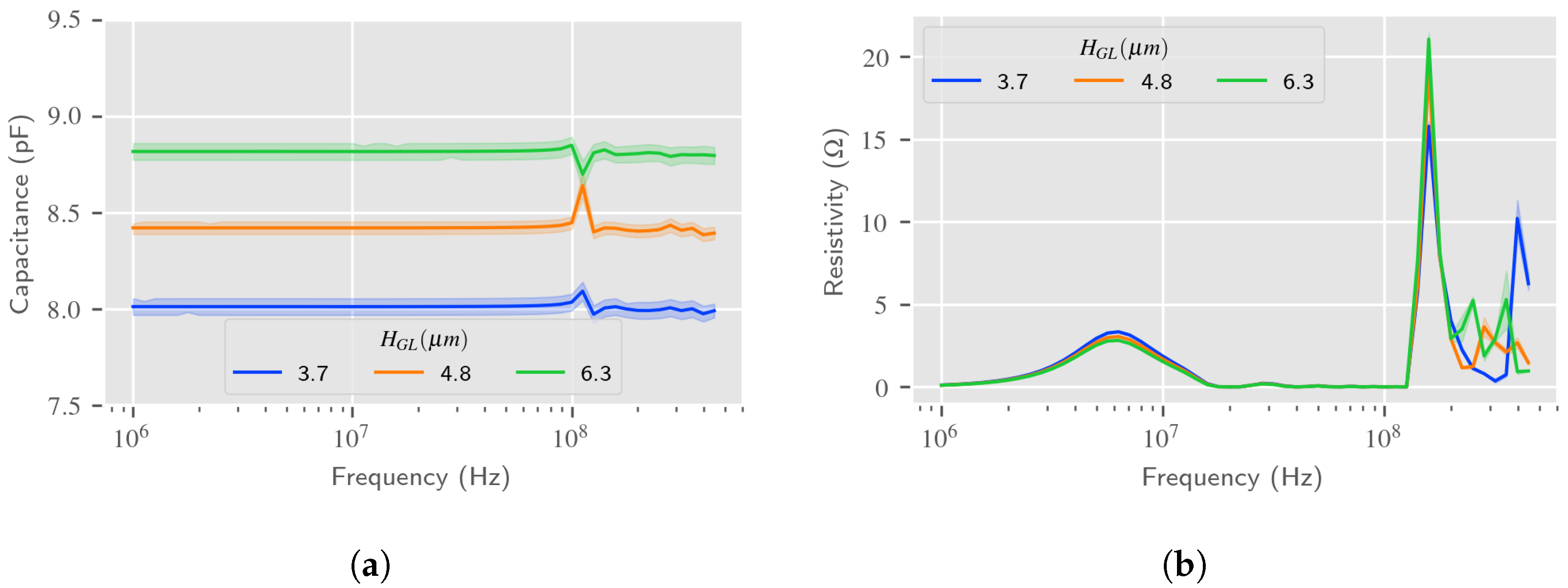
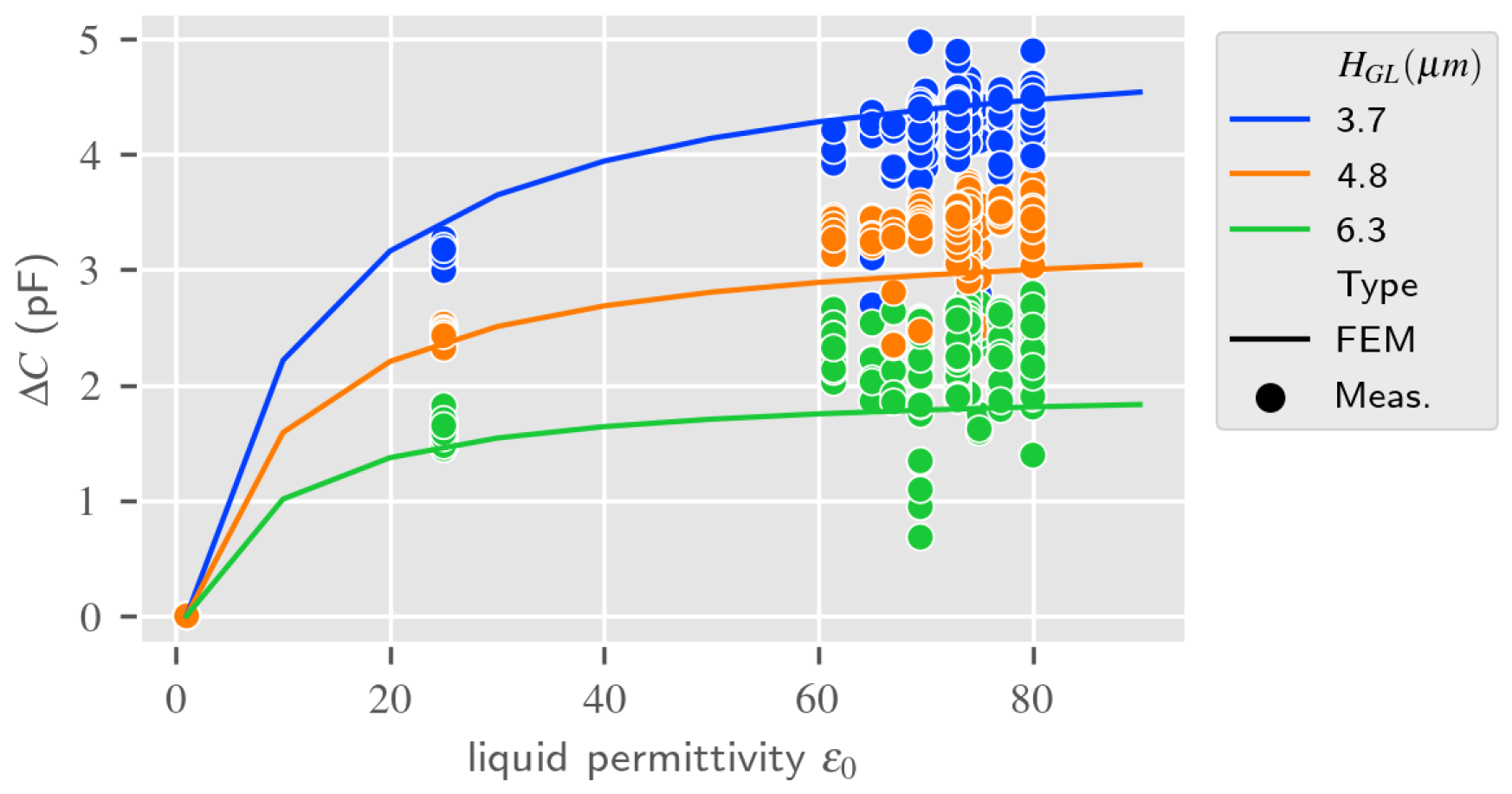
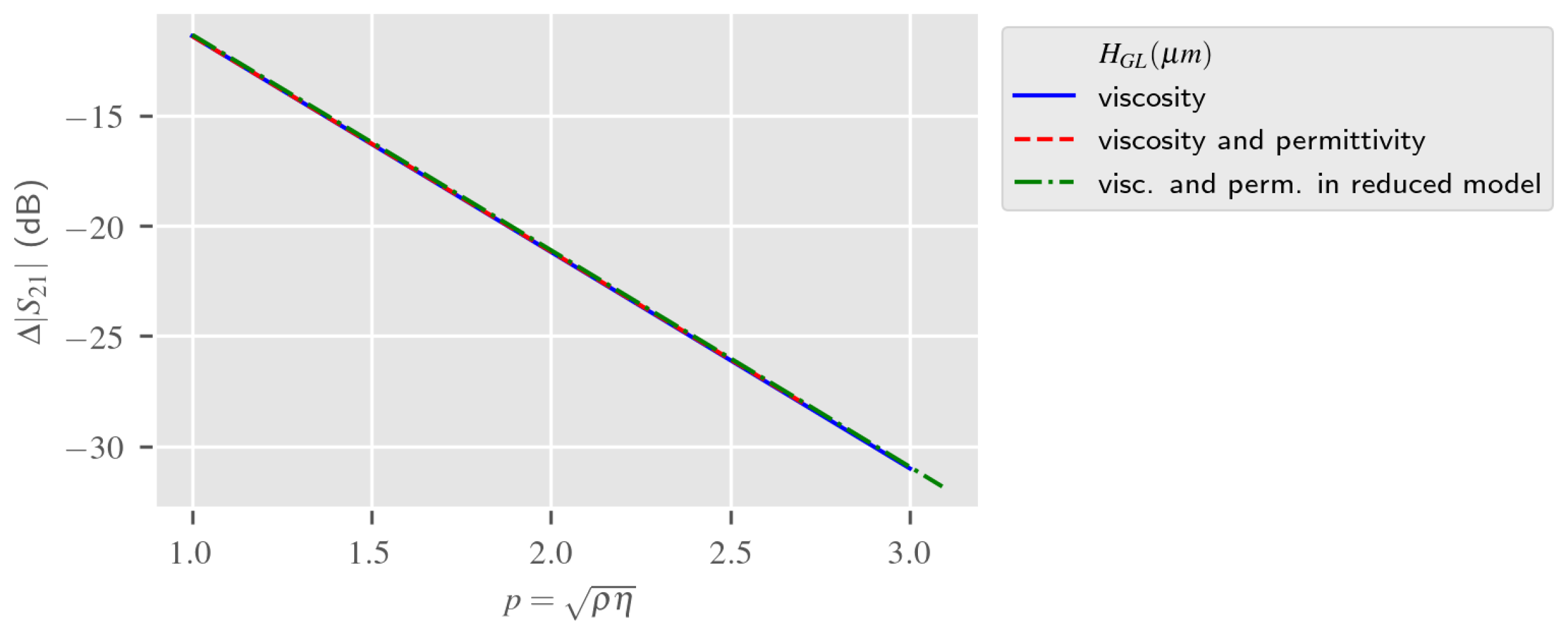
4.3. Discussions on the Love Wave Dielectric Sensing Estimation
5. Results: Love Wave Acoustic and Electro-Acoustic Sensing Estimation
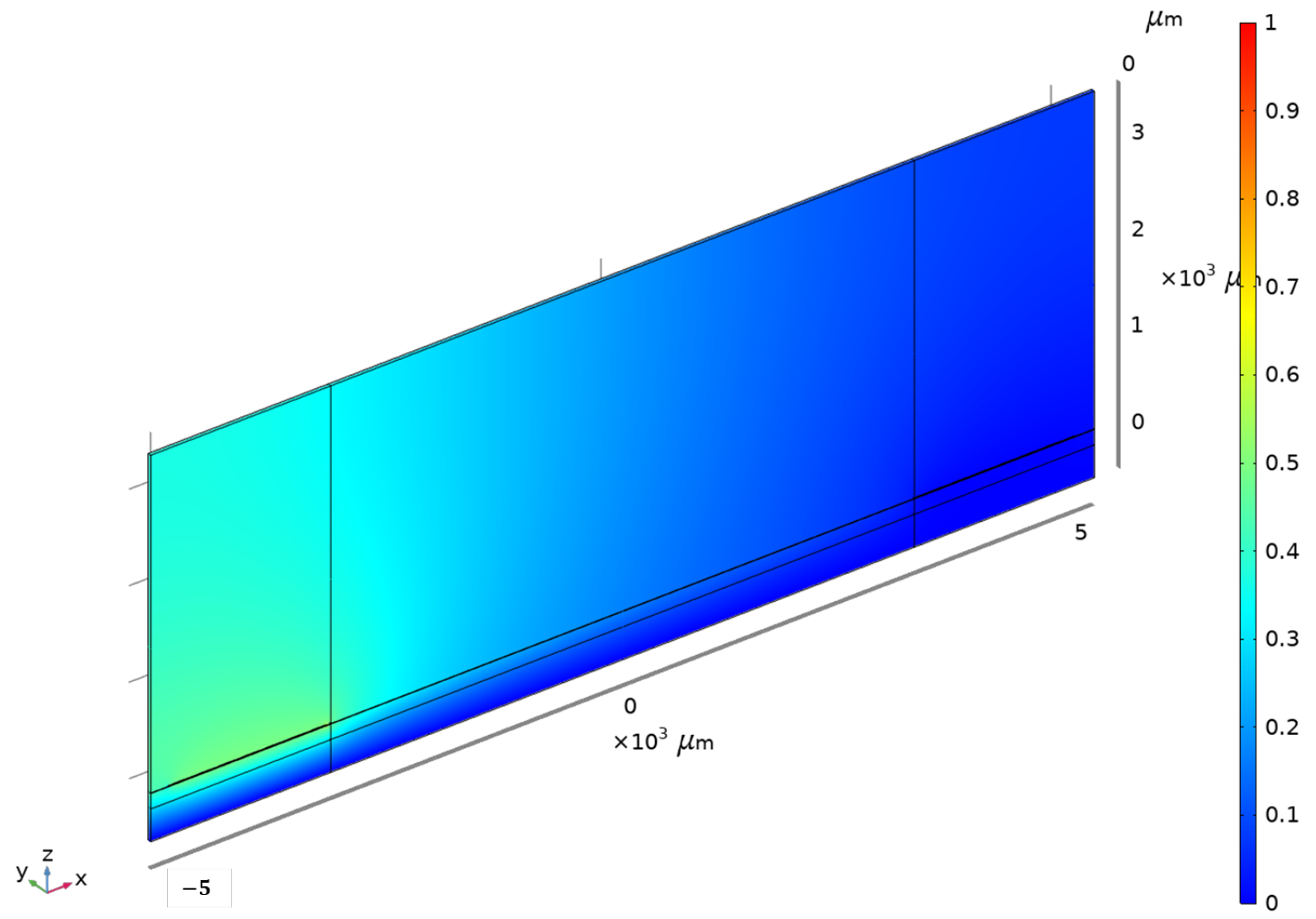
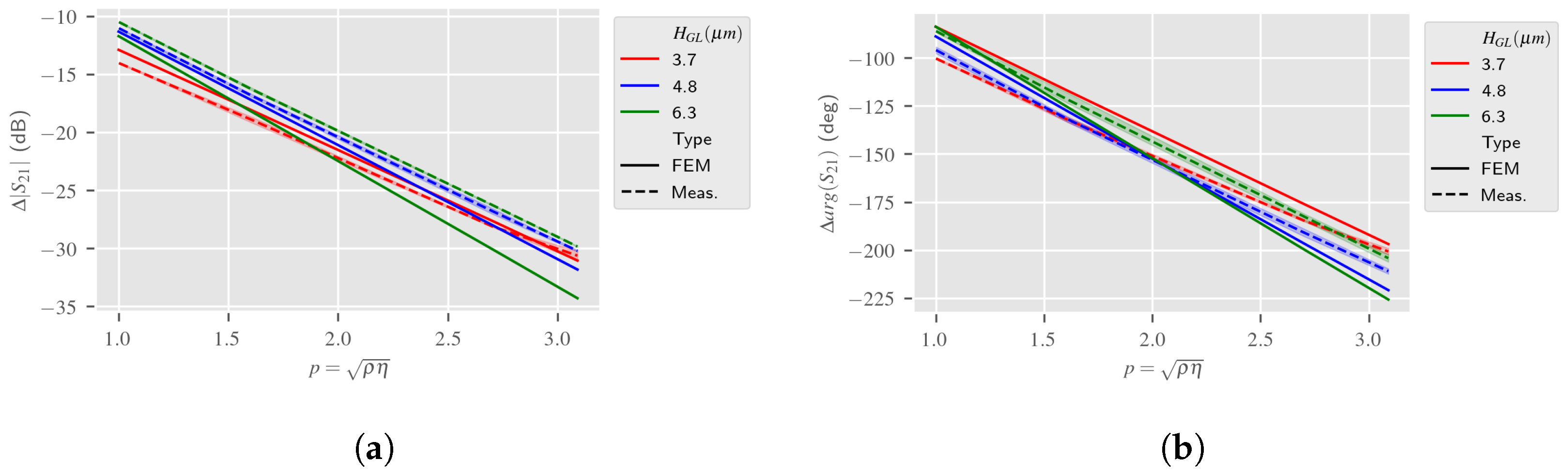
5.1. RVE Model-Based Estimation of Love Wave Device Acoustic Sensing Responses
5.2. 2.5D Model-Based Estimation of Love Wave Electro-Acoustic Sensing Responses
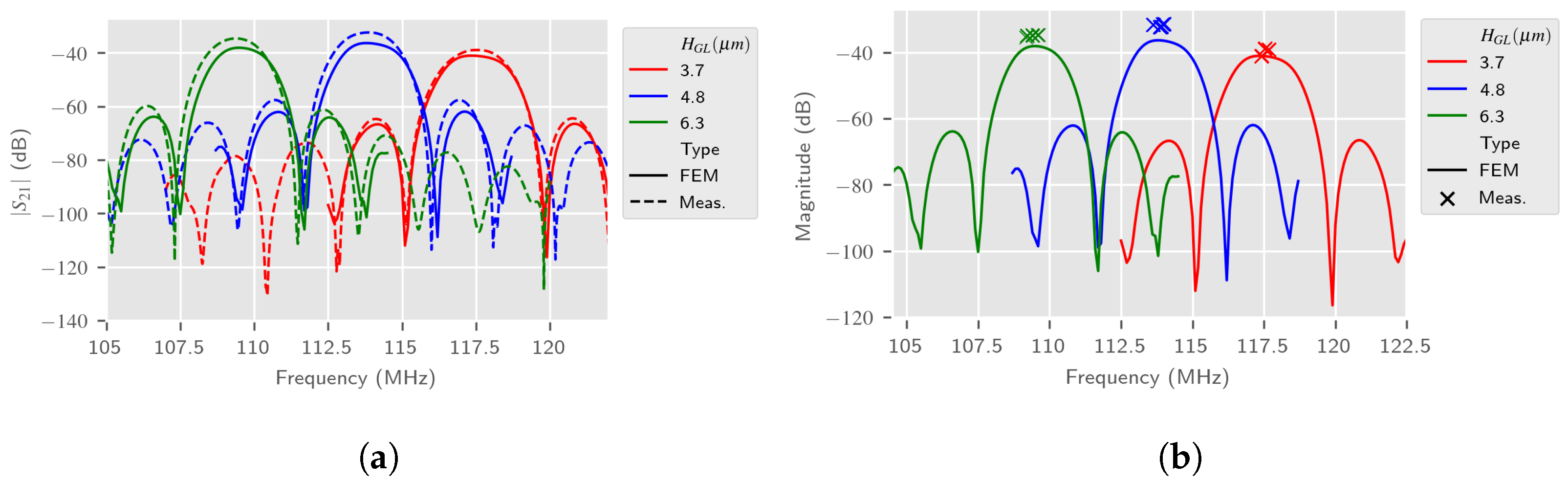
5.2.1. 2.5D Model Simulation Results
5.2.2. Reducing the Computation Time with LW Sensor 2.5D Model
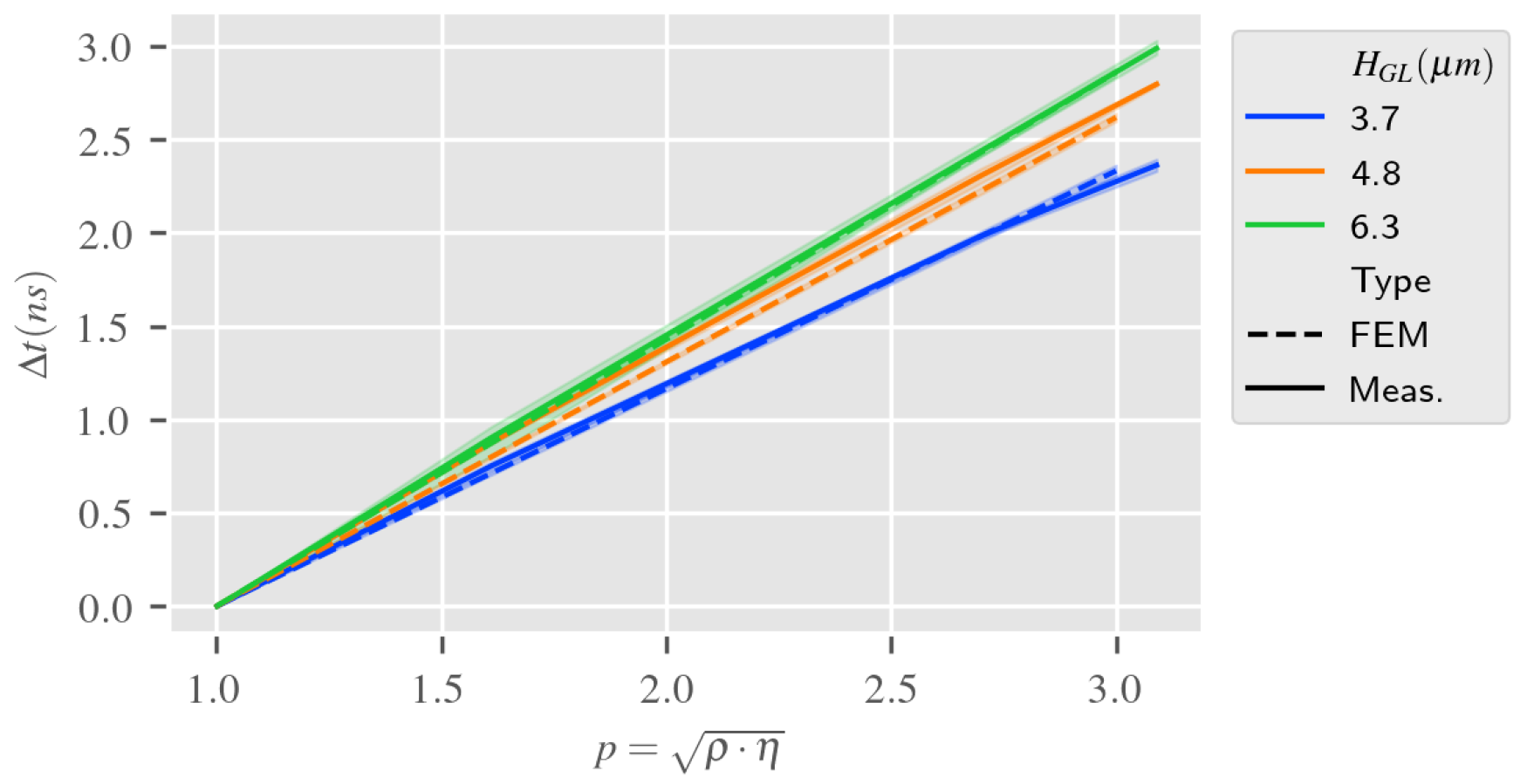
5.3. Discussion about the Electro-Acoustic Sensing Estimation
6. Conclusions and Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Suzuki, Y.; Takeuchi, M.; Nakamura, K.; Hirota, K. Coupled-mode theory of SAW periodic structures. Electron. Commun. Jpn. Part III Fundam. Electron. Sci. 1993, 76, 87–98. [Google Scholar] [CrossRef]
- Park, K.c.; Kagawa, Y.; Tsuchiya, T.; Cho, K.r. Optimization of the frequency characteristics in saw filter design. Inverse Probl. Eng. 2000, 8, 473–493. [Google Scholar] [CrossRef]
- Wang, W.; He, S. Theoretical analysis on response mechanism of polymer-coated chemical sensor based Love Wave in viscoelastic media. Sens. Actuators B Chem. 2009, 138, 432–440. [Google Scholar] [CrossRef]
- McHale, G. Generalized concept of shear horizontal acoustic plate mode and Love wave sensors. Meas. Sci. Technol. 2003, 14, 1847–1853. [Google Scholar] [CrossRef]
- Kovacs, G.; Lubking, G.W.; Vellekoop, M.J.; Venema, A. Love Waves for (bio)chemical sensing in liquids. Proc. IEEE Ultrason. Symp. 1992, 1992, 281–285. [Google Scholar] [CrossRef]
- Rocha-Gaso, M.I.; Fernandez-Diaz, R.; Arnau-Vives, A.; March-Iborra, C. Mass sensitivity evaluation of a Love Wave sensor using the 3D Finite Element Method. In Proceedings of the 2010 IEEE International Frequency Control Symposium, Newport Beach, CA, USA, 1–4 June 2010; pp. 228–231. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, J.; Zou, L.; Zou, Y.; Lang, L.; Gao, F.; Hu, N.; Wang, P. A novel sensitive cell-based Love Wave biosensor for marine toxin detection. Biosens. Bioelectron. 2016, 77, 573–579. [Google Scholar] [CrossRef]
- El Baroudi, A.; Le Pommellec, J.Y. Viscoelastic fluid effect on the surface wave propagation. Sens. Actuators A Phys. 2019, 291, 188–195. [Google Scholar] [CrossRef]
- Rube, M.; Tamarin, O.; Sebeloue, M.; Sadli, I.; Hallil, H.; Linguet, L.; Rebiere, D.; Dejous, C. Unconventional Protocol for SAW Sensor: Multi-Physic Response Enrichment in Liquid Medium. IEEE Sens. J. 2022, 22, 11345–11354. [Google Scholar] [CrossRef]
- Rocha-Gaso, M.I.; March-Iborra, C.; Montoya-Baides, A.; Arnau-Vives, A. Surface Generated Acoustic Wave Biosensors for the Detection of Pathogens: A Review. Sensors 2009, 9, 5740. [Google Scholar] [CrossRef] [PubMed]
- Jakoby, B.; Vellekoop, M.J. Viscosity sensing using a Love-wave device. Sens. Actuators A Phys. 1998, 68, 275–281. [Google Scholar] [CrossRef]
- Hashimoto, K.Y. Interdigital Transducers. In Surface Acoustic Wave Devices in Telecommunications; Springer: Berlin/Heidelberg, Germany, 2000; pp. 47–85. [Google Scholar] [CrossRef]
- Luo, W.; Yuan, Y.; Wang, Y.; Fu, Q.; Xia, H.; Li, H. Fast and Accurate Finite Transducer Analysis Method for Wireless Passive Impedance-Loaded SAW Sensors. Sensors 2018, 18, 3988. [Google Scholar] [CrossRef]
- Lysmer, J.; Drake, L. A Finite Element Method for Seismology. Methods Comput. Phys. 1972, 11, 181–216. [Google Scholar] [CrossRef]
- Ventura, P.; Hode, J.; Desbois, J.; Solal, H. Combined FEM and Green’s function analysis of periodic SAW structure, application to the calculation of reflection and scattering parameters. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 1259–1274. [Google Scholar] [CrossRef]
- Ippolito, S.J.; Kalantar-Zadeh, K.; Powell, D.A.; Wlodarski, W. A 3-dimensional finite element approach for simulating acoustic wave propagation in layered SAW devices. Proc. IEEE Ultrason. Symp. 2003, 1, 303–306. [Google Scholar] [CrossRef]
- Achour, B.; Attia, G.; Zerrouki, C.; Fourati, N.; Raoof, K.; Yaakoubi, N. Simulation/Experiment Confrontation, an Efficient Approach for Sensitive SAW Sensors Design. Sensors 2020, 20, 4994. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, K.Y. Surface Acoustic Wave Devices in Telecommunications; Springer: Berlin/Heidelberg, Germany, 2000; Volume 6, p. 103. [Google Scholar] [CrossRef]
- Wang, W.; Lee, K.; Woo, I.; Park, I.; Yang, S. Optimal design on SAW sensor for wireless pressure measurement based on reflective delay line. Sens. Actuators A Phys. 2007, 139, 2–6. [Google Scholar] [CrossRef]
- Banu Priya, R.; Venkatesan, T.; Pandiyarajan, G.; Pandya, H.M. SAW Devices—A Comprehensive Review. J. Environ. Nanotechnol. 2014, 3, 106–115. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Q.; Zhao, X.; Zhi, S.; Qiu, L.; Fu, S.; Wang, W. A General FEM Model for Analysis of Third-Order Nonlinearity in RF Surface Acoustic Wave Devices Based on Perturbation Theory. Micromachines 2022, 13, 1116. [Google Scholar] [CrossRef] [PubMed]
- Ramshani, Z.; Reddy, A.S.; Narakathu, B.B.; Wabeke, J.T.; Obare, S.O.; Atashbar, M.Z. SH-SAW sensor based microfluidic system for the detection of heavy metal compounds in liquid environments. Sens. Actuators B Chem. 2015, 217, 72–77. [Google Scholar] [CrossRef]
- Kustanovich, K.; Yantchev, V.; Doosti, B.A.; Gözen, I.; Jesorka, A. A microfluidics-integrated impedance/surface acoustic resonance tandem sensor. Sens. Bio-Sens. Res. 2019, 25, 100291. [Google Scholar] [CrossRef]
- Hu, X.; Yang, W. Planar capacitive sensors – designs and applications. Sens. Rev. 2010, 30, 24–39. [Google Scholar] [CrossRef]
- Kiełczyński, P.; Szalewski, M.; Balcerzak, A. Effect of a viscous liquid loading on Love Wave propagation. Int. J. Solids Struct. 2012, 49, 2314–2319. [Google Scholar] [CrossRef]
- Rube, M.; Tamarin, O.; Hemour, S.; Sebeloue, M.; Choudhari, A.; Sadli, I.; Linguet, L.; Rebiere, D.; Dejous, C. A behavior-descriptive model of Love Wave sensor in liquid medium for circuit-design and analysis with QucsStudio. In Proceedings of the 2021 IEEE Sensors, 31 October–4 November 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Bruckner, G.; Bardong, J. Wireless Readout of Multiple SAW Temperature Sensors. Sensors 2019, 19, 3077. [Google Scholar] [CrossRef] [PubMed]
- Lurz, F.; Ostertag, T.; Scheiner, B.; Weigel, R.; Koelpin, A. Reader architectures for wireless surface acoustic wave sensors. Sensors 2018, 18, 1734. [Google Scholar] [CrossRef]
- Gongi, W.; Rube, M.; Ben Ouada, H.; Ben Ouada, H.; Tamarin, O.; Dejous, C. Elaboration and Characterization of a New Heavy Metal Sensor Functionalized by Extracellular Polymeric Substances Isolated from a Tunisian Thermophilic Microalga Strain Graesiella sp. Sensors 2023, 23, 803. [Google Scholar] [CrossRef]






| RVE | 2.5D | |
|---|---|---|
| Liquid dielectric properties simulation only () | Possible for | Yes, for all frequencies (tested from 1 MHz up to 1 GHz) |
| Liquid mechanical properties simulation only (, ) | Resonance frequency | All parameters of interest (S-parameters) |
| Liquid electro-mechanical (dielectric and mechanical) properties estimation (, , ) | Simulation of one mechanism at a time | Simulation of both mechanisms |
| Calculation time | 20 s/point | 10 min/point |
| Calculation resources needed | Light (RAM < 8 Go) | Heavy (RAM > 64 Go) |
| Accuracy with measurements for dielectric properties | Good | Good |
| Accuracy with measurements for mechanical properties | Very good | Good and upgradable |
| Accuracy with measurements for dielectric and mechanical properties | Good and upgradable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rube, M.; Tamarin, O.; Choudhari, A.; Sebeloue, M.; Rebiere, D.; Dejous, C. FEM Modeling Strategies: Application to Mechanical and Dielectric Sensitivities of Love Wave Devices in Liquid Medium. Sensors 2024, 24, 2976. https://doi.org/10.3390/s24102976
Rube M, Tamarin O, Choudhari A, Sebeloue M, Rebiere D, Dejous C. FEM Modeling Strategies: Application to Mechanical and Dielectric Sensitivities of Love Wave Devices in Liquid Medium. Sensors. 2024; 24(10):2976. https://doi.org/10.3390/s24102976
Chicago/Turabian StyleRube, Maxence, Ollivier Tamarin, Asawari Choudhari, Martine Sebeloue, Dominique Rebiere, and Corinne Dejous. 2024. "FEM Modeling Strategies: Application to Mechanical and Dielectric Sensitivities of Love Wave Devices in Liquid Medium" Sensors 24, no. 10: 2976. https://doi.org/10.3390/s24102976
APA StyleRube, M., Tamarin, O., Choudhari, A., Sebeloue, M., Rebiere, D., & Dejous, C. (2024). FEM Modeling Strategies: Application to Mechanical and Dielectric Sensitivities of Love Wave Devices in Liquid Medium. Sensors, 24(10), 2976. https://doi.org/10.3390/s24102976






