An Analytical Approach for Naturalistic Cooperative and Competitive EEG-Hyperscanning Data: A Proof-of-Concept Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Paradigm
2.3. Simultaneous Dyadic EEG Recordings
2.4. EEG Data Analysis
2.4.1. EEG Data Preprocessing
2.4.2. Functional Connectivity Estimation
2.4.3. Graph Theoretical Measures
2.4.4. Clustering Procedure
2.4.5. Statistical Analysis
3. Results
3.1. Graph Theoretical Measures
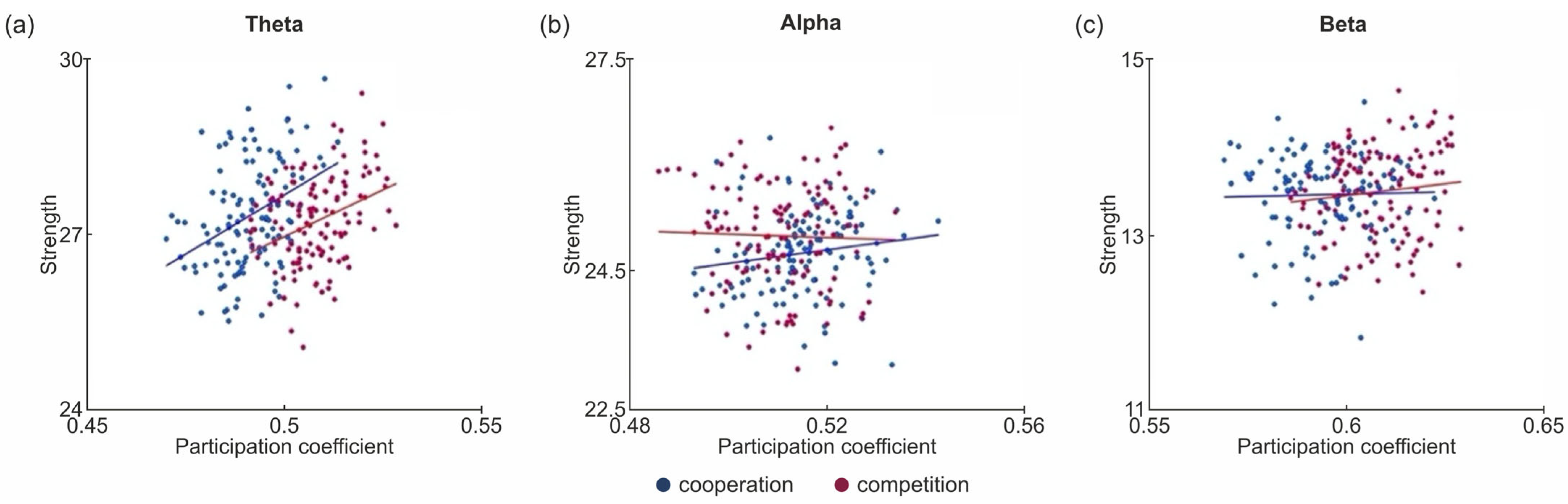
3.1.1. Strength
3.1.2. Participation Coefficient
3.1.3. Local and Global Efficiency
3.2. Results of the Clustering Procedure
4. Discussion
5. Conclusions and Future Directions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Carston, R.; Herbert, H. Clark, Using Language. Cambridge: Cambridge University Press, 1996. Pp. Xi+432. J. Linguist. 1999, 35, 167–222. [Google Scholar] [CrossRef]
- Sebanz, N.; Bekkering, H.; Knoblich, G. Joint Action: Bodies and Minds Moving Together. Trends Cogn. Sci. 2006, 10, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Searle, J.R. Collective Intentions and Actions. In Chapter 19 in “Intentions in Communication”; Cohen, P.R., Morgan, J.L., Pollack, M.E., Eds.; System Development Foundation Benchmark Series; The MIT Press: Cambridge, MA, USA, 1990; ISBN 9780262270540. [Google Scholar] [CrossRef]
- Decety, J.; Sommerville, J. Shared Representations between Self and Other: A Social Cognitive Neuroscience View. Trends Cogn. Sci. 2004, 7, 527–533. [Google Scholar] [CrossRef]
- Deutsch, M. A Theory of Co-Operation and Competition. Hum. Relat. 1949, 2, 129–152. [Google Scholar] [CrossRef]
- Vonk, R. Effects of Cooperative and Competitive Outcome Dependency on Attention and Impression Preferences. J. Exp. Soc. Psychol. 1998, 34, 265–288. [Google Scholar] [CrossRef]
- Krueger, F.; Meyer-Lindenberg, A. Toward a Model of Interpersonal Trust Drawn from Neuroscience, Psychology, and Economics. Trends Neurosci. 2019, 42, 92–101. [Google Scholar] [CrossRef]
- Oullier, O.; Basso, F. Embodied Economics: How Bodily Information Shapes the Social Coordination Dynamics of Decision-Making. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 291–301. [Google Scholar] [CrossRef] [PubMed]
- Sebanz, N.; Knoblich, G. Progress in Joint-Action Research. Curr. Dir. Psychol. Sci. 2021, 30, 138–143. [Google Scholar] [CrossRef]
- Hari, R.; Kujala, M.V. Brain Basis of Human Social Interaction: From Concepts to Brain Imaging. Physiol. Rev. 2009, 89, 453–479. [Google Scholar] [CrossRef]
- Liu, T.; Pelowski, M. Clarifying the Interaction Types in Two-Person Neuroscience Research. Front. Hum. Neurosci. 2014, 8, 276. [Google Scholar] [CrossRef]
- Czeszumski, A.; Eustergerling, S.; Lang, A.; Menrath, D.; Gerstenberger, M.; Schuberth, S.; Schreiber, F.; Rendon, Z.Z.; König, P. Hyperscanning: A Valid Method to Study Neural Inter-Brain Underpinnings of Social Interaction. Front. Hum. Neurosci. 2020, 14, 39. [Google Scholar] [CrossRef]
- Montague, P. Hyperscanning: Simultaneous fMRI during Linked Social Interactions. NeuroImage 2002, 16, 1159–1164. [Google Scholar] [CrossRef]
- Mu, Y.; Cerritos, C.; Khan, F. Neural Mechanisms Underlying Interpersonal Coordination: A Review of Hyperscanning Research. Soc. Personal. Psychol. Compass 2018, 12, e12421. [Google Scholar] [CrossRef]
- Nam, C.S.; Choo, S.; Huang, J.; Park, J. Brain-to-Brain Neural Synchrony During Social Interactions: A Systematic Review on Hyperscanning Studies. Appl. Sci. 2020, 10, 6669. [Google Scholar] [CrossRef]
- Lee, S.; Cho, H.; Kim, K.; Jun, S.C. Simultaneous EEG Acquisition System for Multiple Users: Development and Related Issues. Sensors 2019, 19, 4592. [Google Scholar] [CrossRef] [PubMed]
- Minagawa, Y.; Xu, M.; Morimoto, S. Toward Interactive Social Neuroscience: Neuroimaging Real-World Interactions in Various Populations. Jpn. Psychol. Res. 2018, 60, 196–224. [Google Scholar] [CrossRef]
- Sänger, J.; Lindenberger, U.; Müller, V. Interactive Brains, Social Minds. Commun. Integr. Biol. 2011, 4, 655–663. [Google Scholar] [CrossRef] [PubMed]
- Zamm, A.; Debener, S.; Sebanz, N. The Spontaneous Emergence of Rhythmic Coordination in Turn Taking. Sci. Rep. 2023, 13, 3259. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.M.; Brunet, D. EEG Source Imaging: A Practical Review of the Analysis Steps. Front. Neurol. 2019, 10, 325. [Google Scholar] [CrossRef]
- Gross, J. Magnetoencephalography in Cognitive Neuroscience: A Primer. Neuron 2019, 104, 189–204. [Google Scholar] [CrossRef]
- Filho, E.; Bertollo, M.; Robazza, C.; Comani, S. The Juggling Paradigm: A Novel Social Neuroscience Approach to Identify Neuropsychophysiological Markers of Team Mental Models. Front. Psychol. 2015, 6, 799. [Google Scholar] [CrossRef] [PubMed]
- Filho, E.; Bertollo, M.; Tamburro, G.; Schinaia, L.; Chatel-Goldman, J.; di Fronso, S.; Robazza, C.; Comani, S. Hyperbrain Features of Team Mental Models within a Juggling Paradigm: A Proof of Concept. PeerJ 2016, 4, e2457. [Google Scholar] [CrossRef] [PubMed]
- Müller, V.; Lindenberger, U. Intra- and Interbrain Synchrony and Hyperbrain Network Dynamics of a Guitarist Quartet and Its Audience during a Concert. Ann. N. Y. Acad. Sci. 2023, 1523, 74–90. [Google Scholar] [CrossRef] [PubMed]
- Müller, V.; Sänger, J.; Lindenberger, U. Hyperbrain Network Properties of Guitarists Playing in Quartet. Ann. N. Y. Acad. Sci. 2018, 1423, 198–210. [Google Scholar] [CrossRef] [PubMed]
- Sänger, J.; Müller, V.; Lindenberger, U. Intra- and Interbrain Synchronization and Network Properties When Playing Guitar in Duets. Front. Hum. Neurosci. 2012, 6, 312. [Google Scholar] [CrossRef] [PubMed]
- Babiloni, F.; Cincotti, F.; Mattia, D.; Mattiocco, M.; De Vico Fallani, F.; Tocci, A.; Bianchi, L.; Marciani, M.G.; Astolfi, L. Hypermethods for EEG Hyperscanning. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 3666–3669. [Google Scholar]
- Astolfi, L.; Toppi, J.; Borghini, G.; Vecchiato, G.; Isabella, R.; De Vico Fallani, F.; Cincotti, F.; Salinari, S.; Mattia, D.; He, B.; et al. Study of the Functional Hyperconnectivity between Couples of Pilots during Flight Simulation: An EEG Hyperscanning Study. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 2338–2341. [Google Scholar]
- Fallani, F.D.V.; Nicosia, V.; Sinatra, R.; Astolfi, L.; Cincotti, F.; Mattia, D.; Wilke, C.; Doud, A.; Latora, V.; He, B.; et al. Defecting or Not Defecting: How to “Read” Human Behavior during Cooperative Games by EEG Measurements. PLoS ONE 2010, 5, e14187. [Google Scholar] [CrossRef] [PubMed]
- Astolfi, L.; Toppi, J.; Borghini, G.; Vecchiato, G.; He, E.J.; Roy, A.; Cincotti, F.; Salinari, S.; Mattia, D.; He, B.; et al. Cortical Activity and Functional Hyperconnectivity by Simultaneous EEG Recordings from Interacting Couples of Professional Pilots. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 4752–4755. [Google Scholar]
- Toppi, J.; Borghini, G.; Petti, M.; He, E.J.; Giusti, V.D.; He, B.; Astolfi, L.; Babiloni, F. Investigating Cooperative Behavior in Ecological Settings: An EEG Hyperscanning Study. PLoS ONE 2016, 11, e0154236. [Google Scholar] [CrossRef] [PubMed]
- Venturella, I.; Gatti, L.; Venutelli, M.E.; Balconi, M. When Brains Dialogue by Synchronized or Unsynchronized Languages. Hyperscanning Applications to Neuromanagement. Neuropsychol. Trends 2017, 21, 35–51. [Google Scholar] [CrossRef]
- Stone, D.B.; Tamburro, G.; Filho, E.; di Fronso, S.; Robazza, C.; Bertollo, M.; Comani, S. Hyperscanning of Interactive Juggling: Expertise Influence on Source Level Functional Connectivity. Front. Hum. Neurosci. 2019, 13, 321. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, C.; Wang, F.; Zhang, D. Inter-Brain Amplitude Correlation Differentiates Cooperation from Competition in a Motion-Sensing Sports Game. Soc. Cogn. Affect. Neurosci. 2021, 16, 552–564. [Google Scholar] [CrossRef]
- Sinha, N.; Maszczyk, T.; Zhang, W.; Tan, J.; Dauwels, J. EEG Hyperscanning Study of Inter-Brain Synchrony during Cooperative and Competitive Interaction. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 004813–004818. [Google Scholar] [CrossRef]
- Léné, P.; Karran, A.J.; Labonté-Lemoyne, E.; Sénécal, S.; Fredette, M.; Johnson, K.J.; Léger, P.-M. Is There Collaboration Specific Neurophysiological Activation during Collaborative Task Activity? An Analysis of Brain Responses Using Electroencephalography and Hyperscanning. Brain Behav. 2021, 11, e2270. [Google Scholar] [CrossRef]
- Susnoschi Luca, I.; Putri, F.D.; Ding, H.; Vuckovič, A. Brain Synchrony in Competition and Collaboration During Multiuser Neurofeedback-Based Gaming. Front. Neuroergonomics 2021, 2, 749009. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, A.F.D.C. Hyperscanning: Beyond the Hype. Neuron 2021, 109, 404–407. [Google Scholar] [CrossRef] [PubMed]
- Shamay-Tsoory, S.G.; Mendelsohn, A. Real-Life Neuroscience: An Ecological Approach to Brain and Behavior Research. Perspect Psychol. Sci. 2019, 14, 841–859. [Google Scholar] [CrossRef] [PubMed]
- Kasai, K.; Fukuda, M.; Yahata, N.; Morita, K.; Fujii, N. The Future of Real-World Neuroscience: Imaging Techniques to Assess Active Brains in Social Environments. Neurosci. Res. 2015, 90, 65–71. [Google Scholar] [CrossRef]
- Hakim, U.; De Felice, S.; Pinti, P.; Zhang, X.; Noah, J.; Ono, Y.; Burgess, P.W.; Hamilton, A.; Hirsch, J.; Tachtsidis, I. Quantification of Inter-Brain Coupling: A Review of Current Methods Used in Haemodynamic and Electrophysiological Hyperscanning Studies. NeuroImage 2023, 280, 120354. [Google Scholar] [CrossRef] [PubMed]
- Gugnowska, K.; Novembre, G.; Kohler, N.; Villringer, A.; Keller, P.E.; Sammler, D. Endogenous Sources of Interbrain Synchrony in Duetting Pianists. Cereb. Cortex 2022, 32, 4110–4127. [Google Scholar] [CrossRef] [PubMed]
- Wikström, V.; Saarikivi, K.; Falcon, M.; Makkonen, T.; Martikainen, S.; Putkinen, V.; Cowley, B.U.; Tervaniemi, M. Inter-Brain Synchronization Occurs without Physical Co-Presence during Cooperative Online Gaming. Neuropsychologia 2022, 174, 108316. [Google Scholar] [CrossRef] [PubMed]
- Tamburro, G.; Fiedler, P.; De Fano, A.; Raeisi, K.; Khazaei, M.; Vaquero, L.; Bruña, R.; Oppermann, H.; Bertollo, M.; Filho, E.; et al. An Ecological Study Protocol for the Multimodal Investigation of the Neurophysiological Underpinnings of Dyadic Joint Action. Front. Hum. Neurosci. 2023, 17, 1305331. [Google Scholar] [CrossRef]
- Delorme, A.; Makeig, S. EEGLAB: An Open Source Toolbox for Analysis of Single-Trial EEG Dynamics Including Independent Component Analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef]
- Widmann, A.; Schröger, E.; Maess, B. Digital Filter Design for Electrophysiological Data—A Practical Approach. J. Neurosci. Methods 2015, 250, 34–46. [Google Scholar] [CrossRef] [PubMed]
- Studnicki, A.; Downey, R.J.; Ferris, D.P. Characterizing and Removing Artifacts Using Dual-Layer EEG during Table Tennis. Sensors 2022, 22, 5867. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.-W.; Girolami, M.; Sejnowski, T.J. Independent Component Analysis Using an Extended Infomax Algorithm for Mixed Subgaussian and Supergaussian Sources. Neural Comput. 1999, 11, 417–441. [Google Scholar] [CrossRef] [PubMed]
- Basti, A.; Chella, F.; Guidotti, R.; Ermolova, M.; D’Andrea, A.; Stenroos, M.; Romani, G.L.; Pizzella, V.; Marzetti, L. Looking through the Windows: A Study about the Dependency of Phase-Coupling Estimates on the Data Length. J. Neural Eng. 2022, 19, 016039. [Google Scholar] [CrossRef] [PubMed]
- Bruña, R.; Maestú, F.; Pereda, E. Phase Locking Value Revisited: Teaching New Tricks to an Old Dog. J. Neural Eng. 2018, 15, 056011. [Google Scholar] [CrossRef] [PubMed]
- Lachaux, J.-P.; Rodriguez, E.; Martinerie, J.; Varela, F.J. Measuring Phase Synchrony in Brain Signals. Human Brain Mapping 1999, 8, 194–208. [Google Scholar] [CrossRef]
- Adamovich, T.; Zakharov, I.; Tabueva, A.; Malykh, S. The Thresholding Problem and Variability in the EEG Graph Network Parameters. Sci. Rep. 2022, 12, 18659. [Google Scholar] [CrossRef]
- Redcay, E.; Moran, J.; Mavros, P.; Tager-Flusberg, H.; Gabrieli, J.; Whitfield-Gabrieli, S. Intrinsic Functional Network Organization in High-Functioning Adolescents with Autism Spectrum Disorder. Front. Hum. Neurosci. 2013, 7, 573. [Google Scholar] [CrossRef] [PubMed]
- Power, J.D.; Schlaggar, B.L.; Lessov-Schlaggar, C.N.; Petersen, S.E. Evidence for Hubs in Human Functional Brain Networks. Neuron 2013, 79, 798–813. [Google Scholar] [CrossRef]
- Müller, V.; Sänger, J.; Lindenberger, U. Intra- and Inter-Brain Synchronization during Musical Improvisation on the Guitar. PLoS ONE 2013, 8, e73852. [Google Scholar] [CrossRef]
- Bullmore, E.T.; Bassett, D.S. Brain Graphs: Graphical Models of the Human Brain Connectome. Annu. Rev. Clin. Psychol. 2011, 7, 113–140. [Google Scholar] [CrossRef]
- Rubinov, M.; Kötter, R.; Hagmann, P.; Sporns, O. Brain Connectivity Toolbox: A Collection of Complex Network Measurements and Brain Connectivity Datasets. NeuroImage 2009, 47, S169. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex Network Measures of Brain Connectivity: Uses and Interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective Dynamics of ‘Small-World’ Networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The K-Means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Jain, A.K. Data Clustering: 50 Years beyond K-Means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Chong, B. K-Means Clustering Algorithm: A Brief Review. Acad. J. Comput. Inf. Sci. 2021, 4, 37–40. [Google Scholar] [CrossRef]
- Calinski, T.; Harabasz, J. A Dendrite Method for Cluster Analysis. Comm. Stats.—Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Bridge, P.D.; Sawilowsky, S.S. Increasing Physicians’ Awareness of the Impact of Statistics on Research Outcomes: Comparative Power of the t-Test and Wilcoxon Rank-Sum Test in Small Samples Applied Research. J. Clin. Epidemiol. 1999, 52, 229–235. [Google Scholar] [CrossRef]
- Gorjan, D.; Gramann, K.; Pauw, K.D.; Marusic, U. Removal of Movement-Induced EEG Artifacts: Current State of the Art and Guidelines. J. Neural Eng. 2022, 19, 011004. [Google Scholar] [CrossRef]
- Mihajlović, V.; Patki, S.; Grundlehner, B. The Impact of Head Movements on EEG and Contact Impedance: An Adaptive Filtering Solution for Motion Artifact Reduction. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 5064–5067. [Google Scholar]
- Visser, A.; Büchel, D.; Lehmann, T.; Baumeister, J. Continuous Table Tennis Is Associated with Processing in Frontal Brain Areas: An EEG Approach. Exp. Brain Res. 2022, 240, 1899–1909. [Google Scholar] [CrossRef]
- Studnicki, A.; Ferris, D.P. Parieto-Occipital Electrocortical Dynamics during Real-World Table Tennis. eNeuro 2023, 10, 1–20. [Google Scholar] [CrossRef]
- Yu, R.; Zhou, X. Brain Responses to Outcomes of One’s Own and Other’s Performance in a Gambling Task. NeuroReport 2006, 17, 1747–1751. [Google Scholar] [CrossRef]
- van Dijk, H.; Schoffelen, J.-M.; Oostenveld, R.; Jensen, O. Prestimulus Oscillatory Activity in the Alpha Band Predicts Visual Discrimination Ability. J. Neurosci. 2008, 28, 1816–1823. [Google Scholar] [CrossRef]
- Kang, S.K.; Hirsh, J.B.; Chasteen, A.L. Your Mistakes Are Mine: Self-Other Overlap Predicts Neural Response to Observed Errors. J. Exp. Soc. Psychol. 2010, 46, 229–232. [Google Scholar] [CrossRef]
- Leng, Y.; Zhou, X. Modulation of the Brain Activity in Outcome Evaluation by Interpersonal Relationship: An ERP Study. Neuropsychologia 2010, 48, 448–455. [Google Scholar] [CrossRef]
- Samaha, J.; Postle, B.R. The Speed of Alpha-Band Oscillations Predicts the Temporal Resolution of Visual Perception. Curr. Biol. 2015, 22, 2985–2990. [Google Scholar] [CrossRef]
- Balconi, M.; Vanutelli, M.E. Functional EEG Connectivity during Competition. BMC Neurosci. 2018, 19, 63. [Google Scholar] [CrossRef]
- Aumann, T.D.; Prut, Y. Do Sensorimotor β-Oscillations Maintain Muscle Synergy Representations in Primary Motor Cortex? Trends Neurosci. 2015, 38, 77–85. [Google Scholar] [CrossRef]
- Baker, S.N. Oscillatory Interactions between Sensorimotor Cortex and the Periphery. Curr. Opin. Neurobiol. 2007, 17, 649–655. [Google Scholar] [CrossRef]
- Adhikari, B.M.; Epstein, C.M.; Dhamala, M. Enhanced Brain Network Activity in Complex Movement Rhythms: A Simultaneous Functional Magnetic Resonance Imaging and Electroencephalography Study. Brain Connect. 2018, 8, 68–81. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, H.; Xie, T.; Liu, Y.; Chen, J.; Long, J. Movement Speed Effects on Beta-Band Oscillations in Sensorimotor Cortex during Voluntary Activity. J. Neurophysiol. 2020, 124, 352–359. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.W.; Ofori, E.; Misra, G.; Hess, C.W.; Vaillancourt, D.E. Beta-Band Activity and Connectivity in Sensorimotor and Parietal Cortex Are Important for Accurate Motor Performance. NeuroImage 2017, 144, 164–173. [Google Scholar] [CrossRef] [PubMed]
- Milioni, F.; Leite, J.V.d.M.; Beneke, R.; de Poli, R.A.B.; Papoti, M.; Zagatto, A.M. Table Tennis Playing Styles Require Specific Energy Systems Demands. PLoS ONE 2018, 13, e0199985. [Google Scholar] [CrossRef] [PubMed]
- Martin, C.; Favier-Ambrosini, B.; Mousset, K.; Brault, S.; Zouhal, H.; Prioux, J. Influence of Playing Style on the Physiological Responses of Offensive Players in Table Tennis. J. Sports Med. Phys. Fit. 2015, 55, 1517–1523. [Google Scholar]
- Acquadro, M.A.S.; Congedo, M.; De Riddeer, D. Music Performance As an Experimental Approach to Hyperscanning Studies. Front. Hum. Neurosci. 2016, 10, 242. [Google Scholar] [CrossRef]


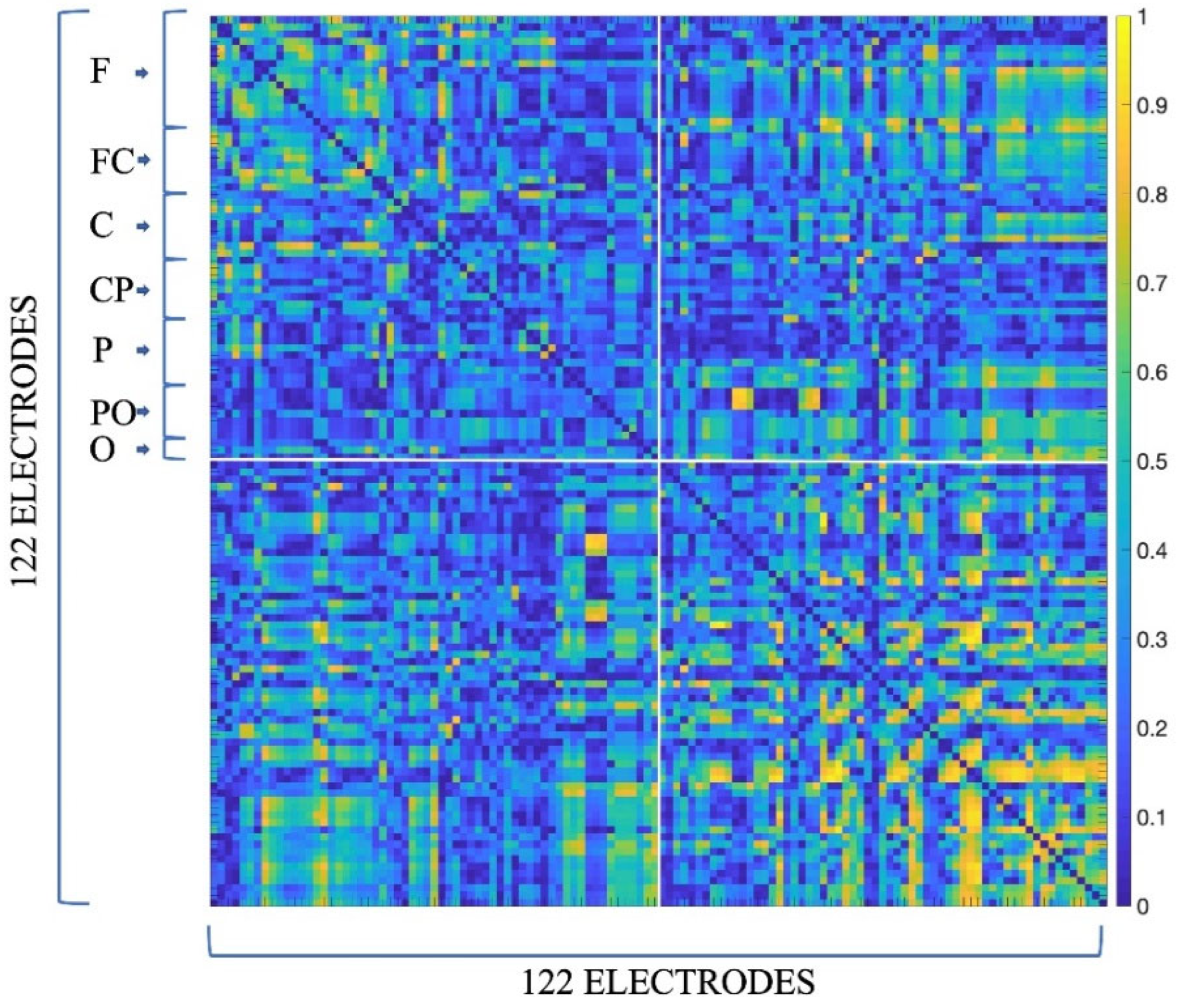
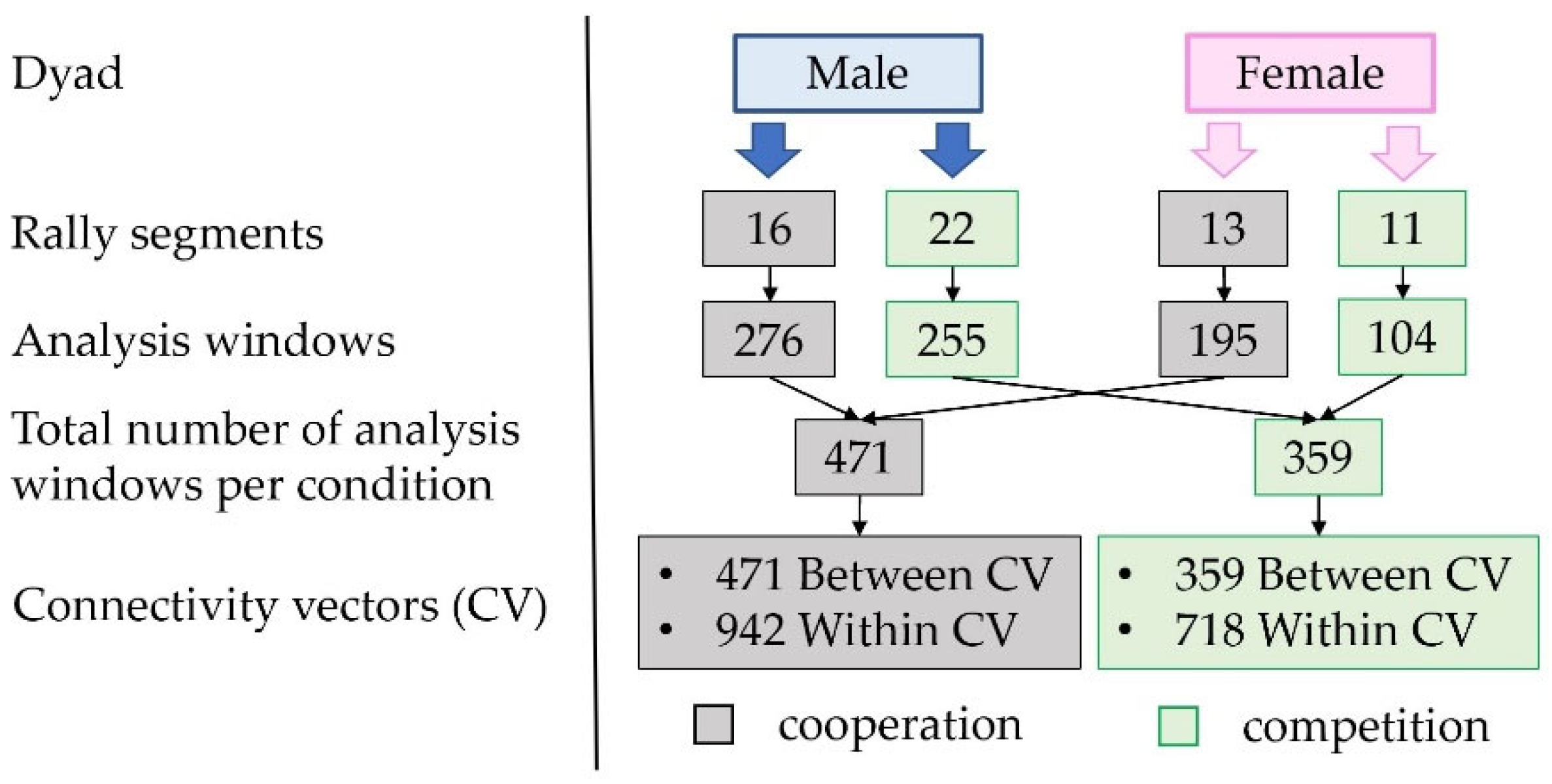


| N. Dyadic EEG Datasets | Gender | Age (year) | EEG Sampling Frequency (Hz) | Recording’s Condition | Total Recording Duration (m) |
|---|---|---|---|---|---|
| 2 | male | 18 | 1024 | cooperative | 8.14 |
| 31 | competitive | 16.27 | |||
| female | 19 | cooperative | 8.27 | ||
| 21 | competitive | 16.53 |
| Condition | Dyad Gender | No. of Rallies | Mean ± STD (s) | Range (s) | Median (s) | 5th and 95th Percentiles (s) | Total Duration of Concatenated EEG Trials (s) |
|---|---|---|---|---|---|---|---|
| COOP | male | 16 | 7.80 ± 4.20 | (3.30 ÷ 18.70) | 6.50 | 3.45; 17.11 | 157.00 |
| female | 13 | 6.70 ± 3.40 | (3.50 ÷ 12.60) | 5.40 | 3.52; 12.48 | 113.40 | |
| COMP | male | 22 | 5.00 ± 1.40 | (3.20 ÷ 8.20) | 4.85 | 3.32; 7.54 | 153.90 |
| female | 11 | 3.90 ± 1.50 | (3.00 ÷ 7.40) | 3.40 | 3.01; 7.35 | 65.30 |
| Graph Theoretical Measure | Within Matrices | Between Matrices | Hyperbrain Matrices |
|---|---|---|---|
| Participation coefficient | ✓ | ||
| Strength | ✓ | ✓ | ✓ |
| Global efficiency (GE) | ✓ | ✓ | |
| Local efficiency (LE) | ✓ | ✓ |
| Theta | Alpha | Beta | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Connectivity Map | Condition | Mean ± STD (s) | Median (Percentiles) (s) | p | Mean ± STD (s) | Median (Percentiles) (s) | p | Mean ± STD (s) | Median (Percentiles) (s) | p |
| Within | COOP | 13.82 ± 0.28 | 13.80 (13.44; 14.24) | 0.34 | 12.37 ± 0.26 | 12.35 (11.95; 12.85) | <0.001 | 6.72 ± 0.17 | 6.72 (6.43; 7.00) | <0.01 |
| COMP | 13.77 ± 0.26 | 13.75 (13.32; 14.17) | 13.04 ± 0.29 | 13.07 (12.57; 13.56) | 6.83 ± 0.17 | 6.83 (6.55; 7.12) | ||||
| Between | COOP | 13.51 ± 0.63 | 13.50 (12.51; 14.42) | 0.46 | 12.37 ± 0.32 | 12.36 (11.80; 12.88) | <0.001 | 6.75 ± 0.30 | 6.78 (6.14; 7.15) | <0.01 |
| COMP | 13.46 ± 0.53 | 13.49 (12.60; 14.39) | 11.96 ± 0.47 | 11.97 (11.26; 12.74) | 6.68 ± 0.21 | 6.66 (6.33; 7.04) | ||||
| Theta | Alpha | Beta | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Connectivity Map | Condition | Mean ± STD (s) | Median (Percentiles) (s) | p | Mean ± STD (s) | Median (Percentiles) (s) | p | Mean ± STD (s) | Median (Percentiles) (s) | p |
| Hyperbrain | COOP | 0.50 ± 0.01 | 0.50 (0.48; 0.51) | <0.001 | 0.51 ± 0.01 | 0.51 (0.49; 0.52) | <0.001 | 0.57 ± 0.01 | 0.57 (0.55; 0.60) | <0.001 |
| COMP | 0.55 ± 0.01 | 0.55 (0.53; 0.57) | 0.55 ± 0.01 | 0.55 (0.54; 0.58) | 0.60 ± 0.01 | 0.59 (0.57; 0.61) | ||||
| Condition | Theta | Alpha | Beta | |
|---|---|---|---|---|
| COOP | R | 0.37 | 0.15 | 0.03 |
| p | <0.001 | 0.09 | 0.80 | |
| COMP | R | 0.35 | −0.03 | 0.11 |
| p | <0.001 | 0.73 | 0.22 |
| Theta | Alpha | Beta | ||||||
|---|---|---|---|---|---|---|---|---|
| Connectivity Map | Metric | Condition | Mean ± STD (s) | p | Mean ± STD (s) | p | Mean ± STD (s) | p |
| Median (Percentiles) (s) | Median (Percentiles) (s) | Median (Percentiles) (s) | ||||||
| Within | LE | COOP | 0.372 ± 0.010 | 0.308 | 0.372 ± 0.007 | 0.594 | 0.365 ± 0.009 | 0.691 |
| 0.373 (0.354; 0.383) | 0.372 (0.363; 0.385) | 0.366 (0.351; 0.380) | ||||||
| COMP | 0.371 ± 0.009 | 0.373 ± 0.009 | 0.365 ± 0.009 | |||||
| 0.372 (0.355; 0.385) | 0.372 (0.360; 0.388) | 0.366 (0.349; 0.378) | ||||||
| GE | COOP | 0.689 ± 0.021 | 0.647 | 0.693 ± 0.014 | 0.007 ** | 0.698 ± 0.014 | 0.257 | |
| 0. 694 (0.645; 0.715) | 0. 693 (0.671; 0.721) | 0. 699 (0.677; 0.723) | ||||||
| COMP | 0.693 ± 0.019 | 0.700 ± 0.017 | 0.701 ± 0.016 | |||||
| 0. 693 (0.660; 0.721) | 0. 699 (0.672; 0.731) | 0. 700 (0.672; 0.727) | ||||||
| LE-GE | COOP | <0.001 | <0.001 | <0.001 | ||||
| COMP | <0.001 | <0.001 | <0.001 | |||||
| Hyperbrain | LE | COOP | 0.748 ± 0.006 | 0.672 | 0.744 ± 0.005 | 0.662 | 0.729 ± 0.005 | 0.544 |
| 0. 749 (0.739; 0.757) | 0. 744 (0.735; 0.751) | 0. 728 (0.721; 0.738) | ||||||
| COMP | 0.748 ± 0.007 | 0.745 ± 0.005 | 0.728 ± 0.004 | |||||
| 0. 747 (0.739; 0.759) | 0. 745 (0.734; 0.752) | 0. 728 (0.723; 0.736) | ||||||
| GE | COOP | 0.698 ± 0.001 | 0.563 | 0.699 ± 0.001 | 0.622 | 0.700 ± 0.001 | 0.050 | |
| 0. 698 (0.696; 0.700) | 0. 699 (0.698; 0.700) | 0. 700 (0.700; 0.700) | ||||||
| COMP | 0.698 ± 0.001 | 0.699 ± 0.001 | 0.700 ± 0.001 | |||||
| 0. 698 (0.696; 0.700) | 0. 699 (0.698; 0.700) | 0. 700 (0.700; 0.700) | ||||||
| LE-GE | COOP | <0.001 | <0.001 | <0.001 | ||||
| COMP | <0.001 | <0.001 | <0.001 | |||||
| Dyad Gender | Subject | Cooperation | Competition | |||
|---|---|---|---|---|---|---|
| Cluster 1 (%) | Cluster 2 (%) | Cluster 1 (%) | Cluster 2 (%) | |||
| Theta | female | P1 | 60 | 40 | 61 | 39 |
| P2 | 45 | 55 | 57 | 43 | ||
| male | P1 | 41 | 59 | 54 | 46 | |
| P2 | 50 | 50 | 57 | 43 | ||
| Alpha | female | P1 | 45 | 55 | 50 | 50 |
| P2 | 57 | 43 | 55 | 45 | ||
| male | P1 | 62 | 38 | 44 | 56 | |
| P2 | 45 | 55 | 51 | 49 | ||
| Beta | female | P1 | 44 | 56 | 46 | 54 |
| P2 | 43 | 57 | 53 | 47 | ||
| male | P1 | 50 | 50 | 57 | 43 | |
| P2 | 56 | 44 | 54 | 46 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamburro, G.; Bruña, R.; Fiedler, P.; De Fano, A.; Raeisi, K.; Khazaei, M.; Zappasodi, F.; Comani, S. An Analytical Approach for Naturalistic Cooperative and Competitive EEG-Hyperscanning Data: A Proof-of-Concept Study. Sensors 2024, 24, 2995. https://doi.org/10.3390/s24102995
Tamburro G, Bruña R, Fiedler P, De Fano A, Raeisi K, Khazaei M, Zappasodi F, Comani S. An Analytical Approach for Naturalistic Cooperative and Competitive EEG-Hyperscanning Data: A Proof-of-Concept Study. Sensors. 2024; 24(10):2995. https://doi.org/10.3390/s24102995
Chicago/Turabian StyleTamburro, Gabriella, Ricardo Bruña, Patrique Fiedler, Antonio De Fano, Khadijeh Raeisi, Mohammad Khazaei, Filippo Zappasodi, and Silvia Comani. 2024. "An Analytical Approach for Naturalistic Cooperative and Competitive EEG-Hyperscanning Data: A Proof-of-Concept Study" Sensors 24, no. 10: 2995. https://doi.org/10.3390/s24102995
APA StyleTamburro, G., Bruña, R., Fiedler, P., De Fano, A., Raeisi, K., Khazaei, M., Zappasodi, F., & Comani, S. (2024). An Analytical Approach for Naturalistic Cooperative and Competitive EEG-Hyperscanning Data: A Proof-of-Concept Study. Sensors, 24(10), 2995. https://doi.org/10.3390/s24102995










