Hadamard Error-Correcting Codes and Their Application in Digital Watermarking
Abstract
1. Introduction
2. One-Dimensional Hadamard Error-Correcting Code
2.1. Hadamard Matrices
2.2. Generation of Hadamard Code
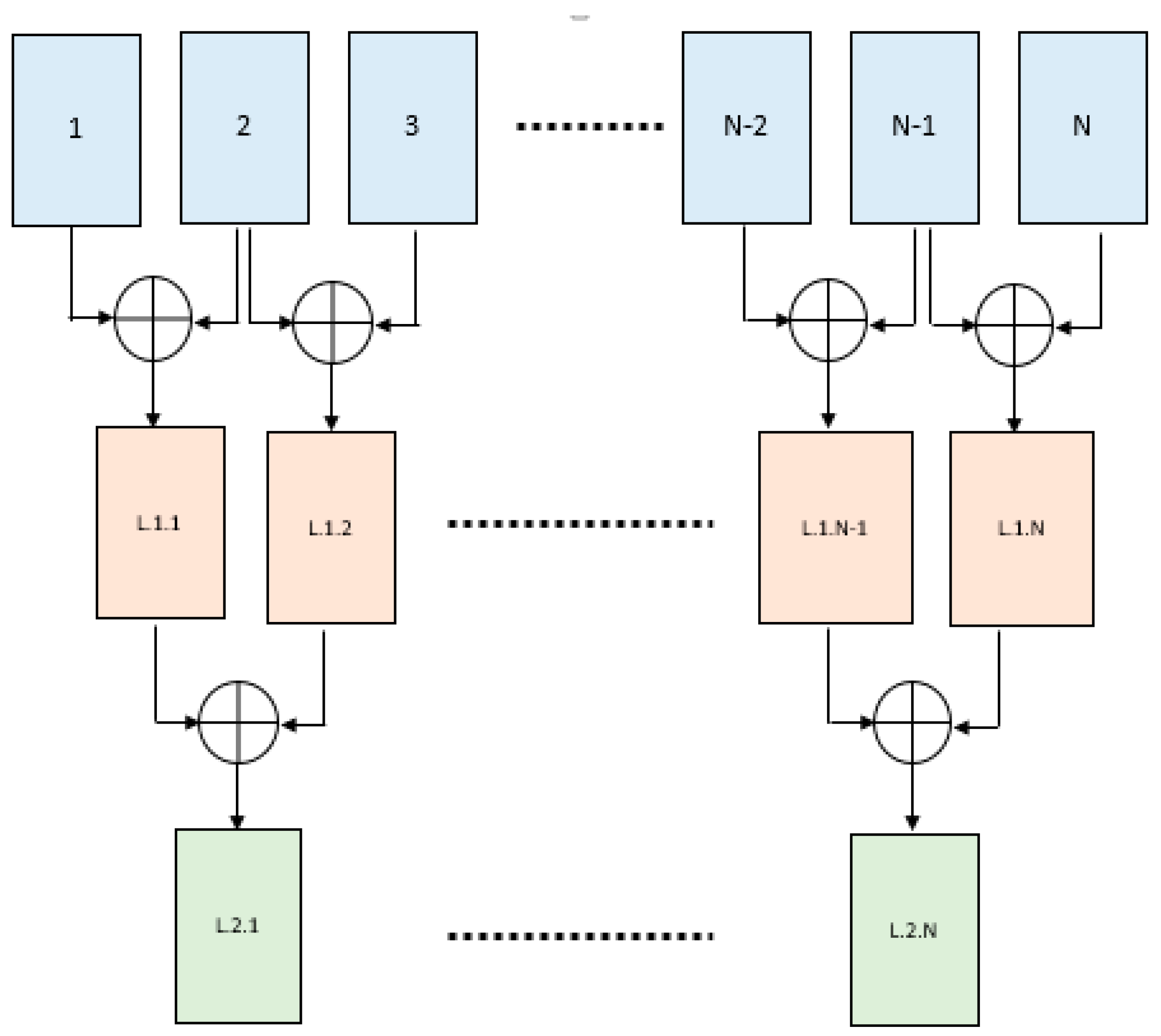
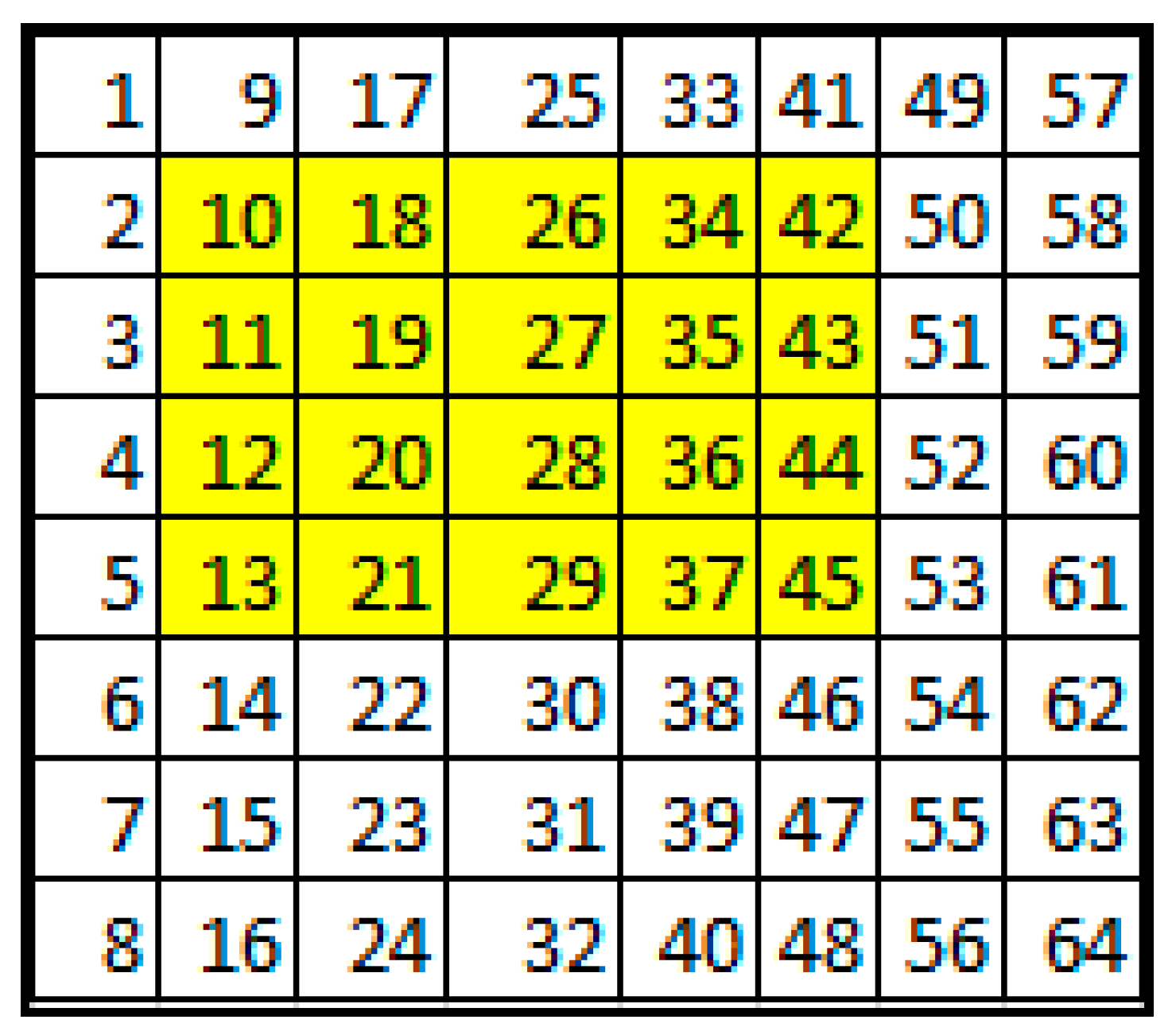
2.3. Decoding of Hadamard Code
- The Hadamard Code [8,4,4] is 8-bit long and can transmit 16 different messages. Only one error can be recovered unambiguously.
- General rule for the Hadamard Code: if the length of the Hadamard Code is , then errors can be corrected. In the case of , only one error can be corrected.
2.4. One-Dimensional Half-Mode Hadamard Code
3. Two-Dimensional Hadamard Error-Correcting Code
4. Enhanced Hadamard Code
- ∘
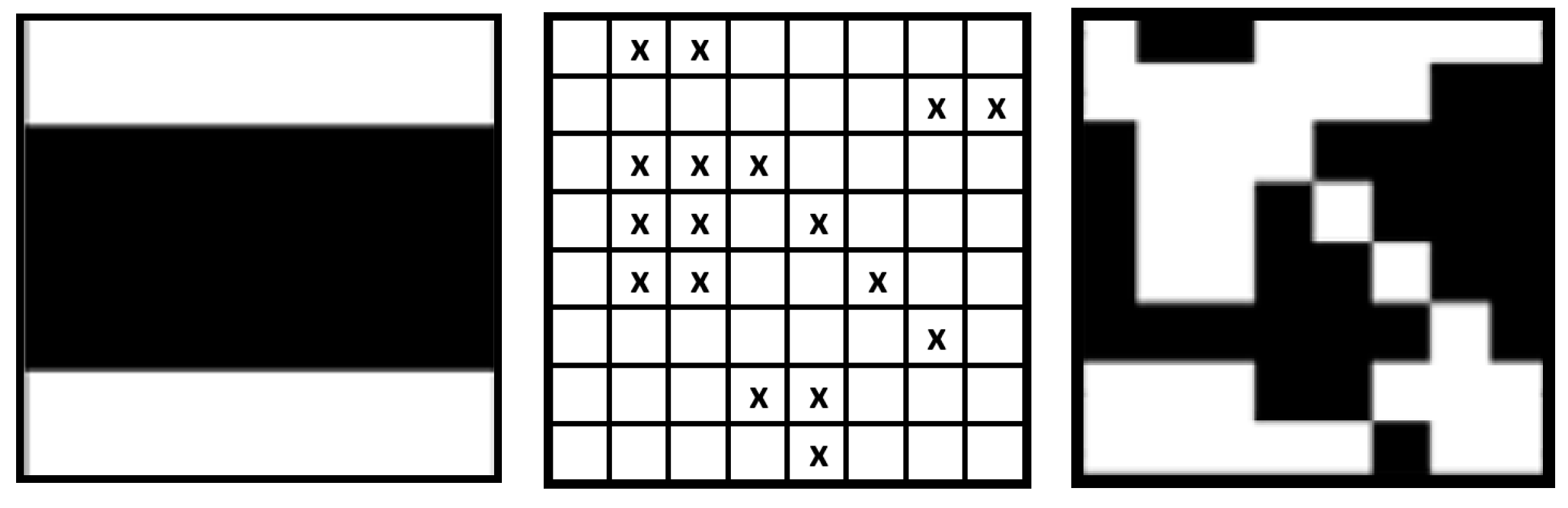
- The tainted basis image (A) is broken down into its individual rows (B).
- ∘
- The 1D Hadamard decoding process is executed to every row. Rows that contain only one error are decoded error-free; all their errors are removed. In the example, these are rows No. 6 and 8. In Part (C), these rows are depicted error-free.
- ∘
- The rows are reassembled (D). There are 15 fewer mistakes in the updated pattern than there were in the previous one.
- ∘
- The Hadamard decoding procedure is applied according to Equation (21) and the Code Book from Table 3. An error-free pattern is the end product: (E).
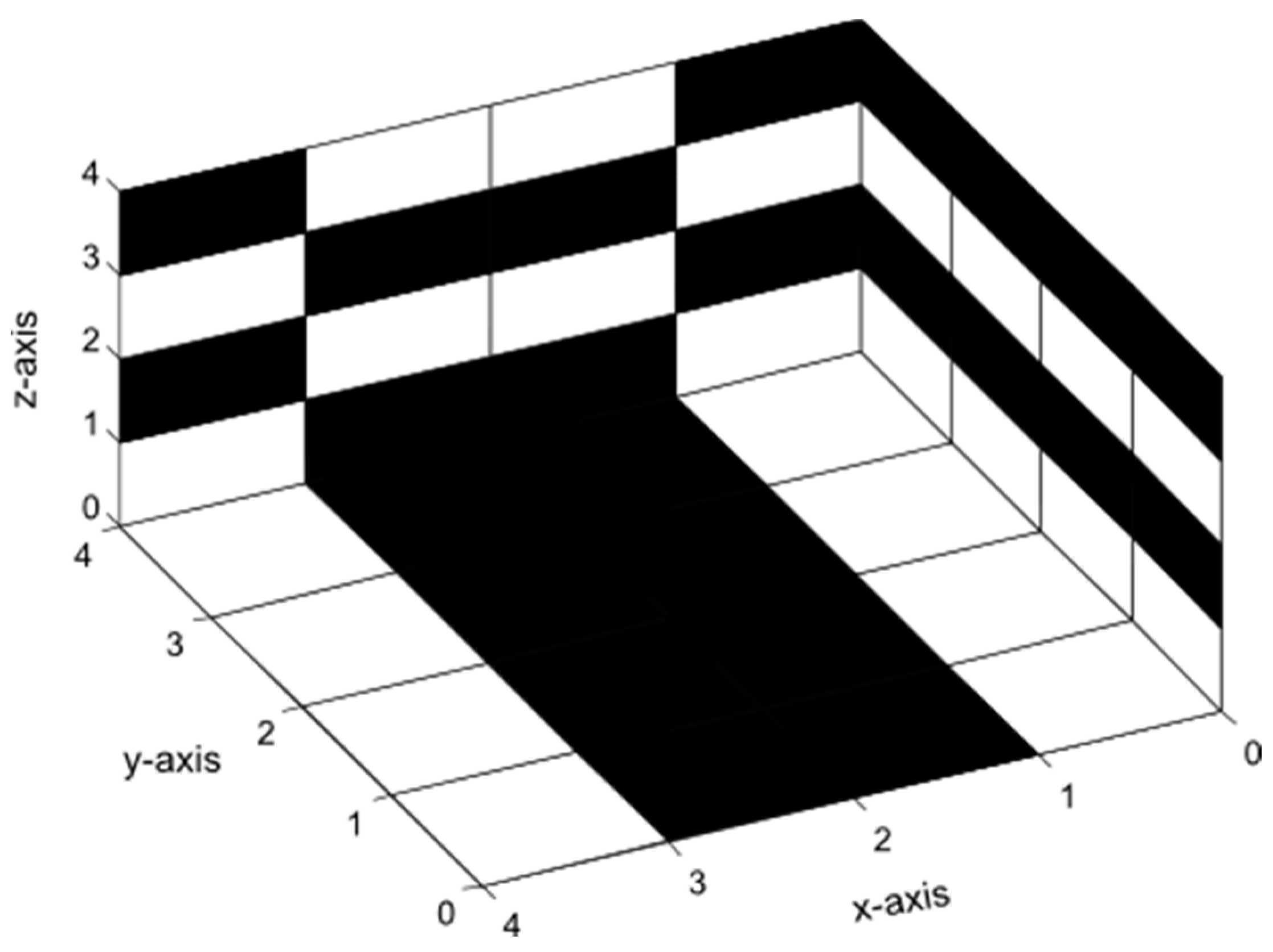
Enhanced 3D Hadamard Error-Correcting Code
5. Utilization of Enhanced Hadamard Code in Watermarking Technology and Its Outcomes
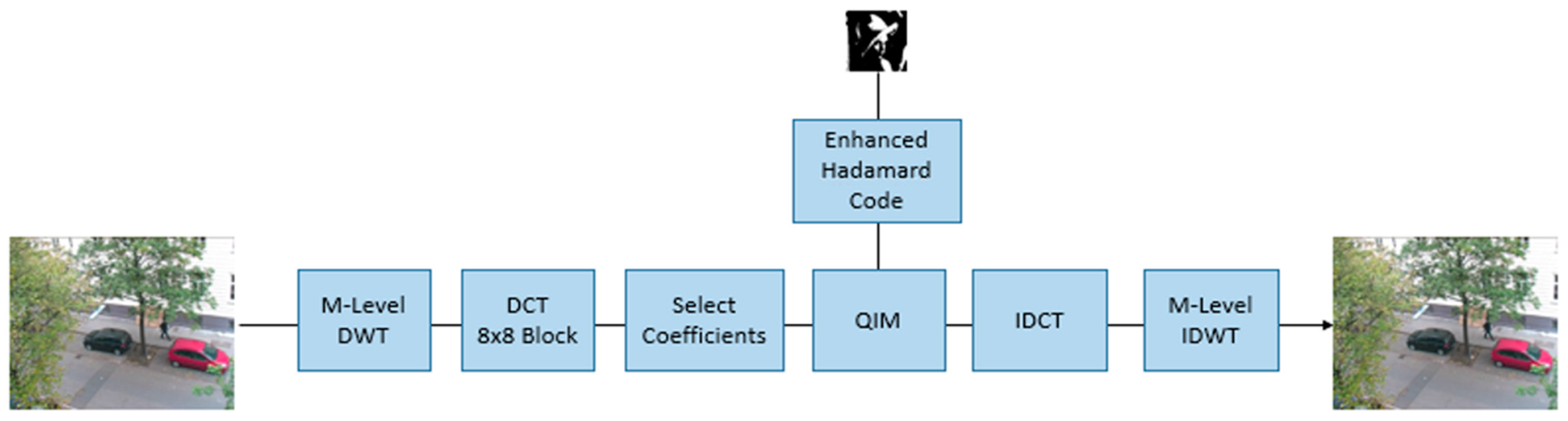
5.1. Proposed Scheme for Embedding Watermarks
5.1.1. Multi-Level DWT
5.1.2. Choice of Embedded Coefficients
5.2. Investigation of Robustness with 3D Enhanced Hadamard Error-Correcting Code
- Read 10 bits from the watermark. This determines the message word.
- According to the Code Book, find the corresponding basic images and the associated codeword. The codeword in this case has a length of 512 bits.
- Select 512 coefficients from DCT blocks.
- Embed the codeword into the selected coefficients through QIM (Quantization Index Modulation).
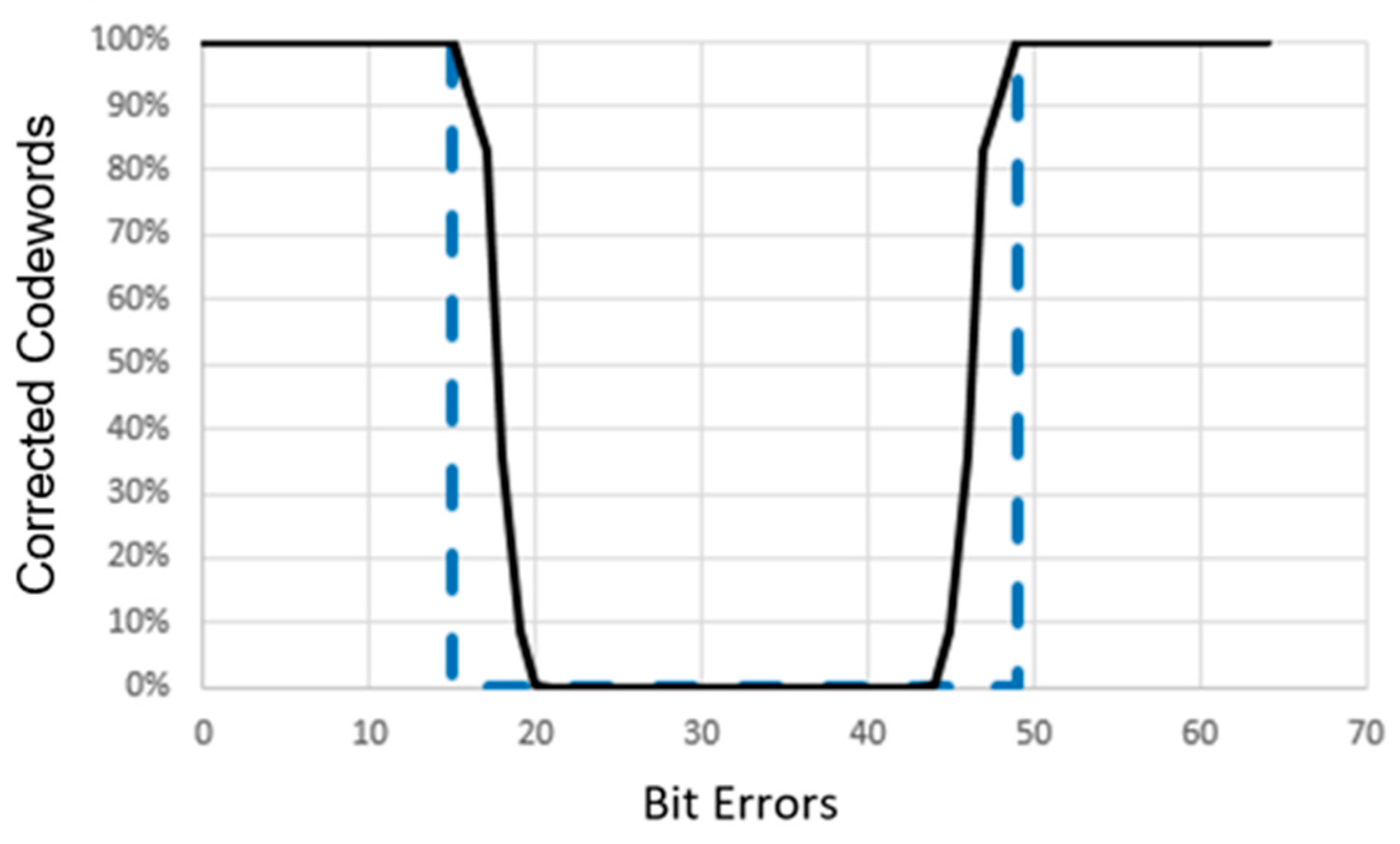
5.3. An Analysis of the 3D Enhanced Hadamard Code Compared to the Reed–Solomon Code
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kashani, Z.H.; Shiva, M. BCH Coding and Multi-hop Communication in Wireless Sensor Networks. In Proceedings of the 2006 IFIP International Conference on Wireless and Optical Communications Networks, Bangalore, India, 11–13 April 2016. [Google Scholar]
- Seferoglu, H.; Altunbasak, Y.; Gurbuz, O.; Ercetin, O. Rate distortion optimized joint ARQ-FEC scheme for real-time wireless multimedia. In Proceedings of the IEEE International Conference on Communications (ICC 2005), Seoul, Republic of Korea, 16–20 May 2005; Volume 2, pp. 1190–1194. [Google Scholar]
- Sartipi, M.; Fekri, F. Source and channel coding inwireless sensor networks using LDPC codes. In Proceedings of the2004 First Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks (IEEE SECON 2004), Santa Clara, CA, USA, 4–7 October 2004; pp. 309–316. [Google Scholar]
- Mambou, E.N.; Tonnellier, T.; Hashemi, S.A.; Gross, W.J. Efficient Flicker-Free FEC Codes Using Knuth’s Balancing Algorithm for VLC. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Lee, H.; Kwon, J.K. Turbo code-based error correction scheme for dimmable visible light communication systems. IEEE Photonics Technol. Lett. 2012, 24, 1463–1465. [Google Scholar] [CrossRef]
- Fang, J.; Che, Z.; Yu, X. An efficient flicker-free FEC coding scheme for dimmable visible light communication based on polar codes. IEEE Photonics J. 2017, 9, 7903310. [Google Scholar] [CrossRef]
- Plotkin, M. Binary Code with specified minimum distance. IRE Trans. Inf. Theory 1960, 6, 445–450. [Google Scholar] [CrossRef]
- Bose, R.C.; Shrikhande, S.S. A note on the result in the theory of code construction. Inf. Control 1965, 2, 183–194. [Google Scholar] [CrossRef][Green Version]
- Peterson, W.W. Error Correcting Codes; The M.I.T. Press, Massachusetts Institute of Technology: Cambridge, MA, USA; John & Wiley & Sons: New York, NY, USA, 1961. [Google Scholar]
- Levenshtein, V.I. Application of Hadamard matrices to a problem in coding. Probl. Cybernatics 1964, 5, 166–184. [Google Scholar]
- Combinatoric in Space, The Mariner 9 Telemetry System. Available online: https://www.scribd.com/document/496261228/Ppt-Mariner-9-Code (accessed on 10 February 2024).
- Agaian, S.; Sarukhanyan, H.; Egiazarian, K.; Astola, J. Hadamard Transforms; SPIE: Washington, DC, USA, 2011. [Google Scholar]
- Horadam, K.J. Hadamard Matrices; Prinston University Press: Princeton, NJ, USA, 2006; ISBN 9780691119212. [Google Scholar]
- Dziech, A.; Wassermann, J. Multidimensional Enhanced Hadamard Error Correcting Code In Comparison with Reed-Solomon Code in Video-Watermarking Applications. WSEAS Trans. Signal Process. 2017, 13, 196–207. [Google Scholar]
- Swanson, M.D.; Kobayashi, M.; Tewfik, A.H. Multimedia Data-Embedding and Watermarking Technologies. Proc. IEEE 1998, 86, 1064–1087. [Google Scholar] [CrossRef]
- Lin, S.D.; Chen, C.-F. A Robust DCT-Based Watermarking for Copyright Protection. IEEE Trans. Consum. Electron. 2000, 46, 415–421. [Google Scholar] [CrossRef]
- Wickler, S.B.; Bhargava, V.K. Reed-Solomon Codes and Their Applications; IEEE Press: Hoboken, NJ, USA, 1994; ISBN 0-7803-5391-9. [Google Scholar]
- Dziech, A.; Wassermann, J. Application of Enhanced Hadamard Error Correcting Code in Video-Watermarking and his comparison to Reed-Solomon code. MATEC Web Conf. 2017, 125, 05007. [Google Scholar] [CrossRef]
- Chan, P.-W.; Lyu, M.R. A DWT-Based Digital Video Watermarking Scheme with Error Correcting Code. In Information and Communications Security; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; LNCS 2836; pp. 202–213. [Google Scholar]
- Zhao, D.; Chen, G.; Liu, W. A Chaos-Based Robust Wavelet-Domain Watermarking Algorithm. Chaos Solut. Fractals 2004, 22, 47–54. [Google Scholar]
- Cox, I.J.; Killian, J.; Leighton, F.L.; Shamoon, T. Secure Spread Spectrum Watermarking for Multimedia. IEEE Trans. Image Process. 1997, 6, 1673–1687. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Wornell, W.G. Quantization Index Modulation for Digital Watermarking and Information Embedding of Multimedia. J. VLSI Signal Process. 2001, 27, 7–33. [Google Scholar] [CrossRef]
- Hartung, F.; Kutter, M. Multimedia Watermarking Techniques. Proc. IEEE 1999, 87, 1079–1107. [Google Scholar] [CrossRef]







| Message Word | Hadamard Vector | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | |
| 0 | 0 | 1 | 0 | 1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | |
| 0 | 0 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | |
| 0 | 1 | 0 | 1 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | |
| 0 | 1 | 1 | 0 | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | |
| 1 | 0 | 0 | 0 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | |
| 1 | 0 | 0 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | |
| 1 | 0 | 1 | 0 | −1 | −1 | 1 | 1 | −1 | −1 | 1 | 1 | |
| 1 | 0 | 1 | 1 | −1 | 1 | 1 | −1 | − 1 | 1 | 1 | −1 | |
| 1 | 1 | 0 | 0 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | −1 | |
| 1 | 1 | 1 | 0 | −1 | −1 | 1 | 1 | 1 | 1 | −1 | −1 | |
| 1 | 1 | 1 | 1 | −1 | 1 | 1 | −1 | 1 | −1 | −1 | 1 | |
| Message | Hadamard Vector | Codeword | ||||||||||||||||||
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||
| 0 | 1 | 0 | 1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| 0 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | ||
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | ||
| 1 | 1 | 0 | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | ||
| Message | Basis Image | Matrix Element | Codeword |
|---|---|---|---|
| 1 0 0 0 0 |  | S(1,1) | 0000000000000000 |
| 1 0 0 0 1 |  | S(1,2) | 0101010101010101 |
| 1 0 0 1 0 |  | S(1,3) | 0011001100110011 |
| 1 0 0 1 1 |  | S(1,4) | 0000111111110000 |
| 1 0 1 0 0 |  | S(2,1) | 0000111100001111 |
| 1 0 1 0 1 |  | S(2,2) | 0101101001011010 |
| 1 0 1 1 0 |  | S(2,3) | 0011110000111100 |
| 1 0 1 1 1 |  | S(2,4) | 0110100101101001 |
| 1 1 0 0 0 |  | S(3,1) | 0000000011111111 |
| 1 1 0 0 1 |  | S(3,2) | 0101010110101010 |
| 1 1 0 1 0 |  | S(3,3) | 0011001111001100 |
| 1 1 0 1 1 |  | S(3,4) | 0110011010011001 |
| 1 1 1 0 0 |  | S(4,1) | 0000111111110000 |
| 1 1 1 0 1 |  | S(4,2) | 0101101010100101 |
| 1 1 1 1 0 |  | S(4,3) | 0011110011000011 |
| 1 1 1 1 1 |  | S(4,4) | 0110100110010110 |
| Data Rate | Compression Ratio | DWT Levels | Delta QIM | Extracted Watermark | SSIM Watermarking | SSIM Video |
|---|---|---|---|---|---|---|
| 6 Mbit/s | 1:200 | 16 | 11 |  | 1 | 0.95 |
| 5 Mbit/s | 1:240 | 16 | 11 |  | 1 | 0.95 |
| 4 Mbit/s | 1:300 | 16 | 11 |  | 0.92 | 0.93 |
| 3 Mbit/s | 1:400 | 16 | 11 |  | 0.89 | 0.91 |
| 2 Mbit/s | 1:600 | 16 | 11 |  | 0.56 | 0.90 |
| Data Rate | EHC | Error % | Reed–Solomon | Error % |
|---|---|---|---|---|
| 5 Mbit/s |  | 0 |  | 17.5 |
| 4 Mbit/s |  | 1.7 |  | 27.6 |
| 3 Mbit/s |  | 6.8 |  | 35.3 |
| 2 Mbit/s |  | 41.2 |  | 40.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Windisch, M.; Wassermann, J.; Leba, M.; Stoicuta, O. Hadamard Error-Correcting Codes and Their Application in Digital Watermarking. Sensors 2024, 24, 3062. https://doi.org/10.3390/s24103062
Windisch M, Wassermann J, Leba M, Stoicuta O. Hadamard Error-Correcting Codes and Their Application in Digital Watermarking. Sensors. 2024; 24(10):3062. https://doi.org/10.3390/s24103062
Chicago/Turabian StyleWindisch, Michael, Jakob Wassermann, Monica Leba, and Olimpiu Stoicuta. 2024. "Hadamard Error-Correcting Codes and Their Application in Digital Watermarking" Sensors 24, no. 10: 3062. https://doi.org/10.3390/s24103062
APA StyleWindisch, M., Wassermann, J., Leba, M., & Stoicuta, O. (2024). Hadamard Error-Correcting Codes and Their Application in Digital Watermarking. Sensors, 24(10), 3062. https://doi.org/10.3390/s24103062







