Broken Rotor Bar Detection Based on Steady-State Stray Flux Signals Using Triaxial Sensor with Random Positioning
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
4. Data Analysis
5. Results
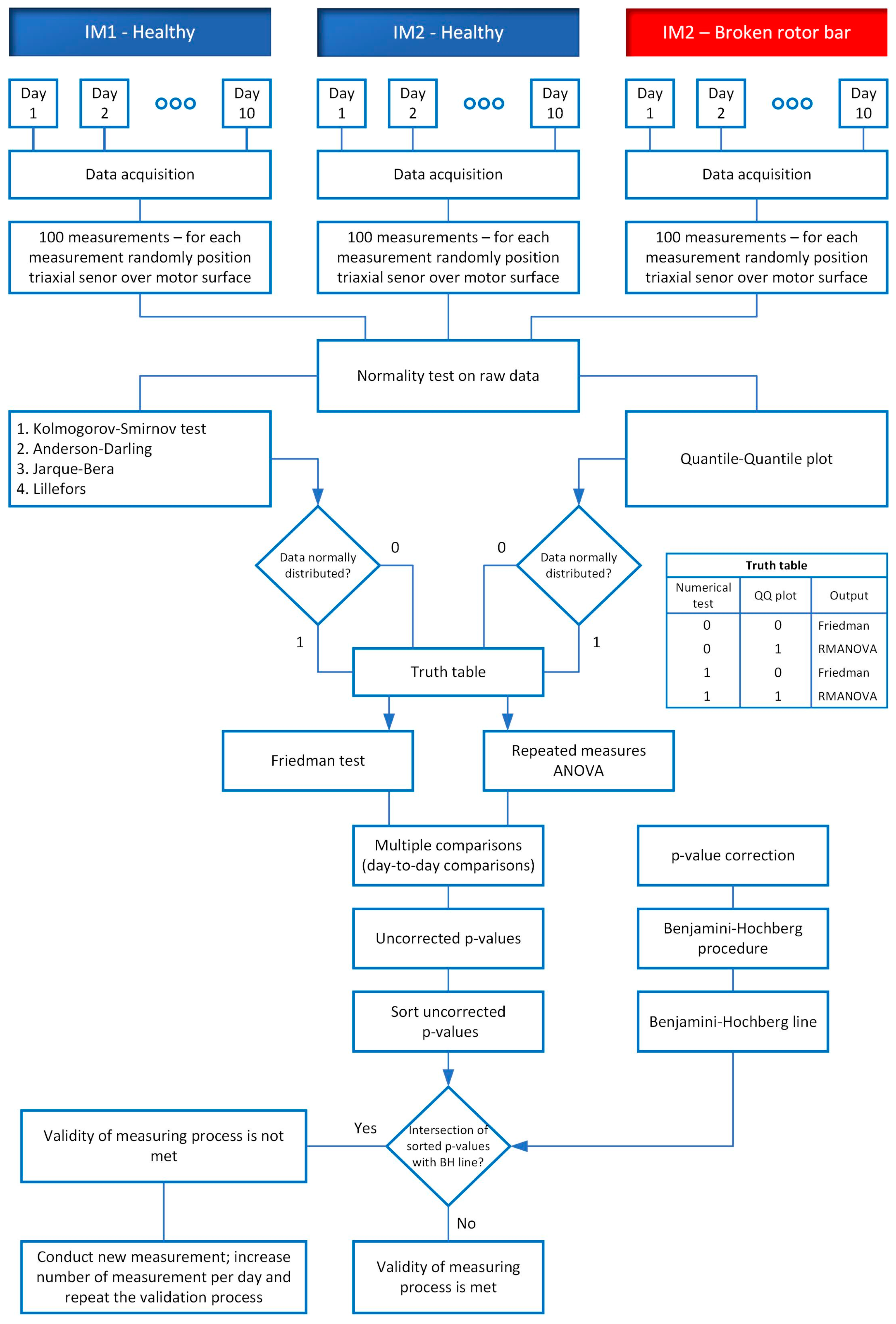
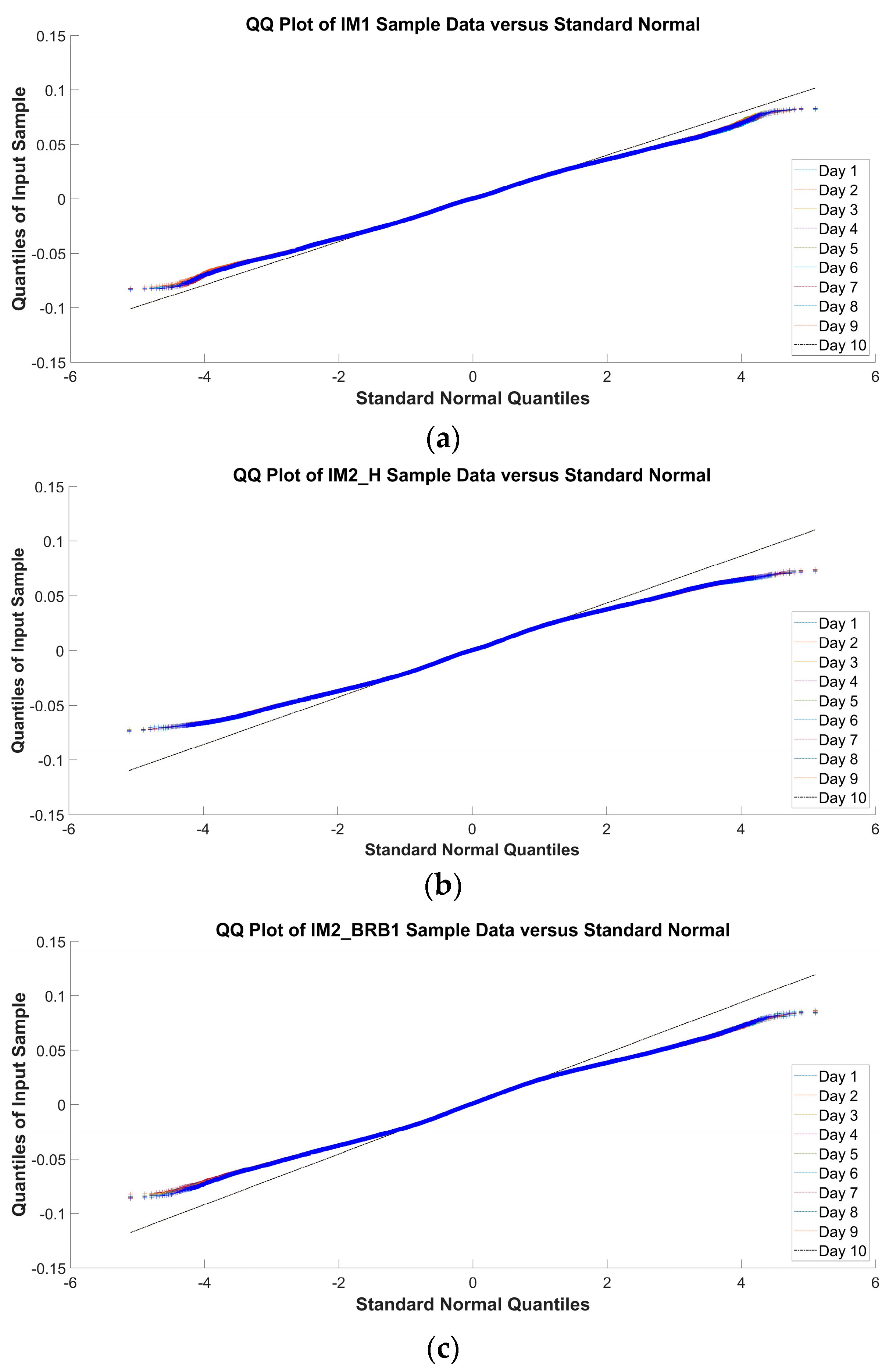
5.1. Normality Assumption
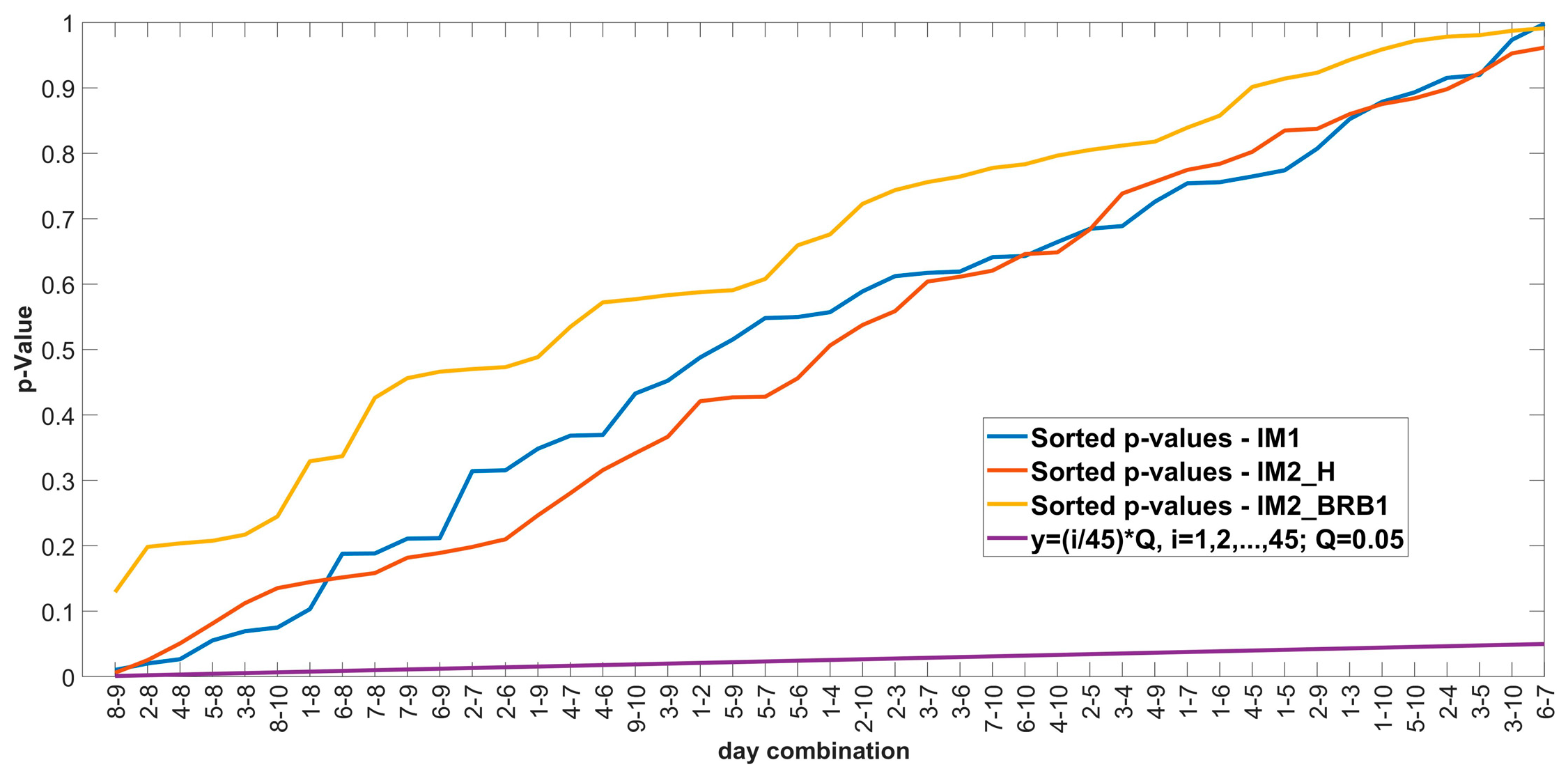
5.2. Non-Parametric Approach
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Souza, D.F.; Salotti, F.A.M.; Sauer, I.L.; Tatizawa, H.; De Almeida, A.T.; Kanashiro, A.G. A Performance Evaluation of Three-Phase Induction Electric Motors between 1945 and 2020. Energies 2022, 15, 2002. [Google Scholar] [CrossRef]
- Gundewar, S.K.; Kane, P.V. Condition Monitoring and Fault Diagnosis of Induction Motor. J. Vib. Eng. Technol. 2021, 9, 643–674. [Google Scholar] [CrossRef]
- Shang, K.; Zhang, Y.; Galea, M.; Brusic, V.; Korposh, S. Fibre Optic Sensors for the Monitoring of Rotating Electric Machines: A Review. Opt. Quant. Electron. 2021, 53, 75. [Google Scholar] [CrossRef]
- Kumar, R.R.; Andriollo, M.; Cirrincione, G.; Cirrincione, M.; Tortella, A. A Comprehensive Review of Conventional and Intelligence-Based Approaches for the Fault Diagnosis and Condition Monitoring of Induction Motors. Energies 2022, 15, 8938. [Google Scholar] [CrossRef]
- Albrecht, P.F.; Appiarius, J.C.; McCoy, R.M.; Owen, E.L.; Sharma, D.K. Assessment of the Reliability of Motors in Utility Applications-Updated. IEEE Trans. Energy Convers. 1986, EC-1, 39–46. [Google Scholar] [CrossRef]
- Thorsen, O.V.; Dalva, M. A Survey of Faults on Induction Motors in Offshore Oil Industry, Petrochemical Industry, Gas Terminals, and Oil Refineries. IEEE Trans. Ind. Appl. 1995, 31, 1186–1196. [Google Scholar] [CrossRef]
- Report of Large Motor Reliability Survey of Industrial and Commercial Installations, Part I. IEEE Trans. Ind. Appl. 1985, IA-21, 853–864. [CrossRef]
- IEEE Recommended Practice for the Design of Reliable Industrial and Commercial Power Systems-Redline; IEEE: Piscataway Township, NJ, USA, 2007; ISBN 978-0-7381-7083-1.
- Zhang, P.; Du, Y.; Habetler, T.G.; Lu, B. A Survey of Condition Monitoring and Protection Methods for Medium-Voltage Induction Motors. IEEE Trans. Ind. Appl. 2011, 47, 34–46. [Google Scholar] [CrossRef]
- Elez, A.; Car, S.; Tvoric, S.; Vaseghi, B. Rotor Cage and Winding Fault Detection Based on Machine Differential Magnetic Field Measurement (DMFM). IEEE Trans. Ind. Appl. 2017, 53, 3156–3163. [Google Scholar] [CrossRef]
- Hassan, O.E.; Amer, M.; Abdelsalam, A.K.; Williams, B.W. Induction Motor Broken Rotor Bar Fault Detection Techniques Based on Fault Signature Analysis—A Review. IET Electr. Power Appl. 2018, 12, 895–907. [Google Scholar] [CrossRef]
- Atta, M.E.E.-D.; Ibrahim, D.K.; Gilany, M.I. Broken Bar Fault Detection and Diagnosis Techniques for Induction Motors and Drives: State of the Art. IEEE Access 2022, 10, 88504–88526. [Google Scholar] [CrossRef]
- Park, Y.; Choi, H.; Shin, J.; Park, J.; Lee, S.B.; Jo, H. Airgap Flux Based Detection and Classification of Induction Motor Rotor and Load Defects During the Starting Transient. IEEE Trans. Ind. Electron. 2020, 67, 10075–10084. [Google Scholar] [CrossRef]
- Henao, H.; Demian, C.; Capolino, G.-A. A Frequency-Domain Detection of Stator Winding Faults in Induction Machines Using an External Flux Sensor. IEEE Trans. Ind. Appl. 2003, 39, 1272–1279. [Google Scholar] [CrossRef]
- Erlicki, M.S.; Porat, Y.; Alexandrovitz, A. Leakage Field Changes of an Induction Motor as Indication of Nonsymmetric Supply. IEEE Trans. Ind. Gen. Appl. 1971, IGA-7, 713–717. [Google Scholar] [CrossRef]
- Mazaheri-Tehrani, E.; Faiz, J. Airgap and Stray Magnetic Flux Monitoring Techniques for Fault Diagnosis of Electrical Machines: An Overview. IET Electr. Power Appl. 2022, 16, 277–299. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Osornio-Rios, R.A.; Antonino-Daviu, J.A.; Razik, H.; Romero-Troncoso, R. Magnetic Flux Analysis for the Condition Monitoring of Electric Machines: A Review. IEEE Trans. Ind. Inf. 2022, 18, 2895–2908. [Google Scholar] [CrossRef]
- Gangsar, P.; Tiwari, R. Signal Based Condition Monitoring Techniques for Fault Detection and Diagnosis of Induction Motors: A State-of-the-Art Review. Mech. Syst. Signal Process. 2020, 144, 106908. [Google Scholar] [CrossRef]
- Ramirez-Nunez, J.A.; Antonino-Daviu, J.A.; Climente-Alarcon, V.; Quijano-Lopez, A.; Razik, H.; Osornio-Rios, R.A.; Romero-Troncoso, R.D.J. Evaluation of the Detectability of Electromechanical Faults in Induction Motors Via Transient Analysis of the Stray Flux. IEEE Trans. Ind. Appl. 2018, 54, 4324–4332. [Google Scholar] [CrossRef]
- Panagiotou, P.A.; Arvanitakis, I.; Lophitis, N.; Antonino-Daviu, J.A.; Gyftakis, K.N. A New Approach for Broken Rotor Bar Detection in Induction Motors Using Frequency Extraction in Stray Flux Signals. IEEE Trans. Ind. Appl. 2019, 55, 3501–3511. [Google Scholar] [CrossRef]
- Iglesias-Martinez, M.E.; Fernandez De Cordoba, P.; Antonino-Daviu, J.A.; Conejero, J.A. Detection of Nonadjacent Rotor Faults in Induction Motors via Spectral Subtraction and Autocorrelation of Stray Flux Signals. IEEE Trans. Ind. Appl. 2019, 55, 4585–4594. [Google Scholar] [CrossRef]
- Iglesias-Martínez, M.; Antonino-Daviu, J.; Fernández De Córdoba, P.; Conejero, J. Rotor Fault Detection in Induction Motors Based on Time-Frequency Analysis Using the Bispectrum and the Autocovariance of Stray Flux Signals. Energies 2019, 12, 597. [Google Scholar] [CrossRef]
- Panagiotou, P.A.; Arvanitakis, I.; Lophitis, N.; Antonino-Daviu, J.A.; Gyftakis, K.N. On the Broken Rotor Bar Diagnosis Using Time–Frequency Analysis: ‘Is One Spectral Representation Enough for the Characterisation of Monitored Signals’? IET Electr. Power Appl. 2019, 13, 932–942. [Google Scholar] [CrossRef]
- Park, Y.; Yang, C.; Kim, J.; Kim, H.; Lee, S.B.; Gyftakis, K.N.; Panagiotou, P.A.; Kia, S.H.; Capolino, G.-A. Stray Flux Monitoring for Reliable Detection of Rotor Faults Under the Influence of Rotor Axial Air Ducts. IEEE Trans. Ind. Electron. 2019, 66, 7561–7570. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Ramirez-Nunez, J.A.; Antonino-Daviu, J.; Osornio-Rios, R.A.; Quijano-Lopez, A.; Razik, H.; Romero-Troncoso, R.J. Automatic Diagnosis of Electromechanical Faults in Induction Motors Based on the Transient Analysis of the Stray Flux via MUSIC Methods. IEEE Trans. Ind. Appl. 2020, 56, 3604–3613. [Google Scholar] [CrossRef]
- Zamudio-Ramírez, I.; Osornio-Ríos, R.A.; Antonino-Daviu, J.A.; Quijano-Lopez, A. Smart-Sensor for the Automatic Detection of Electromechanical Faults in Induction Motors Based on the Transient Stray Flux Analysis. Sensors 2020, 20, 1477. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Choi, H.; Lee, S.B.; Gyftakis, K.N. Search Coil-Based Detection of Nonadjacent Rotor Bar Damage in Squirrel Cage Induction Motors. IEEE Trans. Ind. Appl. 2020, 56, 4748–4757. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Panagiotou, P.A.; Lee, S.B. Generation of Mechanical Frequency Related Harmonics in the Stray Flux Spectra of Induction Motors Suffering From Rotor Electrical Faults. IEEE Trans. Ind. Appl. 2020, 56, 4796–4803. [Google Scholar] [CrossRef]
- Lee, S.B.; Shin, J.; Park, Y.; Kim, H.; Kim, J. Reliable Flux-Based Detection of Induction Motor Rotor Faults From the Fifth Rotor Rotational Frequency Sideband. IEEE Trans. Ind. Electron. 2021, 68, 7874–7883. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Panagiotou, P.A.; Spyrakis, D. Detection of Simultaneous Mechanical Faults in 6-kV Pumping Induction Motors Using Combined MCSA and Stray Flux Methods. IET Electr. Power Appl. 2021, 15, 643–652. [Google Scholar] [CrossRef]
- Biot-Monterde, V.; Navarro-Navarro, Á.; Antonino-Daviu, J.A.; Razik, H. Stray Flux Analysis for the Detection and Severity Categorization of Rotor Failures in Induction Machines Driven by Soft-Starters. Energies 2021, 14, 5757. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Osornio-Rios, R.A.; Antonino-Daviu, J.A. Smart Sensor for Fault Detection in Induction Motors Based on the Combined Analysis of Stray-Flux and Current Signals: A Flexible, Robust Approach. IEEE Ind. Appl. Mag. 2022, 28, 56–66. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Antonino-Daviu, J.A.; Trejo-Hernandez, M.; Osornio-Rios, R.A. Cutting Tool Wear Monitoring in CNC Machines Based in Spindle-Motor Stray Flux Signals. IEEE Trans. Ind. Inf. 2022, 18, 3267–3275. [Google Scholar] [CrossRef]
- Navarro-Navarro, A.; Zamudio-Ramirez, I.; Biot-Monterde, V.; Osornio-Rios, R.A.; Antonino-Daviu, J.A. Current and Stray Flux Combined Analysis for the Automatic Detection of Rotor Faults in Soft-Started Induction Motors. Energies 2022, 15, 2511. [Google Scholar] [CrossRef]
- Biot-Monterde, V.; Navarro-Navarro, A.; Zamudio-Ramirez, I.; Antonino-Daviu, J.A.; Osornio-Rios, R.A. Automatic Classification of Rotor Faults in Soft-Started Induction Motors, Based on Persistence Spectrum and Convolutional Neural Network Applied to Stray-Flux Signals. Sensors 2022, 23, 316. [Google Scholar] [CrossRef]
- Saucedo-Dorantes, J.J.; Elvira-Ortiz, D.A.; Jaen-Cuellar, A.Y.; Antonino-Daviu, J.A.; Osornio-Rios, R.A. Automatic Methodology for Multiple Fault Detection in Induction Motor Under Periodic Low-Frequency Fluctuating Load Based on Stray Flux Signals. IEEE Trans. Energy Convers. 2023, 38, 2744–2753. [Google Scholar] [CrossRef]
- Scheff, S. Fundamental Statistical Principles for the Neurobiologist: A Survival Guide; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2016; ISBN 978-0-12-804753-8. [Google Scholar]
- Guzik, P.; Więckowska, B. Data Distribution Analysis—A Preliminary Approach to Quantitative Data in Biomedical Research. J. Med. Sci. Vol. 2023, 92, e869. [Google Scholar] [CrossRef]
- Hernandez, H. Testing for Normality: What Is the Best Method? 2021, 6, 2021-05. ForsChem Res. Rep. 2021, 6, 2021-05. [Google Scholar] [CrossRef]
- Loy, A.; Follett, L.; Hofmann, H. Variations of Q–Q Plots: The Power of Our Eyes! Am. Stat. 2016, 70, 202–214. [Google Scholar] [CrossRef]
- Kim, T.K. Practical Statistics in Pain Research. Korean J. Pain. 2017, 30, 243–249. [Google Scholar] [CrossRef]
- Muhammad, L.N. Guidelines for Repeated Measures Statistical Analysis Approaches with Basic Science Research Considerations. J. Clin. Investig. 2023, 133, e171058. [Google Scholar] [CrossRef]
- Blanca, M.J.; Arnau, J.; García-Castro, F.J.; Alarcón, R.; Bono, R. Non-Normal Data in Repeated Measures ANOVA: Impact on Type I Error and Power. Psicothema 2023, 35, 21–29. [Google Scholar] [CrossRef]
- Blanca, M.J.; Arnau, J.; García-Castro, F.J.; Alarcón, R.; Bono, R. Repeated Measures ANOVA and Adjusted F-Tests When Sphericity Is Violated: Which Procedure Is Best? Front. Psychol. 2023, 14, 1192453. [Google Scholar] [CrossRef]
- Chen, S.-Y.; Feng, Z.; Yi, X. A General Introduction to Adjustment for Multiple Comparisons. J. Thorac. Dis. 2017, 9, 1725–1729. [Google Scholar] [CrossRef]
- Lee, S.; Lee, D.K. What Is the Proper Way to Apply the Multiple Comparison Test? Korean J. Anesthesiol. 2018, 71, 353–360. [Google Scholar] [CrossRef]
- Lindquist, M.A.; Mejia, A. Zen and the Art of Multiple Comparisons. Psychosom. Med. 2015, 77, 114–125. [Google Scholar] [CrossRef]
- Leday, G.G.R.; Hemerik, J.; Engel, J.; Van Der Voet, H. Improved Family-Wise Error Rate Control in Multiple Equivalence Testing. Food Chem. Toxicol. 2023, 178, 113928. [Google Scholar] [CrossRef]
- Garrido-Trigo, A.; Corraliza, A.M.; Veny, M.; Dotti, I.; Melón-Ardanaz, E.; Rill, A.; Crowell, H.L.; Corbí, Á.; Gudiño, V.; Esteller, M.; et al. Macrophage and Neutrophil Heterogeneity at Single-Cell Spatial Resolution in Human Inflammatory Bowel Disease. Nat. Commun. 2023, 14, 4506. [Google Scholar] [CrossRef]
- Dubitzky, W.; Wolkenhauer, O.; Cho, K.-H.; Yokota, H. (Eds.) Encyclopedia of Systems Biology; Springer Reference: New York, NY, USA, 2013; ISBN 978-1-4419-9862-0. [Google Scholar]
- Pike, N. Using False Discovery Rates for Multiple Comparisons in Ecology and Evolution. Methods Ecol. Evol. 2011, 2, 278–282. [Google Scholar] [CrossRef]
- CKDGen Consortium; Brinster, R.; Köttgen, A.; Tayo, B.O.; Schumacher, M.; Sekula, P. Control Procedures and Estimators of the False Discovery Rate and Their Application in Low-Dimensional Settings: An Empirical Investigation. BMC Bioinform. 2018, 19, 78. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Dehmer, M. Large-Scale Simultaneous Inference with Hypothesis Testing: Multiple Testing Procedures in Practice. MAKE 2019, 1, 653–683. [Google Scholar] [CrossRef]
- Nahm, F.S. Nonparametric Statistical Tests for the Continuous Data: The Basic Concept and the Practical Use. Korean J. Anesthesiol. 2016, 69, 8. [Google Scholar] [CrossRef] [PubMed]
- Krzywinski, M.; Altman, N. Nonparametric Tests. Nat. Methods 2014, 11, 467–468. [Google Scholar] [CrossRef] [PubMed]
- Mowla, M.R.; Gonzalez-Morales, J.D.; Rico-Martinez, J.; Ulichnie, D.A.; Thompson, D.E. A Comparison of Classification Techniques to Predict Brain-Computer Interfaces Accuracy Using Classifier-Based Latency Estimation. Brain Sci. 2020, 10, 734. [Google Scholar] [CrossRef] [PubMed]
- Pereira, D.G.; Afonso, A.; Medeiros, F.M. Overview of Friedman’s Test and Post-Hoc Analysis. Commun. Stat. Simul. Comput. 2015, 44, 2636–2653. [Google Scholar] [CrossRef]

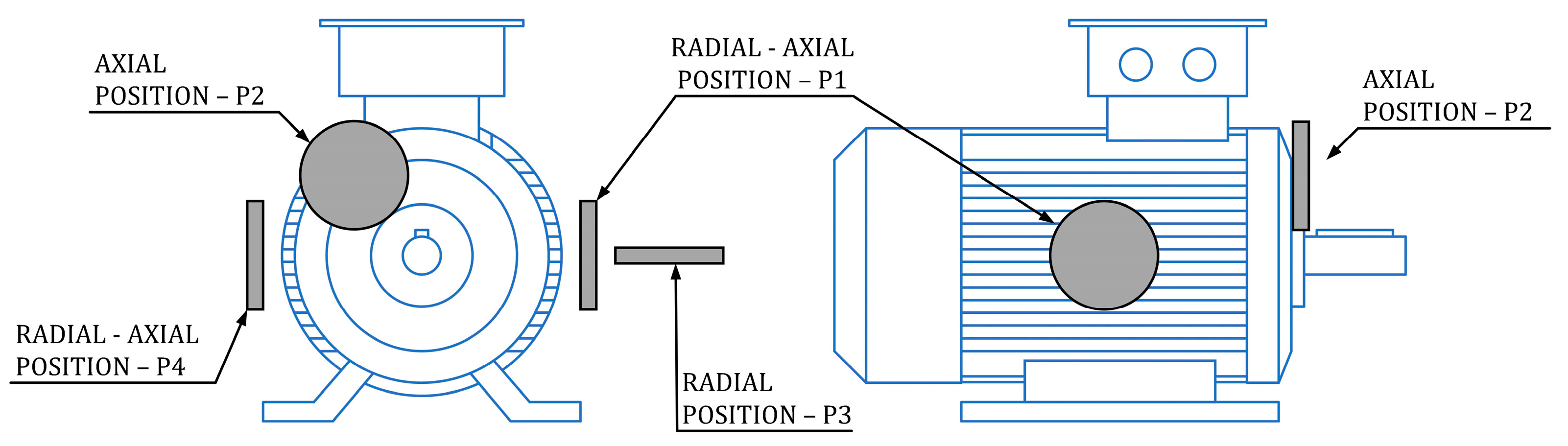






| Reference | Sensor Position (Ref. to Figure 2) | Sensor—Type and Dimensions | Fault Detection Method | Analysed Fault | Tested SCIM Rated Power/ Facility/Motor Supply |
|---|---|---|---|---|---|
| [19] | P1, P2, P3 | Circular coil; N = 1000; Inner φ = 3.9 cm; Outer φ = 8 cm; Height 1 cm | STFT DWT | Misalignment Misal. + 1 BRB Misal. + 2 BRB (adjacent) | M1: 1.1 kW M2: 0.75 kW Lab. Start-up Line supply |
| [20] | P1 | Circular coil; N = 1000 Inner φ = 3.9 cm Outer φ = 8 cm Height 1 cm | STFT FFT | 2 BRB (adjacent, half pole pitch and one pole pitch) | M: 1.1 kW Lab. Steady state Line supply |
| [21] | P1, P2 | Circular coil; N = 1000 Inner φ = 3.9 cm Outer φ = 8 cm Height 1 cm | FFT Spectral subtraction Autocorrelation | 2 BRB (5 combinations) | M: 1.1 kW Lab. Steady state Line supply |
| [22] | P1, P2, P3, P4 | Circular coil; N = 1000 Inner φ = 3.9 cm Outer φ = 8 cm Height 1 cm | Bispectrum Autocorrelation | 1 BRB | M: 1.1 kW Lab. Steady state And Start-up Line supply |
| [23] | P1 | Circular coil Nc =1000 Inner φ = 3.9 cm Outer φ = 8 cm Height 1 cm | STFT | 1 BRB 2 BRB (adjacent) | M: 1.1 kW Lab. Steady state Line supply |
| [24] | P1 | Helmholtz coil Nc =320 Inner φ = 121 cm Outer φ = 155 cm | FFT | 1 BRB 2 BRB | M1:5.5 kW Lab. Steady state Line supply M2,3: 280 kW, 6.6 kV, Field test Steady state Line supply |
| [25] | P1, P2, P3 | Circular coil Nc =1000 Inner φ = 3.9 cm Outer φ = 8 cm Height 1 cm | MUSIC FFNN | 1 BRB 2 BRB | M1: 1.1 kW M2: 7.5 kW Lab. Start-up Line supply |
| [26] | P1, P2 | Triaxial stray flux sensor Three hall sensors perpendicular axis to each other Allegro—A1325 | STFT Statistical parameters LDA dimensionality reduction FFNN | Misalignment Misal. + 1 BRB Misal. + 2 BRB (adjacent) | M:0.74 kW Lab. Start-up Line supply |
| [27] | P1 | Circular coil Nc = 320 | FFT STFT | 1 BRB 2 BRB (adjacent) 2 BRB (non-adjacent; 90° el. apart) | M: 7.5 hp Lab. Start-up and steady state Line supply |
| [28] | P1 | Square body Nc = 1500 copper wire φ = 0.1 mm Inner square length 40 mm Outer square length 50 mm Height 4.5 mm | FFT | 1 BRB | M:4 kW Lab. Steady state Line supply |
| [29] | P1 | Circular coil Nc =300 (as stated in text) | FFT | 1 BRB 2 BRB adjacent 2 BRB non-adjacent Load unbalance Misalignment Eccentricity | M1:7.5 kW M2: 5.5 kW M3: 2.0 kW M4: 5.5 kW Lab. Steady state Line supply |
| [30] | P1 | Square body Nc = 3500 Inner square length 40 mm Outer square length 50 mm Height 4.5 mm | FFT | Misalignment Eccentricity Bearing fault | M1:750 kW M2: 750 kW M3: 240 kW M4: 240 kW Field testing Steady state Line supply |
| [31] | P1, P2, P3 | Circular coil Nc =1000 Inner φ = 65 mm Outer φ = 80 mm Height 15 mm | FFT STFT | 1 BRB 2 BRB (adjacent) | M: 1.1 kW Lab. Start-up and steady state 4 soft-starters |
| [32] | P1 | Triaxial stray flux sensor Three perpendicular hall-effect sensors | STFT FFNN | 1 BRB 2 BRB (adjacent) Misalignment | M1: 1 hp M2: 1.47 hp Lab. Start-up Line supply |
| [33] | P1 | Triaxial stray flux sensor Three hall sensors mounted perpendicular on a PCB board | DWT FFNN | Cutting tool wear evaluation | M1: 3.7 kW Line supply |
| [34] | P1 | The text description of the coil does not match the coil presented in the paper | STFT LDA FFNN | 1 BRB 2 BRB (adjacent) | M: 1.1 kW Lab. Start-up and steady-state 4 soft-starters |
| [35] | P1 | Circular coil Nc =1000 Inner φ = 6.5 cm Outer φ = 8 cm Height 1.5 cm | Persistence spectrum CNN | 1 BRB 2 BRB (adjacent) | M: 1.1 kW Lab. Start-up and steady-state 4 soft-starters |
| [36] | P1 | Triaxial stray flux sensor Three perpendicular hall-effect sensors | Self-Organizing Maps NN | 1/2 BRB 1 BRB Unbalance Misalignment | M: 1.5 kW Lab. Fluctuating load VFD supply |
| Manufacturer: Siemens; Type: 1AV3082B 1LE10030DB222AB4 | |||||||
|---|---|---|---|---|---|---|---|
| V | Hz | kW | A | PF | RPM | EFF-CL | ETA % |
| 400 Y | 50 | 0.55 | 1.26 | 0.78 | 1440 | IE3 | 80.8 |
| Test | Motor | p-Value | |||||||||
| Day 1 | Day 2 | Day 3 | Day 4 | Day 5 | Day 6 | Day 7 | Day 8 | Day 9 | Day 10 | ||
| One-sample Kolmogorov–Smirnov | IM1 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| IM2_H | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| IM2_BRB1 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| Anderson-Darling | IM1 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| IM2_H | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| IM2_BRB1 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| Jarque-Bera | IM1 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| IM2_H | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| IM2_BRB1 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| Lilliefors | IM1 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| IM2_H | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| IM2_BRB1 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| W | ChiStat | DF | p-Value | |
|---|---|---|---|---|
| IM1 | 0.99999 | 41.49 | 44 | 0.5798 |
| IM2_H | 0.99999 | 33.811 | 44 | 0.86671 |
| IM2_BRB1 | 0.99999 | 36.867 | 44 | 0.76842 |
| SumSq | DF | MeanSq | F | p-Value | ||
|---|---|---|---|---|---|---|
| IM1 | (Intercept): day | 0.0032546 | 9 | 0.00036162 | 1.0344 | 0.40934 |
| Error(day) | 9439.4 | 2.7 × 107 | 0.00034961 | |||
| IM2_H | (Intercept): day | 0.0037357 | 9 | 0.00041508 | 1.0644 | 0.38553 |
| Error(day) | 10,529 | 2.7 × 107 | 0.00038995 | |||
| IM2_BRB1 | (Intercept): day | 0.0015375 | 9 | 0.00017084 | 0.41369 | 0.92853 |
| Error(day) | 11,150 | 2.7 × 107 | 0.00041296 |
| W | ChiStat | DF | p-Value |
|---|---|---|---|
| 1 | 36.631 | 44 | 0.77698 |
| SumSq | DF | MeanSq | F | p-Value | |
|---|---|---|---|---|---|
| (Intercept): day | 0.0013094 | 9 | 0.00014549 | 0.37871 | 0.94548 |
| Motor | 8.6033 | 2 | 4.3017 | 10413 | 0 |
| Motor: day | 0.0072185 | 18 | 0.00040103 | 1.0439 | 0.40485 |
| Error(day) | 31,118 | 8.1 × 107 | 0.00038417 | 1 | 0.5 |
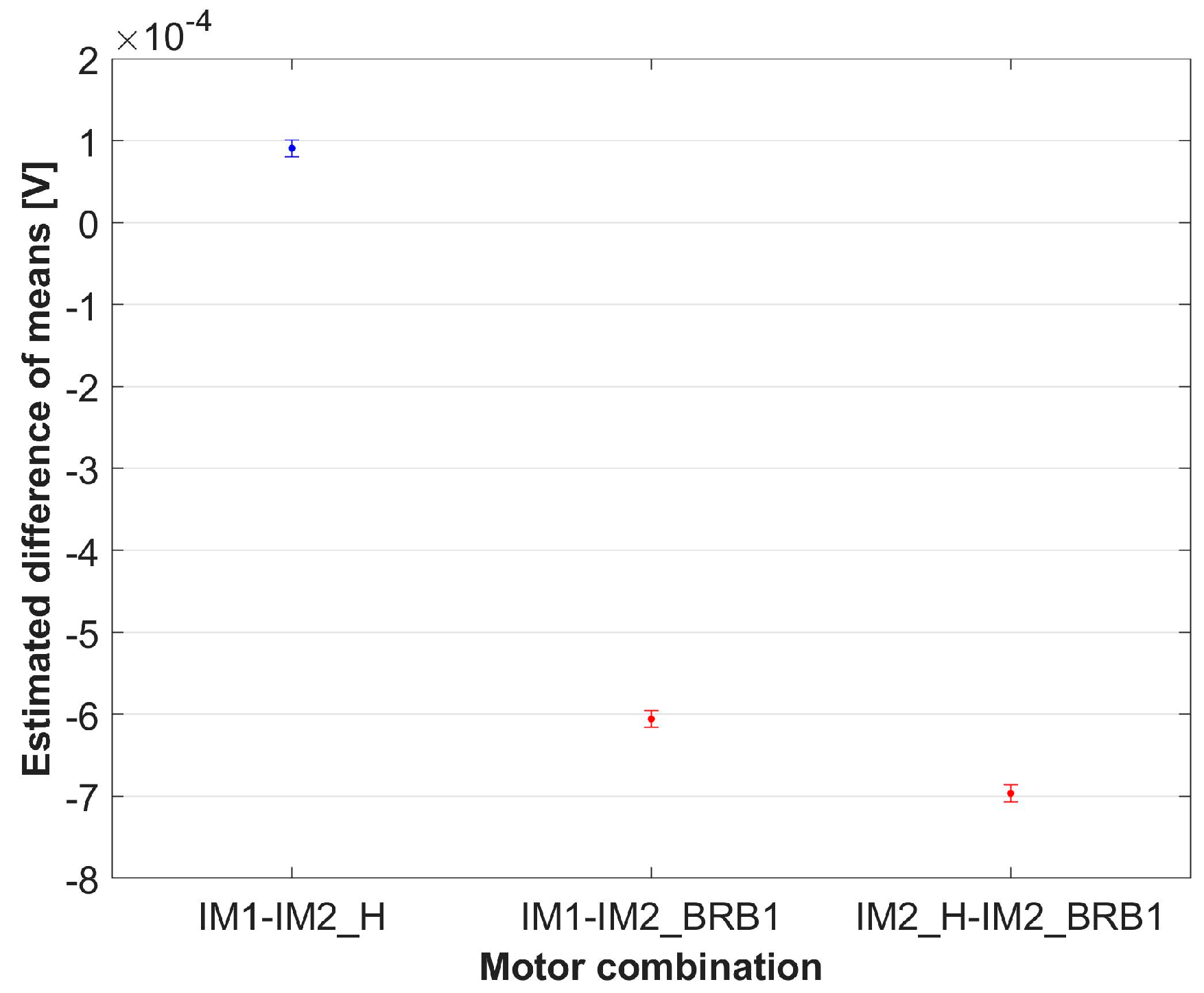
| Motor 1 | Motor 2 | Difference | StdErr | p-Value | Lower | Upper |
|---|---|---|---|---|---|---|
| IM1 | IM2_H | 9.0766 × 10−5 | 5.2479 × 10−6 | 5.0809 × 10−67 | 8.048 × 10−5 | 0.00010105 |
| IM1 | IM2_BRB1 | −0.00060576 | 5.2479 × 10−6 | 0 | −0.00061605 | −0.00059548 |
| IM2_H | IM2_BRB1 | −0.00069653 | 5.2479 × 10−6 | 5.0809 × 10−67 | −0.00070681 | −0.00068624 |
| Reference | Motor Combination | Percentage Difference in Estimated Differences in Means |
|---|---|---|
| IM1–IM2_H | IM1–IM2_BRB1 | 767.40% |
| IM2_H–IM2_BRB1 | 867.40% |
| SS | df | MS | Chi-sq | Prob>Chi-sq | ||
|---|---|---|---|---|---|---|
| IM1 | Columns | 92.7364 | 9 | 10.304 | 10.13 | 0.34 |
| Error | 247,166,451.7636 | 26,999,991 | 9.1543 | |||
| Total | 247,166,544.5 | 29,999,999 | ||||
| IM2_H | Columns | 104.678 | 9 | 11.6309 | 11.43 | 0.2471 |
| Error | 247,189,783.322 | 26,999,991 | 9.1552 | |||
| Total | 247,189,888 | 29,999,999 | ||||
| IM2_BRB1 | Columns | 62.6033 | 9 | 6.95593 | 6.84 | 0.654 |
| Error | 247,200,721.8967 | 26,999,991 | 9.15559 | |||
| Total | 247,200,784.5 | 29,999,999 |
| SS | df | MS | Chi-sq | Prob>Chi-sq | |
|---|---|---|---|---|---|
| Columns | 1.8583 × 104 | 2 | 9.2914 × 103 | 1.8647 × 104 | 0 |
| Error | 5.9776 × 107 | 59,999,998 | 0.9963 | ||
| Total | 5.9795 × 107 | 89,999,999 | 0.00038417 |
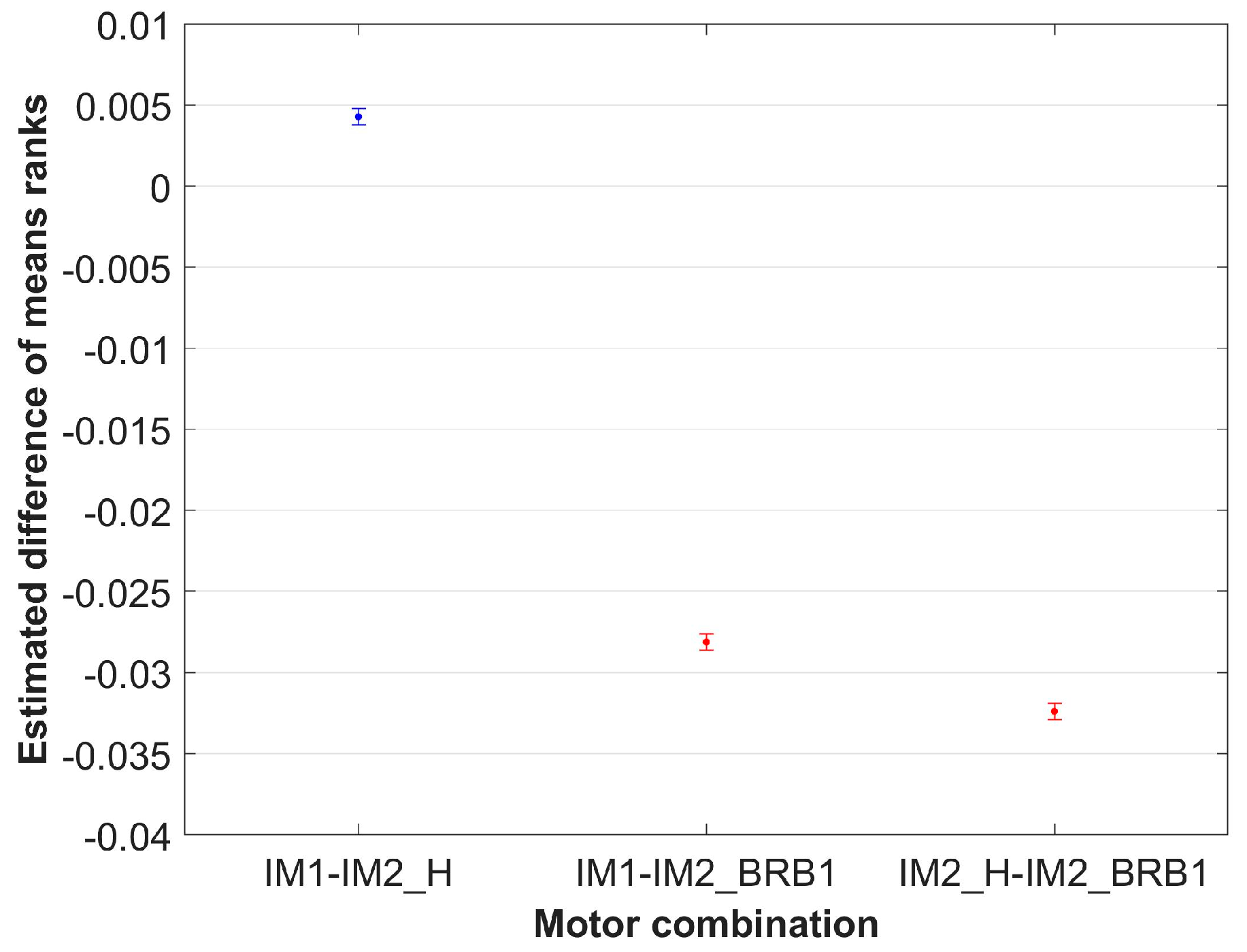
| Motor 1 | Motor 2 | Difference | p-Value | Lower | Upper |
|---|---|---|---|---|---|
| IM1 | IM2_H | 0.0042759 | 8.3828 × 10−62 | 0.0037707 | 0.0047811 |
| IM1 | IM2_BRB1 | −0.028118 | 0 | −0.028623 | −0.027613 |
| IM2_H | IM2_BRB1 | −0.032394 | 0 | −0.032899 | −0.031889 |
| Reference | Motor Combination | Percentage Difference in Estimated Differences in Mean Ranks |
|---|---|---|
| IM1–IM2_H | IM1–IM2_BRB1 | 757.60% |
| IM2_H–IM2_BRB1 | 857.60% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zubčić, M.; Pavić, I.; Matić, P.; Polak, A. Broken Rotor Bar Detection Based on Steady-State Stray Flux Signals Using Triaxial Sensor with Random Positioning. Sensors 2024, 24, 3080. https://doi.org/10.3390/s24103080
Zubčić M, Pavić I, Matić P, Polak A. Broken Rotor Bar Detection Based on Steady-State Stray Flux Signals Using Triaxial Sensor with Random Positioning. Sensors. 2024; 24(10):3080. https://doi.org/10.3390/s24103080
Chicago/Turabian StyleZubčić, Marko, Ivan Pavić, Petar Matić, and Adam Polak. 2024. "Broken Rotor Bar Detection Based on Steady-State Stray Flux Signals Using Triaxial Sensor with Random Positioning" Sensors 24, no. 10: 3080. https://doi.org/10.3390/s24103080
APA StyleZubčić, M., Pavić, I., Matić, P., & Polak, A. (2024). Broken Rotor Bar Detection Based on Steady-State Stray Flux Signals Using Triaxial Sensor with Random Positioning. Sensors, 24(10), 3080. https://doi.org/10.3390/s24103080







