Crossing-Point Estimation in Human–Robot Navigation—Statistical Linearization versus Sigma-Point Transformation
Abstract
:1. Introduction
- An investigation of uncertainties of possible intersection areas originating from sensor noise or system uncertainties.
- A direct and inverse transformation of the error variables at the intersection areas for two input variables (orientation angles) and two output variables (intersection coordinates).
- An extension of the method from two to six input variables (two orientation angles and four position coordinates).
- An exploration of the formulations of fuzzy versions.
- A formulation of the problem by the sigma-point transformation and corresponding comparison of the two methods.
- The statistical linearization, which linearizes the nonlinearity around the operating area at the intersection. The means and standard deviations on the input parameters positions (orientations) are transformed through the linearized nonlinear system to obtain the means and standard deviations of the output parameters (the position of intersection).
- The sigma-point transformation, which calculates the so-called sigma points of the input distribution, including the mean and covariance of the input. The sigma points are directly propagated through the nonlinear system [12,13,14] to obtain the means and covariance of the output and, with this, the standard deviations of the output (the position of intersection). The advantage of the sigma-point transformation is that it captures the first- and second-order statistics of a random variable, whereas the statistical linearization approximates a random variable only by its first order. However, the computational complexity of the extended Kalman filter (EKF, differential approach) and unscented Kalman filter (UKF, sigma-point approach) is of the same order [13].
2. Related Work
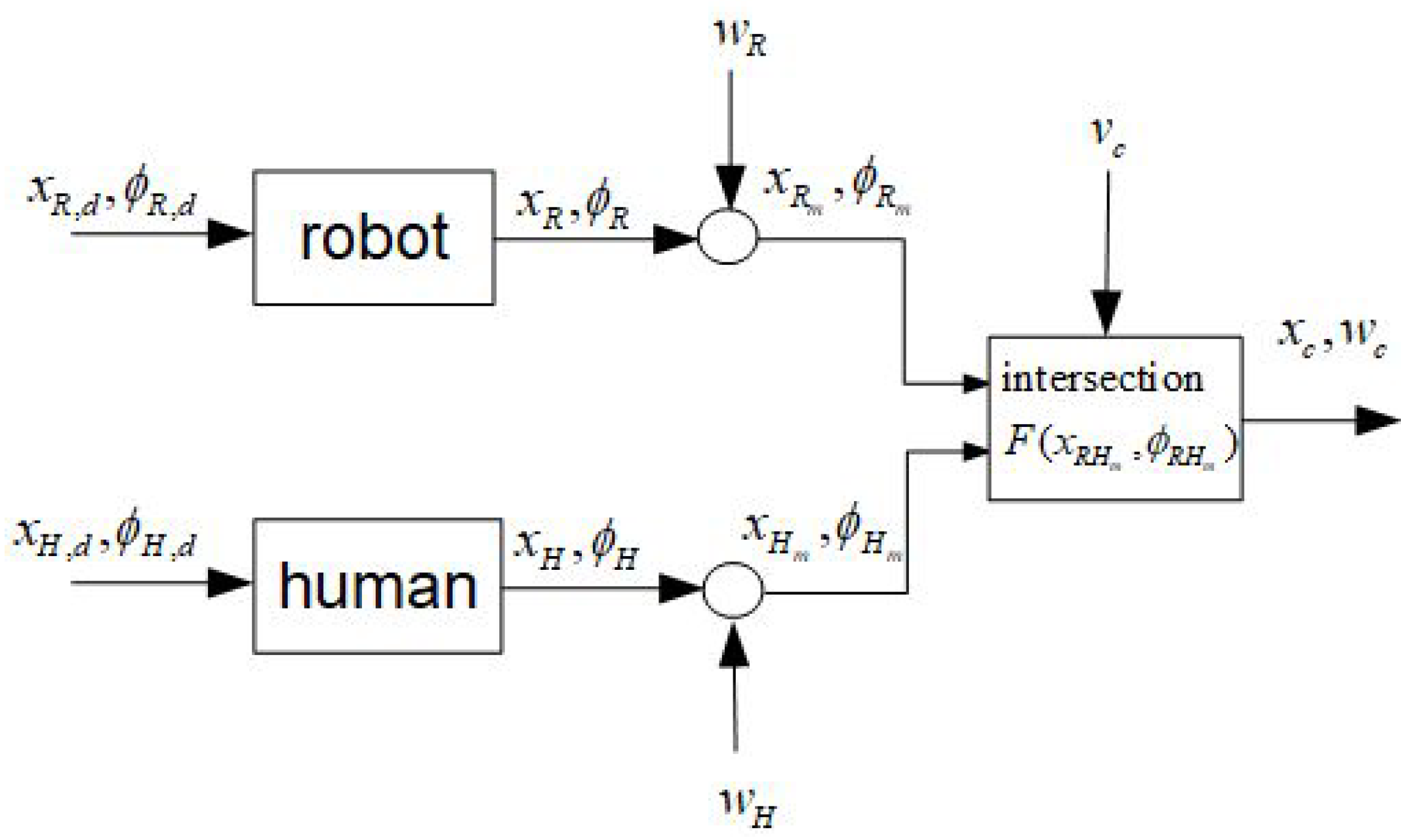
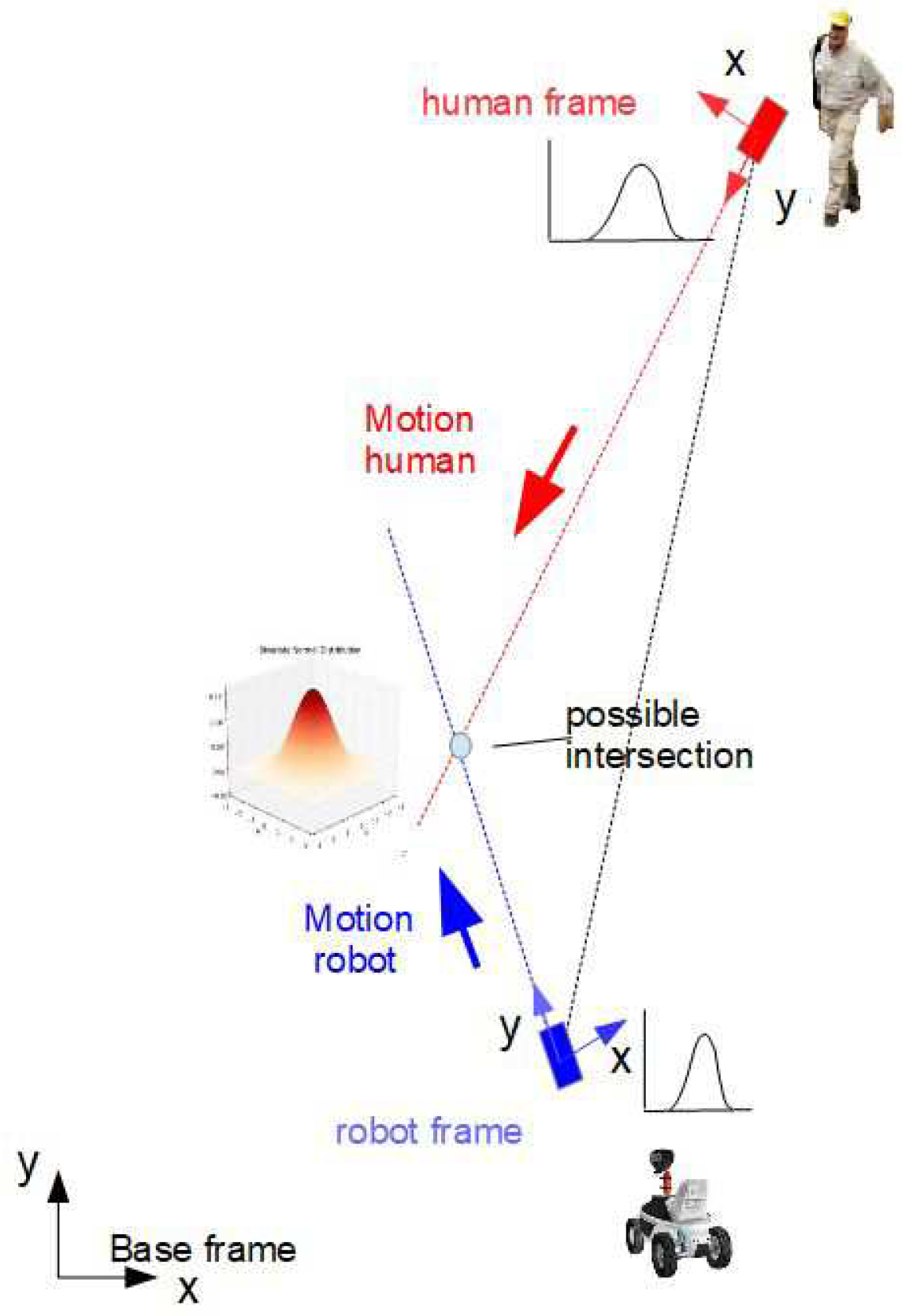
3. Computation of Intersections
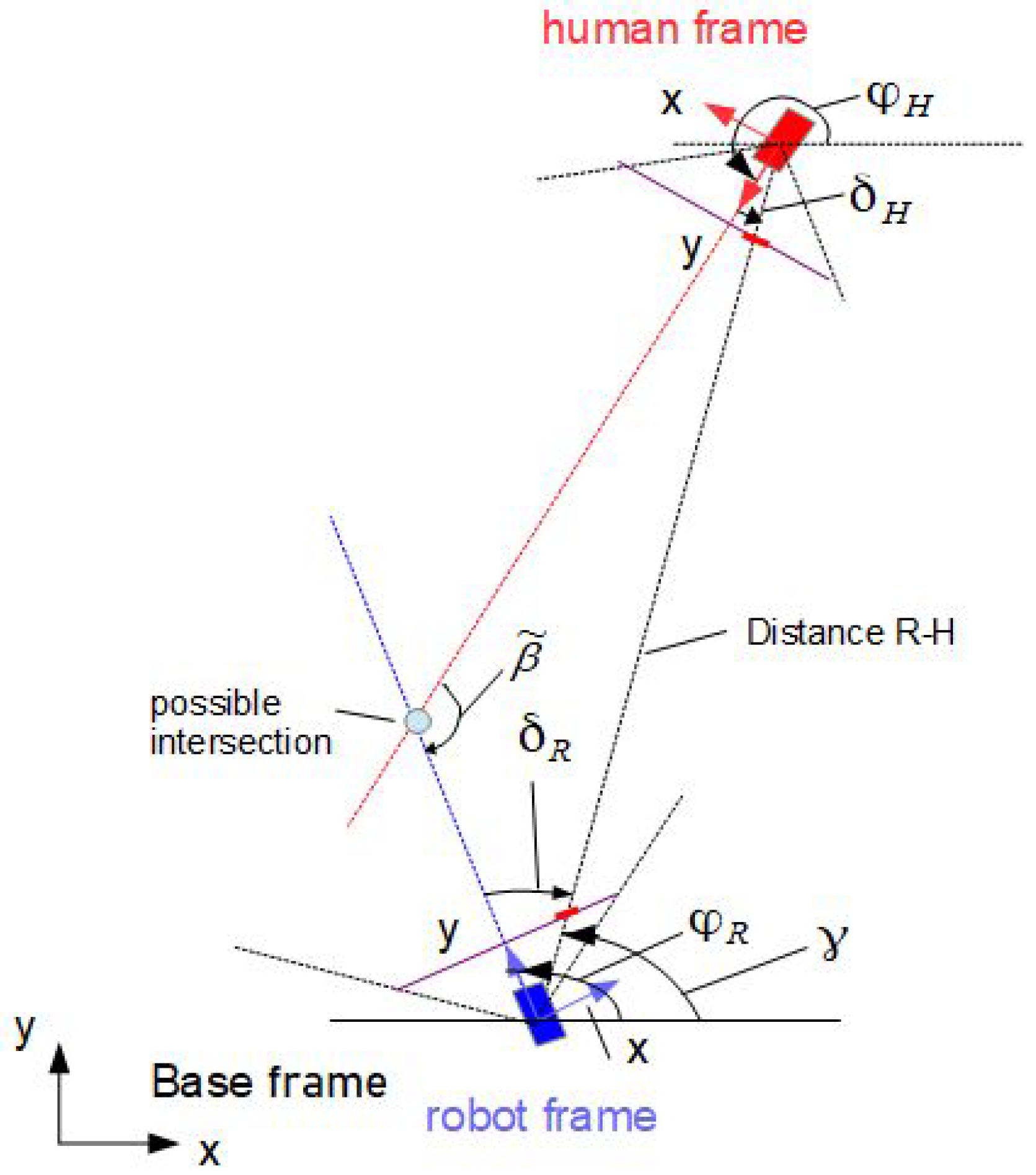
3.1. Geometrical Relations
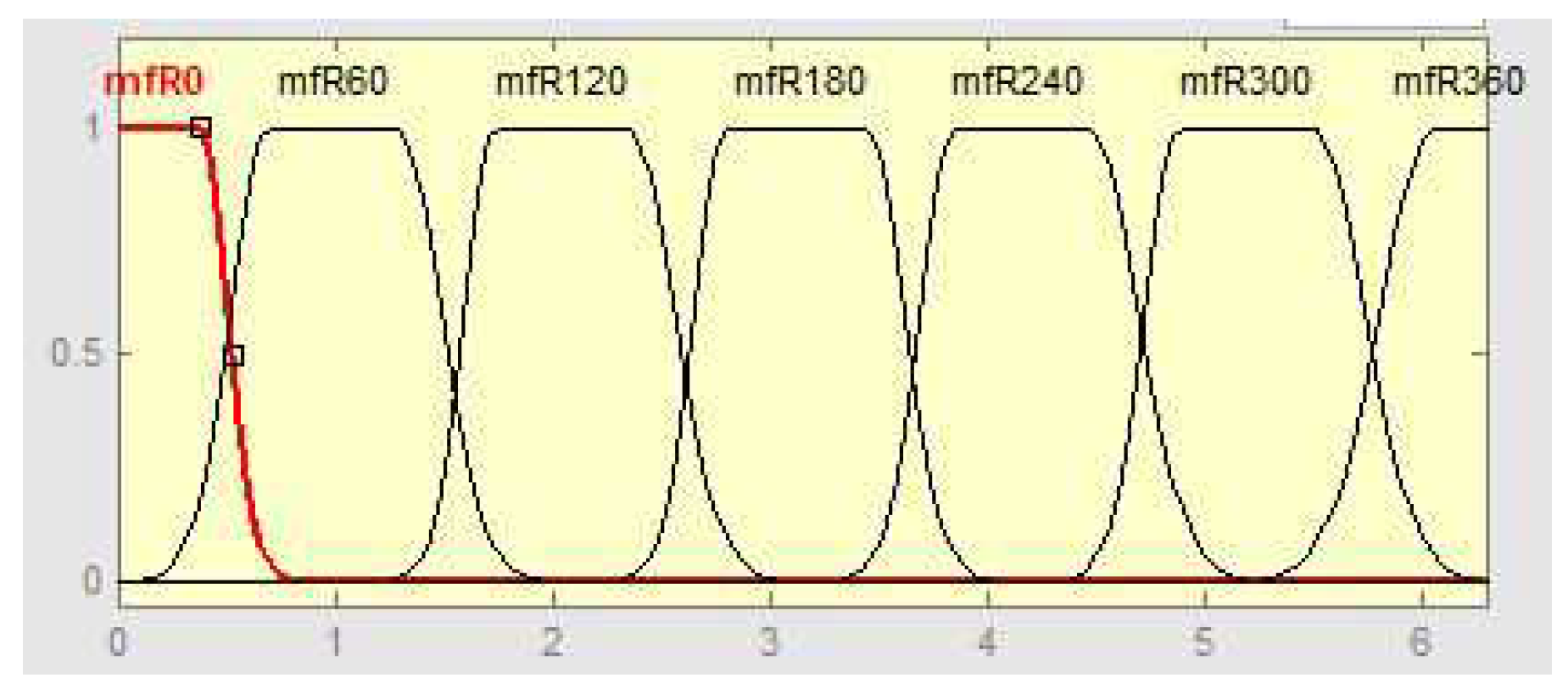
3.2. Computation of Intersections—Fuzzy Approach
3.3. Differential Approach
4. Transformation of Gaussian Distributions
4.1. General Assumptions
4.2. Statistical Linearization, Two Inputs–Two Outputs
4.2.1. Output Distribution
4.2.2. Fuzzy Solution
4.2.3. Inverse Solution
4.3. Six Inputs–Two Outputs
4.3.1. Inverse Solution
4.3.2. Fuzzy Approach
- -
- Define the operation points ;
- -
- Compute , and at from (33);
- -
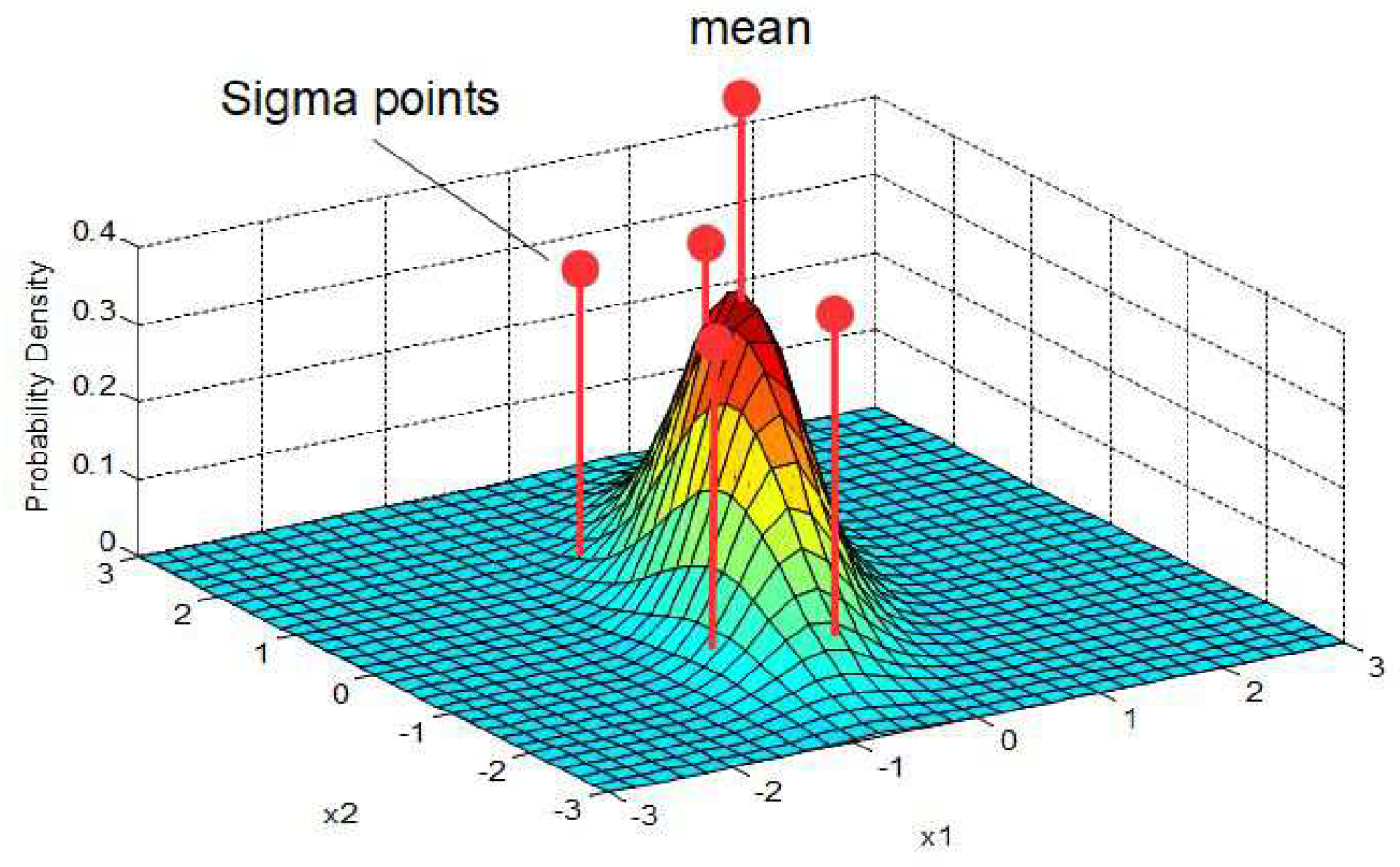
5. Sigma-Point Transformation
- —the mean at time ;
- —the covariance matrix;
- —the initial state with the known mean ;
- .
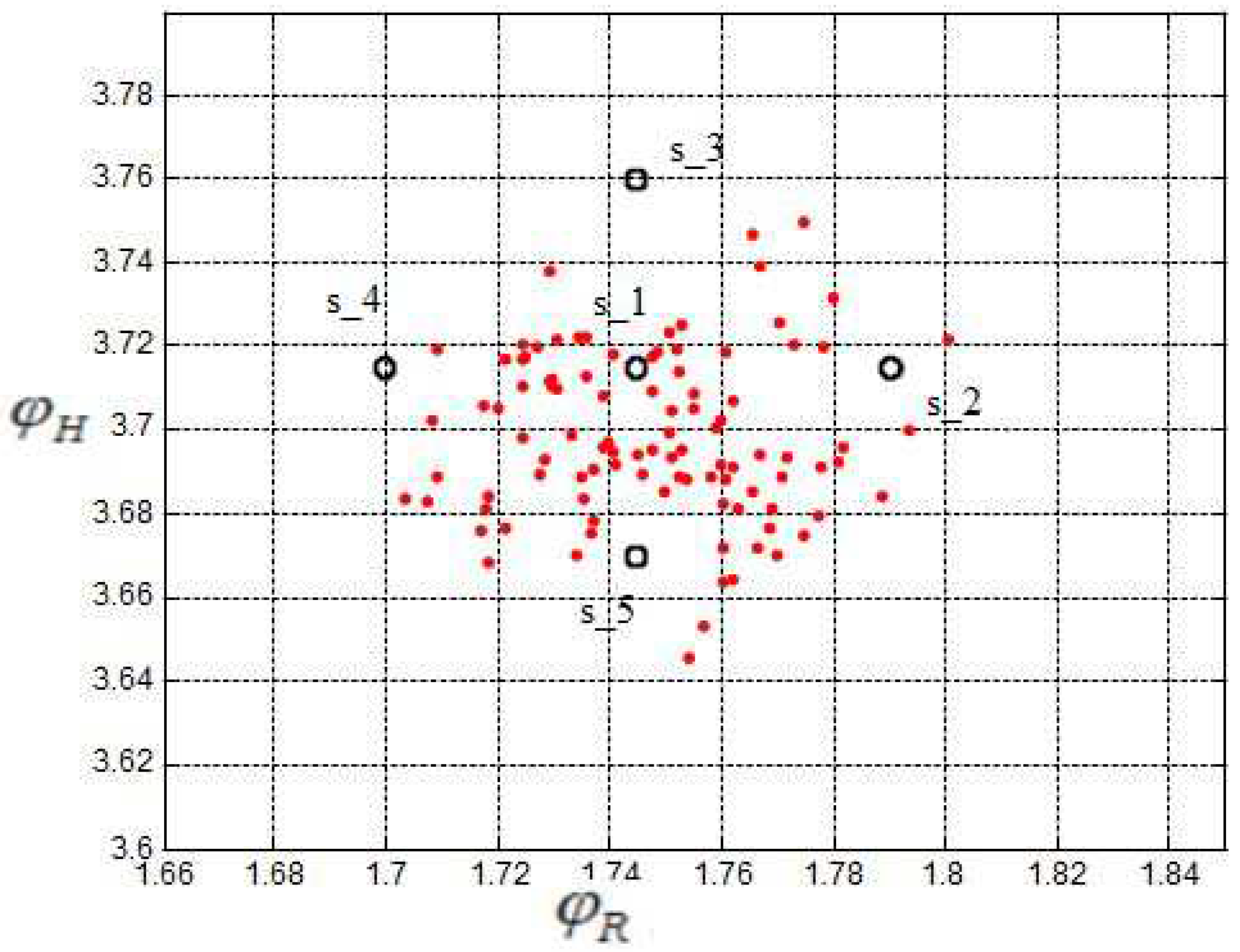
5.1. Selection of Sigma Points
5.2. Model Forecast Step
5.3. Measurement Update Step
5.4. Data Assimilation Step
- The 2 inputs, 2 outputs (2 orientation angles and 2 crossing coordinates);
- The 6 inputs, 2 outputs (2 orientation angles and 4 position coordinates, and 2 crossing coordinates).
5.5. Sigma Points—Fuzzy Solutions
5.6. Inverse Solution
5.7. Six-Inputs–Two-Outputs
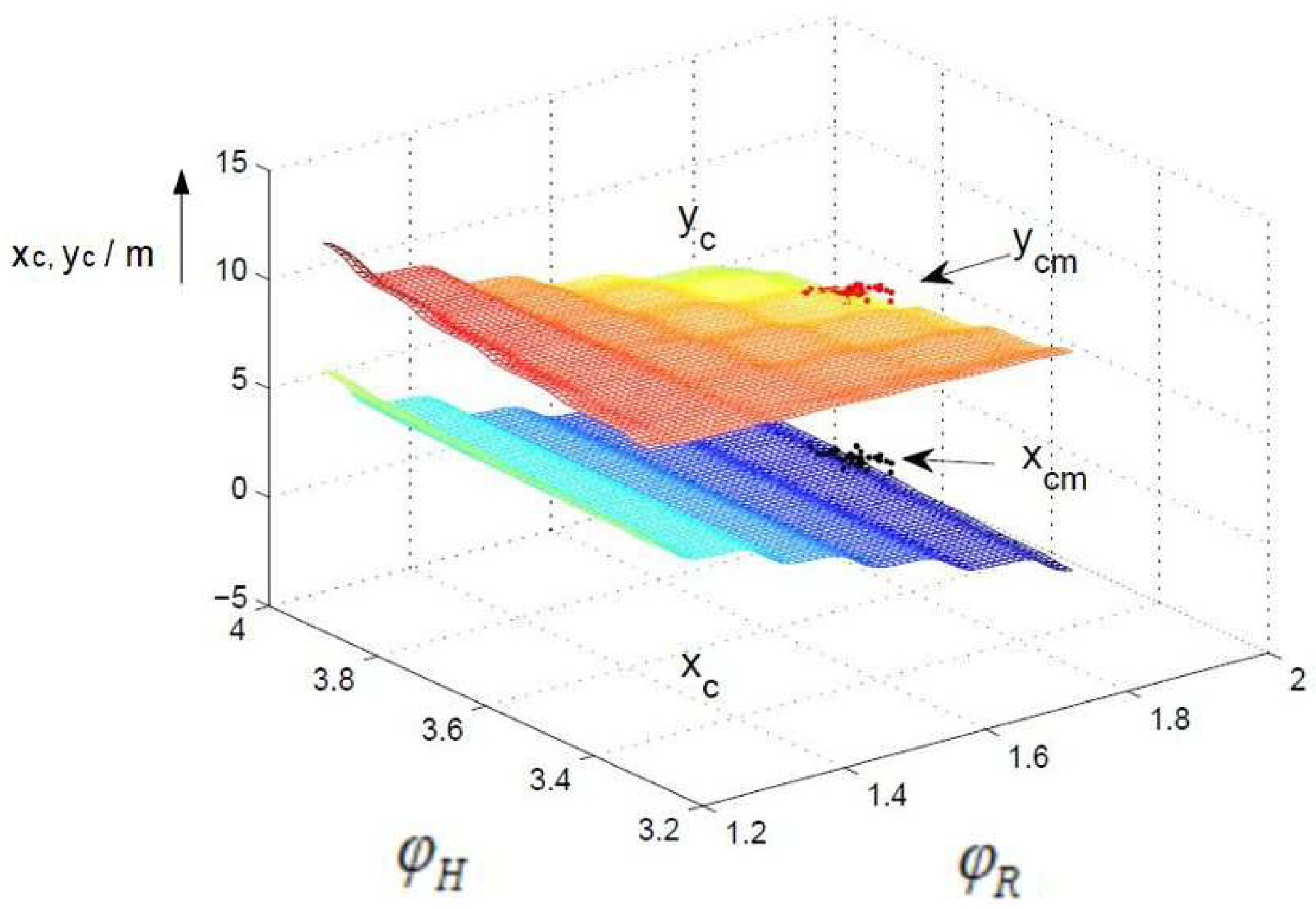
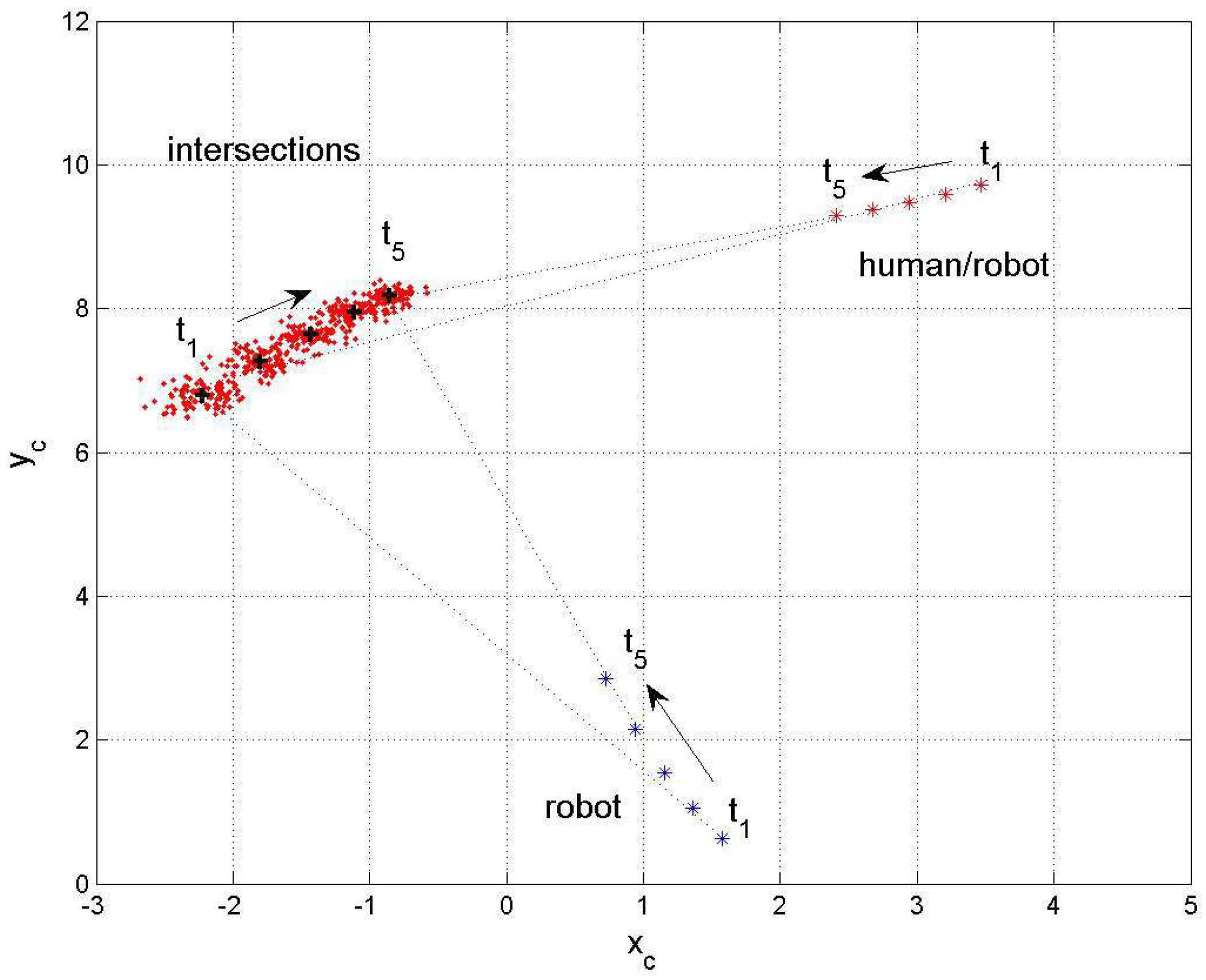
6. Simulation Results
- m;
- m;
- rad = 102°;
- rad = 212°.
- and are corrupted by Gaussian noise with standard deviations (std) of rad, , and rad, .
6.1. Statistical Linearization
6.2. Sigma-Point Method
- m
- m
- with the velocities
- m/s;
- m/s;
- m/s;
- m/s.
- k is the time step.

- rad;
- rad.
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, St. Louis, MI, USA, 25–28 March 1985; p. 500505. [Google Scholar]
- Firl, J. Probabilistic Maneuver Recognition in Traffic Scenarios. Ph.D. Thesis, KIT Karlsruhe Institute of Technology, Karlsruhe, Germany, 2014. [Google Scholar]
- Luo, W.; Xing, J.; Milan, A.; Zhang, X.; Liu, W.; Zhao, X.; Kim, T. Multiple object tracking: A literature review. Artif. Intell. 2021, 293, 103448. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Chou, C. Multiple target tracking in occlusion area with interacting object models in urban environments. Robot. Auton. Syst. 2018, 103, 68–82. [Google Scholar] [CrossRef]
- Kassner, M.; Patera, W.; Bulling, A. Pupil: An open source platform for pervasive eye tracking and mobile gaze-based interaction. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, DC, USA, 13–17 September 2014; pp. 1151–1160. [Google Scholar]
- Bruce, J.; Wawer, J.; Vaughan, R. Human-robot rendezvous by co-operative trajectory signals. In Proceedings of the 10th ACM/IEEE International Conference on Human-Robot Interaction Workshop on Human-Robot Teaming, Portland, OR, USA, 2–5 March 2015; pp. 1–2. [Google Scholar]
- Kunwar, F.; Benhabib, B. Advanced predictive guidance navigation for mobile robots: A novel strategy for rendezvous in dynamic settings. Intern. J. Smart Sens. Intell. Syst. 2008, 1, 858–890. [Google Scholar] [CrossRef]
- Palm, R.; Lilienthal, A. Fuzzy logic and control in human-robot systems: Geometrical and kinematic considerations. In Proceedings of the WCCI 2018: 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 827–834. [Google Scholar]
- Palm, R.; Driankov, D. Fuzzy inputs. In Fuzzy Sets and Systems—Special Issue on Modern Fuzzy Control; IEEE: Piscataway, NJ, USA, 1994; pp. 315–335. [Google Scholar]
- Foulloy, L.; Galichet, S. Fuzzy control with fuzzy inputs. IEEE Trans. Fuzzy Syst. 2003, 11, 437–449. [Google Scholar] [CrossRef]
- Banelli, P. Non-linear transformations of gaussians and gaussian-mixtures with implications on estimation and information theory. IEEE Trans. Inf. Theory 2013. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Merwe, R.v.d.; Wan, E.; Julier, S.J. Sigma-point kalman filters for nonlinear estimation and sensor-fusion: Applications to integrated navigation. In Proceedings of the AIAA 2004, Guidance, Navigation and Control Conference, Portland, OR, USA, 28 June–1 July 2004. [Google Scholar]
- Terejanu, G.A. Unscented Kalman Filter Tutorial; Department of Computer Science and Engineering University at Buffalo: Buffalo, NY, USA, 2011. [Google Scholar]
- Odry, Á.; Kecskes, I.; Sarcevic, P.; Vizvari, Z.; Toth, A.; Odry, P. A novel fuzzy-adaptive extended kalman filter for real-time attitude estimation of mobile robots. Sensors 2020, 20, 803. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Song, Y.; Li, Q. Robust iterated sigma point fastslam algorithm for mobile robot simultaneous localization and mapping. Chin. J. Mech. Eng. 2011, 24, 693. [Google Scholar] [CrossRef]
- Bittler, J.; Bhounsule, P.A. Hybrid unscented kalman filter: Application to the simplest walker. In Proceedings of the 3rd Modeling, Estimation and Control Conference MECC, Lake Tahoe, NV, USA, 2–5 October 2023. [Google Scholar]
- Alireza, S.D.; Shahri, M. Vision based simultaneous localization and mapping using sigma point kalman filter. In Proceedings of the 2011 IEEE International Symposium on Robotic and Sensors Environments (ROSE), Montreal, QC, Canada, 17–18 September 2011. [Google Scholar]
- Xue, Z.; Schwartz, H. A comparison of several nonlinear filters for mobile robot pose estimation. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation (ICMA), Kagawa, Japan, 4–7 August 2013. [Google Scholar]
- Lyu, Y.; Pan, Q.; Lv, J. Unscented transformation-based multi-robot collaborative self-localization and distributed target tracking. Appl. Sci. 2019, 9, 903. [Google Scholar] [CrossRef]
- Raitoharju, M.; Piche, R. On computational complexity reduction methods for kalman filter extensions. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 2–19. [Google Scholar] [CrossRef]
- Palm, R.; Lilienthal, A. Uncertainty and fuzzy modeling in human-robot navigation. In Proceedings of the 11th Joint International Computer Conference (IJCCI 2019), Vienna, Austria, 17–19 September 2019; pp. 296–305. [Google Scholar]
- Palm, R.; Lilienthal, A. Fuzzy geometric approach to collision estimation under gaussian noise in human-robot interaction. In Proceedings of the Computational Intelligence: 11th International Joint Conference, IJCCI 2019, Vienna, Austria, 17–19 September 2019; Springer: Cham, Switzerland; pp. 191–221. [Google Scholar]
- Schaefer, J.; Strimmer, K. A shrinkage to large scale covariance matrix estimation and implications for functional genomics. Stat. Appl. Genet. Mol. Biol. 2005, 4, 32. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y. Learning the Unscented Kalman Filter. 2021. Available online: https://www.mathworks.com/matlabcentral/fileexchange/18217-learning-the-unscented-kalman-filter (accessed on 14 May 2024).





| Input Std | 0.02 Gauss, Bell Shaped (GB) | Gauss | 0.05 GB | |||
|---|---|---|---|---|---|---|
| sector size/° | ||||||
| non-fuzz | 0.143 | 0.140 | 0.138 | 0.125 | 0.144 | 0.366 |
| fuzz | 0.220 | 0.184 | 0.140 | 0.126 | 0.144 | 0.367 |
| non-fuzz | 0.160 | 0.144 | 0.138 | 0.126 | 0.142 | 0.368 |
| fuzz | 0.555 | 0.224 | 0.061 | 0.225 | 0.164 | 0.381 |
| non-fuzz | 0.128 | 0.132 | 0.123 | 0.114 | 0.124 | 0.303 |
| fuzz | 0.092 | 0.087 | 0.120 | 0.112 | 0.122 | 0.299 |
| non-fuzz | 0.134 | 0.120 | 0.123 | 0.113 | 0.129 | 0.310 |
| fuzz | 0.599 | 0.171 | 0.034 | 0.154 | 0.139 | 0.325 |
| non-fuzz | 0.576 | 0.541 | 0.588 | 0.561 | 0.623 | 0.669 |
| fuzz | −0.263 | 0.272 | 0.478 | 0.506 | 0.592 | 0.592 |
| non-fuzz | 0.572 | 0.459 | 0.586 | 0.549 | 0.660 | 0.667 |
| fuzz | 0.380 | 0.575 | 0.990 | 0.711 | 0.635 | 0.592 |
| Outputs | Covariance, Computed | Covariance, Measured | , Comp/Meas | , Comp/Meas |
|---|---|---|---|---|
| 2 inputs | ||||
| 2 inputs, stat. lin. | - | - | ||
| 6 inputs | ||||
| Direct solution | ||||
| Inverse solution |
| Outputs | Covariance, Computed | Covariance, Measured | , Comp/Meas | , Comp/Meas |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palm, R.; Lilienthal, A.J. Crossing-Point Estimation in Human–Robot Navigation—Statistical Linearization versus Sigma-Point Transformation. Sensors 2024, 24, 3303. https://doi.org/10.3390/s24113303
Palm R, Lilienthal AJ. Crossing-Point Estimation in Human–Robot Navigation—Statistical Linearization versus Sigma-Point Transformation. Sensors. 2024; 24(11):3303. https://doi.org/10.3390/s24113303
Chicago/Turabian StylePalm, Rainer, and Achim J. Lilienthal. 2024. "Crossing-Point Estimation in Human–Robot Navigation—Statistical Linearization versus Sigma-Point Transformation" Sensors 24, no. 11: 3303. https://doi.org/10.3390/s24113303
APA StylePalm, R., & Lilienthal, A. J. (2024). Crossing-Point Estimation in Human–Robot Navigation—Statistical Linearization versus Sigma-Point Transformation. Sensors, 24(11), 3303. https://doi.org/10.3390/s24113303







