Development of a Method for Soil Tilth Quality Evaluation from Crumbling Roller Baskets Using Deep Machine Learning Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Site Description
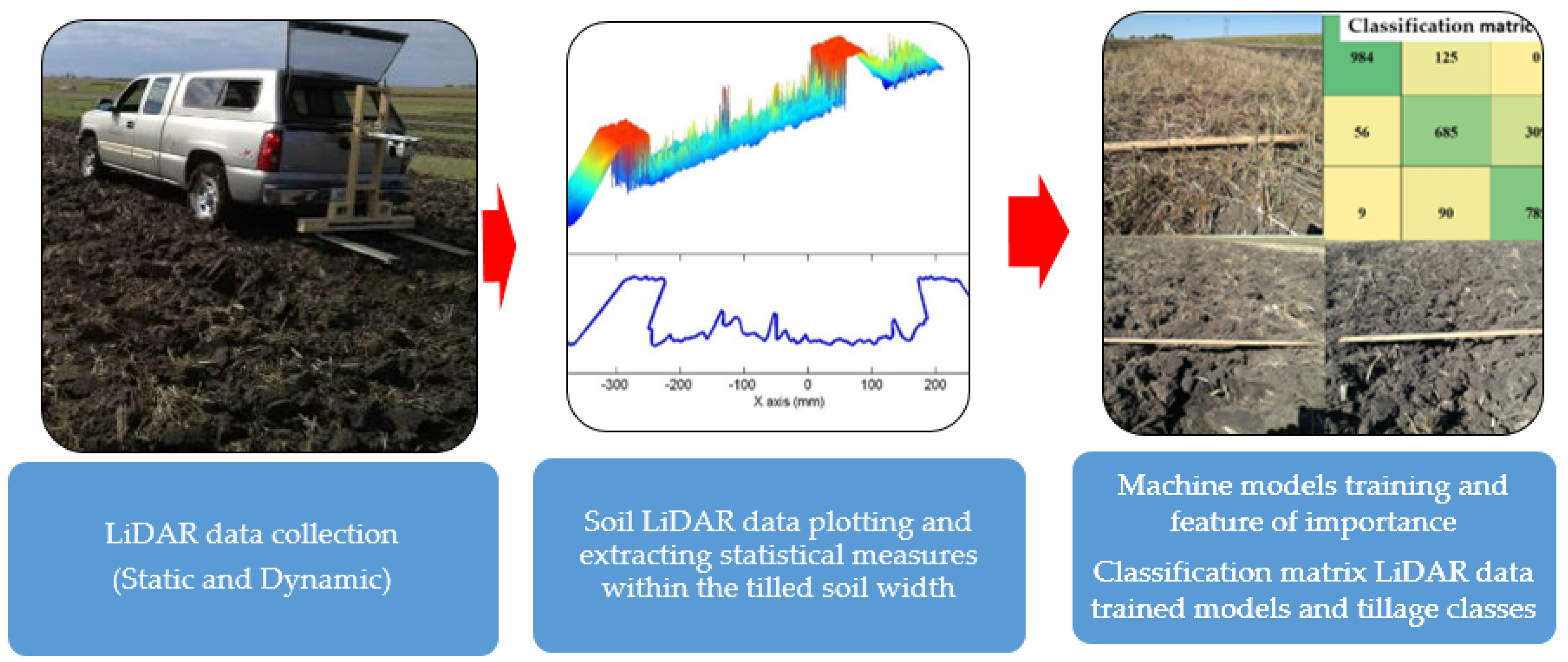
2.2. Data Collection Using Light Detection and Ranging (LiDAR) Unit
2.3. Soil Surface Profile LiDAR Data Analysis
2.4. Statistical Analysis Using Machine Learning Techniques
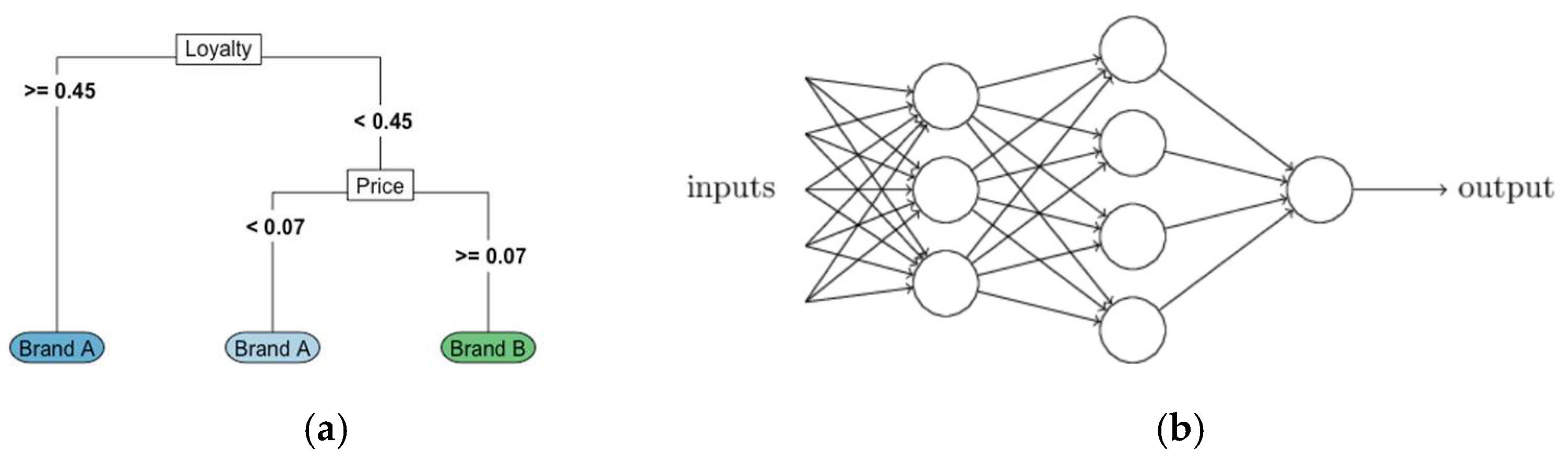
2.4.1. RF Machine Learning Method
2.4.2. SVM Machine Learning Method
2.4.3. NN Machine Learning Method
2.5. VI Soil Surface Machine Learning
3. Results
3.1. Evaluating the Fitness of the Three-Machine Learning Method
Two-Tailed Tests, Permutation Test, Kruskal–Wallis and Analysis of Variance (ANOVA) for the High-Importance Feature Measures
3.2. Discriminatory Analysis
4. Discussion
5. Conclusions
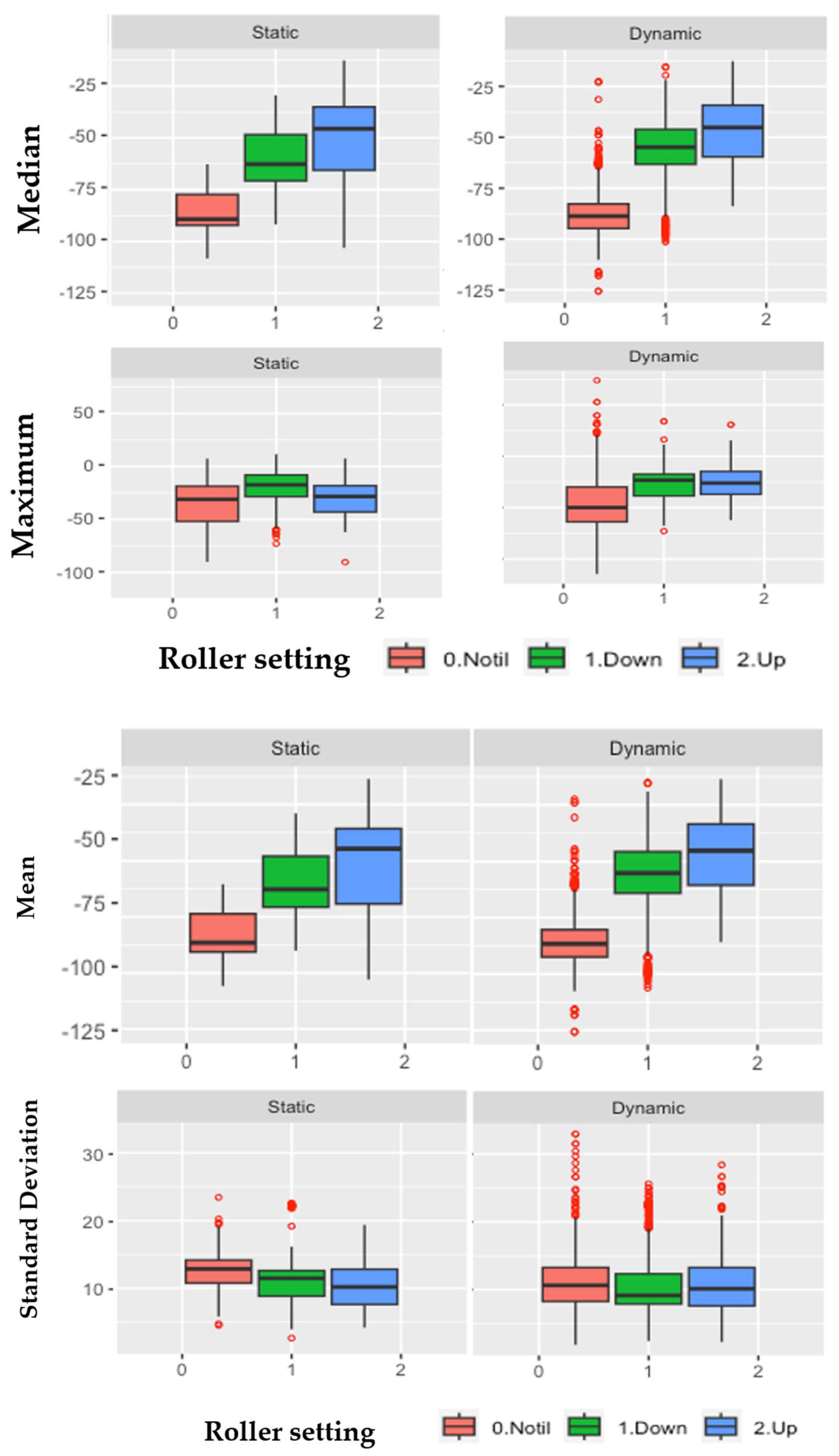
- Machine learning methods were successfully used to evaluate soil tillage quality soil profiles as a function of basket roller pressure settings of disk-ripper-roller baskets on clay loam soil. Three machine learning models (SVM, NN, and RF) were used to select statistical measures of median, mean, maximum, and standard deviation as the top four important features and varied statistically significant by the three roller settings.
- The roller basket down setting induced by applying the maximum hydraulic pressure exerted on disk-ripper soil created more uniform soil tilth characteristics, as quantified by median, mean, maximum, and standard deviation LiDAR soil profiles as compared to soil tilth created from roller basket up. The baseline reference of no-till (crop residue surfaces) without tillage was statistically different from the two soil profiles of the two basket roller settings.
- A comparison of LiDAR data collection using static (stop-go) and dynamic (on-the-go) methods appeared to show a similar classification of the tilled soil tilth after applying the machine learning models and discrimination analysis, with the data from the dynamic LiDAR data set creating higher standard deviation and outliers.
- The proposed machine learning analysis techniques from static and dynamic LiDAR soil data sets can further integrate digitalized soil tilth classes into an operator control display for manual or automated adjustment of roller basket settings from disk-ripper-roller basket tillage passes of combination tillage implements.
- Further research could be helpful in evaluating the proposed techniques for comparing tillage operations of various primary and secondary tillage implements and soil tilth classified trained using machine learning on crop growth and crop yield effects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sewell, M.C. Tillage: A Review of the Literature. J. Am. Soc. Agron. 1919, 2, 269–290. [Google Scholar] [CrossRef]
- Gill, W.R.; Vanden Berg, G.E. Soil Dynamics in Tillage and Traction, Handbook 316; Agricultural Research Service, U.S. Department of Agriculture: Washington, DC, USA, 1968.
- Raper, R.L.; Reeves, D.W.; Burmester, C.H.; Schwab, E.B. Tillage depth, tillage timing, and cover crop effects on cotton yield, soil strength, and tillage energy requirements. Appl. Eng. Agric. 2000, 16, 379–385. [Google Scholar] [CrossRef]
- Karlen, D.L.; Cynthia, A.; Cambardella, J.L.K.; Colvin, T.S. Soil quality response to long-term tillage and crop rotation practices. Soil Tillage Res. 2013, 133, 54–64. [Google Scholar] [CrossRef]
- ASAE S414.2, SAE S414.2 MAR2009 (R2023); Terminology and Definitions for Agricultural Tillage Implements. ASAE: St. Joseph, MI, USA, 2018.
- Colvin, T.S.; Erbach, D.C.; Buchele, W.F.; Cruse, R.M. Tillage index based on created soil conditions. Trans. ASAE 1984, 27, 370–371. [Google Scholar] [CrossRef]
- Karlen, D.L.; Erbach, D.C.; Kaspar, T.C.; Colvin, T.S.; Berry, E.C.; Timmons, D.R. Soil tilth: A review of past perceptions and future needs. Soil Sci. Soc. Am. J. 1990, 54, 153–161. [Google Scholar] [CrossRef]
- Ball, B.C.; Guimarães, R.M.L.; Cloy, J.M.; Hargreaves, P.R.; Shepherd, T.G.; McKenzie, B.M. Visual soil evaluation: A summary of some applications and potential developments for agriculture. Soil Tillage Res. 2017, 173, 114–124. [Google Scholar] [CrossRef]
- Singh, K.K.; Colvin, T.S.; Erbach, D.C.; Mughal, A.Q. Tilth index: An approach to quantifying soil tilth. Trans. ASAE 1992, 35, 1777–1785. [Google Scholar] [CrossRef]
- Adam, K.M.; Erbach, D.C. Secondary Tillage Tool Effect on Soil Aggregation. Trans. ASAE 1992, 35, 1771–1779. [Google Scholar] [CrossRef]
- Bogrekci, I.; Godwin, R.J. Development of an image-processing technique for soil tilth sensing. Biosyst. Eng. 2007, 97, 323–331. [Google Scholar] [CrossRef]
- Fanigliulo, R.; Antonucci, F.; Figorilli, S.; Pock, D.; Pallottino, F.; Fornaciari, L.; Grilli, R.; Costa, C. Light Drone-Based Application to Assess Soil Tillage Quality Parameters. Sensors 2020, 20, 728. [Google Scholar] [CrossRef] [PubMed]
- Model, L.M.; Thomsen, J.E.; Baartman, M.; Barneveld, R.J.; Starkloff, T.; Stolte, J. Soil surface roughness: Comparing old and new measuring methods and application in a soil erosion. Soil 2015, 1, 399–410. [Google Scholar] [CrossRef]
- Gee, G.W.; Bauder, J.W. Particle-Size Analysis in Methods of Soil Analysis, Part 1, Monograph 9, 2nd ed.; American Society of Agronomy: Madison, WI, USA, 1986. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon and organic matter, Part-3 Methods of soil analysis. In Chemical Method, 1st ed.; American Society of Agronomy: Madison, WI, USA, 1996. [Google Scholar]
- D4318-10; Standard Test Method for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. ASTM International: West Conshohocken, PA, USA, 2010.
- Ghorbani, S. Simulation of Soil-to-Tool Interaction Using Discrete Element Method (DEM) and Multibody Dynamics (MBD) Coupling. Ph.D. Thesis, Iowa State University, Ames, IO, USA, 2019. Available online: https://www.proquest.com/docview/2242967820?pqorigsite=gscholar&fromopenview=true&sourcetype=Dissertations%20&%20Theses (accessed on 24 January 2024).
- Tonietto, L.; Veronez, M.R.; Kazmierczak, C.S.; Arnold, D.C.M.; Costa, C.A. New Method for Evaluating Surface Roughness Parameters Acquired by Laser Scanning. Sci. Rep. 2019, 9, 15038. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Krauss, C.; Do, X.A.; Huck, N. Deep neural networks, gradient-boosted trees, random forests: Statistical arbitrage on the S&P 500. Eur. J. Oper. Res. 2017, 259, 689–702. [Google Scholar]
- Wu, X.; Kumar, V. The Top Ten Algorithms in Data Mining; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Zwillinger, D.; Kokoska, S. CRC Standard Probability and Statistics Tables and Formulae; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Iqbal, M.; Marley, S.J.; Erbach, D.C.; Kaspar, T.C. An Evaluation of Seed Furrow Smearing. Trans. ASAE 1998, 41, 1243–1248. [Google Scholar] [CrossRef]
- Hoogmoed, W.B.; Cadena-Zapata, M.; Perdok, U.D. Laboratory assessment of the workable range of soils in the tropical zone of Veracruz, Mexico. Soil Tillage Res. 2003, 74, 169–178. [Google Scholar] [CrossRef]
- Gholamy, A.; Kreinovich, V.; Kosheleva, O. Why 70/30 or 80/20 Relation Between Training and Testing Sets: A Pedagogical Explanation. 2018. Departmental Technical Reports (CS). 1209. Available online: https://scholarworks.utep.edu/cs_techrep/1209 (accessed on 1 May 2024).
- Vân Anh Huynh-Thu, Y.S.; Wehenkel, L.; Geurts, P. Statistical interpretation of machine learning-based feature importance scores for biomarker discovery. Bioinformatics 2012, 28, 1766–1774. [Google Scholar] [CrossRef] [PubMed]

| Percent Particle Size (%) 1 (Std) | Soil Moisture Content (%, d.b.) (Std) | Organic Matter 2 (%) (Std) | PL, Wp 3 (d.b., %) | LL, WL 3 (d.b., %) | ||||
|---|---|---|---|---|---|---|---|---|
| Sand | Silt | Clay | No Till | Roller Basket Up | Roller Basket Down | |||
| 27.5 | 43.3 | 29.2 | 18.68 | 18.32 | 18.06 | 4.7 | 23.2 | 31.9 |
| (2.5) | (3.8) | (1.4) | (1.11) | (0.78) | (0.87) | (0.2) | (1.9) | (0.5) |
| Parameter | SVM | NN | RF |
|---|---|---|---|
| Feature Importance | |||
| Median | 0.231 | 0.228 | 0.224 |
| Mean | 0.137 | 0.199 | 0.219 |
| Maximum | 0.143 | 0.281 | 0.048 |
| Standard deviation | 0.227 | 0.277 | 0.071 |
| Mode | 0.06 | 0.094 | 0.083 |
| Minimum | 0.114 | 0.197 | 0.038 |
| Kurtosis | 0.128 | 0.18 | 0.092 |
| Skewness | 0.128 | 0.18 | 0.092 |
| Roughness Coefficient | 0.083 | 0.178 | 0.039 |
| Parameter | SVM | NN | RF |
|---|---|---|---|
| Feature Importance | |||
| Median | 0.155 | 0.251 | 0.164 |
| Mean | 0.193 | 0.198 | 0.204 |
| Maximum | 0.095 | 0.158 | 0.089 |
| Standard deviation | 0.120 | 0.142 | 0.081 |
| Mode | 0.074 | 0.267 | 0.084 |
| Minimum | 0.021 | 0.025 | 0.108 |
| Kurtosis | 0.055 | 0.120 | 0.109 |
| Skewness | 0.182 | 0.167 | 0.108 |
| Roughness coefficient | 0.07 | 0.043 | 0.053 |
| Static LiDAR Data Set (a) | ||
| Parameter | Permutation Test | Kruskal–Wallis |
| Median | T = 40.7 (p < 0.0001) | Χ2 = 1746.2 (p < 0.0001) |
| Mean | T = 38.9 (p < 0.0001) | Χ2 = 1585.6 (p < 0.0001) |
| Maximum | T = 10.43 (p < 0.0001) | Χ2 = 117.17 (p < 0.0001) |
| Standard deviation | T = 13.25 (p < 0.0001) | Χ2 = 291.16 (p < 0.0001) |
| Dynamic LiDAR Data Set (b) | ||
| Parameter | Permutation Test | Kruskal–Wallis |
| Median | T = 40 (p < 0.0001) | Χ2 = 1625.6 (p < 0.0001) |
| Mean | T = 38 (p < 0.0001) | Χ2 = 1551.2 (p < 0.0001) |
| Maximum | T = 22.6 (p < 0.0001) | Χ2 = 488.4 (p < 0.0001)) |
| Standard deviation | T = 2.4291 (p = 0.04) | Χ2 = 18.025 (p = 0.0001) |
| Static LiDAR Data Set (a) | ||||
| Median (Std) (mm) | Mean (Std) (mm) | Maximum (Std) (mm) | Standard Deviation (Std) (mm) | |
| Basket down | −57.37 (12.62) | −57.14 (13.00) | −24.02 (17.14) | 11.04 (3.97) |
| Basket up | −50.18 (15.52) | −51.29 (16.49) | −30.81 (15.05) | 10.46 (3.19) |
| Dynamic LiDAR Data Set (b) | ||||
| Median (Std) (mm) | Mean (Std) (mm) | Maximum (Std) (mm) | Standard Deviation (Std) (mm) | |
| Basket down | −55.29 (14.42) | −55.22 (15.05) | −27.33 (15.10) | 11.14 (5.27) |
| Basket up | −46.37 (15.29) | −46.86 (15.43) | −24.98 (15.34) | 10.73 (3.94) |
| No till | −87.21 (12.57) | −85.31 (12.57) | −45.28 (25.50) | 11.22 (4.43) |
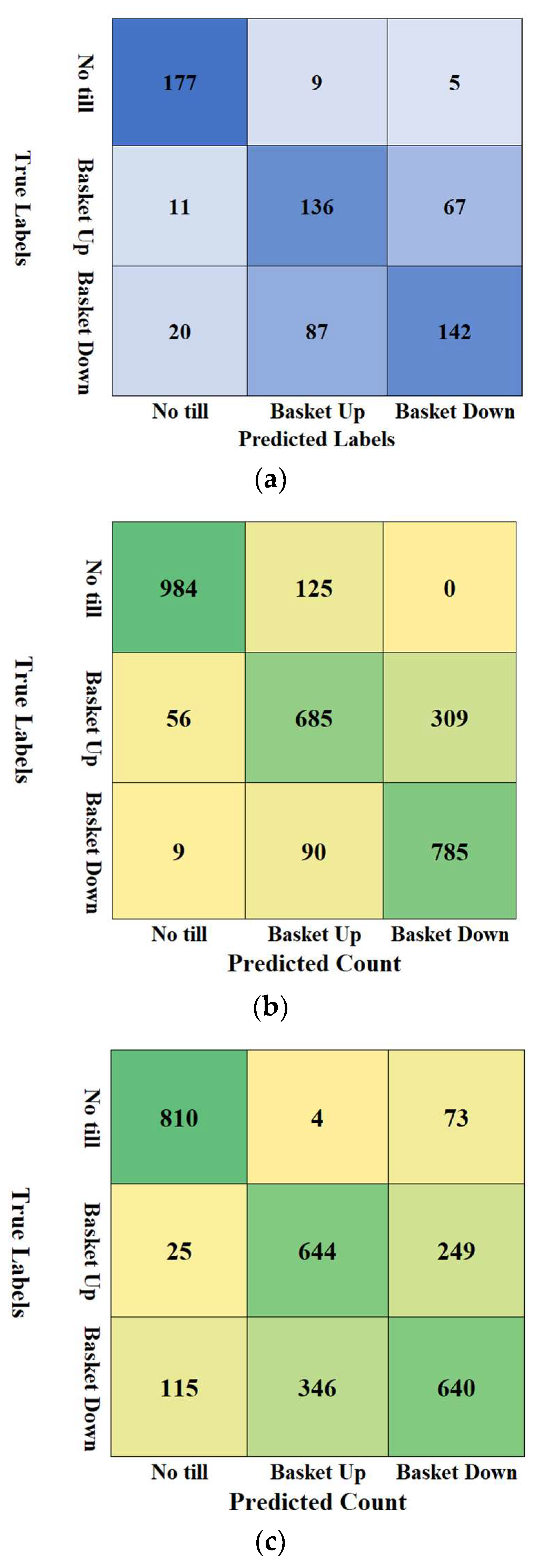
| Visible Imaging Analysis (a) | ||||
| Predicted Labels | ||||
| No till | Basket Up | Basket Down | ||
| True Labels | No till | 92.67% | 4.71% | 2.62% |
| Basket Up | 5.14% | 63.55% | 31.31% | |
| Basket Down | 8.03% | 34.94% | 57.03% | |
| Static LiDAR Data Set (b) | ||||
| Predicted Labels | ||||
| No till | Basket Up | Basket Down | ||
| True Labels | No till | 88.73% | 11.27% | 0.00% |
| Basket Up | 5.33% | 65.24% | 29.43% | |
| Basket Down | 1.02% | 10.18% | 88.80% | |
| Dynamic LiDAR Data Set (c) | ||||
| Predicted Labels | ||||
| No till | Basket Up | Basket Down | ||
| True Labels | No till | 91.32% | 0.45% | 8.23% |
| Basket Up | 2.72% | 70.15% | 27.12% | |
| Basket Down | 10.45% | 31.43% | 58.13% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tekeste, M.Z.; Guo, J.; Habtezgi, D.; He, J.-H.; Waz, M. Development of a Method for Soil Tilth Quality Evaluation from Crumbling Roller Baskets Using Deep Machine Learning Models. Sensors 2024, 24, 3379. https://doi.org/10.3390/s24113379
Tekeste MZ, Guo J, Habtezgi D, He J-H, Waz M. Development of a Method for Soil Tilth Quality Evaluation from Crumbling Roller Baskets Using Deep Machine Learning Models. Sensors. 2024; 24(11):3379. https://doi.org/10.3390/s24113379
Chicago/Turabian StyleTekeste, Mehari Z., Junxian Guo, Desale Habtezgi, Jia-Hao He, and Marcin Waz. 2024. "Development of a Method for Soil Tilth Quality Evaluation from Crumbling Roller Baskets Using Deep Machine Learning Models" Sensors 24, no. 11: 3379. https://doi.org/10.3390/s24113379
APA StyleTekeste, M. Z., Guo, J., Habtezgi, D., He, J.-H., & Waz, M. (2024). Development of a Method for Soil Tilth Quality Evaluation from Crumbling Roller Baskets Using Deep Machine Learning Models. Sensors, 24(11), 3379. https://doi.org/10.3390/s24113379






