The Fault Diagnosis of Rolling Bearings Is Conducted by Employing a Dual-Branch Convolutional Capsule Neural Network
Abstract
1. Introduction
2. The Foundational Theory
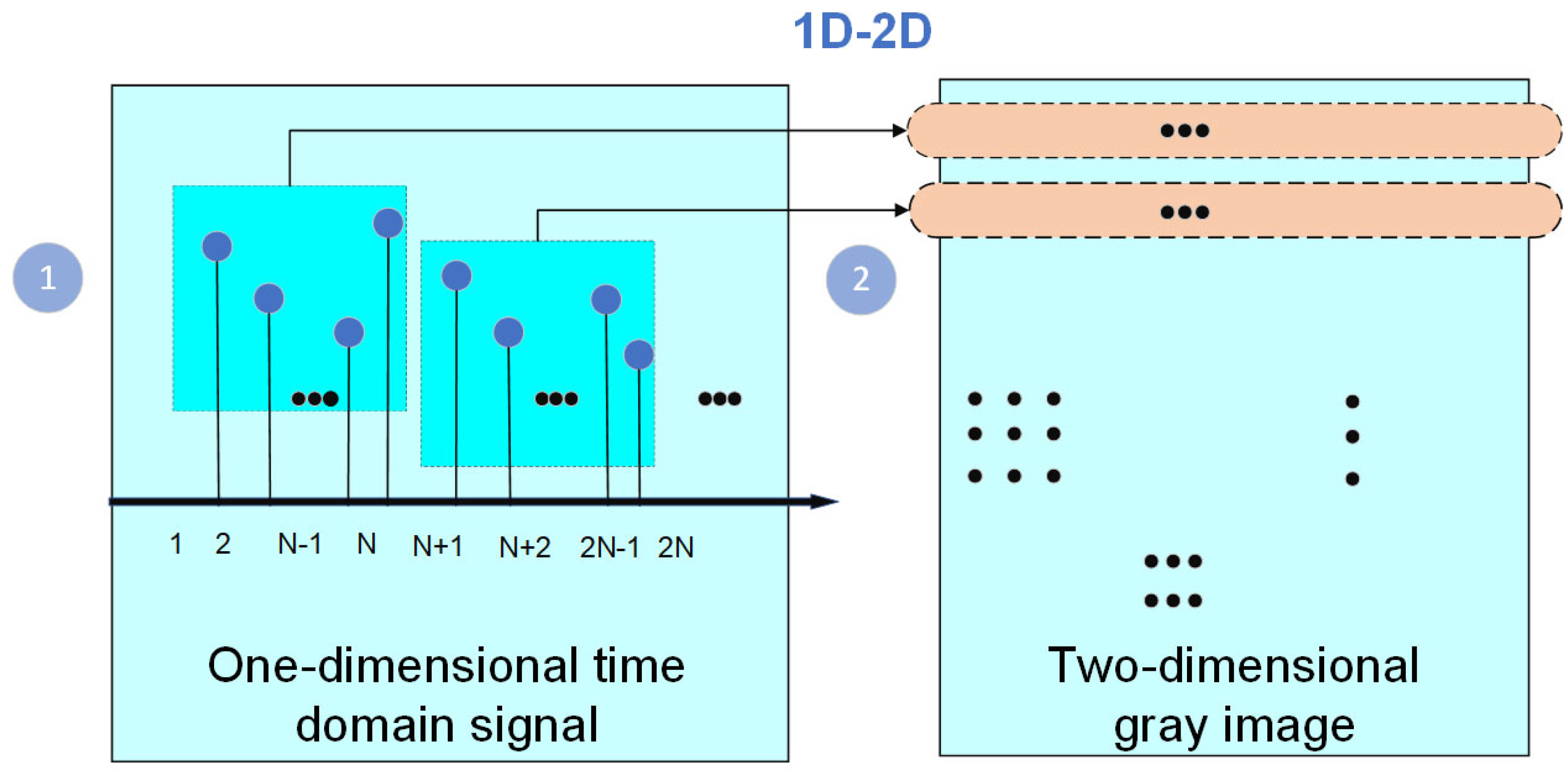
2.1. Preprocessing of Grayscale Images
- Re-scale the one-dimensional temporal signal to ensure its values are normalized within the range of 0 and 1;
- The normalized signal is sampled at fixed time intervals to obtain a discrete temporal signal;
- Employ interpolation techniques to estimate the continuous temporal signal by leveraging the neighboring sampling points;
- Each point on the continuous curve corresponds to a pixel point on the grayscale image. The value of each point on the curve is then converted to the grayscale value of the corresponding pixel by selecting the appropriate grayscale mapping method.
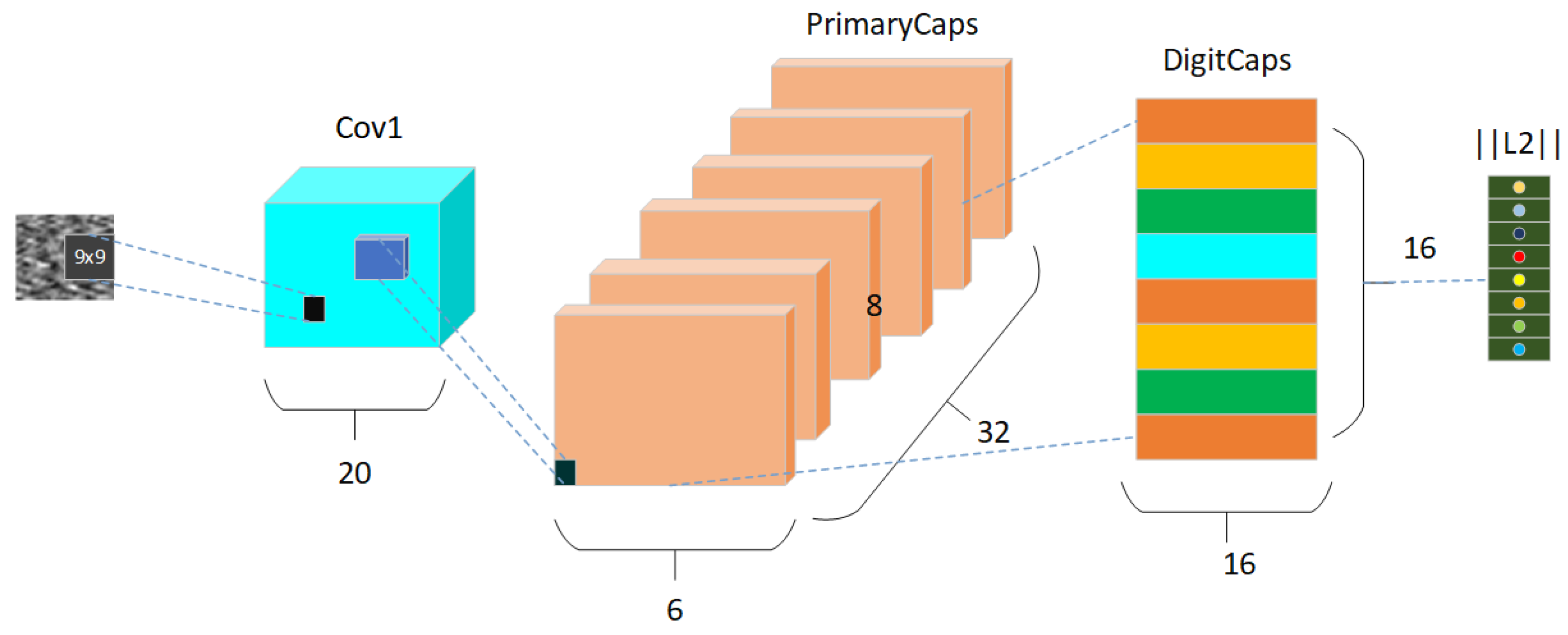
2.2. Capsule Neural Network
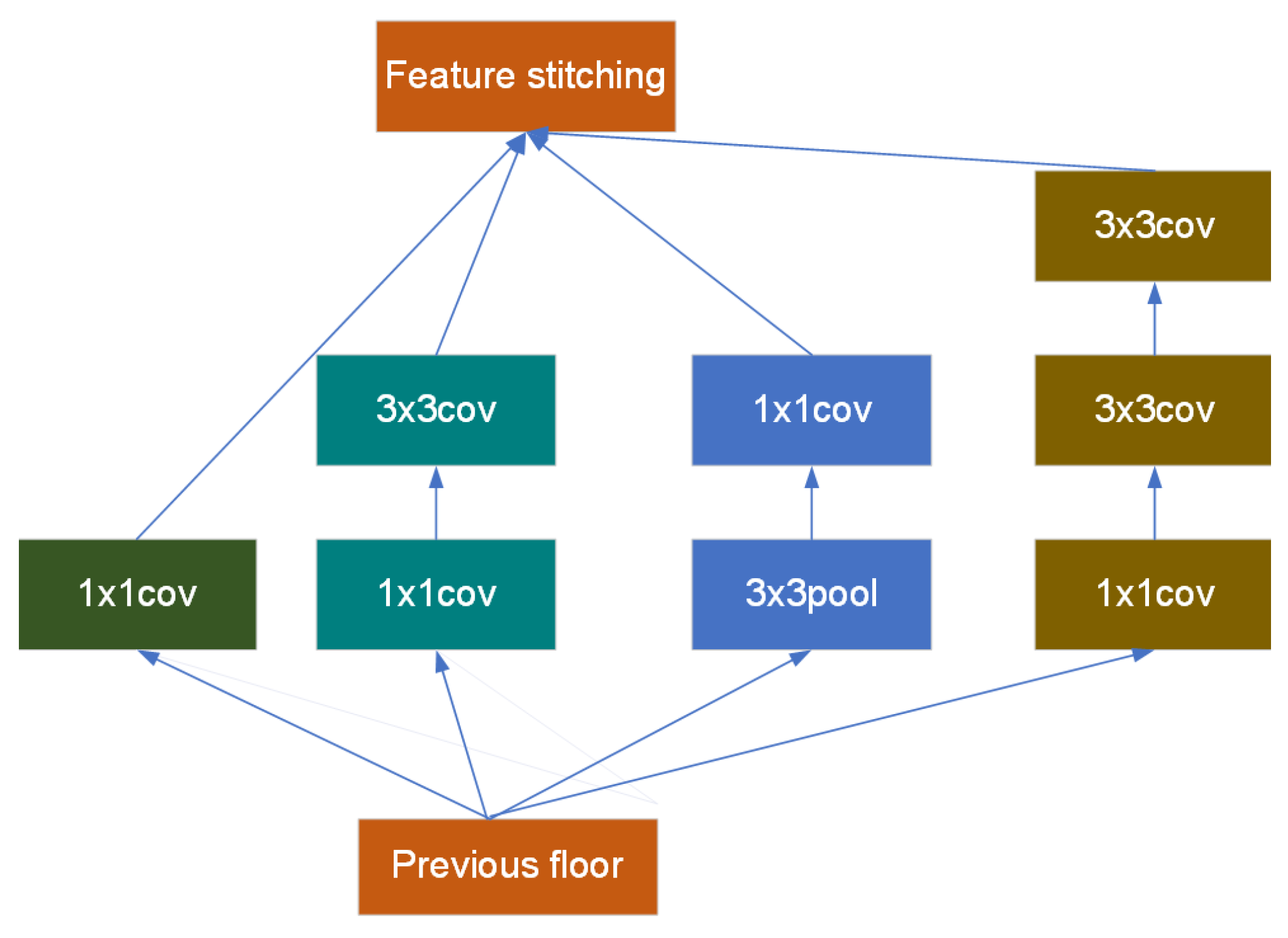
2.3. Inception Module
2.4. The Attention Mechanism in Coordinate Automata (CA)
- The input feature map is globally average pooled in both width and height directions to obtain feature maps in both dimensions;
- The two parallel stages are merged by transposing the width and height onto the same dimension; they are then stacked together to combine their respective features. At this point, we obtain a feature layer of [C, 1, H + W], which undergoes further processing using convolution + normalization + activation functions to extract additional features;
- The merged feature layer is subsequently separated back into two parallel stages: [C, 1, H] and [C, W]. They are obtained through transposition resulting in two separate layers: one with shape [C, H, 1] and another with shape [C, W];
- The number of channels is adjusted by employing 1 × 1 convolution, followed by the application of the sigmoid function to obtain attention weights on the width and height dimensions. These weights are then multiplied with the original features, resulting in the output.
3. An Enhanced Approach for Fault Diagnosis in Capsule Networks
3.1. Development of a Dual-Branch Convolutional Capsule Neural Network for the Diagnosis of Rolling Bearing Faults Model
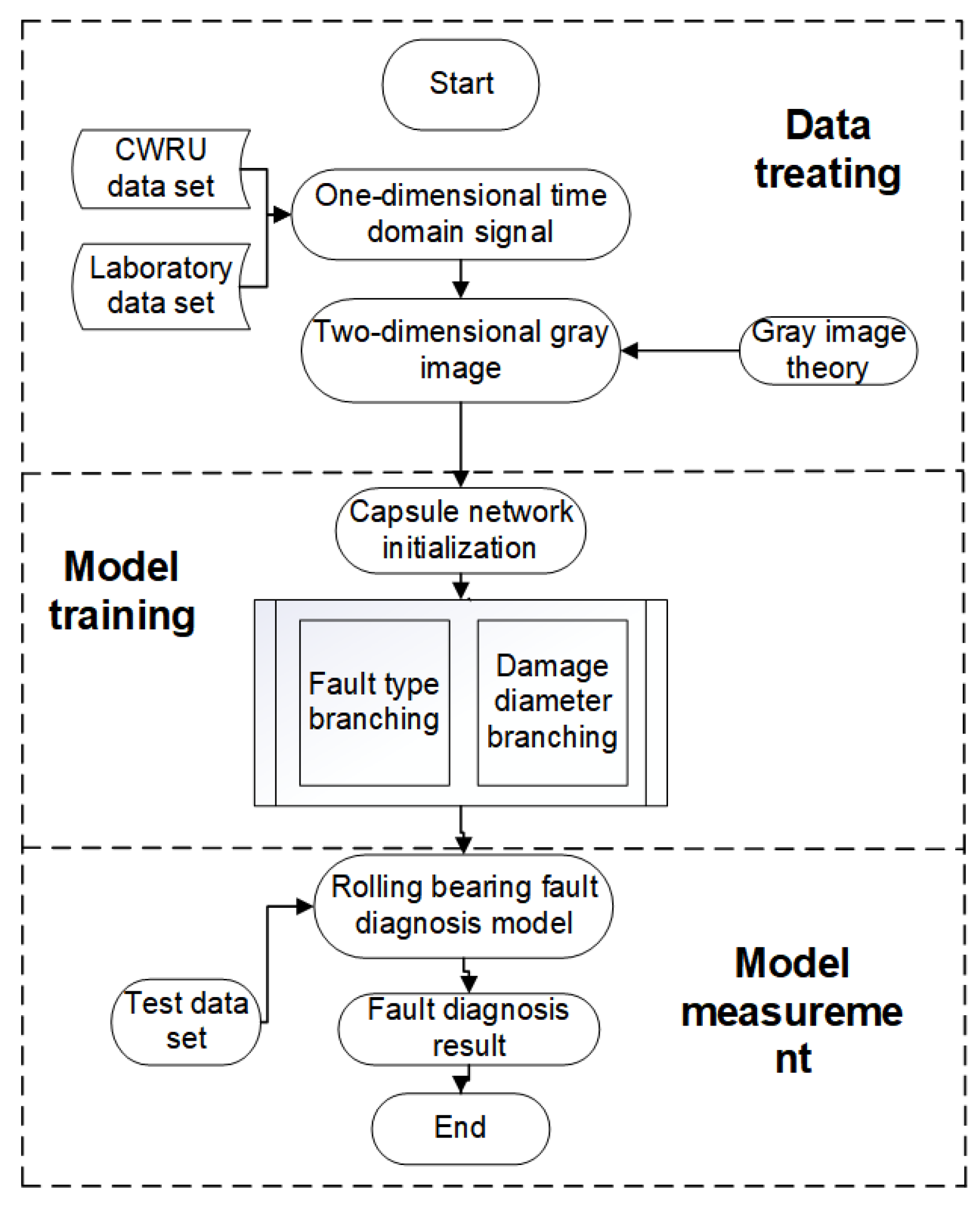
3.2. Process for Diagnosing Faults in Rolling Bearings
4. Experimental Design and Analysis of Results
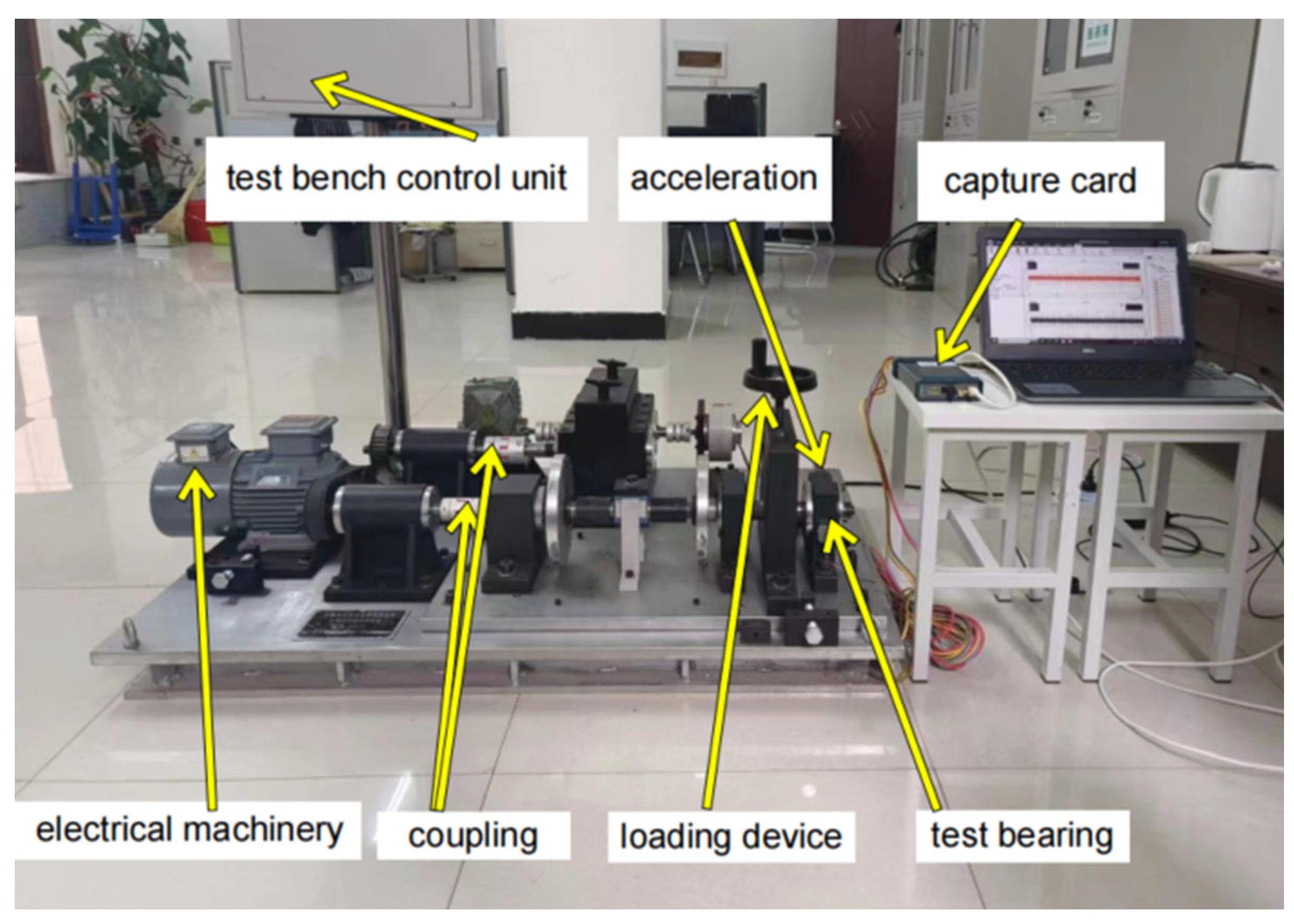
4.1. Establishment of the CWRU Bearing Dataset
4.2. Model Parameter Configuration
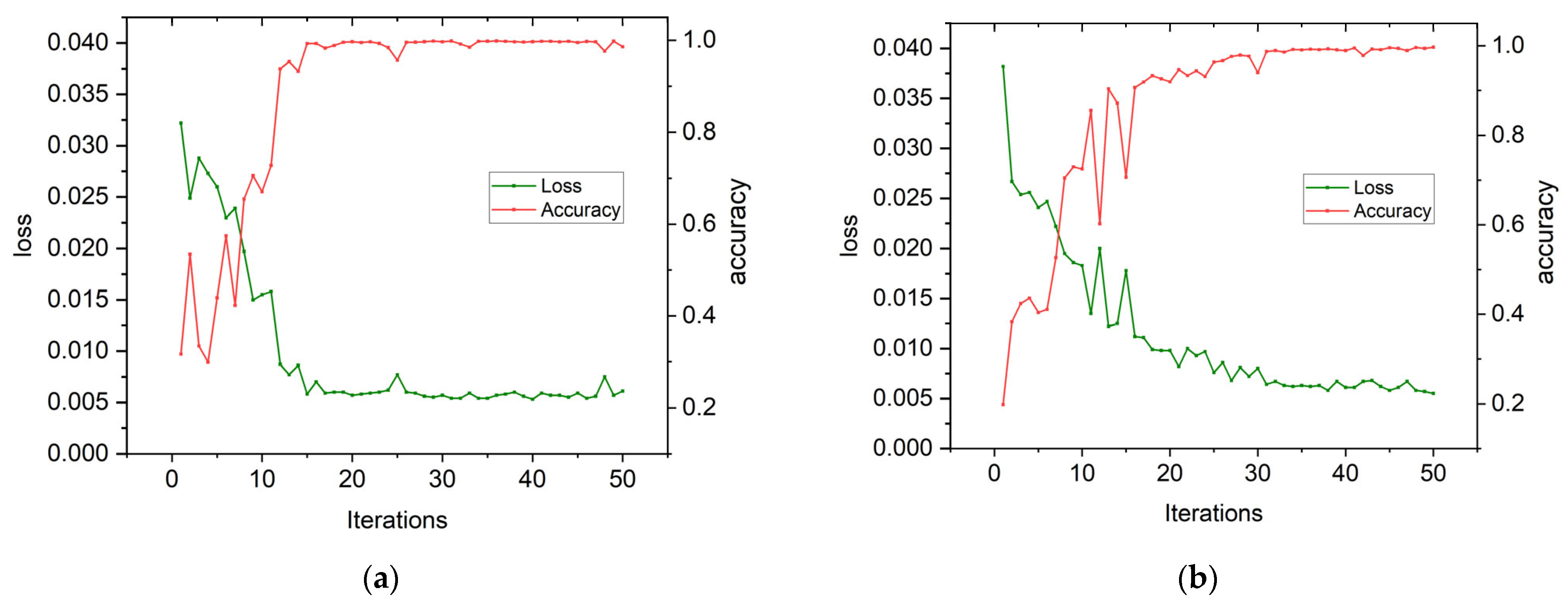
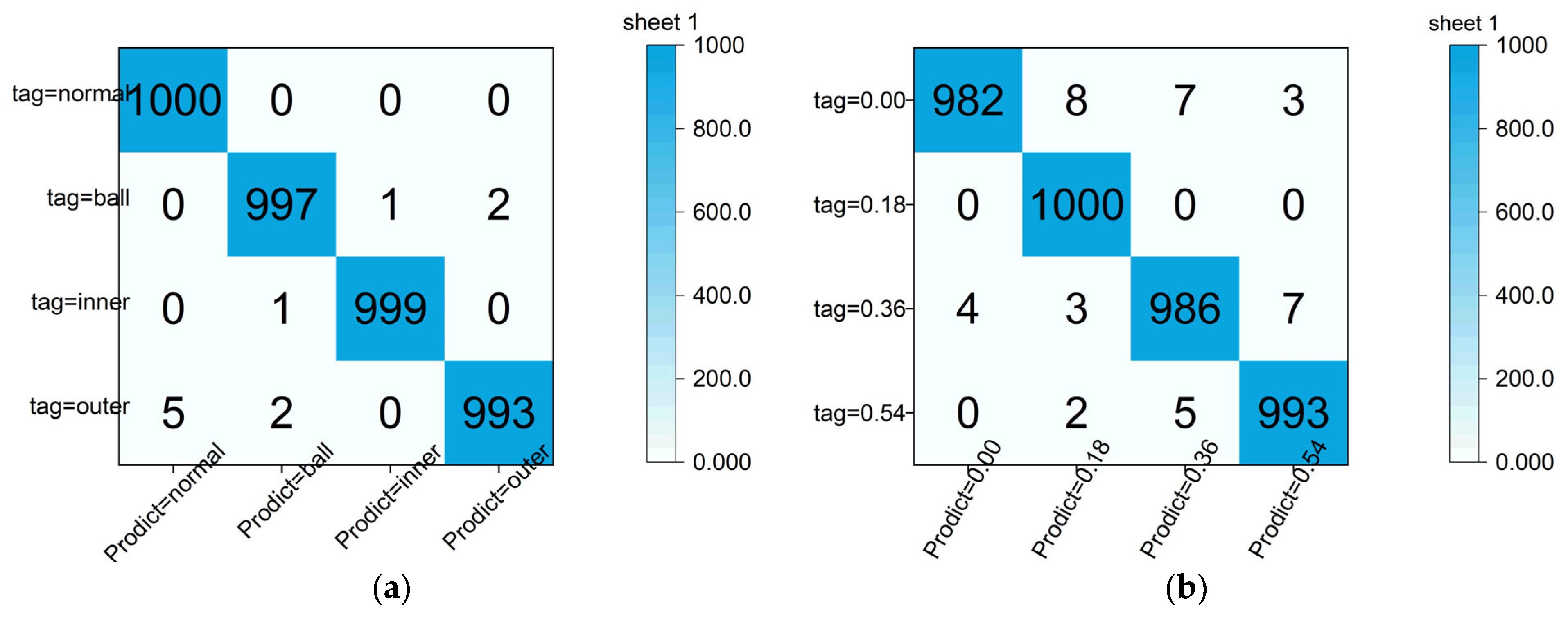
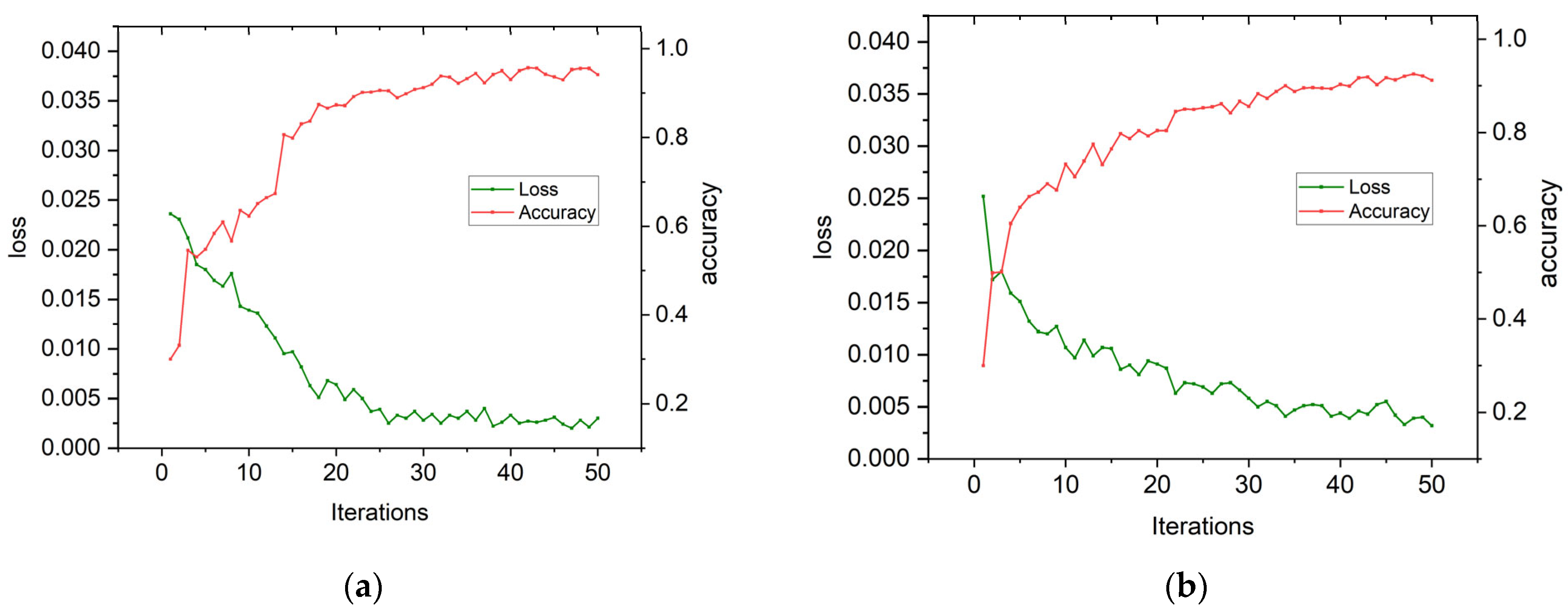
4.3. Analysis of Experimental Results for CWRU Bearing Data
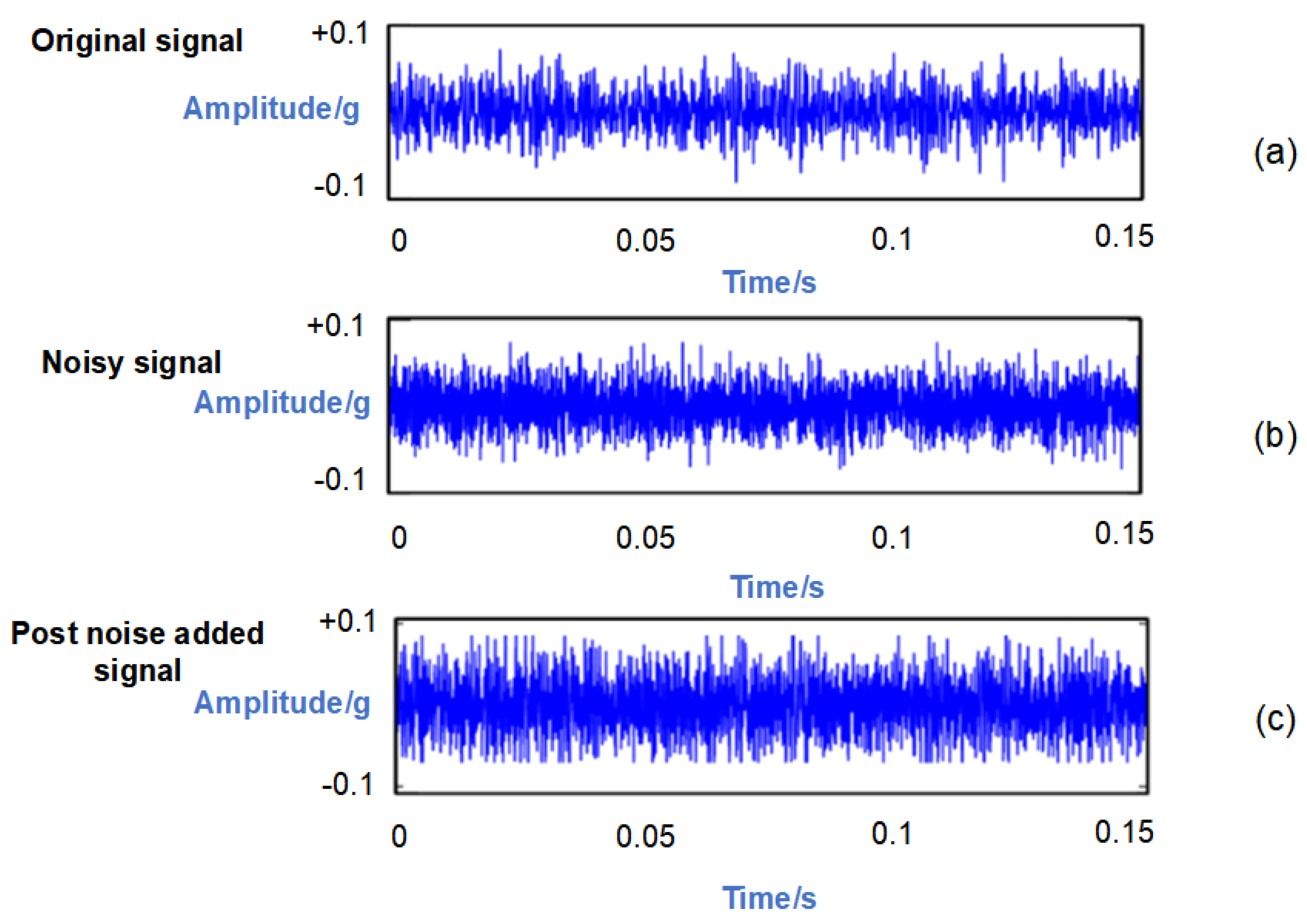
4.4. Experimental Evaluation of Noise Addition for Performance Testing
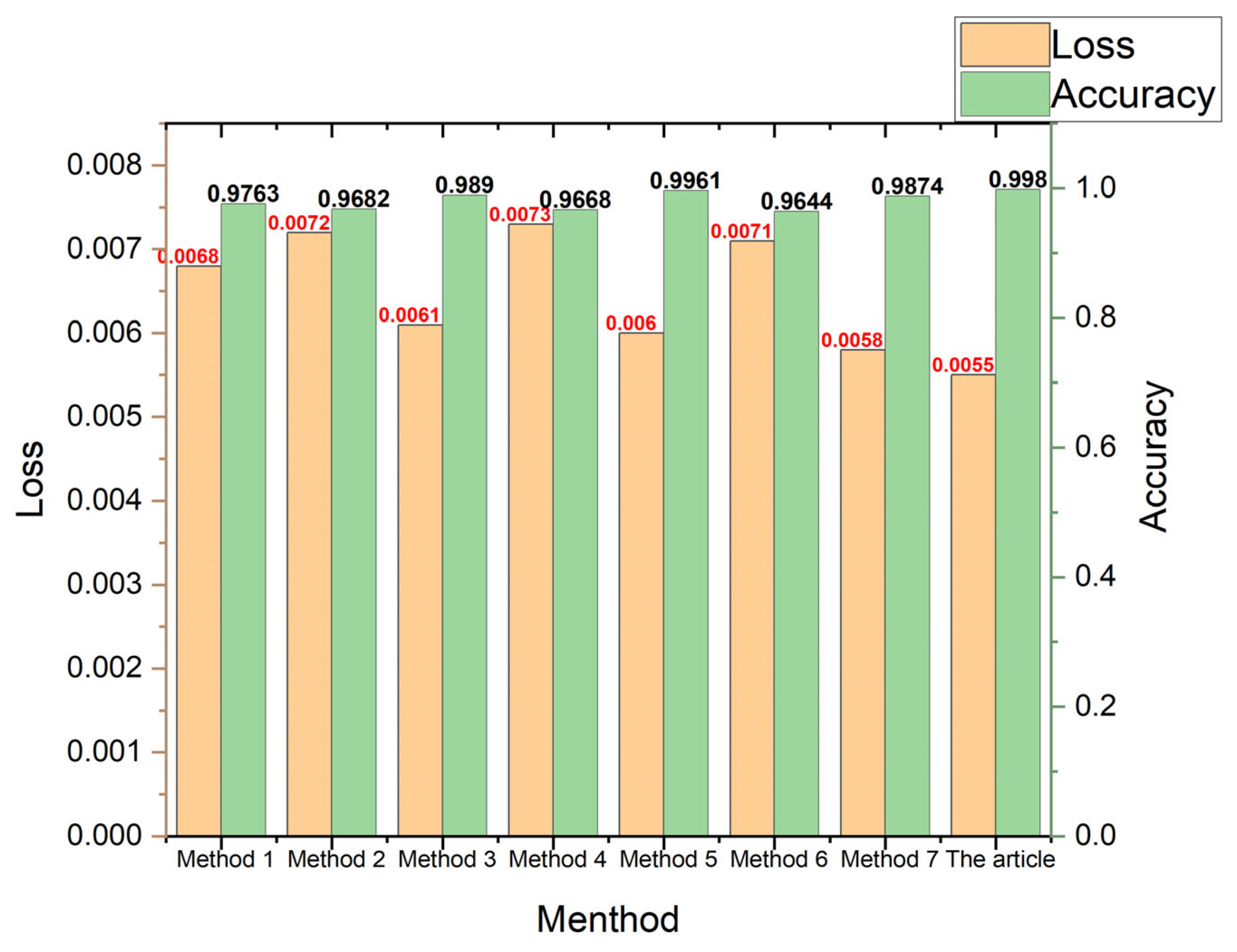
4.5. Comparative Validation of Diagnostic Efficacy across Diverse Algorithms
- In reference [22], a single tag is utilized for data labeling. The vibration signals undergo a short-time Fourier transform, and the resulting time-frequency feature maps are inputted into a convolutional neural network (CNN) with adjusted parameters tailored for fault diagnosis. Data labeling remains consistent with a single tag. The result is method 1 in Figure 13;
- In reference [24], data are annotated using a single tag, followed by feature extraction through a two-dimensional convolutional layer. The extracted features are then fed into capsule layers for fault diagnosis, where both primary and digit capsule layers employ dynamic routing algorithms to transform the feature vectors. The result is method 3 in Figure 13;
- In reference [25], a singular label is employed to annotate the data, while one-dimensional temporal signals are fed into capsule neural networks for feature extraction. The fault diagnosis task is accomplished by leveraging two convolutional layers within the capsule neural network. The result is method 4 in Figure 13;
- In reference [26], data are annotated with a single tag, and we propose a TF-RCNN model based on the utilization of time–frequency regions. This model leverages multiple regions characterized by TFR features, while also incorporating an attention module to enhance the classification efficacy for different types through advanced classification strategies. The result is method 5 in Figure 13;
- Reference [27] introduces a single tag for labeling and proposes a multi-ensemble approach for rolling bearing fault diagnosis based on deep autoencoders (DAE). Multiple DAEs are trained with different activation functions to extract type-specific features, which are then merged into a feature pool. The final result is determined through majority voting among the classifiers of each sample set. The result is method 6 in Figure 13;
- In reference [28], data were annotated with a singular label, proposing an enhanced AlexNet model for the diagnosis of rolling bearings. The optimal pre-training was determined based on the classification diagnostic rate. A modified calculation model was selected to reduce the parameter count and mitigate overfitting. Superior classification results were achieved by incorporating mixed concepts using classifiers. The result is method 7 in Figure 13.
4.6. Revising the Model’s Performance Generalization Verification
5. Conclusions
- The article proposes a novel diagnostic model for rolling bearings, which enables the identification of both fault type and damage diameters through a dual-branch structure. By effectively leveraging fault information to extract more intricate features, it significantly enhances the accuracy of diagnosis. Moreover, the adoption of a one-hot encoding binary labeling method reduces dimensionality and facilitates feature extraction in each branch while ensuring high precision;
- The model was validated using the CWRU bearing dataset and a self-made dataset. The experimental results demonstrate that both branches of the model exhibit high accuracy, achieving an average accuracy of 99.8% for each branch on the CWRU dataset and an average accuracy of 94.25% for each branch on the self-made dataset. In comparison to four other fault diagnosis algorithm models in the existing literature, this model demonstrates a superior fault recognition rate and provides more comprehensive diagnostic information;
- The model’s robustness against noise and superior generalization ability are demonstrated through experiments involving noise addition and evaluation of generalization performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Liu, B. Residual analysis and parameter estimation of uncertain differential equations. Fuzzy Optim. Decis. Mak. 2022, 21, 513–530. [Google Scholar] [CrossRef]
- Ng, Y.S.; Srinivasan, R. Multi-agent based collaborative fault detection and identification in chemical processes. Eng. Appl. Artif. Intell. 2010, 23, 934–949. [Google Scholar] [CrossRef]
- Skowronek, K.; Barszcz, T.; Antoni, J.; Zimroz, R.; Wyłomańska, A. Assessment of background noise properties in time and time–frequency domains in the context of vibration-based local damage detection in real environment. Mech. Syst. Signal Process. 2023, 199, 110465. [Google Scholar] [CrossRef]
- Żuławiński, W.; Antoni, J.; Zimroz, R.; Wyłomańska, A. Applications of robust statistics for cyclostationarity detection in non-Gaussian signals for local damage detection in bearings. Mech. Syst. Signal Process. 2024, 214, 111367. [Google Scholar] [CrossRef]
- Mauricio, A.; Smith, W.A.; Randall, R.B.; Antoni, J.; Gryllias, K. Improved Envelope Spectrum via Feature Optimisation-gram (IESFOgram): A novel tool for rolling element bearing diagnostics under non-stationary operating conditions. Mech. Syst. Signal Process. 2020, 144, 106891. [Google Scholar] [CrossRef]
- Peng, H.-M.; Wang, X.-K.; Wang, T.-L.; Liu, Y.-H.; Wang, J.-Q. Extended failure mode and effect analysis approach based on hesitant fuzzy linguistic Z-numbers for risk prioritisation of nuclear power equipment failures. J. Intell. Fuzzy Syst. 2021, 40, 10489–10505. [Google Scholar] [CrossRef]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An Introduction to Deep Reinforcement Learning. Found. Trends Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef]
- Guo, P.; Liu, Z.; Lu, H.; Wang, Z. Hyperspectral Image Classification Based on Stacked Contractive Autoencoder Combined with Adaptive Spectral-Spatial Information. IEEE Access 2021, 9, 96404–96415. [Google Scholar] [CrossRef]
- Pouryahya, M.; Oh, J.H.; Mathews, J.C.; Belkhatir, Z.; Moosmüller, C.; Deasy, J.O.; Tannenbaum, A.R. Pan-Cancer Prediction of Cell-Line Drug Sensitivity Using Network-Based Methods. Int. J. Mol. Sci. 2022, 23, 1074. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, Y.; Liang, J. A self-adaptive gradient descent search algorithm for fully-connected neural networks. Neurocomputing 2022, 478, 70–80. [Google Scholar] [CrossRef]
- Yin, C.; Wang, Y.; Ma, G.; Wang, Y.; Sun, Y.; He, Y. Weak fault feature extraction of rolling bearings based on improved ensemble noise-reconstructed EMD and adaptive threshold denoising. Mech. Syst. Signal Process. 2022, 171, 108834. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. Bearing fault diagnosis based on adaptive mutiscale fuzzy entropy and support vector machine. J. Vibroengineering 2015, 17, 1188–1202. [Google Scholar]
- Lu, W.; Mao, H.; Lin, F.; Chen, Z.; Fu, H.; Xu, Y. Recognition of rolling bearing running state based on genetic algorithm and convolutional neural network. Adv. Mech. Eng. 2022, 14, 168781322210956. [Google Scholar] [CrossRef]
- Ameer, I.; Bolucu, N.; Sidorov, G.; Can, B. Emotion Classification in Texts over Graph Neural Networks: Semantic Representation is Better Than Syntactic. IEEE Access 2023, 11, 56921–56934. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Luo, Y.; Jiang, J.; Zhu, J.; Huang, Q.; Li, W.; Wang, Y.; Gao, Y. A Caps-Ubi Model for Protein Ubiquitination Site Prediction. Front. Plant Sci. 2022, 13, 884903. [Google Scholar] [CrossRef]
- Zhou, Y.; Jin, L.; Ma, G.; Xu, X. Quaternion Capsule Neural Network with Region Attention for Facial Expression Recognition in Color Images. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 893–912. [Google Scholar] [CrossRef]
- Yang, B.; Bao, W.; Wang, J. Active disease-related compound identification based on capsule network. Brief. Bioinform. 2022, 23, 462. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Wang, Y.; Li, Z.; Li, N.; Su, J. A novel effective and efficient capsule network via bottleneck residual block and automated gradual pruning. Comput. Electr. Eng. 2019, 80, 106481. [Google Scholar] [CrossRef]
- Li, Z.; Lu, C.; Wang, X.; Ban, S. A two-branch convolutional neural network fault diagnosis method considering rolling bearing fault location and damage degree. Sci. Technol. Eng. 2022, 22, 1441–1448. [Google Scholar]
- Min, Q.; He, J.-J.; Yu, P.; Fu, Y. Incremental Fault Diagnosis Method Based on Metric Feature Distillation and Improved Sample Memory. IEEE Access 2023, 11, 46015–46025. [Google Scholar] [CrossRef]
- Li, G.; Deng, C.; Wu, J.; Chen, Z.; Xu, X. Rolling Bearing Fault Diagnosis Based on Wavelet Packet Transform and Convolutional Neural Network. Appl. Sci. 2020, 10, 770. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3859–3869. [Google Scholar]
- Jiang, G.-J.; Li, D.-Z.; Feng, K.; Li, Y.; Zheng, J.; Ni, Q.; Li, H. Rolling Bearing Fault Diagnosis Based On Convolutional Capsule Network. J. Dyn. Monit. Diagn. 2023, 2, 260. [Google Scholar] [CrossRef]
- Huo, C.; Jiang, Q.; Shen, Y.; Qian, C.; Zhang, Q. New transfer learning fault diagnosis method of rolling bearing based on ADC-CNN and LATL under variable conditions. Measurement 2022, 188, 110587. [Google Scholar] [CrossRef]
- Kong, X.; Mao, G.; Wang, Q.; Ma, H.; Yang, W. A multi-ensemble method based on deep auto-encoders for fault diagnosis of rolling bearings. Measurement 2020, 151, 107132. [Google Scholar] [CrossRef]
- Mohiuddin, M.; Islam, S.; Islam, S.; Miah, S.; Niu, M.-B. Intelligent Fault Diagnosis of Rolling Element Bearings Based on Modified AlexNet. Sensors 2023, 23, 7764. [Google Scholar] [CrossRef]




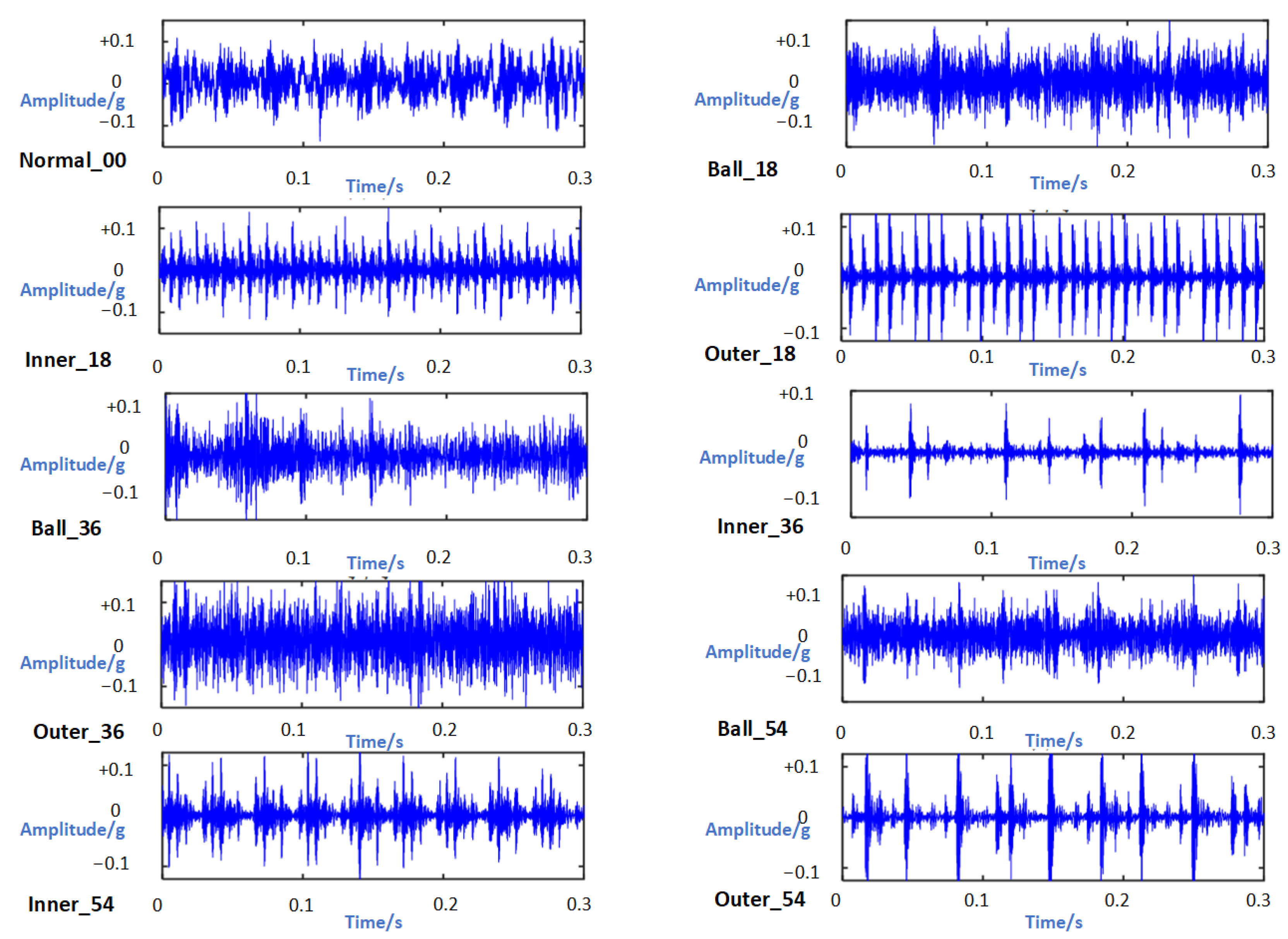

| Data Type | The Original Label | Label 1 | Label 2 |
|---|---|---|---|
| ball_18 | 0 | [1,0,0,0] | [0,1,0,0] |
| ball_36 | 1 | [1,0,0,0] | [0,0,1,0] |
| ball_54 | 2 | [1,0,0,0] | [0,0,0,1] |
| inner_18 | 3 | [0,1,0,0] | [0,1,0,0] |
| inner_36 | 4 | [0,1,0,0] | [0,0,1,0] |
| inner_54 | 5 | [0,1,0,0] | [0,0,0,1] |
| normal_00 | 6 | [0,0,1,0] | [1,0,0,0] |
| outer_18 | 7 | [0,0,0,1] | [0,1,0,0] |
| outer_36 | 8 | [0,0,0,1] | [0,0,1,0] |
| outer_54 | 9 | [0,0,0,1] | [0,0,0,1] |
| Number of Storeys | The Name of the Structure | Structural Parameters | Number of Channels | The Size of the Output |
|---|---|---|---|---|
| Input | (28, 28) | 1 | 28 × 28 | |
| 1 | (The Inception module) | |||
| Branch 1 | (1, 1, 1) | 48 | 28 × 28 | |
| Branch 2 | (1, 1, 1)/(3, 3, 1)/(3, 3, 1) | 48 | 28 × 28 | |
| Branch 3 | (1, 1, 1)/(3, 3, 1) | 64 | 28 × 28 | |
| Branch 4 | (3, 3, 1)/(1, 1, 1) | 64 | 28 × 28 | |
| 2 | CA attention mechanism | |||
| 3 | Basic capsule layer | (9, 9, 2) | 32 | 6 × (8) |
| 4 | Numeric capsule layer | (10, 16, 1) | 256 | 16 × (10) |
| 5 | Fully connected capsule layer | (256/1024) | 10 × (8) | |
| 6 | Output layer | (1024/10) |
| Amplitude Branching | −3 db | 3 db | 6 db | 9 db | ||||
|---|---|---|---|---|---|---|---|---|
| Failure Type | Damage Diameter | Failure Type | Damage Diameter | Failure Type | Damage Diameter | Failure Type | Damage Diameter | |
| Dataset 1 | 94.65% | 95.26% | 96.53% | 95.32% | 97.53% | 96.53% | 97.68% | 97.32% |
| Dataset 2 | 97.34% | 96.33% | 98.68% | 97.07% | 99.03% | 97.61% | 98.47% | 98.55% |
| Data Types | Training Set (Quantity) | Test Set (Quantity) | Loading Condition |
|---|---|---|---|
| ball_18 | 1600 | 400 | Under-loaded |
| ball_36 | 1600 | 400 | Under-loaded |
| ball_54 | 1600 | 400 | Under-loaded |
| inner_18 | 1600 | 400 | Under-loaded |
| inner_36 | 1600 | 400 | Under-loaded |
| inner_54 | 1600 | 400 | Under-loaded |
| normal_00 | 1600 | 400 | Under-loaded |
| outer_18 | 1600 | 400 | Under-loaded |
| outer_36 | 1600 | 400 | Under-loaded |
| outer_54 | 1600 | 400 | Under-loaded |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Liu, J.; Lin, F. The Fault Diagnosis of Rolling Bearings Is Conducted by Employing a Dual-Branch Convolutional Capsule Neural Network. Sensors 2024, 24, 3384. https://doi.org/10.3390/s24113384
Lu W, Liu J, Lin F. The Fault Diagnosis of Rolling Bearings Is Conducted by Employing a Dual-Branch Convolutional Capsule Neural Network. Sensors. 2024; 24(11):3384. https://doi.org/10.3390/s24113384
Chicago/Turabian StyleLu, Wanjie, Jieyu Liu, and Fanhao Lin. 2024. "The Fault Diagnosis of Rolling Bearings Is Conducted by Employing a Dual-Branch Convolutional Capsule Neural Network" Sensors 24, no. 11: 3384. https://doi.org/10.3390/s24113384
APA StyleLu, W., Liu, J., & Lin, F. (2024). The Fault Diagnosis of Rolling Bearings Is Conducted by Employing a Dual-Branch Convolutional Capsule Neural Network. Sensors, 24(11), 3384. https://doi.org/10.3390/s24113384








