The Influence of Fatigue, Recovery, and Environmental Factors on the Body Stability of Construction Workers
Abstract
:1. Introduction
2. Literature Review
3. Methodology
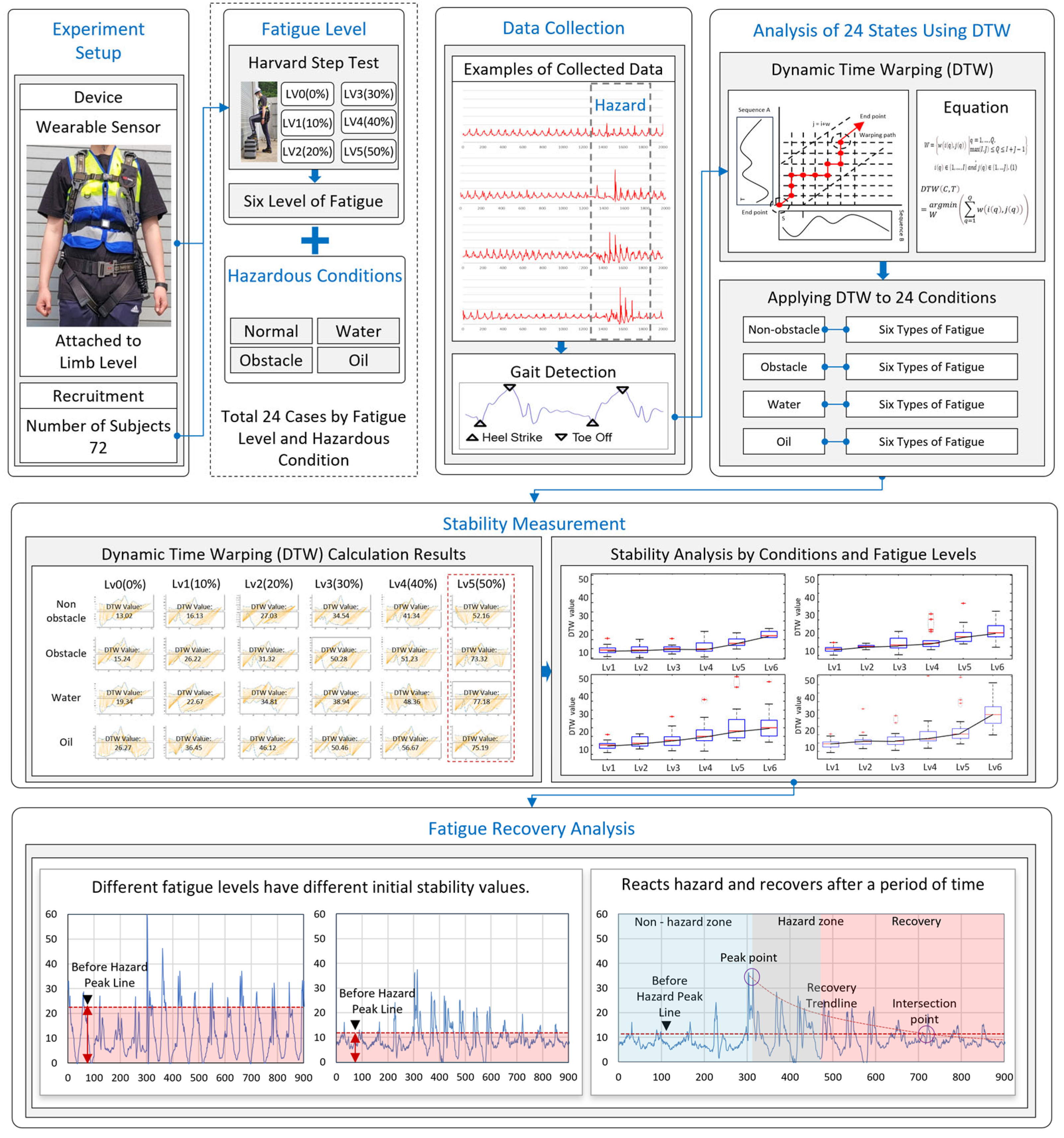
3.1. Research Framework
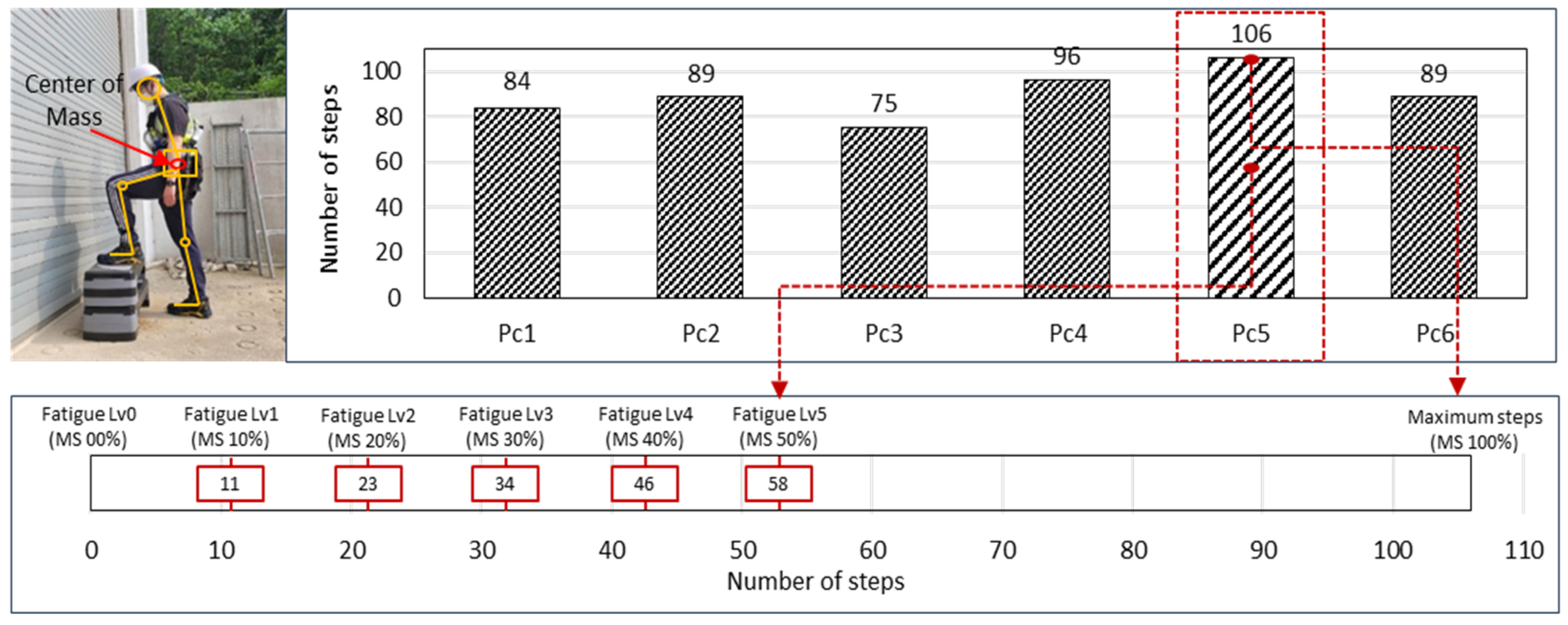
3.2. Experimental Design
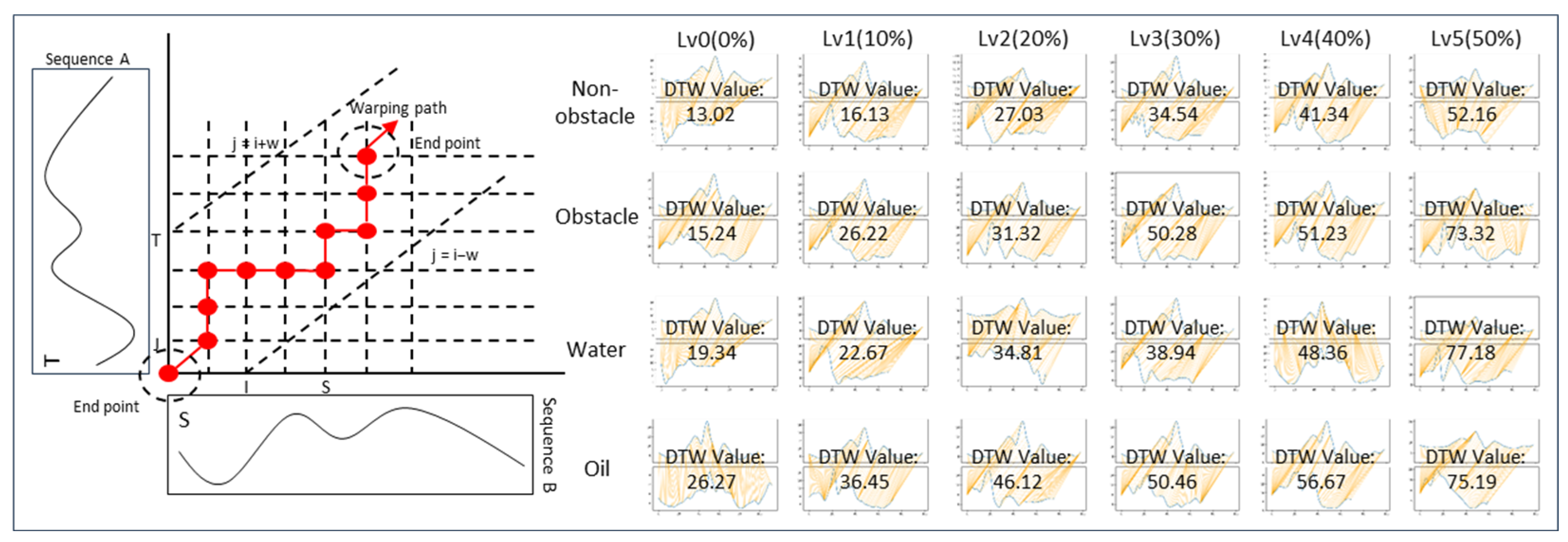
3.3. Body Stability Analysis Using the DTW Algorithm
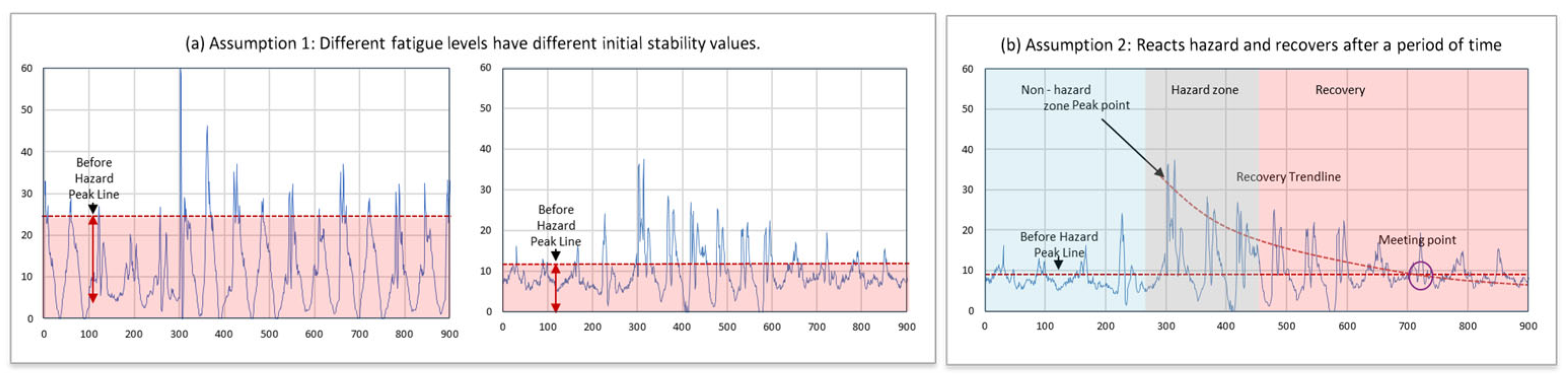
3.4. Body Stability Recovery Based on Fatigue Levels
4. Result
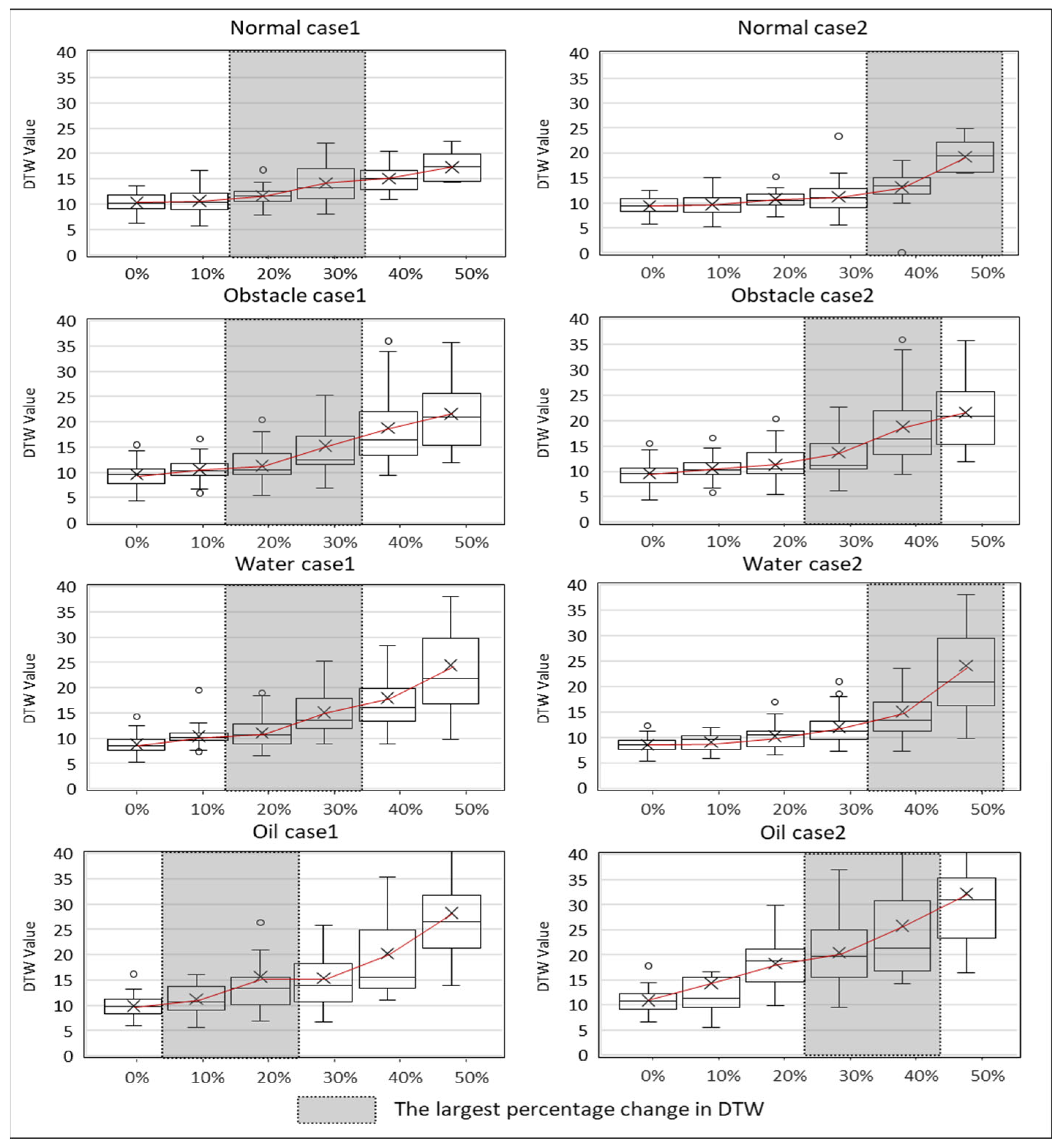
4.1. Investigation of Body Stability Changes Due to Fatigue in Various Construction Environments Using DTW Analysis
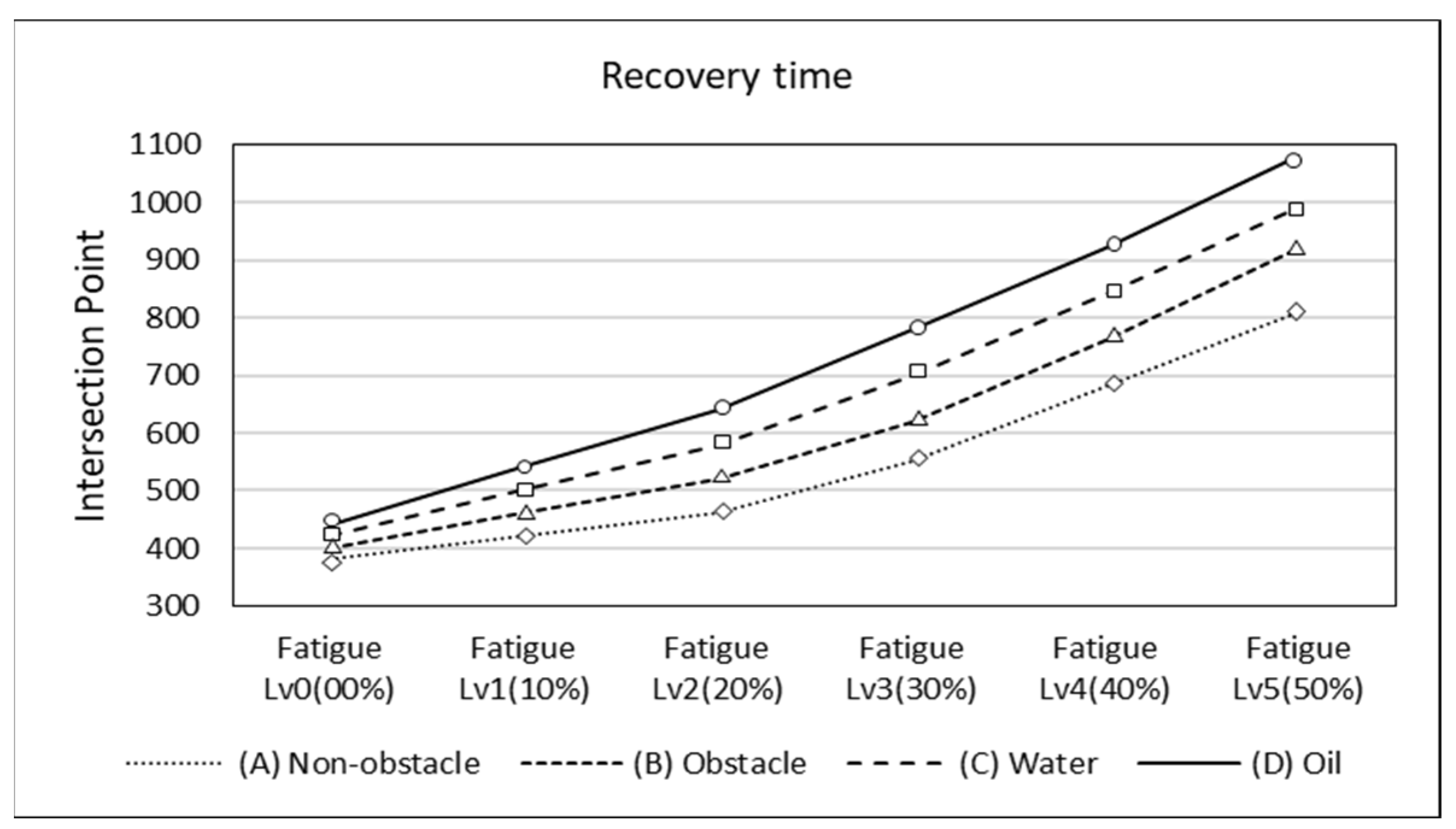
4.2. Results of Body Stability Recovery Analysis for Six Fatigue Levels
4.3. Comparative Analysis of Fatigue Levels and Working Environment Conditions on Overall Worker Stability and Recovery Time
5. Discussion
5.1. Changes in Body Stability According to Fatigue Levels and Hazard Types
5.2. Impact of Fatigue Levels and Hazard Proximity on Worker Body Stability in Construction Environments
5.3. Contributions and Limitations
5.4. Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, W.-R.; Leclercq, S.; Lockhart, T.E.; Haslam, R. State of Science: Occupational Slips, Trips and Falls on the Same Level. Ergonomics 2016, 59, 861–883. [Google Scholar] [CrossRef] [PubMed]
- Tetteh, M. Critical Risk Factors in Accident Causation in the Construction Industry—Perception of Construction. Ph.D. Thesis, University of Education, Winneba, Ghana, 2018. [Google Scholar]
- Cheng, C.; Shen, Z. Mechanism and Measurements of Fall Due to Loss-of-Balance for Construction Workers. In Construction Research Congress; ASCE: Reston, VA, USA, 2018; pp. 400–411. [Google Scholar] [CrossRef]
- Kim, H.; Ahn, C.R.; Yang, K. Identifying Safety Hazards Using Collective Bodily Responses of Workers. J. Constr. Eng. Manag. 2017, 143, 04016090. [Google Scholar] [CrossRef]
- Choi, D.H. Case Study for Preventing Construction Site Fall Accidents. Ph.D. Thesis, Korean Institute of Construction Engineering and Management, Seoul, Republic of Korea, 2019. Korean Journal of Construction Engineering and Management, 2019, Volume 20, No. 6, pp. 82–89. [Google Scholar]
- Neal, A.; Griffin, M.A. A Study of the Lagged Relationships among Safety Climate, Safety Motivation, Safety Behavior, and Accidents at the Individual and Group Levels. J. Appl. Psychol. 2006, 91, 946–953. [Google Scholar] [CrossRef] [PubMed]
- Vigneshkumar, C.; Salve, U.R. A Scientometric Analysis and Review of Fall from Height Research in Construction. Constr. Econ. Build. 2020, 20, 17–35. [Google Scholar] [CrossRef]
- Courtney, T.K.; Sorock, G.S.; Manning, D.P.; Collins, J.W.; Holbein-Jenny, M.A. Occupational Slip, Trip, and Fall-Related Injuries Can the Contribution of Slipperiness Be Isolated? Ergonomics 2001, 44, 1118–1137. [Google Scholar] [CrossRef] [PubMed]
- Wimer, B.; Pan, C.; Lutz, T.; Hause, M.; Warren, C.; Dong, R.; Xu, S. Evaluating the Stability of a Freestanding Mast Climbing Work Platform. J. Saf. Res. 2017, 62, 163–172. [Google Scholar] [CrossRef]
- Umer, W.; Li, H.; Lu, W.; Szeto, G.P.Y.; Wong, A.Y.L. Development of a Tool to Monitor Static Balance of Construction Workers for Proactive Fall Safety Management. Autom. Constr. 2018, 94, 438–448. [Google Scholar] [CrossRef]
- Maynard, W.S. Prevention through Design-Slips, Trips and Falls. In Proceedings of the ASSE Professional Development Conference and Exposition, Las Vegas, NV, USA, 24–27 June 2013. [Google Scholar]
- Alabdulkarim, S.; Nussbaum, M.A. Influences of Different Exoskeleton Designs and Tool Mass on Physical Demands and Performance in a Simulated Overhead Drilling Task. Appl. Ergon. 2019, 74, 55–66. [Google Scholar] [CrossRef] [PubMed]
- Antwi-Afari, M.F.; Li, H.; Edwards, D.J.; Pärn, E.A.; Seo, J.; Wong, A. Effects of Different Weights and Lifting Postures on Balance Control Following Repetitive Lifting Tasks in Construction Workers. Int. J. Build. Pathol. Adapt. 2017, 35, 247–263. [Google Scholar] [CrossRef]
- Chander, H.; Knight, A.C.; Garner, J.C.; Wade, C.; Carruth, D.W.; DeBusk, H.; Hill, C.M. Impact of Military Type Footwear and Workload on Heel Contact Dynamics during Slip Events. Int. J. Ind. Ergon. 2018, 66, 18–25. [Google Scholar] [CrossRef]
- Paillard, T. Effects of General and Local Fatigue on Postural Control: A Review. Neurosci. Biobehav. Rev. 2012, 36, 162–176. [Google Scholar] [CrossRef]
- Horak, F.B. Postural Orientation and Equilibrium: What Do We Need to Know about Neural Control of Balance to Prevent Falls? Age Ageing 2006, 35, ii7–ii11. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.; Lee, S.; Seo, J. Simulation-Based Assessment of Workers’ Muscle Fatigue and Its Impact on Construction Operations. J. Constr. Eng. Manag. 2016, 142, 04016063. [Google Scholar] [CrossRef]
- Hursh, S.R.; Redmond, D.P.; Johnson, M.L.; Thorne, D.R.; Belenky, G.; Balkin, T.J.; Storm, W.F.; Miller, J.C.; Eddy, D.R. Fatigue Models for Applied Research in Warfighting. Aviat. Space Environ. Med. 2004, 75, A44–A53. [Google Scholar]
- Williamson, A.; Lombardi, D.A.; Folkard, S.; Stutts, J.; Courtney, T.K.; Connor, J.L. The Link between Fatigue and Safety. Accid. Anal. Prev. 2011, 43, 498–515. [Google Scholar] [CrossRef] [PubMed]
- Granata, K.P.; Gottipati, P. Fatigue Influences the Dynamic Stability of the Torso. Ergonomics 2008, 51, 1258–1271. [Google Scholar] [CrossRef]
- Chang, F.-L.; Sun, Y.-M.; Chuang, K.-H.; Hsu, D.-J. Work Fatigue and Physiological Symptoms in Different Occupations of High-Elevation Construction Workers. Appl. Ergon. 2009, 40, 591–596. [Google Scholar] [CrossRef]
- Lee, W. Occupational Fatigue Prediction for Entry-Level Construction Workers in Material Handling Activities Using Wearable Sensors. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2018. [Google Scholar]
- Enshassi, A.E.; Shakalaih, S.S. Construction Workers Fall Accidents from Scaffolding in Gaza Strip. Master’s Thesis, Korean Institute of Construction Engineering and Management, Seoul, Republic of Korea, 2015. Korean Construction Management Conference—Program & Proceedings, 2015, Volume 6, pp. 65–70. [Google Scholar]
- Jebelli, H. Assessing Gait and Postural Stability of Construction Workers Using Wearable Wireless Sensor Networks. Master’s Thesis, Department of Construction Engineering and Management, University of Nebraska-Lincoln, Lincoln, NE, USA, 2015. [Google Scholar]
- A Look at Falls, Slips, and Trips in the Construction Industry: The Economics Daily: U.S. Bureau of Labor Statistics. Available online: https://www.bls.gov/opub/ted/2022/a-look-at-falls-slips-and-trips-in-the-construction-industry.htm (accessed on 25 March 2024).
- Antwi-Afari, M.F.; Li, H. Fall Risk Assessment of Construction Workers Based on Biomechanical Gait Stability Parameters Using Wearable Insole Pressure System. Adv. Eng. Inform. 2018, 38, 683–694. [Google Scholar] [CrossRef]
- Duan, P.; Zhou, J. Cascading Vulnerability Analysis of Unsafe Behaviors of Construction Workers from the Perspective of Network Modeling. Eng. Constr. Archit. Manag. 2021, 30, 1037–1060. [Google Scholar] [CrossRef]
- Jebelli, H.; Ahn, C.R.; Stentz, T.L. Fall Risk Analysis of Construction Workers Using Inertial Measurement Units: Validating the Usefulness of the Postural Stability Metrics in Construction. Saf. Sci. 2016, 84, 161–170. [Google Scholar] [CrossRef]
- DiDomenico, A.; McGorry, R.W.; Huang, Y.-H.; Blair, M.F. Perceptions of Postural Stability after Transitioning to Standing among Construction Workers. Saf. Sci. 2010, 48, 166–172. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Umer, W.; Wang, H.; Xing, X.; Zhao, S.; Hou, J. Identification and Classification of Construction Equipment Operators’ Mental Fatigue Using Wearable Eye-Tracking Technology. Autom. Constr. 2020, 109, 103000. [Google Scholar] [CrossRef]
- Qu, X. Development and Evaluation of Postural Control Models for Lifting Motions and Balance Control. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2008. [Google Scholar]
- Chan, M. Fatigue: The Most Critical Accident Risk in Oil and Gas Construction. Constr. Manag. Econ. 2011, 29, 341–353. [Google Scholar] [CrossRef]
- Yu, Y.; Li, H.; Yang, X.; Kong, L.; Luo, X.; Wong, A.Y.L. An Automatic and Non-Invasive Physical Fatigue Assessment Method for Construction Workers. Autom. Constr. 2019, 103, 1–12. [Google Scholar] [CrossRef]
- Heng, P.P.; Yusoff, H.M.; Hod, R. Individual Evaluation of Fatigue at Work to Enhance the Safety Performance in the Construction Industry: A Systematic Review. PLoS ONE 2024, 19, e0287892. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Nnaji, C.; Khan, M.S.; Ibrahim, A.; Lee, D.; Park, C. Risk Factors and Emerging Technologies for Preventing Falls from Heights at Construction Sites. Autom. Constr. 2023, 153, 104955. [Google Scholar] [CrossRef]
- Pei, H.P.; Yusoff, H.m.; Hod, R.; Ja’afar, M.H. The Influence of Work Environmental Risk Factors on Fatigue in The Construction Industry: A Review of Literature: International Journal of Public Health Research. Int. J. Public Health Res. 2023, 13, 1732–1742. [Google Scholar] [CrossRef]
- Escobar-Linero, E.; Domínguez-Morales, M.; Sevillano, J.L. Worker’s Physical Fatigue Classification Using Neural Networks. Expert Syst. Appl. 2022, 198, 116784. [Google Scholar] [CrossRef]
- Lee, S.-J.; Yoon, H.-K. A Systematic Review of Human-Centric Lighting Design of Circadian Rhythm in Architectural Environments. J. Archit. Inst. Korea 2022, 38, 141–151. [Google Scholar] [CrossRef]
- Jebelli, H.; Ahn, C.R.; Stentz, T.L. Comprehensive Fall-Risk Assessment of Construction Workers Using Inertial Measurement Units: Validation of the Gait-Stability Metric to Assess the Fall Risk of Iron Workers. J. Comput. Civ. Eng. 2016, 30, 04015034. [Google Scholar] [CrossRef]
- Yu, Y.; Li, H.; Yang, X.; Umer, W. Estimating Construction Workers’ Physical Workload by Fusing Computer Vision and Smart Insole Technologies. In Proceedings of the 35th International Symposium on Automation and Robotics in Construction (ISARC 2018), Berlin, Germany, 20–25 July 2018. [Google Scholar]
- Alvanchi, A.; Lee, S.; AbouRizk, S. Dynamics of Working Hours in Construction. J. Constr. Eng. Manag. 2012, 138, 66–77. [Google Scholar] [CrossRef]
- Yu, Y. Automatic Physical Fatigue Assessment for Construction Workers Based on Computer Vision and Pressure Insole Sensor. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2020. [Google Scholar]
- Adaptation and Validation of an Analytical Localized Muscle Fatigue Model for Workplace Tasks—ProQuest. Available online: https://www.proquest.com/docview/1652862824?pq-origsite=gscholar&fromopenview=true&sourcetype=Dissertations%20&%20Theses (accessed on 14 March 2024).
- Hwang, S.; Lee, S. Wristband-Type Wearable Health Devices to Measure Construction Workers’ Physical Demands. Autom. Constr. 2017, 83, 330–340. [Google Scholar] [CrossRef]
- Jebelli, H.; Hwang, S.; Lee, S. EEG-Based Workers’ Stress Recognition at Construction Sites. Autom. Constr. 2018, 93, 315–324. [Google Scholar] [CrossRef]
- Zhang, L.; Diraneyya, M.M.; Ryu, J.; Haas, C.T.; Abdel-Rahman, E.M. Jerk as an Indicator of Physical Exertion and Fatigue. Autom. Constr. 2019, 104, 120–128. [Google Scholar] [CrossRef]
- Lewis, C. Resistance Training in Untrained Individuals: Impact of Light Repetition Ranges on Improvements in Fat Free Mass. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2013. [Google Scholar]
- Mosier, E.M. The Effects of Vertical Jump Fatigue and Sprint Fatigue on Total-Body Biomechanics. Ph.D. Thesis, University of Kansas, Lawrence, KS, USA, 2018. [Google Scholar]
- Rota, S.; Morel, B.; Saboul, D.; Rogowski, I.; Hautier, C. Influence of Fatigue on Upper Limb Muscle Activity and Performance in Tennis. J. Electromyogr. Kinesiol. 2014, 24, 90–97. [Google Scholar] [CrossRef]
- Ahn, C.R.; Lee, S.; Sun, C.; Jebelli, H.; Yang, K.; Choi, B. Wearable Sensing Technology Applications in Construction Safety and Health. J. Constr. Eng. Manag. 2019, 145, 03119007. [Google Scholar] [CrossRef]
- Santos, B.R.; Larivière, C.; Delisle, A.; Plamondon, A.; Boileau, P.-É.; Imbeau, D. A Laboratory Study to Quantify the Biomechanical Responses to Whole-Body Vibration: The Influence on Balance, Reflex Response, Muscular Activity and Fatigue. Int. J. Ind. Ergon. 2008, 38, 626–639. [Google Scholar] [CrossRef]
- Chen, S.; Bangaru, S.S.; Yigit, T.; Trkov, M.; Wang, C.; Yi, J. Real-Time Walking Gait Estimation for Construction Workers Using a Single Wearable Inertial Measurement Unit (IMU). In Proceedings of the 2021 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Delft, The Netherlands, 12–16 July 2021; pp. 753–758. [Google Scholar]
- Bonato, P.; Ebenbichler, G.R.; Roy, S.H.; Lehr, S.; Posch, M.; Kollmitzer, J.; Della Croce, U. Muscle Fatigue and Fatigue-Related Biomechanical Changes During a Cyclic Lifting Task. Spine 2003, 28, 1810. [Google Scholar] [CrossRef]
- Badami, S.V. A Comparative Study of Physical Fitness Index and Predicted Maximum Aerobic Capacity Between Students of Medical Education and Physical Education. Ph.D. Thesis, Rajiv Gandhi University of Health Sciences (India), Bengaluru, India, 2013. [Google Scholar]
- de Ruiter, C.J.; Kooistra, R.D.; Paalman, M.I.; de Haan, A. Initial Phase of Maximal Voluntary and Electrically Stimulated Knee Extension Torque Development at Different Knee Angles. J. Appl. Physiol. 2004, 97, 1693–1701. [Google Scholar] [CrossRef]
- Jeong, Y.-S.; Jeong, M.K.; Omitaomu, O.A. Weighted Dynamic Time Warping for Time Series Classification. Pattern Recognit. 2011, 44, 2231–2240. [Google Scholar] [CrossRef]
- Moraffah, R.; Sheth, P.; Karami, M.; Bhattacharya, A.; Wang, Q.; Tahir, A.; Raglin, A.; Liu, H. Causal Inference for Time Series Analysis: Problems, Methods and Evaluation. Knowl. Inf. Syst. 2021, 63, 3041–3085. [Google Scholar] [CrossRef]
- Zhao, J.; Itti, L. shapeDTW: Shape Dynamic Time Warping. Pattern Recognit. 2018, 74, 171–184. [Google Scholar] [CrossRef]
- Zhang, Z.; Tavenard, R.; Bailly, A.; Tang, X.; Tang, P.; Corpetti, T. Dynamic Time Warping under Limited Warping Path Length. Inf. Sci. 2017, 393, 91–107. [Google Scholar] [CrossRef]
- Bankó, Z.; Abonyi, J. Correlation Based Dynamic Time Warping of Multivariate Time Series. Expert Syst. Appl. 2012, 39, 12814–12823. [Google Scholar] [CrossRef]




| Study | Methodology | Sensor Types Used | Environmental Conditions Considered | Fatigue Assessment Method | Key Findings |
|---|---|---|---|---|---|
| Duan et al. (2021) [31] | work modeling of unsafe behaviors | Open pose camera system | High-altitude work | Not specified | Analyzed changes in posture and stability during high-altitude work. |
| Ebell et al. (2016) [32] | Fall risk analysis using wearable sensors | Wearable IMU devices | Construction site | Gait pattern analysis | Found that fall risks can be assessed using postural stability metrics from wearable sensors. |
| Li et al. (2020) [33] | Mental fatigue classification using eye-tracking | Wearable eye-tracking device | Simulated construction environment | Eye-tracking fatigue assessment | Classified mental fatigue of construction equipment operators using eye-tracking technology. |
| Yu et al. (2019) [34] | Physical workload estimation | Wearable insole pressure system | Construction site | Machine learning algorithms | Developed methods to estimate physical workload using computer vision and insole pressure data. |
| Escobar-Linero et al. (2022) [35] | Physical fatigue classification using neural networks | EMG sensors | Laboratory | Neural network analysis | Used neural networks to classify worker physical fatigue based on EMG sensor data. |
| Chan (2011) [36] | Analysis of fatigue as a critical accident risk | Not specified | Oil and gas construction sites | Observation and interviews | Identified fatigue as a critical factor contributing to accidents in the oil and gas construction sector. |
| This Study (2024) | Body stability analysis using DTW | IMU sensors | Non-obstacle, obstacle, water, oil | HST: until failure, with fatigue levels set at 10–50% | Demonstrated significant increases in DTW values as fatigue levels increased and identified the importance of fatigue management. |
| Fatigue Level (%) | Participants Reporting Significant Fatigue | Total Participants | Percentage Reporting Significant Fatigue (%) |
|---|---|---|---|
| 30 | 5 | 72 | 6.94 |
| 40 | 15 | 72 | 20.83 |
| 50 | 28 | 72 | 38.89 |
| 60 | 13 | 72 | 18.06 |
| 70 | 11 | 72 | 15.28 |
| Height (cm) | Weight (kg) | Age (Years) | |
|---|---|---|---|
| Mean | 175.67 | 74.95 | 54.23 |
| Median | 173.74 | 67.28 | 52.01 |
| Standard Deviation | 6.54 | 15.21 | 3.21 |
| Min Value | 163.45 | 56.98 | 45.11 |
| Max Value | 178.7 | 87.35 | 58.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jo, D.; Kim, H. The Influence of Fatigue, Recovery, and Environmental Factors on the Body Stability of Construction Workers. Sensors 2024, 24, 3469. https://doi.org/10.3390/s24113469
Jo D, Kim H. The Influence of Fatigue, Recovery, and Environmental Factors on the Body Stability of Construction Workers. Sensors. 2024; 24(11):3469. https://doi.org/10.3390/s24113469
Chicago/Turabian StyleJo, Daehwi, and Hyunsoo Kim. 2024. "The Influence of Fatigue, Recovery, and Environmental Factors on the Body Stability of Construction Workers" Sensors 24, no. 11: 3469. https://doi.org/10.3390/s24113469
APA StyleJo, D., & Kim, H. (2024). The Influence of Fatigue, Recovery, and Environmental Factors on the Body Stability of Construction Workers. Sensors, 24(11), 3469. https://doi.org/10.3390/s24113469






