Exploring the Use of Cold Atmospheric Plasma for Sound and Vibration Generation
Abstract
:1. Introduction
1.1. Wavefront Visualization
1.2. Mechanical Excitation
2. Materials and Methods
2.1. Wavefront Visualization
2.2. Mechanical Excitation
3. Results and Discussion
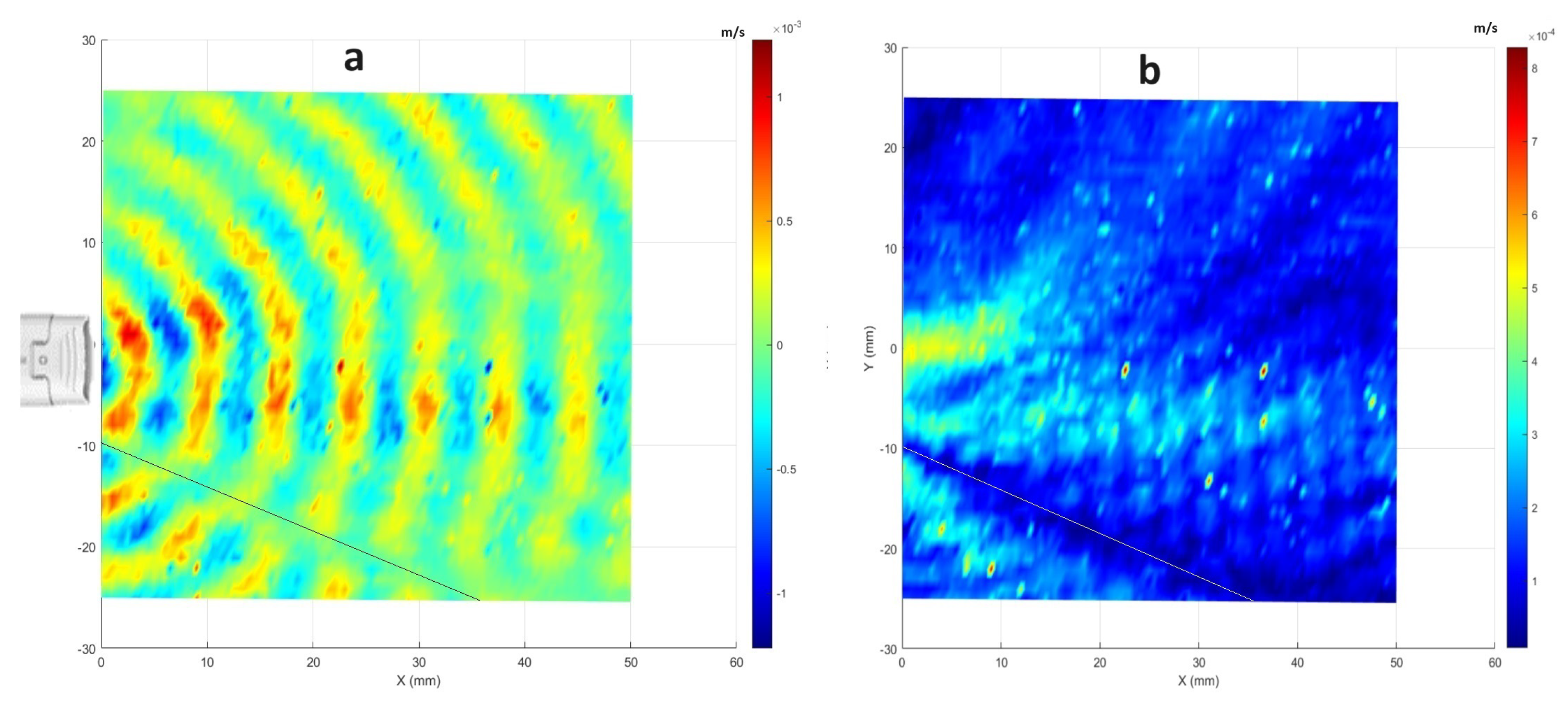
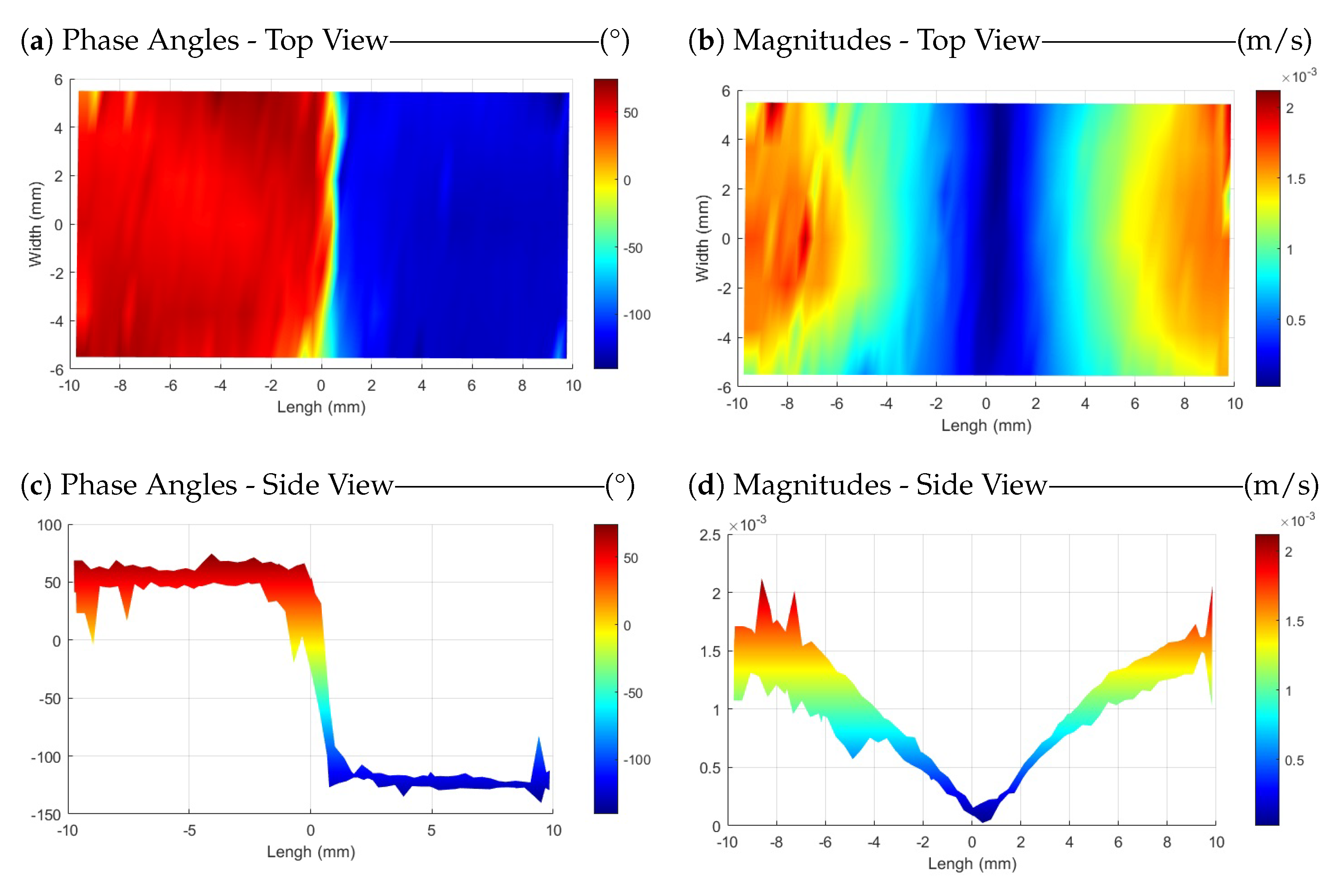
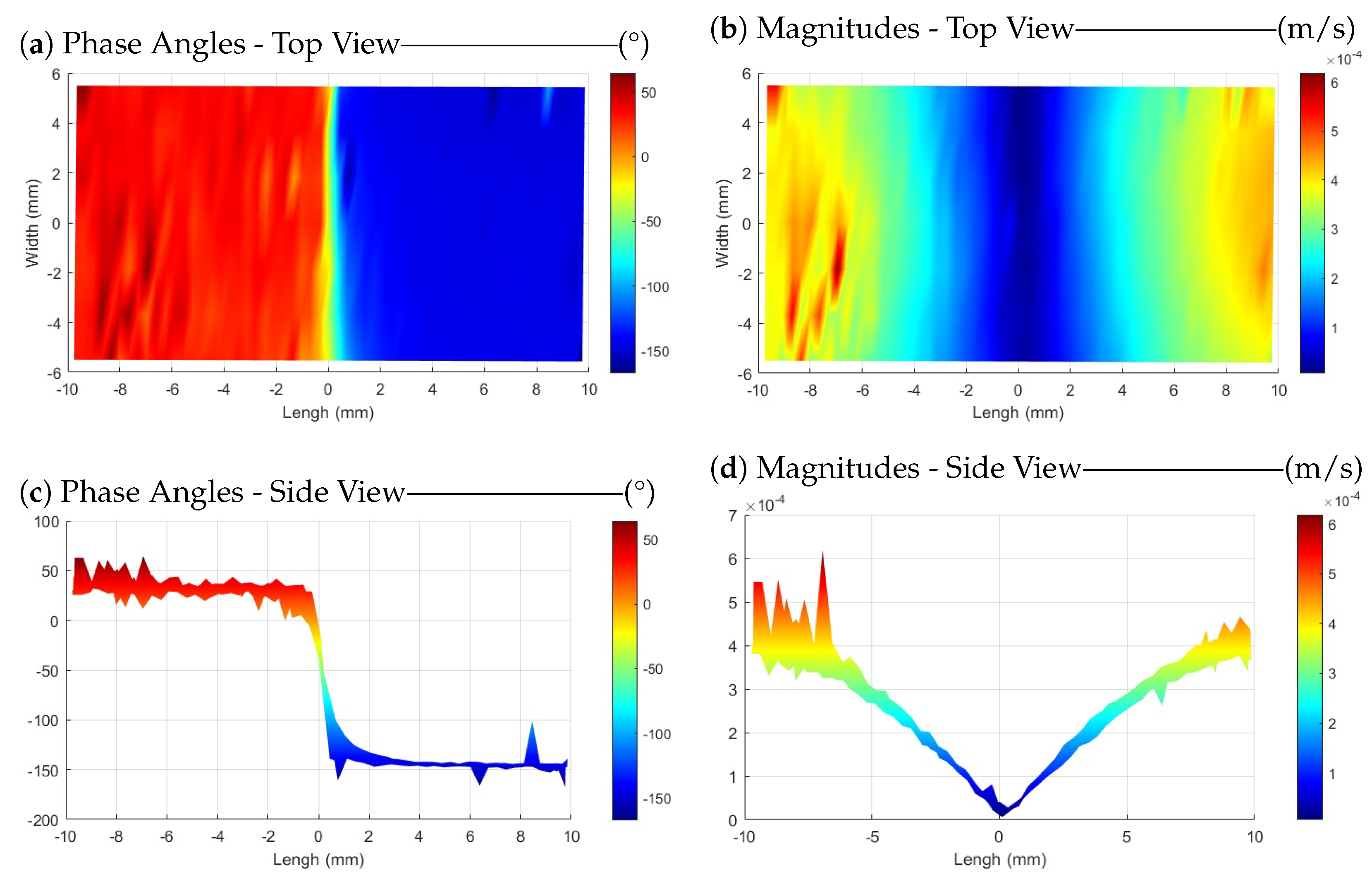
3.1. Wavefront Visualization
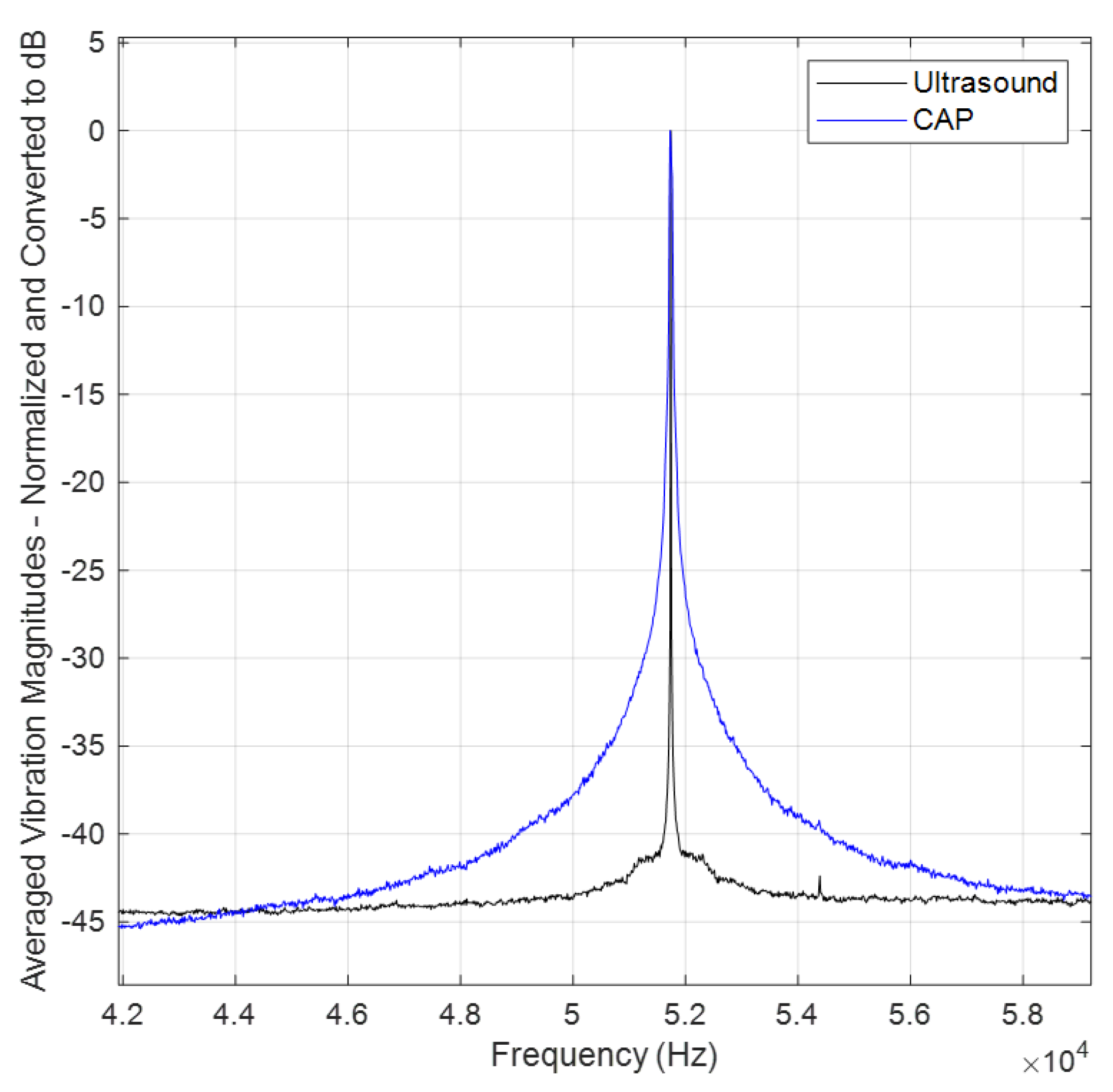
3.2. Mechanical Excitation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LDV | Laser Doppler Vibrometer |
| CAP | cold atmospheric plasma |
| PMMA | polymethyl methacrylate |
| FFT | Fast Fourier Transform |
| PT | piezoelectric transformer |
| SNR | signal-to-noise ratio |
References
- Neuhaus, S.; Padeste, C.; Solak, H.H.; Spencer, N.D. Functionalization of fluoropolymer surfaces with nanopatterned polyelectrolyte brushes. Polymer 2010, 51, 4037–4043. [Google Scholar] [CrossRef]
- Stawarczyk, B.; Thrun, H.; Eichberger, M.; Roos, M.; Edelhoff, D.; Schweiger, J.; Schmidlin, P.R. Effect of different surface pretreatments and adhesives on the load-bearing capacity of veneered 3-unit PEEK FDPs. J. Prosthet. Dent. 2015, 114, 666–673. [Google Scholar] [CrossRef] [PubMed]
- Ito, Y.; Okawa, T.; Fujii, T.; Tanaka, M. Influence of plasma treatment on surface properties of zirconia. J. Osaka Dent. Univ. 2016, 50, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Ito, Y.; Okawa, T.; Fukumoto, T.; Tsurumi, A.; Tatsuta, M.; Fujii, T.; Tanaka, J.; Tanaka, M. Influence of atmospheric pressure low-temperature plasma treatment on the shear bond strength between zirconia and resin cement. J. Prosthodont. Res. 2016, 60, 289–293. [Google Scholar] [CrossRef] [PubMed]
- Fridman, A. Plasma Chemistry I; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Sakudo, A.; Shintani, H. Sterilization and Disinfection by Plasma: Sterilization Mechanisms, Biological and Medical Applications; Nova Science Publishers: Hauppauge, NY, USA, 2011; pp. 1–239. [Google Scholar]
- Korzec, D.; Hoppenthaler, F.; Burger, D.; Andres, T.; Nettesheim, S. Atmospheric pressure plasma jet powered by piezoelectric direct discharge. Plasma Process. Polym. 2020, 17, 2000053. [Google Scholar] [CrossRef]
- Korzec, D.; Hoppenthaler, F.; Nettesheim, S. Piezoelectric Direct Discharge: Devices and Applications. Plasma 2021, 4, 1–41. [Google Scholar] [CrossRef]
- Korzec, D.; Hoppenthaler, F.; Andres, T.; Guentner, S.; Lerach, S. Application of Nitrogen Piezoelectric Direct Discharge for Increase in Surface Free Energy of Polymers. Plasma 2022, 5, 111–129. [Google Scholar] [CrossRef]
- Molin, N.E.; Zipser, L. Optical Methods of Today for Visualizing Sound Fields in Musical Acoustics. Acta Acust. United Acust. 2004, 90, 618–628. [Google Scholar]
- Vanlanduit, S.; Vanherzeele, J.; Guillaume, P.; De Sitter, G. Absorption measurement of acoustic materials using a scanning laser Doppler vibrometer. J. Acoust. Soc. Am. 2005, 117, 1168. [Google Scholar] [CrossRef]
- Longo, R.; Vanlanduit, S.; Arroud, G.; Guillaume, P. Underwater Acoustic Wavefront Visualization by Scanning Laser Doppler Vibrometer for the Characterization of Focused Ultrasonic Transducers. Sensors 2015, 15, 19925–19936. [Google Scholar] [CrossRef] [PubMed]
- Malkin, R.; Todd, T.; Robert, D. A simple method for quantitative imaging of 2D acoustic fields using refracto-vibrometry. J. Sound Vib. 2014, 333, 4473–4482. [Google Scholar] [CrossRef]
- Behrendt, R. Measuring the 3D propagation of sound waves using scanning laser vibrometry. In Proceedings of the Berlin Beamforming Conference, Berlin, Germany, 19–20 February 2008. [Google Scholar]
- Nakamura, K.; Hirayama, M.; Ueha, S. Measurements of air-borne ultrasound by detecting the modulation in optical refractive index of air. In Proceedings of the 2002 IEEE Ultrasonics Symposium, Munich, Germany, 8–11 October 2002; Volume 1, pp. 609–612. [Google Scholar]
- Castellini, P.; Revel, G.; Scalise, L. Measurement of vibrational modal parameters using laser pulse excitation techniques. Measurement 2004, 35, 163–179. [Google Scholar] [CrossRef]
- Vanlanduit, S.; Daerden, F.; Guillaume, P. Experimental modal testing using pressurized air excitation. J. Sound Vib. 2007, 299, 83–98. [Google Scholar] [CrossRef]
- Pézerat, C.; Leclère, Q.; Totaro, N.; Pachebat, M. Identification of vibration excitations from acoustic measurements using near field acoustic holography and the force analysis technique. J. Sound Vib. 2009, 326, 540–556. [Google Scholar] [CrossRef]
- Lin, C.Y. Design and Analysis of Piezoelectric Transformer Converters. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, Virginia, 1997. [Google Scholar]
- TDK Electronics. Cold Plasma from a Single Component. In Applications & Cases; TDK Electronics: München, Germany, 2014; Available online: https://www.tdk-electronics.tdk.com/en/373562/tech-library/articles/applications-cases/applications-cases/cold-plasma-from-a-single-component/1109546 (accessed on 31 October 2014).
- CUI Devices. CUSA-TR60-06-2200-W68 Ultrasonic Transceiver Datasheet. Available online: https://www.cuidevices.com/product/sensors/ultrasonic-sensors/ultrasonic-transceivers/cusa-tr60-06-2200-w68 (accessed on 8 May 2022).
- Hasheminejad, N.; Vanlanduit, S.; Ghalandari, T.; Pierron, F.; Vuye, C. Into a rapid polymer characterization employing optical measurement systems and high-power ultrasonic excitation. Polymer 2024, 294, 126730. [Google Scholar] [CrossRef]





| Parameter Description | Parameter Value |
|---|---|
| Operating frequency (kHz) | 50 |
| Weight (g) | 8.0 ± 1.6 |
| (mm) | 72 × 6 × 2.8 |
| Material | PZT (lead–zirconate–titanate) |
| Maximum operating power (W) | 8.0 |
| Input control board voltage (V) | 24 |
| Parameter Description | Parameter Value |
|---|---|
| Dimensions D × H (mm) | 14 × 9 |
| Detectable Range (m) | 0.3 to 6 |
| Frequency (kHz) | 48 |
| Rated Voltage (Vp-p) | 150 |
| Directivity (°) | 60 |
| Operating Temp Range (°C) | −40 to 80 |
| Excitation Source | Max. Measured Velocity in Refracto-Vibrometry [m/s] | Max. Measured Longitudinal Velocity (at with Sample Surface) [m/s] |
|---|---|---|
| Ultrasound | * | |
| Plasma | * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaderi, N.; Hasheminejad, N.; Dirckx, J.; Vanlanduit, S. Exploring the Use of Cold Atmospheric Plasma for Sound and Vibration Generation. Sensors 2024, 24, 3518. https://doi.org/10.3390/s24113518
Ghaderi N, Hasheminejad N, Dirckx J, Vanlanduit S. Exploring the Use of Cold Atmospheric Plasma for Sound and Vibration Generation. Sensors. 2024; 24(11):3518. https://doi.org/10.3390/s24113518
Chicago/Turabian StyleGhaderi, Nasser, Navid Hasheminejad, Joris Dirckx, and Steve Vanlanduit. 2024. "Exploring the Use of Cold Atmospheric Plasma for Sound and Vibration Generation" Sensors 24, no. 11: 3518. https://doi.org/10.3390/s24113518
APA StyleGhaderi, N., Hasheminejad, N., Dirckx, J., & Vanlanduit, S. (2024). Exploring the Use of Cold Atmospheric Plasma for Sound and Vibration Generation. Sensors, 24(11), 3518. https://doi.org/10.3390/s24113518







