Early Warning for Continuous Rigid Frame Bridges Based on Nonlinear Modeling for Temperature-Induced Deflection
Abstract
1. Introduction
2. Theory
2.1. Nonlinear Modeling for the TID Based on the KPCA-SVM
2.1.1. Kernel Principal Component Analysis
2.1.2. Support Vector Machine
2.2. Sensitivity Analysis of the TID to Bridge Degradation
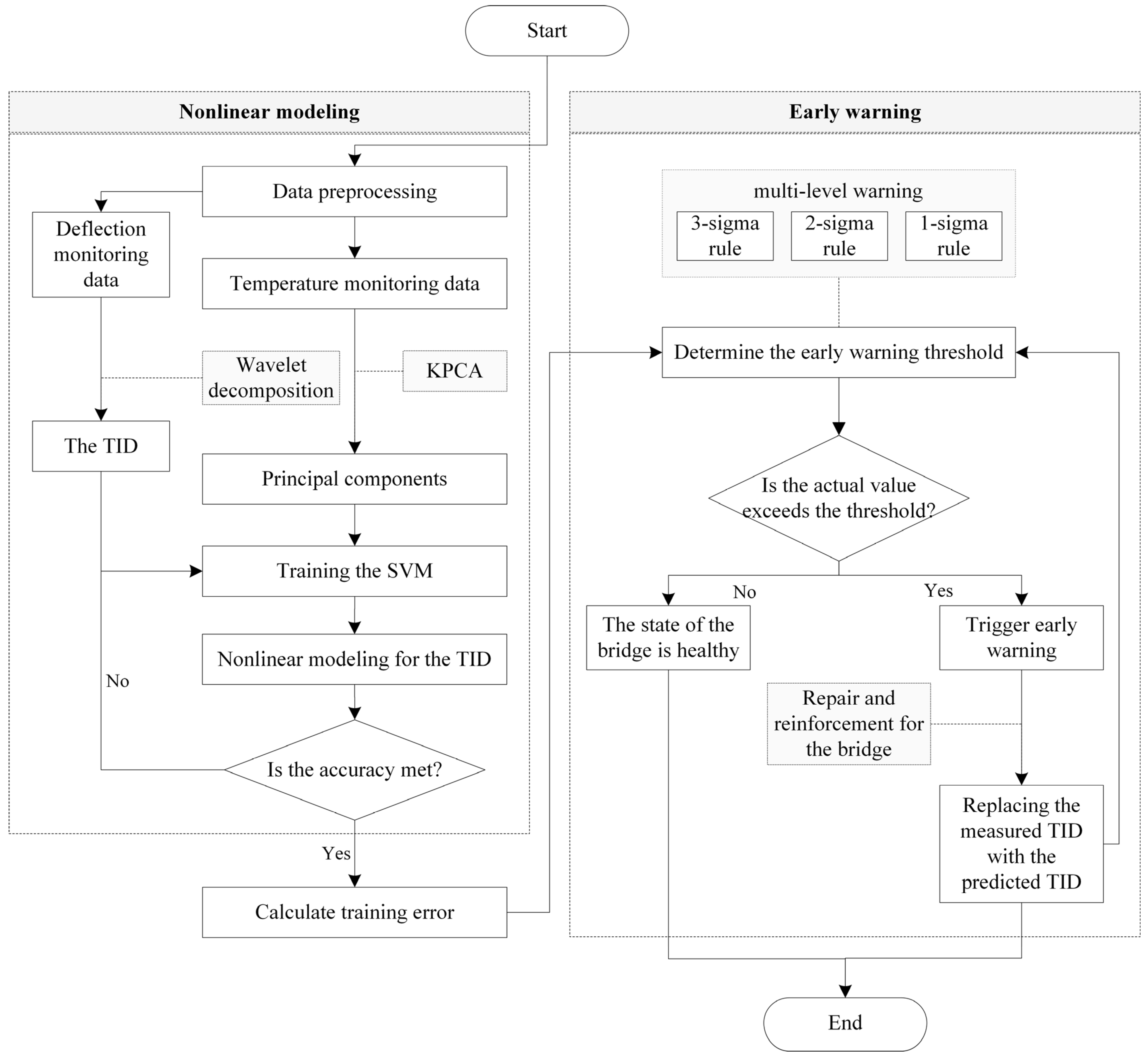
2.3. Flow Chart for the Proposed Early Warning Method
- (1)
- Preprocess the data from the SHM system to obtain temperature monitoring values and deflection monitoring values, and use wavelet decomposition techniques to extract the TID.
- (2)
- Perform kernel principal component analysis on the temperature monitoring values to extract the principal components that reflect temperature gradient information across the bridge cross-section.
- (3)
- Use the results of kernel principal component analysis as inputs and the TID as outputs of the SVM to conduct a regression analysis of deflection responses under temperature influence.
- (4)
- Set warning thresholds based on the statistical characteristics of the TID prediction errors to achieve early warnings for bridges.
- (5)
- When the early warning is triggered, take repair and reinforcement measures to bring the bridge back to an intact state, and replace the measured TID with the predicted TID during the process of repair and reinforcement.
3. Introduction of the SHM System and Data Analysis
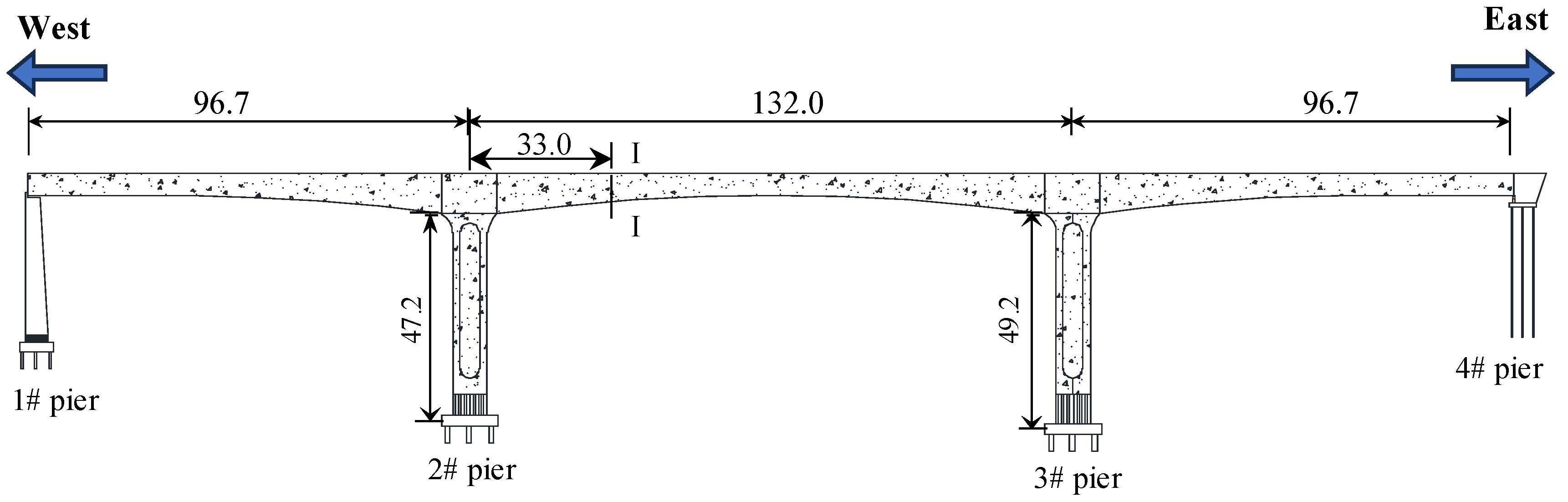
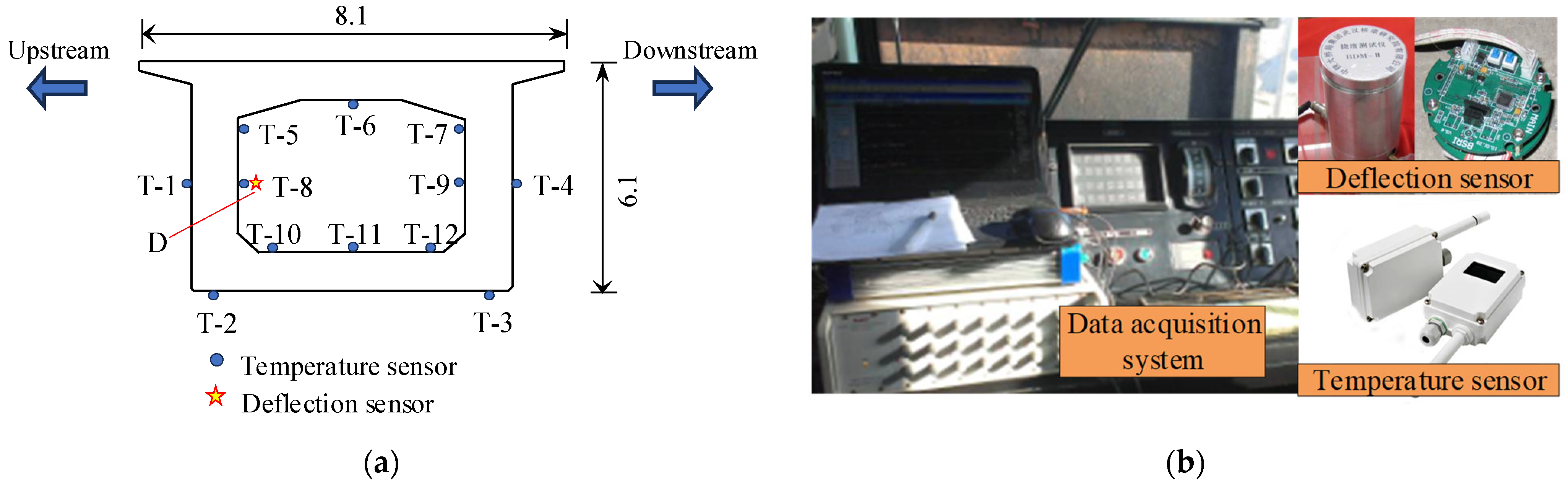
3.1. Health Monitoring System of the Yellow River Bridge
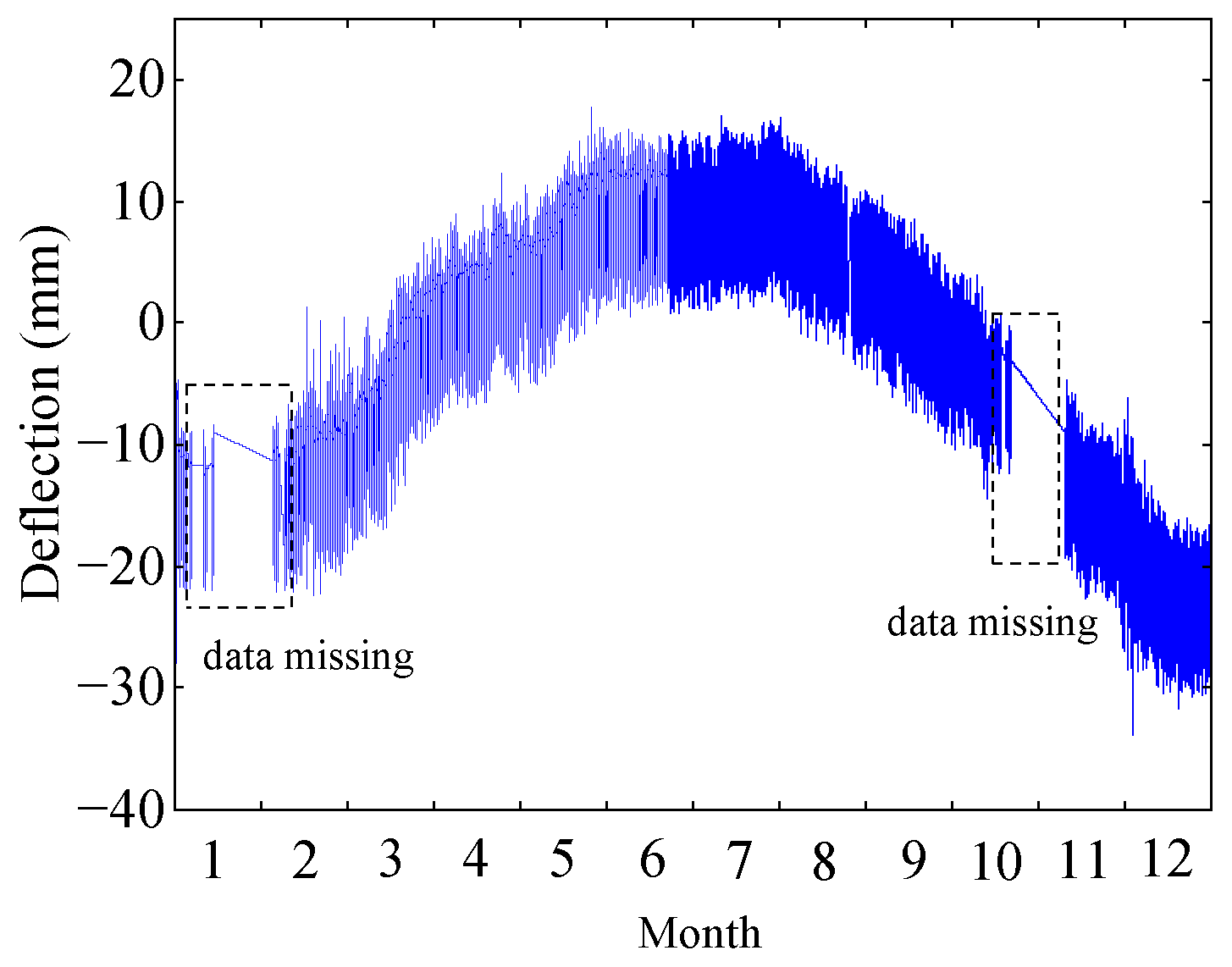
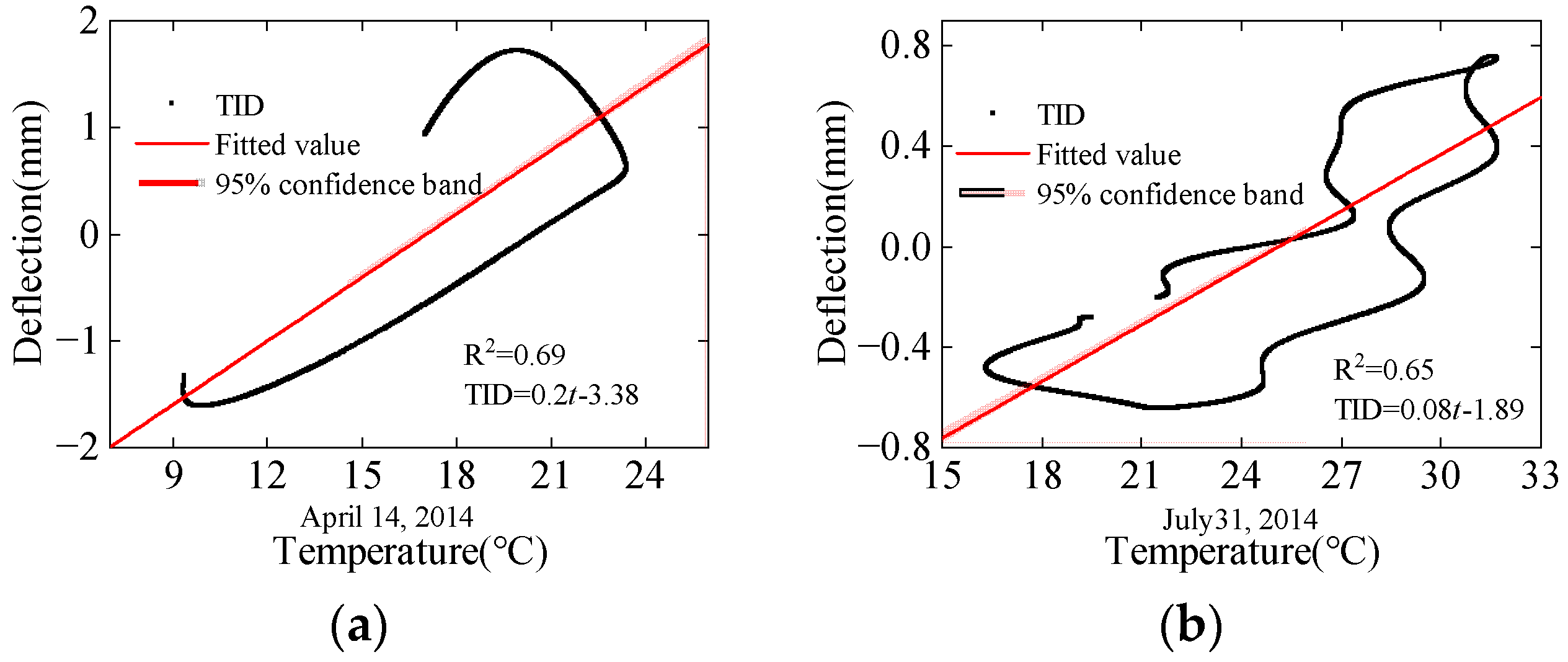
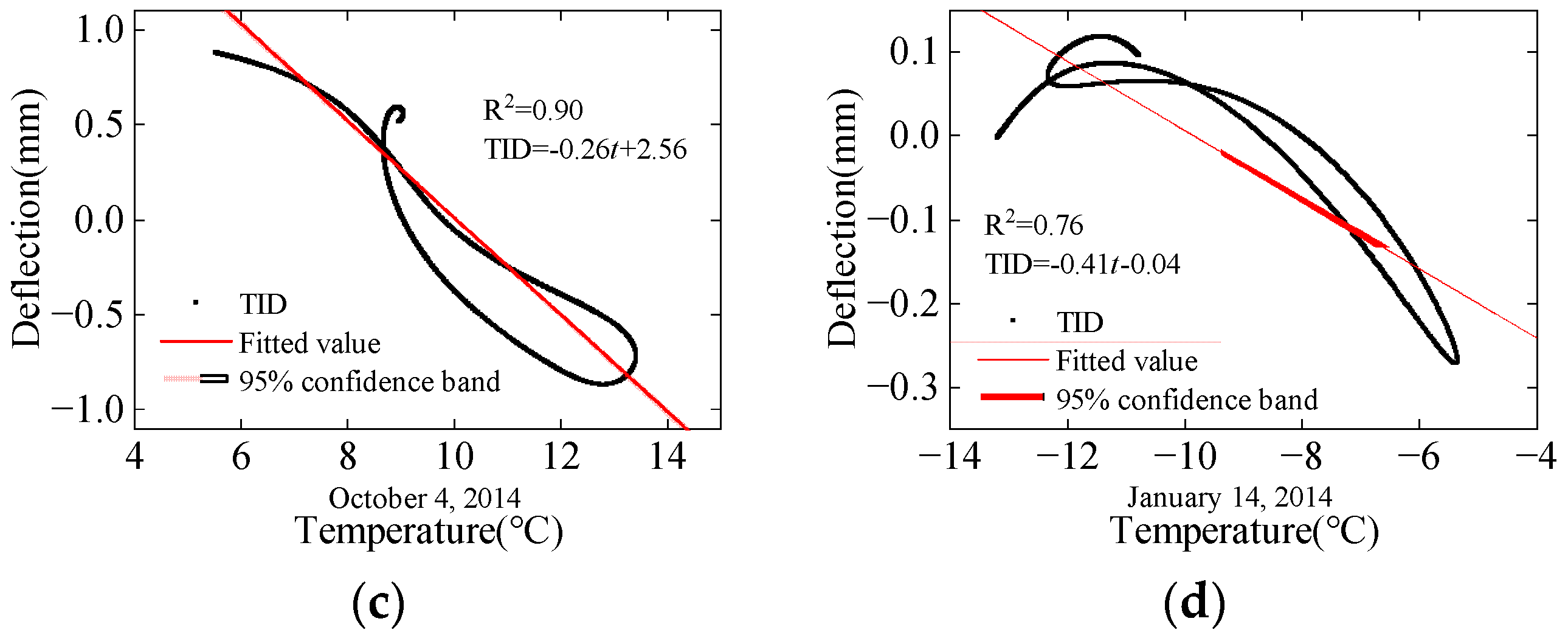
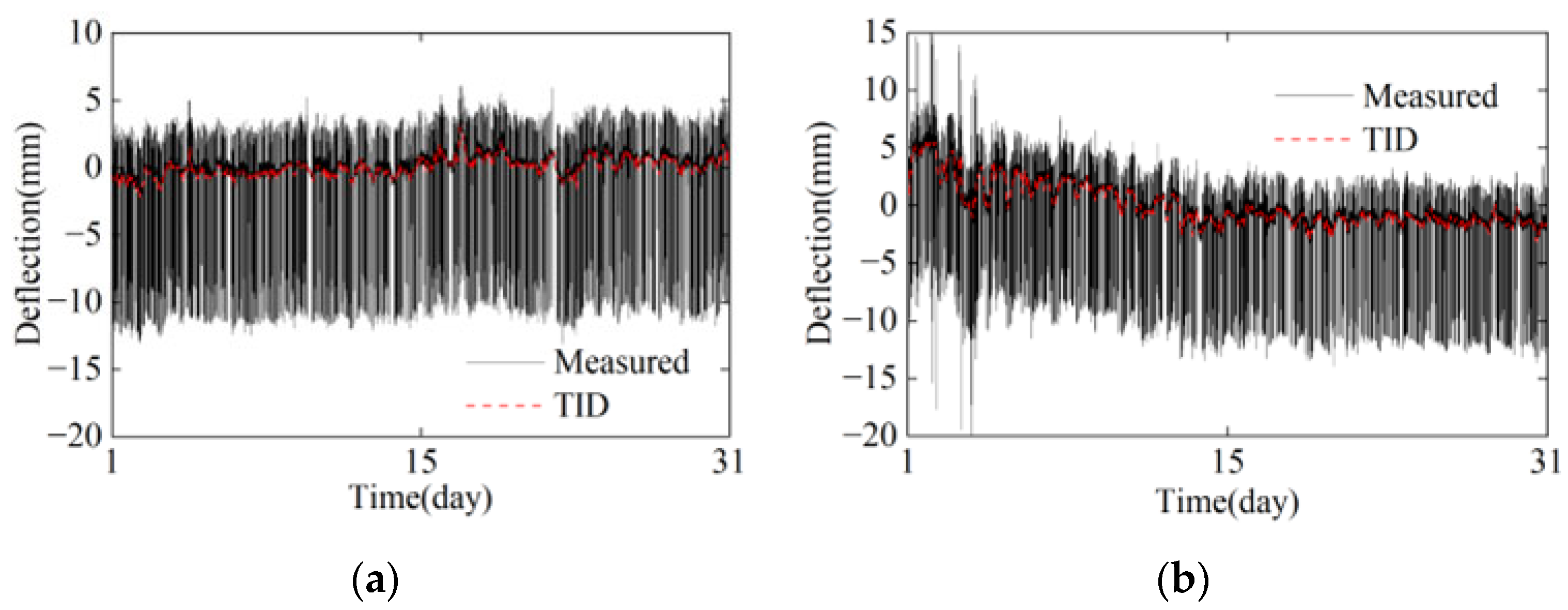
3.2. Analysis for Deflection Data
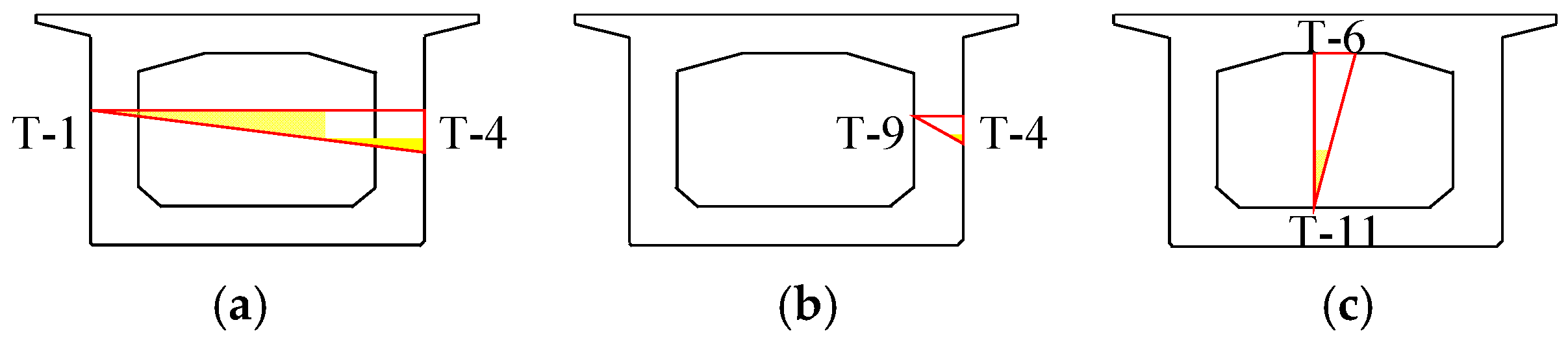
3.3. Cross-Section Temperature Gradient Analysis
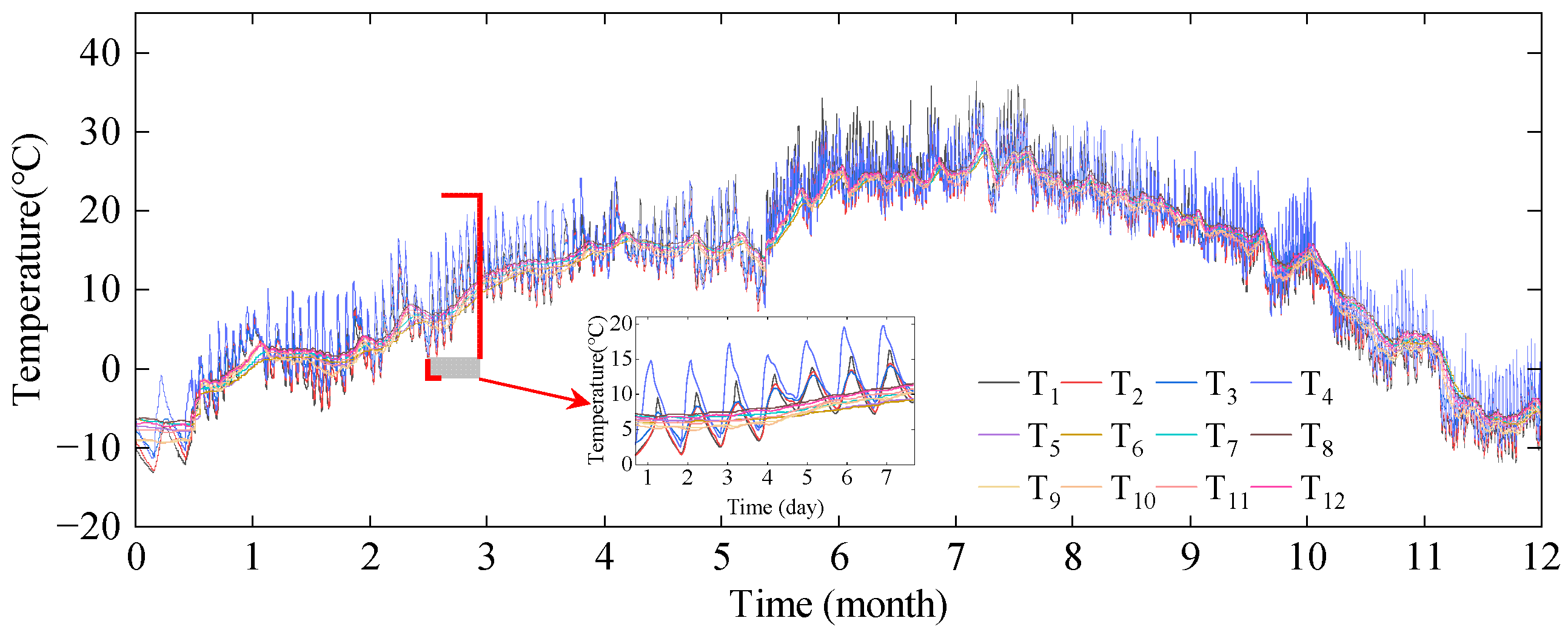
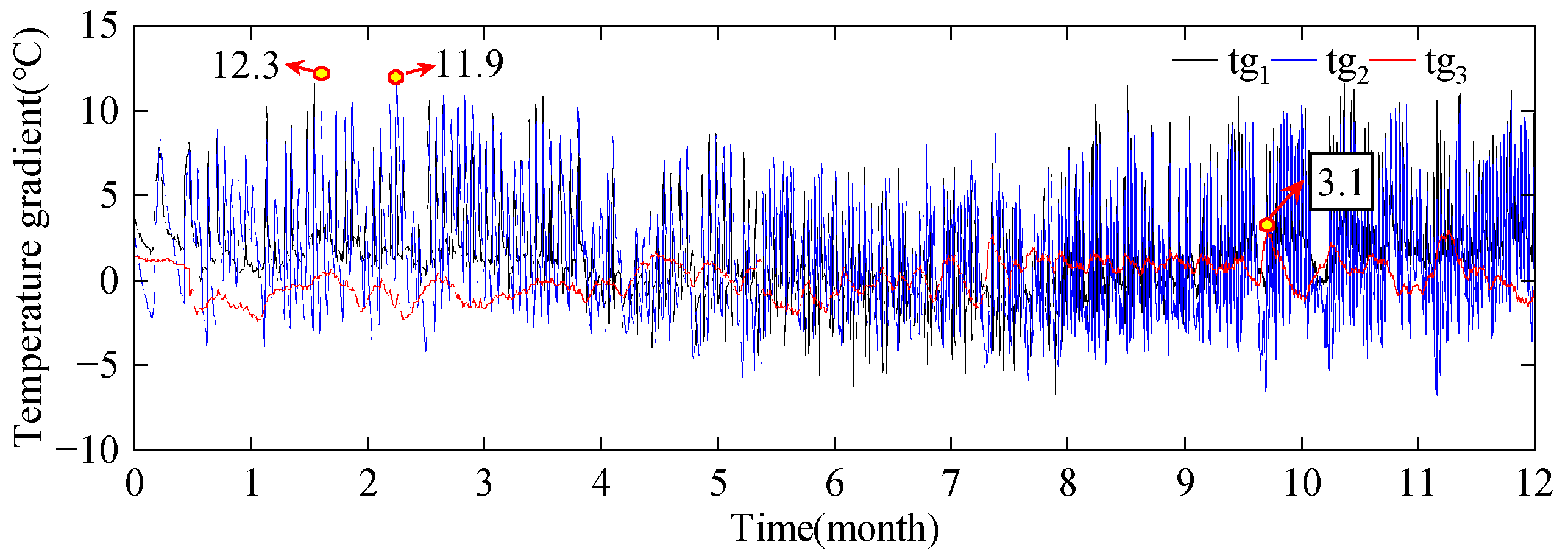
3.3.1. Patterns of Temperature Variation
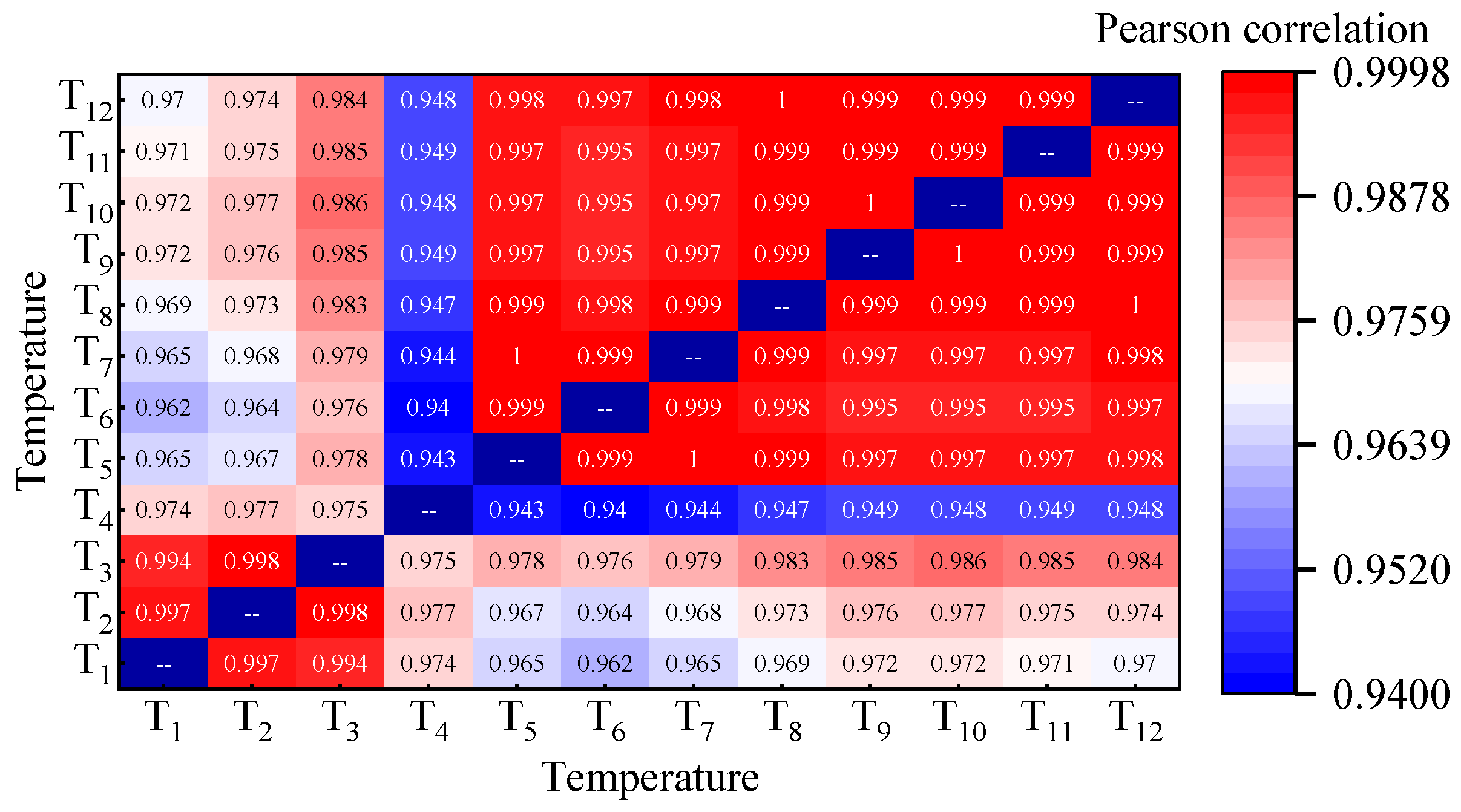
3.3.2. Temperature Correlation Analysis
4. Nonlinear Modeling for the TID
4.1. Temperature Principal Component
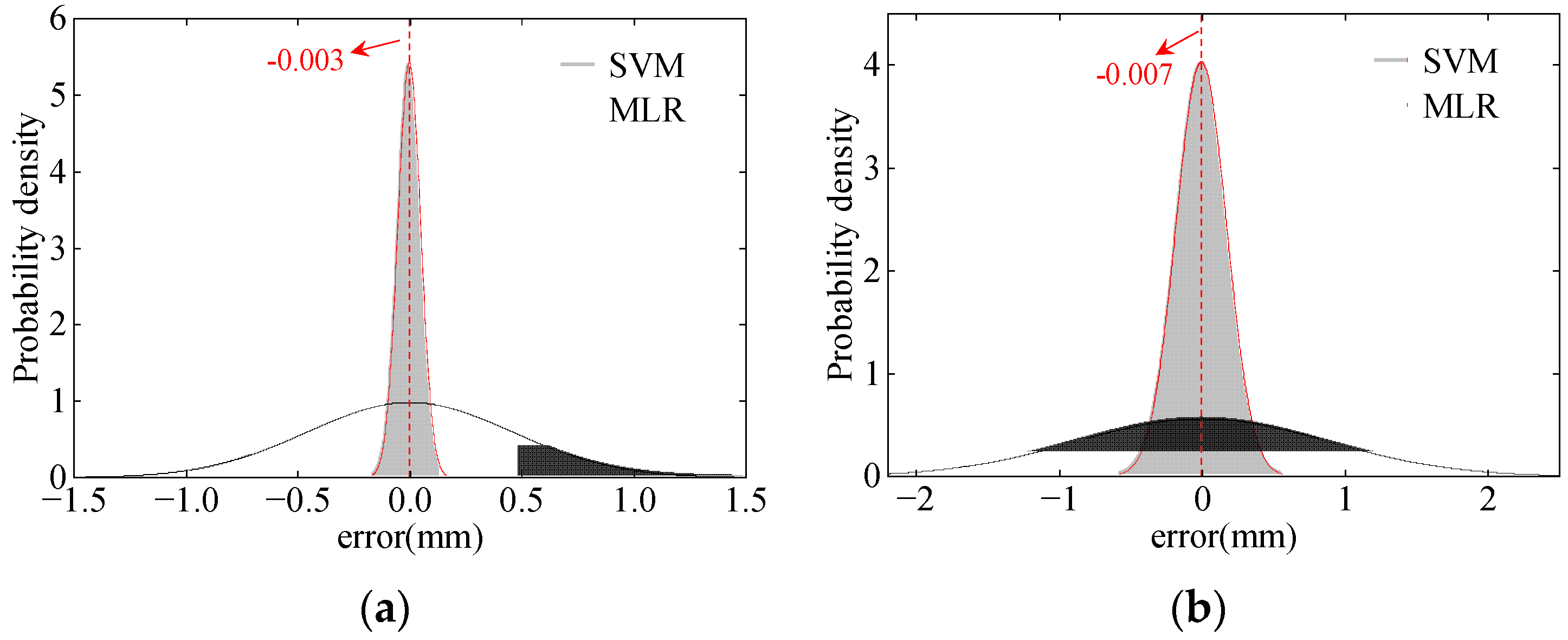
4.2. Nonlinear Modeling for the TID
5. Early Warning for Bridges
5.1. Selection of the Warning Threshold
5.2. Selection of the Training Set
6. Conclusions
- (1)
- The deflection response of the bridge is consistent with the trend of structural temperature changes, following sinusoidal function patterns over one year and one day. Due to the time-lag effect, the linear regression analysis between temperature and the TID results in a circular pattern. It is difficult for both the simple linear and multiple linear regression to accurately predict the TID.
- (2)
- Temperature monitoring values at different points on the cross-section of the concrete box girder bridge exhibit two forms of variation: inside and outside of the box. The outside box has higher absolute temperatures and greater fluctuations, while the inside box has lower absolute temperatures and smoother fluctuations. The Pearson correlation coefficients of temperature monitoring values from different points are greater than 0.94, but the peak times differ, and there is a significant temperature gradient across the cross-section of the concrete box girder.
- (3)
- Extracting temperature gradient information from the bridge cross-section using the KPCA-SVM algorithm allows for the establishment of an accurate nonlinear TID prediction model while significantly reducing the computational burden. The prediction model achieves the coefficients of determination (R2) greater than 0.98. The KPCA-SVM algorithm demonstrates a strong generalization ability, with the correlation coefficient of prediction results remaining above 0.95 even when the ratio of the training set to the validation set is reduced to 1:1.
- (4)
- The TID can be used as an indicator for continuous rigid frame bridge performance degradation. Setting the TID early warning thresholds based on the statistical patterns of KPCA-SVM algorithm training errors enables dynamic warnings for bridges, and the implementation of multi-level warnings can be achieved by a simple adjustment of parameters. A combination of early warning systems and on-site manual inspections provides important safeguards for the safe operation of bridges.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, X.; Song, X.; Cai, C.S.; Li, G.; Xiong, W. Early warning for abnormal strains of continuous bridges using a proposed temperature-strain mapping model. Smart Mater. Struct. 2023, 32, 125018. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, W.; Zhang, A.; Wu, N.; Liu, Z. Structural Damage Identification Based on Variable-Length Elements and an Improved Genetic Algorithm for Railway Bridges. Appl. Sci. 2022, 12, 5706. [Google Scholar] [CrossRef]
- Tan, D.; Guo, T.; Luo, H.; Ji, B.; Tao, Y.; Li, A. Dynamic Threshold Cable-Stayed Bridge Health Monitoring System Based on Temperature Effect Correction. Sensors 2023, 23, 8826. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yi, T.-H.; Yang, D.-H.; Li, H.-N.; Liu, H. Early Warning of Abnormal Bridge Frequencies Based on a Local Correlation Model under Multiple Environmental Conditions. J. Bridge Eng. 2023, 28, 04022139. [Google Scholar] [CrossRef]
- Yu, S.; Ou, J. Structural Health Monitoring and Model Updating of Aizhai Suspension Bridge. J. Aerosp. Eng. 2017, 30, 4016009. [Google Scholar] [CrossRef]
- Han, Q.; Ma, Q.; Xu, J.; Liu, M. Structural health monitoring research under varying temperature condition: A review. J. Civ. Struct. Health Monit. 2021, 11, 149–173. [Google Scholar] [CrossRef]
- Fu, M.; Liang, Y.; Feng, Q.; Wu, B.; Tang, G. Research on the Application of Multi-Source Data Analysis for Bridge Safety Monitoring in the Reconstruction and Demolition Process. Buildings 2022, 12, 1195. [Google Scholar] [CrossRef]
- Zhao, H.-W.; Ding, Y.-L.; Nagarajaiah, S.; Li, A.-Q. Behavior Analysis and Early Warning of Girder Deflections of a Steel-Truss Arch Railway Bridge under the Effects of Temperature and Trains: Case Study. J. Bridge Eng. 2019, 24, 05018013. [Google Scholar] [CrossRef]
- Xia, Q.; Cheng, Y.; Zhang, J.; Zhu, F. In-Service Condition Assessment of a Long-Span Suspension Bridge Using Temperature-Induced Strain Data. J. Bridge Eng. 2017, 22, 04016124. [Google Scholar] [CrossRef]
- Zhu, F.; Yu, Y.; Li, P.; Zhang, J. The Multi-Scale Model Method for U-Ribs Temperature-Induced Stress Analysis in Long-Span Cable-Stayed Bridges through Monitoring Data. Sustainability 2023, 15, 9149. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, J.; Hu, J.; Ye, Z.; Deng, Z.; Wan, N. Nonlinear modeling of temperature-induced bearing displacement of long-span single-pier rigid frame bridge based on DCNN-LSTM. Case Stud. Therm. Eng. 2024, 53, 103897. [Google Scholar] [CrossRef]
- Zhu, Q.-X.; Wang, H.; Mao, J.-X.; Wan, H.-P.; Zheng, W.-Z.; Zhang, Y.-M. Investigation of Temperature Effects on Steel-Truss Bridge Based on Long-Term Monitoring Data: Case Study. J. Bridge Eng. 2020, 25, 05020007. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, H.; Spencer, B.F.; Mao, J. Mapping of Temperature-Induced Response Increments for Monitoring Long-Span Steel Truss Arch Bridges Based on Machine Learning. J. Struct. Eng. 2022, 148, 04022034. [Google Scholar] [CrossRef]
- Li, S.; Xin, J.; Jiang, Y.; Wang, C.; Zhou, J.; Yang, X. Temperature-induced deflection separation based on bridge deflection data using the TVFEMD-PE-KLD method. J. Civ. Struct. Health Monit. 2023, 13, 781–797. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, H.; Cao, H.; Zhang, X.; Zhang, A.; Wu, N.; Liu, Z. Separation of Temperature-Induced Response for Bridge Long-Term Monitoring Data Using Local Outlier Correction and Savitzky-Golay Convolution Smoothing. Sensors 2023, 23, 2632. [Google Scholar] [CrossRef]
- An, L.; Li, D.; Yuan, P.; Chen, P. An Analytical Algorithm for Determining Optimal Thin-Walled Hollow Pier Configuration with Sunlight Temperature Differences. Buildings 2023, 13, 1208. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, Y.; Chen, B.; Fujino, Y. Analytical solution to temperature-induced deformation of suspension bridges. Mech. Syst. Sig. Process. 2020, 139, 106568. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, Y.; Fujino, Y. Analytical formulas of beam deflection due to vertical temperature difference. Eng. Struct. 2021, 240, 112366. [Google Scholar] [CrossRef]
- Wang, G.-X.; Ding, Y.-L.; Song, Y.-S.; Wu, L.-Y.; Yue, Q.; Mao, G.-H. Detection and Location of the Degraded Bearings Based on Monitoring the Longitudinal Expansion Performance of the Main Girder of the Dashengguan Yangtze Bridge. J. Perform. Constr. Facil. 2016, 30, 04015074. [Google Scholar] [CrossRef]
- Wu, G.-M.; Yi, T.-H.; Yang, D.-H.; Li, H.-N.; Liu, H. Early Warning Method for Bearing Displacement of Long-Span Bridges Using a Proposed Time-Varying Temperature-Displacement Model. J. Bridge Eng. 2021, 26, 04021068. [Google Scholar] [CrossRef]
- Yue, Z.; Ding, Y.; Zhao, H.; Wang, Z. Mechanics-Guided optimization of an LSTM network for Real-Time modeling of Temperature-Induced deflection of a Cable-Stayed bridge. Eng. Struct. 2022, 252, 113619. [Google Scholar] [CrossRef]
- Yue, Z.; Ding, Y.; Zhao, H.; Wang, Z. Ultra-high precise Stack-LSTM-CNN model of temperature-induced deflection of a cable-stayed bridge for detecting bridge state driven by monitoring data. Structures 2022, 45, 110–125. [Google Scholar] [CrossRef]
- Sun, Z.; Lou, P.; Huang, X. Temperature gradient of ballastless track in large daily temperature difference region and its influence on dynamic responses of vehicle-track-bridge system. Alex. Eng. J. 2023, 85, 114–131. [Google Scholar] [CrossRef]
- Xia, Z.; Guo, J.; Yue, Z.; Ding, Y.; Wang, Z.; Sun, S. Digital Model of Deflection of a Cable-Stayed Bridge Driven by Deep Learning and Big Data Optimized via PCA-LGBM. Sustainability 2023, 15, 9623. [Google Scholar] [CrossRef]
- Yan, Y.; Wu, X.; Wu, Z. Bridge safety monitoring and evaluation based on hesitant fuzzy set. Alex. Eng. J. 2022, 61, 1183–1200. [Google Scholar] [CrossRef]
- Li, G.; Ran, R.J.; Fang, J.; Peng, H.; Wang, S.M. Early Warning for the Construction Safety Risk of Bridge Projects Using a RS-SSA-LSSVM Model. Adv. Civ. Eng. 2021, 2021, 4449451. [Google Scholar] [CrossRef]
- Qu, B.; Huang, Y.; She, J.; Liao, P.; Lai, X. Forecasting and early warning of bridge monitoring information based on a multivariate time series ARDL model. Phys. Chem. Earth 2024, 133, 103533. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, H.; Spencer, B.F., Jr. Investigation on the mapping for temperature-induced responses of a long-span steel truss arch bridge. Struct. Infrastruct. Eng. 2024, 20, 232–249. [Google Scholar] [CrossRef]
- Li, J.-X.; Yi, T.-H.; Qu, C.-X.; Li, H.-N.; Liu, H. Early Warning for Abnormal Cable Forces of Cable-Stayed Bridges Considering Structural Temperature Changes. J. Bridge Eng. 2023, 28, 04022137. [Google Scholar] [CrossRef]
- Xiao, T.; Hong, Y.; Xu, J.; Pu, Q.; Wen, X. Performance evaluation of cable-stayed bridge expansion joints based on Lasso dimensionality reduction and temperature-displacement-correlation model. Adv. Struct. Eng. 2024, 27, 981–994. [Google Scholar] [CrossRef]
- Zoubir, H.; Rguig, M.; El Aroussi, M.; Chehri, A.; Saadane, R. Concrete Bridge Crack Image Classification Using Histograms of Oriented Gradients, Uniform Local Binary Patterns, and Kernel Principal Component Analysis. Electronics 2022, 11, 3357. [Google Scholar] [CrossRef]
- Lan, Y.F.; Zhang, Y.Q.; Lin, W.W. Diagnosis algorithms for indirect bridge health monitoring via an optimized AdaBoost-linear SVM. Eng. Struct. 2023, 275, 115239. [Google Scholar] [CrossRef]
- Zhan, Y.L.; Fan, Z.H.; Huang, Y.Y.; Zhang, Z.Q.; Shao, J.H.; An, J.W. Study on shrinkage and creep effect of steel truss-stiffened continuous rigid frame bridge considering variable temperature and relative humidity. Structures 2024, 61, 106120. [Google Scholar] [CrossRef]
- Yuan, Z.Y.; Ng, P.L.; Bacinskas, D.; Du, J.S. Analysis of non-uniform shrinkage effect in box girder sections for long-span continuous rigid frame bridge. Balt. J. Road Bridge Eng. 2018, 13, 146–155. [Google Scholar] [CrossRef]
- Wu, N.; Yang, H.; Afsar, H.; Wang, B.; Fan, J. Analysis of Train–Track–Bridge Coupling Vibration Characteristics for Heavy-Haul Railway Based on Virtual Work Principle. Sensors 2023, 23, 8550. [Google Scholar] [CrossRef]
- Yang, H.; Wu, N.; Zhang, W.; Liu, Z.; Fan, J.; Wang, C. Dynamic Response of Spatial Train-Track-Bridge Interaction System Due to Unsupported Track Using Virtual Work Principle. Appl. Sci. 2022, 12, 6156. [Google Scholar] [CrossRef]
- Xu, X.; Ren, Y.; Huang, Q.; Zhao, D.-Y.; Tong, Z.-J.; Chang, W.-J. Thermal response separation for bridge long-term monitoring systems using multi-resolution wavelet-based methodologies. J. Civ. Struct. Health Monit. 2020, 10, 527–541. [Google Scholar] [CrossRef]






| Model | July | December | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| SVM | 0.99 | 0.08 | 0.06 | 0.98 | 0.10 | 0.07 |
| MLR | 0.47 | 0.51 | 0.40 | 0.78 | 0.88 | 0.68 |
| Ω | R2 | RMSE | MAE |
|---|---|---|---|
| 9:1 | 0.98 | 0.093 | 0.065 |
| 8:2 | 0.98 | 0.100 | 0.065 |
| 7:3 | 0.97 | 0.117 | 0.074 |
| 6:4 | 0.96 | 0.126 | 0.078 |
| 5:5 | 0.95 | 0.144 | 0.089 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Yang, H.; Liu, W.; Ye, Z.; Pei, J.; Liu, Z.; Fan, J. Early Warning for Continuous Rigid Frame Bridges Based on Nonlinear Modeling for Temperature-Induced Deflection. Sensors 2024, 24, 3587. https://doi.org/10.3390/s24113587
Jiang L, Yang H, Liu W, Ye Z, Pei J, Liu Z, Fan J. Early Warning for Continuous Rigid Frame Bridges Based on Nonlinear Modeling for Temperature-Induced Deflection. Sensors. 2024; 24(11):3587. https://doi.org/10.3390/s24113587
Chicago/Turabian StyleJiang, Liangwei, Hongyin Yang, Weijun Liu, Zhongtao Ye, Junwen Pei, Zhangjun Liu, and Jianfeng Fan. 2024. "Early Warning for Continuous Rigid Frame Bridges Based on Nonlinear Modeling for Temperature-Induced Deflection" Sensors 24, no. 11: 3587. https://doi.org/10.3390/s24113587
APA StyleJiang, L., Yang, H., Liu, W., Ye, Z., Pei, J., Liu, Z., & Fan, J. (2024). Early Warning for Continuous Rigid Frame Bridges Based on Nonlinear Modeling for Temperature-Induced Deflection. Sensors, 24(11), 3587. https://doi.org/10.3390/s24113587







