Theoretical and Experimental Analysis of Single-Arm Bimodal Plasmo-Photonic Refractive Index Sensors
Abstract
:1. Introduction
2. Sensitivity Calculations
3. Numerical Validation
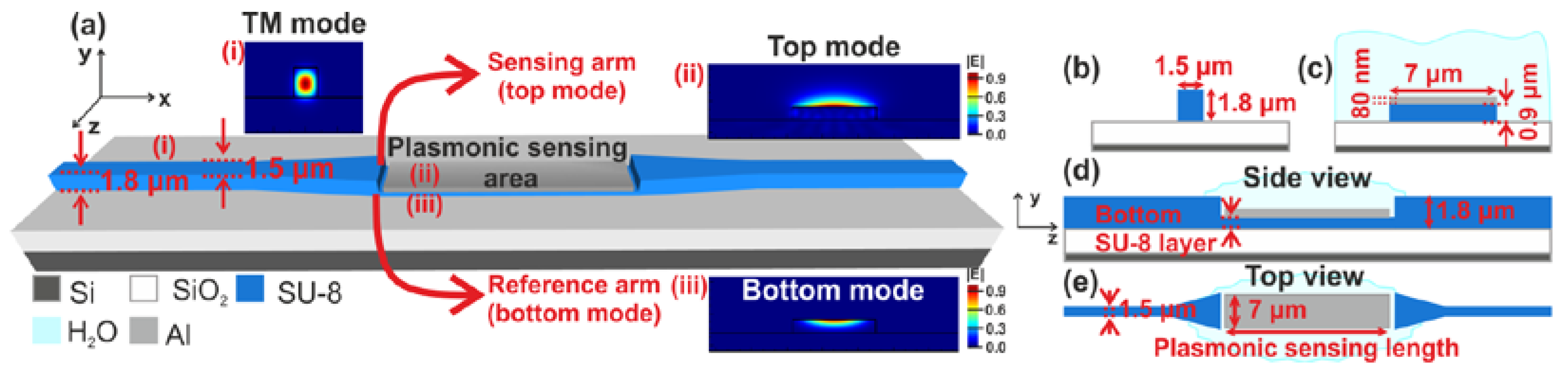
4. Fabrication
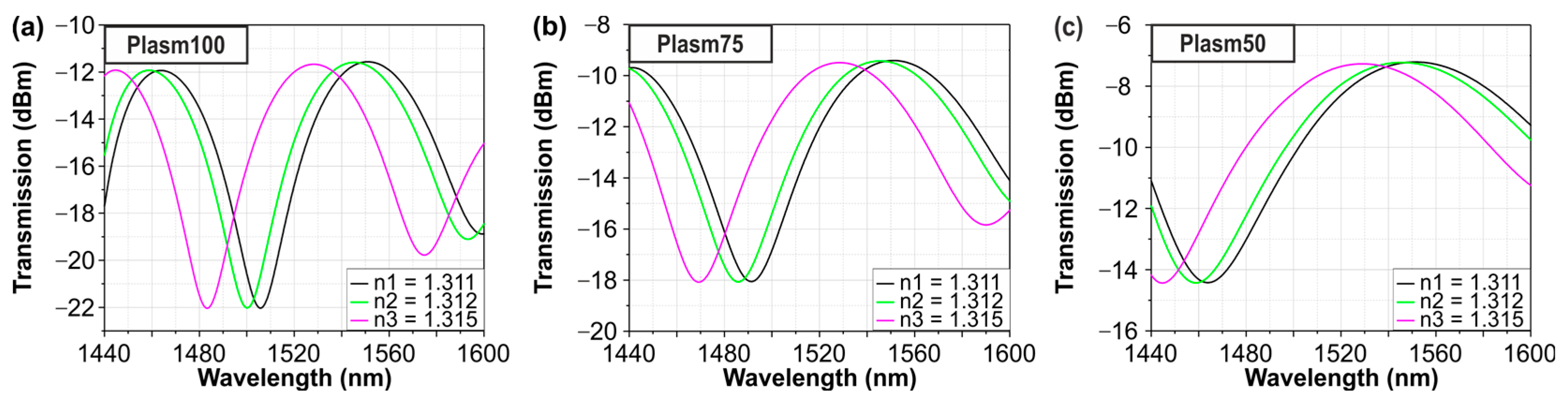
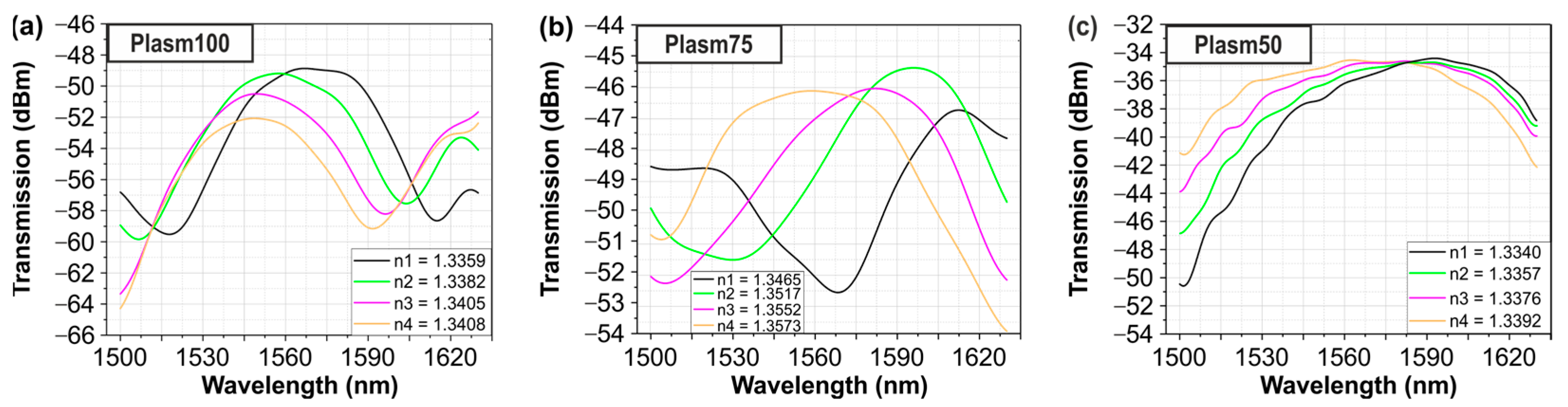
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.; Tu, X.; Kim, K.W.; Kee, J.S.; Shin, Y.; Han, K.; Yoon, Y.J.; Lo, G.Q.; Park, M.K. Highly sensitive Mach-Zehnder interferometer biosensor based on silicon nitride slot waveguide. Sens. Actuators B Chem. 2013, 188, 681–688. [Google Scholar] [CrossRef]
- Sepúlveda, B.; Del Rio, J.S.; Moreno, M.; Blanco, F.J.; Mayora, K.; Domínguez, C.; Lechuga, L.M. Optical biosensor microsystems based on the integration of highly sensitive Mach-Zehnder interferometer devices. J. Opt. A Pure Appl. Opt. 2006, 8, 561–566. [Google Scholar] [CrossRef]
- TalebiFard, S.; Schmidt, S.; Shi, W.; Wu, W.; Jaeger, N.A.; Kwok, E.; Ratner, D.M.; Chrostowski, L. Optimized sensitivity of silicon-on-insulator (SOI) strip waveguide resonator sensor. Biomed. Opt. Express 2017, 8, 500–511. [Google Scholar] [CrossRef] [PubMed]
- Claes, T.; Molera, J.G.; De Vos, K.; Schacht, E.; Baets, R.; Bienstman, P. Label-Free Biosensing with a Slot-Waveguide-Based Ring Resonator in Silicon on Insulator. IEEE Photonics J. 2009, 1, 197–204. [Google Scholar] [CrossRef]
- Khan, A.; Krupin, O.; Lisicka-Skrzek, E.; Berini, P. Mach-Zehnder refractometric sensor using long-range surface plasmon waveguides. Appl. Phys. Lett. 2013, 103, 111108. [Google Scholar] [CrossRef]
- Wong, W.R.; Fan, H.; Adikan, F.R.M.; Berini, P. Multichannel Long-Range Surface Plasmon Waveguides for Parallel Biosensing. J. Light. Technol. 2018, 36, 5536–5546. [Google Scholar] [CrossRef]
- Soler, M.; Lechuga, L.M. Principles, technologies, and applications of plasmonic biosensors. J. Appl. Phys. 2021, 129, 111102. [Google Scholar] [CrossRef]
- Manolis, T.; Dabos, G.; Pleros, N.; Chmielak, B.; Giesecke, A.L.; Porschatis, C.; Cegielski, P.J.; Markey, L.; Weeber, J.-C.; Dereux, A.; et al. Plasmonics co-integrated with silicon nitride photonics for high sensitivity interferometric biosensing. Opt. Express 2019, 27, 17102. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Dai, D.; Thylén, L.; Wosinski, L. Double-Slot Hybrid Plasmonic Ring Resonator Used for Optical Sensors and Modulators. Photonics 2015, 2, 1116–1130. [Google Scholar] [CrossRef]
- Debackere, P.; Scheerlinck, S.; Bienstman, P.; Baets, R. Surface plasmon interferometer in silicon-on-insulator: Novel concept for an integrated biosensor. Opt. Express 2006, 14, 7063–7072. [Google Scholar] [CrossRef] [PubMed]
- Chatzianagnostou, E.; Dabos, G.; Manolis, A.; Markey, L.; Weeber, J.-C.; Dereux, A.; Tsiokos, D.; Pleros, N. Ultra-compact single-arm interferometric plasmonic sensor co-integrated on a TiO2 photonic waveguide platform. In Integrated Optics: Devices, Materials, and Technologies XXIII; SPIE: San Francisco, CA, USA, 2019; Volume 10921. [Google Scholar]
- Dante, S.; Duval, D.; Fariña, D.; González-Guerrero, A.B.; Lechuga, L.M. Linear readout of integrated interferometric biosensors using a periodic wavelength modulation. Laser Photonics Rev. 2015, 9, 248–255. [Google Scholar] [CrossRef]
- Torrijos-Morán, L.; Lisboa, B.D.; Soler, M.; Lechuga, L.M.; García-Rupérez, J. Integrated optical bimodal waveguide biosensors: Principles and applications. Results Opt. 2022, 9, 100285. [Google Scholar] [CrossRef]
- Hassan, K.; Weeber, J.-C.; Markey, L.; Dereux, A.; Pitilakis, A.; Tsilipakos, O.; Kriezis, E.E. Thermo-optic plasmo-photonic mode interference switches based on dielectric loaded waveguides. Appl. Phys. Lett. 2011, 99, 241110. [Google Scholar] [CrossRef]
- Liang, Y.; Zhao, M.; Wu, Z.; Morthier, G. Bimodal Waveguide Interferometer RI Sensor Fabricated on Low-Cost Polymer Platform. IEEE Photonics J. 2019, 11, 6801108. [Google Scholar] [CrossRef]
- Fotiadis, K.; Chatzianagnostou, E.; Spasopoulos, D.; Simos, S.; Bellas, D.V.; Bhalerao, O.; Suckow, S.; Schall-Giesecke, A.L.; Lemme, M.; Weeber, J.-C.; et al. A High-Sensitivity Bi-modal Plasmo-photonic Refractive Index Sensor. ACS Photonics 2023, 10, 2580–2588. [Google Scholar] [CrossRef]
- Chatzianagnostou, E.; Manolis, A.; Miliou, A.; Tsiokos, D.; Pleros, N. Theory and Sensitivity Optimization of Plasmo-photonic Mach-Zehnder Interferometric Sensors. J. Light. Technol. 2021, 39, 5206–5217. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids I–III; Academic Press: Orlando, FL, USA, 1998. [Google Scholar]
- Moran, L.T.; Griol, A.; Ruperez, J.G. Experimental study of subwavelength grating bimodal waveguides as ultrasensitive interferometric sensors. Opt. Lett. 2019, 44, 4702–4705. [Google Scholar] [CrossRef] [PubMed]
- Szunerits, S.; Boukherroub, R. Sensing using localized surface plasmon resonance sensors. ChemComm 2012, 48, 8999–9010. [Google Scholar]
- Xu, Y.; Wu, L.; Ang, L.K. Surface Exciton Polaritons: A Promising Mechanism for Refractive-Index Sensing. Phys. Rev. Appl. 2019, 12, 024029. [Google Scholar] [CrossRef]
- Chu, Y.S.; Hsu, W.H.; Lin, C.W.; Wang, W.S. Surface plasmon resonance sensors using silica-on-silicon optical waveguides. Microw. Opt. Technol. Lett. 2006, 48, 955–957. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fotiadis, K.; Chatzianagnostou, E.; Spasopoulos, D.; Simos, S.; Bellas, D.V.; Bhalerao, O.; Suckow, S.; Lemme, M.C.; Lidorikis, E.; Pleros, N. Theoretical and Experimental Analysis of Single-Arm Bimodal Plasmo-Photonic Refractive Index Sensors. Sensors 2024, 24, 3705. https://doi.org/10.3390/s24123705
Fotiadis K, Chatzianagnostou E, Spasopoulos D, Simos S, Bellas DV, Bhalerao O, Suckow S, Lemme MC, Lidorikis E, Pleros N. Theoretical and Experimental Analysis of Single-Arm Bimodal Plasmo-Photonic Refractive Index Sensors. Sensors. 2024; 24(12):3705. https://doi.org/10.3390/s24123705
Chicago/Turabian StyleFotiadis, Konstantinos, Evangelia Chatzianagnostou, Dimosthenis Spasopoulos, Stelios Simos, Dimitris V. Bellas, Omkar Bhalerao, Stephan Suckow, Max C. Lemme, Elefterios Lidorikis, and Nikos Pleros. 2024. "Theoretical and Experimental Analysis of Single-Arm Bimodal Plasmo-Photonic Refractive Index Sensors" Sensors 24, no. 12: 3705. https://doi.org/10.3390/s24123705
APA StyleFotiadis, K., Chatzianagnostou, E., Spasopoulos, D., Simos, S., Bellas, D. V., Bhalerao, O., Suckow, S., Lemme, M. C., Lidorikis, E., & Pleros, N. (2024). Theoretical and Experimental Analysis of Single-Arm Bimodal Plasmo-Photonic Refractive Index Sensors. Sensors, 24(12), 3705. https://doi.org/10.3390/s24123705







