Classification of Visually Induced Motion Sickness Based on Phase-Locked Value Functional Connectivity Matrix and CNN-LSTM
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
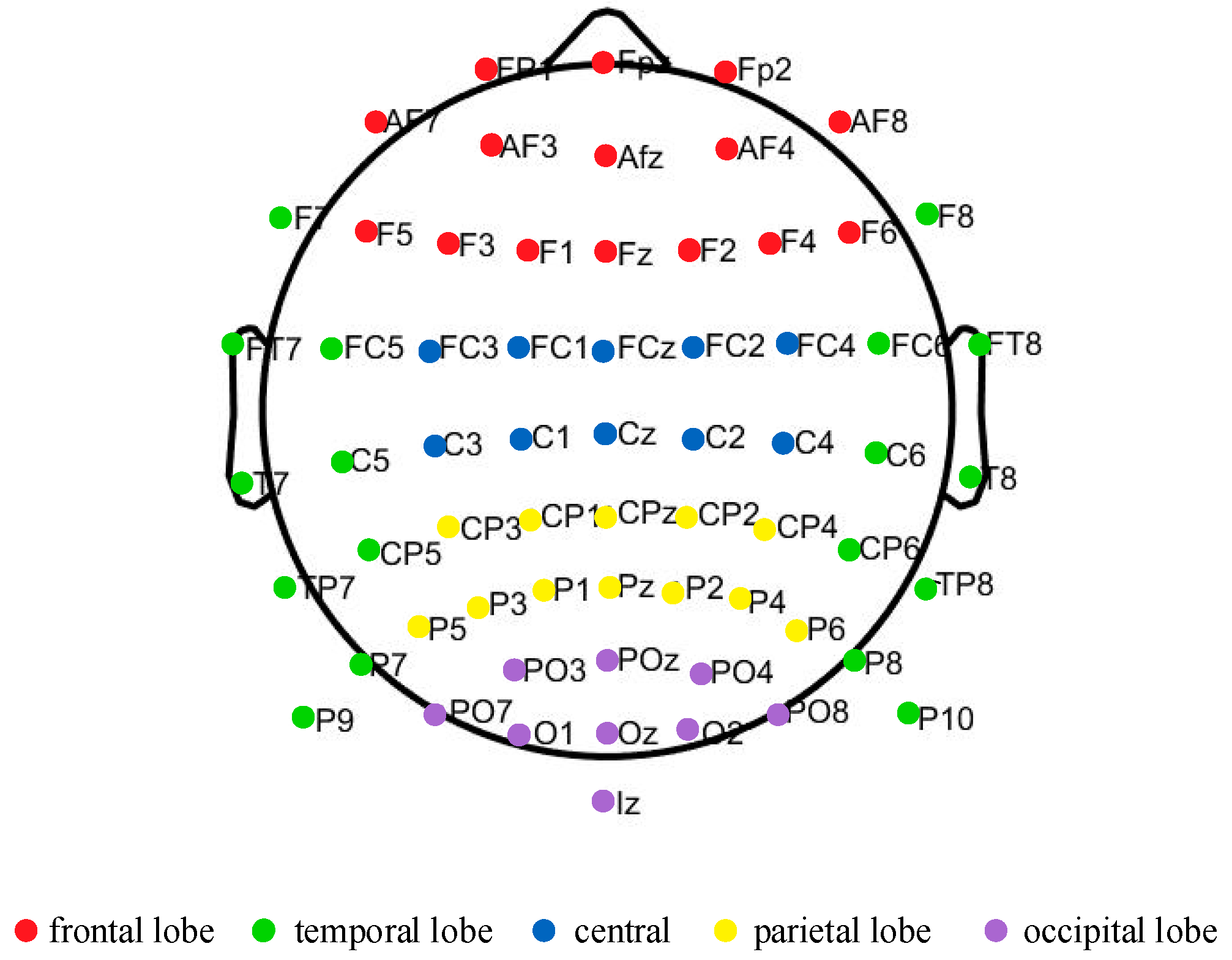
2.2. Experiment Platform Construction
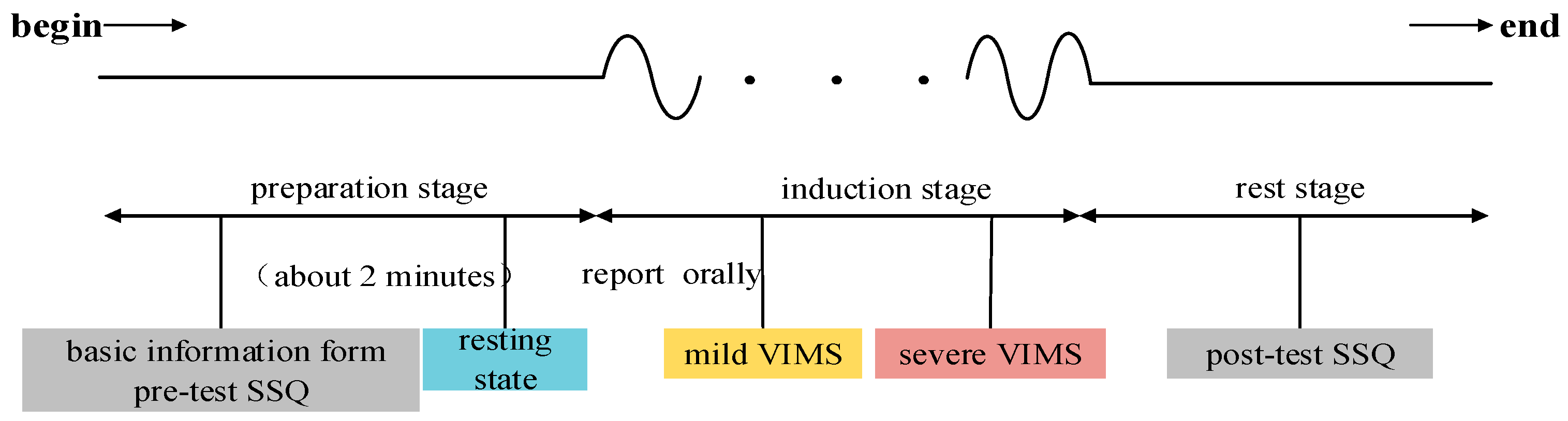
2.3. Experimental Procedure
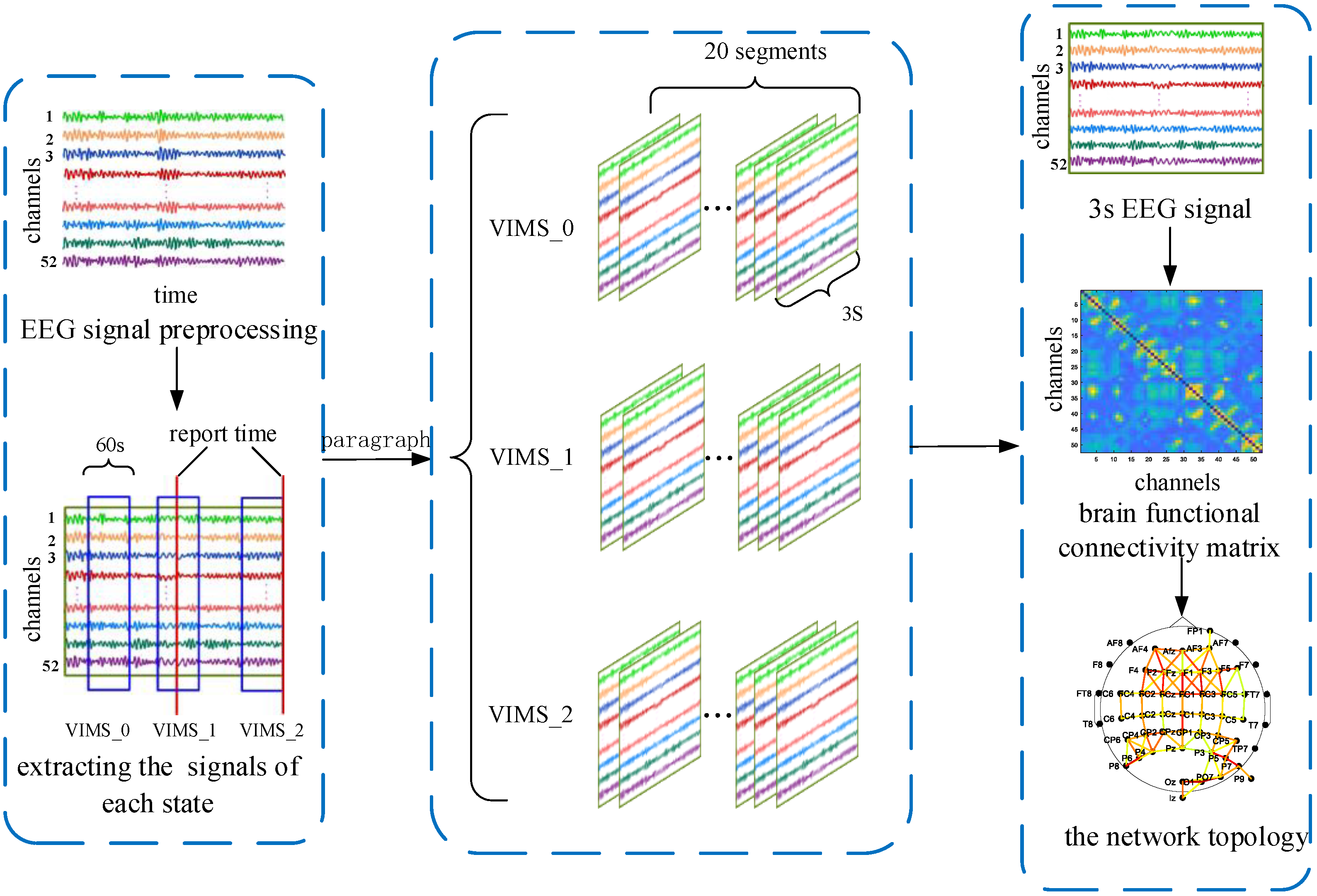
2.4. EEG Signal Preprocessing
2.5. PLV Functional Connectivity Matrix Construction
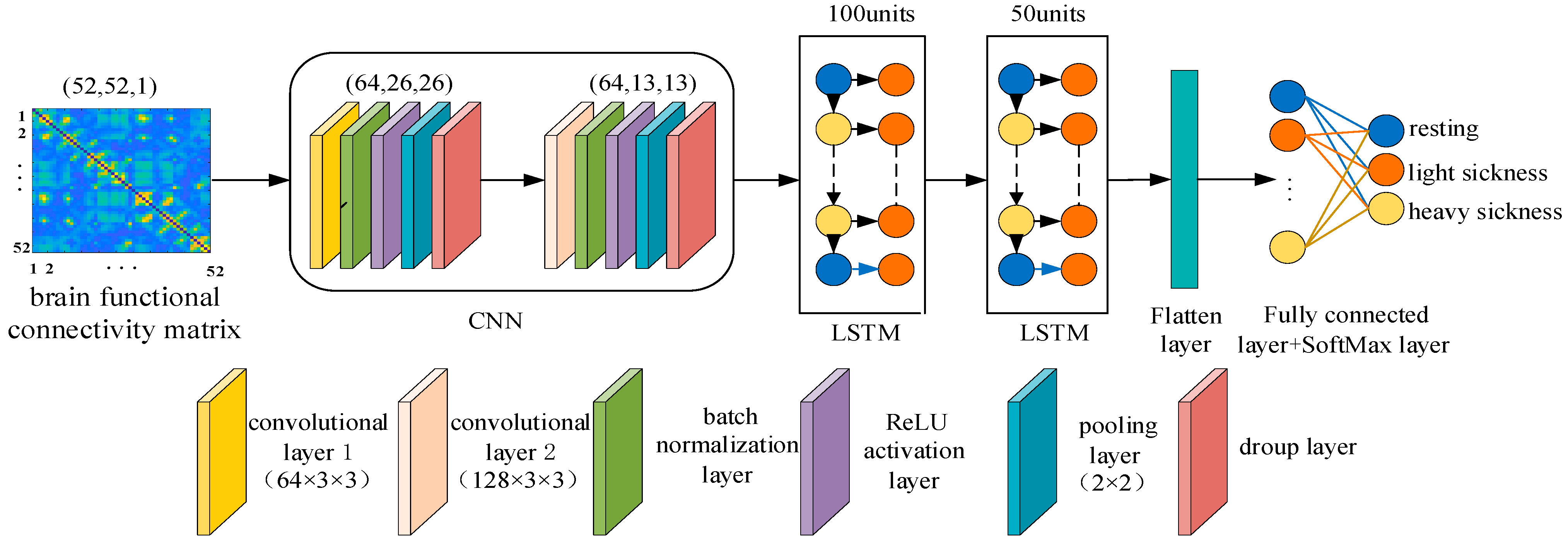
2.6. Classification Modeling
2.7. Performance Evaluation Methods
3. Results and Discussion
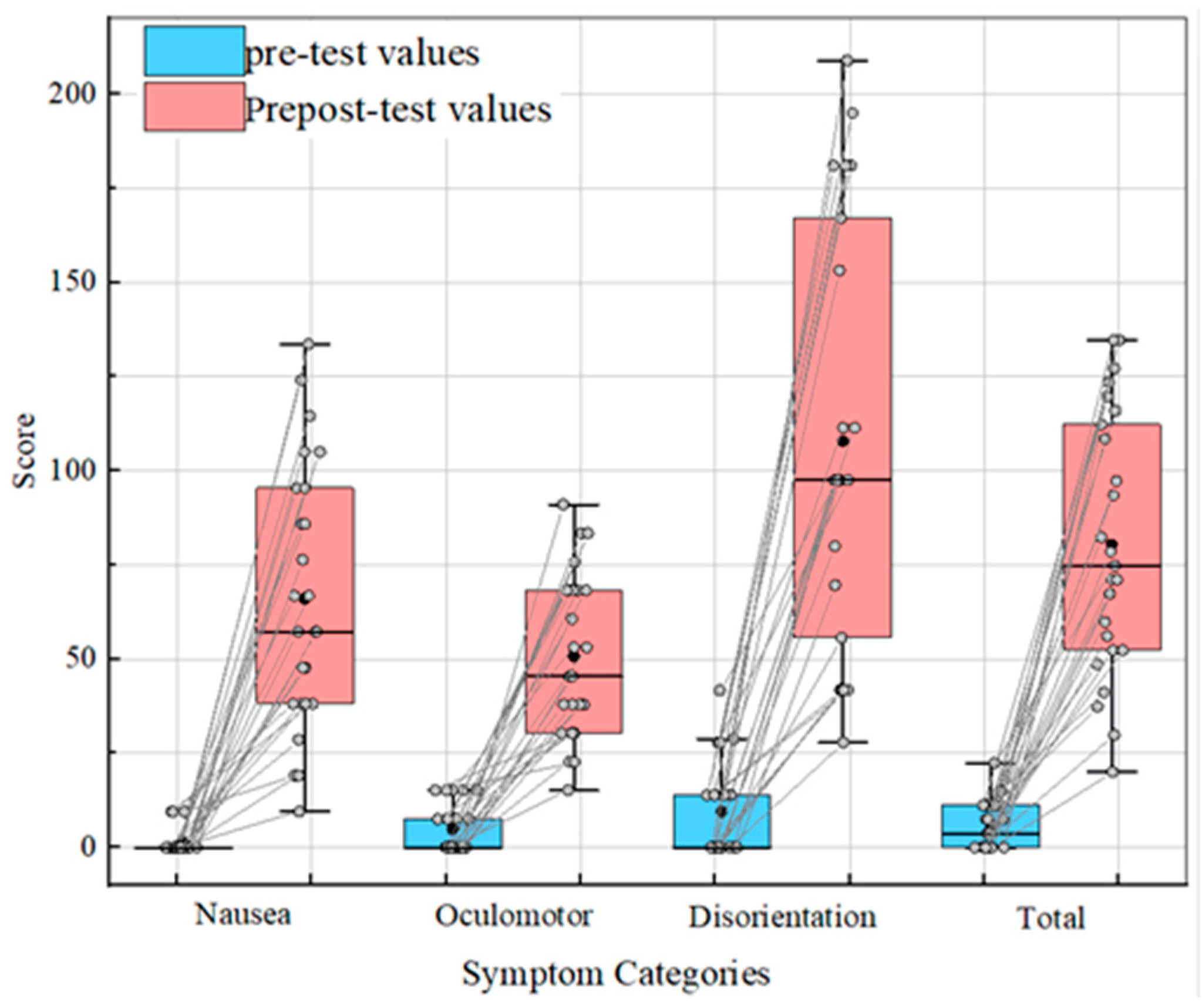
3.1. SSQ Analysis
3.2. Functional Connectivity Matrix
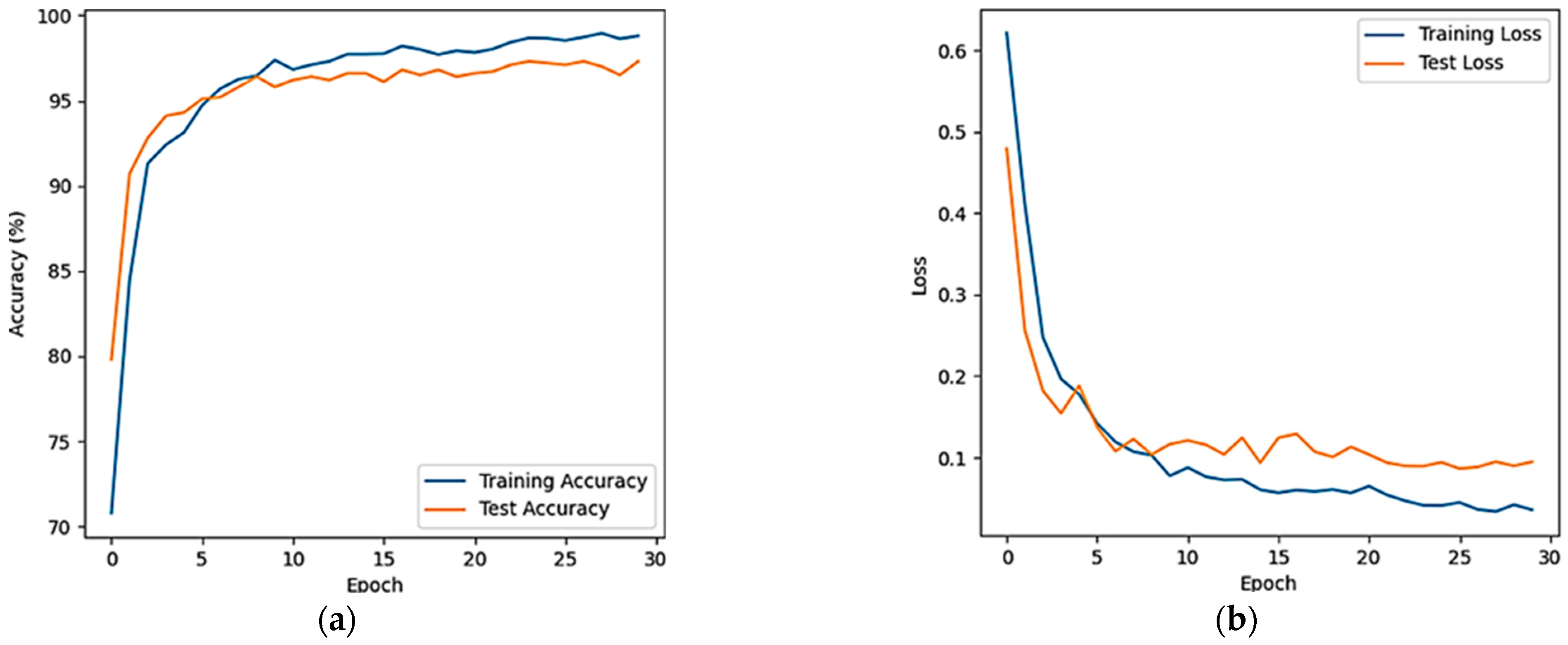
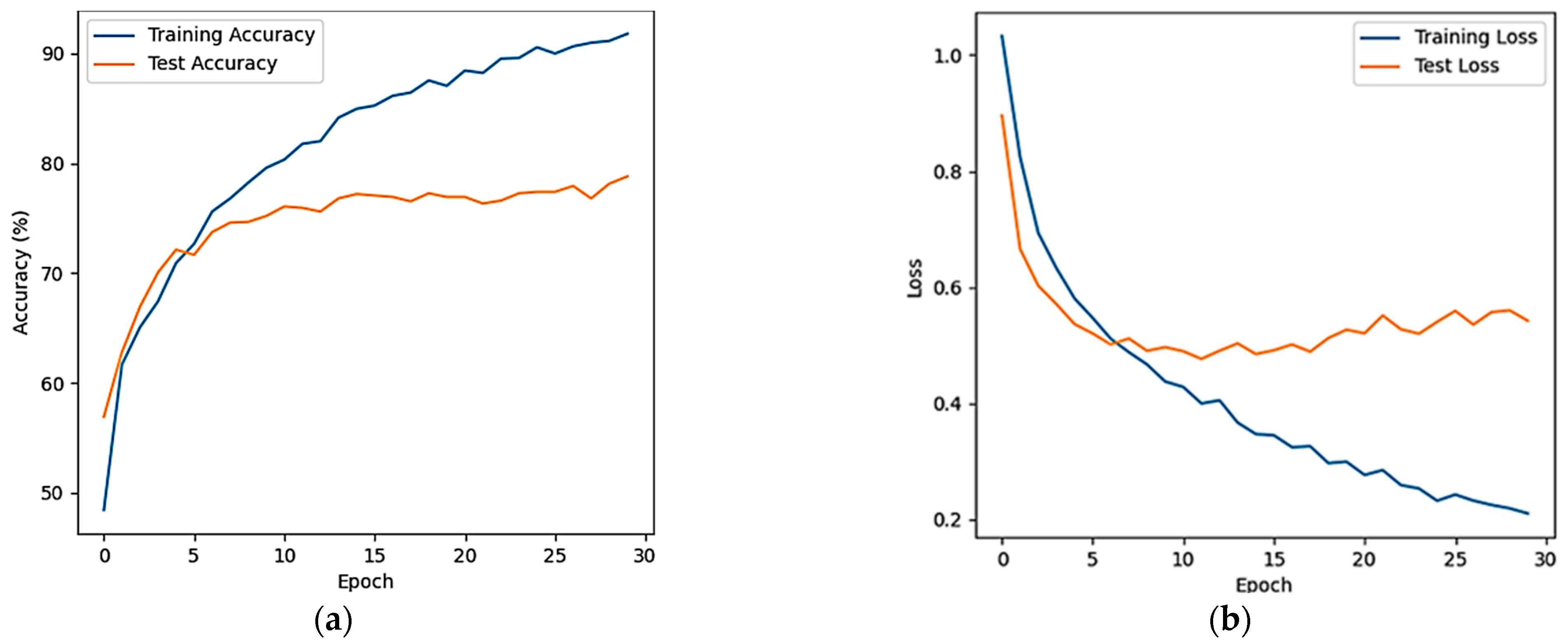
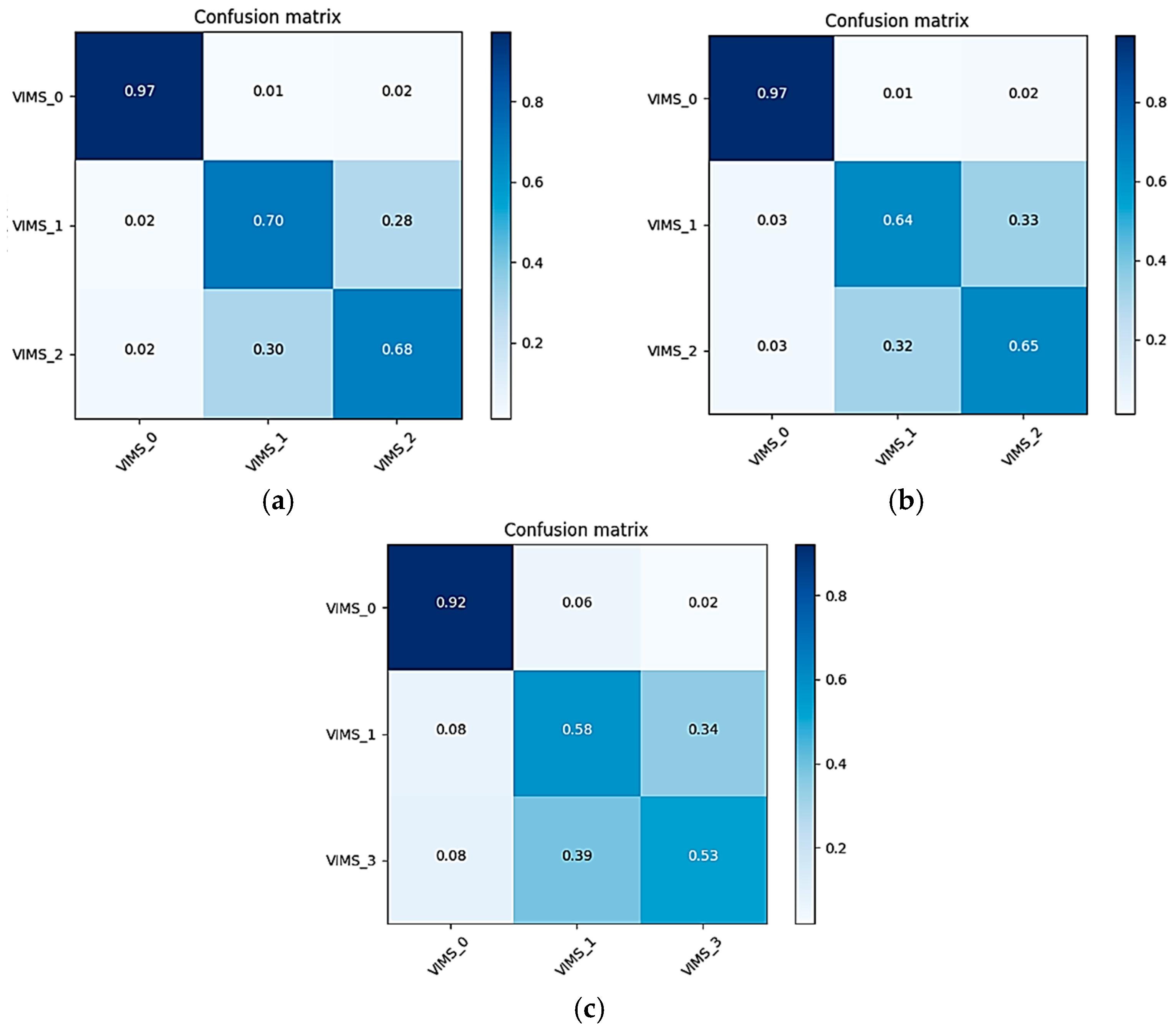
3.3. Classified Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chattha, U.A.; Janjua, U.I.; Anwar, F.; Madni, T.M.; Cheema, M.F.; Janjua, S.I. Motion sickness in virtual reality: An em-pirical evaluation. IEEE Access 2020, 8, 130486–130499. [Google Scholar] [CrossRef]
- Kim, H.K.; Park, J.; Choi, Y.; Choe, M. Virtual reality sickness questionnaire (vrsq): Motion sickness measurement index in a virtual reality environment. Appl. Ergon. 2018, 69, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Sugita, N.; Yoshizawa, M.; Abe, M.; Tanaka, A.; Nitta, S.I. Evaluation of adaptation to visually induced motion sickness by using physiological index associated with baroreflex function. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; Volume 2007, pp. 303–306. [Google Scholar]
- Ahn, M.H.; Park, J.H.; Jeon, H.; Lee, H.J.; Hong, S.K. Temporal dynamics of visually induced motion perception and neural evidence of alterations in the motion perception process in an immersive virtual reality environment. Front. Neurosci. 2020, 14, 600839. [Google Scholar] [CrossRef]
- Yang, J.; Zhai, G.; Duan, H. Predicting the visual saliency of the people with vims. In Proceedings of the 2019 IEEE Visual Communications and Image Processing (VCIP), Sydney, Australia, 1–4 December 2019. [Google Scholar]
- Nesbitt, K.; Davis, S.; Blackmore, K.; Nalivaiko, E. Correlating reaction time and nausea measures with raditional measures of cybersickness. Disp. Technol. Appl. 2017, 48, 1–8. [Google Scholar]
- Li, X.; Zhu, C.; Xu, C.; Zhu, J.; Wu, S. Vr motion sickness recognition by using eeg rhythm energy ratio based on wavelet packet transform. Comput. Methods Programs Biomed. 2019, 188, 105266. [Google Scholar] [CrossRef]
- Krokos, E.; Varshney, A. Quantifying vr cybersickness using eeg. Virtual Real. 2022, 26, 77–89. [Google Scholar] [CrossRef]
- Islam, R.; Lee, Y.; Jaloli, M.; Muhammad, I.; Zhu, D.; Rad, P.; Huang, Y.; Quarles, J. Automatic detection and prediction of cy-bersickness severity using deep neural networks from user physiological signals. In Proceedings of the 2020 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Porto de Galinhas, Brazil, 9–13 November 2020; pp. 400–411. [Google Scholar]
- Shimada, S.; Ikei, Y.; Nishiuchi, N.; Yem, V. Study of cybersickness prediction in real time using eye tracking data. In Proceedings of the 2023 IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW), Shanghai, China, 25–29 March 2023; pp. 871–872. [Google Scholar]
- Gruden, T.; Popovi, N.B.; Stojmenova, K.; Jakus, G.; Miljkovi, N.; Tomaži, S.; Sodnik, J. Electrogastrography in autonomous vehiclesn objective method for assessment of motion sickness in simulated driving environments. Sensors 2021, 21, 550. [Google Scholar] [CrossRef]
- Irmak, T.; Pool, D.M.; Happee, R. Objective and subjective responses to motion sickness: The group and the individual. Exp. Brain Res. 2021, 239, 515–531. [Google Scholar] [CrossRef]
- Sugita, N.; Yoshizawa, M.; Tanaka, A.; Abe, K.; Chiba, S.; Yambe, T.; Nitta, S.-I. Quantitative evaluation of effects of visually- induced motion sickness based on causal coherence functions between blood pressure and heart rate. Displays 2008, 29, 167–175. [Google Scholar] [CrossRef]
- Lim, H.K.; Ji, K.; Woo, Y.S.; Han, D.U.; Jang, K.M. Test-retest reliability of the virtual reality sickness evaluation using elec-troencephalography (eeg). Neurosci. Lett. 2020, 743, 135589. [Google Scholar] [CrossRef]
- Lin, Y.-T.; Chien, Y.-Y.; Wang, H.-H.; Lin, F.-C.; Huang, Y.-P. The quantization of cybersickness level using eeg and ecg for virtual reality headounted display. SID Symp. Dig. Tech. Pap. 2018, 49, 862–865. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Duann, J.-R.; Chuang, S.-W.; Lin, C.-L.; Ko, L.-W.; Jung, T.-P.; Lin, C.-T. Spatial and temporal eeg dynamics of motion sickness. NeuroImage 2010, 49, 2862–2870. [Google Scholar] [CrossRef] [PubMed]
- Vidaurre, C.; Krämer, N.; Blankertz, B.; Schlögl, A. Time domain parameters as a feature for eeg-based brain–computer 524 interfaces. Neural Netw. 2009, 22, 1313–1319. [Google Scholar] [CrossRef]
- Zhao, L.; Chong, L.; Ji, L.; Yang, T. EEG characteristics of motion sickness subjectts in automatic driving mode based on virtual reality tests. J. Tsinghua Univ. Sci. Technol. 2019, 60, 993–998. [Google Scholar]
- Dai, G.; Yang, C.; Liu, Y.; Jiang, T.; Mgaya, G.B. A dynamic multi-reduction algorithm for brain functional connection pathways analysis. Symmetry 2019, 11, 701. [Google Scholar] [CrossRef]
- Islam, M.R.; Islam, M.M.; Rahman, M.M.; Mondal, C.; Singha, S.K.; Ahmad, M.; Awal, A.; Islam, M.S.; Moni, M.A. Eeg channel correlation based model for emotion recognition. Comput. Biol. Med. 2021, 136, 104757. [Google Scholar] [CrossRef]
- Zhu, L.; Su, C.; Zhang, J.; Cui, G.; Cichocki, A.; Zhou, C.; Li, J. Eeg-based approach for recognizing human social emotion perception. Adv. Eng. Inform. 2020, 46, 101191. [Google Scholar] [CrossRef]
- Moon, S.-E.; Jang, S.; Lee, J.-S. Convolutional neural network approach for eeg-based emotion recognition using brain con-nectivity and its spatial information. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2556–2560. [Google Scholar]
- Kang, J.-S.; Park, U.; Gonuguntla, V.; Veluvolu, K.C.; Lee, M. Human implicit intent recognition based on the phase synchrony of eeg signals. Pattern Recognit. Lett. 2015, 66, 144–152. [Google Scholar] [CrossRef]
- di Biase, L.; Ricci, L.; Caminiti, M.L.; Pecoraro, P.M.; Carbone, S.P.; Di Lazzaro, V. Quantitative high density eeg brain con-nectivity evaluation in parkinson disease: The phase locking value (plv). J. Clin. Med. 2023, 12, 1450. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C. Research on EEG Detection and Evaluation Method of VR Motion Sickness. Master’s Thesis, China Jiliang University, Hangzhou, China, 2020. [Google Scholar]
- Hua, C.; Chai, L.; Zhou, Z.; Xu, C.; Liu, J. Automatic eeg detection of virtual reality motion sickness in resting state based on variational mode decomposition. J. Eletronic Meas. Instrum. 2024, 38, 171–181. [Google Scholar]
- Yildirim, C. A review of deep learning approaches to eeg-based classification of cybersickness in virtual reality. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Virtual Reality (AIVR), Utrecht, The Netherlands, 14–18 December 2020. [Google Scholar]
- Hua, C.; Chai, L.; Yan, Y.; Liu, J.; Wang, Q.; Fu, R.; Zhou, Z. Assessment of virtual reality motion sickness severity based on eeg via lstm/bilstm. IEEE Sens. J. 2023, 23, 24839–24848. [Google Scholar] [CrossRef]
- Fransson, P.A.; Patel, M.; Jensen, H.; Lundberg, M.; Tjernstrm, F.; Magnusson, M.; Hansson, E.E. Postural instability in an immersive virtual reality adapts with repetition and includes directional and gender specific effects. Sci. Rep. 2019, 9, 3168. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, R.S.; Lane, N.E.; Berbaum, K.S.; Lilienthal, M.G. Simulator sickness questionnaire: An enhanced method for quantifying simulator sickness. Int. J. Aviat. Psychol. 1993, 3, 203–220. [Google Scholar] [CrossRef]
- Nam, S.; Jang, K.-M.; Kwon, M.; Lim, H.K.; Jeong, J. Electroencephalogram microstates and functional connectivity of cyber-sickness. Front. Hum. Neurosci. 2022, 16, 857768. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, A.; Ding, L. Machine learning assessment of visually induced motion sickness levels based on multiple biosignals. Biomed. Signal Process. Control 2019, 49, 202–211. [Google Scholar] [CrossRef]
- Liu, R.; Cui, S.; Zhao, Y.; Chen, X.; Yi, L.; Hwang, A.D. Vimsnet: An effective network for visually induced motion sickness detection. Signal Image Video Process. 2022, 16, 2029–2036. [Google Scholar] [CrossRef]
- Lin, C.-T.; Tsai, S.-F.; Ko, L.-W. Eeg-based learning system for online motion sickness level estimation in a dynamic vehicle environment. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1689–1700. [Google Scholar]
- Mawalid, M.A.; Khoirunnisa, A.Z.; Purnomo, M.H.; Wibawa, A.D. Classification of eeg signal for detecting cybersickness through time domain feature extraction using naïve bayes. In Proceedings of the 2018 International Conference on Computer Engineering, Network and Intelligent Multimedia (CENIM), Surabaya, Indonesia, 26–27 November 2018; pp. 29–34. [Google Scholar]
- Hyder, R.; Kamel, N.; Tang, T.B.; Bornot, J. Brain source localization techniques: Evaluation study using simulated eeg data. In Proceedings of the 2014 IEEE Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysia, 8–10 December 2014; pp. 942–947. [Google Scholar]
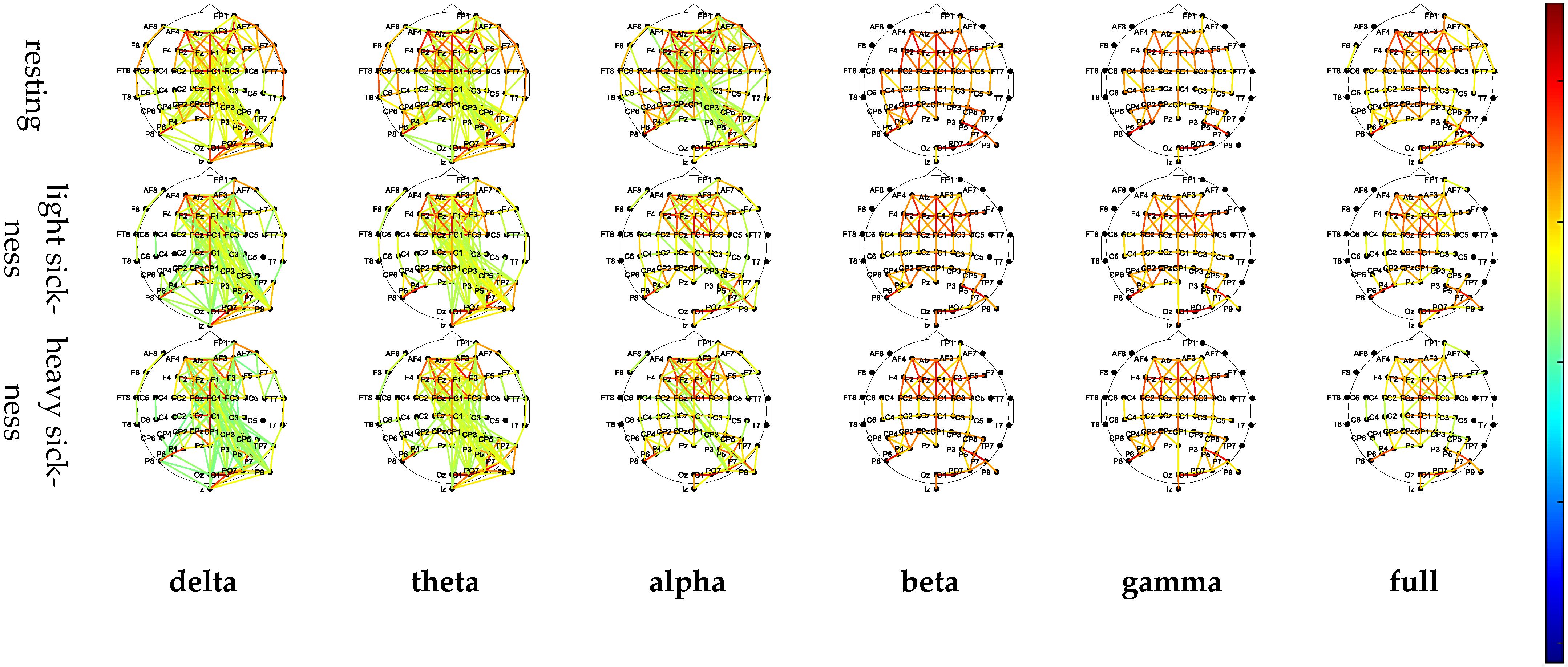
| Delta | Theta | Alpha | Beta | Gamma | Full | ||
|---|---|---|---|---|---|---|---|
| resting |  |  | 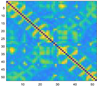 | 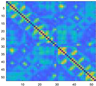 |  |  | |
| light sickness |  |  |  | 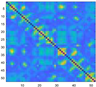 |  |  | |
| heavy sickness |  |  |  | 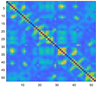 | 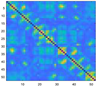 |  |  |
| Model | Two-Class Average Accuracy ± Standard Deviation (%) | Three-Class Average Accuracy ± Standard Deviation (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SVM | CNN-2 | LSTM | CNN-LSTM | SVM | CNN-1 | CNN-2 | CNN-3 | LSTM | CNN-LSTM | |
| Full | 94.48 ± 1.40 | 95.00 ± 1.30 | 85.71 ± 2.88 | 97.09 ± 0.80 | 72.80 ± 2.14 | 74.60 ± 3.59 | 76.46 ± 3.31 | 61.73 ± 2.58 | 70.78 ± 1.58 | 78.60 ± 1.48 |
| Delta | 77.80 ± 1.81 | 82.48 ± 1.96 | 75.03 ± 2.24 | 82.79 ± 1.03 | 56.13 ± 2.58 | 60.27 ± 2.21 | 61.80 ± 2.07 | 52.34 ± 3.24 | 50.67 ± 3.12 | 64.27 ± 0.92 |
| Theta | 89.52 ± 1.76 | 92.44 ± 2.02 | 88.83 ± 3.42 | 93.20 ± 1.81 | 61.33 ± 2.99 | 61.20 ± 2.39 | 62.67 ± 2.64 | 57.47 ± 3.45 | 55.72 ± 2.27 | 68.14 ± 2.22 |
| Alpha | 90.63 ± 3.15 | 91.48 ± 2.88 | 89.32 ± 1.58 | 95.10 ± 1.16 | 64.67 ± 2.76 | 66.33 ± 3.50 | 67.59 ± 3.30 | 60.46 ± 2.46 | 58.96 ± 2.75 | 71.74 ± 2.60 |
| Beta | 98.78 ± 0.64 | 97.99 ± 0.83 | 92.27 ± 1.46 | 98.96 ± 0.45 | 76.07 ± 2.58 | 80.20 ± 1.94 | 80.86 ± 1.71 | 64.13 ± 2.31 | 63.27 ± 3.93 | 83.94 ± 2.43 |
| Gamma | 98.94 ± 0.59 | 99.40 ± 0.37 | 97.56 ± 0.92 | 99.56 ± 0.34 | 80.80 ± 2.16 | 84.32 ± 2.97 | 84.60 ± 2.34 | 67.13 ± 3.91 | 72.70 ± 1.41 | 86.94 ± 1.38 |
| Studies | Feature Extraction | Classification Model | Two-Class Average Accuracy ± Standard Deviation (%) | Three-Class Average Accuracy ± Standard Deviation (%) |
|---|---|---|---|---|
| Hua et al. [26] | Variational mode decomposition, sample entropy, permutation entropy, center frequency | SVM classifier | 98.3% | - |
| Li et al. [32] | Power spectral density and PCA | Voting classifier | 76.3% | - |
| Liu et al. [33] | Raw EEG data | VIMSNet | 96.7% | - |
| Lin et al. [34] | Power spectrum analysis and PCA | Fuzzy neural network | 82% | - |
| Mawalid et al. [35] | Time domain feature | Naive Bayes classifier | 83.8% | - |
| Zhu et al. [25] | Rhythm wavelet packetEnergy proportion | polynomial-SVM KNN RBF-SVM | 79.25% 77.5% 73.83% | 68.15% 70.37% 64.07% |
| This study | Brain functions connect networks | CNN-LSTM | 99.56% | 86.54% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Z.; Liu, X.; Li, W.; Li, X.; Wang, Q. Classification of Visually Induced Motion Sickness Based on Phase-Locked Value Functional Connectivity Matrix and CNN-LSTM. Sensors 2024, 24, 3936. https://doi.org/10.3390/s24123936
Shen Z, Liu X, Li W, Li X, Wang Q. Classification of Visually Induced Motion Sickness Based on Phase-Locked Value Functional Connectivity Matrix and CNN-LSTM. Sensors. 2024; 24(12):3936. https://doi.org/10.3390/s24123936
Chicago/Turabian StyleShen, Zhenqian, Xingru Liu, Wenqiang Li, Xueyan Li, and Qiang Wang. 2024. "Classification of Visually Induced Motion Sickness Based on Phase-Locked Value Functional Connectivity Matrix and CNN-LSTM" Sensors 24, no. 12: 3936. https://doi.org/10.3390/s24123936
APA StyleShen, Z., Liu, X., Li, W., Li, X., & Wang, Q. (2024). Classification of Visually Induced Motion Sickness Based on Phase-Locked Value Functional Connectivity Matrix and CNN-LSTM. Sensors, 24(12), 3936. https://doi.org/10.3390/s24123936




