A Novel Generalized Nested Array MIMO Radar for DOA Estimation with Increased Degrees of Freedom and Low Mutual Coupling
Abstract
1. Introduction
2. Signal Model
3. Generalized Nested Array MIMO Radar Configuration
3.1. Review of Sum Co-Array and Difference Co-Array
3.2. Reformulation of Generalized Nested Array
3.3. Design Principle for GNA-MIMO Radar
3.4. Properties of the GNA-MIMO Radar
3.5. Optimal M and N
4. Performance Analysis
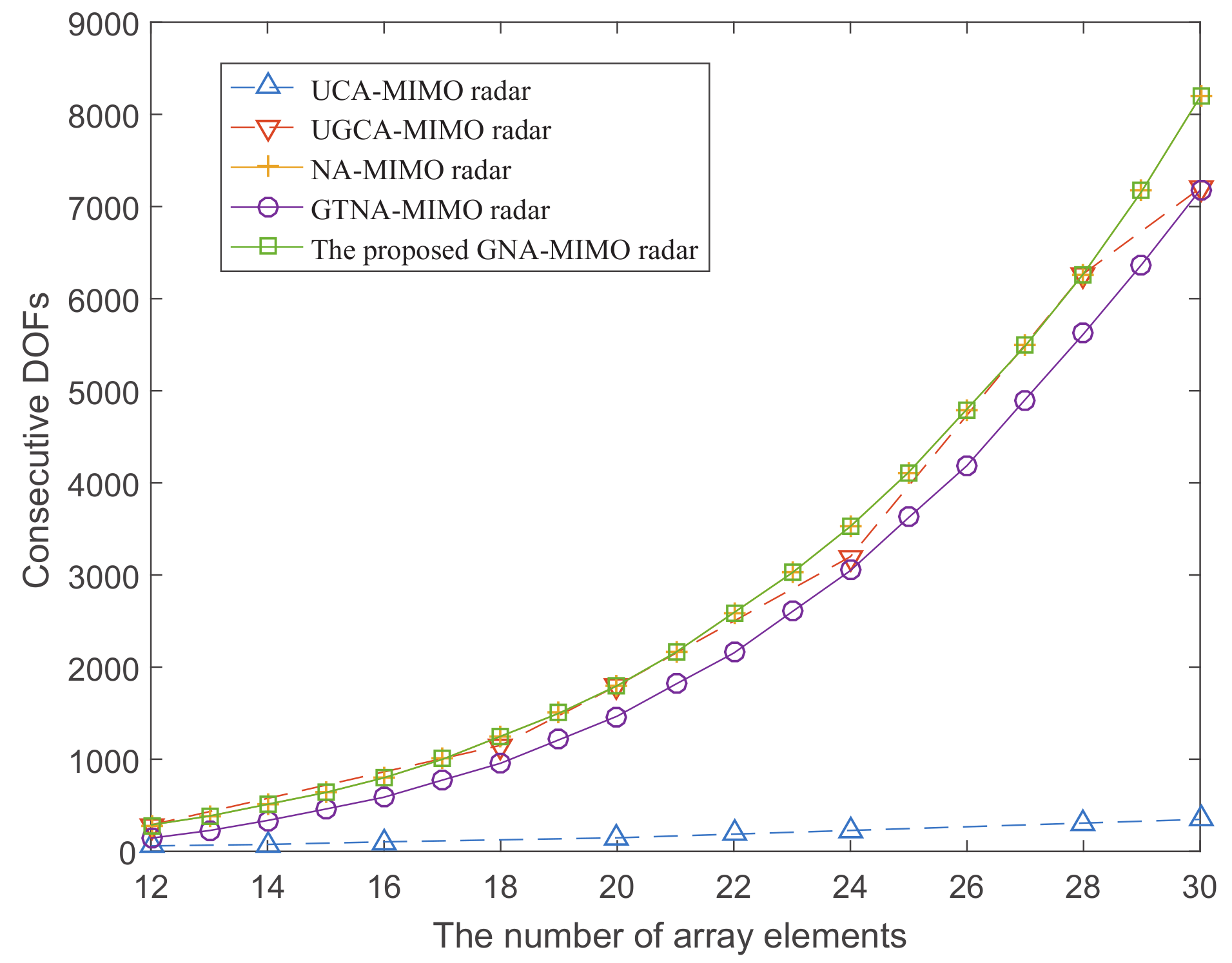
4.1. The Consecutive DOFs
4.2. The Mutual Coupling Leakage Rate
4.3. The CRB Bound
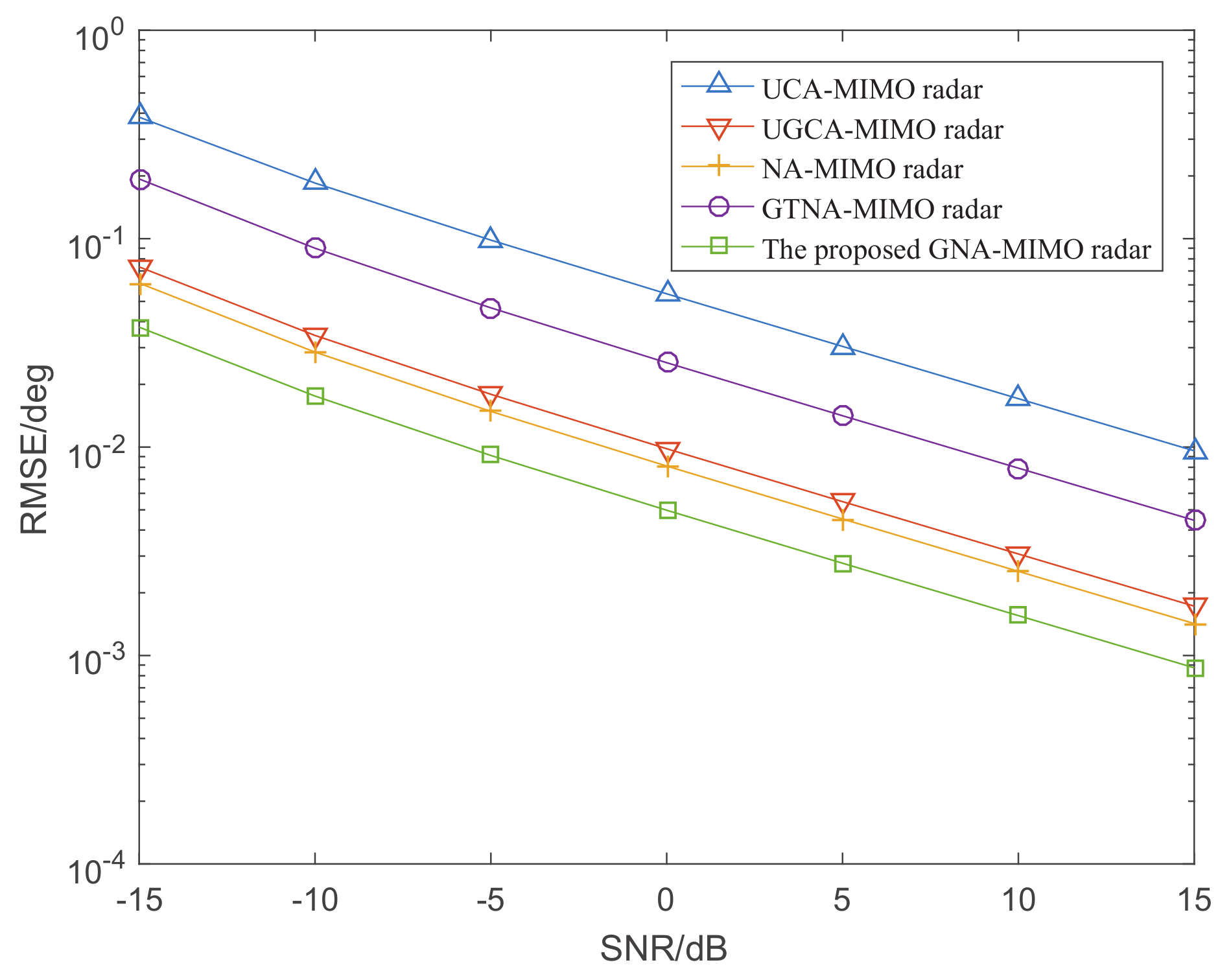
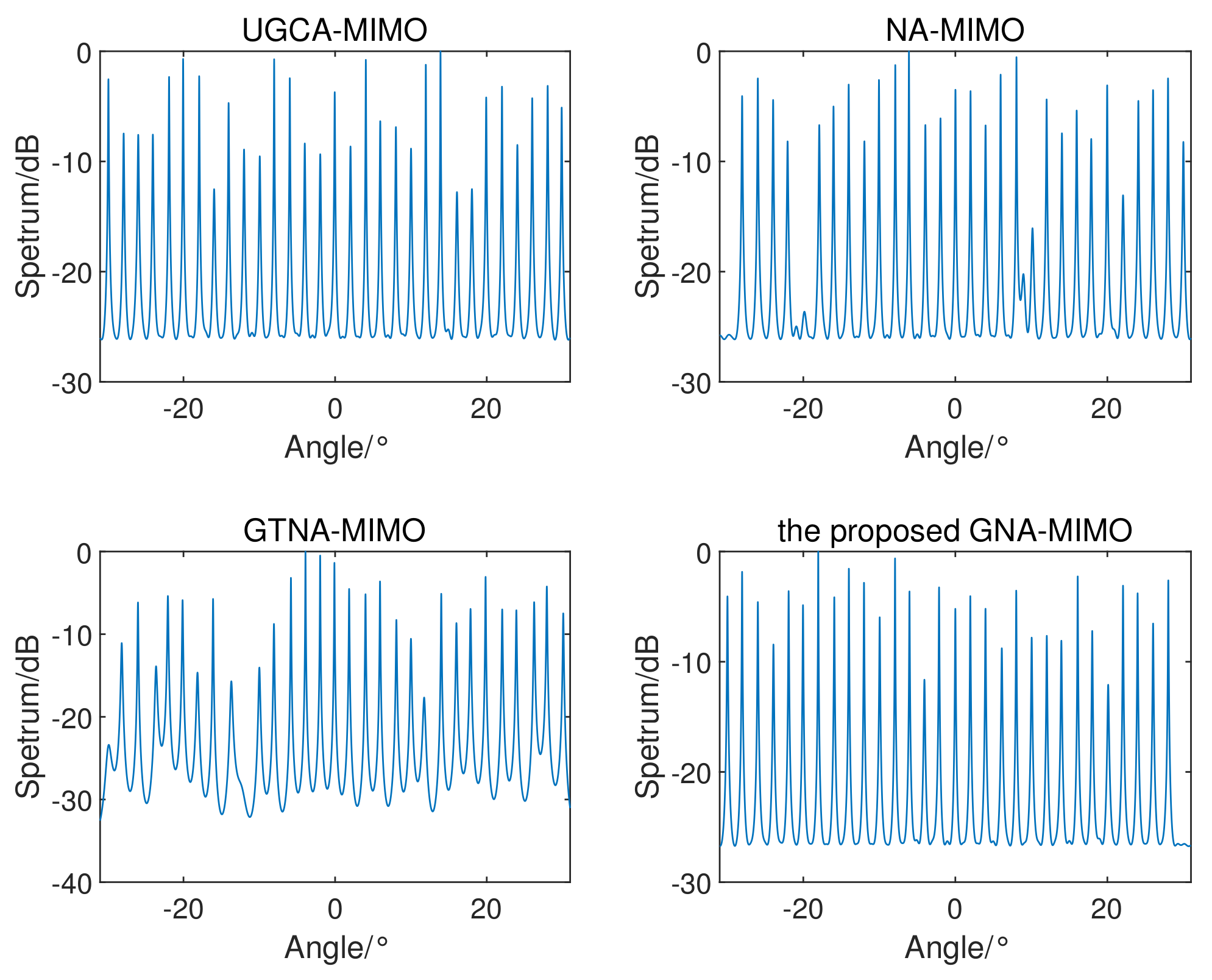
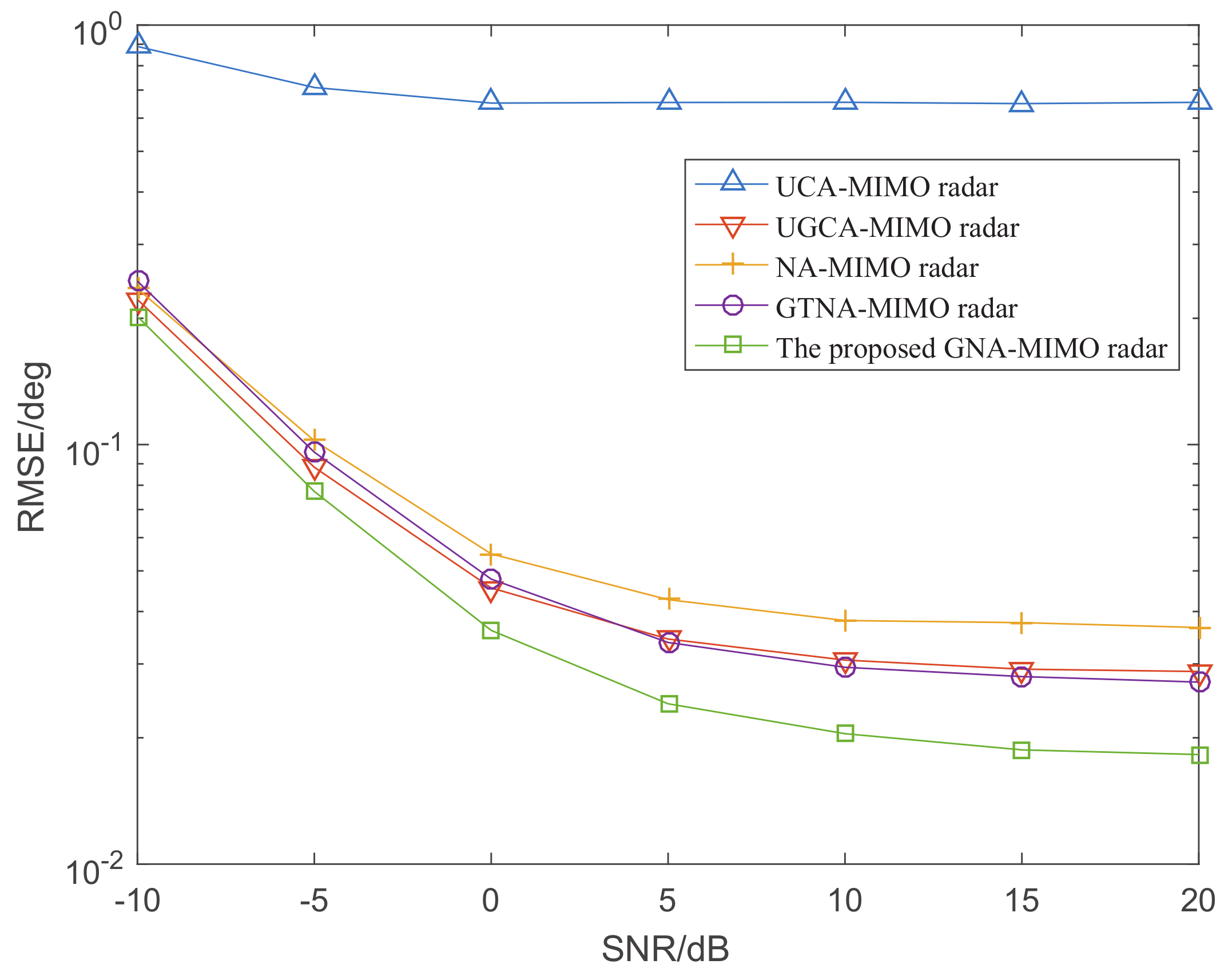
5. Simulation Results
5.1. MUSIC Spectrum
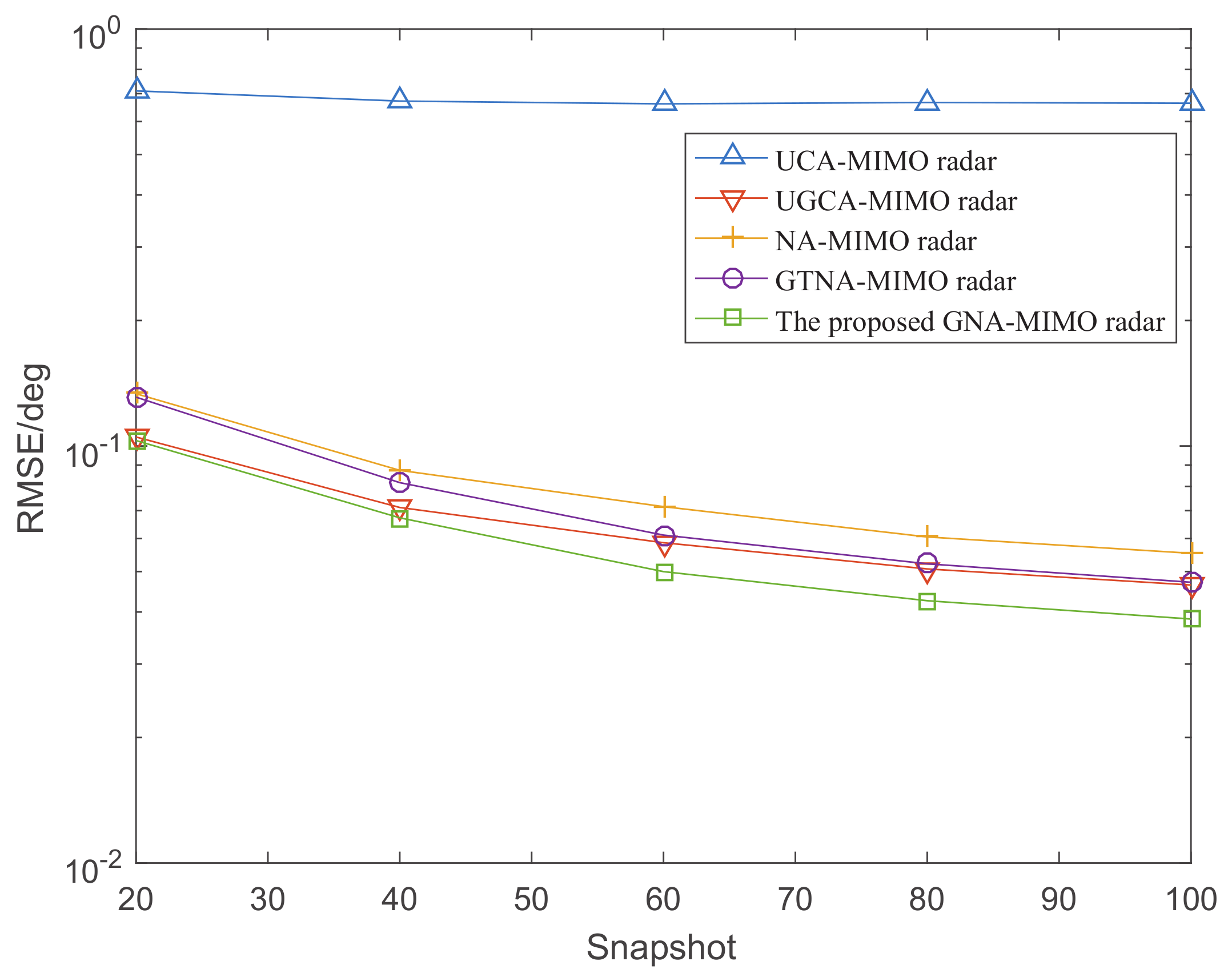
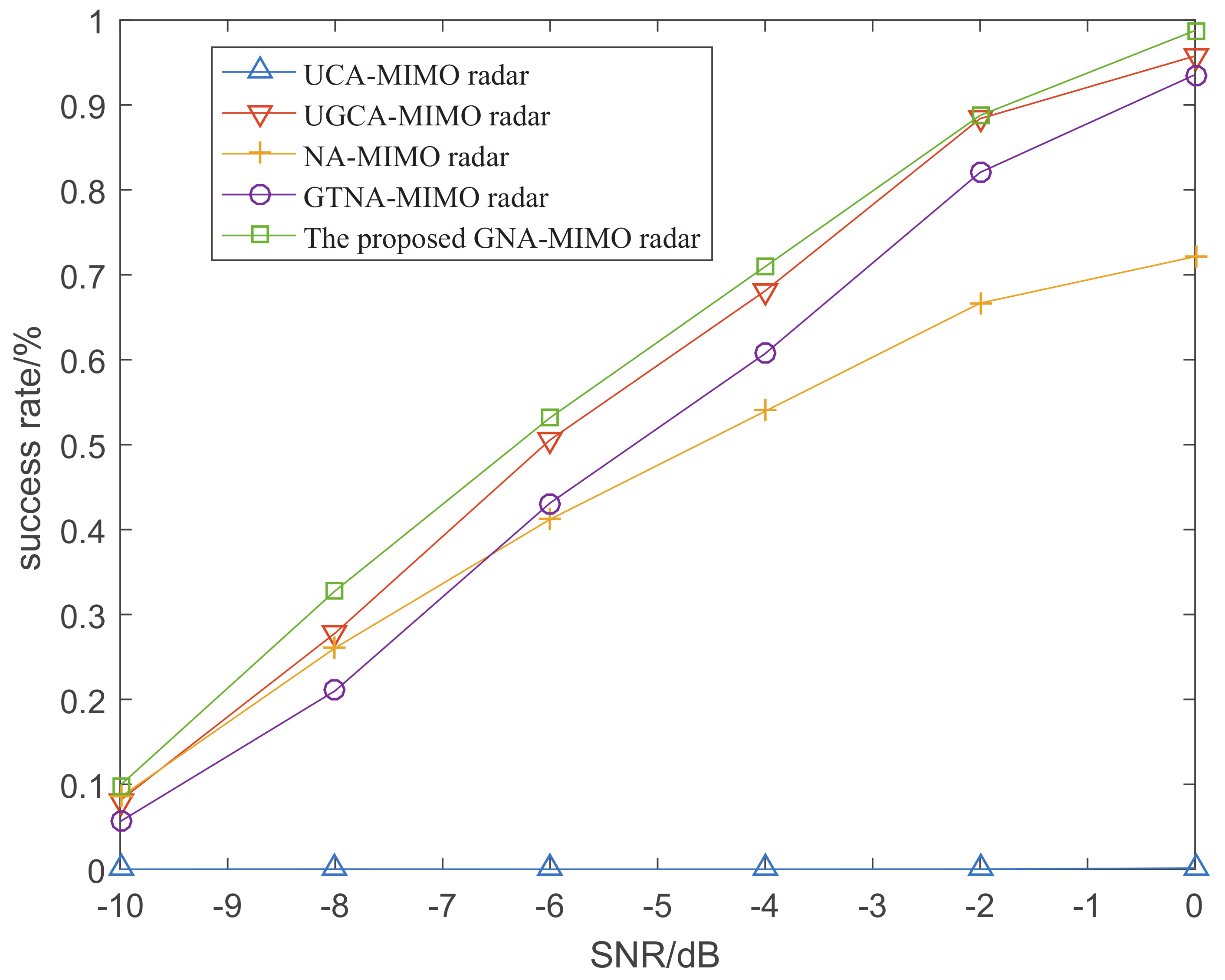
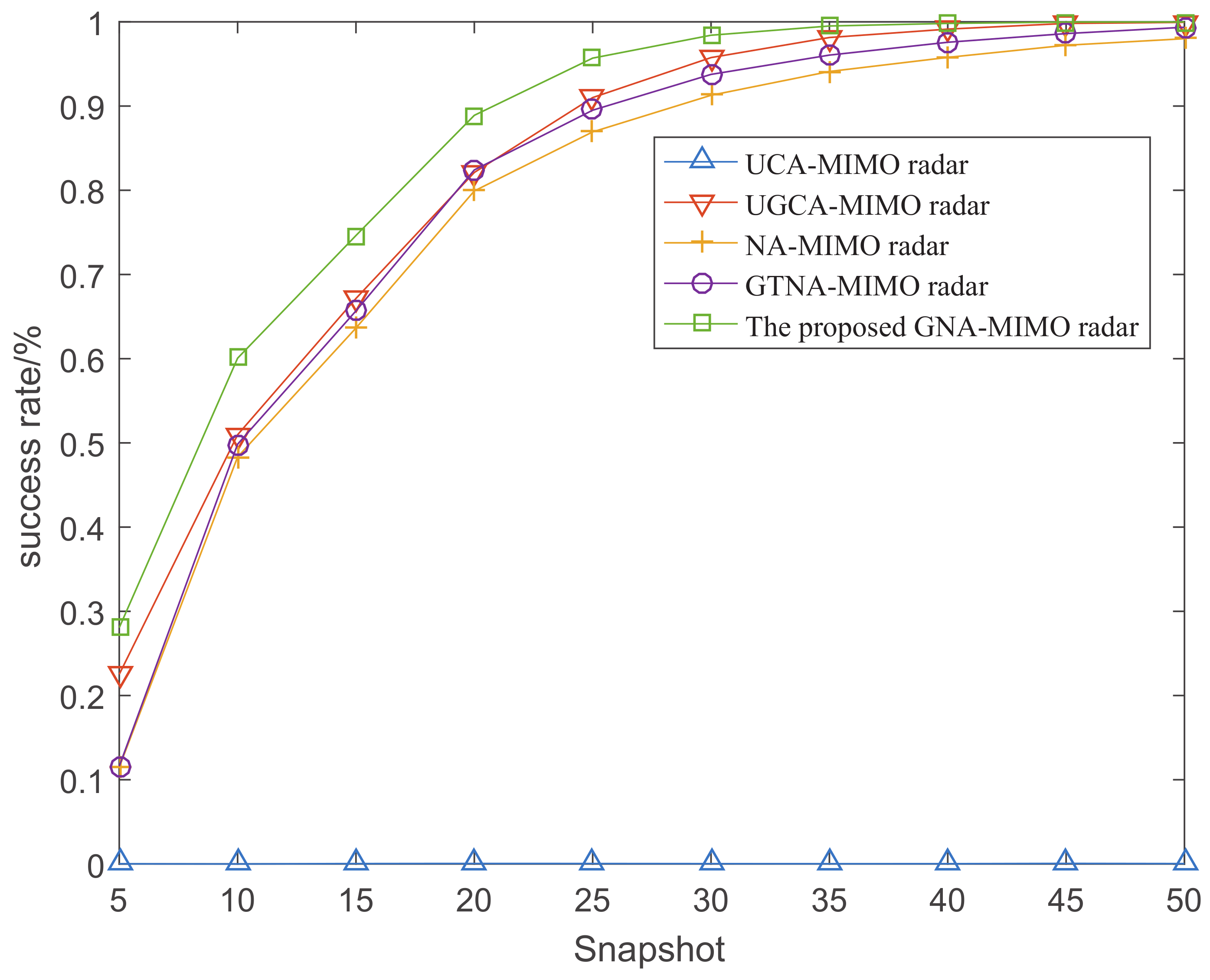
5.2. The RMSE Performance versus SNR and Snapshots
5.3. Resolution Performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Cao, R. Direction of Arrival Estimation: Introduction; Wiley: London, UK, 2017. [Google Scholar]
- Qin, S.; Zhang, Y.D.; Amin, M.G.; Zoubir, A. Generalized coprime sampling of Toeplitz matrices. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 4468–4472. [Google Scholar]
- Zhang, X.; Lai, X.; Zheng, W.; Wang, Y. Sparse Array Design for DOA Estimation of Non-Circular Signals: Reduced Co-Array Redundancy and Increased DOF. IEEE Sens. J. 2021, 21, 27928–27937. [Google Scholar] [CrossRef]
- Lai, X.; Zhang, X.; Zheng, W.; Ma, P. Spatially Smoothed Tensor-Based Method for Bistatic Co-Prime MIMO Radar With Hole-Free Sum-Difference Co-Array. IEEE Trans. Veh. Technol. 2022, 71, 3889–3899. [Google Scholar] [CrossRef]
- Bliss, D.W.; Forsythe, K.W. Multiple-input multiple-output (MIMO) radar and imaging: Degrees of freedom and resolution. In Proceedings of the The Thrity-Seventh Asilomar Conference on Signals, Systems Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 1, pp. 54–59. [Google Scholar]
- Cao, Y.; Zhang, Z.; Dai, F.; Xie, R. Fast DOA estimation for monostatic MIMO radar with arbitrary array configurations. In Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011; Volume 1, pp. 959–962. [Google Scholar]
- Yang, M.; Sun, L.; Yuan, X.; Chen, B. A New Nested MIMO Array With Increased Degrees of Freedom and Hole-Free Difference Coarray. IEEE Signal Process. Lett. 2018, 25, 40–44. [Google Scholar] [CrossRef]
- Wandale, S.; Ichige, K. A Nested Array Geometry with Enhanced Degrees of Freedom and Hole-Free Difference Coarray. In Proceedings of the 2021 29th European Signal Processing Conference (EUSIPCO), Dublin, Ireland, 23–27 August 2021; pp. 1905–1909. [Google Scholar]
- Chen, C.Y.; Vaidyanathan, P.P. Minimum redundancy MIMO radars. In Proceedings of the 2008 IEEE International Symposium on Circuits and Systems (ISCAS), Seattle, WA, USA, 18–21 May 2008; pp. 45–48. [Google Scholar]
- Liao, G.; Jin, M.; Li, J. A two-step approach to construct minimum redundancy MIMO radars. In Proceedings of the 2009 International Radar Conference “Surveillance for a Safer World” (RADAR 2009), Bordeaux, France, 12–16 October 2009; pp. 1–4. [Google Scholar]
- Dong, J.; Li, Q.; Guo, W. A Combinatorial Method for Antenna Array Design in Minimum Redundancy MIMO Radars. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 1150–1153. [Google Scholar] [CrossRef]
- Dong, J.; Shi, R.; Lei, W.; Guo, Y. Minimum Redundancy MIMO Array Synthesis by means of Cyclic Difference Sets. Int. J. Antennas Propag. 2013, 2013, 323521. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing With Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing With Co-Prime Samplers and Arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Zhang, X.; Zhou, H. Generalized Nested Array: Optimization for Degrees of Freedom and Mutual Coupling. IEEE Commun. Lett. 2018, 22, 1208–1211. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized coprime array configurations. In Proceedings of the 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruna, Spain, 22–25 June 2014; pp. 529–532. [Google Scholar]
- Li, J.; Zhang, X. Direction of Arrival Estimation of Quasi-Stationary Signals Using Unfolded Coprime Array. IEEE Access 2017, 5, 6538–6545. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. DOA estimation of mixed coherent and uncorrelated signals exploiting a nested MIMO system. In Proceedings of the 2014 IEEE Benjamin Franklin Symposium on Microwave and Antenna Sub-systems for Radar, Telecommunications, and Biomedical Applications (BenMAS), Philadelphia, PA, USA, 26 September 2014; pp. 1–3. [Google Scholar]
- Qin, S.; Zhang, Y.D.; Amin, M.G. DOA estimation of mixed coherent and uncorrelated targets exploiting coprime MIMO radar. Digit. Signal Process. 2017, 61, 26–34. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, X.; Shi, J. Sparse Extension Array Geometry for DOA Estimation With Nested MIMO Radar. IEEE Access 2017, 5, 9580–9586. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Zhang, X.; Sun, F.; Zheng, W.; Xiao, Y. Generalized Co-Prime MIMO Radar for DOA Estimation With Enhanced Degrees of Freedom. IEEE Sens. J. 2018, 18, 1203–1212. [Google Scholar] [CrossRef]
- BouDaher, E.; Ahmad, F.; Amin, M.G. Sparsity-Based Direction Finding of Coherent and Uncorrelated Targets Using Active Nonuniform Arrays. IEEE Signal Process. Lett. 2015, 22, 1628–1632. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, G.; Zhou, H.; Zhu, M.; Zhang, F. DOA Estimation of a Novel Generalized Nested MIMO Radar with High Degrees of Freedom and Hole-Free Difference Coarray. Math. Probl. Eng. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Shaikh, A.H.; Dang, X.; Ahmed, T.; Huang, D. New Transmit-Receive Array Configurations for the MIMO Radar With Enhanced Degrees of Freedom. IEEE Commun. Lett. 2020, 24, 1534–1538. [Google Scholar] [CrossRef]
- Wei, Z. DOA Estimation of Single-Base Unfolded Co-prime Array MIMO Radar. J. Nanjing Univ. Posts Telecommun. Nat. Sci. Ed. 2019, 39, 8. [Google Scholar]
- Wei, Z.; Qiang, W.; Jun, T.; Wei, Z.; Yingjie, P. Dimensionality Reduction Estimation of DOD and DOA for Dual-Base Unfolded Co-prime Array MIMO Radar. J. Nanjing Univ. Posts Telecommun. Nat. Sci. Ed. 2020, 40, 7. [Google Scholar]
- Yulei, Z.; Guoping, H.; Hao, Z.; Shijie, Y.; Feilong, Z. DOA Estimation of High-Degree-of-Freedom Low-Mutual-Coupling Generalized Second-Order Nested MIMO Radar. Syst. Eng. Electron. 2021, 43, 2819–2827. [Google Scholar]
- Hao, H.; Lai, X.; Han, S.; Zhang, X. Unfolded augmented co-prime array for MIMO radar: Low mutual coupling and high degree of freedom perspective. J. Appl. Sci. 2023, 41, 911–925. [Google Scholar]
- Li, J.; He, Y.; Ma, P.; Zhang, X.; Wu, Q. Direction of Arrival Estimation Using Sparse Nested Arrays With Coprime Displacement. IEEE Sens. J. 2021, 21, 5282–5291. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar Diversity Means Superiority. In MIMO Radar Signal Processing; IEEE: Piscataway, NJ, USA, 2009; pp. 1–64. [Google Scholar]
- Huang, Y.; Liao, G.; Li, J.; Wang, H. Sum and difference coarray based MIMO radar array optimization with its application for DOA estimation. Multidimens. Syst. Signal Process. 2017, 28, 1–20. [Google Scholar] [CrossRef]


| When M Is | The Optimal | The Optimal , |
|---|---|---|
| Even | , | |
| Odd | , | , |
| The Total Number of Physical Radar Elements | The Closed-Form Expression of Consecutive DOFs | |
|---|---|---|
| UCA-MIMO radar in [20] | ||
| GTNA-MIMO radar in [19] | ||
| NA-MIMO radar in [19] | ||
| UGCA-MIMO radar in [24] | ||
| The proposed GNA-MIMO radar | Equation (14) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Bi, Z.; Chen, Y.; Hao, H. A Novel Generalized Nested Array MIMO Radar for DOA Estimation with Increased Degrees of Freedom and Low Mutual Coupling. Sensors 2024, 24, 3952. https://doi.org/10.3390/s24123952
Yang Z, Bi Z, Chen Y, Hao H. A Novel Generalized Nested Array MIMO Radar for DOA Estimation with Increased Degrees of Freedom and Low Mutual Coupling. Sensors. 2024; 24(12):3952. https://doi.org/10.3390/s24123952
Chicago/Turabian StyleYang, Zhongtian, Zhengyang Bi, Ye Chen, and Honghao Hao. 2024. "A Novel Generalized Nested Array MIMO Radar for DOA Estimation with Increased Degrees of Freedom and Low Mutual Coupling" Sensors 24, no. 12: 3952. https://doi.org/10.3390/s24123952
APA StyleYang, Z., Bi, Z., Chen, Y., & Hao, H. (2024). A Novel Generalized Nested Array MIMO Radar for DOA Estimation with Increased Degrees of Freedom and Low Mutual Coupling. Sensors, 24(12), 3952. https://doi.org/10.3390/s24123952





