Multi-Parameter Characterization of Liquid-to-Ice Phase Transition Using Bulk Acoustic Waves
Abstract
:1. Introduction
2. Materials and Methods
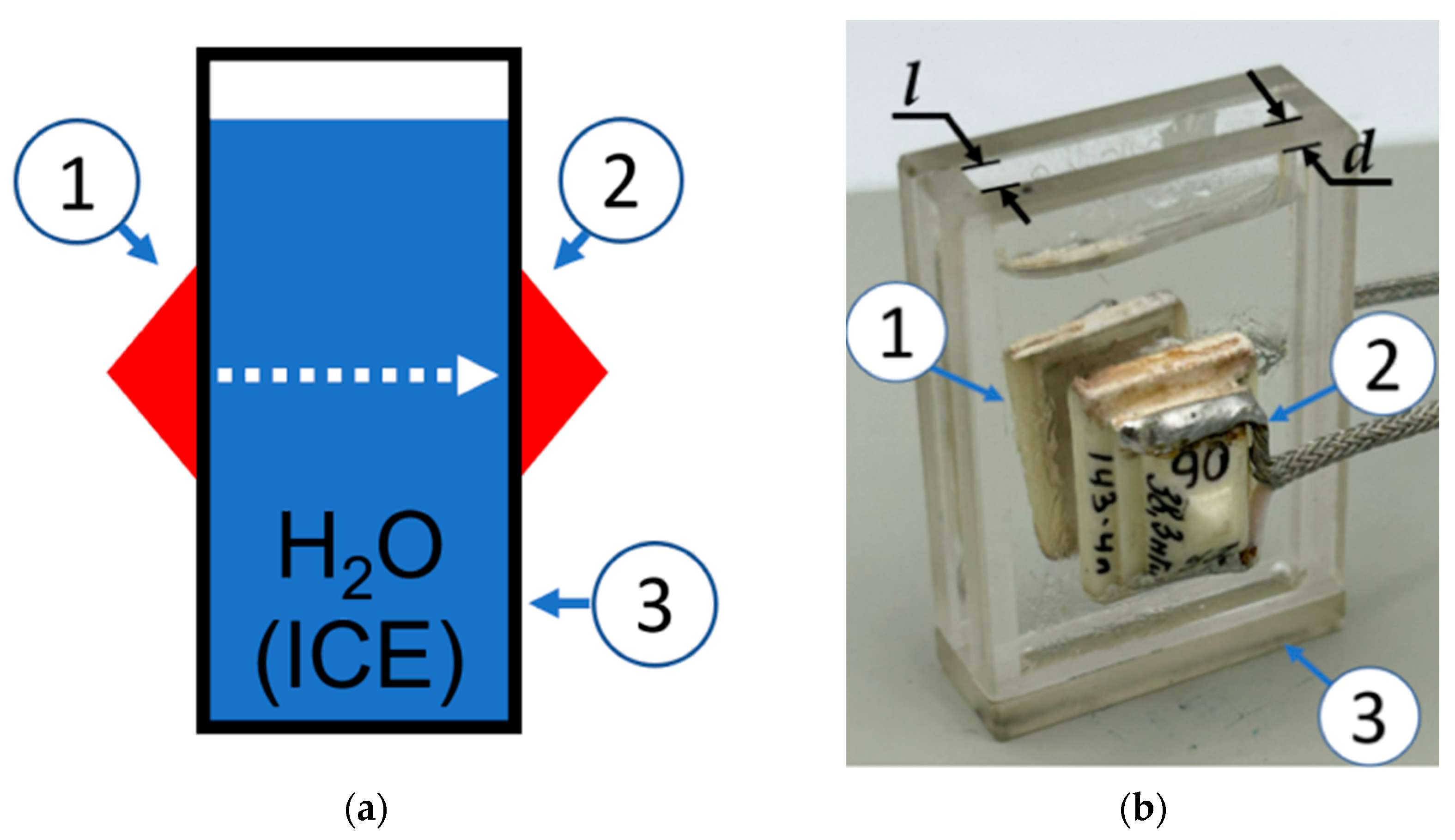
2.1. Design of a BAW Sensor for Registration of Liquid-to-Ice Phase Transition
2.2. Design of a BAW Sensor for Ice Homogeneity Control
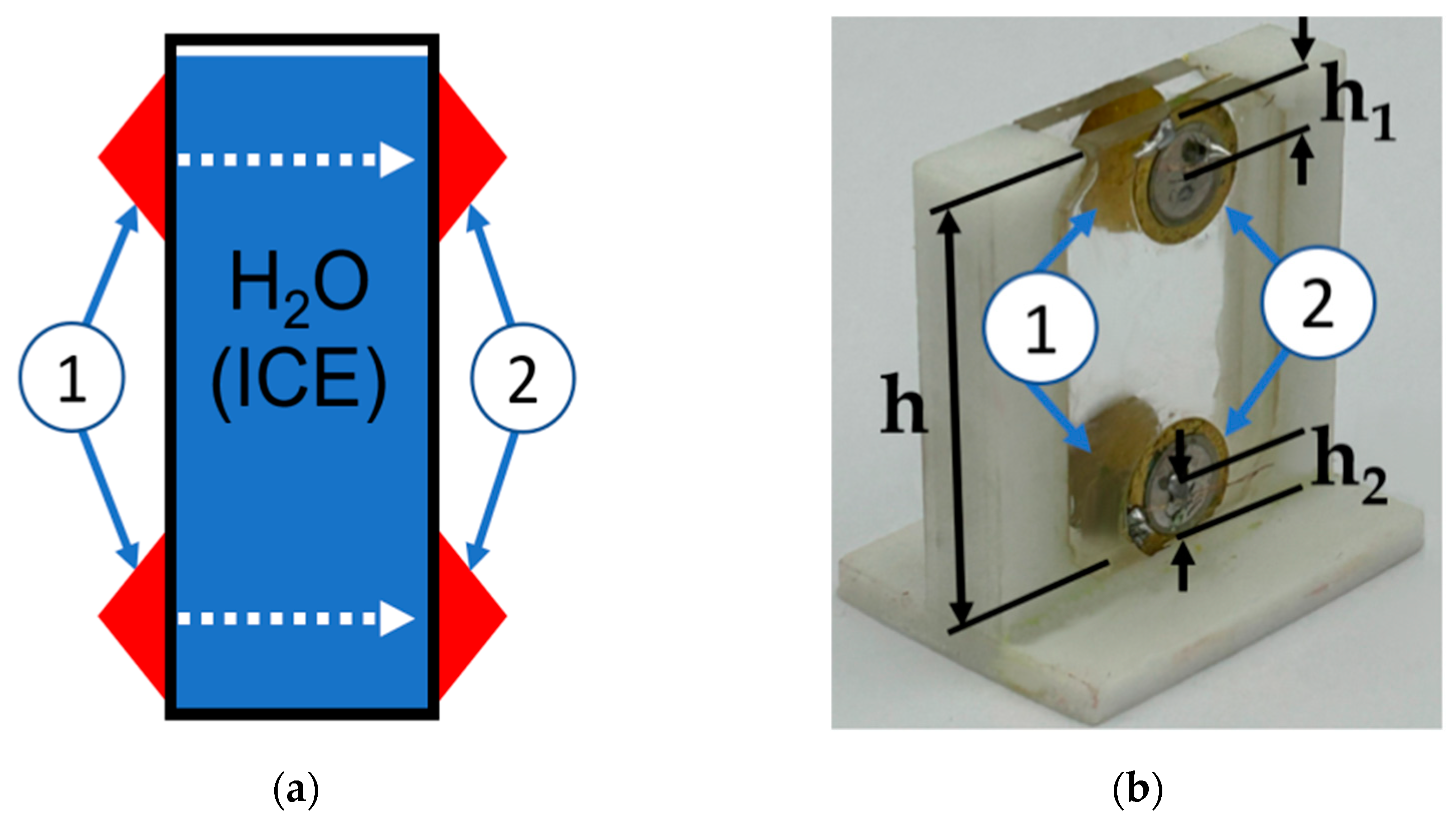
2.3. Design of a Dual BAW Sensor for Simultaneous Detection of Two Liquid-to-Ice Transformations
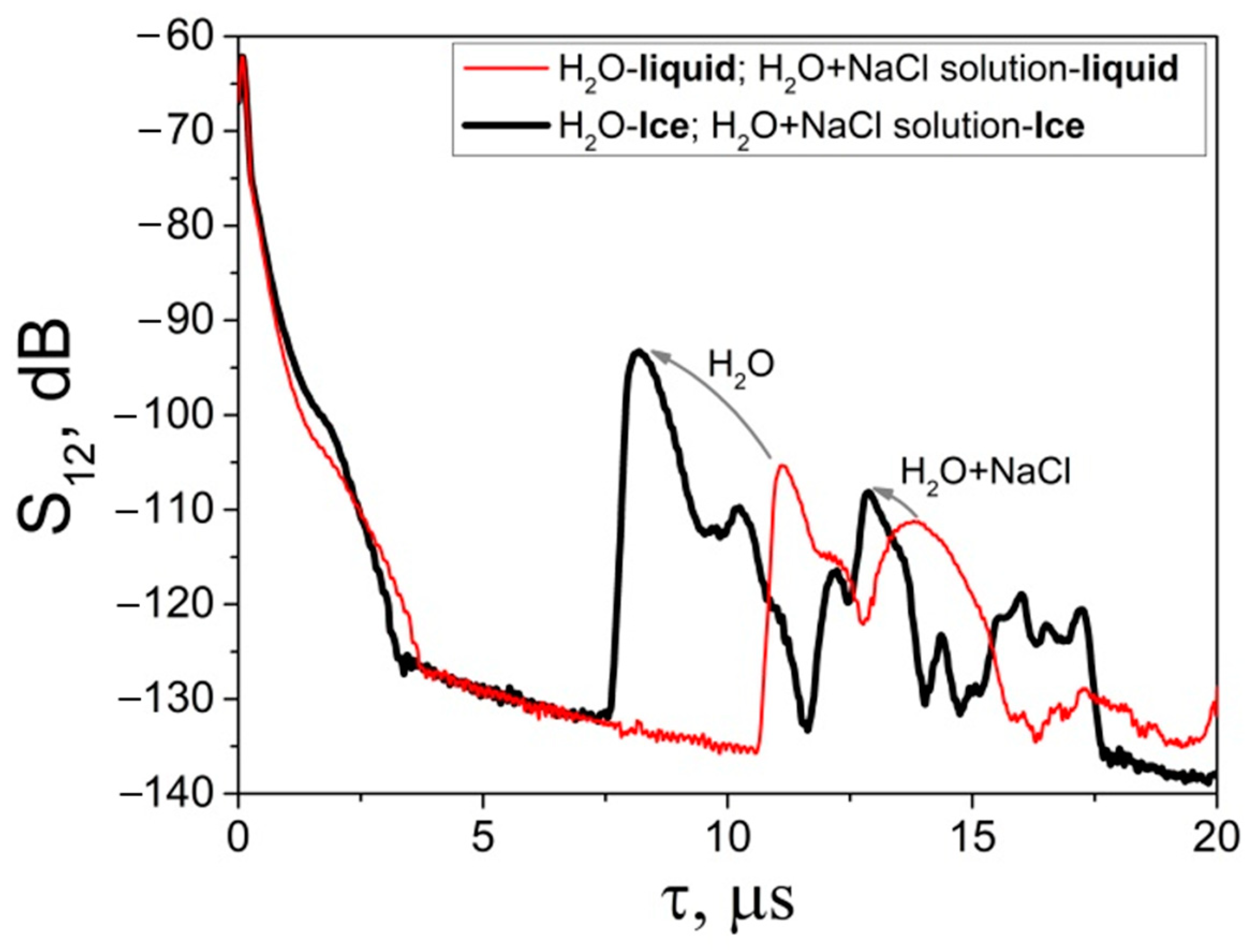
3. Results and Discussion
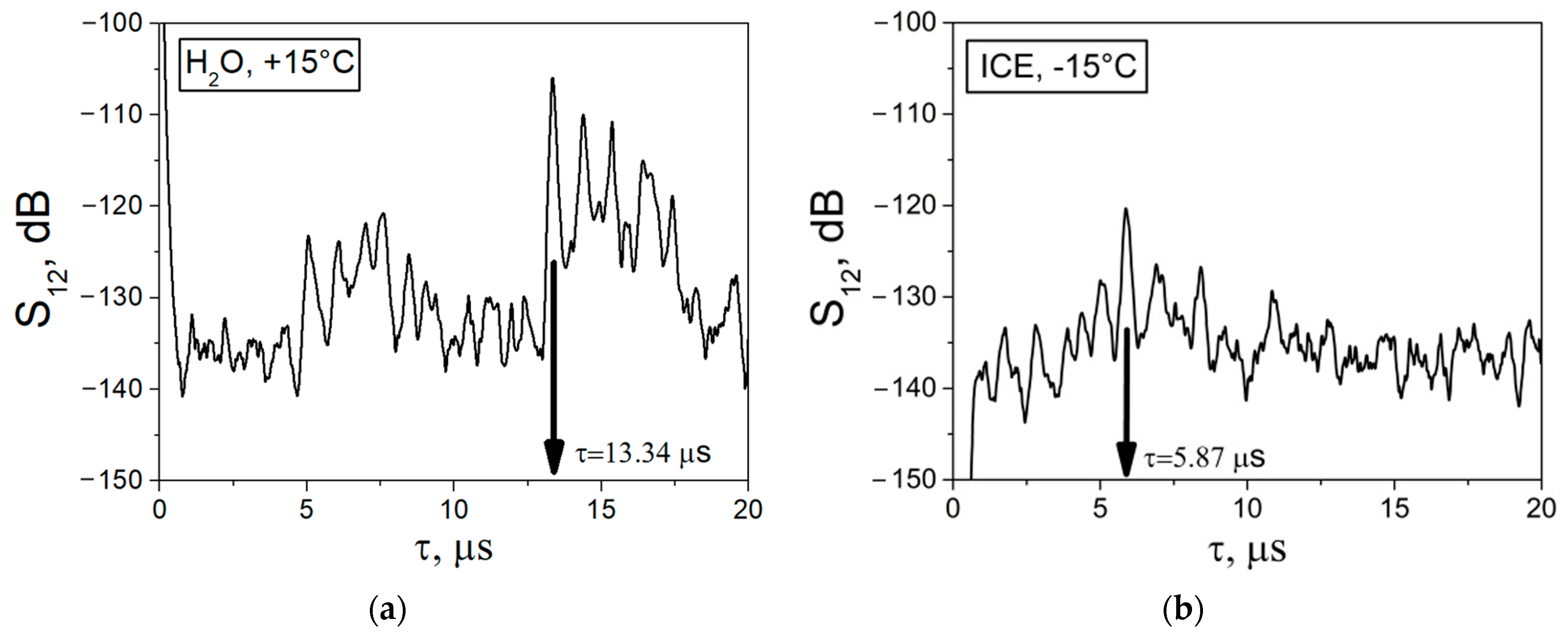
3.1. Registration of Liquid-to-Ice Phase Transition Using the Developed BAW Sensor
3.2. Ice Homogeneity Control Using the Developed LBAW Sensor
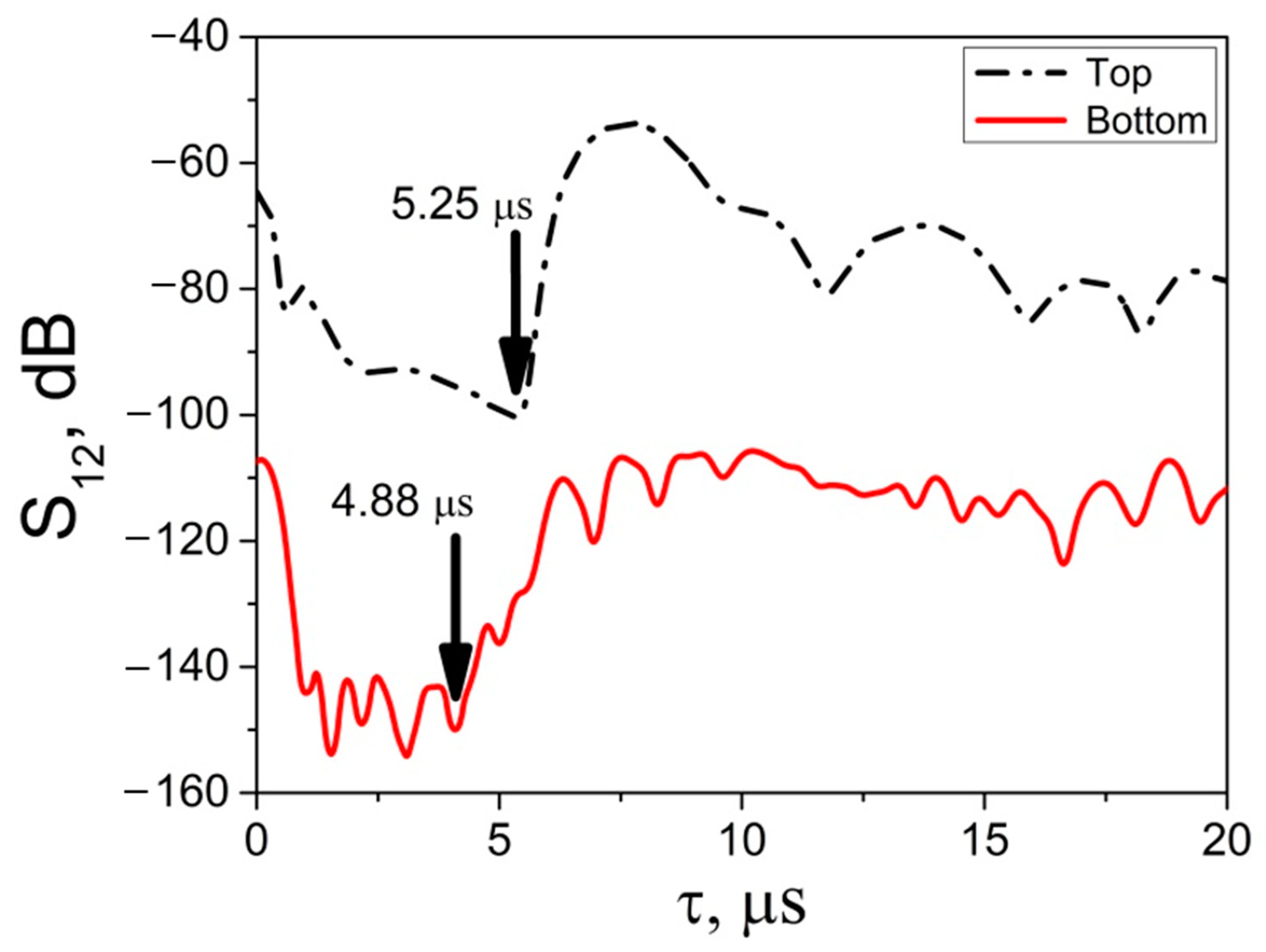
3.3. Simultaneous Detection of Two Liquid-to-Ice Transformations Using the Dual BAW Sensor Developed
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Parron, P.; Leblond, J.; Meijer, P.H. The Physics of Phase Transitions; Springer: Berlin, Germany, 2006. [Google Scholar]
- Wang, Y.; Li, F.; Fang, W.; Li, Y.; Sun, C.; Men, Z. Influence of Si quantum dots on water molecules icing. J. Molec. Liq. 2019, 291, 111315. [Google Scholar] [CrossRef]
- Zhu, X.; Yuan, Q.; Zhao, Y.-P. Phase transitions of a water overlayer on charged graphene: From electromelting to electrofreezing. Nanoscale 2014, 6, 5432–5437. [Google Scholar] [CrossRef] [PubMed]
- Bovo, L.; Rouleau, C.M.; Prabhakaran, D.; Bramwell, S.T. Phase transitions in few-monolayer spin ice films. Nat. Commun. 2019, 10, 1219. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Kahan, T.F. Physical characterization of frozen aqueous solutions containing sodium chloride and humic acid at environmentally relevant temperatures. ACS Earth Space Chem. 2020, 4, 305–310. [Google Scholar] [CrossRef]
- Eisenberg, D.; Kauzmann, W. The Structure and Properties of Water; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Caliskan, F.; Hajiyev, C. A review of in-flight detection and identification of aircraft icing and reconfigurable control. Prog. Aerosp. Sci. 2013, 60, 12–34. [Google Scholar] [CrossRef]
- Barthod, C.; Prasad, M.; Bouillot, J.; Galez, C.; Farzaneh, M. High electric field measurement and ice detection using a safe probe near power installations. Sens. Actuators A Phys. 2004, 113, 140–146. [Google Scholar] [CrossRef]
- Ikiades, A. Fiber optic ice sensor for measuring ice thickness, type, and the freezing fraction on aircraft wings. Aerospace 2023, 10, 31. [Google Scholar] [CrossRef]
- Zhang, C.; Xiao, C.; Li, S.; Yan, H.; Liu, D. A Novel fiber-optic ice sensor to identify ice types based on total reflection. Sensors 2023, 23, 3996. [Google Scholar] [CrossRef] [PubMed]
- Wagih, M.; Shi, J. Toward the optimal antenna-based wireless sensing strategy: An ice sensing case study. IEEE Open J. Antennas Propag. 2022, 3, 687–699. [Google Scholar] [CrossRef]
- Jinesh, K.; Frenken, J. Experimental evidence for ice formation at room temperature. Phys. Rev. Lett. 2008, 101, 036101. [Google Scholar] [CrossRef]
- Varadan, V.K.; Varadan, V.V.; Bao, X.-K. IDT, SAW and MEMS sensors for measuring deflection, acceleration and ice detection of aircraft. Proc. SPIE 1997, 3046, 209–219. [Google Scholar]
- Vellekoop, M.J.; Jakoby, B.; Bastemeijer, J. A love-wave ice detector. In Proceedings of the 1999 IEEE Ultrasonics Symposium, Lake Tahoe, NV, USA, 17–20 October 1999; pp. 453–456. [Google Scholar]
- Wang, W.; Yin, Y.; Jia, Y.; Liu, M.; Liang, Y.; Zhang, Y.; Lu, M. Development of Love wave based device for sensing icing process with fast response. J. Electr. Eng. Technol. 2020, 15, 1245–1254. [Google Scholar] [CrossRef]
- Schulmeyer, P.; Weihnacht, M.; Schmidt, H. A Dual-mode surface acoustic wave delay line for the detection of ice on 64°-rotated Y-cut lithium niobate. Sensors 2024, 24, 2292. [Google Scholar] [CrossRef] [PubMed]
- Pavey, K.; Hunter, A.; Paul, F. Real-time evaluation of macromolecular surface modified quartz crystal resonant sensors under cryogenic stress for biological applications. Biosens. Bioelectron. 2003, 18, 1349–1354. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Rose, J.L. Ice detection and classification on an aircraft wing with ultrasonic shear horizontal guided waves. IEEE Trans. Ultras. Ferroel. Freq. Contr. 2009, 56, 334–343. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Wang, Q.; Liu, M.; Zhang, J.; Zhou, L. Robust and quantitative characterization of aircraft icing with mode and frequency selective ultrasonic guided wave. Ultrasonics 2023, 127, 106846. [Google Scholar] [CrossRef] [PubMed]
- Hughes, R.S.; Martin, S.J.; Frye, J.C.; Ricco, A.J. Liquid-solid phase transition detection with acoustic plate mode sensors: Application to icing of surfaces. Sens. Act. A Phys. 1990, A21–A23, 693–699. [Google Scholar] [CrossRef]
- Anisimkin, V.; Kolesov, V.; Kuznetsova, A.; Shamsutdinova, E.; Kuznetsova, I. An analysis of the water-to-ice phase transition using acoustic plate waves. Sensors 2021, 21, 919. [Google Scholar] [CrossRef]
- Anisimkin, V.I.; Voronova, N.V. New modification of the acoustic Lamb waves and its application for liquid and ice sensing. Ultrasonics 2021, 116, 106496. [Google Scholar] [CrossRef]
- Kuznetsova, I.; Zaitsev, B.; Seleznev, E.; Verona, E. Gasoline identifier based on SH0 plate acoustic wave. Ultrasonics 2016, 70, 34–37. [Google Scholar] [CrossRef]
- Gao, H.; Rose, J.L. Ultrasonic guided wave tomography for ice detection. Ultrasonics 2016, 67, 212–219. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, Y.; Li, W.; Wu, D.; Zhao, N.; Zhu, C. Study on freezing characteristics of the surface water film over glaze ice by using an ultrasonic pulse-echo technique. Ultrasonics 2022, 126, 106804. [Google Scholar] [CrossRef] [PubMed]
- Dukhin, A.S.; Goetz, P.J. Fundamentals of acoustics in liquids. Stud. Interface Sci. 2002, 15, 75–99. [Google Scholar] [CrossRef]
- Kielczynski, P. Application of Acoustic Waves to Investigate the Physical Properties of Liquids at High Pressure. In Acoustic Waves; Dissanayake, D.W., Ed.; Sciyo: Rijeka, Croatia, 2010; Chapter 14; pp. 317–340. [Google Scholar]
- Kielczynski, P. The Application of Ultrasonics for Oil Characterization, Ultrasound in Food Processing: Recent Advances, 1st ed.; Villamiel, M., Montilla, A., García-Pérez, J.V., Cárcel, J.A., Benedito, J., Eds.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Jones, G.A.; Ferreira, A.M.G.; Kulessa, B.; Schimmel, M.; Berbellini, A.; Morelli, A. Constraints on the cryohydrological warming of firn and ice in Greenland from Rayleigh wave ellipticity data. Geophys. Res. Lett. 2023, 50, e2023GL103673. [Google Scholar] [CrossRef]
- Berbellini, A.; Schimmel, M.; Ferreira, A.M.G.; Morelli, A. Constraining S-wave velocity using Rayleigh wave ellipticity from polarization analysis of seismic noise. Geophys. J. Int. 2019, 216, 1817–1830. [Google Scholar] [CrossRef]
- Ono, S.; Wasa, K.; Hayakawa, S. SAW properties in ZnO-SiO2 layered structure. Wave Electron. 1977, 3, 35–49. [Google Scholar]
- Auld, B.A. Acoustic Fields and Waves in Solids; Willey-Interscience Publication: Hoboken, NJ, USA, 1973; Volume 1. [Google Scholar]
- Del Grosso, V.A.; Mader, C.W. Speed of sound in pure water. J. Acoust. Soc. Am. 1972, 52, 1442–1446. [Google Scholar] [CrossRef]
- Gammon, P.H.; Kiefte, H.; Clouter, M.J.; Denner, W.W. Elastic constants of artificial ice and natural ice samples by Brillouin spectroscopy. J. Glaciol. 1983, 29, 433–460. [Google Scholar] [CrossRef]
- Fukuhara, M.; Sanpei, A. High temperature-elastic moduli and internal dilational and shear frictions of fused quartz. Jpn. J. Appl. Phys. 1994, 33, 2890–2893. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Theory of Elasticity; Pergamon Press: London, UK, 1959. [Google Scholar]
- Viktorov, I.A. Rayleigh and Lamb Waves: Physical Theory and Applications; Plenum Press: New York, NY, USA, 1970. [Google Scholar]
- Makkonen, L. Models for the growth of rime, glaze, icicles and wet snow on structures. Phil. Trans. R. Soc. Lond. A 2000, 358, 2913–2939. [Google Scholar] [CrossRef]


| , μs | , km/s | , dB/mm | , μs | , km/s | , dB/mm | , μs | , km/s | |
|---|---|---|---|---|---|---|---|---|
| Present paper | 13.34 | 1.4 ± 0.1 | 1.9 ± 0.5 | 5.87 | 3.5 ± 0.2 | 3.8 ± 0.5 | 0.84 | 5.96 ± 0.1 |
| Other papers | - | 1.466 ± 0.003 [33] | - | - | 3.6 ± 0.1 [34] | - | - | 5.97 [35] |
| , μs | , km/s | , dB/mm | , μs | , km/s | |
|---|---|---|---|---|---|
| Present paper | 3.4 | 1.7 ± 0.2 | 6.1 ± 0.5 | 1.44 | 3.76 ± 0.1 |
| Other papers | - | 1.929 ± 0.02 [34] | - | - | 3.76 [35] |
| , km/s | , km/s | , km/s | , dB/mm | , dB/mm | , dB/mm | σice |
|---|---|---|---|---|---|---|
| 3.5 ± 0.2 | 1.7 ± 0.2 | 1.6 ± 0.2 | 3.8 ± 0.5 | 6.1 ± 0.2 | 4 ± 0.5 | 0.35 ± 0.04 |
| Transducers Position | , km/s | , dB/mm |
|---|---|---|
| Top | 4.2 ± 0.2 | 0.7 ± 0.2 |
| Bottom | 4.7 ± 0.2 | 3.8 ± 0.5 |
| Liquid Phase | Solid Phase | ||||
|---|---|---|---|---|---|
| H2O | H2O + 0.9% NaCl | Pure Ice | Salty Ice | ||
| τlq, μs | 10.2 ± 0.5 | 11.8 ± 0.5 | τice, μs | 7.5 ± 0.5 | 11.2 ± 0.5 |
| , m/s | 1500 | 1100 | , m/s | 3500 | 1250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smirnov, A.; Anisimkin, V.; Voronova, N.; Kashin, V.; Kuznetsova, I. Multi-Parameter Characterization of Liquid-to-Ice Phase Transition Using Bulk Acoustic Waves. Sensors 2024, 24, 4010. https://doi.org/10.3390/s24124010
Smirnov A, Anisimkin V, Voronova N, Kashin V, Kuznetsova I. Multi-Parameter Characterization of Liquid-to-Ice Phase Transition Using Bulk Acoustic Waves. Sensors. 2024; 24(12):4010. https://doi.org/10.3390/s24124010
Chicago/Turabian StyleSmirnov, Andrey, Vladimir Anisimkin, Natalia Voronova, Vadim Kashin, and Iren Kuznetsova. 2024. "Multi-Parameter Characterization of Liquid-to-Ice Phase Transition Using Bulk Acoustic Waves" Sensors 24, no. 12: 4010. https://doi.org/10.3390/s24124010
APA StyleSmirnov, A., Anisimkin, V., Voronova, N., Kashin, V., & Kuznetsova, I. (2024). Multi-Parameter Characterization of Liquid-to-Ice Phase Transition Using Bulk Acoustic Waves. Sensors, 24(12), 4010. https://doi.org/10.3390/s24124010








