Effect of Biomass Water Dynamics in Cosmic-Ray Neutron Sensor Observations: A Long-Term Analysis of Maize–Soybean Rotation in Nebraska
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Description of SWC Datasets
2.3. Description of CRNS Data
2.4. Biomass Water Equivalent Measurements
2.5. Statistical Analysis of BWE on Neutron Intensity
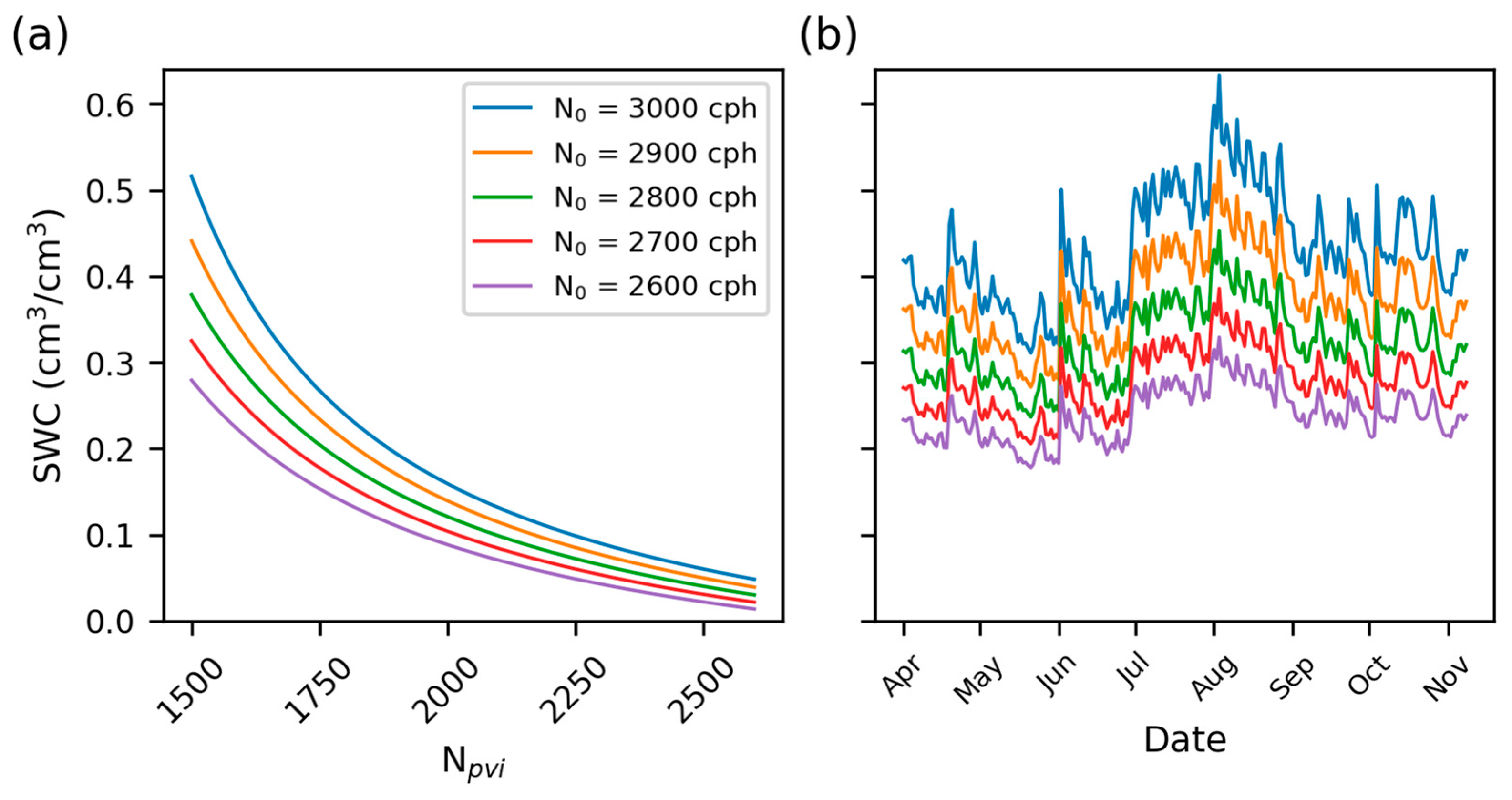
3. Results
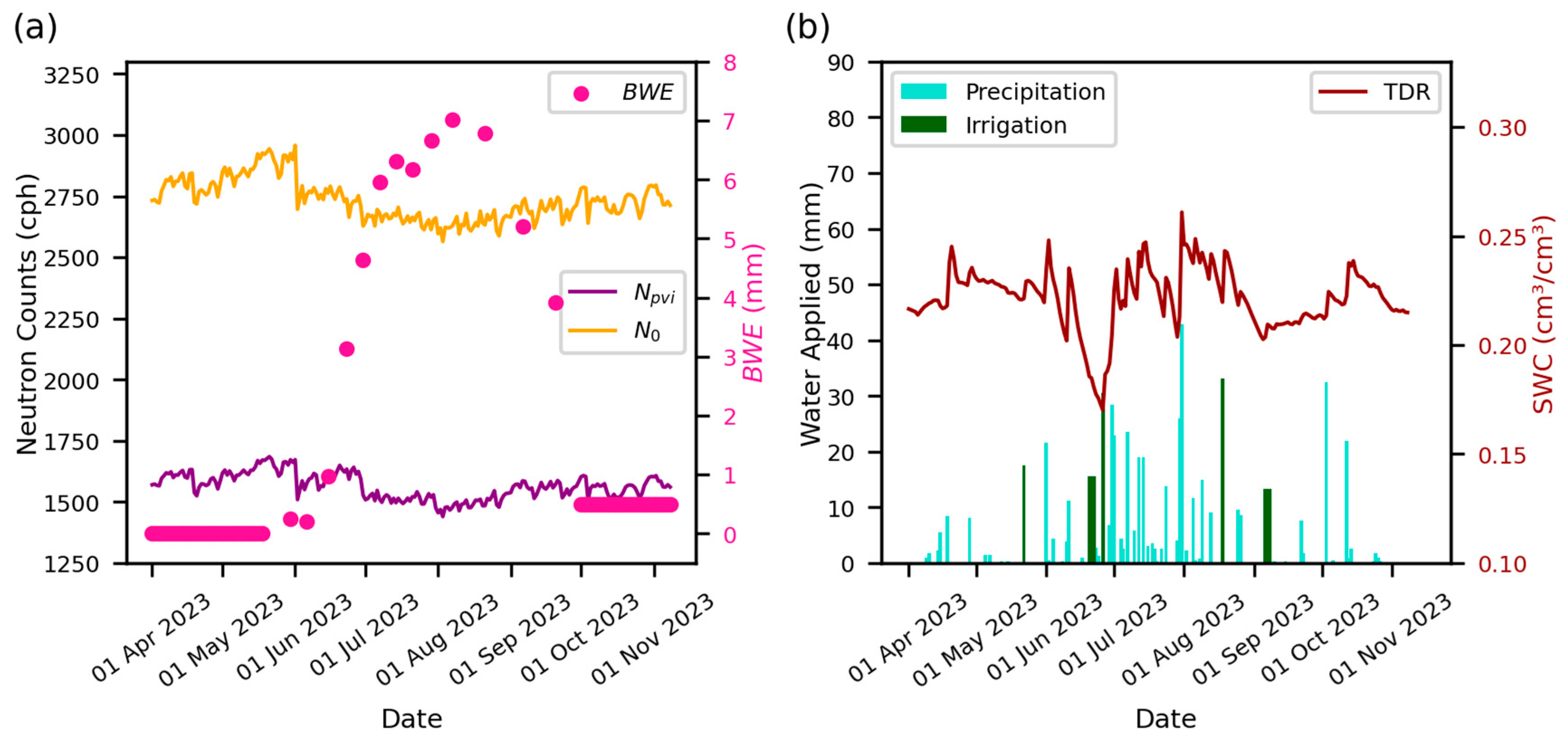
3.1. Overview of SWC, BWE, and CRNS at Study Sites
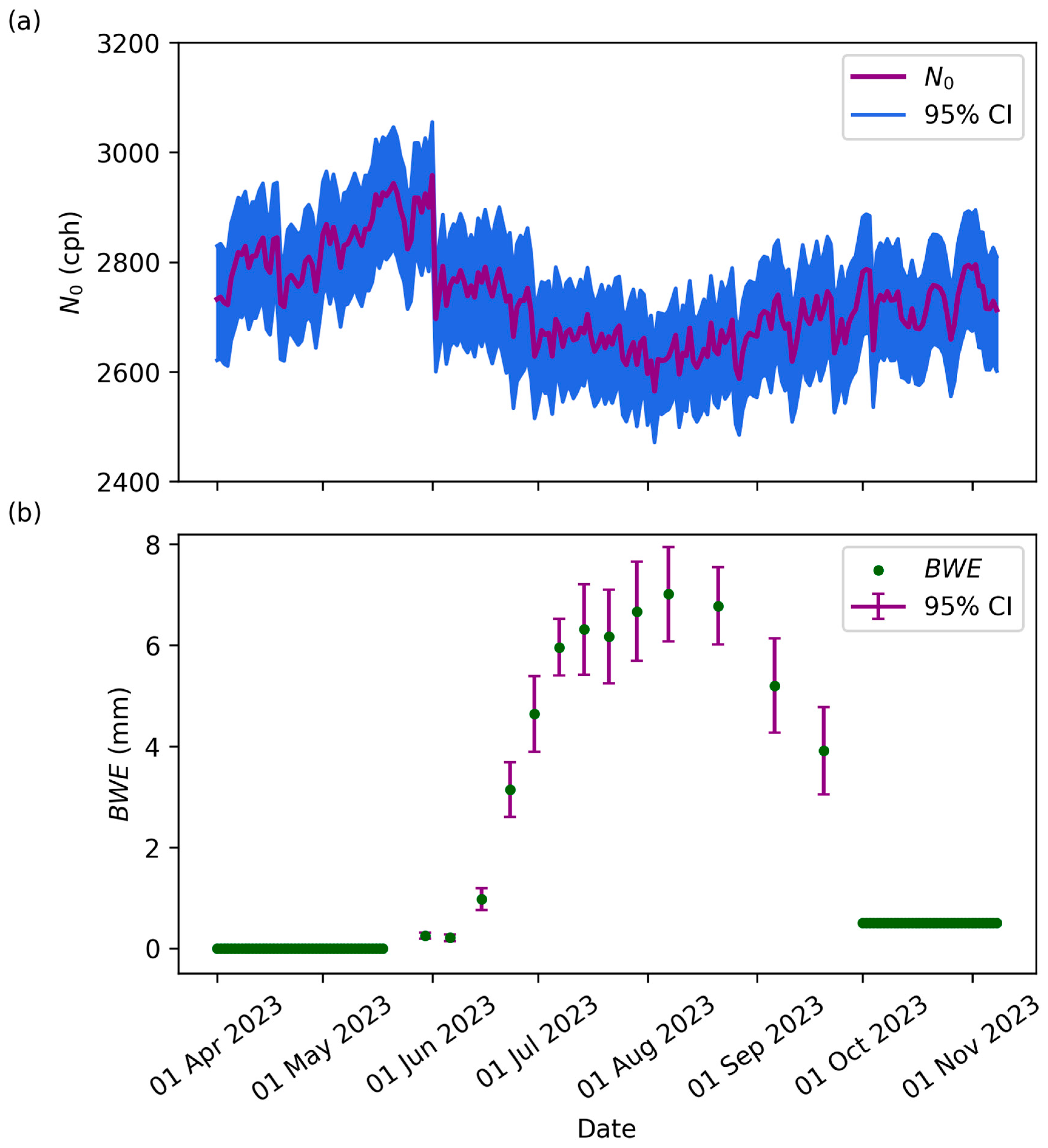
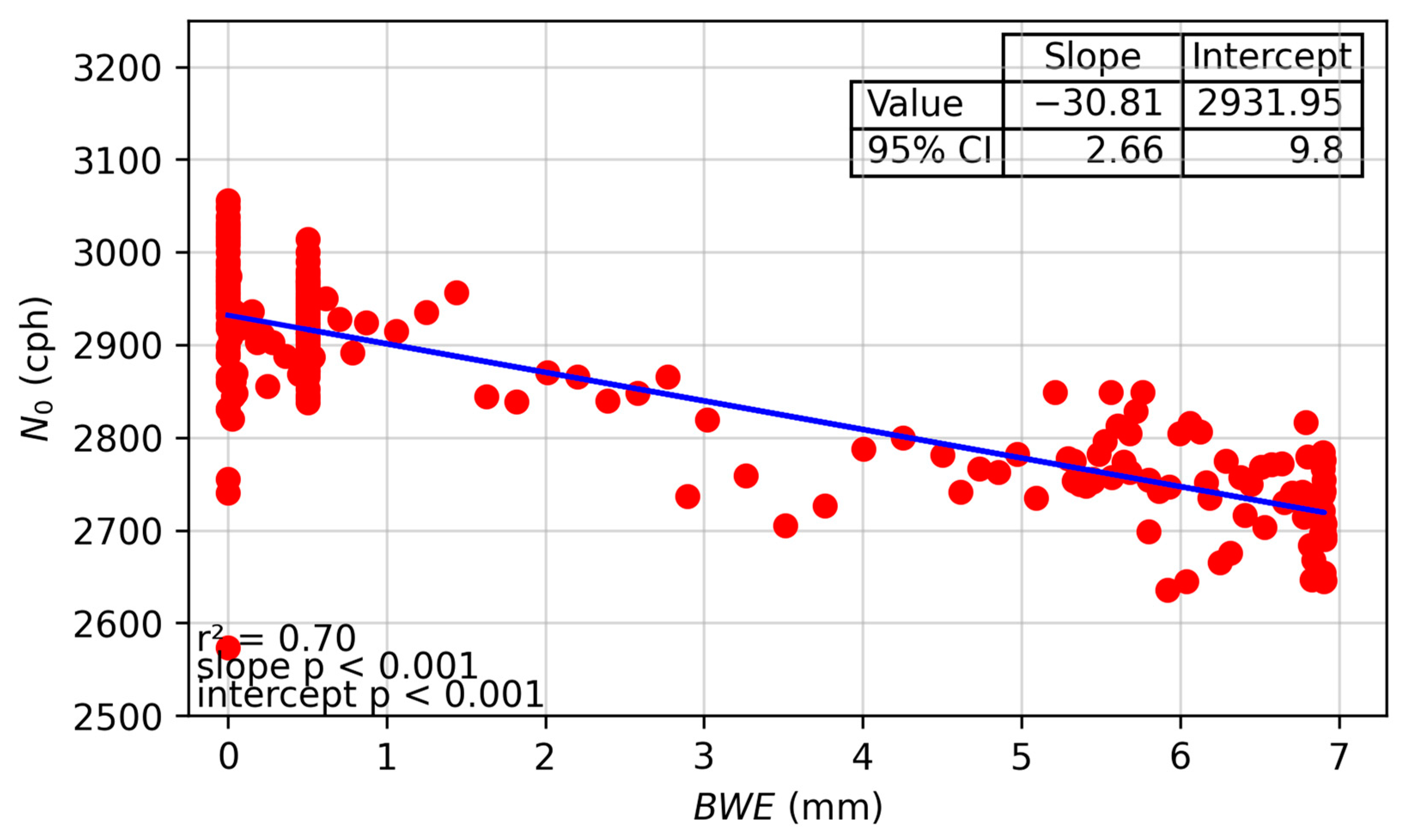
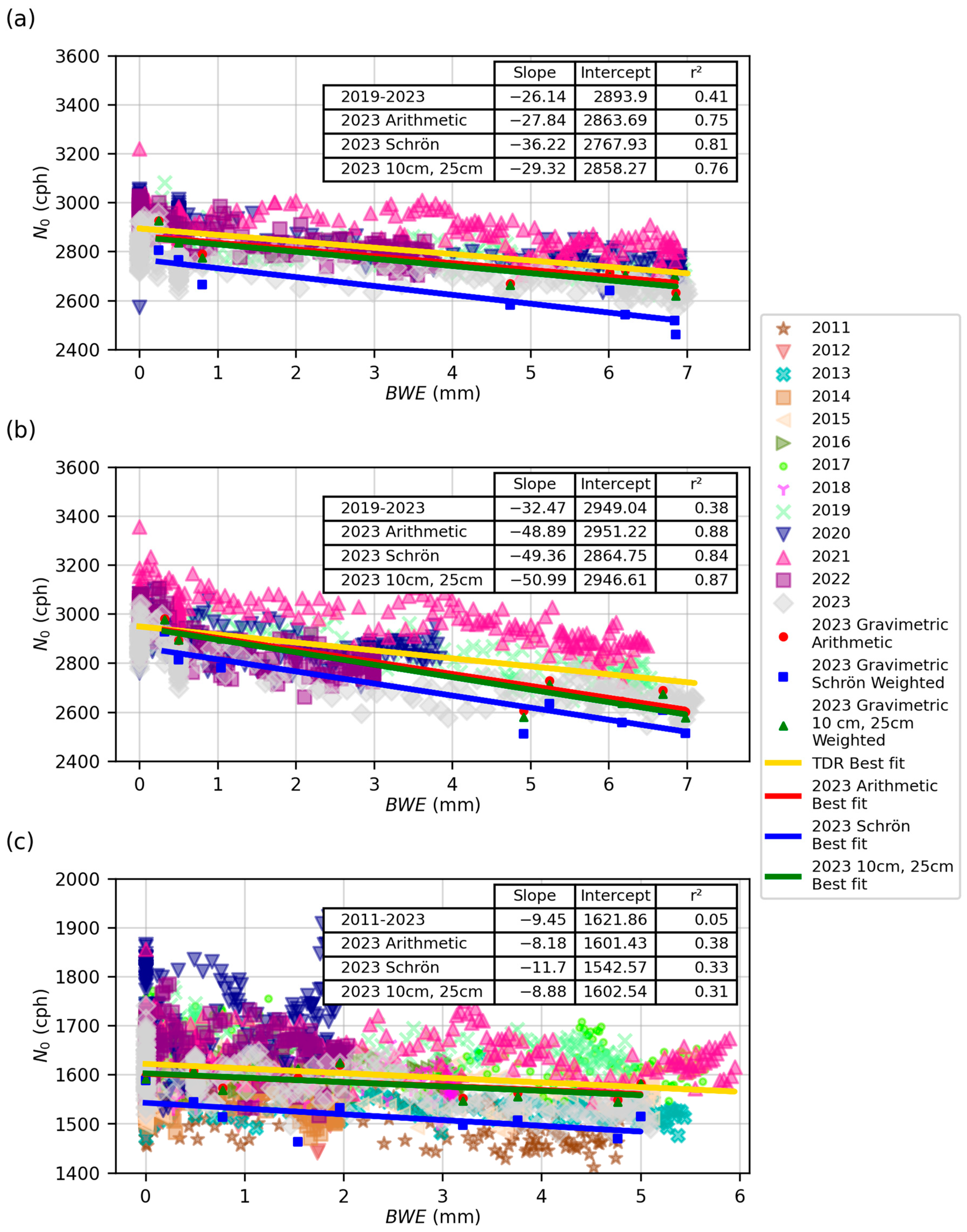
3.2. Influence of BWE on Neutron Intensity
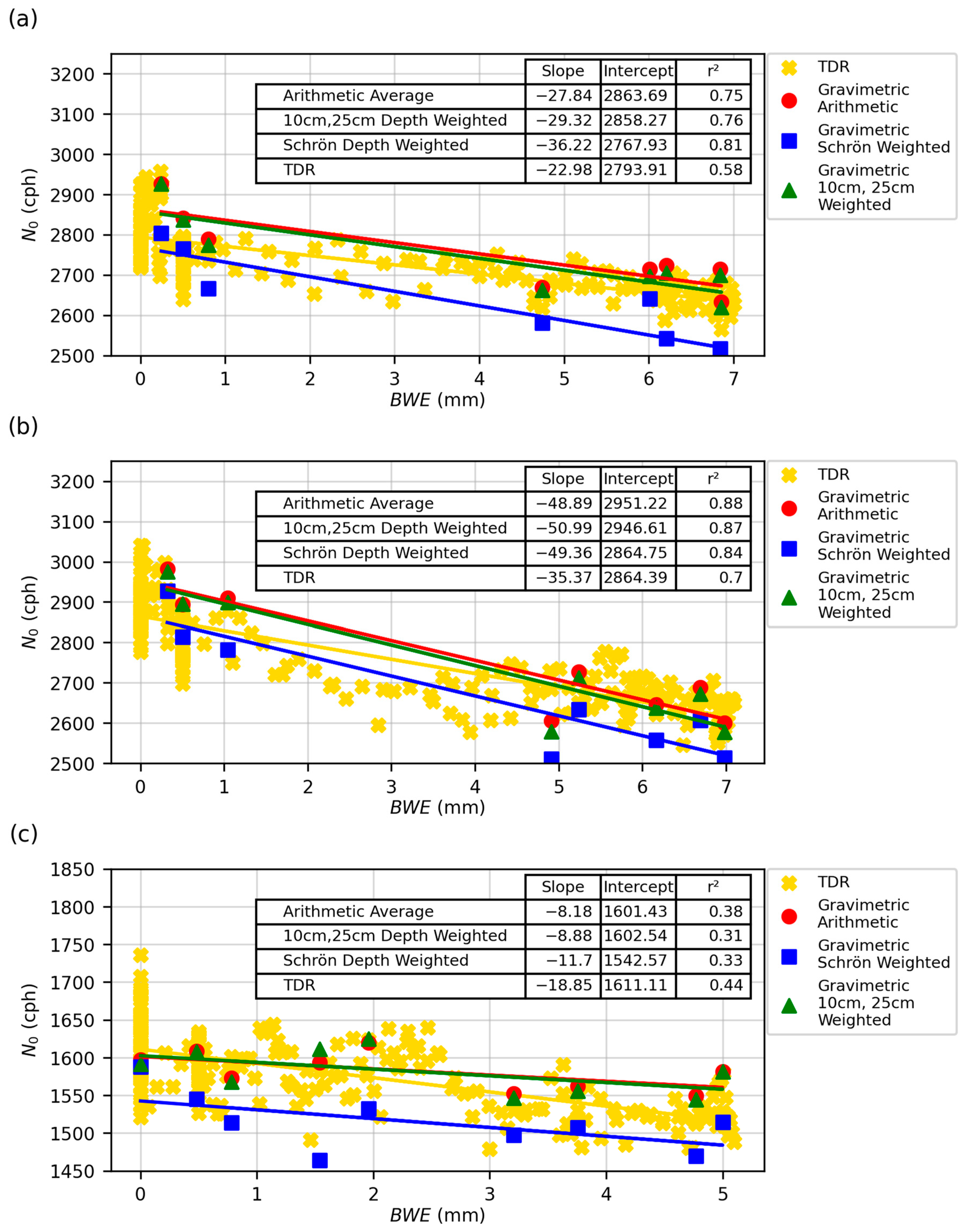
3.3. TDR vs. Gravimetric Sampling
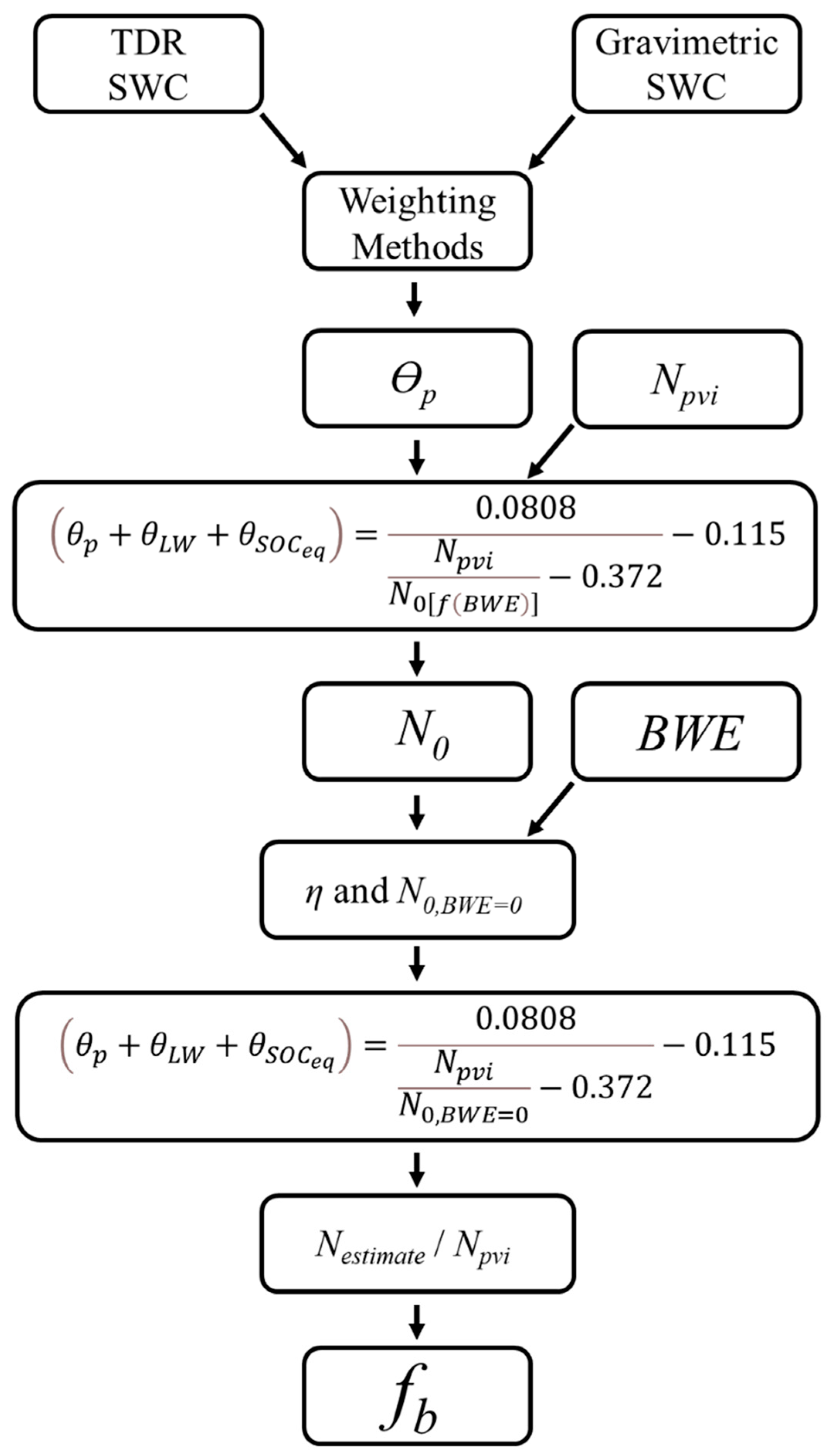
3.4. Proposed Biomass Correction Factor, fb
4. Discussion
4.1. Relationship between N0 and BWE
4.2. Sparse TDR Network vs. Gravimetric Sampling
4.3. Vegetation Correction Factor
4.4. Variations in Sensor Type
4.5. Limitations of Study and Future Directions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations. United Nations Food and Agriculture Organization: How to Feed the World in 2050; United Nations: New York, NY, USA, 2015. [Google Scholar]
- van Dijk, M.; Morley, T.; Rau, M.L.; Saghai, Y. A meta-analysis of projected global food demand and population at risk of hunger for the period 2010–2050. Nat. Food 2021, 2, 494–501. [Google Scholar] [CrossRef] [PubMed]
- AQUASTAT—FAO. AQUASTAT—FAO’s Global Information System on Water and Agriculture. Available online: https://www.fao.org/aquastat/en/overview/methodology/water-use (accessed on 7 February 2024).
- Ewaid, S.H.; Abed, S.A.; Al-Ansari, N. Assessment of Main Cereal Crop Trade Impacts on Water and Land Security in Iraq. Agronomy 2020, 10, 98. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Dold, C. Water-Use Efficiency: Advances and Challenges in a Changing Climate. Front. Plant Sci. 2019, 10, 429990. [Google Scholar] [CrossRef] [PubMed]
- Sharma, B.; Molden, D.; Cook, S. Water use efficiency in agriculture: Measurement, current situation and trends. In Managing Water and Fertilizer for Sustainable Agricultural Intensification; International Fertiliser Association: Paris, France, 2015. [Google Scholar]
- United States Department of Agriculture, National Agricultural Statistics Service. 2018 Irrigation and Water Management Survey. Census of Agriculture; 2017. Available online: https://www.nass.usda.gov/Publications/AgCensus/2017/Online_Resources/Farm_and_Ranch_Irrigation_Survey/FRIS.txt (accessed on 27 January 2024).
- Zhang, J.; Guan, K.; Peng, B.; Jiang, C.; Zhou, W.; Yang, Y.; Pan, M.; Franz, T.E.; Heeren, D.M.; Rudnick, D.R.; et al. Challenges and opportunities in precision irrigation decision-support systems for center pivots. Environ. Res. Lett. 2021, 16, 053003. [Google Scholar] [CrossRef]
- Zreda, M.; Desilets, D.; Ferré, T.P.A.; Scott, R.L. Measuring soil moisture content non-invasively at intermediate spatial scale using cosmic-ray neutrons. Geophys. Res. Lett. 2008, 35, L21402. [Google Scholar] [CrossRef]
- Köhli, M.; Schrön, M.; Zreda, M.; Schmidt, U.; Dietrich, P.; Zacharias, S. Footprint characteristics revised for field-scale soil moisture monitoring with cosmic-ray neutrons. Water Resour. Res. 2015, 51, 5772–5790. [Google Scholar] [CrossRef]
- Schrön, M.; Köhli, M.; Scheiffele, L.; Iwema, J.; Bogena, H.R.; Lv, L.; Martini, E.; Baroni, G.; Rosolem, R.; Weimar, J.; et al. Improving calibration and validation of cosmic-ray neutron sensors in the light of spatial sensitivity. Hydrol. Earth Syst. Sci. 2017, 21, 5009–5030. [Google Scholar] [CrossRef]
- Francke, T.K.O.; Heistermann, M.; Köhli, M.; Budach, C.; Schrön, M.; Oswald, S.E. Assessing the Feasibility of a Directional Cosmic-ray Neutron Sensing Sensor for Estimating Soil Moisture; Universität Potsdam: Potsdam, Germany, 2022. [Google Scholar] [CrossRef]
- Andreasen, M.; Jensen, K.H.; Desilets, D.; Franz, T.E.; Zreda, M.; Bogena, H.R.; Looms, M.C. Status and Perspectives on the Cosmic-Ray Neutron Method for Soil Moisture Estimation and Other Environmental Science Applications. Vadose Zone J. 2017, 16. [Google Scholar] [CrossRef]
- Baroni, G.; Scheiffele, L.M.; Schrön, M.; Ingwersen, J.; Oswald, S.E. Uncertainty, sensitivity and improvements in soil moisture estimation with cosmic-ray neutron sensing. J. Hydrol. 2018, 564, 873–887. [Google Scholar] [CrossRef]
- Zreda, M.; Shuttleworth, W.J.; Zeng, X.; Zweck, C.; Desilets, D.; Franz, T.; Rosolem, R. COSMOS: The COsmic-ray Soil Moisture Observing System. Hydrol. Earth Syst. Sci. 2012, 16, 4079–4099. [Google Scholar] [CrossRef]
- Desilets, D.; Zreda, M. Footprint diameter for a cosmic-ray soil moisture probe: Theory and Monte Carlo simulations. Water Resour. Res. 2013, 49, 3566–3575. [Google Scholar] [CrossRef]
- Köhli, M.; Weimar, J.; Schrön, M.; Baatz, R.; Schmidt, U. Soil Moisture and Air Humidity Dependence of the Above-Ground Cosmic-Ray Neutron Intensity. Front. Water 2021, 2, 544847. [Google Scholar] [CrossRef]
- Desilets, D.; Zreda, M.; Ferré, T.P.A. Nature’s neutron probe: Land surface hydrology at an elusive scale with cosmic rays. Water Resour. Res. 2010, 46, W11505. [Google Scholar] [CrossRef]
- Andreasen, M.; Jensen, K.H.; Bogena, H.; Desilets, D.; Zreda, M.; Looms, M.C. Cosmic Ray Neutron Soil Moisture Estimation Using Physically Based Site-Specific Conversion Functions. Water Resour. Res. 2020, 56, e2019WR026588. [Google Scholar] [CrossRef]
- McJannet, D.; Franz, T.; Hawdon, A.; Boadle, D.; Baker, B.; Almeida, A.; Silberstein, R.; Lambert, T.; Desilets, D. Field testing of the universal calibration function for determination of soil moisture with cosmic-ray neutrons. Water Resour. Res. 2014, 50, 5235–5248. [Google Scholar] [CrossRef]
- Rosolem, R.; Shuttleworth, W.J.; Zreda, M.; Franz, T.E.; Zeng, X.; Kurc, S.A. The Effect of Atmospheric Water Vapor on Neutron Count in the Cosmic-Ray Soil Moisture Observing System. J. Hydrometeorol. 2013, 14, 1659–1671. [Google Scholar] [CrossRef]
- Franz, T.E.; Zreda, M.; Rosolem, R.; Hornbuckle, B.K.; Irvin, S.L.; Adams, H.; Kolb, T.E.; Zweck, C.; Shuttleworth, W.J. Ecosystem-scale measurements of biomass water using cosmic ray neutrons. Geophys. Res. Lett. 2013, 40, 3929–3933. [Google Scholar] [CrossRef]
- McJannet, D.L.; Desilets, D. Incoming Neutron Flux Corrections for Cosmic-Ray Soil and Snow Sensors Using the Global Neutron Monitor Network. Water Resour. Res. 2023, 59, e2022WR033889. [Google Scholar] [CrossRef]
- Baatz, R.; Bogena, H.R.; Hendricks Franssen, H.-J.; Huisman, J.A.; Montzka, C.; Vereecken, H. An empirical vegetation correction for soil water content quantification using cosmic ray probes. Water Resour. Res. 2015, 51, 2030–2046. [Google Scholar] [CrossRef]
- Vather, T.; Everson, C.S.; Franz, T.E. The Applicability of the Cosmic Ray Neutron Sensor to Simultaneously Monitor Soil Water Content and Biomass in an Acacia mearnsii Forest. Hydrology 2020, 7, 48. [Google Scholar] [CrossRef]
- Franz, T.E.; Wang, T.; Avery, W.; Finkenbiner, C.; Brocca, L. Combined analysis of soil moisture measurements from roving and fixed cosmic ray neutron probes for multiscale real-time monitoring. Geophys. Res. Lett. 2015, 42, 3389–3396. [Google Scholar] [CrossRef]
- Heistermann, M.; Francke, T.; Scheiffele, L.; Dimitrova Petrova, K.; Budach, C.; Schrön, M.; Trost, B.; Rasche, D.; Güntner, A.; Döpper, V.; et al. Three years of soil moisture observations by a dense cosmic-ray neutron sensing cluster at an agricultural research site in north-east Germany. Earth Syst. Sci. Data 2023, 15, 3243–3262. [Google Scholar] [CrossRef]
- Tian, Z.; Li, Z.; Liu, G.; Li, B.; Ren, T. Soil water content determination with cosmic-ray neutron sensor: Correcting aboveground hydrogen effects with thermal/fast neutron ratio. J. Hydrol. 2016, 540, 923–933. [Google Scholar] [CrossRef]
- Jakobi, J.; Huisman, J.A.; Vereecken, H.; Diekkrüger, B.; Bogena, H.R. Cosmic Ray Neutron Sensing for Simultaneous Soil Water Content and Biomass Quantification in Drought Conditions. Water Resour. Res. 2018, 54, 7383–7402. [Google Scholar] [CrossRef]
- Andreasen, M.; Jensen, K.H.; Desilets, D.; Zreda, M.; Bogena, H.R.; Looms, M.C. Cosmic-ray neutron transport at a forest field site: The sensitivity to various environmental conditions with focus on biomass and canopy interception. Hydrol. Earth Syst. Sci. 2017, 21, 1875–1894. [Google Scholar] [CrossRef]
- Andreasen, M.; Kragh, S.J.; Meyer, R.; Jensen, K.H.; Looms, M.C. Mapping spatiotemporal soil moisture in highly heterogeneous agricultural landscapes using mobile dual-spectra cosmic-ray neutron sensing. Vadose Zone J. 2023, 22, e20287. [Google Scholar] [CrossRef]
- Serrano, L.; Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Peñuelas, J. Deriving Water Content of Chaparral Vegetation from AVIRIS Data. Remote Sens. Environ. 2000, 74, 570–581. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Estimation of vegetation water content and photosynthetic tissue area from spectral reflectance: A comparison of indices based on liquid water and chlorophyll absorption features. Remote Sens. Environ. 2003, 84, 526–537. [Google Scholar] [CrossRef]
- Avery, W.A.; Finkenbiner, C.; Franz, T.E.; Wang, T.; Nguy-Robertson, A.L.; Suyker, A.; Arkebauer, T.; Muñoz-Arriola, F. Incorporation of globally available datasets into the roving cosmic-ray neutron probe method for estimating field-scale soil water content. Hydrol. Earth Syst. Sci. 2016, 20, 3859–3872. [Google Scholar] [CrossRef]
- Coopersmith, E.J.; Cosh, M.H.; Daughtry, C.S.T. Field-scale moisture estimates using COSMOS sensors: A validation study with temporary networks and Leaf-Area-Indices. J. Hydrol. 2014, 519, 637–643. [Google Scholar] [CrossRef]
- Baatz, R.; Bogena, H.R.; Hendricks Franssen, H.-J.; Huisman, J.A.; Qu, W.; Montzka, C.; Vereecken, H. Calibration of a catchment scale cosmic-ray probe network: A comparison of three parameterization methods. J. Hydrol. 2014, 516, 231–244. [Google Scholar] [CrossRef]
- Hawdon, A.; McJannet, D.; Wallace, J. Calibration and correction procedures for cosmic-ray neutron soil moisture probes located across Australia. Water Resour. Res. 2014, 50, 5029–5043. [Google Scholar] [CrossRef]
- Rivera Villarreyes, C.A.; Baroni, G.; Oswald, S.E. Integral quantification of seasonal soil moisture changes in farmland by cosmic-ray neutrons. Hydrol. Earth Syst. Sci. 2011, 15, 3843–3859. [Google Scholar] [CrossRef]
- Hornbuckle, B.; Irvin, S.; Franz, T.; Rosolem, R.; Zweck, C. The potential of the COSMOS network to be a source of new soil moisture information for SMOS and SMAP. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1243–1246. [Google Scholar] [CrossRef]
- Franz, T.E.; Zreda, M.; Rosolem, R.; Ferre, T.P.A. A universal calibration function for determination of soil moisture with cosmic-ray neutrons. Hydrol. Earth Syst. Sci. 2013, 17, 453–460. [Google Scholar] [CrossRef]
- Heidbüchel, I.; Güntner, A.; Blume, T. Use of cosmic-ray neutron sensors for soil moisture monitoring in forests. Hydrol. Earth Syst. Sci. 2016, 20, 1269–1288. [Google Scholar] [CrossRef]
- Baroni, G.; Oswald, S.E. A scaling approach for the assessment of biomass changes and rainfall interception using cosmic-ray neutron sensing. J. Hydrol. 2015, 525, 264–276. [Google Scholar] [CrossRef]
- Jakobi, J.; Huisman, J.A.; Fuchs, H.; Vereecken, H.; Bogena, H.R. Potential of Thermal Neutrons to Correct Cosmic-Ray Neutron Soil Moisture Content Measurements for Dynamic Biomass Effects. Water Resour. Res. 2022, 58, e2022WR031972. [Google Scholar] [CrossRef]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-Scale Biomass Estimators for United States Tree Species. For. Sci. 2003, 49, 12–35. [Google Scholar] [CrossRef]
- Soil Survey Staff. Natural Resources Conservation Service, & United States Department of Agriculture. Web Soil Survey [Dataset]. Available online: https://websoilsurvey.nrcs.usda.gov/app/ (accessed on 20 February 2023).
- Suyker, A. AmeriFlux BASE US-Ne1 Mead—Irrigated Continuous Maize Site, Ver. 16-5, AmeriFlux AMP, (Dataset); AmeriFlux: New York, NY, USA, 2024. [CrossRef]
- Suyker, A. AmeriFlux BASE US-Ne2 Mead—Irrigated Maize-Soybean Rotation Site, Ver. 16-5, AmeriFlux AMP, (Dataset); AmeriFlux: New York, NY, USA, 2024. [CrossRef]
- Suyker, A. AmeriFlux BASE US-Ne3 Mead—Rainfed Maize-Soybean Rotation Site, Ver. 16-5, AmeriFlux AMP, (Dataset); AmeriFlux: New York, NY, USA, 2024. [CrossRef]
- Franz, T.E.; Zreda, M.; Rosolem, R.; Ferre, T.P.A. Field Validation of a Cosmic-Ray Neutron Sensor Using a Distributed Sensor Network. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Iwema, J.; Rosolem, R.; Baatz, R.; Wagener, T.; Bogena, H.R. Investigating temporal field sampling strategies for site-specific calibration of three soil moisture–neutron intensity parameterisation methods. Hydrol. Earth Syst. Sci. 2015, 19, 3203–3216. [Google Scholar] [CrossRef]
- Franz, T.E.; Wahbi, A.; Zhang, J.; Vreugdenhil, M.; Heng, L.; Dercon, G.; Strauss, P.; Brocca, L.; Wagner, W. Practical Data Products From Cosmic-Ray Neutron Sensing for Hydrological Applications. Front. Water 2020, 2. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Heistermann, M.; Francke, T.; Schrön, M.; Oswald, S.E. Technical Note: Revisiting the general calibration of cosmic-ray neutron sensors to estimate soil water content. Hydrol. Earth Syst. Sci. Discuss. 2023, 2023, 1–18. [Google Scholar] [CrossRef]
- Andreasen, M.; Jensen, K.H.; Zreda, M.; Desilets, D.; Bogena, H.; Looms, M.C. Modeling cosmic ray neutron field measurements. Water Resour. Res. 2016, 52, 6451–6471. [Google Scholar] [CrossRef]
- Köhli, M.; Schrön, M.; Zacharias, S.; Schmidt, U. URANOS v1.0—The Ultra Rapid Adaptable Neutron-Only Simulation for Environmental Research. Geosci. Model Dev. 2023, 16, 449–477. [Google Scholar] [CrossRef]




| Method | Method Summary | Pro | Con | fb | Source |
|---|---|---|---|---|---|
| Thermal/ Epithermal Ratio | Uses bare and moderated sensors to determine the ratio between thermal and epithermal neutrons | Minimizes need for soil sampling, easy to measure, many applications | Requires two detectors, limited validation, several assumptions | Biomass presence reduces N0 by 13.8% for 13.7 kg/m2 dry biomass [25] linear relationship between ratio and biomass present | [19,25,28,29,30,31] |
| BWE | Weigh plants wet, oven dry, weigh plants dry, remove cellulose signal | Accurate, accounts for all parts of plants, used for ground truthing of other methods | Destructive, time-consuming, poor temporal resolution, one sample may not represent field | Linear relationship can be used to correct for vegetation, 1% decrease in N0 per mm BWE added | [26] |
| Remote Sensing | Satellite measurements taken to estimate biomass | Generally inexpensive, easily measured, large-scale coverage, non-destructive | Poor spatial and temporal resolution, atmospheric interference, complex analysis, lack of ground validation | No direct values reported, many studies discuss potential for an fb | [32,33,34,35] |
| Above-Ground Biomass | Measurements of AGB through several methods (destructive, allometric, etc.) | Accurate, reasonable biomass estimates, cost effective | Does not account for belowground biomass, labor-intensive, does not capture field variability | One study uses [24] correction, most studies report linear N0 and AGB relationship, no direct fb values reported, but need is addressed | [22,27,36,37,38] |
| Plant Allometry | Uses easily measured plant parts to estimate biomass of whole plant | Easy to measure and allows predictive power in growing biomass | Does not capture biomass variations and field variability, complex calculations | Biomass relationship listed as linear in some studies and non-linear in others, no direct fb reported | [39,40,41] |
| Scaling | Linear scaling approach used to upscale soil moisture measurements | Low cost, can be used at different time intervals (daily vs. seasonal trend), easy to upscale or downscale | Requires point water measurements, needs N0 calibration, relies heavily on z* and vertical weighting | No fb reported, reported that fast-growing biomass (e.g., maize) adds ~7 mm of BWE | [42] |
| Combination of Methods | Uses at least two methods listed above | Allows cross validation, more comprehensive study, and limits measurement bias | Adds complexity, requires more resources, introduces potential error sources | 0.9% per kg/m2 of dry AGB or per 2 kg/m2 of BWE [22], Other studies report an fb is needed, but do not quantify | [20,24,43] |
| 2023 CSP1 | 2023 CSP2 | 2023 CSP3 | 2011 CSP3 | Value Used | |
|---|---|---|---|---|---|
| 0.055 | 0.059 | 0.06 | 0.0375 | 0.058 | |
| 0.0113 | 0.0067 | 0.0097 | 0.006 | 0.0092 | |
| 1.40 ± 0.25 | 1.42 ± 0.17 | 1.43 ± 0.38 | 1.42 ± 0.17 | 1.42 |
| Year | CSP1 Intercept | CSP1 Slope | CSP2 Intercept | CSP2 Slope | CSP3 Intercept | CSP3 Slope | CSP1 η | CSP2 η | CSP3 η |
|---|---|---|---|---|---|---|---|---|---|
| 2023 Grav. Arithmetic | 2863.69 ± 79.0 | −27.84 ± 16.1 | 2951.22 ± 88.5 | −48.89 ± 18.4 | 1601.43 ± 27.6 | −8.18 ± 9.3 | −0.97 | −1.66 | −0.51 |
| 2023 Grav. Schrön et al. | 2767.93 ± 86.5 | −36.22 ± 17.7 | 2864.75 ± 102.7 | −49.36 ± 21.4 | 1542.57 ± 44.1 | −11.7 ± 44.1 | −1.31 | −1.72 | −0.76 |
| 2023 Grav. 10, 25 cm Wt. | 2858.27 ± 80.4 | −29.32 ± 16.4 | 2946.61 ± 94.6 | −50.99 ± 19.7 | 1602.54 ± 34.8 | −8.88 ± 11.7 | −1.03 | −1.73 | −0.55 |
| 2023 | 2793.91 ± 9.9 | −22.98 ± 2.6 | 2864.39 ± 11.8 | −35.37 ± 3.1 | 1611.11 ± 7.0 | −18.85 ± 2.8 | −0.82 | −1.23 | −1.17 |
| 2022 | 2918.41 ± 9.7 | −40.84 ± 5.7 | 2957.0 ± 9.6 | −67.36 ± 7.2 | 1644.22 ± 7.0 | −11.95 ± 8.1 | −1.40 | −2.28 | −0.73 |
| 2021 | 2920.98 ± 11.9 | −13.28 ± 3.4 | 3044.36 ± 13.5 | −24.99 ± 3.9 | 1663.1 ± 7.5 | −7.91 ± 2.4 | −0.45 | −0.82 | −0.48 |
| 2020 | 2931.95 ± 9.8 | −30.81 ± 2.7 | 2935.68 ± 10.5 | −30.98 ± 6.4 | 1688.51 ± 14.3 | 28.64 ± 15.3 | −1.05 | −1.06 | 1.70 |
| 2019 | 2888.29 ± 14.1 | −27.27 ± 3.4 | 2935.06 ± 14.7 | −34.32 ± 3.5 | 1661.97 ± 6.7 | −9.12 ± 2.6 | −0.94 | −1.17 | −0.55 |
| 2018 | 1627.93 ± 7.2 | −17.5 ± 4.0 | −1.07 | ||||||
| 2017 | 1667.4 ± 8.0 | −11.79 ± 2.6 | −0.71 | ||||||
| 2016 | 1651.59 ± 5.7 | −21.61 ± 3.8 | −1.31 | ||||||
| 2015 | 1584.47 ± 8.1 | −2.11 ± 3.0 | −0.13 | ||||||
| 2014 | 1583.61 ± 7.4 | −21.05 ± 7.6 | −1.33 | ||||||
| 2013 | 1556.41 ± 5.1 | −4.67 ± 1.9 | −0.30 | ||||||
| 2012 | 1574.7 ± 6.7 | −12.04 ± 8.6 | −0.76 | ||||||
| 2011 | 1542.13 ± 7.6 | −12.16 ± 3.0 | −0.79 | ||||||
| TDR Avg. | 2890.7 ± 11.1 | −27.0 ± 3.5 | 2947.3 ± 12.0 | −38.6 ± 4.8 | 1614.1 ± 7.0 | −12.6 ± 4.2 | −0.9 ± 0.3 | −1.3 ± 0.4 | −0.59 ± 0.4 |
| Field and Weighting Method | Neutron Intensity Reduction (% per mm BWE) |
|---|---|
| CSP1 Schrön et al. | 1.309 |
| CSP2 Schrön et al. | 1.723 |
| CSP3 Schrön et al. | 0.758 |
| CSP1 Arithmetic | 0.972 |
| CSP2 Arithmetic | 1.639 |
| CSP3 Arithmetic | 0.511 |
| CSP1 10, 25 cm | 1.026 |
| CSP2 10, 25 cm | 1.730 |
| CSP3 10, 25 cm | 0.554 |
| CSP1 TDR | 0.903 |
| CSP2 TDR | 1.101 |
| CSP3 TDR | 0.583 |
| CRS-2000/B Average | 1.300 ± 0.24 |
| CRS-1000/B Average | 0.602 ± 0.11 |
| Gravimetric Average | 1.136 ± 0.32 |
| TDR Average | 0.862 ± 0.30 |
| Overall Average | 1.067 ± 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morris, T.C.; Franz, T.E.; Becker, S.M.; Suyker, A.E. Effect of Biomass Water Dynamics in Cosmic-Ray Neutron Sensor Observations: A Long-Term Analysis of Maize–Soybean Rotation in Nebraska. Sensors 2024, 24, 4094. https://doi.org/10.3390/s24134094
Morris TC, Franz TE, Becker SM, Suyker AE. Effect of Biomass Water Dynamics in Cosmic-Ray Neutron Sensor Observations: A Long-Term Analysis of Maize–Soybean Rotation in Nebraska. Sensors. 2024; 24(13):4094. https://doi.org/10.3390/s24134094
Chicago/Turabian StyleMorris, Tanessa C., Trenton E. Franz, Sophia M. Becker, and Andrew E. Suyker. 2024. "Effect of Biomass Water Dynamics in Cosmic-Ray Neutron Sensor Observations: A Long-Term Analysis of Maize–Soybean Rotation in Nebraska" Sensors 24, no. 13: 4094. https://doi.org/10.3390/s24134094
APA StyleMorris, T. C., Franz, T. E., Becker, S. M., & Suyker, A. E. (2024). Effect of Biomass Water Dynamics in Cosmic-Ray Neutron Sensor Observations: A Long-Term Analysis of Maize–Soybean Rotation in Nebraska. Sensors, 24(13), 4094. https://doi.org/10.3390/s24134094






