Human Activity Recording Based on Skin-Strain-Actuated Microfluidic Pumping in Asymmetrically Designed Micro-Channels
Abstract
:1. Introduction
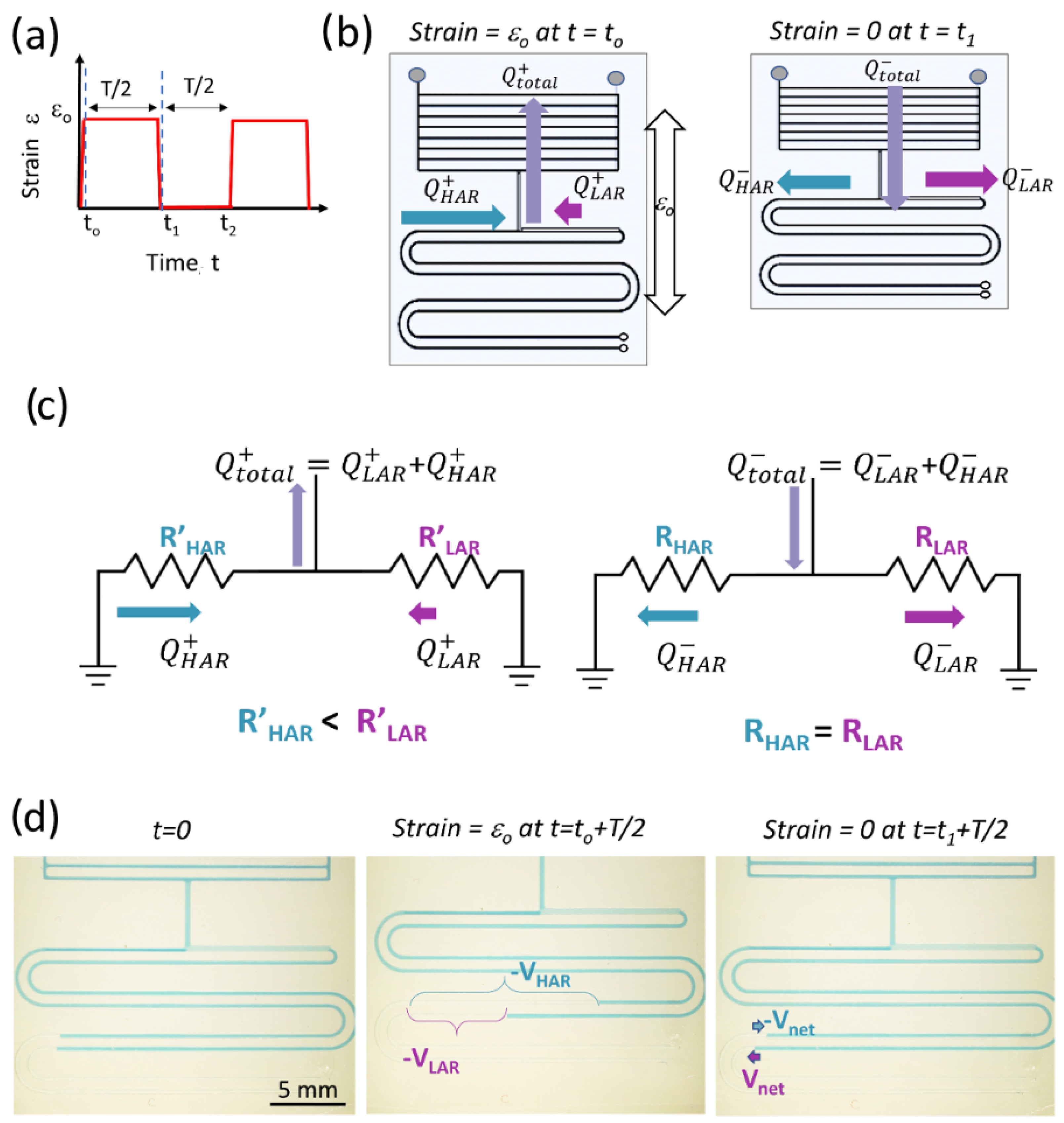
2. Device Design and Operation Mechanism
Equivalent Electrical Circuit Model for Pumping Efficiency Calculation
3. Materials and Methods
3.1. Fabrication of Molds
3.2. Fabrication of Devices
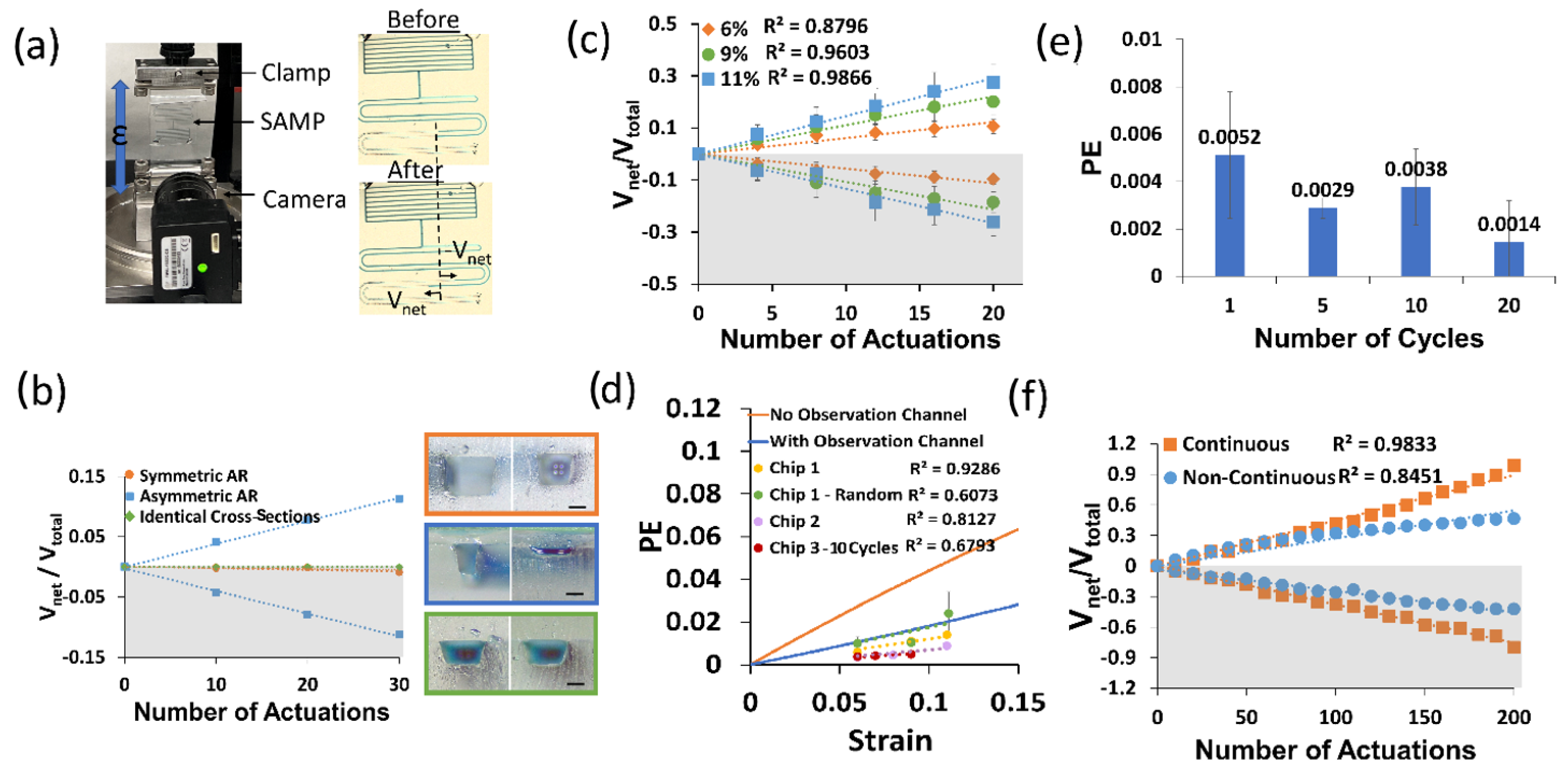
3.3. Benchtop Characterization
3.4. DIC Experimentation Methods
4. Results
4.1. Benchtop Experiments
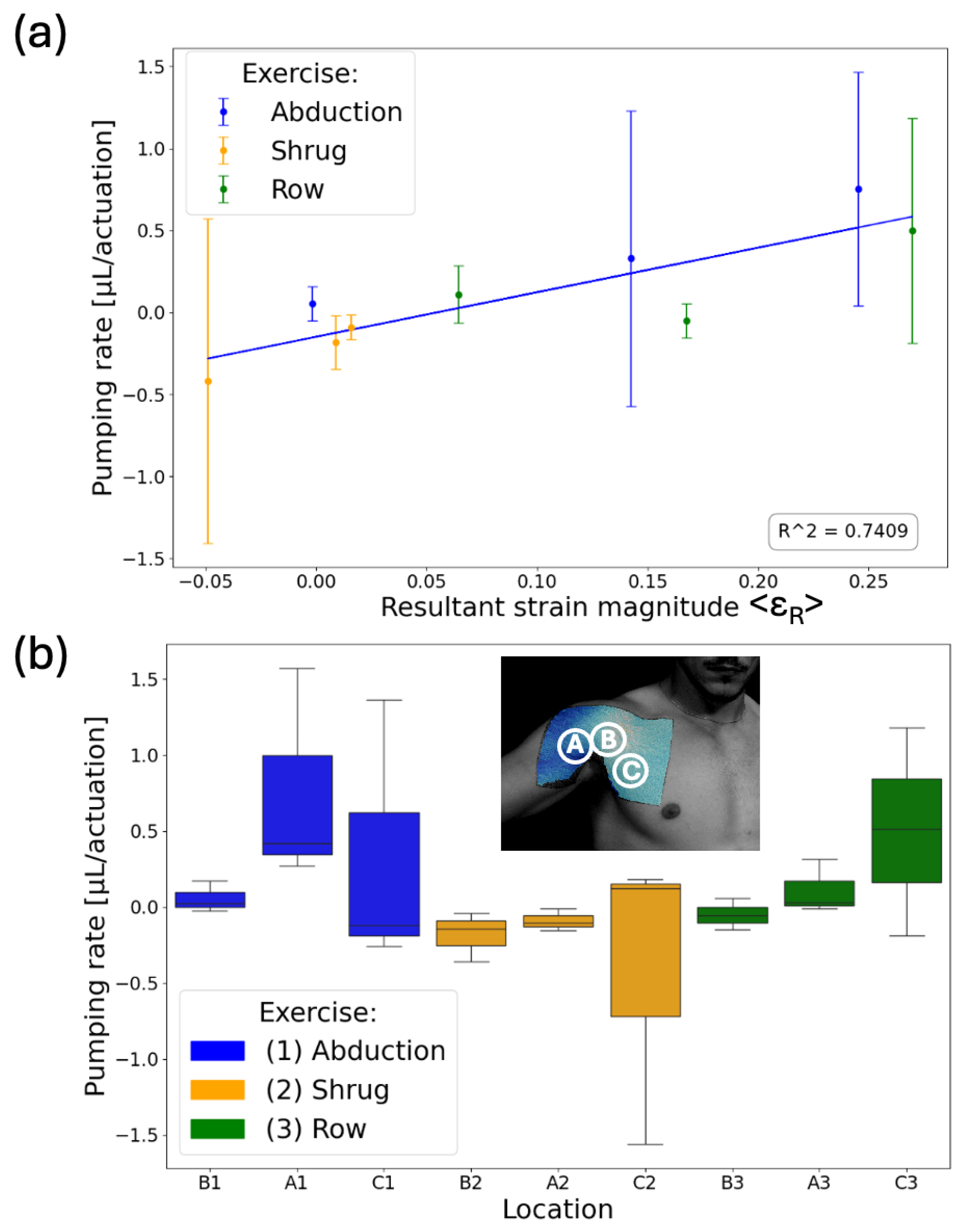
4.2. Human Volunteer Experiments
4.2.1. Wrist Experiments
4.2.2. Shoulder Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, Z.; Li, W.; Bao, Y.; Han, F.; Gao, L.; Xu, J.; Ma, Y.; Han, D.; Niu, L. Breathable and Skin-Mountable Strain Sensor with Tunable Stretchability, Sensitivity, and Linearity via Surface Strain Delocalization for Versatile Skin Activities’ Recognition. ACS Appl. Mater. Interfaces 2018, 10, 42826–42836. [Google Scholar] [CrossRef] [PubMed]
- Nishikawa, T.; Yamane, H.; Matsuhisa, N.; Miki, N. Stretchable Strain Sensor with Small but Sufficient Adhesion to Skin. Sensors 2023, 23, 1774. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Xu, Y.; Cheng, Y.; Xue, M.; Deng, M.; Jaffrezic-Renault, N.; Guo, Z. Recent advances in skin-like wearable sensors: Sensor design, health monitoring, and intelligent auxiliary. Sens. Diagn. 2022, 1, 686–708. [Google Scholar] [CrossRef]
- Yadav, A.K.; Yadav, N.; Wu, Y.; RamaKrishna, S.; Hongyu, Z. Wearable strain sensors: State-of-the-art and future applications. Mater. Adv. 2023, 4, 1444–1459. [Google Scholar] [CrossRef]
- Cho, Y.; Kim, K.; Kim, D.; Bissannagari, M.; Lee, J.; Hong, W.; Kwon, H.-J.; Jang, J.E.; Kang, H. Stretchable Substrate Surface-Embedded Inkjet-Printed Strain Sensors for Design Customizable On-Skin Healthcare Electronics. ACS Appl. Electron. Mater. 2023, 6, 3147–3157. [Google Scholar] [CrossRef]
- Zhao, L.; Ling, Q.; Fan, X.; Gu, H. Self-Healable, Adhesive, Anti-Drying, Freezing-Tolerant, and Transparent Conductive Organohydrogel as Flexible Strain Sensor, Triboelectric Nanogenerator, and Skin Barrier. ACS Appl. Mater. Interfaces 2023, 15, 40975–40990. [Google Scholar] [CrossRef] [PubMed]
- Javaid, A.; Zulfiqar, M.H.; Saleem, M.S.; Khan, M.A.; Massoud, Y.; Mehmood, M.Q. Skin-Mount Textile-Based Flexible Strain Sensors for Physiotherapy. Adv. Eng. Mater. 2024, 26, 2301138. [Google Scholar] [CrossRef]
- Lu, D.; Chu, Y.; Liao, S.; Li, W.; Cai, Y.; Wei, Q.; Wang, Q. Highly sensitive fabric strain sensor with double-layer conductive networks for joint rehabilitation therapy. Compos. Sci. Technol. 2022, 230, 109778. [Google Scholar] [CrossRef]
- Lu, S.; Chen, D.; Liu, C.; Jiang, Y.; Wang, M. A 3-D finger motion measurement system via soft strain sensors for hand rehabilitation. Sens. Actuators A Phys. 2019, 285, 700–711. [Google Scholar] [CrossRef]
- Ye, S.; Feng, S.; Huang, L.; Bian, S. Recent Progress in Wearable Biosensors: From Healthcare Monitoring to Sports Analytics. Biosensors 2020, 10, 205. [Google Scholar] [CrossRef] [PubMed]
- Baker, L.B.; Model, J.B.; Barnes, K.A.; Anderson, M.L.; Lee, S.P.; Lee, K.A.; Brown, S.D.; Reimel, A.J.; Roberts, T.J.; Nuccio, R.P.; et al. Skin-interfaced microfluidic system with personalized sweating rate and sweat chloride analytics for sports science applications. Sci. Adv. 2020, 6, eabe3929. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Liao, S.; Chu, Y.; Cai, Y.; Wei, Q.; Chen, K.; Wang, Q. Highly Durable and Fast Response Fabric Strain Sensor for Movement Monitoring Under Extreme Conditions. Adv. Fiber Mater. 2023, 5, 223–234. [Google Scholar] [CrossRef]
- Yang, K.; McErlain-Naylor, S.A.; Isaia, B.; Callaway, A.; Beeby, S. E-Textiles for Sports and Fitness Sensing: Current State, Challenges, and Future Opportunities. Sensors 2024, 24, 1058. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Yang, S.; Zhao, P.; Zhang, J.; Yang, Y.; Ye, X.; Zhao, X.; Cui, N.; Tong, Y.; Liu, Y.; et al. Skin-like Ultrasensitive Strain Sensor for Full-Range Detection of Human Health Monitoring. ACS Appl. Mater. Interfaces 2020, 12, 13287–13295. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Guo, X.; Xu, Z.; Wu, Q.; Chen, J.; Wu, J.; Dai, Y.; Qu, L.; Huang, Z. Highly sensitive and stretchable strain sensors based on serpentine-shaped composite films for flexible electronic skin applications. Compos. Sci. Technol. 2020, 197, 108215. [Google Scholar] [CrossRef]
- Xu, H.; Lv, Y.; Qiu, D.; Zhou, Y.; Zeng, H.; Chu, Y. An ultra-stretchable, highly sensitive and biocompatible capacitive strain sensor from an ionic nanocomposite for on-skin monitoring. Nanoscale 2019, 11, 1570–1578. [Google Scholar] [CrossRef] [PubMed]
- Yepes, L.R.; Demir, E.; Lee, J.Y.; Sun, R.; Smuck, M.; Araci, I.E. Skin Mountable Capillaric Strain Sensor with Ultrahigh Sensitivity and Direction Specificity. Adv. Mater. Technol. 2020, 5, 2000631. [Google Scholar] [CrossRef]
- Gasvoda, H.; Cmager, N.; Altay, R.; Lee, J.Y.; Araci, I.E. Integration of capillaric strain sensors toward recognition of human movements. Sensors Diagn. 2023, 2, 212–224. [Google Scholar] [CrossRef]
- Hu, T.; Sheng, B. A Highly Sensitive Strain Sensor with Wide Linear Sensing Range Prepared on a Hybrid-Structured CNT/Ecoflex Film via Local Regulation of Strain Distribution. ACS Appl. Mater. Interfaces 2024, 16, 21061–21072. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Bossuyt, F.M.; Adam, N.C.; Zambrano, B.L.; Stauffer, F.; Rennhard, P.; Gubler, R.; Küng, R.; Abramovic, S.; Useini, V.; et al. A Stretchable Strain Sensor System for Wireless Measurement of Musculoskeletal Soft Tissue Strains. Adv. Mater. Technol. 2023, 8, 2202041. [Google Scholar] [CrossRef]
- Wang, S.; Fang, Y.; He, H.; Zhang, L.; Li, C.; Ouyang, J. Wearable Stretchable Dry and Self-Adhesive Strain Sensors with Conformal Contact to Skin for High-Quality Motion Monitoring. Adv. Funct. Mater. 2021, 31, 2007495. [Google Scholar] [CrossRef]
- Shukla, P.; Saxena, P.; Madhwal, D.; Singh, Y.; Bhardwaj, N.; Samal, R.; Kumar, V.; Jain, V.K. Prototyping a wearable and stretchable graphene-on-PDMS sensor for strain detection on human body physiological and joint movements. Microchim. Acta 2024, 191, 301. [Google Scholar] [CrossRef] [PubMed]
- Ku, M.; Kim, J.; Won, J.-E.; Kang, W.; Park, Y.-G.; Park, J.; Lee, J.-H.; Cheon, J.; Lee, H.H.; Park, J.-U. Smart, soft contact lens for wireless immunosensing of cortisol. Sci. Adv. 2020, 6, eabb2891. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Cheng, C.; Yuan, W.; Liu, Z.; Zhu, L.; Li, X.; Lu, Y.; Chen, Z.; Liu, J.; Cui, Z.; et al. Smartphone-based battery-free and flexible electrochemical patch for calcium and chloride ions detections in biofluids. Sens. Actuators B Chem. 2019, 297, 126743. [Google Scholar] [CrossRef]
- Bandodkar, A.J.; Choi, J.; Lee, S.P.; Jeang, W.J.; Agyare, P.; Gutruf, P.; Wang, S.; Sponenburg, R.A.; Reeder, J.T.; Schon, S.; et al. Soft, Skin-Interfaced Microfluidic Systems with Passive Galvanic Stopwatches for Precise Chronometric Sampling of Sweat. Adv. Mater. 2019, 31, e1902109. [Google Scholar] [CrossRef] [PubMed]
- Kong, L.; Li, W.; Zhang, T.; Ma, H.; Cao, Y.; Wang, K.; Zhou, Y.; Shamim, A.; Zheng, L.; Wang, X.; et al. Wireless Technologies in Flexible and Wearable Sensing: From Materials Design, System Integration to Applications. Adv. Mater. 2024, e2400333. [Google Scholar] [CrossRef] [PubMed]
- Gong, S.; Yap, L.W.; Zhu, B.; Zhai, Q.; Liu, Y.; Lyu, Q.; Wang, K.; Yang, M.; Ling, Y.; Lai, D.T.H.; et al. Local Crack-Programmed Gold Nanowire Electronic Skin Tattoos for In-Plane Multisensor Integration. Adv. Mater. 2019, 31, e1903789. [Google Scholar] [CrossRef]
- Chen, W.; Yao, Y.; Chen, T.; Shen, W.; Tang, S.; Lee, H.K. Application of smartphone-based spectroscopy to biosample analysis: A review. Biosens. Bioelectron. 2021, 172, 112788. [Google Scholar] [CrossRef]
- Yüzer, E.; Doğan, V.; Kılıç, V.; Şen, M. Smartphone embedded deep learning approach for highly accurate and automated colorimetric lactate analysis in sweat. Sens. Actuators B Chem. 2022, 371, 132489. [Google Scholar] [CrossRef]
- Tu, E.; Pearlmutter, P.; Tiangco, M.; Derose, G.; Begdache, L.; Koh, A. Comparison of Colorimetric Analyses to Determine Cortisol in Human Sweat. ACS Omega 2020, 5, 8211–8218. [Google Scholar] [CrossRef]
- Liu, W.; Cheng, H.; Wang, X. Skin-interfaced colorimetric microfluidic devices for on-demand sweat analysis. npj Flex. Electron. 2023, 7, 43. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, J.; Lu, Q.; Zhang, J.; Li, Y.; Pang, Y.; Yang, C.; Wang, Q.; Kong, D. Stretchable and Sweat-Wicking Patch for Skin-Attached Colorimetric Analysis of Sweat Biomarkers. ACS Sens. 2024, 9, 1515–1524. [Google Scholar] [CrossRef] [PubMed]
- Kant, T.; Shrivas, K.; Tejwani, A.; Tandey, K.; Sharma, A.; Gupta, S. Progress in the design of portable colorimetric chemical sensing devices. Nanoscale 2023, 15, 19016–19038. [Google Scholar] [CrossRef] [PubMed]
- Ardalan, S.; Hosseinifard, M.; Vosough, M.; Golmohammadi, H. Towards smart personalized perspiration analysis: An IoT-integrated cellulose-based microfluidic wearable patch for smartphone fluorimetric multi-sensing of sweat biomarkers. Biosens. Bioelectron. 2020, 168, 112450. [Google Scholar] [CrossRef] [PubMed]
- Deng, M.; Li, X.; Song, K.; Yang, H.; Wei, W.; Duan, X.; Ouyang, X.; Cheng, H.; Wang, X. Skin-Interfaced Bifluidic Paper-Based Device for Quantitative Sweat Analysis. Adv. Sci. 2024, 11, e2306023. [Google Scholar] [CrossRef] [PubMed]
- Koh, A.; Kang, D.; Xue, Y.; Lee, S.; Pielak, R.M.; Kim, J.; Hwang, T.; Min, S.; Banks, A.; Bastien, P.; et al. A soft, wearable microfluidic device for the capture, storage, and colorimetric sensing of sweat. Sci. Transl. Med. 2016, 8, 366ra165. [Google Scholar] [CrossRef] [PubMed]
- Baker, L.B.; Seib, M.S.; Barnes, K.A.; Brown, S.D.; King, M.A.; De Chavez, P.J.D.; Qu, S.; Archer, J.; Wolfe, A.S.; Stofan, J.R.; et al. Skin-Interfaced Microfluidic System with Machine Learning-Enabled Image Processing of Sweat Biomarkers in Remote Settings. Adv. Mater. Technol. 2022, 7, 2200249. [Google Scholar] [CrossRef]
- Ghaffari, R.; Choi, J.; Raj, M.S.; Chen, S.; Lee, S.P.; Reeder, J.T.; Aranyosi, A.J.; Leech, A.; Li, W.; Schon, S.; et al. Soft Wearable Systems for Colorimetric and Electrochemical Analysis of Biofluids. Adv. Funct. Mater. 2019, 30, 1907269. [Google Scholar] [CrossRef]
- Araci, I.E.; Su, B.; Quake, S.R.; Mandel, Y. An implantable microfluidic device for self-monitoring of intraocular pressure. Nat. Med. 2014, 20, 1074–1078. [Google Scholar] [CrossRef] [PubMed]
- Agaoglu, S.; Diep, P.; Martini, M.; Kt, S.; Baday, M.; Araci, I.E. Ultra-sensitive microfluidic wearable strain sensor for intraocular pressure monitoring. Lab Chip 2018, 18, 3471–3483. [Google Scholar] [CrossRef]
- Bohm, S.; Phi, H.B.; Moriyama, A.; Runge, E.; Strehle, S.; König, J.; Cierpka, C.; Dittrich, L. Highly efficient passive Tesla valves for microfluidic applications. Microsyst. Nanoeng. 2022, 8, 97. [Google Scholar] [CrossRef] [PubMed]
- Klammer, I.; Buchenauer, A.; Fassbender, H.; Schlierf, R.; Dura, G.; Mokwa, W.; Schnakenberg, U. Numerical analysis and characterization of bionic valves for microfluidic PDMS-based systems. J. Micromech. Microeng. 2007, 17, S122–S127. [Google Scholar] [CrossRef]
- Fadl, A.; Zhang, Z.; Geller, S.; Tölke, J.; Krafczyk, M.; Meyer, D. The effect of the microfluidic diodicity on the efficiency of valve-less rectification micropumps using Lattice Boltzmann Method. Microsyst. Technol. 2009, 15, 1379–1387. [Google Scholar] [CrossRef]
- Kim, D.; Beebe, D.J. A bi-polymer micro one-way valve. Sens. Actuators A Phys. 2007, 136, 426–433. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, H.; Wang, Y.; Zhao, W.; Han, M.; Zhang, H. A time sequential microfluid sensor with Tesla valve channels. Nano Res. 2023, 16, 11667–11673. [Google Scholar] [CrossRef]
- Groisman, A.; Quake, S.R. A Microfluidic Rectifier: Anisotropic flow resistance at low reynolds numbers. Phys. Rev. Lett. 2004, 92, 094501. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, Q.M.; Abouezzi, J.; Ristroph, L. Early turbulence and pulsatile flows enhance diodicity of Tesla’s macrofluidic valve. Nat. Commun. 2021, 12, 2884. [Google Scholar] [CrossRef] [PubMed]
- Reeder, J.T.; Xue, Y.; Franklin, D.; Deng, Y.; Choi, J.; Prado, O.; Kim, R.; Liu, C.; Hanson, J.; Ciraldo, J.; et al. Resettable skin interfaced microfluidic sweat collection devices with chemesthetic hydration feedback. Nat. Commun. 2019, 10, 5513. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhao, X.; Yang, W.; Xu, F.; Chen, B.; Peng, J.; Huang, J.; Mi, S. Stretch-driven microfluidic chip for nucleic acid detection. Biotechnol. Bioeng. 2021, 118, 3559–3568. [Google Scholar] [CrossRef] [PubMed]
- Mishra, N.; Garland, N.T.; Hewett, K.A.; Shamsi, M.; Dickey, M.D.; Bandodkar, A.J. A Soft Wearable Microfluidic Patch with Finger-Actuated Pumps and Valves for On-Demand, Longitudinal, and Multianalyte Sweat Sensing. ACS Sens. 2022, 7, 3169–3180. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Cheng, M.; Huang, J.; Liu, Y.; Chen, Y.; Xiao, Y.; Chen, S.; Ouyang, X.; Cheng, H.; Wang, X. Strain-Tunable Microfluidic Devices with Crack and Wrinkle Microvalves for Microsphere Screening and Fluidic Logic Gates. ACS Appl. Mater. Interfaces 2021, 13, 36849–36858. [Google Scholar] [CrossRef] [PubMed]
- Bruus, H. Theoretical Microfluidics; Oxford University Press (OUP): Oxford, UK, 1997. [Google Scholar]
- Chossat, J.-B.; Park, Y.-L.; Wood, R.J.; Duchaine, V. A soft strain sensor based on ionic and metal liquids. IEEE Sens. J. 2013, 13, 3405–3414. [Google Scholar] [CrossRef]
- Araci, I.E.; Agaoglu, S.; Lee, J.Y.; Yepes, L.R.; Diep, P.; Martini, M.; Schmidt, A. Flow stabilization in wearable microfluidic sensors enables noise suppression. Lab Chip 2019, 19, 3899–3908. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Feng, S.; Nag, A.; Afsarimanesh, N.; Han, T.; Mukhopadhyay, S.C. Recent Progress in 3D Printed Mold-Based Sensors. Sensors 2020, 20, 703. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Huang, N.; Xu, F.; Tong, J.; Chen, Z.; Gui, X.; Fu, Y.; Lao, C. 3D printing technologies for flexible tactile sensors toward wearable electronics and electronic skin. Polymers 2018, 10, 629. [Google Scholar] [CrossRef] [PubMed]
- Bazaz, S.R.; Kashaninejad, N.; Azadi, S.; Patel, K.; Asadnia, M.; Jin, D.; Warkiani, M.E. Rapid Softlithography Using 3D-Printed Molds. Adv. Mater. Technol. 2019, 4, 1900425. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 Years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Solav, D.; Silverstein, A. DuoDIC: 3D Digital Image Correlation in MATLAB. J. Open Source Softw. 2022, 7, 4279. [Google Scholar] [CrossRef]
- Obropta, E.W.; Newman, D.J. Skin strain fields at the shoulder joint for mechanical counter pressure space suit development. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016; pp. 1–9. [Google Scholar]
- Xu, X.; Li, Z.; Hu, M.; Zhao, W.; Dong, S.; Sun, J.; He, P.; Yang, J. High Sensitivity and Antifreeze Silver Nanowire/Eutectic Gel Strain Sensor for Human Motion and Healthcare Monitoring. IEEE Sens. J. 2024, 24, 5928–5935. [Google Scholar] [CrossRef]
- Kumaresan, Y.; Mishra, S.; Ozioko, O.; Chirila, R.; Dahiya, R. Ultra-High Gauge Factor Strain Sensor with Wide-Range Stretchability. Adv. Intell. Syst. 2022, 4, 2200043. [Google Scholar] [CrossRef]
- Yu, T.; Lü, X.; Bao, W. High electrical self-healing flexible strain sensor based on MWCNT- polydimethylsiloxane elastomer with high gauge factor and wide measurement range. Compos. Sci. Technol. 2023, 238, 110049. [Google Scholar] [CrossRef]
- Xue, F.; Peng, Q.; Ding, R.; Li, P.; Zhao, X.; Zheng, H.; Xu, L.; Tang, Z.; Zhang, X.; He, X. Ultra-sensitive, highly linear, and hysteresis-free strain sensors enabled by gradient stiffness sliding strategy. npj Flex. Electron. 2024, 8, 14. [Google Scholar] [CrossRef]
- Araromi, O.A.; Graule, M.A.; Dorsey, K.L.; Castellanos, S.; Foster, J.R.; Hsu, W.-H.; Passy, A.E.; Vlassak, J.J.; Weaver, J.C.; Walsh, C.J.; et al. Ultra-sensitive and resilient compliant strain gauges for soft machines. Nature 2020, 587, 219–224. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Fuh, H.-R.; Lv, Y.; Chen, K.-Q.; Tsai, T.-Y.; Wu, Y.-R.; Shieh, T.-H.; Hung, K.-M.; Li, J.; Zhang, D.; et al. Giant gauge factor of Van der Waals material based strain sensors. Nat. Commun. 2021, 12, 2018. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Chen, J.; Chang, X.; Xu, Y.; Zhao, G.; Zhu, Y.; Li, Y. A highly stretchable strain sensor with both an ultralow detection limit and an ultrawide sensing range. J. Mater. Chem. A 2021, 9, 1795–1802. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Asghar, W.; Liu, Y.; Li, F.; Sun, D.; Hu, C.; Wu, Z.; Shang, J.; Yu, Z.; et al. Liquid Metal-Based Strain Sensor with Ultralow Detection Limit for Human–Machine Interface Applications. Adv. Intell. Syst. 2021, 3, 2000235. [Google Scholar] [CrossRef]
- Li, J.; Yao, Z.; Meng, X.; Zhang, X.; Wang, Z.; Wang, J.; Ma, G.; Liu, L.; Zhang, J.; Niu, S.; et al. High-Fidelity, Low-Hysteresis Bionic Flexible Strain Sensors for Soft Machines. ACS Nano 2024, 18, 2520–2530. [Google Scholar] [CrossRef] [PubMed]
- Bi, P.; Zhang, M.; Li, S.; Lu, H.; Wang, H.; Liang, X.; Liang, H.; Zhang, Y. Ultra-sensitive and wide applicable strain sensor enabled by carbon nanofibers with dual alignment for human machine interfaces. Nano Res. 2022, 16, 4093–4099. [Google Scholar] [CrossRef]
- Schulze, C.; Knaack, F.; Goosmann, M.; Mittelmeier, W.; Bader, R. Kontinuierliche passive Bewegungstherapie (CPM-Therapie) in der orthopädischen Rehabilitation am Schultergelenk—Eine Literaturübersicht [Continuous Passive Motion in Orthopaedic Rehabilitation of the Shoulder Girdle—A Literature Survey]. Die Rehabil. 2021, 60, 364–373. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askar, C.B.; Cmager, N.; Altay, R.; Araci, I.E. Human Activity Recording Based on Skin-Strain-Actuated Microfluidic Pumping in Asymmetrically Designed Micro-Channels. Sensors 2024, 24, 4207. https://doi.org/10.3390/s24134207
Askar CB, Cmager N, Altay R, Araci IE. Human Activity Recording Based on Skin-Strain-Actuated Microfluidic Pumping in Asymmetrically Designed Micro-Channels. Sensors. 2024; 24(13):4207. https://doi.org/10.3390/s24134207
Chicago/Turabian StyleAskar, Caroline Barbar, Nick Cmager, Rana Altay, and I. Emre Araci. 2024. "Human Activity Recording Based on Skin-Strain-Actuated Microfluidic Pumping in Asymmetrically Designed Micro-Channels" Sensors 24, no. 13: 4207. https://doi.org/10.3390/s24134207





