Pulsed Laser-Bleaching Semiconductor and Photodetector
Abstract
1. Introduction
2. Materials and Methods
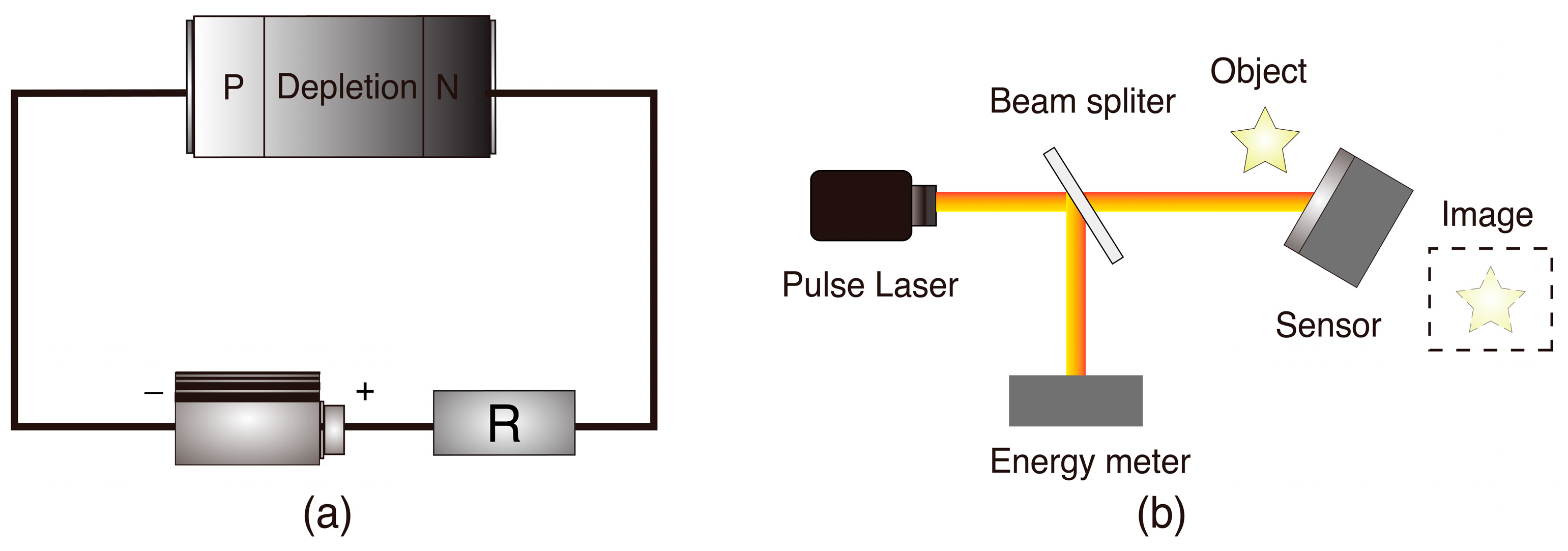
2.1. The Model of Pulsed Laser Bleaching Semiconductor
2.2. The Model Pulsed Laser Bleaching Photodetector
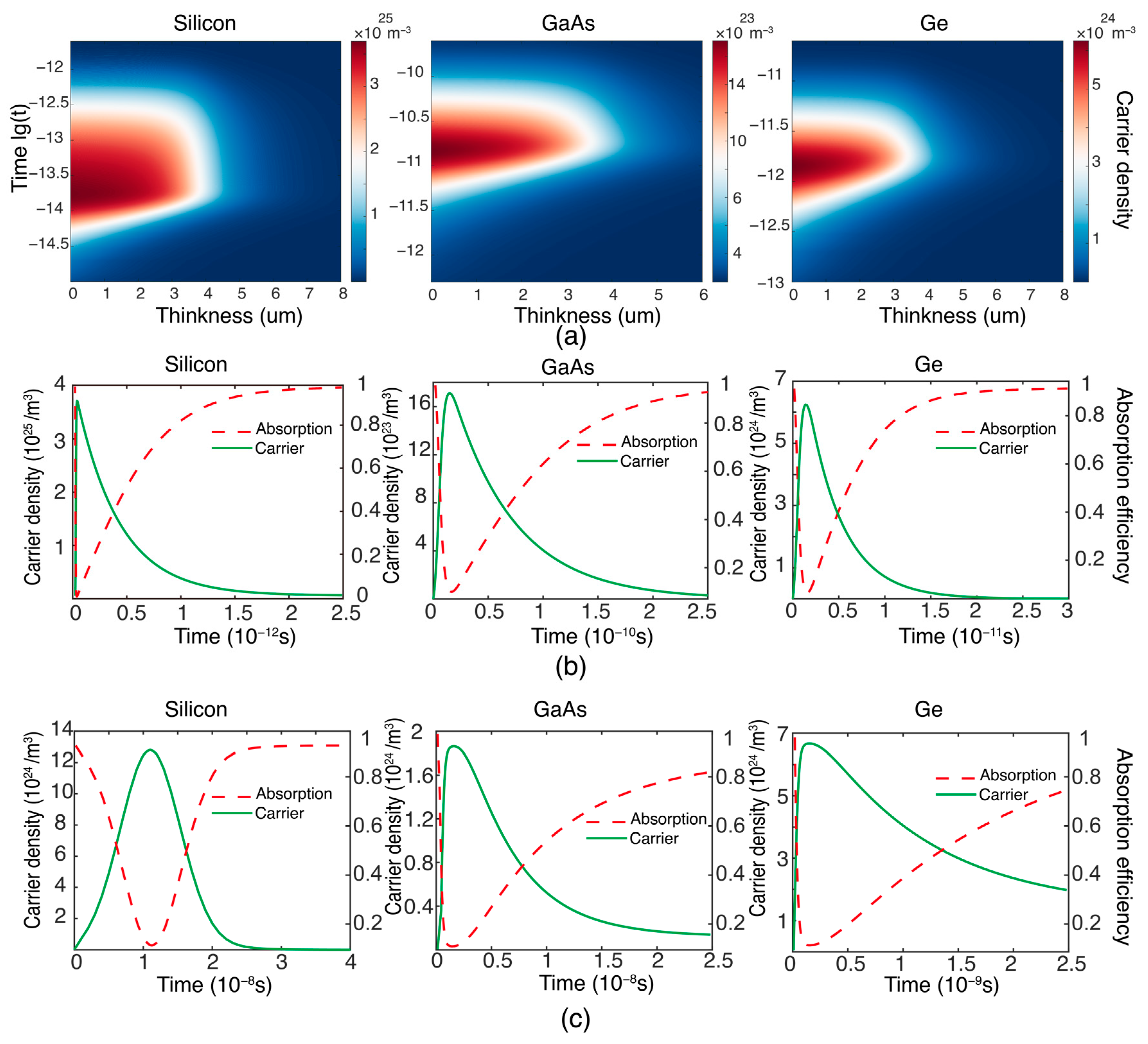
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Camposeo, A.; Persano, L.; Farsari, M.; Pisignano, D. Additive manufacturing: Applications and directions in photonics and optoelectronics. Adv. Opt. Mater. 2019, 7, 1800419. [Google Scholar] [CrossRef] [PubMed]
- Hegazy, M.A.; Abd El-Hameed, A.M. Characterization of CdSe-nanocrystals used in semiconductors for aerospace applications: Production and optical properties. NRIAG J. Astron. Geophys. 2014, 3, 82–87. [Google Scholar] [CrossRef]
- Maini, A.K. Battlefield Lasers and Opto-electronics Systems. Def. Sci. J. 2010, 60, 189–196. [Google Scholar] [CrossRef]
- Walkey, C.; Sykes, E.A.; Chan, W.C. Application of semiconductor and metal nanostructures in biology and medicine. ASH Educ. Program Book 2009, 2009, 701–707. [Google Scholar] [CrossRef] [PubMed]
- González, A.; Fang, Z.; Socarras, Y.; Serrat, J.; Vázquez, D.; Xu, J.; López, A.M. Pedestrian detection at day/night time with visible and FIR cameras: A comparison. Sensors 2016, 16, 820. [Google Scholar] [CrossRef] [PubMed]
- Piprek, J. Semiconductor Optoelectronic Devices: Introduction to Physics and Simulation; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Velicu, S.; Grein, C.; Emelie, P.; Itsuno, A.; Philips, J.; Wijewarnasuriya, P. MWIR and LWIR HgCdTe infrared detectors operated with reduced cooling requirements. J. Electron. Mater. 2010, 39, 873–881. [Google Scholar] [CrossRef]
- Bendib, A.; Bendib-Kalache, K.; Deutsch, C. Optical breakdown threshold in fused silica with femtosecond laser pulses. Laser Part. Beams 2013, 31, 523–529. [Google Scholar] [CrossRef]
- Di Cicco, A.; Polzoni, G.; Gunnella, R.; Trapananti, A.; Minicucci, M.; Rezvani, S.; Catone, D.; Di Mario, L.; Pelli Cresi, J.; Turchini, S. Broadband optical ultrafast reflectivity of Si, Ge and GaAs. Sci. Rep. 2020, 10, 17363. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.; Sun, J.; Lu, Y.; Jiang, L. Ultrafast dynamics observation during femtosecond laser-material interaction. Int. J. Extrem. Manuf. 2019, 1, 032004. [Google Scholar] [CrossRef]
- Othonos, A. Probing ultrafast carrier and phonon dynamics in semiconductors. J. Appl. Phys. 1998, 83, 1789–1830. [Google Scholar] [CrossRef]
- Zhang, F.; Li, S.; Chen, A.; Jiang, Y.; Li, S.; Jin, M. Ultrafast dynamical process of Ge irradiated by the femtosecond laser pulses. High Power Laser Sci. Eng. 2016, 4, e12. [Google Scholar] [CrossRef]
- Klingshirn, C.F. Semiconductor Optics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Sundaram, S.; Mazur, E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat. Mater. 2002, 1, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Rafailov, M.K. Ultrafast bandgap photonics. In Micro-and Nanotechnology Sensors, Systems, and Applications III; SPIE: Bellingham, WA, USA, 2011; pp. 652–663. [Google Scholar]
- Rafailov, M.K. Ultrafast bandgap photonics: Meta-stability of transient states. In Ultrafast Bandgap Photonics; SPIE: Bellingham, WA, USA, 2016; pp. 205–209. [Google Scholar]
- Xu, Z.; Zhang, J.; Lin, X.; Shao, B.; Yang, P. Negative response of hgcdte photodiode induced by nanosecond laser pulse. In Proceedings of the Fourth International Symposium on Laser Interaction with Matter, Chengdu, China, 6–9 November 2016; SPIE: Bellingham, WA, USA, 2017; pp. 41–46. [Google Scholar]
- Zewail, A.H. Laser femtochemistry. Science 1988, 242, 1645–1653. [Google Scholar] [CrossRef] [PubMed]
- Niedzwiedzki, D.M.; Sullivan, J.O.; Polívka, T.; Birge, R.R.; Frank, H.A. Femtosecond time-resolved transient absorption spectroscopy of xanthophylls. J. Phys. Chem. B 2006, 110, 22872–22885. [Google Scholar] [CrossRef] [PubMed]
- Ohkita, H.; Cook, S.; Astuti, Y.; Duffy, W.; Tierney, S.; Zhang, W.; Heeney, M.; McCulloch, I.; Nelson, J.; Bradley, D.D. Charge carrier formation in polythiophene/fullerene blend films studied by transient absorption spectroscopy. J. Am. Chem. Soc. 2008, 130, 3030–3042. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Rueda, J.; Puerto, D.; Siegel, J.; Galvan-Sosa, M.; Solis, J. Plasma dynamics and structural modifications induced by femtosecond laser pulses in quartz. Appl. Surf. Sci. 2012, 258, 9389–9393. [Google Scholar] [CrossRef]
- Pan, C.; Wang, Q.; Sun, J.; Wang, F.; Sun, J.; Wang, G.; Lu, Y.; Jiang, L. Dynamics and its modulation of laser-induced plasma and shockwave in femtosecond double-pulse ablation of silicon. Appl. Phys. Express 2019, 13, 012006. [Google Scholar] [CrossRef]
- Wang, K.; Yao, C.; Wu, Y.; Wang, X.; Wang, Y.; Li, P. Laser-interfered studies in HgCdTe infrared focal plane array detector by high-repetition-rate mid-infrared supercontinuum fiber laser. Opt. Laser Technol. 2023, 163, 109433. [Google Scholar] [CrossRef]
- Zuodong, X.; Jianmin, Z.; Xinwei, L.; Bibo, S. Transient response degradation of HgCdTe photovoltaic detectors under irradiation of nanosecond laser. Infrared Laser Eng. 2018, 47, 106001-0106001. [Google Scholar] [CrossRef]
- Dou, X.; Sun, X. Model of transient bleaching effect of the direct bandgap semiconductor induced by femtosecond laser. Zhongguo Jiguang(Chin. J. Lasers) 2012, 39, 0602007-6. [Google Scholar]
- Dou, X.; Sun, X.; Li, H.; Chen, X. The study of transient bleaching effect of indirect bandgap semiconductors induced by femtosecond laser. Optik 2015, 126, 3267–3271. [Google Scholar]
- Abdelmalek, A.; Kotsedi, L.; Bedrane, Z.; Amara, E.-H.; Girolami, M.; Maaza, M. Optical and thermal behavior of germanium thin films under femtosecond laser irradiation. Nanomaterials 2022, 12, 3786. [Google Scholar] [CrossRef] [PubMed]
- Principi, E.; Giangrisostomi, E.; Mincigrucci, R.; Beye, M.; Kurdi, G.; Cucini, R.; Gessini, A.; Bencivenga, F.; Masciovecchio, C. Extreme ultraviolet probing of nonequilibrium dynamics in high energy density germanium. Phys. Rev. B 2018, 97, 174107. [Google Scholar] [CrossRef]
- Du, L.; Sun, J.; Zhang, R. Transient response analysis of photoconductive detector under ultra-short laser pulse radiation. Optik 2013, 124, 6577–6581. [Google Scholar] [CrossRef]
- Meng, Q.; Yu, J.; Zhong, Z.; Ye, R.; Zhang, B. Damage threshold prediction of crystal materials irradiated by femtosecond lasers based on ionization model and two-temperature model. Opt. Mater. 2015, 46, 444–449. [Google Scholar] [CrossRef]
- Kuzmany, H. Solid-State Spectroscopy: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Green, M.A. Intrinsic concentration, effective densities of states, and effective mass in silicon. J. Appl. Phys. 1990, 67, 2944–2954. [Google Scholar] [CrossRef]
- Li, M.; Menon, S.; Nibarger, J.P.; Gibson, G.N. Ultrafast electron dynamics in femtosecond optical breakdown of dielectrics. Phys. Rev. Lett. 1999, 82, 2394. [Google Scholar] [CrossRef]
- Tanimura, H.; Kanasaki, J.i.; Tanimura, K.; Sjakste, J.; Vast, N. Ultrafast relaxation dynamics of highly excited hot electrons in silicon. Phys. Rev. B 2019, 100, 035201. [Google Scholar] [CrossRef]
- Gonzalez, B.; Palankovski, V.; Kosina, H.; Hernandez, A.; Selberherr, S. An energy relaxation time model for device simulation. Solid-State Electron. 1999, 43, 1791–1795. [Google Scholar] [CrossRef]
- Selberherr, S. Analysis and Simulation of Semiconductor Devices; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhang, Y.; Dou, X.; Li, F.; Sun, X. The response characteristics of avalanche photodiodes to ultrashort pulsed laser. Infrared Phys. Technol. 2015, 73, 226–231. [Google Scholar] [CrossRef]
- Chuang, S.L. Physics of Photonic Devices; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kopytko, M.; Sobieski, J.; Gawron, W.; Kębłowski, A.; Piotrowski, J. Minority carrier lifetime in HgCdTe (100) epilayers and their potential application to background radiation limited MWIR photodiodes. Semicond. Sci. Technol. 2021, 36, 055003. [Google Scholar] [CrossRef]
- Levinshtein, M. Handbook Series on Semiconductor Parameters; World Scientific: Singapore, 1997; Volume 1. [Google Scholar]
- Feng, T.; Chen, G.; Han, H.; Qiao, J. Femtosecond-laser-ablation dynamics in silicon revealed by transient reflectivity change. Micromachines 2021, 13, 14. [Google Scholar] [CrossRef] [PubMed]
- Turchinovich, D.; D’Angelo, F.; Bonn, M. Femtosecond-timescale buildup of electron mobility in GaAs observed via ultrabroadband transient terahertz spectroscopy. Appl. Phys. Lett. 2017, 110, 121102. [Google Scholar] [CrossRef]



| Parameters | Silicon | GaAs | Ge | InAs | InSb | HgCdTe | InAs0.4Sb0.6 |
|---|---|---|---|---|---|---|---|
| (μm) | 0.65 | 0.65 | 1.03 | 2.3 | 5.4 | 10 | 10.4 |
| (eV) | 1.12 | 1.424 | 0.661 | 0.354 | 0.17 | 0.123 | 0.102 |
| (m−3) | 1.5 × 1016 | 2.1 × 1012 | 2 × 1019 | 1 × 1021 | 2 × 1021 | 6.3 × 1018 | 0.8 × 1023 |
| Electron effective mass ) | 1.08 | 0.063 | 1.6 | 0.023 | 0.014 | 0.01 | 0.0104 |
| ) | 0.57 | 0.51 | 0.33 | 0.41 | 0.43 | 0.47 | 0.422 |
| (s) | 10−7 | 2.2 × 10−6 | 3.2 × 10−6 | 1.3 × 10−6 | 5 × 10−8 | 10−6 | 9.4 × 10−7 |
| (s) | 10−7 | 2.2 × 10−6 | 3.2 × 10−6 | 1.3 × 10−6 | 5 × 10−8 | 10−6 | 9.4 × 10−7 |
| (s) | 4 × 10−11 | 5.7 × 10−11 | 3.8 × 10−12 | 6.15 × 10−11 | 5 × 10−11 | 2 × 10−11 | 1 × 10−12 |
| 3.565 | 3.3 | 4 | 3.51 | 4 | 3.54 | 3.7 | |
| 0.5 | 0.46 | 0.722 | 0.54 | 0.415 | 0.11 | 0.126 | |
| (m−3) | 2 × 1023 | 0.3 × 1023 | 6.3 × 1022 | 2 × 1023 | 7.7 × 1020 | 1.5 × 1021 | 2.5 × 1023 |
| (m−3) | 4.9 × 1021 | 1.2 × 1023 | 0.8 × 1022 | 1 × 1023 | 3.85 × 1020 | 1 × 1021 | 1.5 × 1023 |
| (cm2·V−1·s−1) | 1400 | 8500 | 3900 | 40,000 | 7.7 × 104 | 1 × 105 | 2.25 × 104 |
| (cm2·V−1·s−1) | 450 | 400 | 1900 | 500 | 850 | 450 | 500 |
| Laser Parameters | Silicon | GaAs | Ge | InAs | InSb | HgCdTe | InAs0.4Sb0.6 |
|---|---|---|---|---|---|---|---|
| Energy density (mJ/cm2) | 12 | 0.75 | 4.2 | 0.17 | 0.01 | 0.0005 | 0.1 |
| Pulse duration (ps) | 0.01 | 10 | 1 | 10 | 1 | 10 | 0.1 |
| Repetition rate (GHz) | 400 | 4 | 40 | 2 | 2.5 | 4 | 200 |
| Laser Parameters | Silicon | GaAs | Ge | InAs | InSb | HgCdTe | InAs0.4Sb0.6 |
|---|---|---|---|---|---|---|---|
| Energy density (mJ/cm2) | 13 | 1.7 | 3 | 0.15 | 0.05 | 0.005 | 0.05 |
| Pulse duration (ps) | 10,000 | 1000 | 100 | 1000 | 100,000 | 100 | 10 |
| Repetition rate (MHz) | 25 | 40 | 400 | 40 | 2 | 400 | 4000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Chen, F.; Zhang, Z.; Tang, X.; Zhu, M.; Sun, J.; Chen, Y.; Zhang, X.; Yu, J.; Zhang, Y. Pulsed Laser-Bleaching Semiconductor and Photodetector. Sensors 2024, 24, 4226. https://doi.org/10.3390/s24134226
Huang C, Chen F, Zhang Z, Tang X, Zhu M, Sun J, Chen Y, Zhang X, Yu J, Zhang Y. Pulsed Laser-Bleaching Semiconductor and Photodetector. Sensors. 2024; 24(13):4226. https://doi.org/10.3390/s24134226
Chicago/Turabian StyleHuang, Chen, Fei Chen, Ze Zhang, Xin Tang, Meng Zhu, Junjie Sun, Yi Chen, Xin Zhang, Jinghua Yu, and Yiwen Zhang. 2024. "Pulsed Laser-Bleaching Semiconductor and Photodetector" Sensors 24, no. 13: 4226. https://doi.org/10.3390/s24134226
APA StyleHuang, C., Chen, F., Zhang, Z., Tang, X., Zhu, M., Sun, J., Chen, Y., Zhang, X., Yu, J., & Zhang, Y. (2024). Pulsed Laser-Bleaching Semiconductor and Photodetector. Sensors, 24(13), 4226. https://doi.org/10.3390/s24134226







