Three-Dimensional Human Posture Recognition by Extremity Angle Estimation with Minimal IMU Sensor
Abstract
:1. Introduction
2. The Material for Estimation by IMU
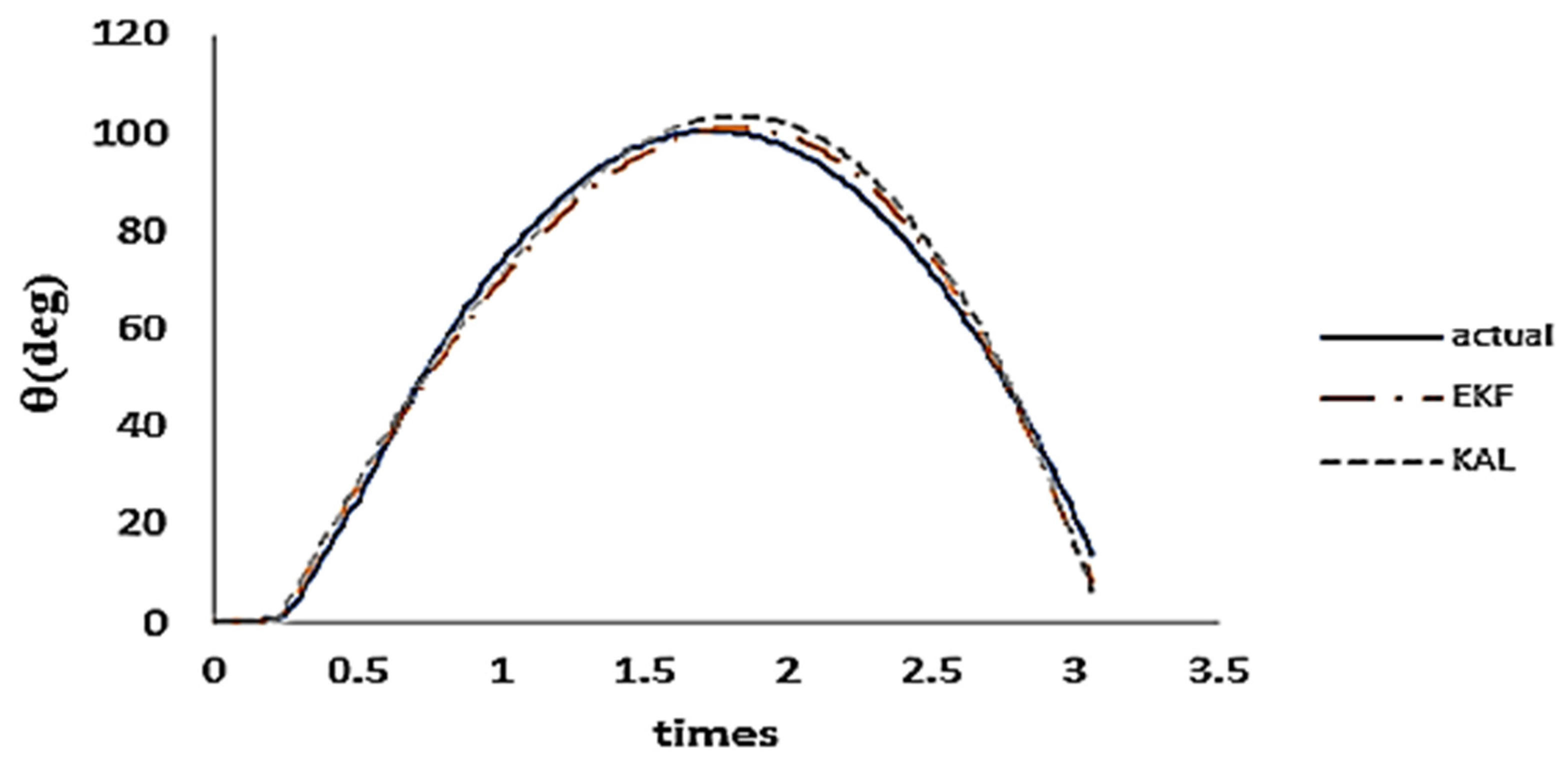
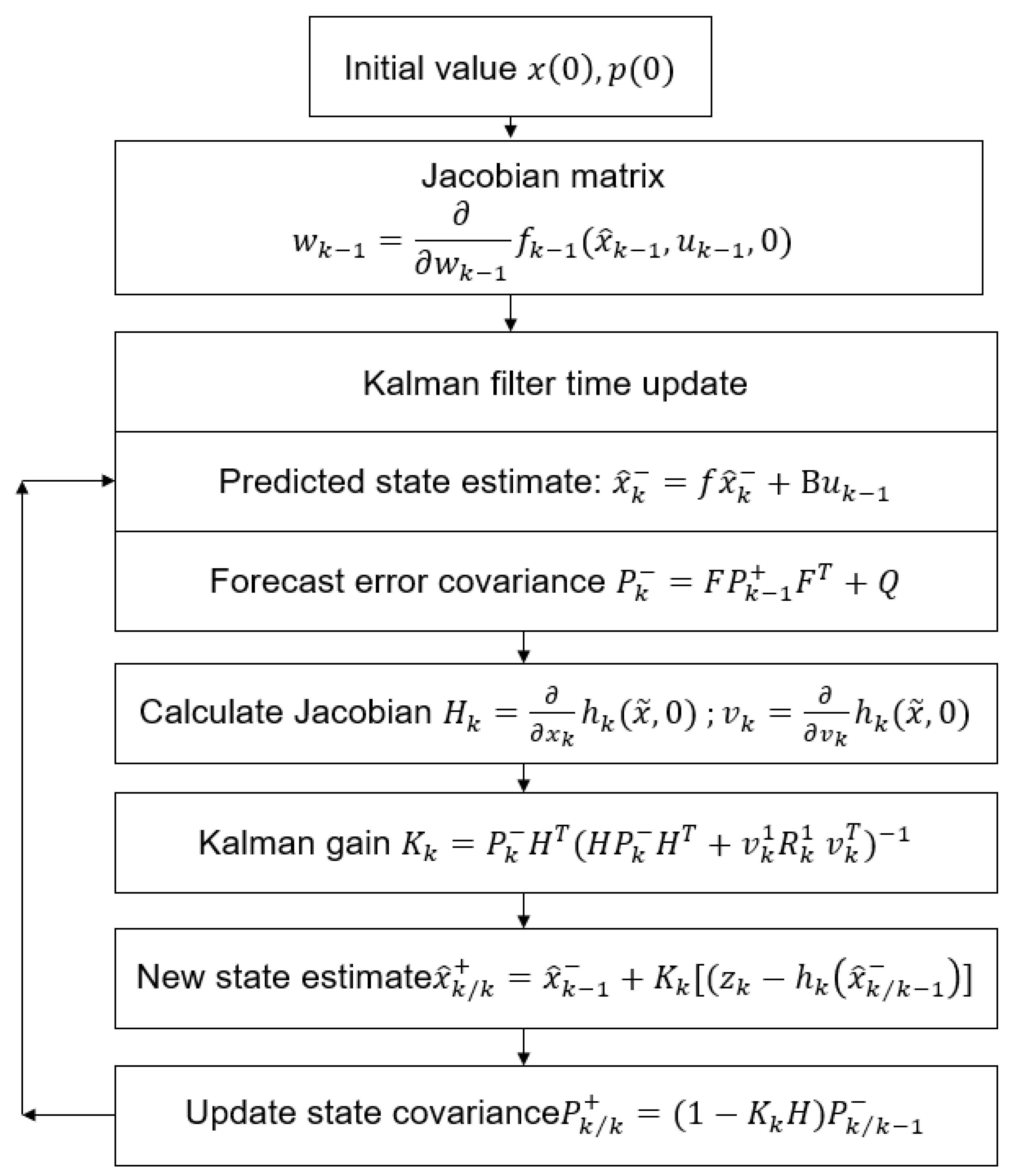
2.1. Extended Kalman Filter
2.2. Mathematical Model for Joint Angle Estimation
- (a) Estimation of upper extremity joint angles
- (b) Estimation of lower extremity joint angles
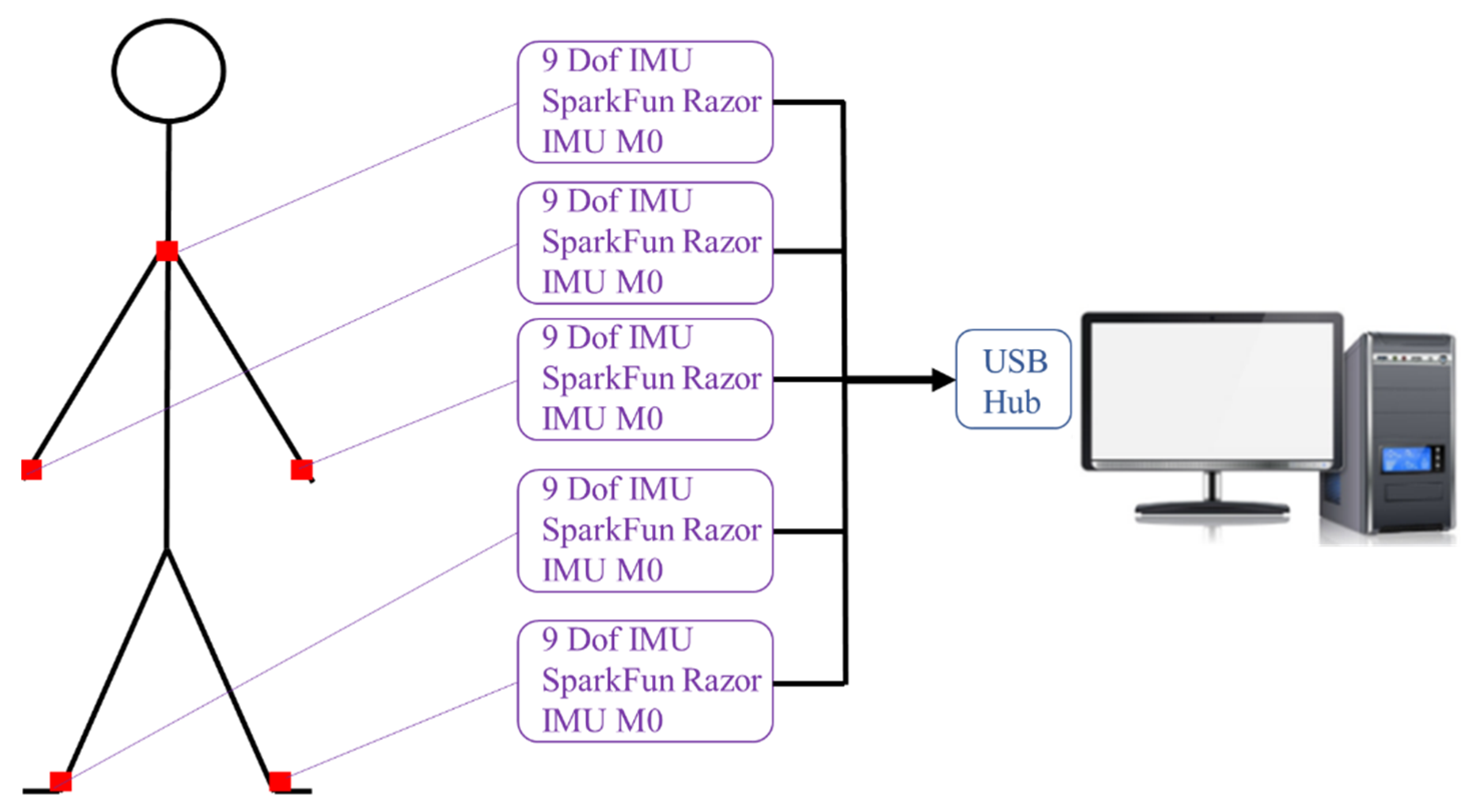
2.3. Minimal IMU Model for Dynamic Motion Observation
2.4. The Impact of IMU Placement Position
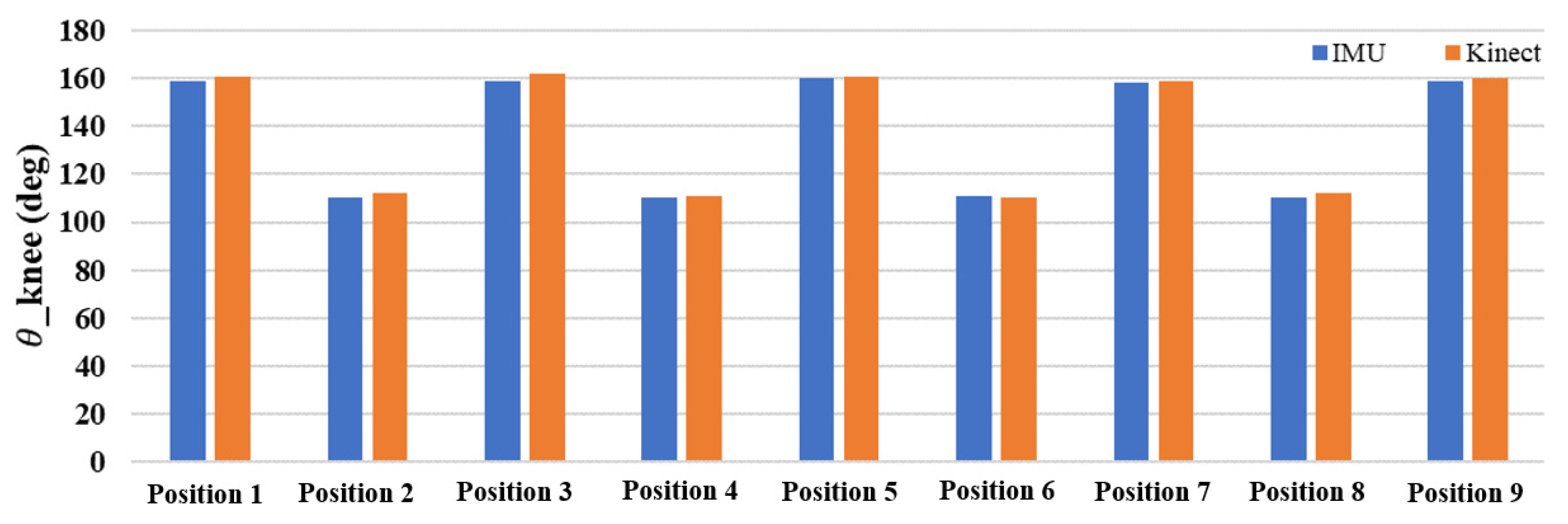
3. Motion Joint Angle Verification
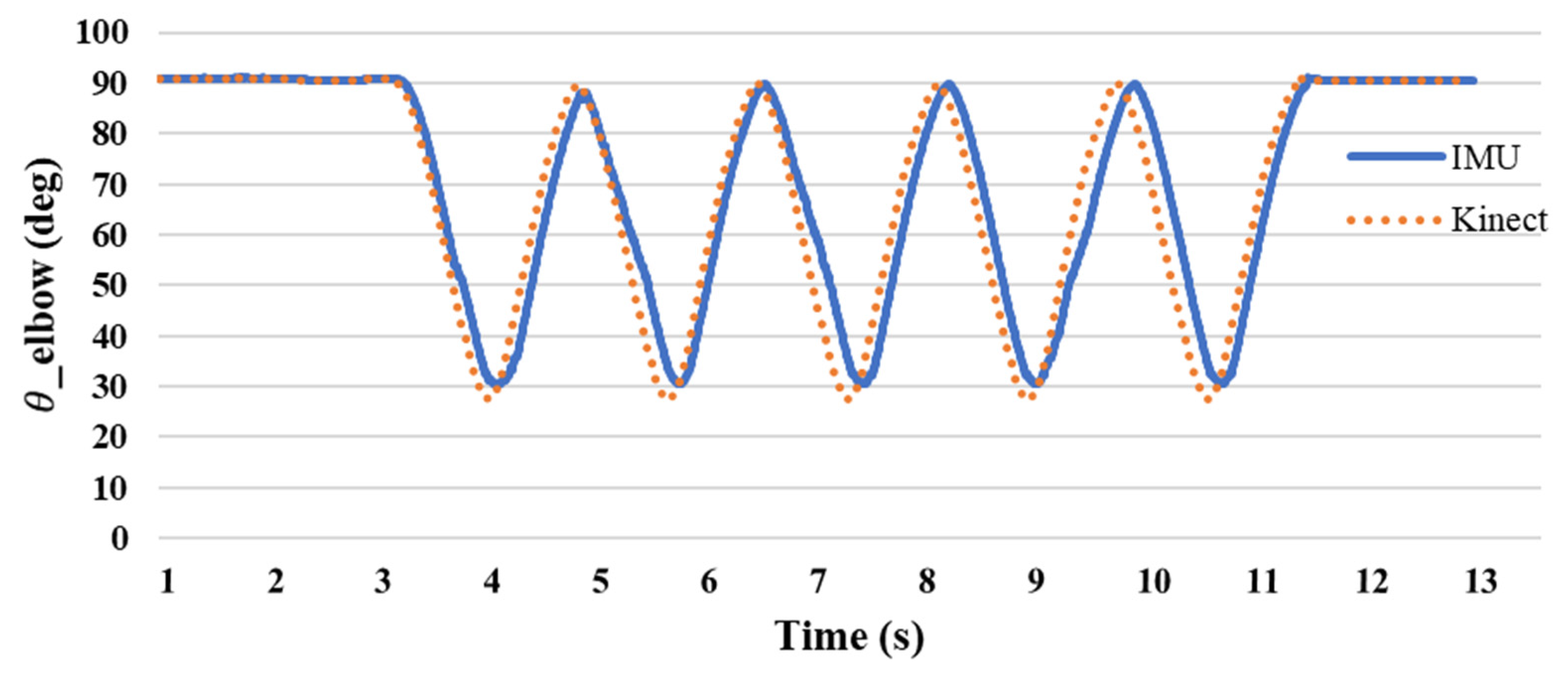
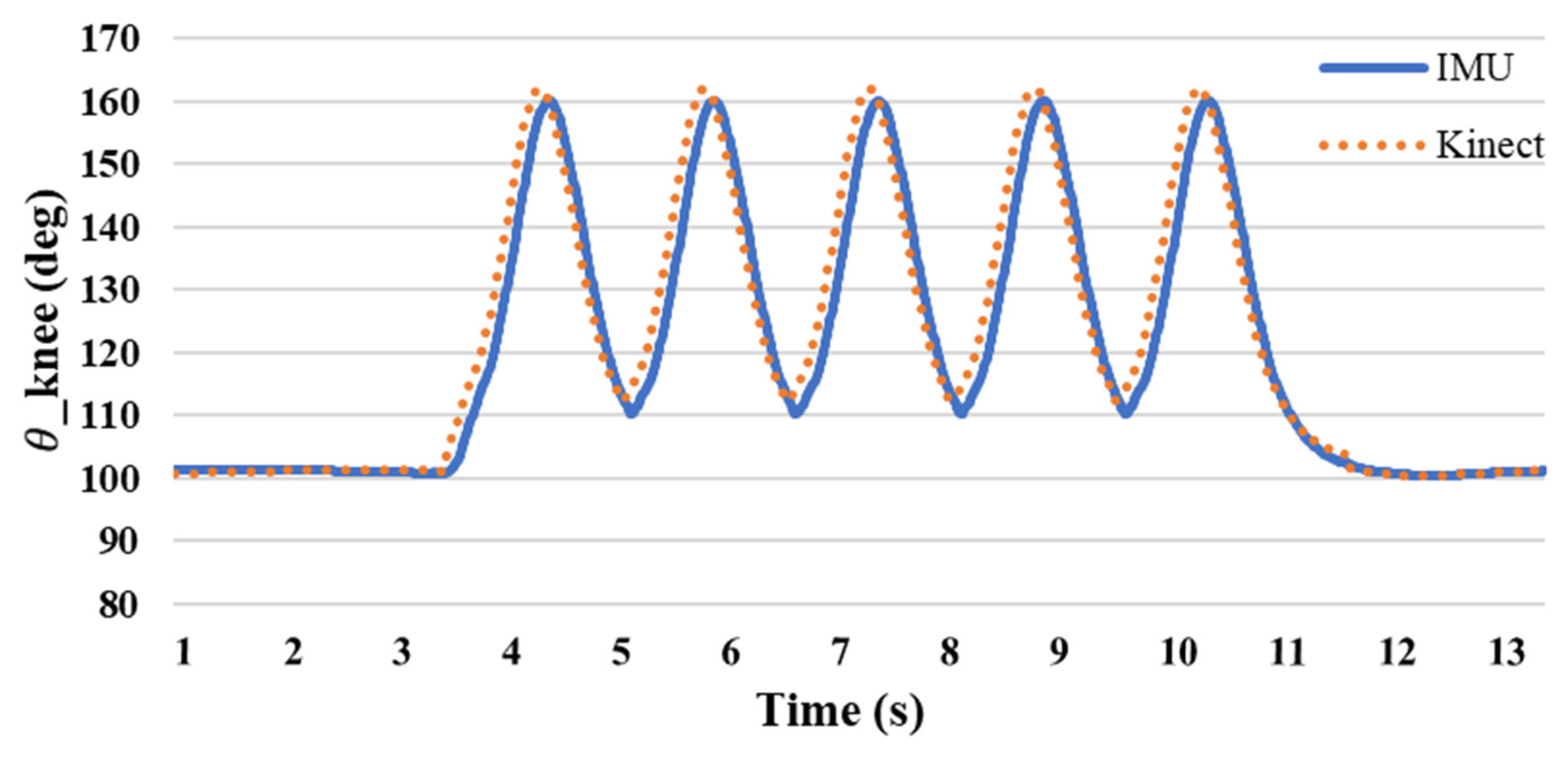
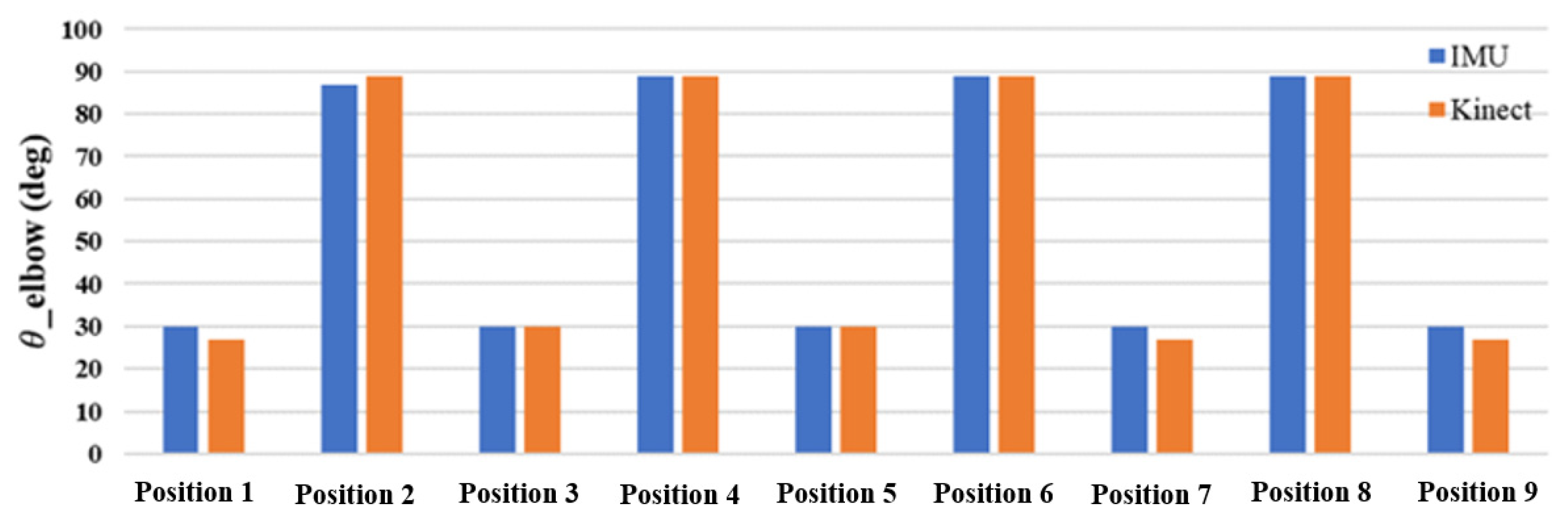
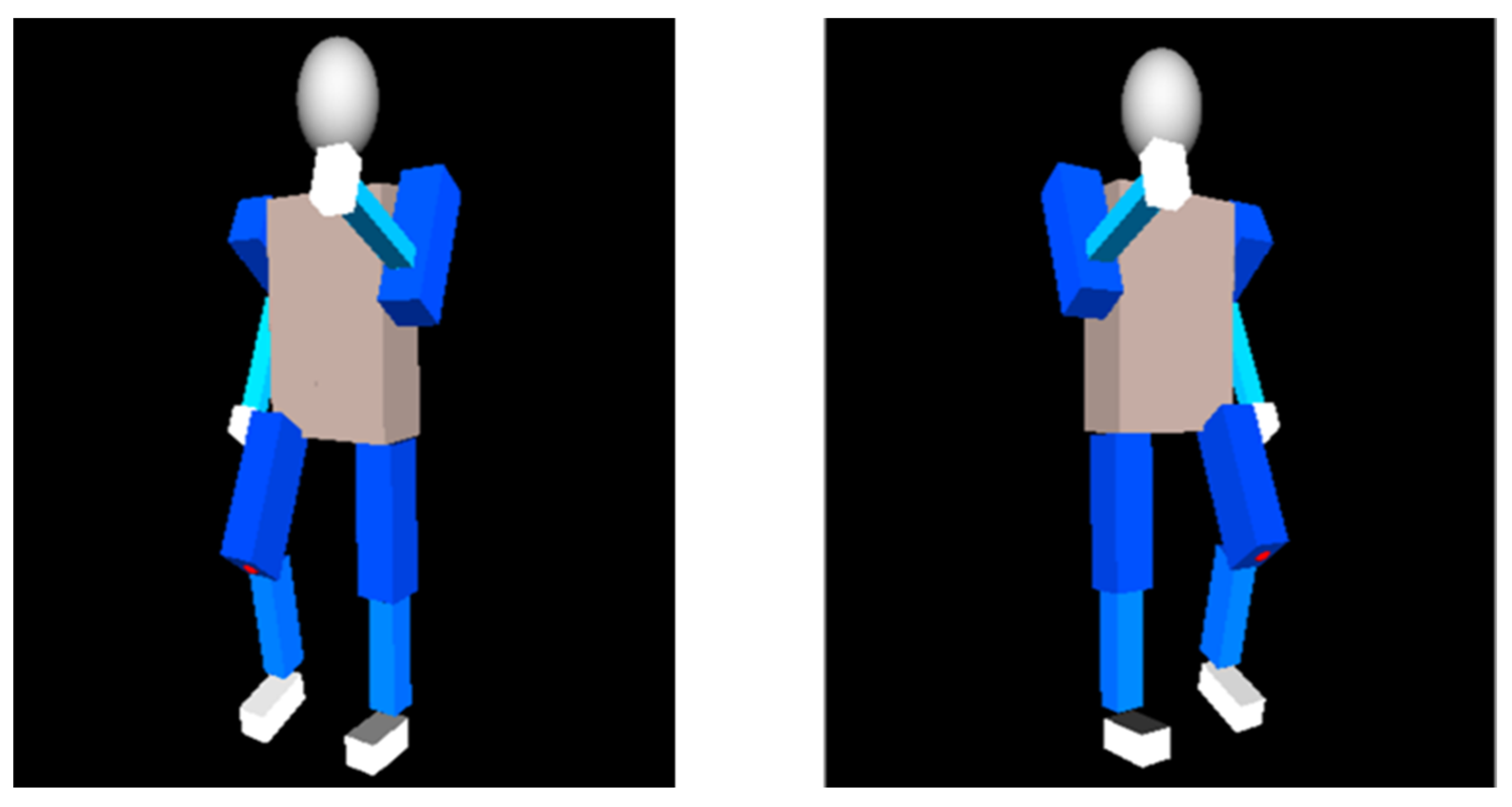
3.1. Image Recognition Technology
3.2. The Difference between Image Recognition Technology and Single-Sensor Estimation of Joint Angle
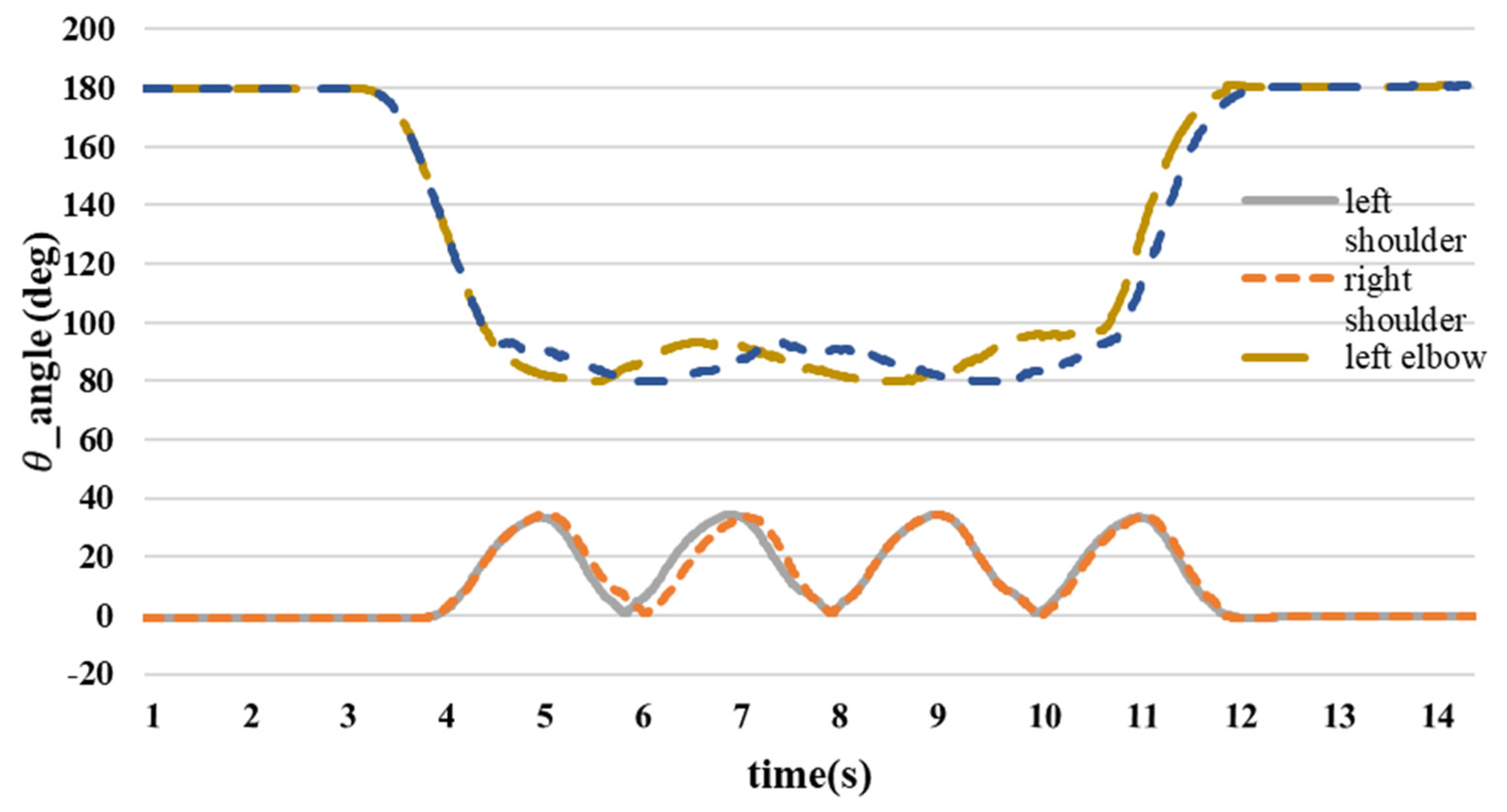
4. Experiment on Human Walking Posture
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lin, C.Y.; Chuang, L.W.; Huang, C.C.; Lin, K.J.; Fahn, C.S. Development of hand posture recognition system for finger gaming robot. In Proceedings of the 2013 International Conference on Advanced Robotics and Intelligent Systems (ARIS), Tainan, Taiwan, 31 May–2 June 2013; pp. 86–91. [Google Scholar] [CrossRef]
- Lee, M.F.R.; Chen, Y.C.; Tsai, C.Y. Deep Learning-Based Human Body Posture Recognition and Tracking for Unmanned Aerial Vehicles. Processes 2022, 10, 2295. [Google Scholar] [CrossRef]
- Yang, X.; Ren, X.; Chen, M.; Wang, L.; Ding, Y. Human Posture Recognition in Intelligent Healthcare. J. Phys. Conf. Ser. 2020, 1437, 012014. [Google Scholar] [CrossRef]
- Hong, Z.; Hong, M.; Wang, N.; Ma, Y.; Zhou, X.; Wang, W. A wearable-based posture recognition system with AI-assisted approach for healthcare IoT. Futur. Gener. Comput. Syst. 2022, 127, 286–296. [Google Scholar] [CrossRef]
- Wang, J.; Qiu, K.; Fu, J.; Peng, H.; Zhu, J. AI Coach: Deep Human Pose Estimation and Analysis for Personalized Athletic Training Assistance. In Proceedings of the 27th ACM International Conference on Multimedia—MM’19, Nice, France, 21–25 October 2019; pp. 374–382. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, X. An improved deep neural network method for an athlete’s human motion posture recognition. Int. J. Inf. Commun. Technol. 2023, 22, 45–59. [Google Scholar] [CrossRef]
- Wang, Q. Application of Human Posture Recognition Based on the Convolutional Neural Network in Physical Training Guidance. Comput. Intell. Neurosci. 2022, 2022, 5277157. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Xiao, B.; Tian, Y.; Wu, Z.; Liu, Q.; Wang, J.; Sun, M.; Liu, X. A Control and Posture Recognition Strategy for Upper-Limb Rehabilitation of Stroke Patients. Wirel. Commun. Mob. Comput. 2021, 2021, 6630492. [Google Scholar] [CrossRef]
- Lahner, C.R. Adult weight measurement: Decoding the terminology used in literature. S. Afr. J. Clin. Nutr. 2019, 32, 28–31. [Google Scholar] [CrossRef]
- Kachlik, D.; Varga, I.; Báča, V.; Musil, V. Variant anatomy and its terminology. Medicina 2020, 56, 713. [Google Scholar] [CrossRef] [PubMed]
- Duren, D.L.; Sherwood, R.J.; Czerwinski, S.A.; Lee, M.; Choh, A.C.; Siervogel, R.M.; Chumlea, W.C. Body composition methods: Comparisons and interpretation. J. Diabetes Sci. Technol. 2008, 2, 1139–1146. [Google Scholar] [CrossRef]
- Gan, Q.; Li, Y.; Wang, G.; Zhang, Y. Application Research of Optical Tracking Point Layout in Computer Motion Capture Technology: Take Walking Motion as an Example. In Proceedings of the 2020 International Conference on Innovation Design and Digital Technology (ICIDDT), Zhenjing, China, 5–6 December 2020; pp. 548–552. [Google Scholar] [CrossRef]
- Li, N.; Dai, Y.; Wang, R.; Shao, Y. Study on Action Recognition Based on Kinect and Its Application in Rehabilitation Training. In Proceedings of the 5th IEEE Fifth International Conference on Big Data and Cloud Computing, Dalian, China, 26–28 August 2015; pp. 265–269. [Google Scholar] [CrossRef]
- Gahlot, A.; Agarwal, P.; Agarwal, A.; Singh, V.; Gautam, A.K. Skeleton based Human Action Recognition using Kinect. Int. J. Comput. Appl. 2016, 21, 975–8887. [Google Scholar]
- Wang, W.J.; Chang, J.W.; Haung, S.F.; Wang, R.J. Human Posture Recognition Based on Images Captured by the Kinect Sensor. Int. J. Adv. Robot. Syst. 2016, 13, 54. [Google Scholar] [CrossRef]
- Jais, H.M.; Mahayuddin, Z.R.; Arshad, H. A review on gesture recognition using kinect. In Proceedings of the 2015 International Conference on Electrical Engineering and Informatics (ICEEI), Denpasar, Indonesia, 10–11 August 2015; pp. 594–599. [Google Scholar] [CrossRef]
- Li, Y.; Chu, Z.; Xin, Y. Posture recognition technology based on kinect. IEICE Trans. Inf. Syst. 2020, E103D, 621–630. [Google Scholar] [CrossRef]
- Yang, D.; Huang, J.; Tu, X.; Ding, G.; Shen, T.; Xiao, X. A Wearable Activity Recognition Device Using Air-Pressure and IMU Sensors. IEEE Access 2019, 7, 6611–6621. [Google Scholar] [CrossRef]
- Zhuang, W.; Chen, Y.; Su, J.; Wang, B.; Gao, C. Design of human activity recognition algorithms based on a single wearable IMU sensor. Int. J. Sens. Netw. 2019, 30, 193–206. [Google Scholar] [CrossRef]
- Valarezo, E.; Rivera, P.; Park, J.M.; Gi, G.; Kim, T.Y.; Al-Antari, M.A.; Al-Masni, M.; Kim, T.S. Human Activity Recognition Using a Single Wrist IMU Sensor via Deep Learning Convolutional and Recurrent Neural Nets Index Terms—Human Activities, Inertial Measurement Units (IMUs), Convolutional Neural Nets (CNN), Recurrent Neural Nets (RNN), HAR System. J. ICT Des. Eng. Technol. Sci. JITDETS 2017, 1, 1–5. [Google Scholar]
- Patterson, M.; McGrath, D.; Caulfield, B. Using a tri-axial accelerometer to detect technique breakdown due to fatigue in distance runners: A preliminary perspective. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 6511–6514. [Google Scholar] [CrossRef]
- Liang, J.; Duan, H.; Li, J.; Sun, H.; Sha, X.; Zhao, Y.; Liu, L. Accurate Estimation of Gait Altitude Using One Wearable IMU Sensor. In Proceedings of the 2018 IEEE 1st International Conference on Micro/Nano Sensors for AI, Healthcare, and Robotics (NSENS), Shenzhen, China, 5–7 December 2018; pp. 64–67. [Google Scholar] [CrossRef]
- Fourati, H. Heterogeneous data fusion algorithm for pedestrian navigation via foot-mounted inertial measurement unit and complementary filter. IEEE Trans. Instrum. Meas. 2015, 64, 221–229. [Google Scholar] [CrossRef]
- Marins, J.L.; Yun, X.; Bachmann, E.R.; McGhee, R.B.; Zyda, M.J. An extended Kalman filter for quaternion-based orientation estimation using MARG sensors. IEEE Int. Conf. Intell. Robot. Syst. 2001, 4, 2003–2011. [Google Scholar] [CrossRef]
- Bachmann, E.R.; Duman, I.; Usta, U.Y.; Mcghee, R.B.; Yun, X.P.; Zyda, M.J. Orientation Tracking for Humans and Robots Using Inertial Sensors A Quaternion Attitude Filter. In Proceedings of the 1999 IEEE International Symposium on Computational Intelligence in Robotics and Automation, Monterey, CA, USA, 8–9 November 1999; pp. 187–194. [Google Scholar]
- Huang, Y.-P.; Chuang, C.-H. An Intelligent Identification Model for Classifying Trembling Patterns of Parkinson’s Disease. In Advances in Swarm Intelligence; Tan, Y., Shi, Y., Li, L., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 215–222. [Google Scholar] [CrossRef]
- Bellitti, P.; Borghetti, M.; Lopomo, N.F.; Sardini, E.; Serpelloni, M. Smart Brace for Static and Dynamic Knee Laxity Measurement. Sensors 2022, 22, 5815. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Lee, S. Fusion Poser: 3D Human Pose Estimation Using Sparse IMUs and Head Trackers in Real Time. Sensors 2022, 22, 4846. [Google Scholar] [CrossRef]
- McGrath, T.; Stirling, L. Body-Worn IMU-Based Human Hip and Knee Kinematics Estimation during Treadmill Walking. Sensors 2022, 22, 2544. [Google Scholar] [CrossRef]
- Slyper, R.; Hodgins, J.K. Action capture with accelerometers. In Proceedings of the Eurographics/ACM SIGGRAPH Symposium on Computer Animation, Dublin, Ireland, 7–9 July 2008; pp. 193–199. [Google Scholar]
- Huang, Y.-P. System and Method Rehabilitation Monitoring System and Method. 82119-TW-PA. Available online: https://rndc.ntut.edu.tw/p/16-1037-107369.php?Lang=en (accessed on 1 April 2024).
- Banos, O.; Calatroni, A.; Damas, M.; Pomares, H.; Roggen, D.; Rojas, I.; Villalonga, C. Opportunistic Activity Recognition in IoT Sensor Ecosystems via Multimodal Transfer Learning. Neural Process. Lett. 2021, 53, 3169–3197. [Google Scholar] [CrossRef]
- Tian, Y.; Meng, X.; Tao, D.; Liu, D.; Feng, C. Upper limb motion tracking with the integration of IMU and Kinect. Neurocomputing 2015, 159, 207–218. [Google Scholar] [CrossRef]
- Hoang, T.; Shiao, Y. New Method for Reduced-Number IMU Estimation in Observing Human Joint Motion. Sensors 2023, 23, 5712. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.P.; Chou, Y.J.; Lee, S.H. An OpenPose-based System for Evaluating Rehabilitation Actions in Parkinson’s Disease. In Proceedings of the 2022 International Automatic Control Conference (CACS), Kaohsiung, Taiwan, 3–6 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, Y.P.; Liu, Y.Y.; Hsu, W.H.; Lai, L.J.; Lee, M.S. Monitoring and assessment of rehabilitation progress on range of motion after total knee replacement by sensor-based system. Sensors 2020, 20, 1703. [Google Scholar] [CrossRef] [PubMed]

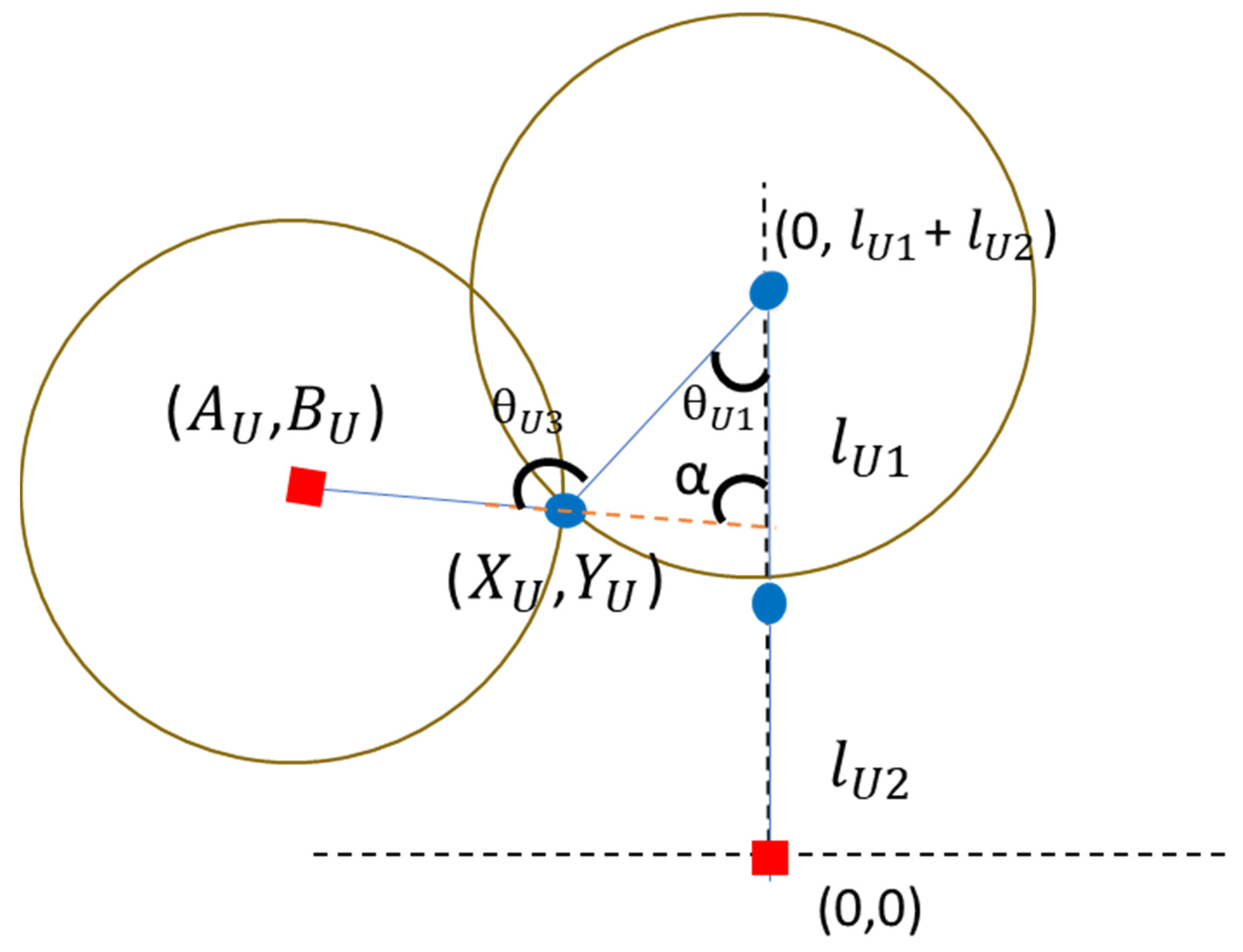

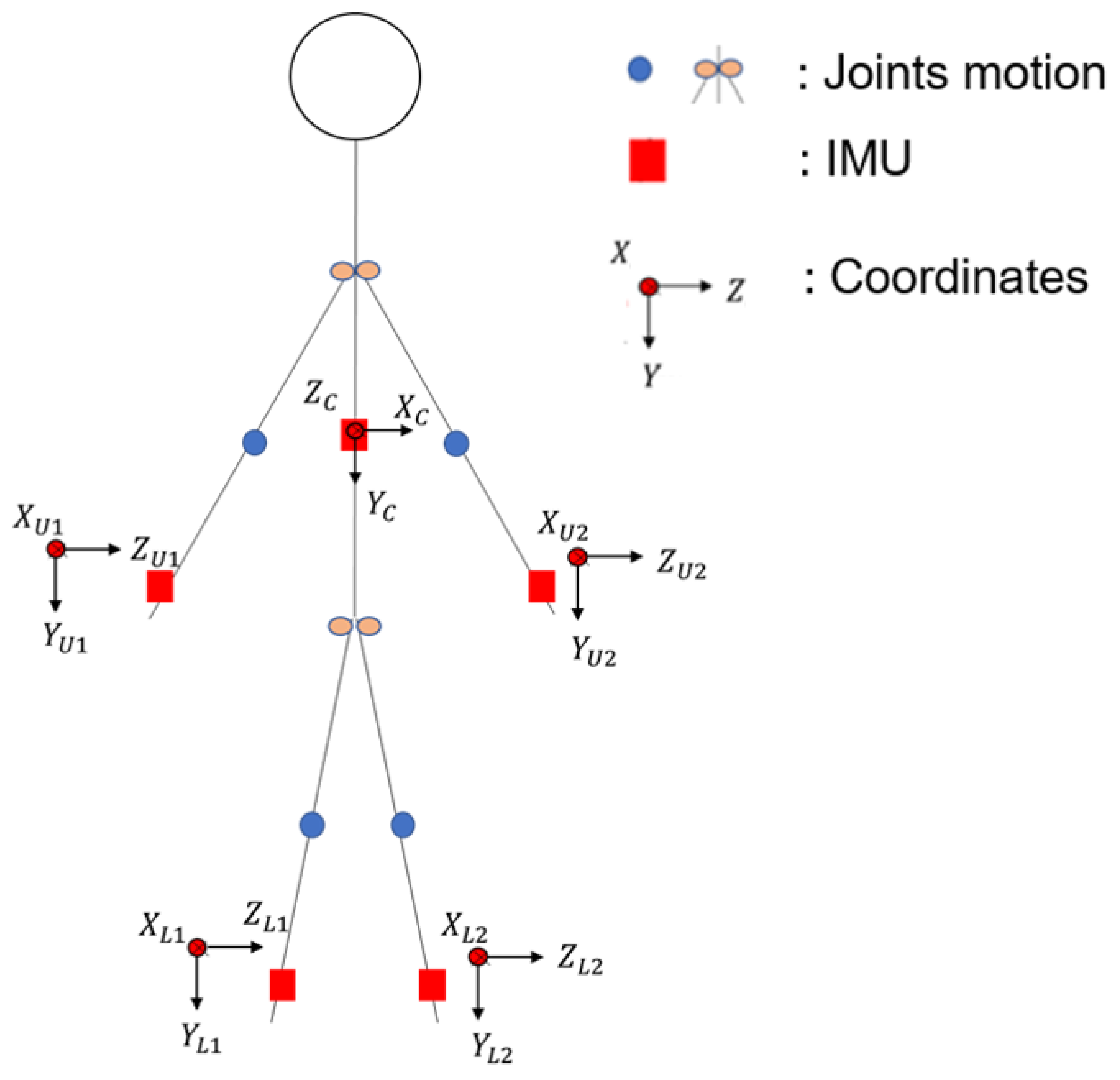
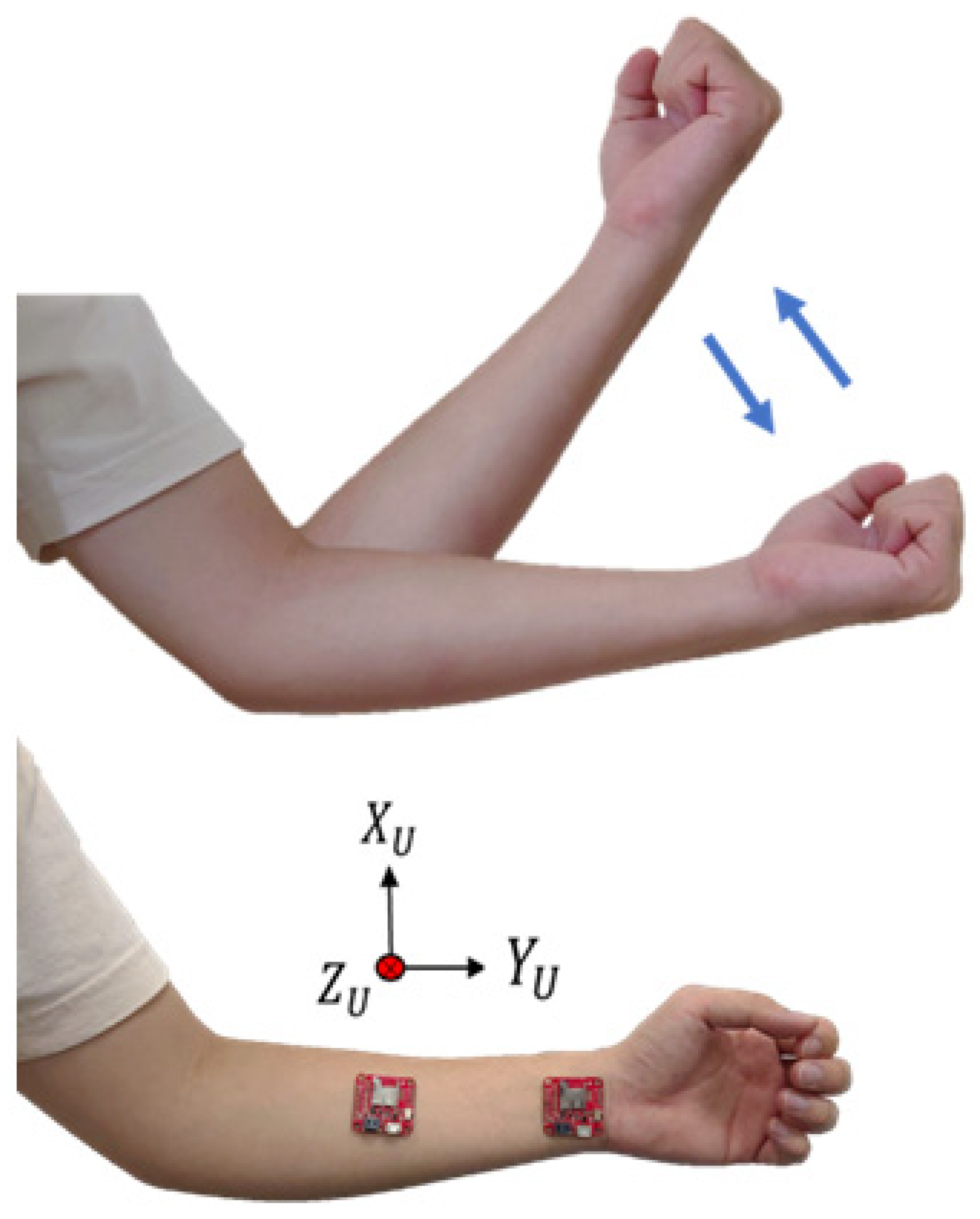
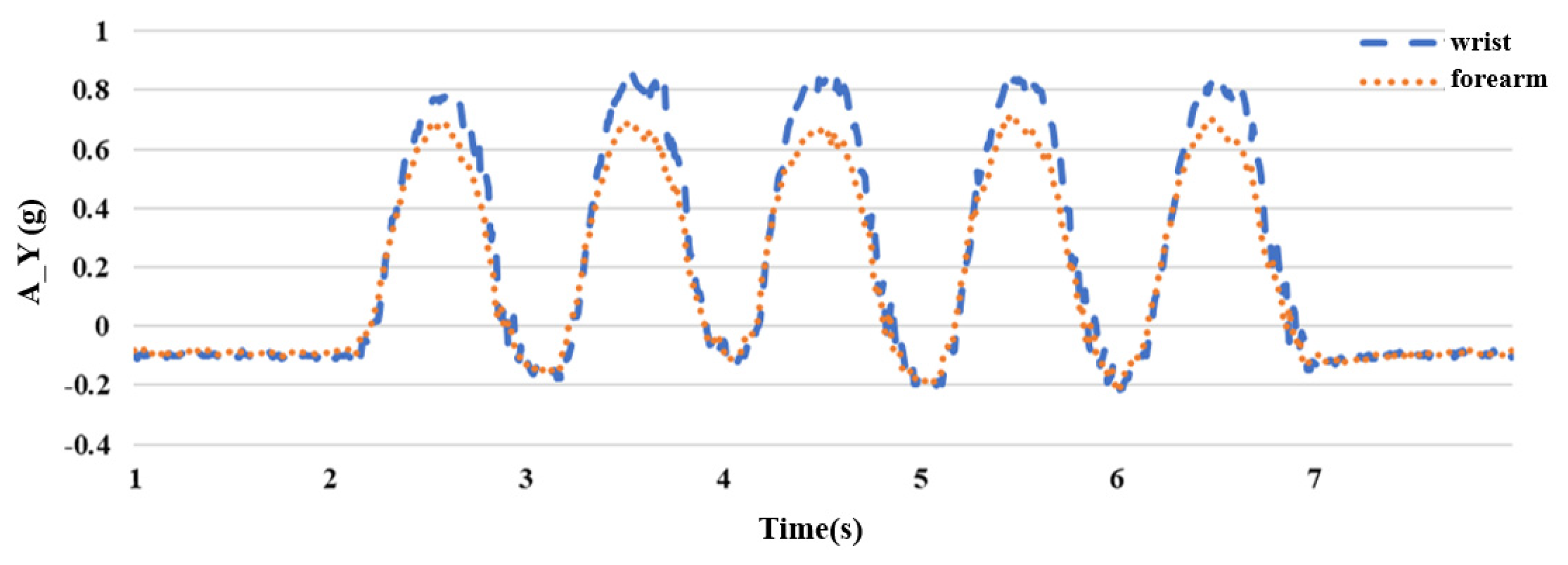


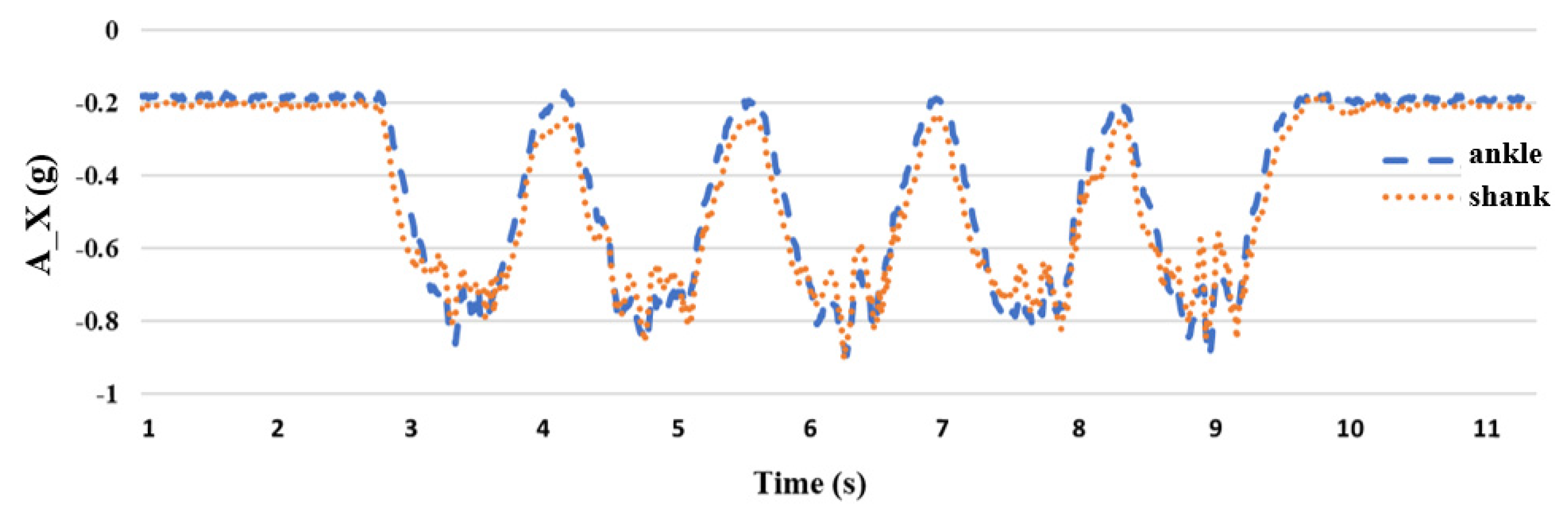
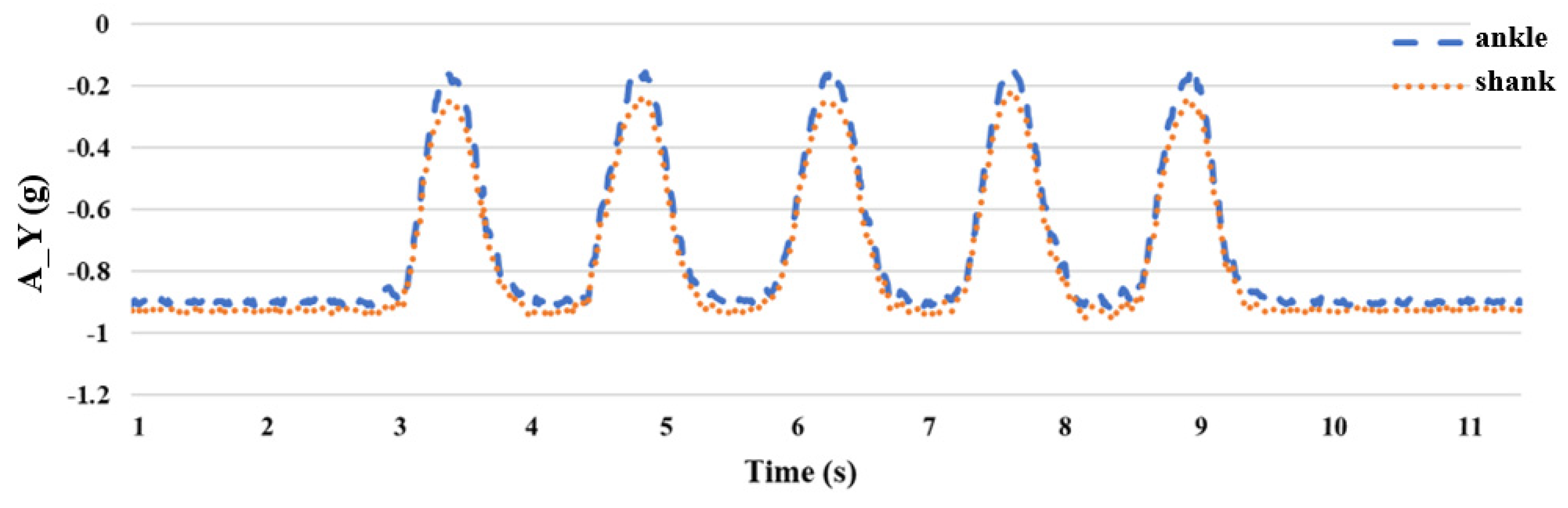
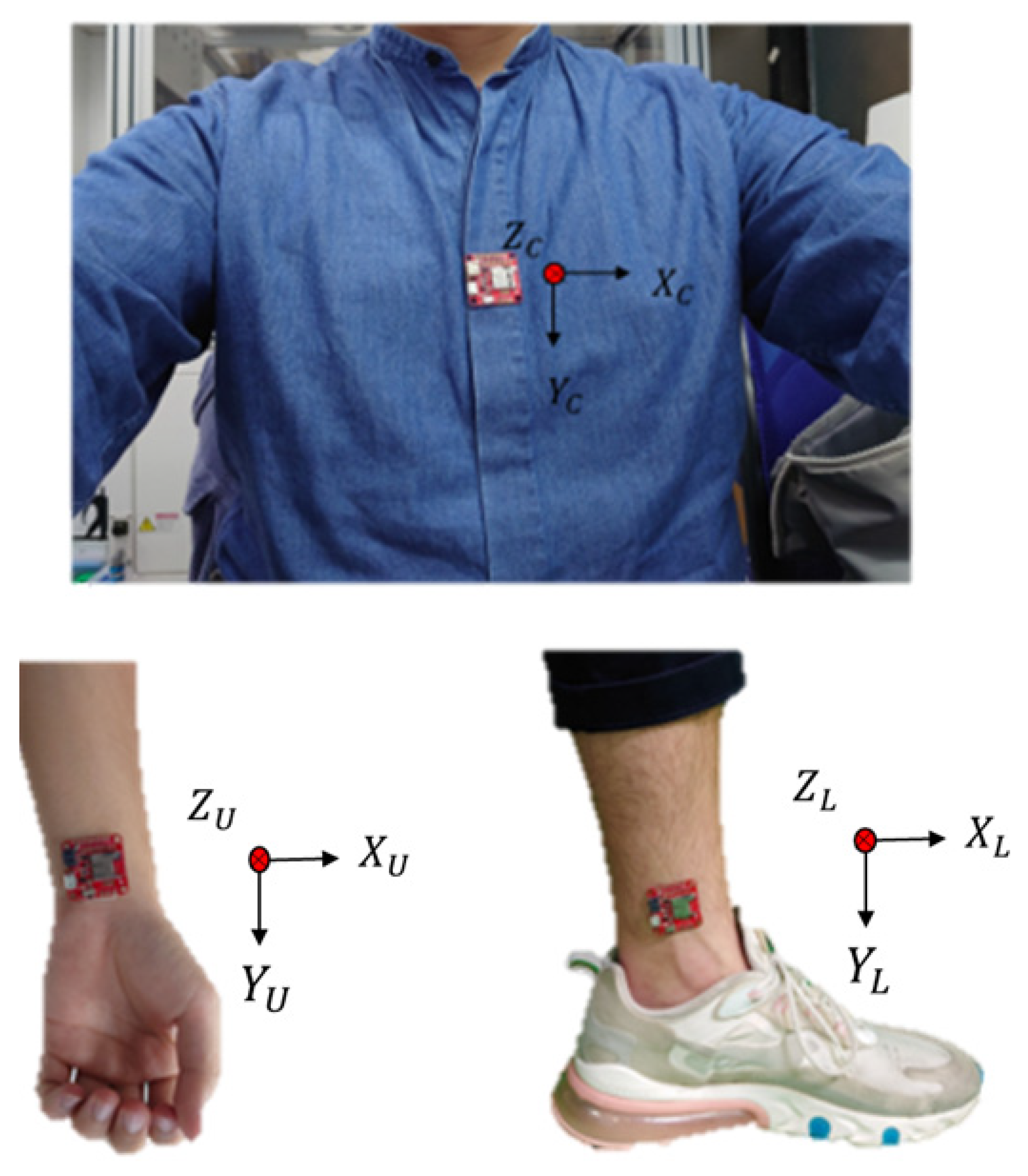



| Symbol | Meaning |
|---|---|
| Upper extremity length | |
| Forearm length | |
| Shoulder angle | |
| α (pitch) | Calculated angles from the IMU |
| Elbow angle | |
| The distance between the IMU coordinates and the origin | |
| The distance between the elbow joint coordinates and the origin |
| Symbol | Meaning |
|---|---|
| Thigh length | |
| Shank length | |
| Hip angle | |
| beta (pitch) | Calculated angles from the IMU |
| Knee angle | |
| , | The distance between the IMU coordinates and the origin |
| , | The distance between the knee joint coordinates and the origin |
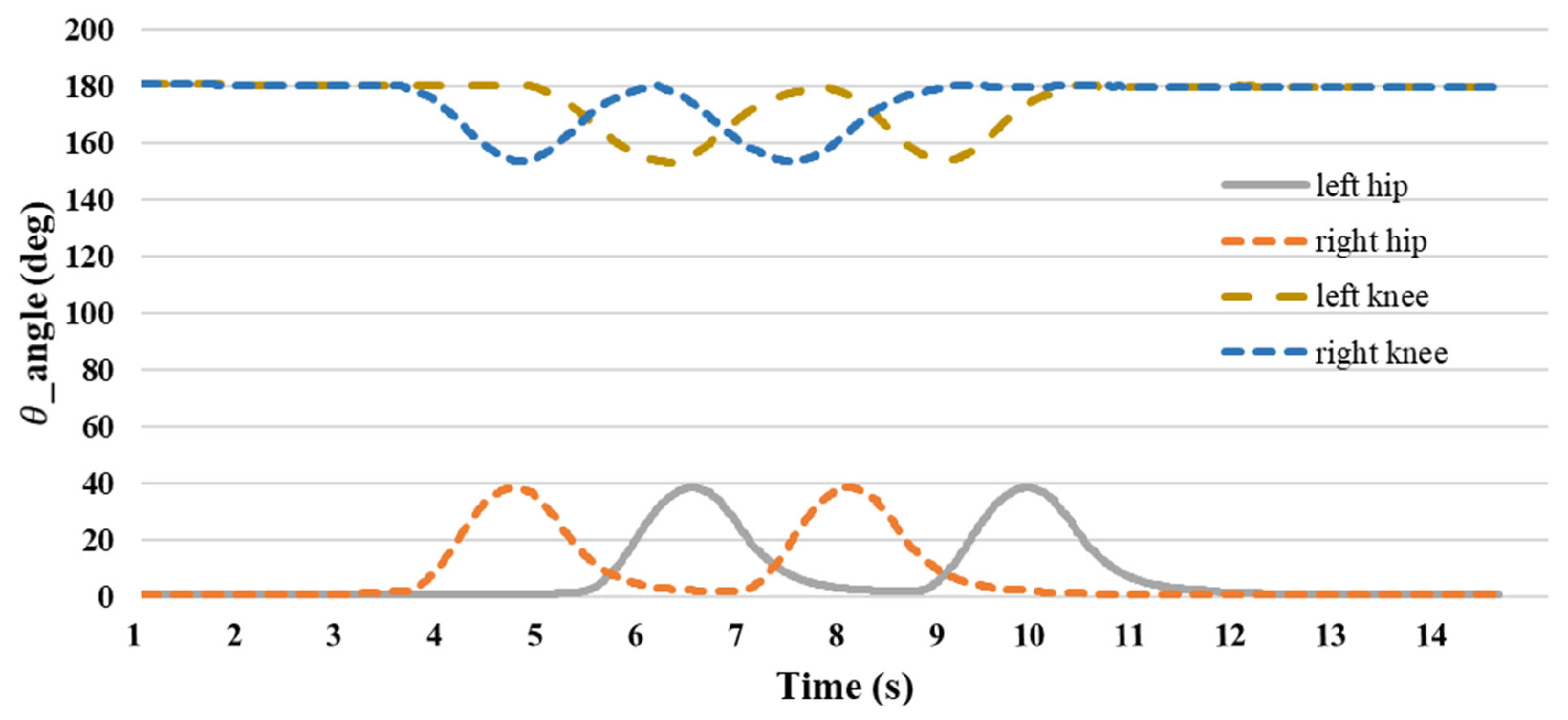
| No | First Cycle | Second Cycle | Variance = ±2 Degree | |||
|---|---|---|---|---|---|---|
| Motion | Initial (Degree) | The Raising of the Left Hand and the Lifting of the Right Foot (Degree) | The Raising of the Right Hand and the Lifting of the Left Foot (Degree) | The Raising of the Left Hand and the Lifting of the Right Foot (Degree) | The Raising of the Right Hand and the Lifting of the Left Foot (Degree) | Finish (Degree) |
| Left shoulder | 1.2 | 33.3 | 34.6 | 34.4 | 33.7 | 1.1 |
| Right shoulder | 1.4 | 34.1 | 33.7 | 34.7 | 33.5 | 1.3 |
| Left elbow | 180.2 | 82.5 | 92.4 | 83.8 | 94.6 | 180.4 |
| Right elbow | 180.5 | 90.8 | 85.2 | 81.3 | 81.8 | 180.6 |
| left hip | 1.1 | 2.4 | 38.7 | 2.4 | 38.5 | 1.2 |
| Right hip | 1.3 | 38.7 | 3.4 | 38.5 | 1.3 | 1.4 |
| Left knee | 180.3 | 180.7 | 153.3 | 179.6 | 153.4 | 180.5 |
| Right knee | 180.4 | 153.5 | 178.7 | 155.7 | 180.5 | 180.3 |
| Limitation | Description | Discussion |
|---|---|---|
| Number of IMU sensors | The study uses five sensors (two on the wrists, two on the ankles, and one on the chest) to track body movements. | Despite a reduction in the number of sensors compared to earlier research, the usage of five sensors might still provide challenges and inconveniences for users in practical applications. Addressing the difficulty of maintaining high precision while further reducing the number of sensors remains a priority. |
| Accuracy of joint angle estimation | The system demonstrates relatively high accuracy with discrepancies within 10° compared to dual IMU sensors and within 5° compared to image recognition technology, but there are still inherent errors. | This level of accuracy may not be enough for applications requiring very high precision, such as in the medical domain or professional sports. Improving the system’s precision is essential to expand its range of applications. |
| Cost and system complexity | The use of multiple sensors and complex algorithms, such as the extended Kalman filter, increases the system’s cost and complexity. | Optimizing cost and reducing system complexity are essential for broader commercial adoption. |
| Scalability and integration | The current system focuses on tracking joint angles of the upper and lower limbs during specific exercises like curling and leg stretching. | In order to have a wider range of uses, it is essential to enhance the system’s capacity to monitor intricate motions and incorporate with other systems, such as machine learning or artificial intelligence, for thorough data analysis. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiao, Y.; Chen, G.-Y.; Hoang, T. Three-Dimensional Human Posture Recognition by Extremity Angle Estimation with Minimal IMU Sensor. Sensors 2024, 24, 4306. https://doi.org/10.3390/s24134306
Shiao Y, Chen G-Y, Hoang T. Three-Dimensional Human Posture Recognition by Extremity Angle Estimation with Minimal IMU Sensor. Sensors. 2024; 24(13):4306. https://doi.org/10.3390/s24134306
Chicago/Turabian StyleShiao, Yaojung, Guan-Yu Chen, and Thang Hoang. 2024. "Three-Dimensional Human Posture Recognition by Extremity Angle Estimation with Minimal IMU Sensor" Sensors 24, no. 13: 4306. https://doi.org/10.3390/s24134306
APA StyleShiao, Y., Chen, G.-Y., & Hoang, T. (2024). Three-Dimensional Human Posture Recognition by Extremity Angle Estimation with Minimal IMU Sensor. Sensors, 24(13), 4306. https://doi.org/10.3390/s24134306






