A Semi-Supervised Adaptive Matrix Machine Approach for Fault Diagnosis in Railway Switch Machine
Abstract
1. Introduction
- (1)
- The incorporation of an adaptive low-rank regularizer selectively retains larger singular values, improving the approximation of the matrix rank and enhancing the extraction of fundamental connections between the rows and columns of matrix data.
- (2)
- The development of a probabilistic output strategy for SAMM, coupled with a semi-supervised learning (SSL) framework that utilizes these outputs to assign high-confidence pseudo-labels to unlabeled samples, effectively mitigating the challenges associated with a lack of labeled data.
- (3)
- The introduction of an adaptive penalty term to address the imbalance in pseudo-label distribution, which adjusts the hinge loss penalty coefficient based on sample quantity to counteract learning biases.
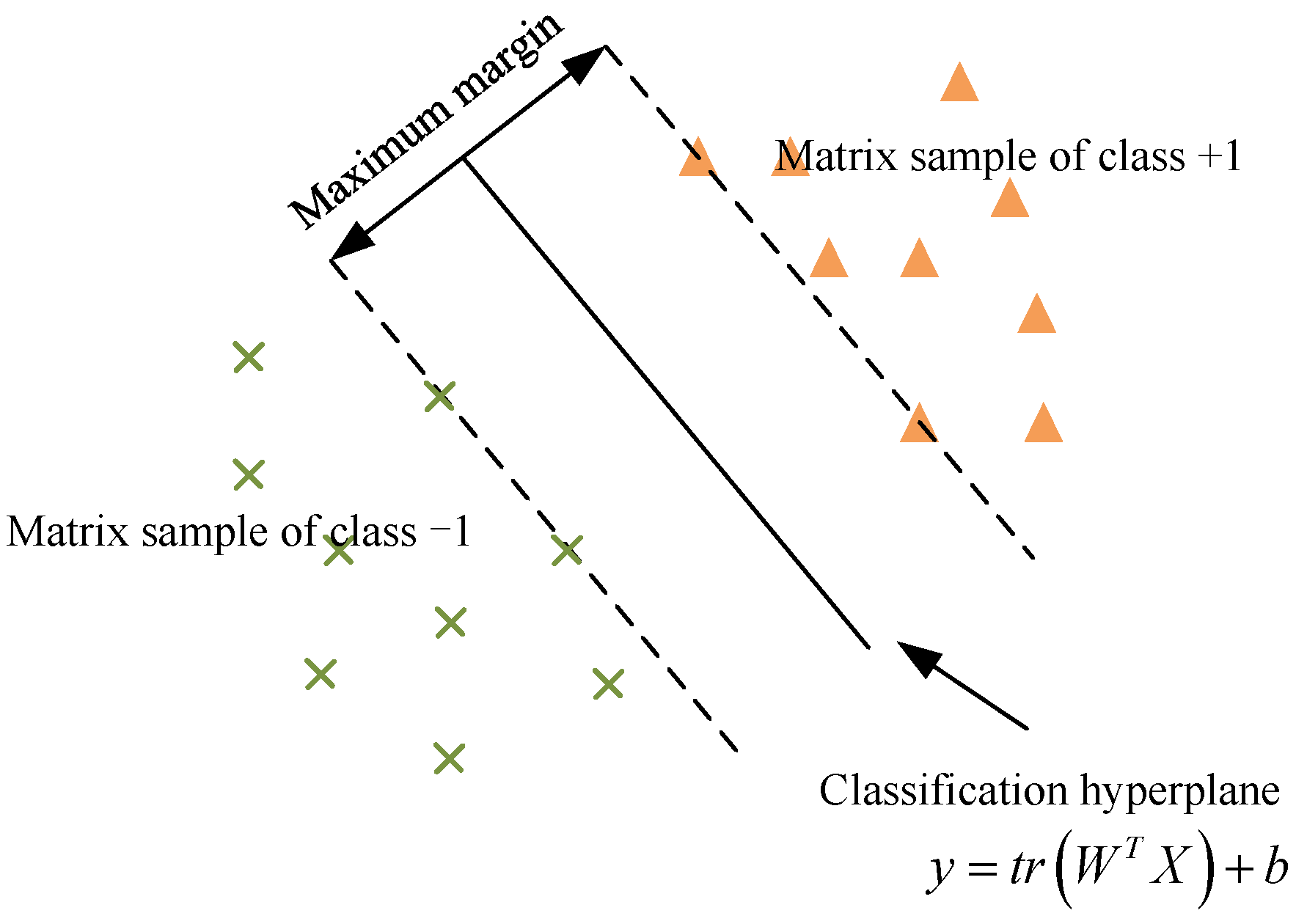
2. Support Matrix Machine
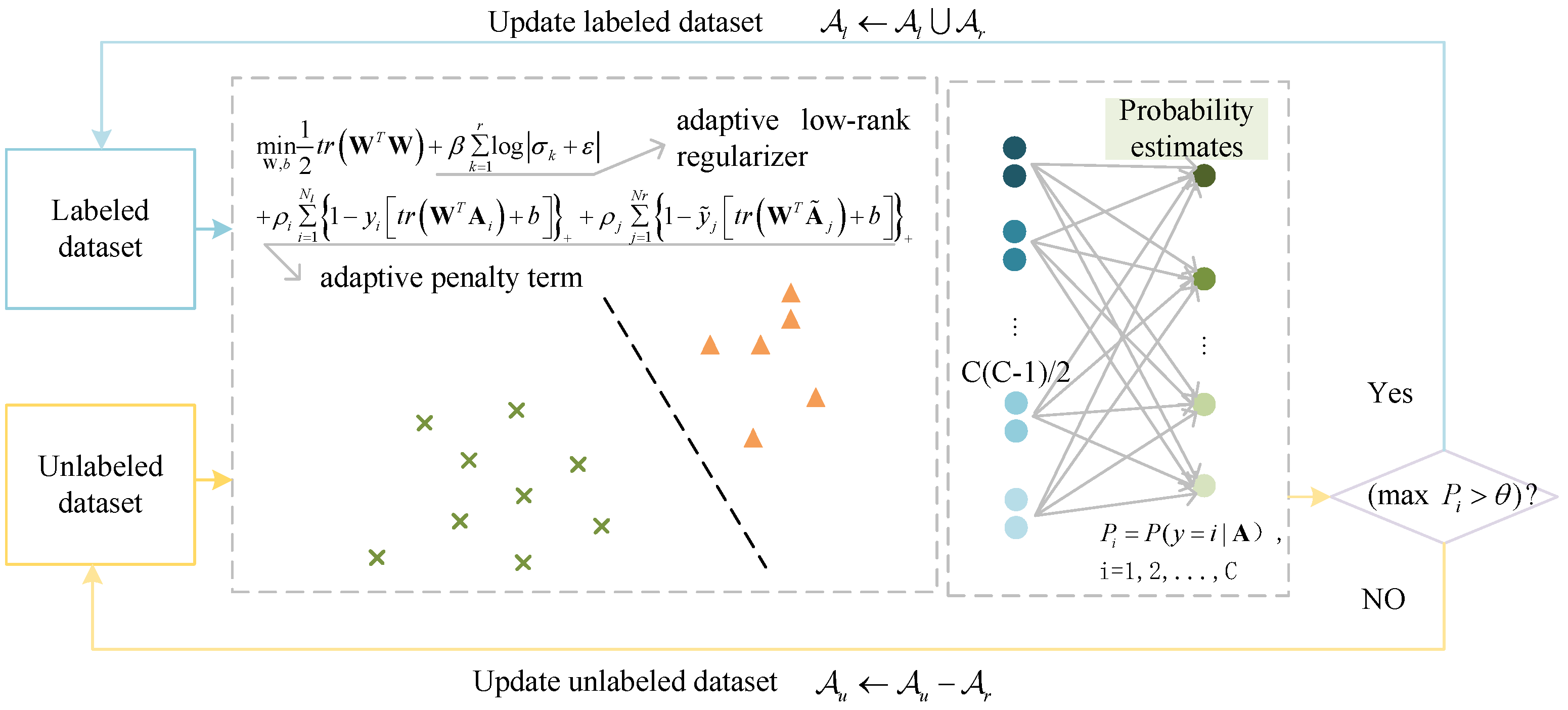
3. Semi-Supervised Adaptive Matrix Machine
3.1. SAMM Model
3.2. SAMM Learning Algorithm
- (1)
- To solve the subproblem of , assume and are held constant, reducing it to a function concerning expressed as:
- (2)
- To address the subproblem concerning , we undertake minimization of the expression encapsulating all terms associated with as outlined in Equation (5).
| Algorithm 1: The learning algorithm for SAMM |
Input: Training set , low-rank coefficient , loss penalty coefficient , step size . Output , b 1. Initialize. While not converging do 2. Update with Equation (8) 4. Update with Equation (6) 5. End 6. Return , b |
3.3. Fault Diagnosis Framework
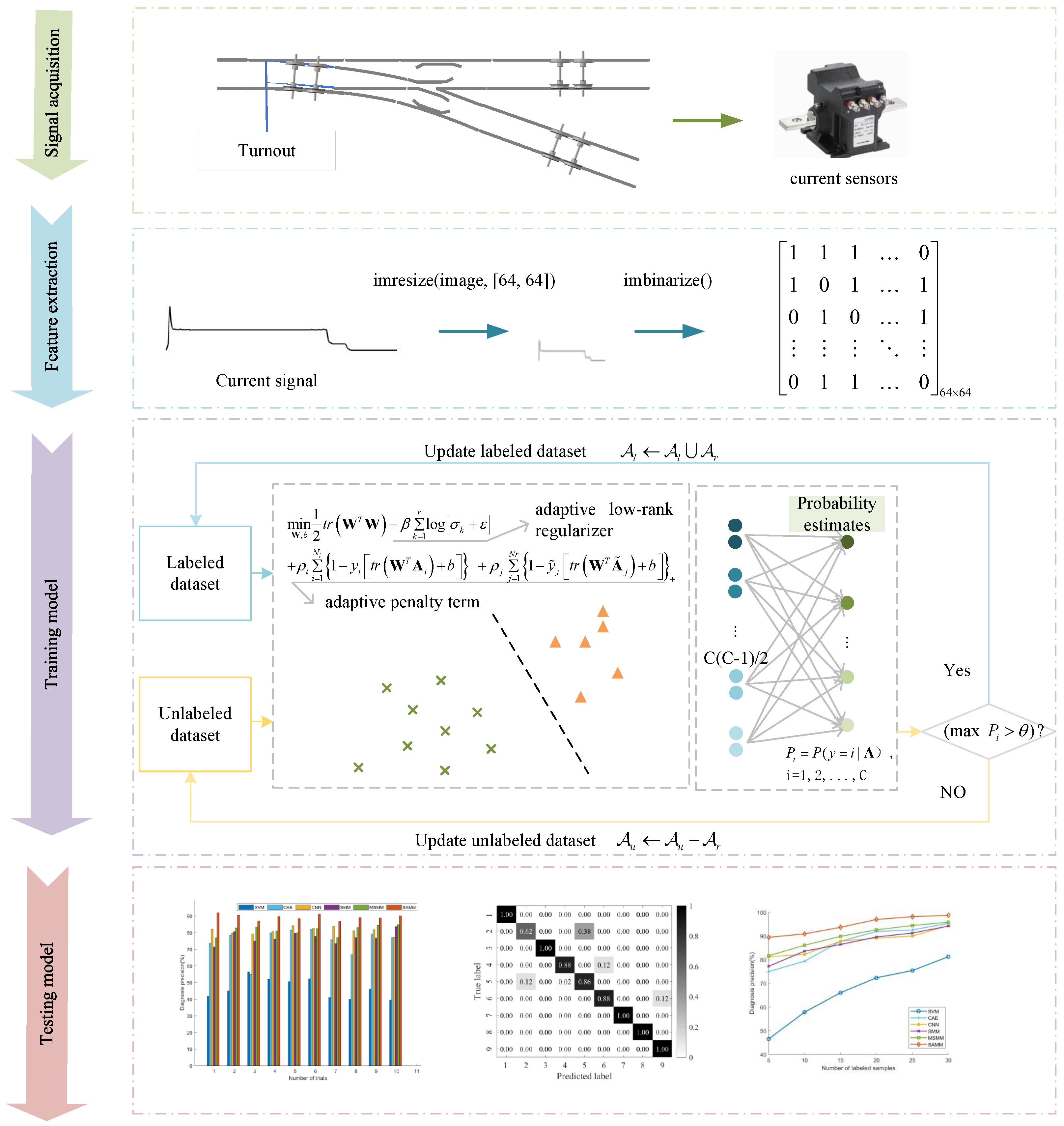
- Step 1: Signal acquisition. Acquire current signals of the switch machine across various fault states.
- Step 2: Feature extraction. Convert continuous current signals into 2D matrix samples via downsampling and binarization techniques, enabling efficient processing and model training.
- Step 3: Train the SAMM Model. Labeled and unlabeled samples from the training dataset are used to build the SAMM model. The model integrates an adaptive low-rank regularizer with an adaptive penalty term, enhancing matrix structure information extraction, and addressing the pseudo-labeling imbalance challenge of semi-supervised learning.
- Step 4: Test the SAMM Model. Predict the switch machine’s fault status by inputting test samples into the SAMM model.
4. Experimental and Discussion
4.1. Description of the Data Set
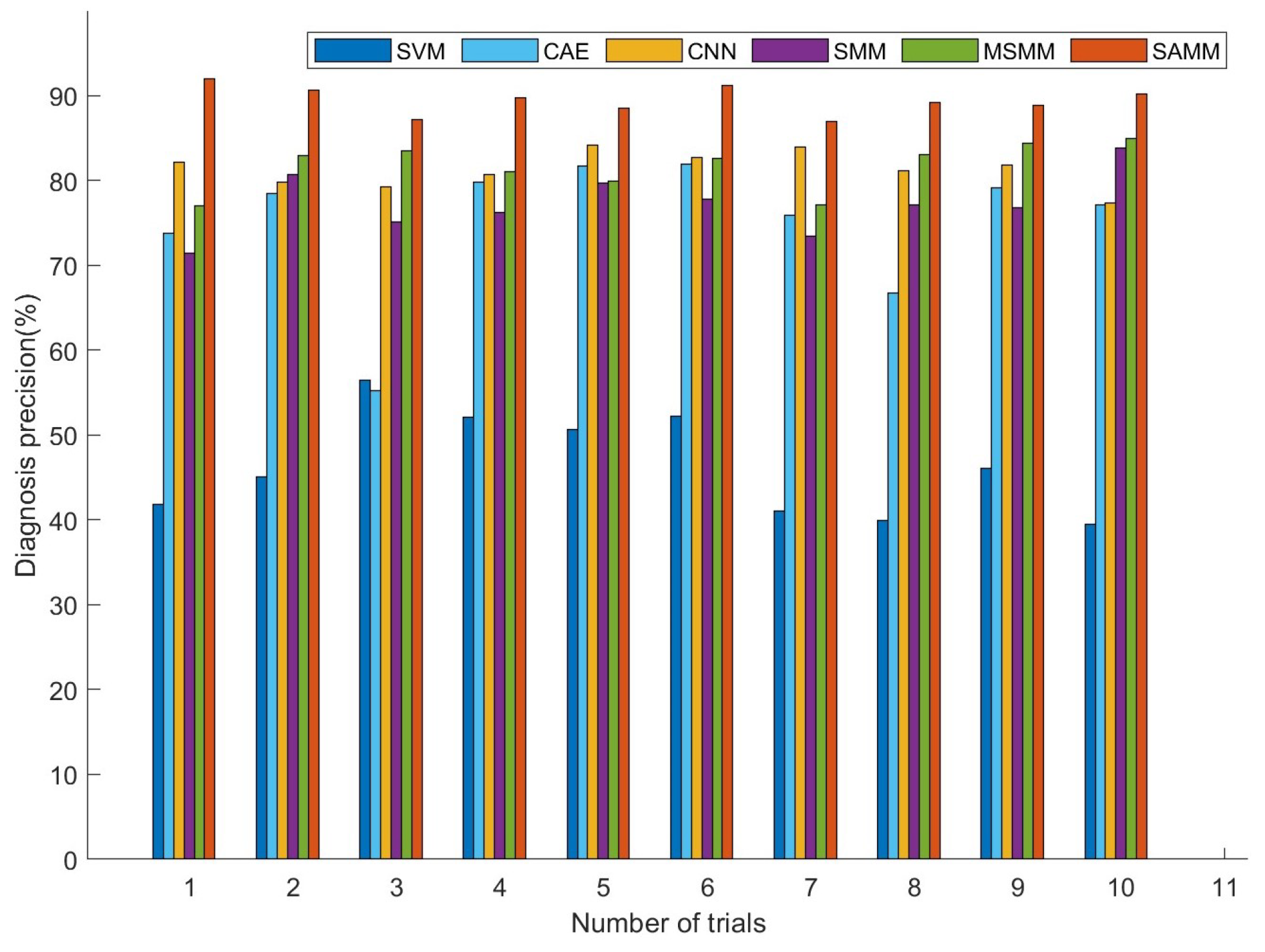
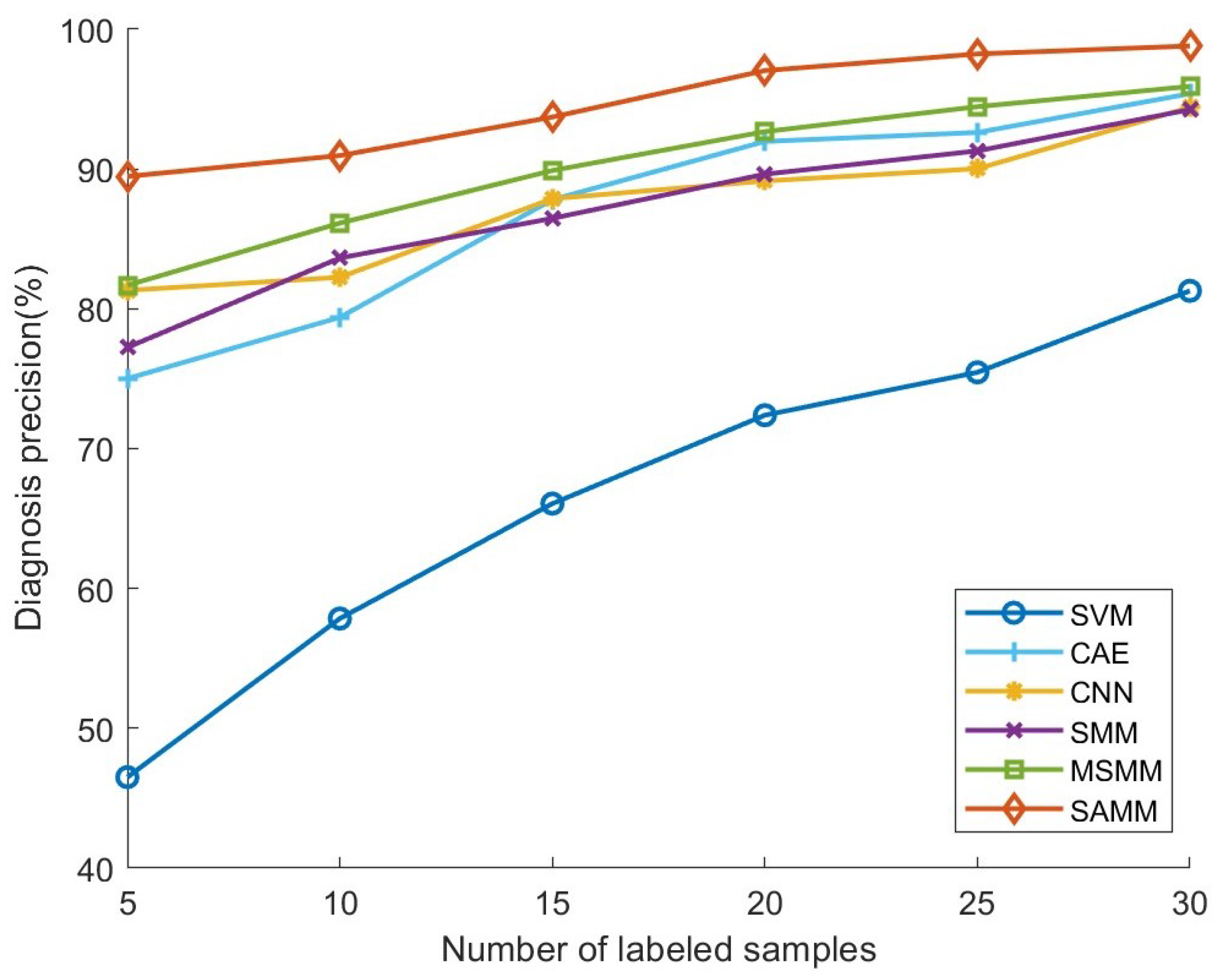
4.2. Comparison Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SVM | Support vector machine |
| CAE | Convolutional autoencoder |
| CNN | Convolutional neural network |
| SMM | Support matrix machine |
| MSMM | Multiclass support matrix machine |
References
- Pyrgidis, C.N. Railway Transportation Systems: Design, Construction and Operation; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Loidolt, M.; Marschnig, S.; Berghold, A. Track geometry quality assessments for turnouts. Transp. Eng. 2023, 12, 100170. [Google Scholar] [CrossRef]
- Mistry, P.; Lane, P.; Allen, P. Railway Point-Operating Machine Fault Detection Using Unlabeled Signaling Sensor Data. Sensors 2020, 20, 2692. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhu, F.; Xu, Z.; Xie, Q.; Lo, S.M.; Tsui, K.L.; Li, L. Knowledge-Informed Wheel Wear Prediction Method for High-Speed Train Using Multisource Signal Data. IEEE Trans. Instrum. Meas. 2024, 73, 3522912. [Google Scholar] [CrossRef]
- Luo, J.; Shao, H.; Lin, J.; Liu, B. Meta-learning with elastic prototypical network for fault transfer diagnosis of bearings under unstable speeds. Reliab. Eng. Syst. Saf. 2024, 245, 110001. [Google Scholar] [CrossRef]
- Kim, H.; Sa, J.; Chung, Y.; Park, D.; Yoon, S. Fault diagnosis of railway point machines using dynamic time warping. Electron. Lett. 2016, 52, 818–819. [Google Scholar] [CrossRef]
- Li, W.; Li, G. Railway’s Turnout Fault Diagnosis Based on Power Curve Similarity. In Proceedings of the 2019 International Conference on Communications, Information System and Computer Engineering (CISCE), Haikou, China, 5–7 July 2019; pp. 112–115. [Google Scholar] [CrossRef]
- Ji, W.; Cheng, C.; Xie, G.; Zhu, L.; Wang, Y.; Pan, L.; Hei, X. An intelligent fault diagnosis method based on curve segmentation and SVM for rail transit turnout. J. Intell. Fuzzy Syst. 2021, 41, 4275–4285. [Google Scholar] [CrossRef]
- Muñoz del Río, A.; Segovia Ramirez, I.; Papaelias, M.; García Márquez, F.P. Pattern recognition based on statistical methods combined with machine learning in railway switches. Expert Syst. Appl. 2024, 238, 122214. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Wang, N.; Long, J.; Tao, T. Fault Diagnosis of Railway Turnout Based on Random Forests. In Proceedings of the 4th International Conference on Electrical and Information Technologies for Rail Transportation (EITRT) 2019; Qin, Y., Jia, L., Liu, B., Liu, Z., Diao, L., An, M., Eds.; Springer: Singapore, 2020; pp. 505–515. [Google Scholar]
- Chen, C.; Li, X.; Huang, K.; Xu, Z.; Mei, M. A Convolutional Autoencoder Based Fault Detection Method for Metro Railway Turnout. Comput. Model. Eng. Sci. 2023, 136, 471–485. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, G.; Dong, W.; Sun, X.; Ji, X. Fault Diagnosis of High-Speed Railway Turnout Based on Convolutional Neural Network. In Proceedings of the 2018 24th International Conference on Automation and Computing (ICAC), Newcastle Upon Tyne, UK, 6–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, D.; Fu, Y.; Qin, N.; Gao, S. Fault diagnosis of high-speed train bogie based on LSTM neural network. Sci. China Inf. Sci. 2020, 64, 119203. [Google Scholar] [CrossRef]
- Yan, S.; Shao, H.; Wang, J.; Zheng, X.; Liu, B. LiConvFormer: A lightweight fault diagnosis framework using separable multiscale convolution and broadcast self-attention. Expert Syst. Appl. 2024, 237, 121338. [Google Scholar] [CrossRef]
- Shao, H.; Zhou, X.; Lin, J.; Liu, B. Few-Shot Cross-Domain Fault Diagnosis of Bearing Driven by Task-Supervised ANIL. IEEE Internet Things J. 2024, 11, 22892–22902. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Yan, K.; Shao, H.; Lin, J. Intelligent fault diagnosis of bevel gearboxes using semi-supervised probability support matrix machine and infrared imaging. Reliab. Eng. Syst. Saf. 2023, 230, 108921. [Google Scholar] [CrossRef]
- Ramírez-Sanz, J.M.; Maestro-Prieto, J.A.; Arnaiz-González, Á.; Bustillo, A. Semi-supervised learning for industrial fault detection and diagnosis: A systemic review. ISA Trans. 2023, 143, 255–270. [Google Scholar] [CrossRef] [PubMed]
- Lao, Z.; He, D.; Jin, Z.; Liu, C.; Shang, H.; He, Y. Few-shot fault diagnosis of turnout switch machine based on semi-supervised weighted prototypical network. Knowl.-Based Syst. 2023, 274, 110634. [Google Scholar] [CrossRef]
- Shi, Z.S.; Du, Y.M.; Du, T.; Shan, G.C. The Turnout Abnormality Diagnosis with Semi-supervised Learning Method. In Proceedings of the 4th International Conference on Electrical and Information Technologies for Rail Transportation (EITRT) 2019; Qin, Y., Jia, L., Liu, B., Liu, Z., Diao, L., An, M., Eds.; Springer: Singapore, 2020; pp. 737–746. [Google Scholar]
- Kim, S.; Park, J.; Kim, W.; Jo, S.H.; Youn, B.D. Learning from even a weak teacher: Bridging rule-based Duval method and a deep neural network for power transformer fault diagnosis. Int. J. Electr. Power Energy Syst. 2022, 136, 107619. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Z.; Lian, L.; Yu, S.X. Debiased Learning from Naturally Imbalanced Pseudo-Labels for Zero-Shot and Semi-Supervised Learning. arXiv 2022, arXiv:2201.01490. [Google Scholar]
- Pirsiavash, H.; Ramanan, D.; Fowlkes, C. Bilinear Classifiers for Visual Recognition. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2009; Volume 22. [Google Scholar]
- Wolf, L.; Jhuang, H.; Hazan, T. Modeling Appearances with Low-Rank SVM. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, C.; Xu, Z.; Mei, M.; Huang, K.; Lo, S.M. Fault Diagnosis Scheme for Railway Switch Machine Using Multi-Sensor Fusion Tensor Machine. Comput. Mater. Contin. 2024, 79, 4533–4549. [Google Scholar] [CrossRef]
- Luo, L.; Xie, Y.; Zhang, Z.; Li, W.J. Support Matrix Machines. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Zheng, Q.; Zhu, F.; Qin, J.; Heng, P.A. Multiclass support matrix machine for single trial EEG classification. Neurocomputing 2018, 275, 869–880. [Google Scholar] [CrossRef]
- Razzak, I. Cooperative Evolution Multiclass Support Matrix Machines. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Li, X.; Li, S.; Wei, D.; Si, L.; Yu, K.; Yan, K. Dynamics simulation-driven fault diagnosis of rolling bearings using security transfer support matrix machine. Reliab. Eng. Syst. Saf. 2024, 243, 109882. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, Y.; Liu, P.; Sun, W.; Li, S.; Fang, X. Saliency detection via double nuclear norm maximization and ensemble manifold regularization. Knowl.-Based Syst. 2019, 183, 12. [Google Scholar] [CrossRef]
- Zhang, Y.; Lei, X.; Pan, Y.; Pedrycz, W. Prediction of disease-associated circRNAs via circRNA–disease pair graph and weighted nuclear norm minimization. Knowl.-Based Syst. 2021, 214, 106694. [Google Scholar] [CrossRef]
- Jia, X.; Feng, X.; Wang, W. Adaptive regularizer learning for low rank approximation with application to image denoising. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 3096–3100. [Google Scholar] [CrossRef]
- Zhu, W.; Peng, B. Sparse and low-rank regularized deep subspace clustering. Knowl.-Based Syst. 2020, 204, 106199. [Google Scholar] [CrossRef]
- Xu, H.; Pan, H.; Zheng, J.; Liu, Q.; Tong, J. Dynamic penalty adaptive matrix machine for the intelligent detection of unbalanced faults in roller bearing. Knowl.-Based Syst. 2022, 247, 108779. [Google Scholar] [CrossRef]
- Parvin, H.; Moradi, P.; Esmaeili, S.; Qader, N.N. A scalable and robust trust-based nonnegative matrix factorization recommender using the alternating direction method. Knowl.-Based Syst. 2019, 166, 92–107. [Google Scholar] [CrossRef]
- Platt, J. Probabilistic Outputs for Support Vector Machines and Comparisons to Regularized Likelihood Methods. Adv. Large Margin Classif. 2000, 10, 61–74. [Google Scholar]
- Wu, T.F.; Lin, C.J.; Weng, R.C. Probability Estimates for Multi-class Classification by Pairwise Coupling. J. Mach. Learn. Res. 2004, 5, 975–1005. [Google Scholar]
- Sohn, K.; Berthelot, D.; Li, C.L.; Zhang, Z.; Carlini, N.; Cubuk, E.D.; Kurakin, A.; Zhang, H.; Raffel, C. FixMatch: Simplifying semi-supervised learning with consistency and confidence. Adv. Neural Inf. Process. Syst. 2020, 33, 596–608. [Google Scholar]
- Cao, Y.; Sun, Y.; Xie, G.; Li, P. A Sound-Based Fault Diagnosis Method for Railway Point Machines Based on Two-Stage Feature Selection Strategy and Ensemble Classifier. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12074–12083. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, Y.; Li, P.; Su, S. Sound Based Degradation Status Recognition for Railway Point Machines Based on Soft-Threshold Wavelet Denoising, WPD, and ReliefF. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]
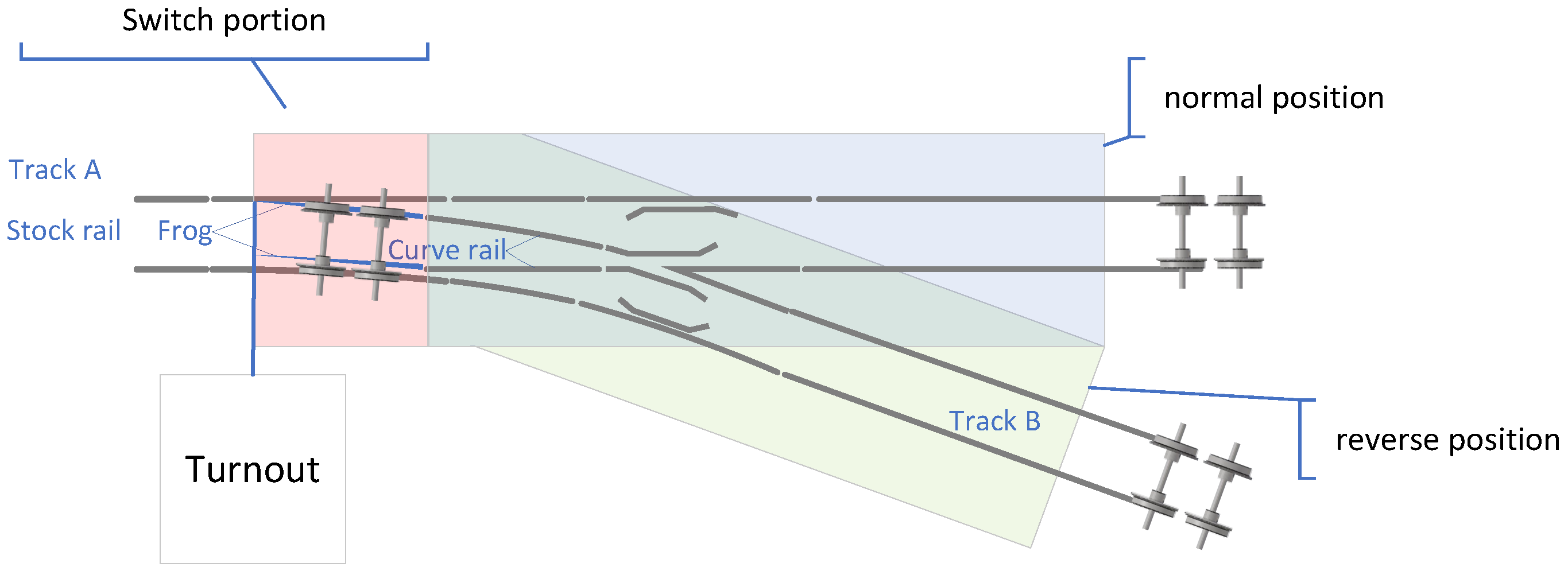
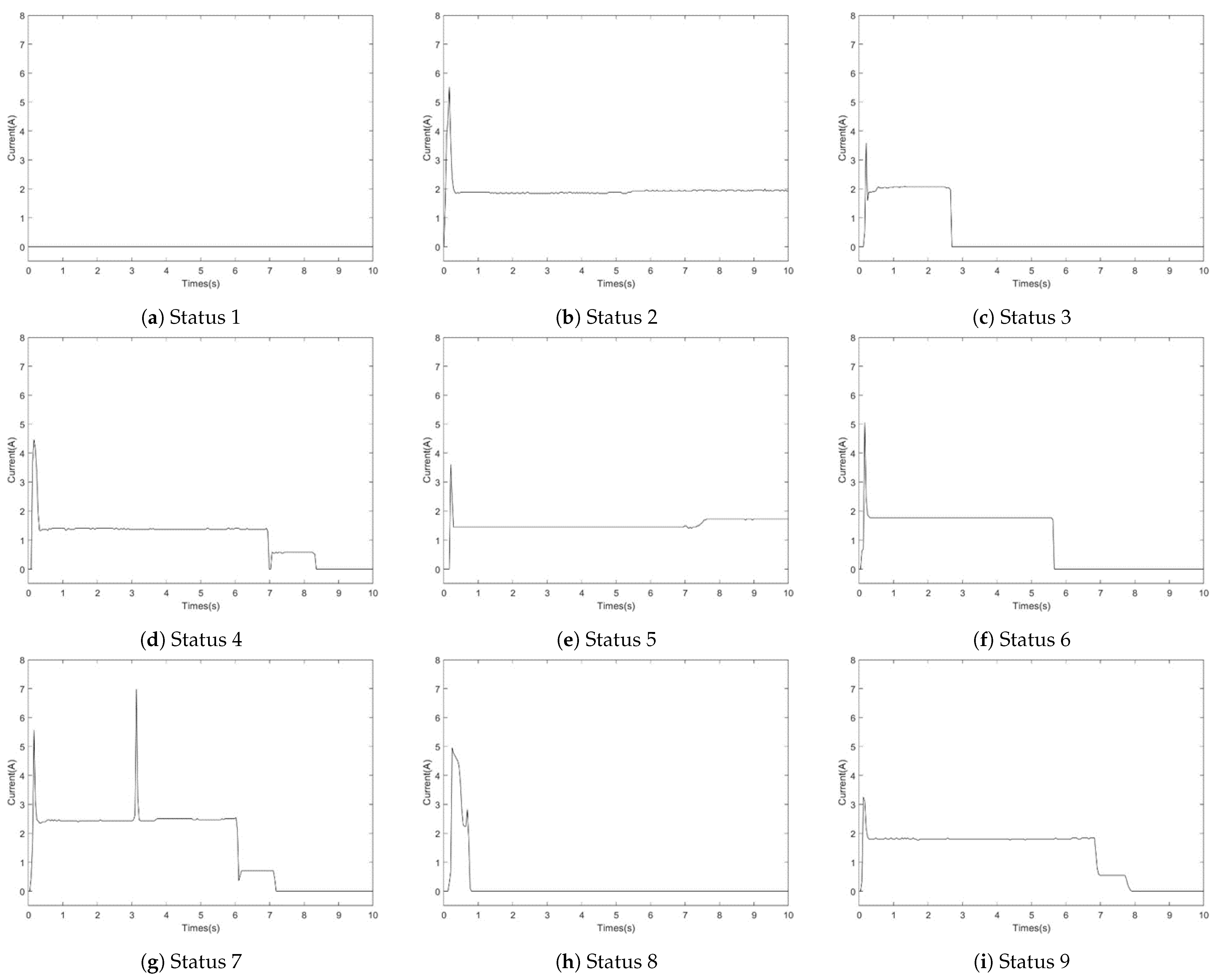

| Label | Fault Phenomenon | Fault Cause |
|---|---|---|
| 1 | Consistently no current | Action circuit malfunction |
| 2 | The current remains constant during release | Mechanical resistance encountered |
| 3 | A sudden drop in current to zero | Insufficient contact or unlocked |
| 4 | The current release time is delayed | Abnormal motor condition |
| 5 | Increase in current during release. | Internal jamming and friction increase |
| 6 | Release without small steps | Abnormality in the indicated circuit |
| 7 | Pulse observed during switching | Poor contact of automatic switch |
| 8 | The curve only maintains 0∼1 s | Phase failure in the starting circuit |
| 9 | Normal state | Normal |
| Data Class | Classified as Pos. | Classified as Neg. |
|---|---|---|
| pos | true positive (tp) | false negative (fn) |
| neg | false positive (fp) | true negative (tn) |
| Model | Number of Labeled Samples in Each Status | |||||
|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | |
| SVM | 40.69% | 54.67% | 65.11% | 68.22% | 71.78% | 80.44% |
| CAE | 72.71% | 77.33% | 87.11% | 91.78% | 91.56% | 95.33% |
| CNN | 79.25% | 80.89% | 85.78% | 88.00% | 88.00% | 94.22% |
| SMM | 74.89% | 82.22% | 84.67% | 89.33% | 89.33% | 93.56% |
| MSMM | 79.78% | 82.00% | 83.78% | 92.44% | 94.44% | 95.11% |
| SAMM | 87.91% | 90.44% | 93.56% | 96.89% | 98.22% | 98.56% |
| Model | Number of Labeled Samples in Each Status | |||||
|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | |
| SVM | 43.25% | 56.21% | 65.59% | 70.25% | 73.57% | 80.87% |
| CAE | 73.83% | 78.35% | 87.46% | 91.88% | 92.08% | 95.36% |
| CNN | 80.24% | 81.57% | 86.81% | 88.57% | 89.00% | 94.32% |
| SMM | 76.04% | 82.92% | 85.56% | 89.48% | 90.31% | 93.90% |
| MSMM | 80.57% | 84.01% | 86.73% | 92.56% | 94.45% | 95.51% |
| SAMM | 89.47% | 90.70% | 93.64% | 96.96% | 98.23% | 98.68% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Xu, Z.; Mei, M.; Lan, M.; Liu, C.; Gao, X. A Semi-Supervised Adaptive Matrix Machine Approach for Fault Diagnosis in Railway Switch Machine. Sensors 2024, 24, 4402. https://doi.org/10.3390/s24134402
Li W, Xu Z, Mei M, Lan M, Liu C, Gao X. A Semi-Supervised Adaptive Matrix Machine Approach for Fault Diagnosis in Railway Switch Machine. Sensors. 2024; 24(13):4402. https://doi.org/10.3390/s24134402
Chicago/Turabian StyleLi, Wenqing, Zhongwei Xu, Meng Mei, Meng Lan, Chuanzhen Liu, and Xiao Gao. 2024. "A Semi-Supervised Adaptive Matrix Machine Approach for Fault Diagnosis in Railway Switch Machine" Sensors 24, no. 13: 4402. https://doi.org/10.3390/s24134402
APA StyleLi, W., Xu, Z., Mei, M., Lan, M., Liu, C., & Gao, X. (2024). A Semi-Supervised Adaptive Matrix Machine Approach for Fault Diagnosis in Railway Switch Machine. Sensors, 24(13), 4402. https://doi.org/10.3390/s24134402






