Relationship of Cycling Power and Non-Linear Heart Rate Variability from Everyday Workout Data: Potential for Intensity Zone Estimation and Monitoring
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Study Design
2.3. Data Analysis
- Data Quality: Artifacts—e.g., missed beats by HR monitors—can significantly affect the DFA-a1 calculation. Hence, the focus of the data analysis was on including workouts with a maximum of 5% artifacts. From the initial data pool, this criterion narrows down the dataset to 2096 workouts (still 21 users), forming 411 10-day workout groups.
- Fatigue Consideration: To mitigate the impact of fatigue, only minutes 5 to 20 of each workout were included in the data analysis. The first 5 min of data were excluded as they are more prone to HRV artifacts due to the HR monitor potentially not having built up sufficient moisture from the athlete’s sweat and the potentially suboptimal position of the chest strap that gets adjusted during the first few minutes of exercising.
- Data Consistency: Inconsistent data, especially during periods without pedaling (where power equals 0), can skew the results. Indeed, while stopping spinning for a few seconds occasionally is not a problem, it becomes one when it is performed for longer times and/or very frequently. In such a situation, a lot of data points with the same power value of 0 and different values of DFA-a1 would be included, significantly spoiling the correlation. To maintain consistency, workouts with prolonged or frequent periods of no pedaling (exclusion of datasets pedaling < 90% of the dataset) were excluded, and data points with a power of 0 were discarded.
- Data Range and Intensity: For a meaningful correlation between power and DFA-a1, a sufficient range of the internal load marker is necessary. Data inclusion focuses on datasets where at least 50% of the data points were within the dynamic range (DFA-a1 < 1.0), which indicates a significant effort level. Data with mostly DFA-a1 > 1.0, typically corresponding to very easy rides, breaks, or resting conditions in healthy individuals, were not processed [22].
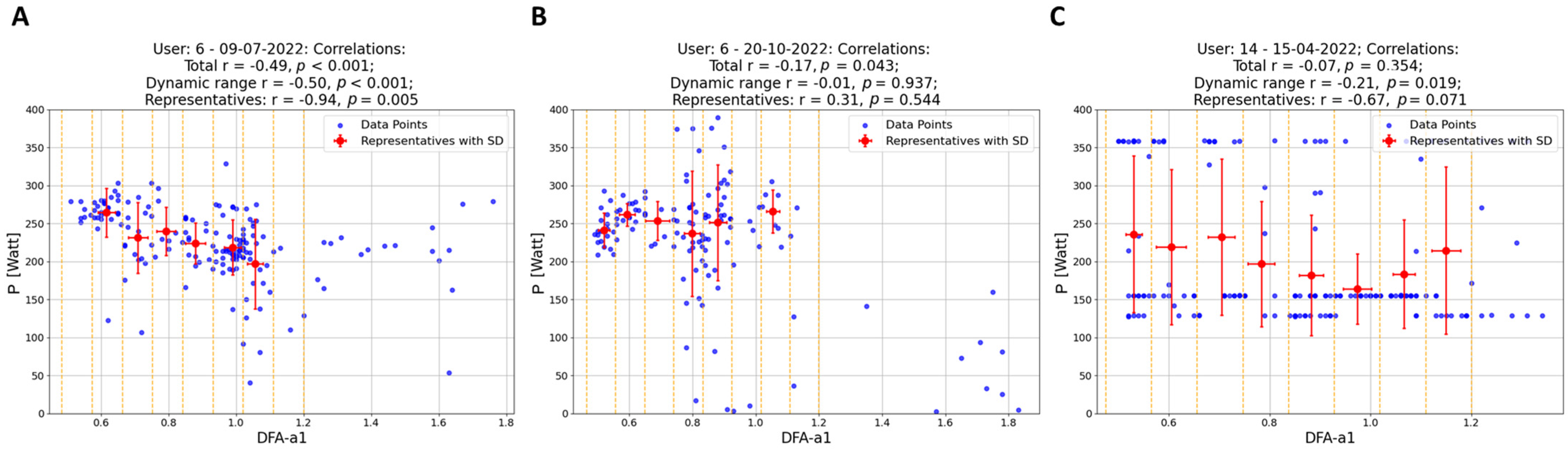
- Data Segmentation: In this study, data points (depicted as blue and light blue data points in Figure 2 and Figure 3) were segmented into intervals based on DFA-a1 levels, delineated by yellow (and purple) dashed lines in these figures. The segmentation methodology varied depending on the dataset. For individual workouts, due to a high sparseness of data points outside the dynamic range (DFA-a1 > 1.0), the data were divided into eight equal-length intervals within the range [a1min, a1*], where a1min represents the minimum DFA-a1 value and a1* is the lesser of DFA-a1 = 1.2 and the maximum DFA-a1 value. For workout groups, two distinct regions were defined: within the dynamic range [a1min, 1.0], data points were segmented into nine equal-length intervals, and in the range [1.0, a1*] (a1* being the lesser of DFA-a1 = 1.8 and the maximum DFA-a1 value), data were divided into five equal-length intervals.
- Representative Points: Within each interval, a representative point was established by averaging both power and DFA-a1 (Pavg, DFA-a1avg) for that interval. These representative points are indicated as red data points in Figure 2 and as red and purple data points in Figure 3. For individual workouts, a representative point is calculated only if the interval contains at least eight data points, while for workout groups, the minimum threshold was ten data points. This method enhances the reliability of the representative points, excluding those derived from an insufficient data quantity.
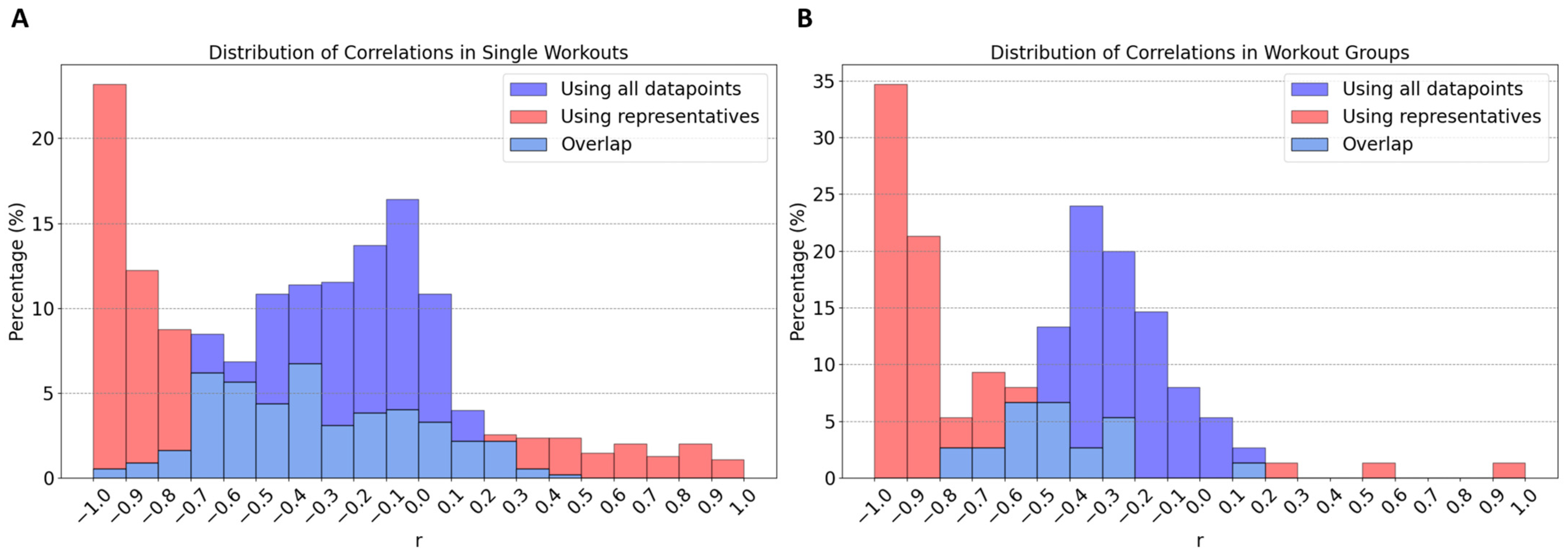
- Correlation of Representatives: Instead of correlating all individual data points, these representative points were correlated. Initially, correlations were computed for individual workouts using the representatives in Figure 2 (indicated as the last correlation value in each plot title). Subsequently, correlations for workout groups were calculated. In this case, two correlation coefficients were derived for each workout group: one using representatives within the dynamic range (red data points) and another incorporating all representatives, if feasible (including both red and purple data points). These two sets of correlation coefficients are presented as the final two values in the plot titles in Figure 3.
2.4. Statistics
3. Results
4. Discussion
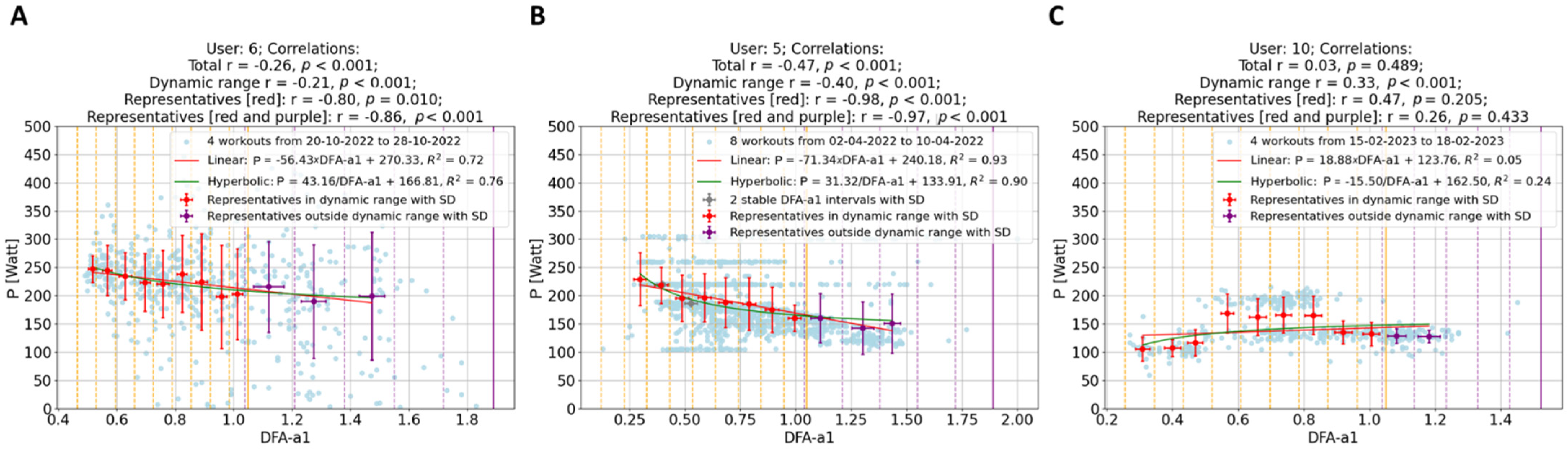
- Reduced Impact of Workout Types: Merging different types of workouts, as seen in the second group (B) in Figure 3, minimizes the influence of workout variety. This results in more generalizable insights.
- Enhanced Significance of Data Points: In the workout groups, data points are more densely packed, making the representatives much more meaningful than in isolated workouts. For example, representatives outside the dynamic range display a clearer behavior, aligning with the expectation that lower power corresponds with lower effort. This phenomenon is evident in Figure 3’s first workout group (A), where workouts with weaker individual correlations (as B in Figure 2) contribute to groups with significantly stronger correlations.
- Identification of Potential Non-Responders: The approach facilitates the detection of non-responders—specified as athletes whose workouts consistently show very weak correlations across almost all their workout groups. In the present analysis of 11 athletes, data revealed no non-responders.
- Modeling: Collecting data over several days allows for a meaningful investigation of the short-term relationship between power and DFA-a1. As demonstrated in Figure 3, it was tested with two types of two-parameter functions for each workout group, linear regression and hyperbolic fit, since a single parameter hyperbolic fit did not fit the data sufficiently well. As detailed in Figure 4, neither model showed a remarkable preference, leading to an analysis of the simpler linear model for its straightforwardness: P = m × DFA-a1 + q.
5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meyer, T.; Lucía, A.; Earnest, C.P.; Kindermann, W. A Conceptual Framework for Performance Diagnosis and Training Prescription from Submaximal Gas Exchange Parameters—Theory and Application. Int. J. Sports Med. 2005, 26 (Suppl. 1), S38–S48. [Google Scholar] [CrossRef] [PubMed]
- Faude, O.; Kindermann, W.; Meyer, T. Lactate threshold concepts: How valid are they? Sports Med. 2009, 39, 469–490. [Google Scholar] [CrossRef]
- Beneke, R.; Leithäuser, R.M.; Ochentel, O. Blood Lactate Diagnostics in Exercise Testing and Training. Int. J. Sports Physiol. Perform. 2011, 6, 8–24. [Google Scholar] [CrossRef]
- Michael, S.; Graham, K.S.; Davis, G.M. Cardiac Autonomic Responses during Exercise and Post-exercise Recovery Using Heart Rate Variability and Systolic Time Intervals—A Review. Front. Physiol. 2017, 8, 301. [Google Scholar] [CrossRef]
- Jamnick, N.A.; Pettitt, R.W.; Granata, C.; Pyne, D.B.; Bishop, D.J. An Examination and Critique of Current Methods to Determine Exercise Intensity. Sports Med. 2020, 50, 1729–1756. [Google Scholar] [CrossRef] [PubMed]
- Poole, D.C.; Rossiter, H.B.; Brooks, G.A.; Gladden, L.B. The anaerobic threshold: 50+ years of controversy. J. Physiol. 2021, 599, 737–767. [Google Scholar] [CrossRef]
- Kaufmann, S.; Gronwald, T.; Herold, F.; Hoos, O. Heart Rate Variability-Derived Thresholds for Exercise Intensity Prescription in Endurance Sports: A Systematic Review of Interrelations and Agreement with Different Ventilatory and Blood Lactate Thresholds. Sports Med. Open 2023, 9, 59. [Google Scholar] [CrossRef] [PubMed]
- Seiler, S.; Haugen, O.; Kuffel, E. Autonomic Recovery after Exercise in Trained Athletes: Intensity and duration effects. Med. Sci. Sports Exerc. 2007, 39, 1366–1373. [Google Scholar] [CrossRef]
- Stanley, J.; Peake, J.M.; Buchheit, M. Cardiac Parasympathetic Reactivation Following Exercise: Implications for Training Prescription. Sports Med. 2013, 43, 1259–1277. [Google Scholar] [CrossRef]
- Van Wijck, K.; Lenaerts, K.; Grootjans, J.; Wijnands, K.A.P.; Poeze, M.; van Loon, L.J.C.; Dejong, C.H.C.; Buurman, W.A. Physiology and pathophysiology of splanchnic hypoperfusion and intestinal injury during exercise: Strategies for evaluation and prevention. Am. J. Physiol. Liver Physiol. 2012, 303, G155–G168. [Google Scholar] [CrossRef]
- Noakes, T.D.; Gibson, A.S.C.; Lambert, E.V. From catastrophe to complexity: A novel model of integrative central neural regulation of effort and fatigue during exercise in humans: Summary and conclusions. Br. J. Sports Med. 2005, 39, 120–124. [Google Scholar] [CrossRef] [PubMed]
- Venhorst, A.; Micklewright, D.; Noakes, T.D. Towards a three-dimensional framework of centrally regulated and goal-directed exercise behaviour: A narrative review. Br. J. Sports Med. 2018, 52, 957–966. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.-K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of Scaling Exponents and Crossover Phenomena in Nonstationary Heartbeat Time Series. CHAOS 1995, 5, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Heneghan, C.; McDarby, G. Establishing the relation between detrended fluctuation analysis and power spectral density analysis for stochastic processes. Phys. Rev. E 2000, 62, 6103–6110. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Ivanov, P.C.; Chen, Z.; Carpena, P.; Stanley, H.E. Effect of trends on detrended fluctuation analysis. Phys. Rev. E 2001, 64 Pt 1, 011114. [Google Scholar] [CrossRef] [PubMed]
- Hautala, A.J.; Mäkikallio, T.H.; Seppänen, T.; Huikuri, H.V.; Tulppo, M.P. Short-term correlation properties of R–R interval dynamics at different exercise intensity levels. Clin. Physiol. Funct. Imaging 2003, 23, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Casties, J.-F.; Mottet, D.; Le Gallais, D. Non-Linear Analyses of Heart Rate Variability During Heavy Exercise and Recovery in Cyclists. Int. J. Sports Med. 2006, 27, 780–785. [Google Scholar] [CrossRef] [PubMed]
- Platisa, M.M.; Gal, V. Correlation properties of heartbeat dynamics. Eur. Biophys. J. 2008, 37, 1247–1252. [Google Scholar] [CrossRef]
- Platisa, M.M.; Mazic, S.; Nestorovic, Z.; Gal, V. Complexity of heartbeat interval series in young healthy trained and untrained men. Physiol. Meas. 2008, 29, 439–450. [Google Scholar] [CrossRef]
- Iannetta, D.; de Almeida Azevedo, R.; Keir, D.A.; Murias, J.M. Establishing the VO2 versus constant-work-rate rela-tionship from ramp-incremental exercise: Simple strategies for an unsolved problem. J. Appl. Physiol. 2019, 127, 1519–1527. [Google Scholar] [CrossRef] [PubMed]
- Gronwald, T.; Rogers, B.; Hoos, O. Fractal Correlation Properties of Heart Rate Variability: A New Biomarker for Intensity Distribution in Endurance Exercise and Training Prescription? Front. Physiol. 2020, 11, 550572. [Google Scholar] [CrossRef] [PubMed]
- Mateo-March, M.; Moya-Ramón, M.; Javaloyes, A.; Sánchez-Muñoz, C.; Clemente-Suárez, V.J. Validity of detrended fluctuation analysis of heart rate variability to determine intensity thresholds in elite cyclists. Eur. J. Sport Sci. 2022, 23, 580–587. [Google Scholar] [CrossRef] [PubMed]
- Rogers, B.; Gronwald, T. Fractal Correlation Properties of Heart Rate Variability as a Biomarker for Intensity Distribution and Training Prescription in Endurance Exercise: An Update. Front. Physiol. 2022, 13, 879071. [Google Scholar] [CrossRef] [PubMed]
- Yates, F. Order and complexity in dynamical systems: Homeodynamics as a generalized mechanics for biology. Math. Comput. Model. 1994, 19, 49–74. [Google Scholar] [CrossRef]
- Yates, F.E. Homeokinetics/Homeodynamics: A Physical Heuristic for Life and Complexity. Ecol. Psychol. 2008, 20, 148–179. [Google Scholar] [CrossRef]
- Kauffman, S.A. At Home in the Universe: The Search for Laws of Self-Organization and Complexity; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Lloyd, D.; Aon, M.A.; Cortassa, S. Why homeodynamics, not homeostasis? Sci. World J. 2001, 1, 133–145. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.N.; Hausdorff, J.M.; Ivanov, P.C.; Peng, C.-K.; Stanley, H.E. Fractal dynamics in physiology: Alterations with disease and aging. Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. 1), 2466–2472. [Google Scholar] [CrossRef] [PubMed]
- De Godoy, M.F. Nonlinear analysis of heart rate variability: A comprehensive review. J. Cardiol. Ther. 2016, 3, 528–533. [Google Scholar] [CrossRef]
- Peltola, M.A. Role of editing of R–R intervals in the analysis of heart rate variability. Front. Physiol. 2012, 3, 148. [Google Scholar] [CrossRef]
- Tarvainen, M.P.; Niskanen, J.-P.; Lipponen, J.A.; Ranta-Aho, P.O.; Karjalainen, P.A. Kubios HRV—Heart rate variability analysis software. Comput. Methods Progr. Biomed. 2014, 113, 210–220. [Google Scholar] [CrossRef] [PubMed]
- Lipponen, J.A.; Tarvainen, M.P. A robust algorithm for heart rate variability time series artefact correction using novel beat classification. J. Med. Eng. Technol. 2019, 43, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Tarvainen, M.P.; Ranta-aho, P.O.; Karjalainen, P.A. An advanced detrending method with application to HRV analysis. IEEE Trans. Biomed. Eng. 2002, 49, 172–175. [Google Scholar] [CrossRef] [PubMed]
- Chan, Y.H. Biostatistics 104: Correlational analysis. Singap. Med. J. 2003, 44, 614–619. [Google Scholar]
- Gronwald, T.; Rogers, B.; Hottenrott, L.; Hoos, O.; Hottenrott, K. Correlation Properties of Heart Rate Variability during a Marathon Race in Recreational Runners: Potential Biomarker of Complex Regulation during Endurance Exercise. J. Sports Sci. Med. 2021, 20, 557–563. [Google Scholar] [CrossRef] [PubMed]
- Rogers, B.; Mourot, L.; Doucende, G.; Gronwald, T. Fractal correlation properties of heart rate variability as a biomarker of endurance exercise fatigue in ultramarathon runners. Physiol. Rep. 2021, 9, e14956. [Google Scholar] [CrossRef] [PubMed]
- Van Hooren, B.; Mennen, B.; Gronwald, T.; Bongers, B.C.; Rogers, B. Correlation properties of heart rate variability to assess the first ventilatory threshold and fatigue in runners. J. Sports Sci. 2023, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Schaffarczyk, M.; Rogers, B.; Reer, R.; Gronwald, T. Fractal correlation properties of HRV as a noninvasive biomarker to assess the physiological status of triathletes during simulated warm-up sessions at low exercise intensity: A pilot study. BMC Sports Sci. Med. Rehabil. 2022, 14, 203. [Google Scholar] [CrossRef]
- Van Hooren, B.; Bongers, B.C.; Rogers, B.; Gronwald, T. The Between-Day Reliability of Correlation Properties of Heart Rate Variability During Running. Appl. Psychophysiol. Biofeedback 2023, 48, 453–460. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andriolo, S.; Rummel, M.; Gronwald, T. Relationship of Cycling Power and Non-Linear Heart Rate Variability from Everyday Workout Data: Potential for Intensity Zone Estimation and Monitoring. Sensors 2024, 24, 4468. https://doi.org/10.3390/s24144468
Andriolo S, Rummel M, Gronwald T. Relationship of Cycling Power and Non-Linear Heart Rate Variability from Everyday Workout Data: Potential for Intensity Zone Estimation and Monitoring. Sensors. 2024; 24(14):4468. https://doi.org/10.3390/s24144468
Chicago/Turabian StyleAndriolo, Stefano, Markus Rummel, and Thomas Gronwald. 2024. "Relationship of Cycling Power and Non-Linear Heart Rate Variability from Everyday Workout Data: Potential for Intensity Zone Estimation and Monitoring" Sensors 24, no. 14: 4468. https://doi.org/10.3390/s24144468
APA StyleAndriolo, S., Rummel, M., & Gronwald, T. (2024). Relationship of Cycling Power and Non-Linear Heart Rate Variability from Everyday Workout Data: Potential for Intensity Zone Estimation and Monitoring. Sensors, 24(14), 4468. https://doi.org/10.3390/s24144468






