A Health Monitoring Model for Circulation Water Pumps in a Nuclear Power Plant Based on Graph Neural Network Observer
Abstract
:1. Introduction
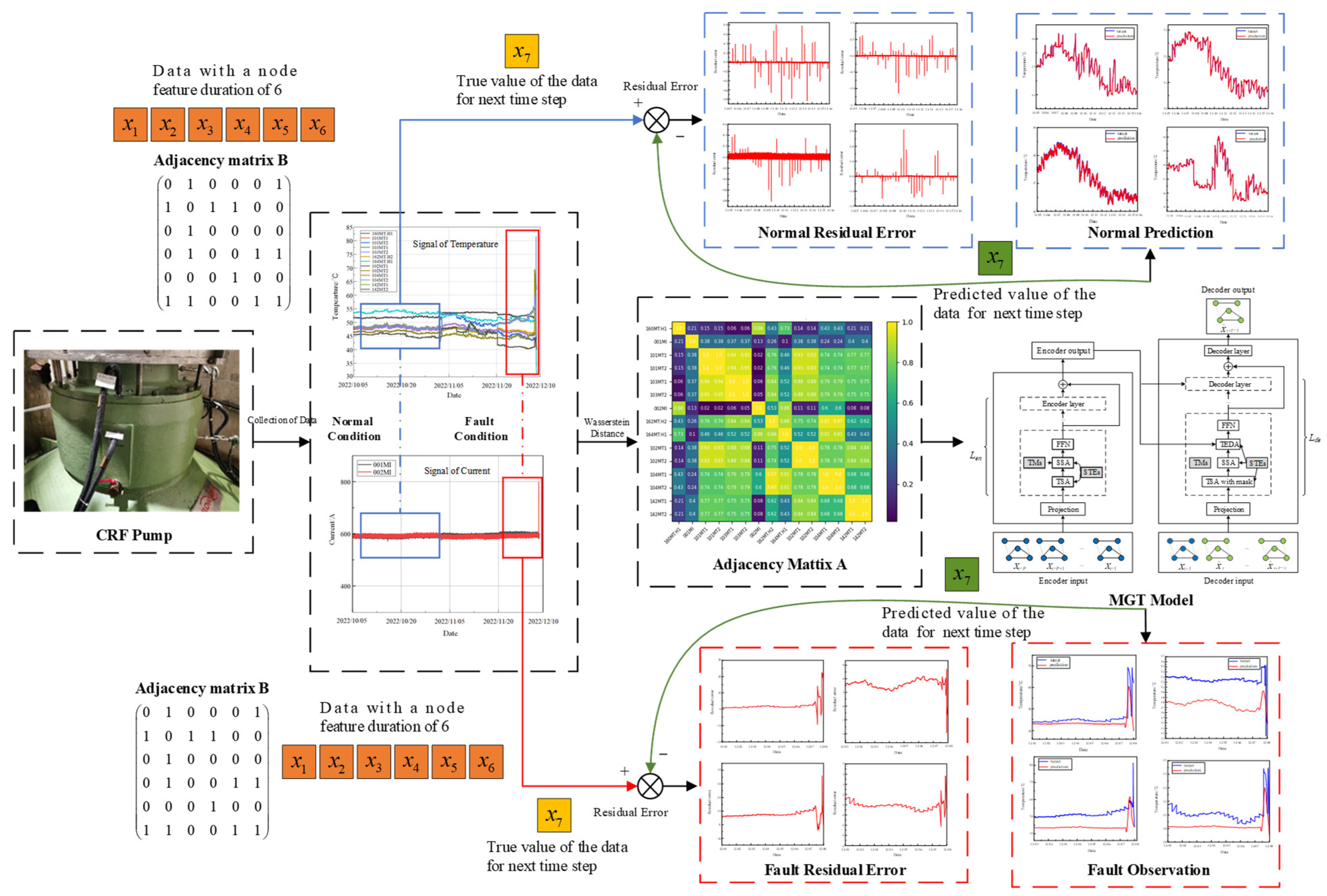
- The concept of graph self-learning is introduced, utilizing a graph self-learning layer to adaptively extract relationships between the multivariate monitoring data of the CRF pump. This approach ensures that the graph neural network is no longer influenced by the diversity of predefined graph structures when predicting the node characteristics within the graph structure.
- The graph structure can be continuously updated during the training process, enabling the system to better handle multiple working conditions and monitor the variable changes in the CRF pumps in nuclear plants over time.
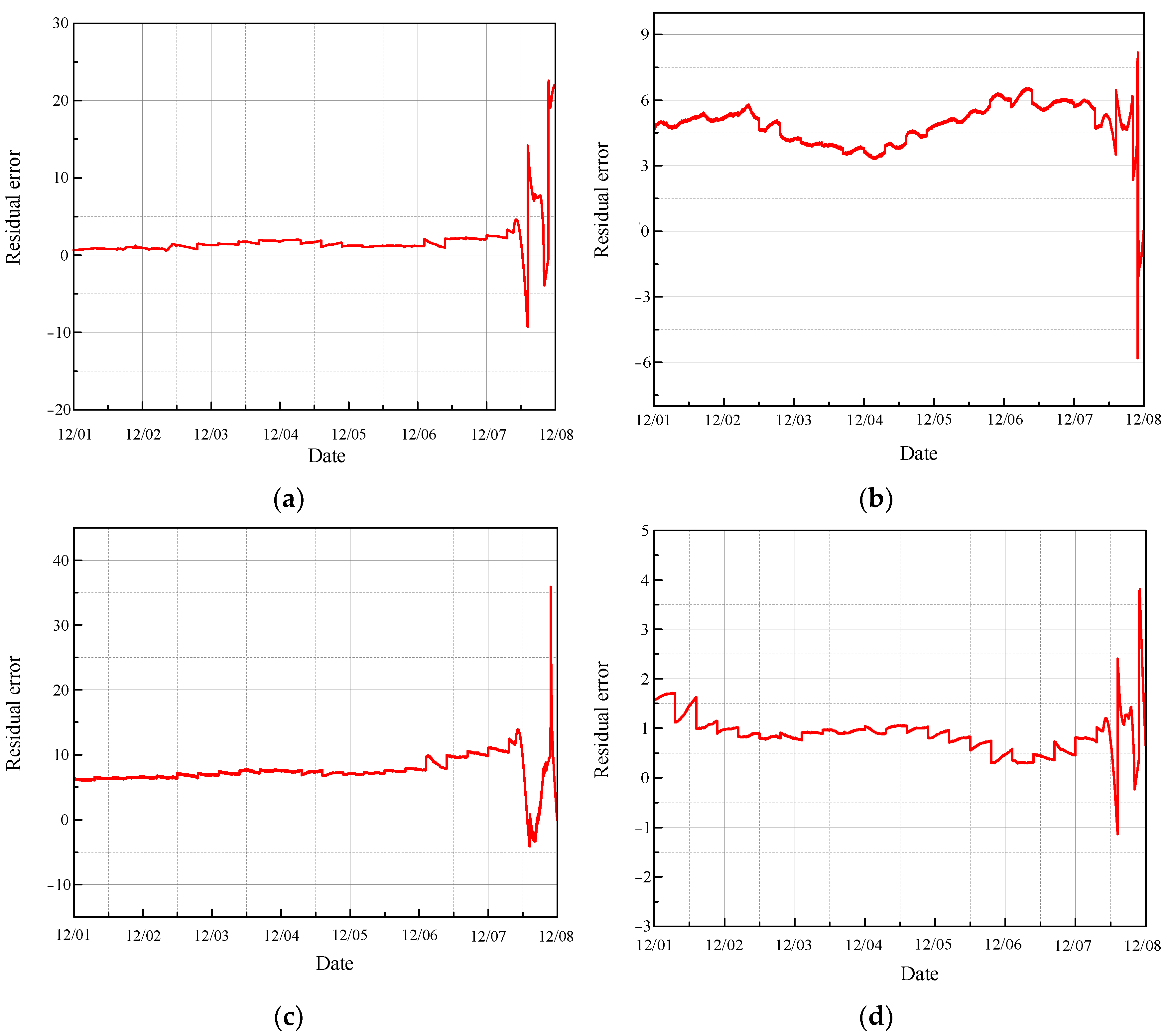
- Combined with the graph self-learning neural network model MGT, a fault observation system for CRF pumps is constructed. By training on normal data to predict conditions during the fault observation phase, the deviations of the actual values from the predicted values within a certain range indicate potential issues that require attention. This system can monitor the fault conditions of CRF pumps and provide early warnings.
2. Methodology
2.1. Quantitative Analysis of Wasserstein Distance
2.2. Meta Graph Transformer
2.2.1. Embedding of Spatial–Temporal
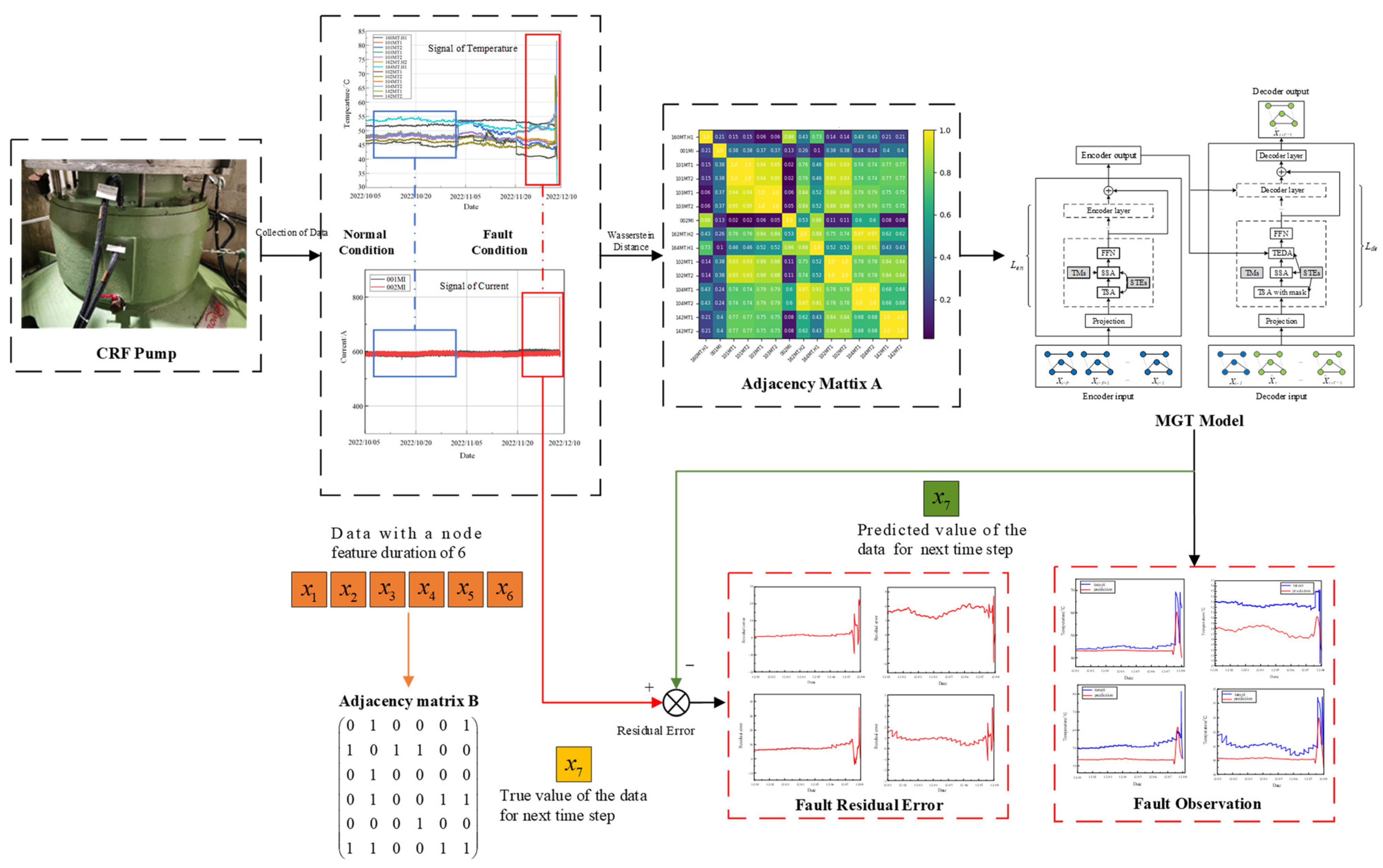
2.2.2. Construction of Adjacency Matrix
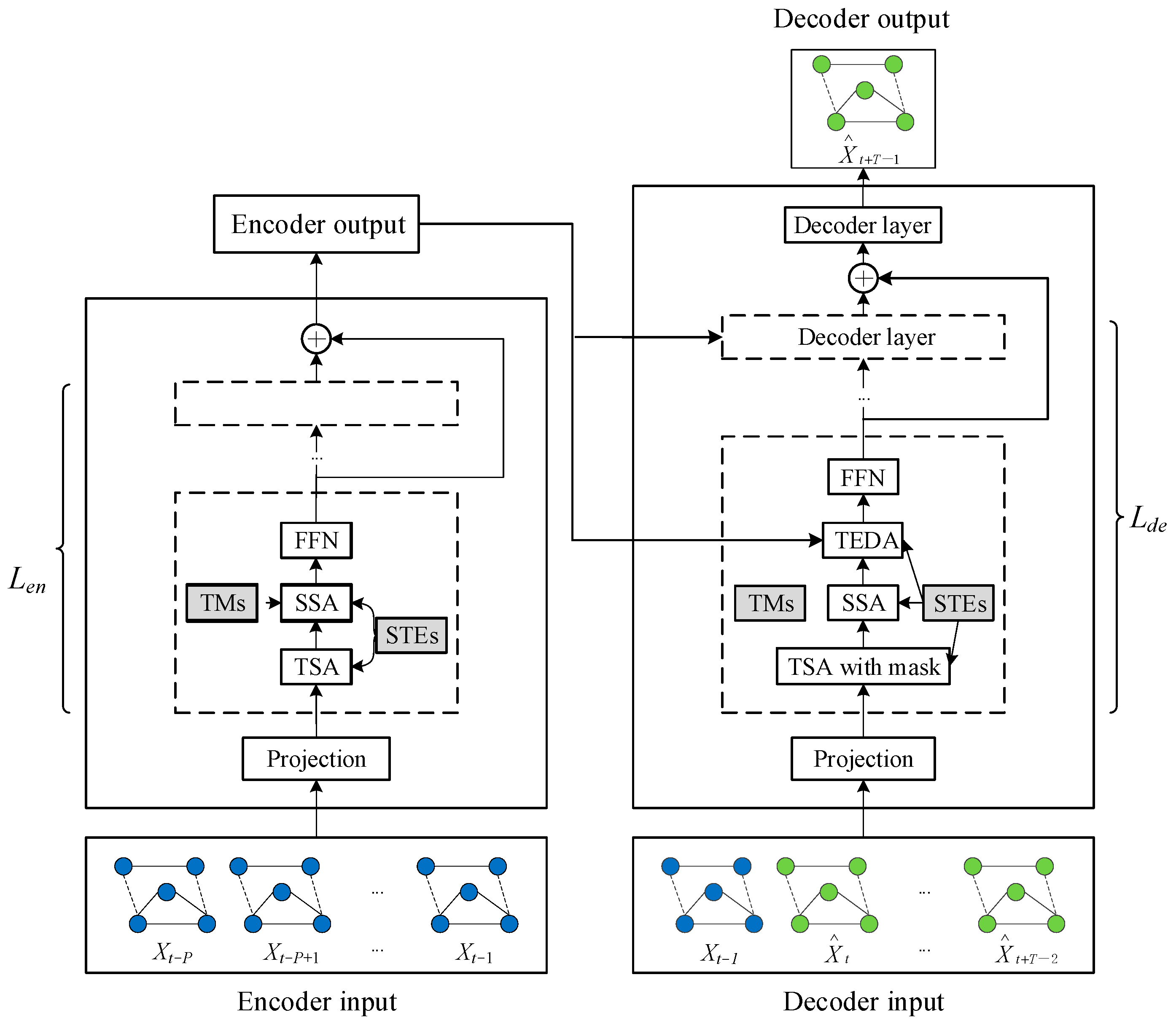
2.2.3. Encoder
2.2.4. Decoder
2.3. MGT Fault Observer
3. Experimental Results and Analysis
3.1. Experimental Setup
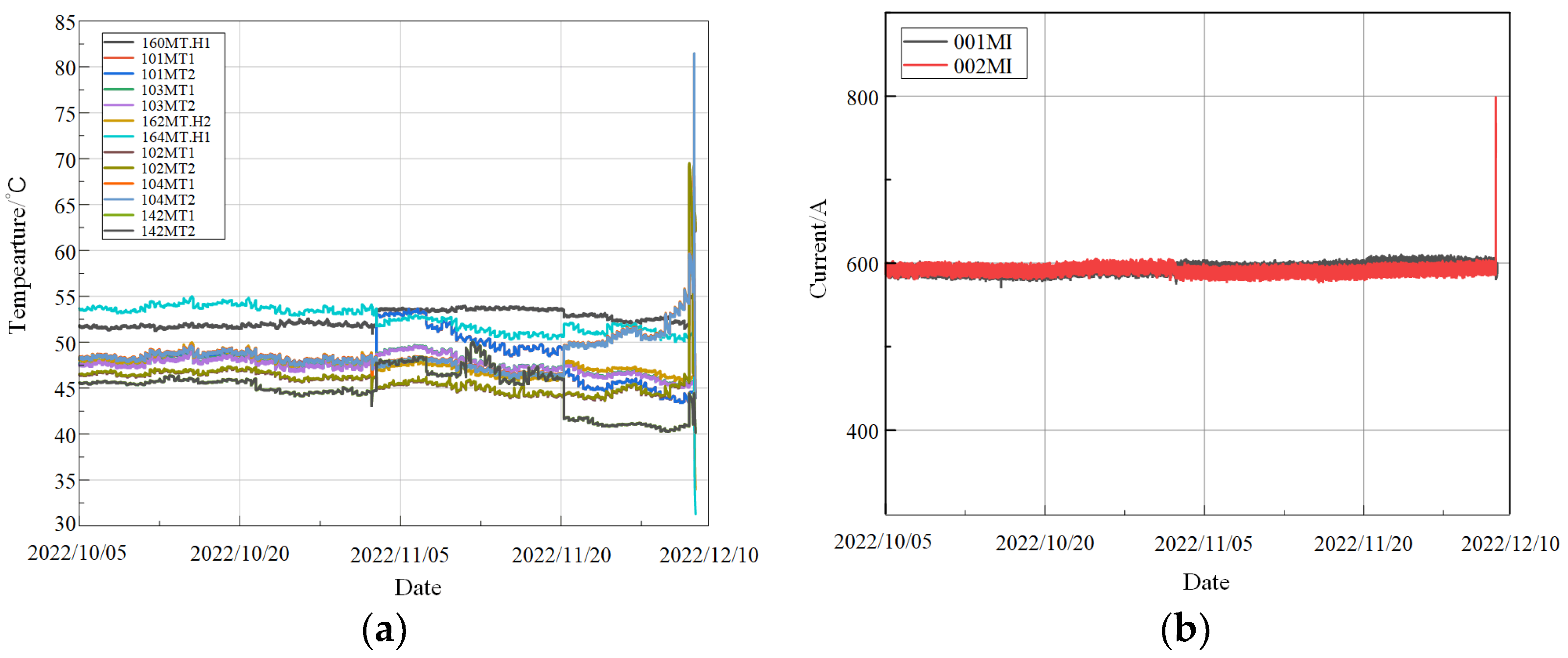
3.1.1. Datasets
3.1.2. MGT Parameter Settings
3.1.3. Evaluation Metrics Settings
3.2. Evaluation of the Proposed Health Monitoring Model
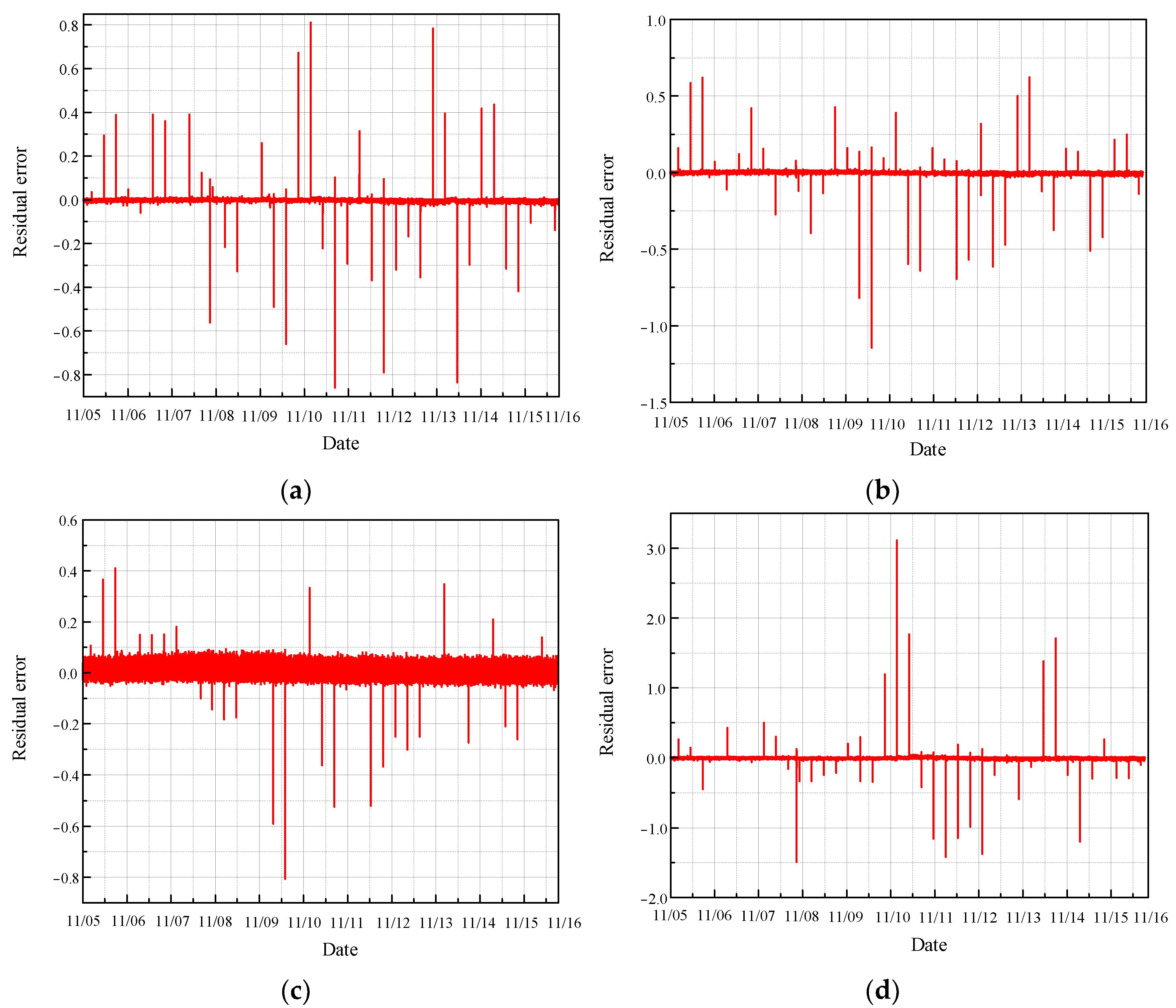
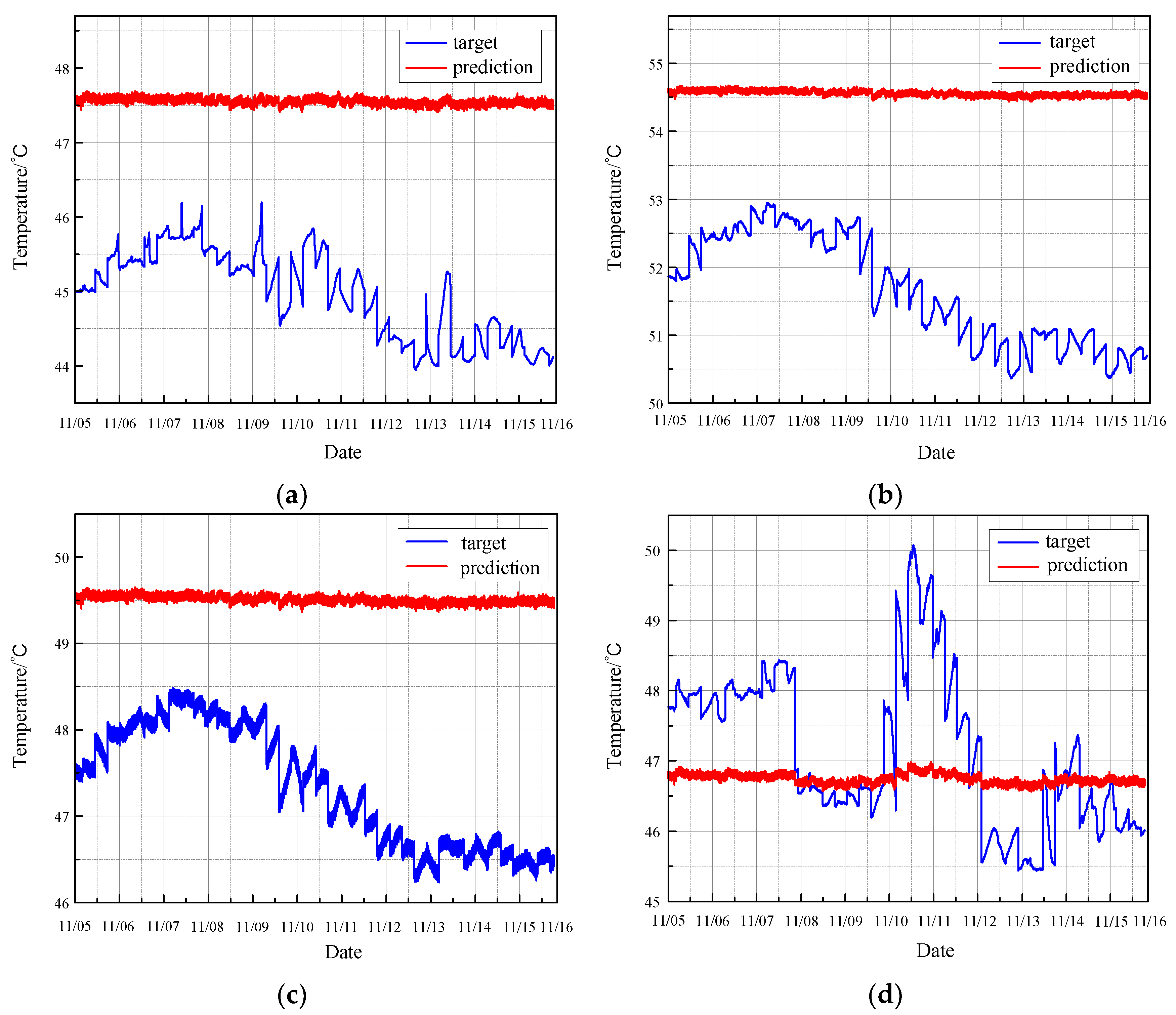
3.2.1. Prediction of Normal Condition
3.2.2. Contrast of Other Methods
- (1)
- Long short-term memory network
- (2)
- Convolutional neural network
- (3)
- Deep AR
- (4)
- Temporal convolutional network
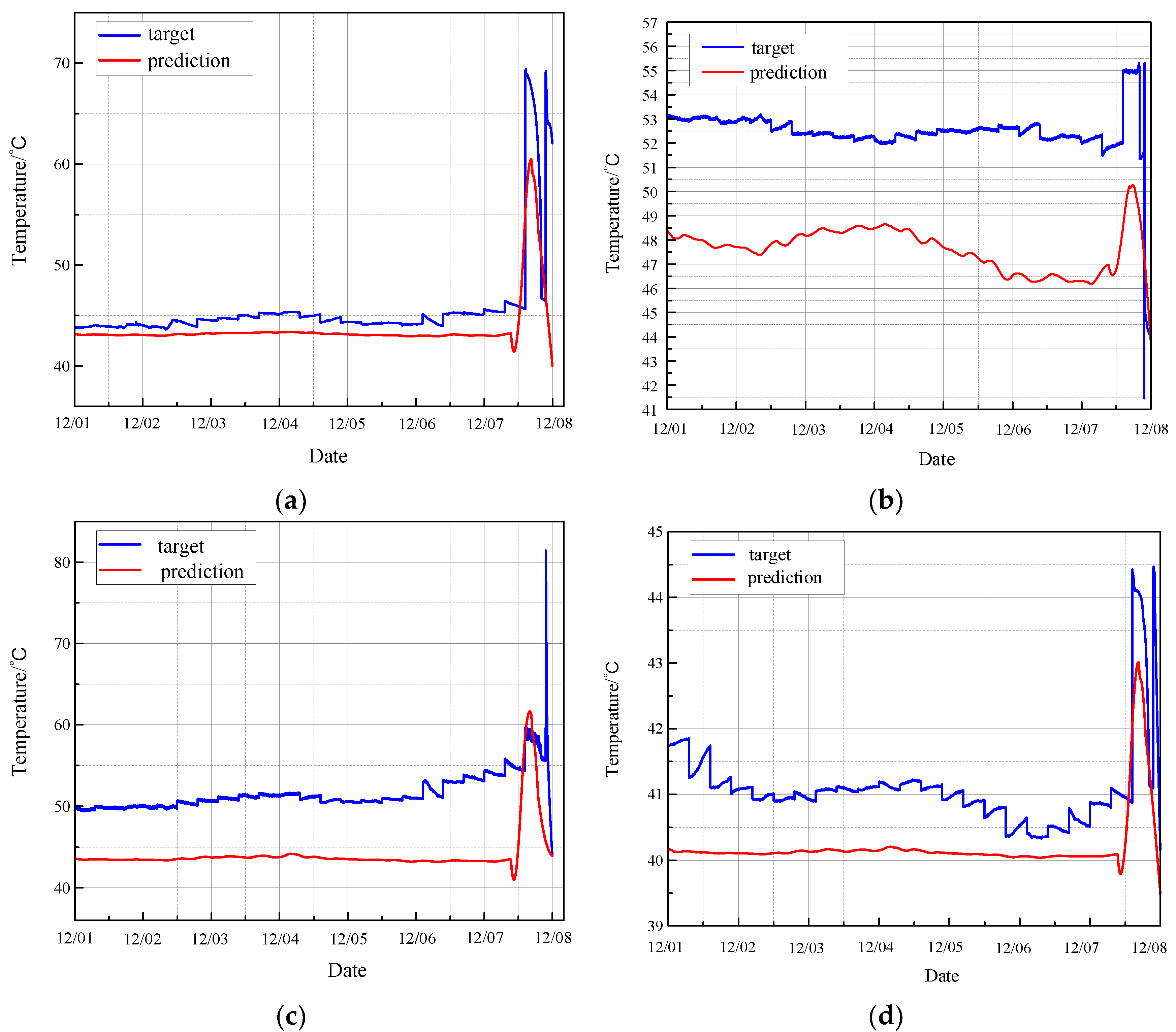
3.2.3. Construction of MGT Observer
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, L.; Liu, D.; Zhou, L.; Wang, F.; Wang, P. Optimal number of circulating water pumps in a nuclear power plant. Nucl. Eng. 2015, 43, 35–41. [Google Scholar] [CrossRef]
- Cheng, W.; Liu, X.; Xing, J.; Chen, X.; Ding, B.; Zhang, R.; Zhou, K.; Huang, Q. AFARN: Domain adaptation for intelligent cross-domain bearing fault diagnosis in nuclear circulating water pump. IEEE Trans. Ind. Inform. 2022, 18, 3229–3239. [Google Scholar] [CrossRef]
- Liu, Z.; Li, M.; Zhu, Z.; Xiao, L.; Nie, C.; Tang, Z. Health State Identification Method of Nuclear Power Main Circulating Pump Based on EEMD and OQGA-SVM. Electronics 2023, 12, 410. [Google Scholar] [CrossRef]
- Hu, G.; Zhou, T.T.; Liu, Q.F. Data-Driven Machine Learning for Fault Detection and Diagnosis in Nuclear Power Plants: A Review. Front. Energy Res. 2023, 9, 135–149. [Google Scholar] [CrossRef]
- Qi, B.; Liang, J.; Tong, J. Fault Diagnosis Techniques for Nuclear Power Plants: A Review from the Artificial Intelligence Perspective. Energies 2023, 16, 1850. [Google Scholar] [CrossRef]
- Agarwal, V.; Neal, K.D.; Mahadevan, S.; Adams, D. Concrete Structural Health Monitoring in Nuclear Power Plants; Idaho National Lab. (INL): Idaho Falls, ID, USA, 2017; Volume 47, pp. 22–35. [Google Scholar]
- Zhao, X.G.; Kim, J.; Warns, K.; Wang, X.Y.; Ramuhalli, P.; Cetiner, S.; Kang, H.G.; Golay, M. Prognostics and Health Management in Nuclear Power Plants: An Updated Method-Centric Review With Special Focus on Data-Driven Methods. OSTI 2023, 56, 123–140. [Google Scholar] [CrossRef]
- Yu, Y.; Peng, M.; Wang, H.; Liu, Y.; Ma, Z.; Cheng, S. Long-term operation monitoring strategy for nuclear power plants based on condition monitoring technologies. ScienceDirect 2023, 78, 341–355. [Google Scholar]
- Mohanty, J.K.; Dash, P.R.; Pradhan, P.K. FMECA analysis and condition monitoring of critical equipment in nuclear power plants. IEEE Trans. Energy Convers. 2023, 13, 45–62. [Google Scholar]
- Hashemian, H.M. On-line monitoring applications in nuclear power plants. ScienceDirect 2023, 45, 229–243. [Google Scholar] [CrossRef]
- Wu, G.; Yuan, D.P.; Yin, J.Y.; Xiao, Y.Q.; Ji, D.X. A Framework for Monitoring and Fault Diagnosis in Nuclear Power Plants Based on Signed Directed Graph Methods. Frontiers 2023, 11, 102–117. [Google Scholar]
- Dong, Z.; Cheng, Z.H.; Zhu, Y.L.; Huang, X.J.; Dong, Y.J.; Zhang, Z.Y. Review on the Recent Progress in Nuclear Plant Dynamical Modeling and Control. Energies 2023, 17, 1443. [Google Scholar] [CrossRef]
- Kot, P.; Muradov, M.; Gkantou, M.; Kamaris, G.S.; Hashim, K.; Yeboah, D. Recent Advancements in Non-Destructive Testing Techniques for Structural Health Monitoring. Appl. Sci. 2021, 11, 2750. [Google Scholar] [CrossRef]
- Yao, Y.T.; Ge, D.C.; Yu, J.; Xie, M. Model-Based Deep Transfer Learning Method to Fault Detection and Diagnosis in Nuclear Power Plants. Frontiers 2023, 10, 789–804. [Google Scholar] [CrossRef]
- Qian, G.S.; Liu, J.Q. A comparative study of deep learning-based fault diagnosis methods for nuclear power plants. ScienceDirect 2023, 67, 1021–1038. [Google Scholar] [CrossRef]
- Dalloul, A.H.; Miramirkhani, F.; Kouhalvandi, L. A Review of Recent Innovations in Remote Health Monitoring for Nuclear Power Plants. Micromachines 2023, 14, 2157. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.S.; Xiong, X.; He, J.; Huang, Y.Y.; Yang, S.X. Fault feature extraction for planetary bearing of CRF pump in nuclear power plant based on TFDC-QPSO-optimised MOMEDA. Meas. Sci. Technol. 2023, 34, 102–120. [Google Scholar] [CrossRef]
- Liu, S.; Xiong, X.; Huang, Y.Y.; Chang, Z.K.; He, J.; Yang, S.X. Health state identification of circulating seawater pump-unit in nuclear power plant based on multi-virtual vibration source fusion in the presence of strong data imbalance. ScienceDirect 2024, 197, 1–20. [Google Scholar] [CrossRef]
- Amin, M.T.; Yao, Y.T.; Yu, J.; Adumene, S. Probabilistic monitoring of nuclear plants using R-vine copula. ScienceDirect 2023, 190, 1–11. [Google Scholar] [CrossRef]
- Wang, R.H.; Chen, H.; Guan, C. A Bayesian inference-based approach for performance prognostics towards uncertainty quantification and its applications on the marine diesel engine. ISA Trans. 2021, 118, 159–173. [Google Scholar] [CrossRef] [PubMed]
- Cheng, W.; Xie, S.S.; Xing, J.; Nie, Z.L.; Chen, X.F.; Liu, Y.L.; Liu, X.; Huang, Q.; Zhang, R.Y. Interactive hybrid model for remaining useful life prediction with uncertainty quantification of bearing in nuclear circulating water pump. IEEE Trans. Ind. Inform. 2023, 19, 541–559. [Google Scholar] [CrossRef]
- Guo, J.Y.; Wang, Z.Y.; Li, H.; Yang, Y.L.; Huang, C.G.; Yazdi, M.; Kang, H.S. A Hybrid Prognosis Scheme for Rolling Bearings Based on a Novel Health Indicator and Nonlinear Wiener Process. Reliab. Eng. Syst. Saf. 2024, 245, 110014. [Google Scholar] [CrossRef]
- He, C.; Ge, D.C.; Yang, M.; Yong, N.; Wang, J.Y.; Yu, J. A data-driven adaptive fault diagnosis methodology for nuclear power systems based on NSGAII-CNN. Ann. Nucl. Energy 2021, 159, 108326. [Google Scholar] [CrossRef]
- Wang, F.; Xiahou, T.; Zhang, X.; He, P.; Yang, T.; Niu, J.; Liu, C.; Liu, Y. Convolutional Preprocessing Transformer-Based Fault Diagnosis for Rectifier-Filter Circuits in Nuclear Power Plants. Reliab. Eng. Syst. Saf. 2024, 249, 110198. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, S.; Zhao, K.; Li, Z.; Yang, Q.; Liu, Z. An Efficient Diagnostic Strategy for Intermittent Faults in Electronic Circuit Systems by Enhancing and Locating Local Features of Faults. IEEE Trans. Ind. Electron. 2021, 68, 1234–1245. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.; Wang, Z.; Hu, N. Ultrafast and Robust Structural Damage Identification Framework Enabled by an Optimized Extreme Learning Machine. Mech. Syst. Signal Process. 2022, 163, 108115. [Google Scholar] [CrossRef]
- Lee, J.; Li, J. An AI-Based Fault Diagnosis Framework for Rotating Machinery Using Deep Learning and Transfer Learning. J. Manuf. Process. 2023, 85, 100–110. [Google Scholar]
- Wang, X.; Zhang, J. Development of an Intelligent Monitoring System for Nuclear Power Plants Based on Multi-Sensor Data Integration. Energies 2023, 16, 2245. [Google Scholar]
- He, Q.; Chen, S.; Wang, Y.; Li, J. Artificial Intelligence Application in Machine Condition Monitoring and Fault Diagnosis. Appl. Sci. 2023, 13, 10243. [Google Scholar]
- Li, X.L.; Xie, L.F.; Deng, B.; Lu, H.H.; Zhu, Y.Y.; Yin, M.; Yin, G.F.; Gao, W.X. Deep Dynamic High-Order Graph Convolutional Network for Wear Fault Diagnosis of Hydrodynamic Mechanical Seal. Reliab. Eng. Syst. Saf. 2024, 247, 1726–1753. [Google Scholar] [CrossRef]
- Wang, H.T.; Dai, X.Y.; Shi, L.C.; Li, M.J.; Liu, Z.L.; Wang, R.H.; Xia, X.H. Data-Augmentation Based CBAM-ResNet-GCN Method for Unbalance Fault Diagnosis of Rotating Machinery. IEEE Access 2024, 12, 547–561. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y. A Novel Multi-Sensor Data Fusion Technique for Fault Detection in Mechanical Systems. Measurement 2022, 178, 109317. [Google Scholar]
- Yu, Y.-C.; Yang, S.-R.; Chuang, S.-W.; Chien, J.-T.; Lee, C.-Y. Pruning Quantized Unsupervised Meta-Learning Degrading Net Solution for Industrial Equipment and Semiconductor Process Anomaly Detection and Prediction. Appl. Sci. 2024, 14, 1708. [Google Scholar] [CrossRef]
- Plaza, E.G.; López, P.J.N.; González, E.M.B. Multi-Sensor Data Fusion for Real-Time Surface Quality Control in Automated Machining Systems. Sensors. 2019, 19, 1566. [Google Scholar]
- Jing, L.; Wang, T.; Zhao, M.; Wang, P. An Adaptive Multi-Sensor Data Fusion Method Based on Deep Convolutional Neural Networks for Fault Diagnosis of Planetary Gearbox. Sensors 2019, 19, 5678. [Google Scholar] [CrossRef]
- Yin, W.; Xia, H.; Wang, Z.; Yang, B.; Zhang, J.; Jiang, Y.; Miyombo, M.E. A fault diagnosis of nuclear power plant rotating machinery based on multi-sensor data fusion. Ann. Nucl. Energy 2020, 123, 45–58. [Google Scholar]
- Wang, M.; Wang, X.; Yang, L.T.; Deng, X.; Yi, L. Multi-sensor fusion based intelligent sensor relocation for health and safety monitoring in BSNs. Inf. Fusion 2020, 54, 61–71. [Google Scholar] [CrossRef]
- Rahman, M.; Ong, Z.C.; Chong, W.T.; Julai, S.; Khoo, S.Y. A Real-time Multi-Sensor Data Fusion System for the Condition Monitoring of Wind Turbines. Renew. Energy 2020, 51, 43–54. [Google Scholar]
- Wang, H.; Sun, W.; He, L.; Zhou, J. Health Monitoring of Nuclear Power Plant Equipment Using Multi-Sensor Data Fusion and Machine Learning. Appl. Sci. 2021, 11, 1234. [Google Scholar]
- Jia, X.; Zheng, H.; Wang, Q.; Yang, T.; Chen, X.; Zhao, Y. Advanced Data Fusion Techniques for Predictive Maintenance in Nuclear Power Plants. J. Nucl. Sci. Technol. 2023, 60, 123–140. [Google Scholar]
- Wang, L.; Chen, H. Meta Graph Transformer for Traffic Flow Prediction. IEEE Trans. Intell. Transp. Syst. 2023, 23, 1245–1257. [Google Scholar]
- Zhang, J.; Li, X. Spatial-Temporal Meta-Graph Learning for Traffic Forecasting. IEEE Trans. Knowl. Data Eng. 2021, 33, 3517–3531. [Google Scholar]
- Liu, B.; Xu, X. Synchronous Spatiotemporal Graph Transformer for Traffic Flow Prediction. IEEE Access 2023, 11, 5634–5647. [Google Scholar]
- Sun, Y.; Zhou, Y. Transport-Hub-Aware Spatial-Temporal Adaptive Graph Transformer for Traffic Prediction. IEEE Trans. Big Data 2022, 8, 234–245. [Google Scholar]
- Zhang, Q.; Chang, W.; Li, C.; Yin, C.; Su, Y.; Xiao, P. Attention-based Spatial-Temporal Graph Transformer for Traffic Flow Prediction. Neural Comput. Appl. 2023, 35, 21827–21839. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, T. Dynamic Spatial-Temporal Graph Convolutional Network for Traffic Forecasting. Expert Syst. Appl. 2024, 240, 122381. [Google Scholar]
- Xu, D.; Ruan, C.; Korpeoglu, E.; Kumar, S.; Achan, K. Inductive Representation Learning on Temporal Graphs. Proc. ACM SIGKDD 2022, 28, 2704–2713. [Google Scholar]
- Hu, Z.; Dong, Y.; Wang, K.; Sun, Y. Heterogeneous Graph Transformer. Proc. ACM SIGKDD 2021, 27, 2704–2713. [Google Scholar]
- Wang, X.; Yu, Z.; Zhang, L. Metapath-guided Heterogeneous Graph Transformer for Social Network Analysis. IEEE Trans. Knowl. Data Eng. 2022, 34, 555–567. [Google Scholar]
- Liu, Q.; Hu, Q.; Lee, C. Hierarchical Graph Transformer with Adaptive Node Sampling for Social Network Analysis. Adv. Neural Inf. Process. Syst. 2022, 35, 21171–21183. [Google Scholar]
- Chen, X.; Zhang, H.; Hu, Y. Variational Non-Autoregressive Graph Transformer Network for Multi-Agent Trajectory Prediction. IEEE Trans. Veh. Technol. 2023, 72, 5634–5647. [Google Scholar] [CrossRef]
- Wang, H.; Li, C. Graph Transformer Networks: Learning Meta-path Graphs to Improve GNNs. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 1634–1645. [Google Scholar]
- Zhou, W.; Zhang, L.; Liu, J. GPDRP: A multimodal framework for drug response prediction with graph transformer. BMC Bioinform. 2023, 24, 541. [Google Scholar]
- Chen, Y.; Li, Y.; Wang, H. AMGDTI: Drug–target interaction prediction based on adaptive meta-graph transformer. Bioinformatics 2023, 39, 101–112. [Google Scholar]
- Wang, Z.; Chen, X. MGDTI: Graph Transformer with Meta-Learning for Drug-Target Interaction Prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 19, 3201–3212. [Google Scholar]
- Sun, J.; Liu, Q. Metapath-aggregated heterogeneous graph neural network for drug–target interaction prediction. Brief. Bioinform. 2022, 24, 211–223. [Google Scholar]
- Han, L.; Zhang, H. TranDTA: Prediction of Drug–Target Binding Affinity Using Transformer. Bioinformatics 2023, 39, btad410. [Google Scholar]
- Li, J.; Wang, S. Hierarchical graph transformer with contrastive learning for protein-protein interaction prediction. Bioinformatics 2022, 38, 234–245. [Google Scholar]
- Zhang, L.; Chen, H. MMGPL: Multimodal Medical Data Analysis with Graph Prompt Learning. BMC Bioinform. 2023, 24, 541. [Google Scholar]
- Sun, Y.; Liu, Q. Meta-HGT: Metapath-aware HyperGraph Transformer for heterogeneous medical data. IEEE Trans. Med. Imaging 2022, 41, 2345–2358. [Google Scholar]
- Wang, X.; Zhang, H. MD-SGT: Multi-dilation Spherical Graph Transformer for unsupervised medical image registration. Comput. Med. Imaging Graph. 2023, 108, 102281. [Google Scholar]
- Chen, Y.; Li, Y. Trans G-net: Transformer and Graph Neural Network based multi-modal data analysis for medical applications. IEEE Trans. Biomed. Eng. 2022, 69, 456–467. [Google Scholar]
- Hou, W.; Zhang, L. Multi-scope Analysis Driven Hierarchical Graph Transformer for Whole Slide Image Based Cancer Survival Prediction. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2023, Proceedings of the 26th International Conference, Vancouver, BC, Canada, 8–12 October 2023; Lecture Notes in Computer Science; Springer: New York, NY, USA, 2023; Volume 14225. [Google Scholar]
- Asadi, S.; Khoshniat, F. Design of a Takagi–Sugeno Fuzzy-Based Sliding Mode Observer for Fault Reconstruction in Nonlinear Systems. Sensors 2022, 22, 10002. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Ji, J.; Kalhori, H. Advanced Fault Diagnosis and Health Monitoring Techniques for Complex Engineering Systems. Sensors 2022, 22, 10002. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Zhang, L. Piecewise Aggregate Approximation Combined with Complete Ensemble Empirical Mode Decomposition for Bearing Fault Diagnosis. Mech. Syst. Signal Process. 2023, 188, 109002. [Google Scholar]
- Zhang, Y.; Hu, L. Fault Propagation Inference Based on a Graph Neural Network for Steam Turbine Systems. Energies 2021, 14, 309. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S. Graph Neural Network-Based Bearing Fault Diagnosis Using Granger Causality. Mech. Syst. Signal Process. 2022, 163, 108202. [Google Scholar]
- Li, X.; Chen, Y. Deep Dynamic High-Order Graph Convolutional Network for Wear Fault Diagnosis. Mech. Syst. Signal Process. 2022, 171, 108908. [Google Scholar]


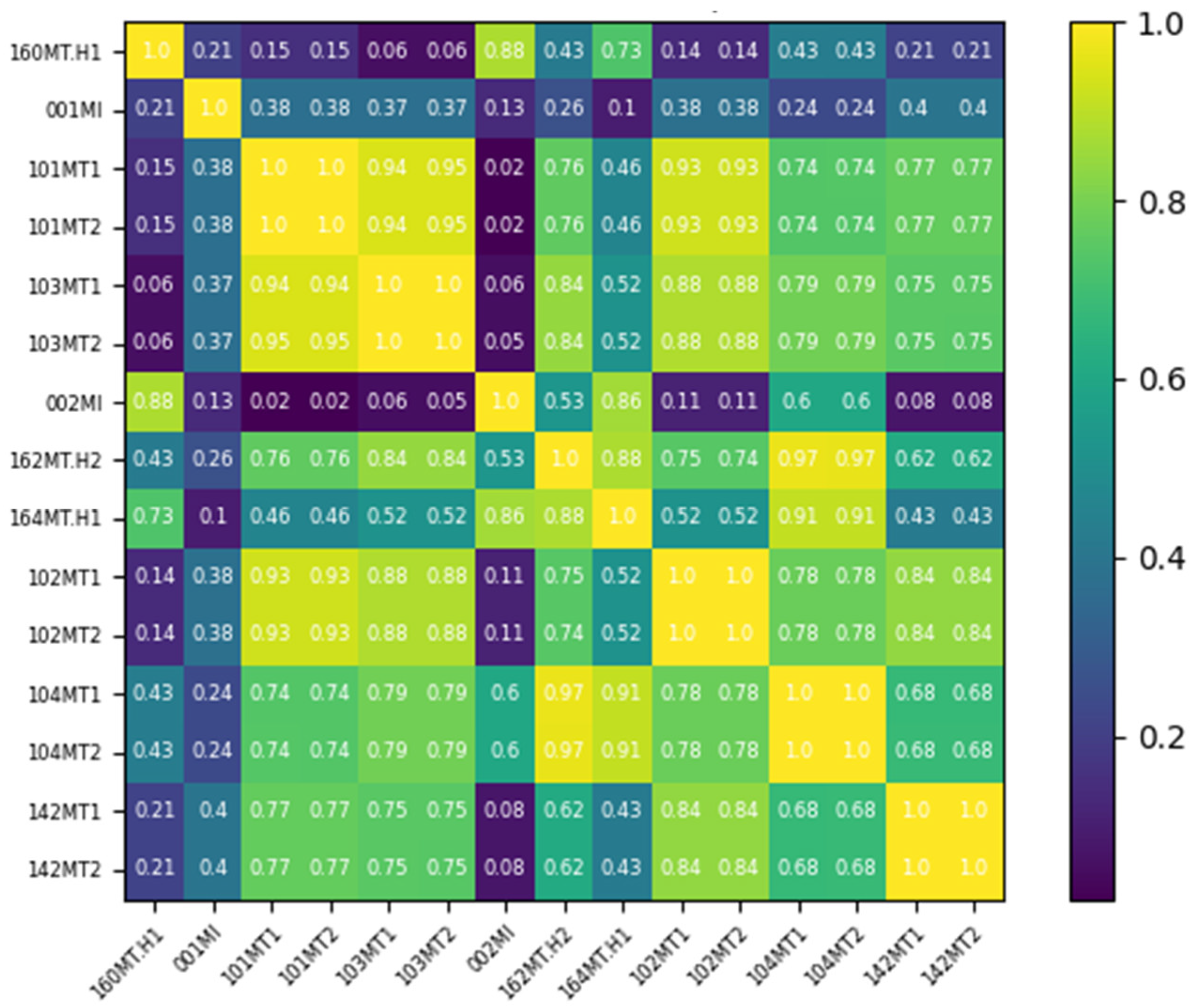








| No. | Code of Measuring Point | Location of Measuring Point | Unit |
|---|---|---|---|
| 1 | 160 MT.H1 | The output thrust bearing of the gearbox | °C |
| 2 | 001 MI | The current of the motor | A |
| 3 | 002 MI | The current of the motor | A |
| 4 | 162 MT.H2 | The top radial bearing of the motor | °C |
| 5 | 164 MT.H1 | The thrust bearing of the motor | °C |
| 6 | 101 MT1 | The upper radial bearing of the pump | °C |
| 7 | 101 MT2 | The upper radial bearing of the pump | °C |
| 8 | 102 MT1 | The upper radial bearing of the pump | °C |
| 9 | 102 MT2 | The upper radial bearing of the pump | °C |
| 10 | 103 MT1 | Pump thrust bearing | °C |
| 11 | 103 MT2 | Pump thrust bearing | °C |
| 12 | 104 MT1 | The thrust bearing of the pump | °C |
| 13 | 104 MT2 | The thrust bearing of the pump | °C |
| 14 | 142 MT1 | The lower radial bearing of the pump | °C |
| 15 | 142 MT2 | The lower radial bearing of the pump | °C |
| Data Type | Date of Data | Length of Data |
|---|---|---|
| Quantitative analysis data | 5 October–16 November | 460,482 |
| Training data | 5 October–19 October | 222,000 |
| Validation data | 20 October–25 October | 70,000 |
| Normal test data | 5 November–16 November | 140,082 |
| Fault test data | 1 December–8 December | 85,000 |
| MAE | MAPE | RMSE | |
|---|---|---|---|
| LSTM | 14.4626 | 1.3612 | 27.7123 |
| CNN | 26.4723 | 3.9569 | 39.5432 |
| TCN | 21.6907 | 2.6734 | 30.5073 |
| Deep AR | 1.2864 | 1.9765 | 4.2572 |
| MGT | 0.5614 | 1.2385 | 2.6554 |
| Model | GPU Type | CPU Cores | Training Time/Hours | Max Memory Usage/GB |
|---|---|---|---|---|
| LSTM | NVIDA GeForce RTX 4090 | 16 | 10 | 32 |
| CNN | 8 | 28 | ||
| TCN | 14 | 35 | ||
| Deep AR | 12 | 30 | ||
| MGT | 9 | 29 |
| Model | Validation Loss | Test Loss | Training Loss | Cross-Validation Mean | Cross-Validation Std Dev |
|---|---|---|---|---|---|
| LSTM | 0.45 | 0.50 | 0.40 | 0.47 | 0.02 |
| CNN | 0.40 | 0.45 | 0.35 | 0.42 | 0.03 |
| TCN | 0.48 | 0.52 | 0.43 | 0.49 | 0.02 |
| Deep AR | 0.42 | 0.47 | 0.38 | 0.44 | 0.03 |
| MGT | 0.38 | 0.43 | 0.34 | 0.40 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Ma, L.; Qing, C.; Zhao, T.; Wang, Z.; Geng, J.; Li, Y. A Health Monitoring Model for Circulation Water Pumps in a Nuclear Power Plant Based on Graph Neural Network Observer. Sensors 2024, 24, 4486. https://doi.org/10.3390/s24144486
Gao J, Ma L, Qing C, Zhao T, Wang Z, Geng J, Li Y. A Health Monitoring Model for Circulation Water Pumps in a Nuclear Power Plant Based on Graph Neural Network Observer. Sensors. 2024; 24(14):4486. https://doi.org/10.3390/s24144486
Chicago/Turabian StyleGao, Jianyong, Liyi Ma, Chen Qing, Tingdi Zhao, Zhipeng Wang, Jie Geng, and Ying Li. 2024. "A Health Monitoring Model for Circulation Water Pumps in a Nuclear Power Plant Based on Graph Neural Network Observer" Sensors 24, no. 14: 4486. https://doi.org/10.3390/s24144486
APA StyleGao, J., Ma, L., Qing, C., Zhao, T., Wang, Z., Geng, J., & Li, Y. (2024). A Health Monitoring Model for Circulation Water Pumps in a Nuclear Power Plant Based on Graph Neural Network Observer. Sensors, 24(14), 4486. https://doi.org/10.3390/s24144486








