Distributed Drive Electric Vehicle Handling Stability Coordination Control Framework Based on Adaptive Model Predictive Control
Abstract
1. Introduction
- This paper proposes a control framework based on AMPC for coordinating handling stability, consisting of a dynamic supervision layer, online optimization layer, and low-level control layer. This framework uses the AMPC strategy to coordinate maneuverability and lateral stability, enhancing the vehicle handling stability.
- In establishing the phase plane stability boundary, the influence of vehicle speed, front wheel steering angle, and road adhesion coefficient on the stability boundary was considered, along with added constraints on the yaw rate and maneuverability to redefine the stability boundary. Based on this, variable weight factors are dynamically quantified in real time, facilitating the coordination of maneuverability and stability control in the online optimization layer.
- A target weight-adaptive AMPC strategy was established, which can adjust the control weights for maneuverability and lateral stability in real time based on the vehicle state, thereby enhancing maneuverability under normal conditions and stability under extreme conditions.
2. Vehicle and Tire Model
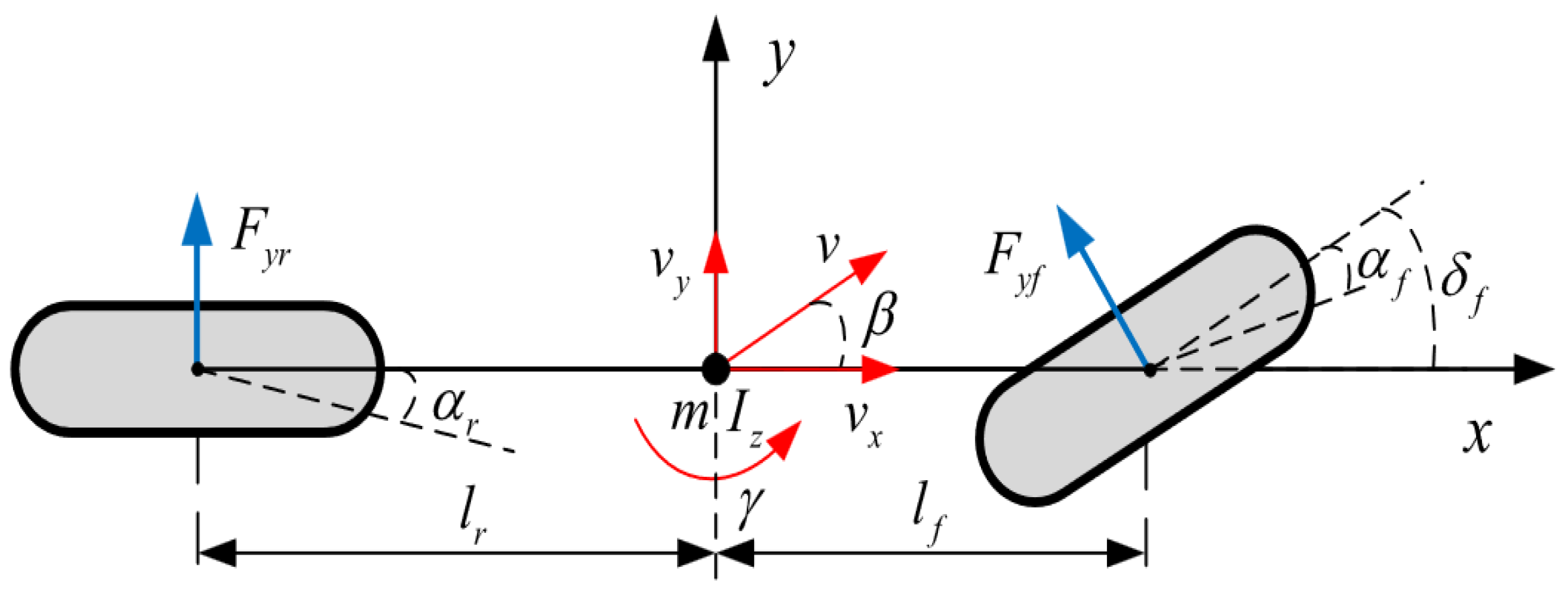
2.1. Vehicle Dynamics Model
2.2. Tire Model
3. Hierarchical Control System Design
3.1. Dynamic Supervision Layer
3.1.1. Phase Plane Portrait Analysis
3.1.2. Varying Weight Factor Design
3.2. Online Optimization Layer
3.2.1. Reference Model
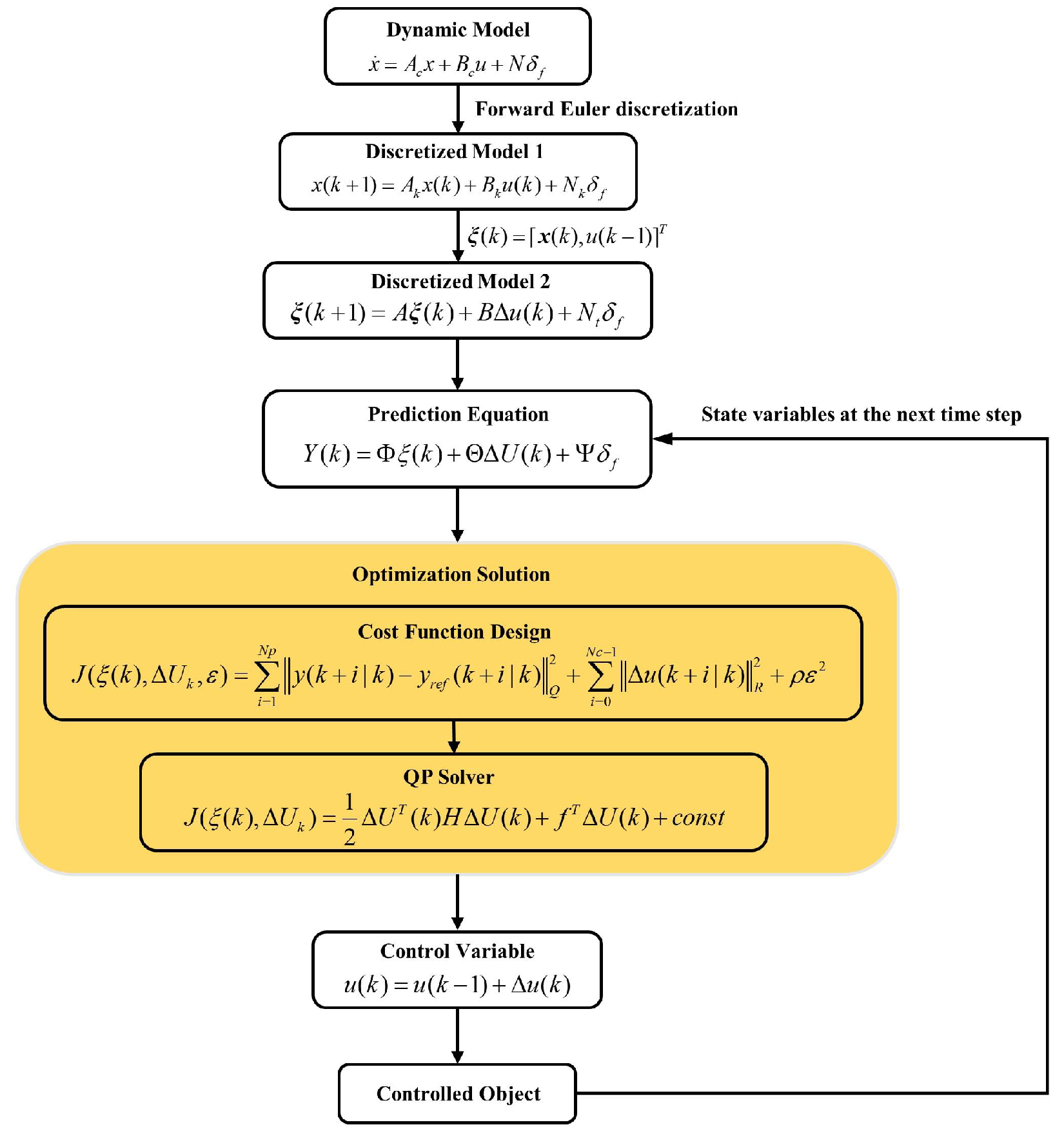
3.2.2. Design of the AMPC Controller
- Control increment constraints:The above equation in the rolling time domain is as follows:Expressed in compact form it is:
- Control variable constraints:As the solve variables in the objective function are in the form of control increments, therefore, the constraints must also be expressed in the form of control increments.where ⊗ represents the Kronecker product symbol.Expressed in compact form this gives:Rearranging the above equation obtains:
- The output constraints are:The above equation in the rolling time domain is:Expressed in a compact form this is:The output constraints can be represented as:Rearranging the above equation obtains:
3.3. Low-Level Control Layer
- Minimum torque distribution error objective functionThe distribution of longitudinal forces for all four wheels must first satisfy the additional yaw torque determined by the stability control system and the longitudinal force demands of the driver. Torque distribution is optimized to minimize the torque distribution error, with the following expression for the objective function:where represents the demand matrix, represents the control efficiency matrix, and represents the control input matrix. is the control demand weighting matrix, used to balance the proportion between the driver’s longitudinal force demands and the additional yaw torque demands, and . and represent the front and rear wheel tracks, and R represents the rolling radius of the wheel.
- Objective function based on the tire utilization rateFor vehicle motion control, the tire–road friction is also an important factor. To obtain good adhesion potentials, the tire force of each tire should stay away from the boundary of corresponding friction ellipse. Therefore, it is necessary to perform torque optimization distribution using the minimum tire utilization rate as the cost function. The expression for the objective function is as follows:where represents the Hessian matrix.
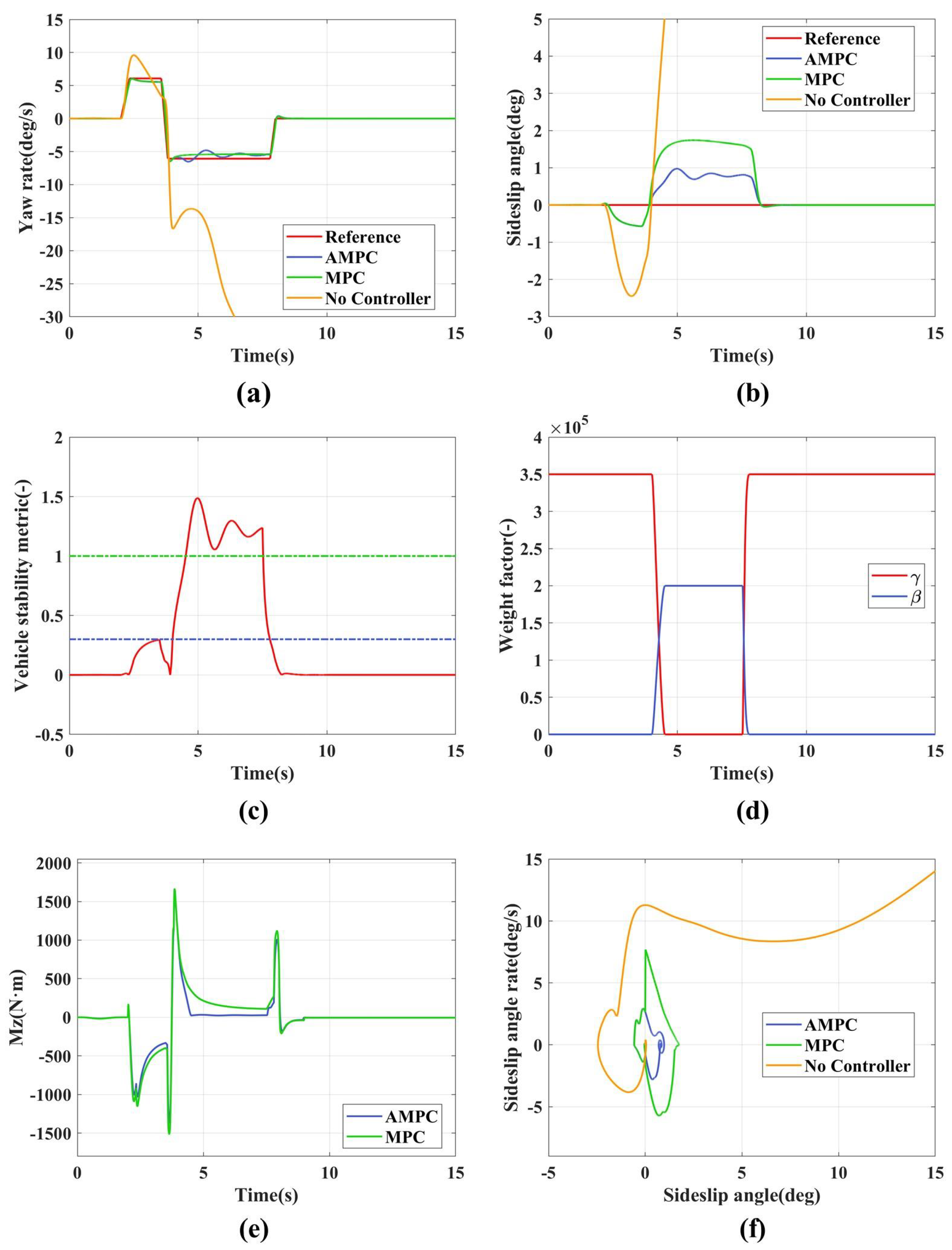
4. Results
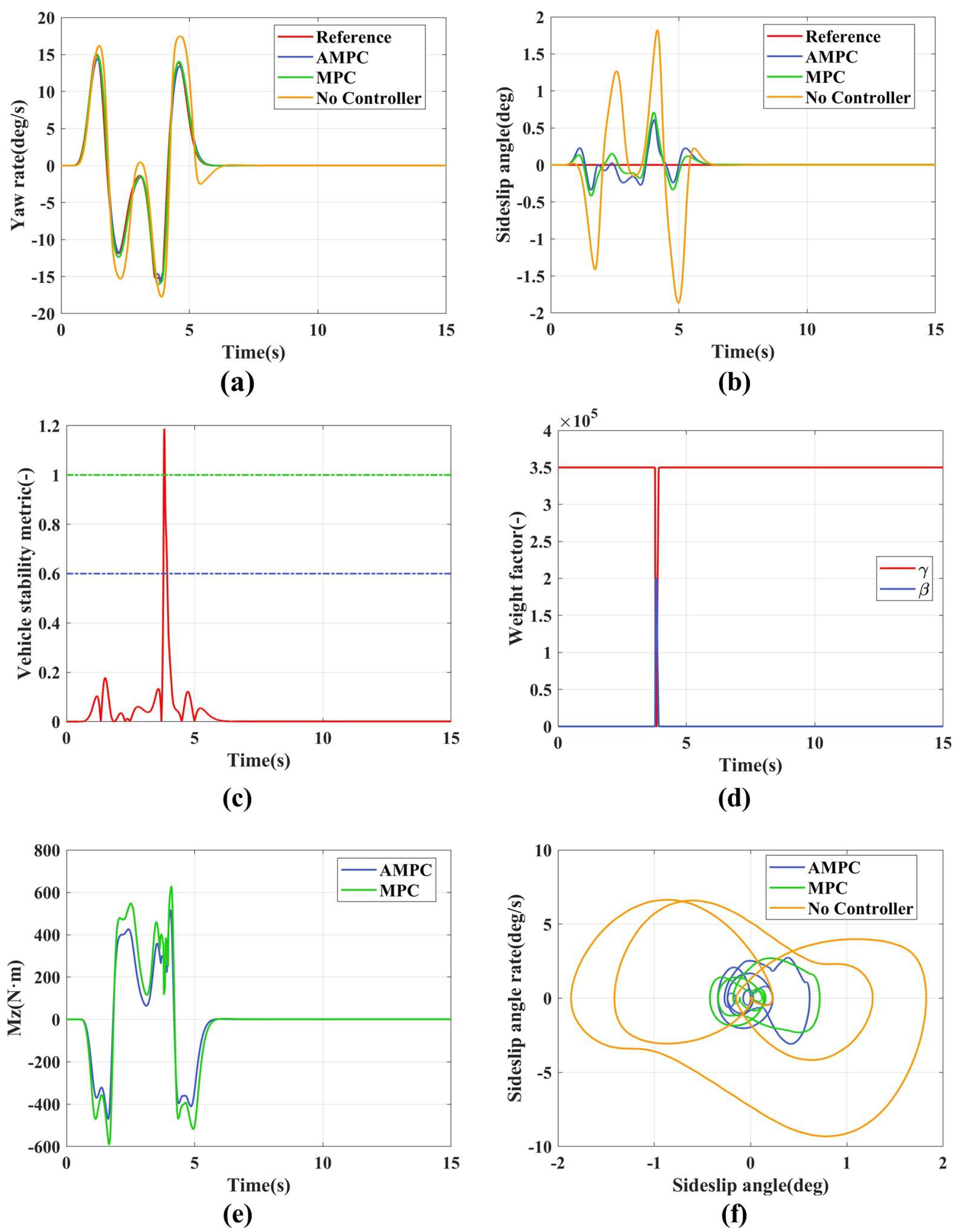
4.1. Double Lane Change
4.1.1. Low Adhesion Double Lane Change
4.1.2. Medium Adhesion Double Lane Change
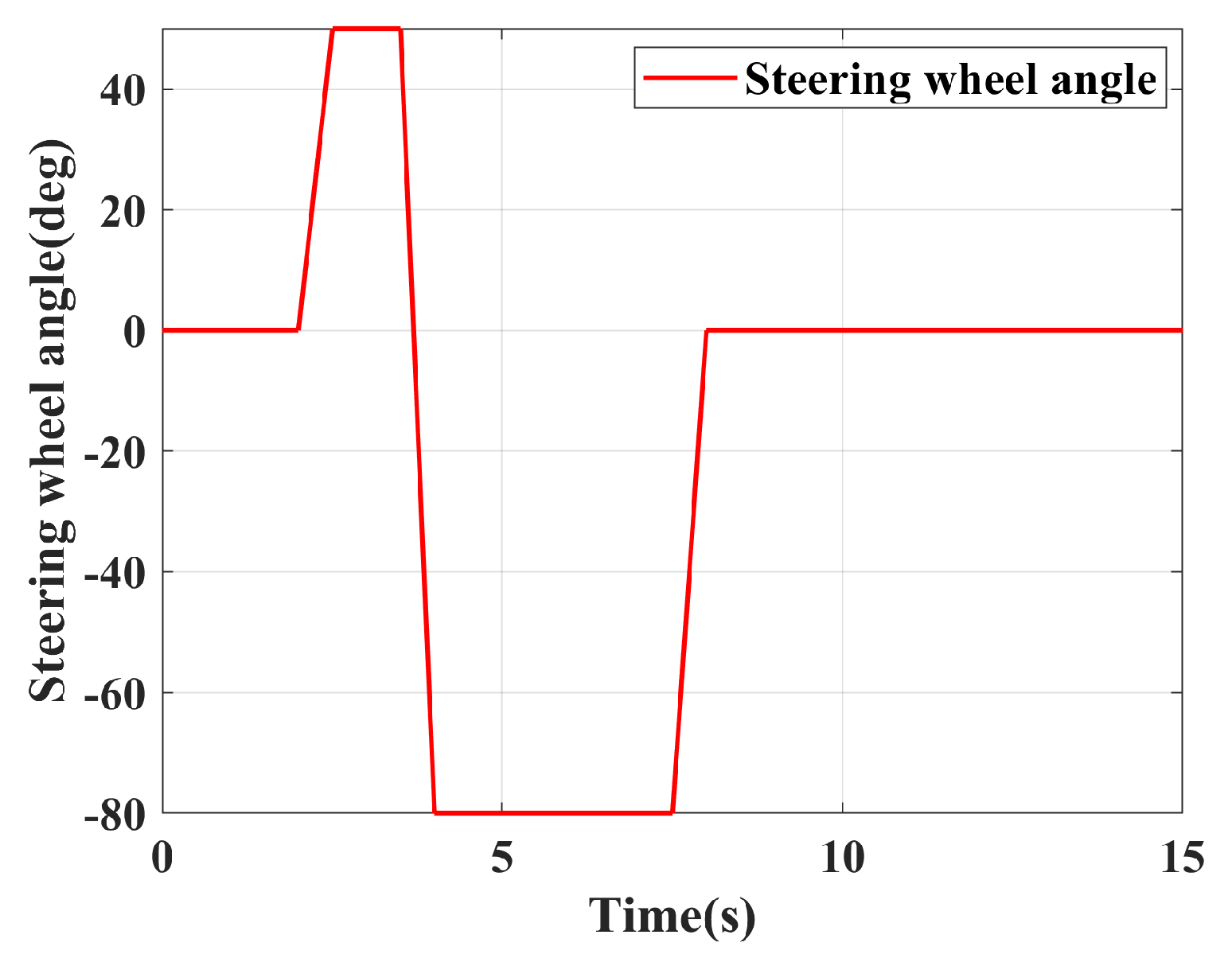
4.2. Fishhook Condition
4.2.1. Low Adhesion Fishhook Condition
4.2.2. High Adhesion Fishhook Condition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, Z.; Zhao, X.; Wang, S.; Yu, Q.; Zhang, H.; Li, Z.; Chai, H.; Han, Q. Extension coordinated control of distributed-driven electric vehicles based on evolutionary game theory. Control. Eng. Pract. 2023, 137, 105583. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, T.; Li, S.; Cheng, S.; Ding, X.; Wang, Z.; Sun, F. Review of Chassis Coordinated Control for Fully Line-Controlled Distributed Drive Electric Vehicles. J. Mech. Eng. 2023, 59, 261–280. [Google Scholar]
- Ataei, M.; Khajepour, A.; Jeon, S. Model predictive control for integrated lateral stability, traction/braking control, and rollover prevention of electric vehicles. Veh. Syst. Dyn. 2019, 58, 49–73. [Google Scholar] [CrossRef]
- Wang, J.; Gao, S.; Wang, K.; Wang, Y.; Wang, Q. Wheel torque distribution optimization of four-wheel independent-drive electric vehicle for energy efficient driving. Control. Eng. Pract. 2021, 110, 104779. [Google Scholar] [CrossRef]
- Liang, J.; Lu, Y.; Wang, F.; Yin, G.; Zhu, X.; Li, Y. A robust dynamic game-based control framework for integrated torque vectoring and active front-wheel steering system. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7328–7341. [Google Scholar] [CrossRef]
- Pugi, L.; Favilli, T.; Berzi, L.; Locorotondo, E.; Pierini, M. Brake blending and torque vectoring of road electric vehicles: A flexible approach based on smart torque allocation. Int. J. Electr. Hybrid Veh. 2020, 12, 87–115. [Google Scholar] [CrossRef]
- Zhao, F.; An, J.; Chen, Q.; Li, Y. Integrated Path Following and Lateral Stability Control of Distributed Drive Autonomous Unmanned Vehicle. World Electr. Veh. J. 2024, 15, 122. [Google Scholar] [CrossRef]
- Mirzaei, M. A new strategy for minimum usage of external yaw moment in vehicle dynamic control system. Transp. Res. Part C Emerg. Technol. 2010, 18, 213–224. [Google Scholar] [CrossRef]
- Goggia, T.; Sorniotti, A.; De Novellis, L.; Ferrara, A.; Gruber, P.; Theunissen, J.; Steenbeke, D.; Knauder, B.; Zehetner, J. Integral sliding mode for the torque-vectoring control of fully electric vehicles: Theoretical design and experimental assessment. IEEE Trans. Veh. Technol. 2014, 64, 1701–1715. [Google Scholar] [CrossRef]
- Tian, Y.; Cao, X.; Wang, X.; Zhao, Y. Four wheel independent drive electric vehicle lateral stability control strategy. IEEE/CAA J. Autom. Sin. 2020, 7, 1542–1554. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, L.; Li, Y.; Li, S.; Liang, Y. Cooperative strategy of trajectory tracking and stability control for 4WID autonomous vehicles under extreme conditions. IEEE Trans. Veh. Technol. 2023, 72, 3105–3118. [Google Scholar] [CrossRef]
- Wang, J.; Lv, S.; Sun, N.; Gao, S.; Sun, W.; Zhou, Z. Torque vectoring control of RWID electric vehicle for reducing driving-wheel slippage energy dissipation in cornering. Energies 2021, 14, 8143. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, K.; Zhang, P.; Yan, F. Direct Yaw Moment Control for Distributed Drive Electric Vehicles Based on Hierarchical Optimization Control Framework. Mathematics 2024, 12, 1715. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, J.; Xiong, L.; Feng, Y. Design of Control Strategy for Improving the Handling Performance of Distributed Drive Electric Vehicles. J. Tongji Univ. Nat. Sci. 2014, 42, 1088–1095. [Google Scholar]
- Woo, S.; Cha, H.; Yi, K.; Jang, S. Active differential control for improved handling performance of front-wheel-drive high-performance vehicles. Int. J. Automot. Technol. 2021, 22, 537–546. [Google Scholar] [CrossRef]
- Ahmadian, N.; Khosravi, A.; Sarhadi, P. Integrated model reference adaptive control to coordinate active front steering and direct yaw moment control. ISA Trans. 2020, 106, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Ding, H.; Huang, Y.; Chen, H.; Guo, K.; Li, Q. An analytical approach to improve vehicle maneuverability via torque vectoring control: Theoretical study and experimental validation. IEEE Trans. Veh. Technol. 2019, 68, 4514–4526. [Google Scholar] [CrossRef]
- Zhu, Z.; Tang, X.; Qin, Y.; Huang, Y.; Hashemi, E. A survey of lateral stability criterion and control application for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10382–10399. [Google Scholar] [CrossRef]
- Liu, W.; Ding, H.; Guo, K.; Zou, B. Application of Centroid Sideslip Angle Phase Diagram in Vehicle ESC System Stability Control. J. Beijing Inst. Technol. 2013, 42–46. [Google Scholar] [CrossRef]
- Farroni, F.; Russo, M.; Russo, R.; Terzo, M.; Timpone, F. A combined use of phase plane and handling diagram method to study the influence of tyre and vehicle characteristics on stability. Veh. Syst. Dyn. 2013, 51, 1265–1285. [Google Scholar] [CrossRef]
- Wang, J.; Luo, Z.; Wang, Y.; Yang, B.; Assadian, F. Coordination control of differential drive assist steering and vehicle stability control for four-wheel-independent-drive EV. IEEE Trans. Veh. Technol. 2018, 67, 11453–11467. [Google Scholar] [CrossRef]
- Chen, W.; Liang, X.; Wang, Q.; Zhao, L.; Wang, X. Extension coordinated control of four wheel independent drive electric vehicles by AFS and DYC. Control. Eng. Pract. 2020, 101, 104504. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, Y.; Zhao, S. Distributed Intelligent Vehicle Path Tracking and Stability Cooperative Control. World Electr. Veh. J. 2024, 15, 89. [Google Scholar] [CrossRef]
- Guo, N.; Zhang, X.; Zou, Y.; Lenzo, B.; Du, G.; Zhang, T. A supervisory control strategy of distributed drive electric vehicles for coordinating handling, lateral stability, and energy efficiency. IEEE Trans. Transp. Electrif. 2021, 7, 2488–2504. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, H.; Shi, J.; Huang, Y.; Chen, H.; Guo, K.; Li, Q. An adaptive backstepping sliding mode controller to improve vehicle maneuverability and stability via torque vectoring control. IEEE Trans. Veh. Technol. 2020, 69, 2598–2612. [Google Scholar] [CrossRef]
- Alipour, H.; Sabahi, M.; Sharifian, M.B.B. Lateral stabilization of a four wheel independent drive electric vehicle on slippery roads. Mechatronics 2015, 30, 275–285. [Google Scholar] [CrossRef]
- Ji, X.; He, X.; Lv, C.; Liu, Y.; Wu, J. A vehicle stability control strategy with adaptive neural network sliding mode theory based on system uncertainty approximation. Veh. Syst. Dyn. 2018, 56, 923–946. [Google Scholar] [CrossRef]
- Ding, S.; Liu, L.; Zheng, W.X. Sliding mode direct yaw-moment control design for in-wheel electric vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6752–6762. [Google Scholar] [CrossRef]
- Guo, N.; Zhang, X.; Zou, Y.; Lenzo, B.; Zhang, T.; Göhlich, D. A fast model predictive control allocation of distributed drive electric vehicles for tire slip energy saving with stability constraints. Control. Eng. Pract. 2020, 102, 104554. [Google Scholar] [CrossRef]
- Jalali, M.; Hashemi, E.; Khajepour, A.; Chen, S.k.; Litkouhi, B. Integrated model predictive control and velocity estimation of electric vehicles. Mechatronics 2017, 46, 84–100. [Google Scholar] [CrossRef]
- Lenzo, B.; Zanchetta, M.; Sorniotti, A.; Gruber, P.; De Nijs, W. Yaw rate and sideslip angle control through single input single output direct yaw moment control. IEEE Trans. Control. Syst. Technol. 2020, 29, 124–139. [Google Scholar] [CrossRef]
- Zhai, L.; Sun, T.; Wang, J. Electronic stability control based on motor driving and braking torque distribution for a four in-wheel motor drive electric vehicle. IEEE Trans. Veh. Technol. 2016, 65, 4726–4739. [Google Scholar] [CrossRef]
- Ružinskas, A.; Sivilevičius, H. Magic formula tyre model application for a tyre-ice interaction. Procedia Eng. 2017, 187, 335–341. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, B.; Wen, G.; Long, L.; Cui, Q. Intervention criterion and control research for active front steering with consideration of road adhesion. Veh. Syst. Dyn. 2018, 56, 553–578. [Google Scholar] [CrossRef]
- Yu, Z.; Leng, B.; Xiong, L.; Feng, Y. Vehicle sideslip angle and yaw rate joint criterion for vehicle stability control. J. Tongji Univ. Nat. Sci. 2015, 43, 1841–1849. [Google Scholar]
- Zhang, D.; Liu, G.; Zhou, H.; Zhao, W. Adaptive sliding mode fault-tolerant coordination control for four-wheel independently driven electric vehicles. IEEE Trans. Ind. Electron. 2018, 65, 9090–9100. [Google Scholar] [CrossRef]






| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Vehicle mass (kg) | 1412 | Yaw Moment of inertia (kg·m2) | 1436.7 |
| Wheelbase (m) | 2.91 | Wheel track (m) | 1.675 (front) 1.675 (rear) |
| Distance from rear axle to center of mass (m) | 1.015 | Distance from rear axle to center of mass (m) | 1.895 |
| Centroid height (m) | 0.54 | Rolling radius (m) | 0.325 |
| Front axle cornering stiffness (N/rad) | −134,900 | Rear axle cornering stiffness (N/rad) | −79,617 |
| Algorithm Simulation | Weight Coefficient |
|---|---|
| AMPC | Adaptive Weight Adjustment (Section 3.2) |
| MPC | Fixed Weight |
| No Controller | - |
| Indicators | Controller | Max | Avg | RMSE |
|---|---|---|---|---|
| Yaw rate error (deg/s) | AMPC | 2.9564 | 0.2435 | 0.4823 |
| MPC | 4.27 | 0.3832 | 0.7644 | |
| Sideslip angle error (deg) | AMPC | 0.8668 | 0.1545 | 0.2896 |
| MPC | 1.712 | 0.3472 | 0.6484 |
| Indicators | Controller | Max | Avg | RMSE |
|---|---|---|---|---|
| Yaw rate error (deg/s) | AMPC | 2.81 | 0.27 | 0.49 |
| MPC | 3.28 | 0.38 | 0.68 | |
| Sideslip angle error (deg) | AMPC | 0.58 | 0.05 | 0.11 |
| MPC | 0.71 | 0.06 | 0.18 |
| Indicators | Controller | Max | Avg | RMSE |
|---|---|---|---|---|
| Yaw rate error (deg/s) | AMPC | 1.76 | 0.22 | 0.4 |
| MPC | 1.76 | 0.24 | 0.41 | |
| Sideslip angle error (deg) | AMPC | 0.97 | 0.25 | 0.42 |
| MPC | 1.74 | 0.48 | 0.85 |
| Indicators | Controller | Max | Avg | RMSE |
|---|---|---|---|---|
| Yaw rate error (deg/s) | AMPC | 1.38 | 0.15 | 0.3 |
| MPC | 1.85 | 0.17 | 0.36 | |
| Sideslip angle error (deg) | AMPC | 0.19 | 0.04 | 0.06 |
| MPC | 0.20 | 0.06 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Dai, Z.; Liu, M.; Xie, Z.; Jiang, Y.; Yang, H.; Xie, D. Distributed Drive Electric Vehicle Handling Stability Coordination Control Framework Based on Adaptive Model Predictive Control. Sensors 2024, 24, 4811. https://doi.org/10.3390/s24154811
Guo J, Dai Z, Liu M, Xie Z, Jiang Y, Yang H, Xie D. Distributed Drive Electric Vehicle Handling Stability Coordination Control Framework Based on Adaptive Model Predictive Control. Sensors. 2024; 24(15):4811. https://doi.org/10.3390/s24154811
Chicago/Turabian StyleGuo, Jianhua, Zhiyuan Dai, Ming Liu, Zhihao Xie, Yu Jiang, Haochun Yang, and Dong Xie. 2024. "Distributed Drive Electric Vehicle Handling Stability Coordination Control Framework Based on Adaptive Model Predictive Control" Sensors 24, no. 15: 4811. https://doi.org/10.3390/s24154811
APA StyleGuo, J., Dai, Z., Liu, M., Xie, Z., Jiang, Y., Yang, H., & Xie, D. (2024). Distributed Drive Electric Vehicle Handling Stability Coordination Control Framework Based on Adaptive Model Predictive Control. Sensors, 24(15), 4811. https://doi.org/10.3390/s24154811





