Investigation of the Zero-Frequency Component of Nonlinear Lamb Waves in a Symmetrical Undulated Plate
Abstract
:1. Introduction
1.1. Second Harmonic Method
1.2. Zero-Frequency Component (ZFC)–Based Method
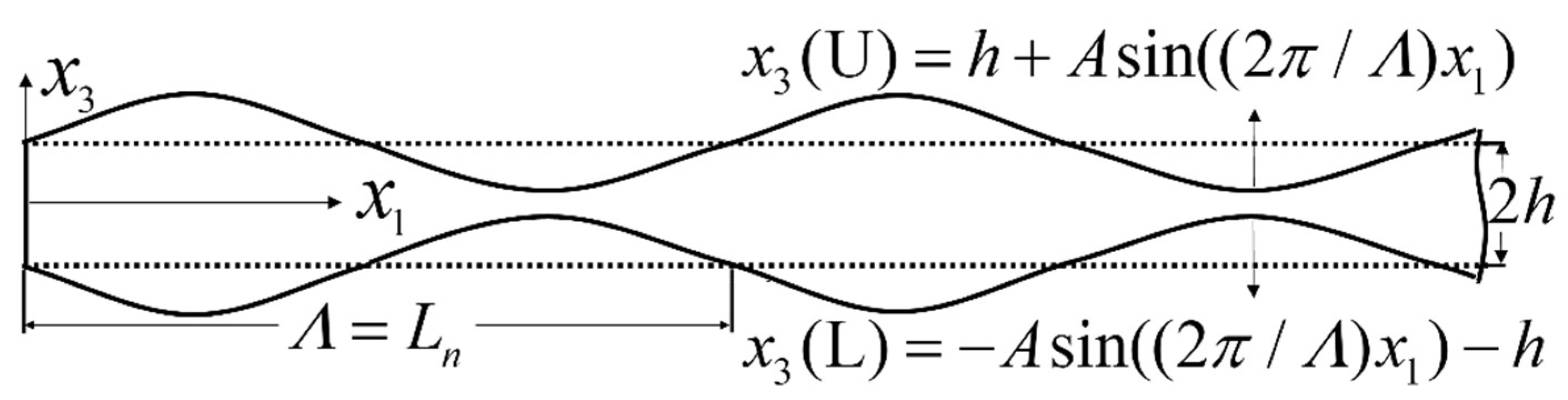
2. Theory
- Determining the inspection frequency. Assuming the spatial period distance () of the second harmonics is equal to the spatial length () of the undulated plate, the frequency of the fundamental wave can be obtained by solving Equation (A1) in Appendix A.
- Determining the location of the detection points. To reduce the error, the distance between two adjacent detection points must be (or an integral number of ).
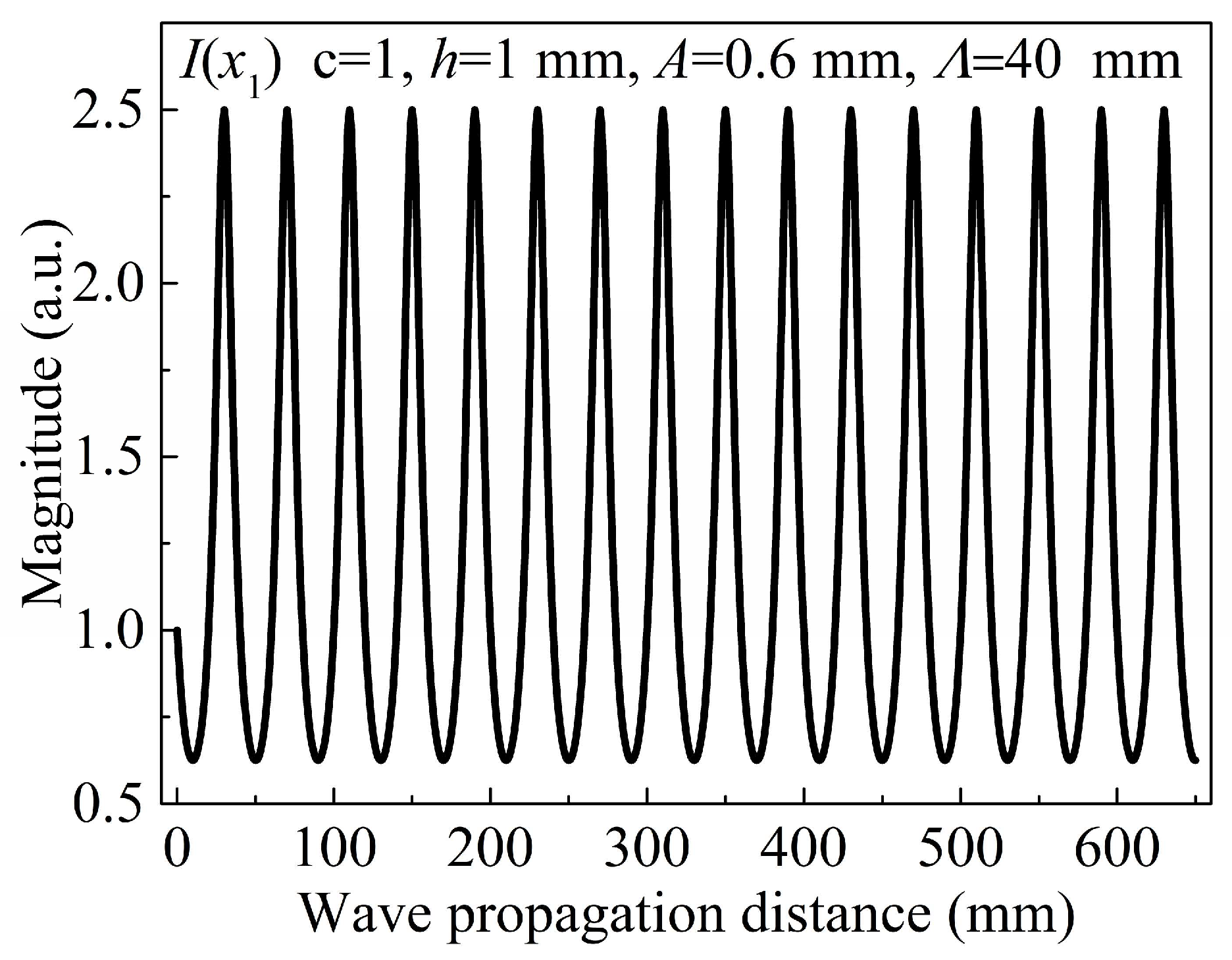
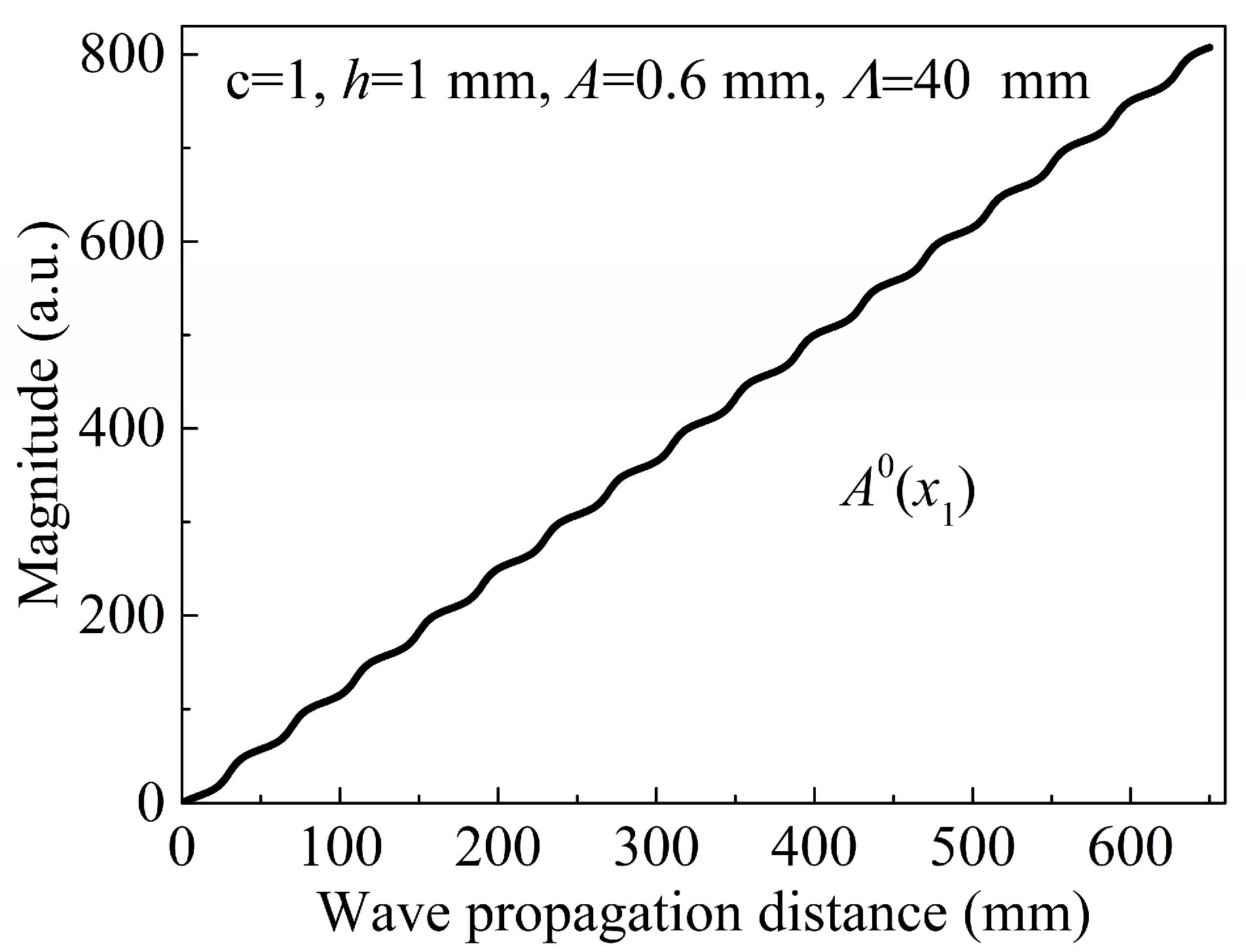
- The fundamental wave in the undulated plate at the selected frequency is excited. Subsequently, the transmitted wave is detected and received at different wave propagation distances along a straight line. The corresponding second harmonic magnitude is obtained by performing the fast Fourier transform on every received signal.
3. Numerical Simulation
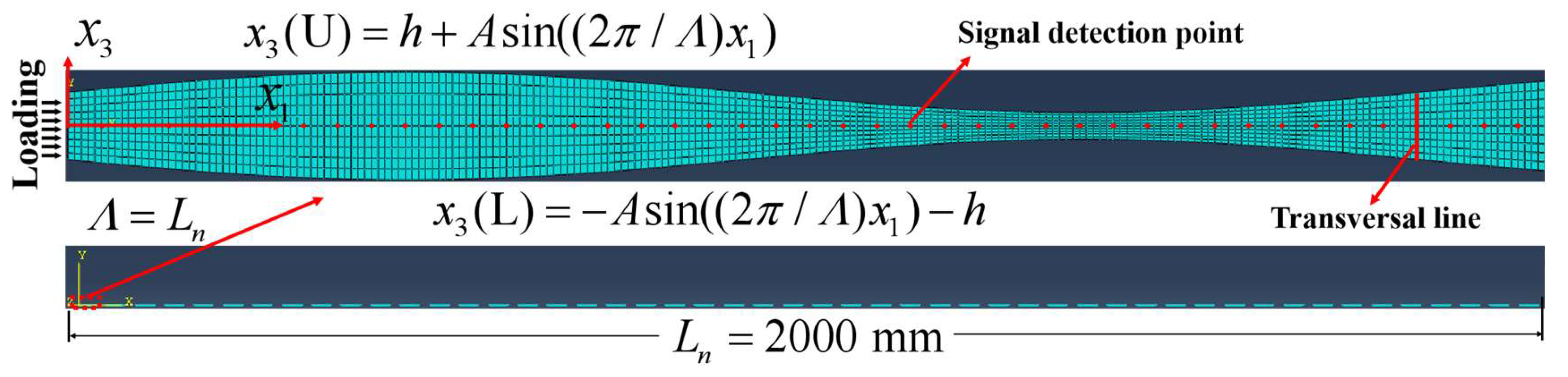
3.1. Simulation Model
3.2. Results and Discussion
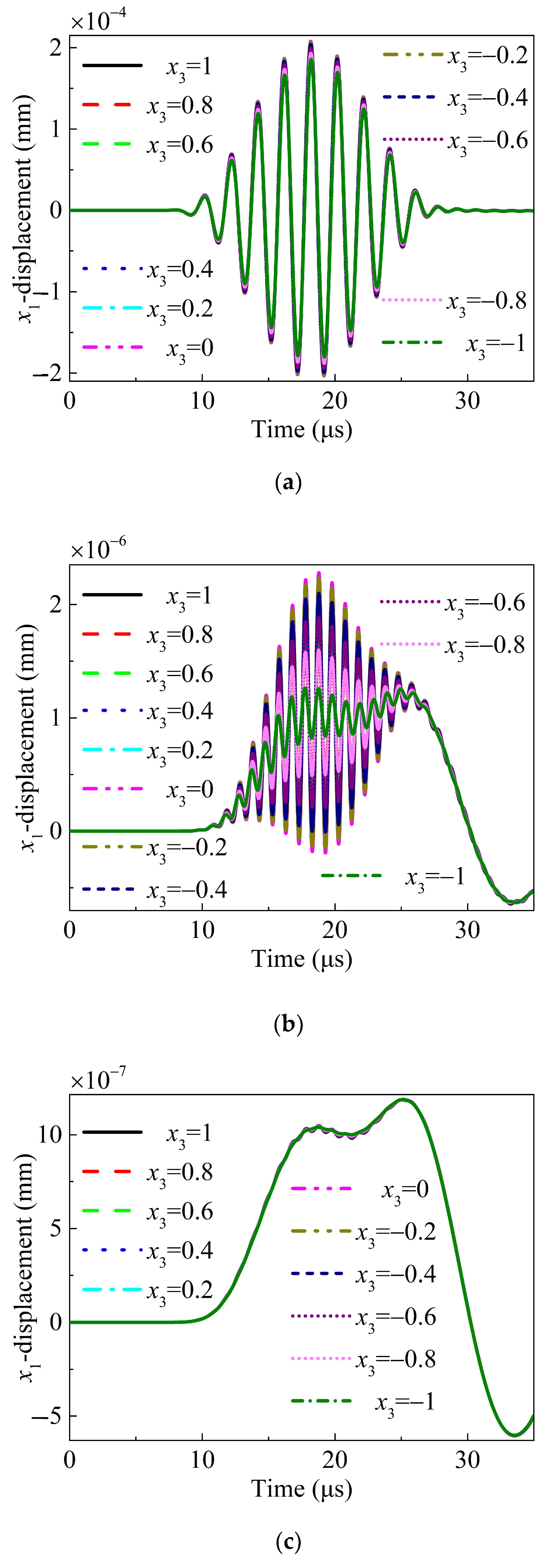
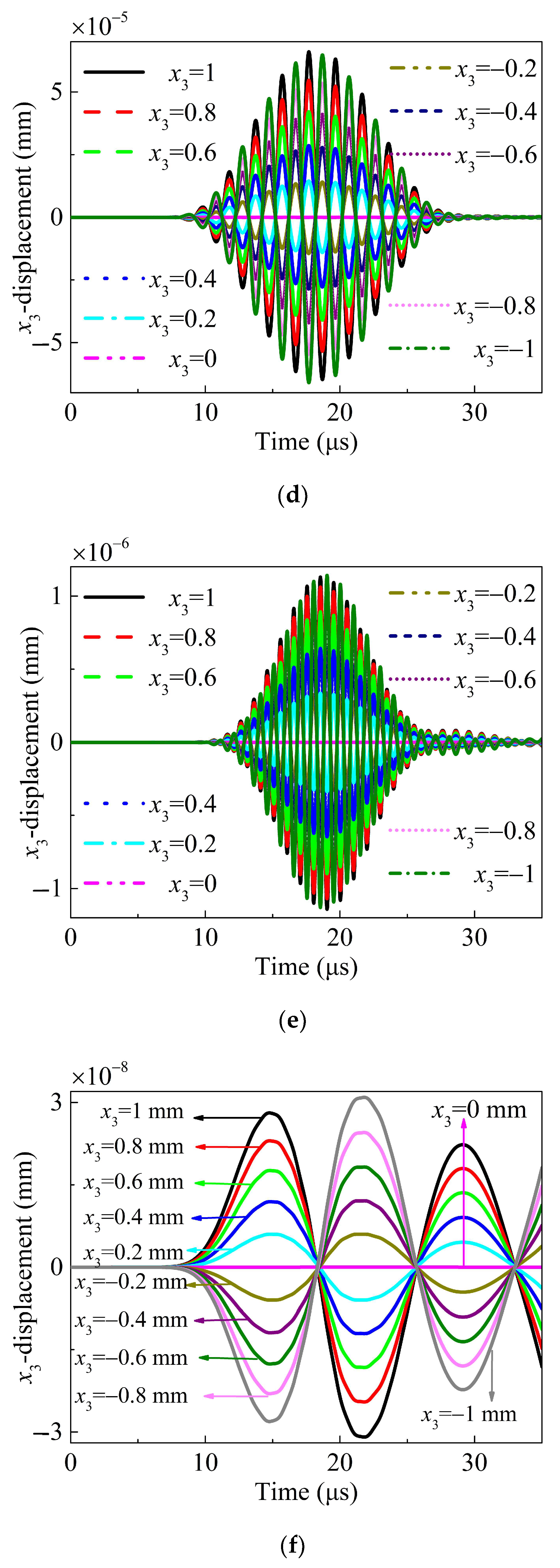
3.2.1. Symmetrical Property
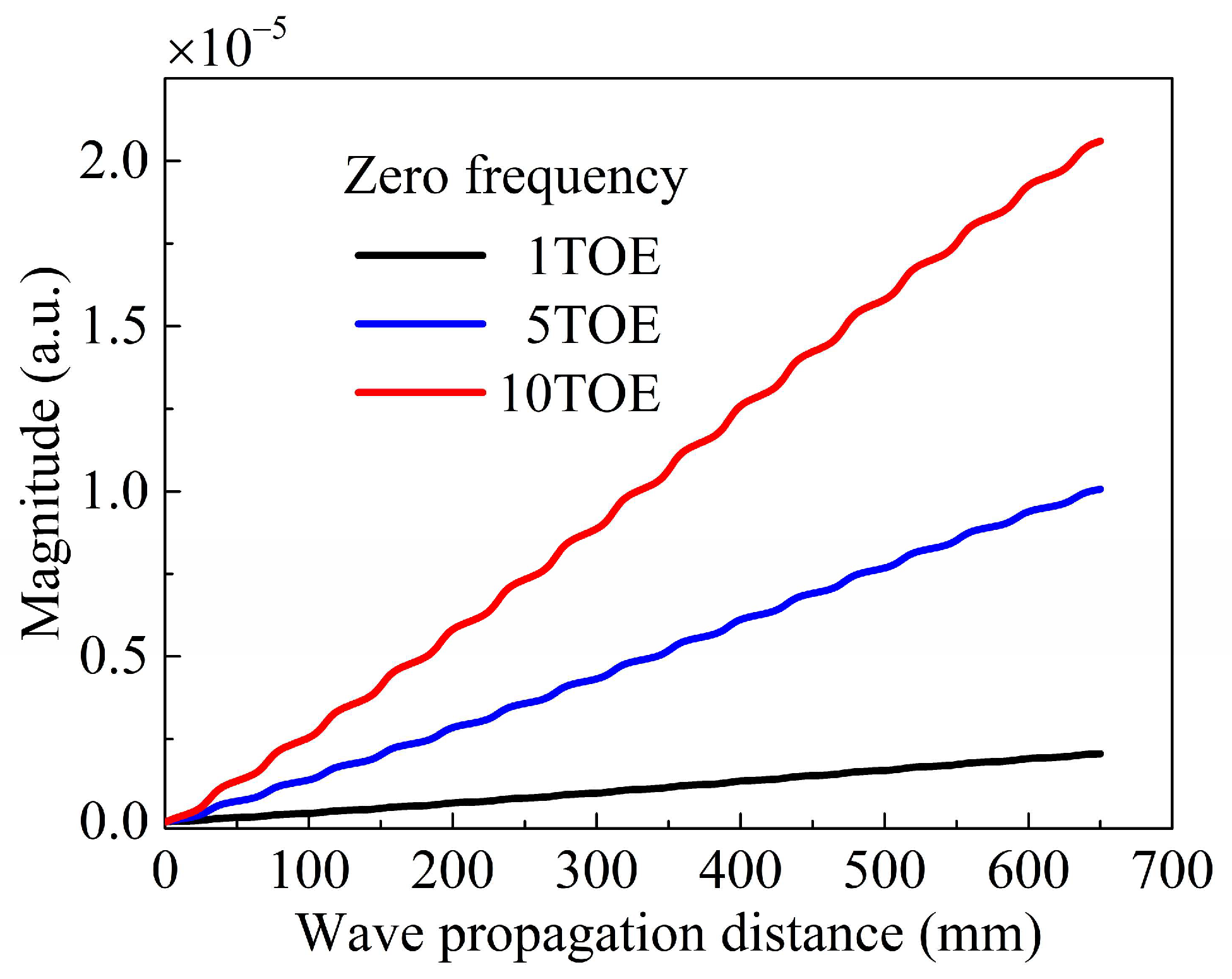
3.2.2. Material Early-Stage Damage Evaluation
4. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kanaris, A.G.; Mouza, A.; Paras, S. Optimal design of a plate heat exchanger with undulated surfaces. Int. J. Therm. Sci. 2009, 48, 1184–1195. [Google Scholar] [CrossRef]
- Mevissen, F.; Meo, M. Nonlinear Ultrasound Crack Detection with Multi-Frequency Excitation—A Comparison. Sensors 2021, 21, 5368. [Google Scholar] [CrossRef] [PubMed]
- Meyendorf, N.; Rosner, H.; Kramb, V.; Sathish, S. Thermo-acoustic fatigue characterization. Ultrasonics 2002, 40, 427–434. [Google Scholar] [CrossRef] [PubMed]
- Sagar, S.; Das, S.; Parida, N.; Bhattacharya, D. Non-linear ultrasonic technique to assess fatigue damage in structural steel. Scripta Mater. 2006, 55, 199–202. [Google Scholar] [CrossRef]
- Zhao, C.; Tanweer, S.; Li, J.; Lin, M.; Zhang, X.; Liu, Y. Nonlinear Guided Wave Tomography for Detection and Evaluation of Early-Life Material Degradation in Plates. Sensors 2021, 21, 5498. [Google Scholar] [CrossRef]
- Deng, M. Cumulative second-harmonic generation of Lamb-mode propagation in a solid plate. J. Appl. Phys. 1999, 85, 3051–3058. [Google Scholar] [CrossRef]
- Deng, M. Analysis of second-harmonic generation of Lamb modes using a modal analysis approach. J. Appl. Phys. 2003, 94, 4152–4159. [Google Scholar] [CrossRef]
- Lima, W.; Hamilton, M. Finite-amplitude waves in isotropic elastic plates. J. Sound Vib. 2003, 265, 819–839. [Google Scholar] [CrossRef]
- Deng, M.; Wang, P.; Lv, X. Experimental observation of cumulative second-harmonic generation of Lamb-wave propagation in an elastic plate. J. Phys. D. Appl. Phys. 2005, 38, 344. [Google Scholar] [CrossRef]
- Bermes, C.; Kim, J.; Qu, J.; Jacobs, L. Experimental characterization of material nonlinearity using Lamb waves. Appl. Phys. Lett. 2007, 90, 219801. [Google Scholar] [CrossRef]
- Bermes, C.; Kim, J.; Qu, J.; Jacobs, L. Nonlinear Lamb waves for the detection of material nonlinearity. Mech. Syst. Signal Process. 2008, 22, 638–646. [Google Scholar] [CrossRef]
- Pruell, C.; Kim, J.; Qu, J.; Jacobs, L. Evaluation of fatigue damage using nonlinear guided waves. Smart Mater. Struct. 2009, 18, 035003. [Google Scholar] [CrossRef]
- Pruell, C.; Kim, J.; Qu, J.; Jacobs, L. A nonlinear-guided wave technique for evaluating plasticity-driven material damage in a metal plate. NDT E Int. 2009, 42, 199–2032. [Google Scholar] [CrossRef]
- Matsuda, N.; Biwa, S. Phase and group velocity matching for cumulative harmonic generation in Lamb waves. J. Appl. Phys. 2011, 109, 094903. [Google Scholar] [CrossRef]
- Li, W.; Cho, Y.; Achenbach, J. Detection of thermal fatigue in composites by second harmonic Lamb waves. Smart Mater. Struct. 2012, 21, 85–93. [Google Scholar] [CrossRef]
- Shui, G.; Wang, Y. Ultrasonic evaluation of early damage of a coating by using second-harmonic generation technique. J. Appl. Phys. 2012, 111, 67. [Google Scholar] [CrossRef]
- Chillara, V.; Lissenden, C. Interaction of guided wave modes in isotropic weakly nonlinear elastic plates: Higher harmonic generation. J. Appl. Phys. 2012, 111, 229–277. [Google Scholar] [CrossRef]
- Xiang, Y.; Deng, M.; Xuan, F.; Liu, C. Effect of precipitate-dislocation interactions on generation of nonlinear Lamb waves in creep-damaged metallic alloys. J. Appl. Phys. 2012, 111, 375. [Google Scholar] [CrossRef]
- Xiang, Y.; Deng, M.; Xuan, F. Creep damage characterization using nonlinear ultrasonic guided wave method: A mesoscale model. J. Appl. Phys. 2014, 115, 044914. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhu, W.; Liu, C.; Xuan, F.; Wang, Y.; Kuang, W. Creep degradation characterization of titanium alloy using nonlinear ultrasonic technique. NDT E Int. 2015, 72, 41–49. [Google Scholar] [CrossRef]
- Deng, M.; Pei, J. Assessment of accumulated fatigue damage in solid plates using nonlinear Lamb wave approach. Appl. Phys. Lett. 2007, 90, 273–277. [Google Scholar] [CrossRef]
- Rauter, N.; Lammering, R. Numerical simulation of elastic wave propagation in isotropic media considering material and geometrical nonlinearities. Smart Mater. Struct. 2015, 24, 045027. [Google Scholar] [CrossRef]
- Shui, G.; Wang, Y.; Huang, P.; Qu, J. Nonlinear ultrasonic evaluation of the fatigue damage of adhesive joints. NDT E Int. 2015, 70, 9–15. [Google Scholar] [CrossRef]
- Wan, X.; Tse, P.; Xu, G.; Tao, F.; Zhang, Q. Analytical and numerical studies of approximate phase velocity matching based nonlinear S0 mode Lamb waves for the detection of evenly distributed microstructural changes. Smart Mater. Struct. 2016, 25, 045023. [Google Scholar] [CrossRef]
- Wan, X.; Zhang, Q. Numerical simulation of nonlinear Lamb waves used in a thin plate for detecting buried micro-cracks. Sensors 2014, 15, 8528–8546. [Google Scholar] [CrossRef] [PubMed]
- Chillara, V.; Lissenden, C. Nonlinear guided waves in plates: A numerical perspective. Ultrasonics 2014, 54, 1553–1558. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Victor, G. Predictive modeling of nonlinear wave propagation for structural health monitoring with piezoelectric wafer active sensors. J. Intel. Mat. Syst. Str. 2014, 25, 506–520. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, Y.; Hu, N.; Liu, Y.; Zhang, Q.; Deng, M. Experimental and numerical study of nonlinear Lamb waves of a low-frequency S0 mode in plates with quadratic nonlinearity. Materials 2018, 11, 2096. [Google Scholar] [CrossRef] [PubMed]
- Shui, G.; Song, X.; Xi, J.; Wang, Y. Experimental characterization of impact fatigue damage in an adhesive bonding using the second harmonics. J. Nondestruct. Eval. 2017, 3, 23. [Google Scholar] [CrossRef]
- Yang, Y.; Ng, C.; Kotousov, A.; Sohn, H.; Lim, H. Second harmonic generation at fatigue cracks by low-frequency Lamb waves: Experimental and numerical studies. Mech. Syst. Signal Process. 2018, 99, 760–773. [Google Scholar] [CrossRef]
- Yang, Y.; Ng, C.; Kotousov, A. Second-order harmonic generation of Lamb wave in prestressed plates. J. Sound Vib. 2019, 460, 114903. [Google Scholar] [CrossRef]
- Jones, G. Interaction of elastic waves in an isotropic solid. J. Acoust. Soc. Am. 1963, 35, 5–10. [Google Scholar] [CrossRef]
- Liu, M.; Tang, G.; Jacobs, L.; Qu, J. Measuring acoustic nonlinearity by collinear mixing waves. In Annual Review of Progress in Quantitative Nondestructive Evaluation; NASA: Washington, DC, USA, 2011. [Google Scholar]
- Tang, G.; Liu, M.; Jacobs, L. Detecting localized plastic strain by a scanning collinear wave mixing method. J. Nondestruct. Eval. 2014, 33, 196–204. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Z.; Cao, P.; Qiu, Y. Experiment and FEM study of one-way mixing of elastic waves with quadratic nonlinearity. NDT E Int. 2015, 72, 33–40. [Google Scholar] [CrossRef]
- He, C.; Jiao, J.; Wu, B.; Meng, X. Nonlinear Lamb wave-mixing technique for micro-crack detection in plates. NDT E Int. 2017, 85, 63–71. [Google Scholar] [CrossRef]
- Hasanian, M.; Lissenden, C. Second order ultrasonic guided wave mutual interactions in plate: Arbitrary angles, internal resonance, and finite interaction region. J. Appl. Phys. 2018, 124, 164904. [Google Scholar] [CrossRef]
- Sun, M.; Xiang, Y.; Deng, M.; Chao, J.; Xuan, F. Scanning non-collinear wave mixing for nonlinear ultrasonic detection and localization of plasticity. NDT E Int. 2018, 93, 1–6. [Google Scholar] [CrossRef]
- Li, W.; Deng, M.; Hu, N.; Xiang, Y. Theoretical analysis and experimental observation of frequency mixing response of ultrasonic Lamb waves. J. Appl. Phys. 2018, 124, 044901. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, Y.; Jacobs, L.; Qu, J. Mixing of collinear plane wave pulses in elastic solids with quadratic nonlinearity. J. Acoust. Soc. Am. 2014, 136, 2389–2404. [Google Scholar] [CrossRef] [PubMed]
- Ishii, Y.; Biwa, S.; Adachi, T. Non-collinear interaction of guided elastic waves in an isotropic plate. J. Sound. Vib. 2018, 419, 390–404. [Google Scholar] [CrossRef]
- Sun, M.; Qu, J. Analytical and numerical investigations of one-way mixing of Lamb waves in a thin plate. Ultrasonics 2020, 108, 106180. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Xiang, Y.; Deng, M.; Tang, B.; Zhu, W.; Xuan, F. Experimental and numerical investigations of nonlinear interaction of counter-propagating Lamb waves. Appl. Phys. Lett. 2019, 114, 119902. [Google Scholar] [CrossRef]
- Ju, T.; Achenbach, J.; Jacobs, L.; Qu, J. Nondestructive evaluation of thermal aging of adhesive joints by using a nonlinear wave mixing technique. NDT E Int. 2019, 103, 62–67. [Google Scholar] [CrossRef]
- Ju, T.; Achenbach, J.; Jacobs, L.; Qu, J. One-way mixing of collinear waves in an adhesive layer. J. Acoust. Soc. Am. 2019, 145, 110–120. [Google Scholar] [CrossRef] [PubMed]
- Aslam, M.; Nagarajan, P.; Remanan, M. Defect localization using nonlinear Lamb wave mixing technique. J. Nondestruct. Eval. 2021, 40, 16. [Google Scholar] [CrossRef]
- Jiao, J.; Li, L.; Gao, X.; Cheng, Q.; He, C.; Wu, B. Application of nonlinear Lamb wave mixing method for residual stress measurement in metal plate. Chin. J. Mech. Eng. 2023, 36, 12. [Google Scholar] [CrossRef]
- Brillouin, L. Sur les tensions de radiation. Ann. Phys. 1925, 4, 528–586. [Google Scholar] [CrossRef]
- Thurston, R.; Shapiro, M. Interpretation of ultrasonic experiments on finite amplitude waves. J. Acoust. Soc. Am. 1967, 41, 276. [Google Scholar] [CrossRef]
- Cantrell, J. Acoustic-radiation stress in solids. I—Theory. Phys. Rev. B 1984, 30, 3214. [Google Scholar] [CrossRef]
- Yost, W.; Cantrell, J. Acoustic-radiation stress in solids. II. Experiment. Phys. Rev. B 1984, 30, 3221–3227. [Google Scholar] [CrossRef]
- Cantrell, J.; Yost, W. Acoustic radiation stress in solids. Ultrason. Symp. 1983, 32, 78–122. [Google Scholar]
- Narasimha, K.; Kannan, E.; Balasubramaniam, K. Simplified experimental technique to extract the acoustic radiation induced static strain in solids. Appl. Phys. Lett. 2007, 91, 1112. [Google Scholar] [CrossRef]
- Jacob, X.; Takatsu, R.; Barriere, C.; Royer, D. Experimental study of the acoustic radiation strain in solids. Appl. Phys. Lett. 2006, 88, 134111–134113. [Google Scholar] [CrossRef]
- Narasimha, K.T.; Kannan, E.; Balasubramaniam, K. Issues on the pulse-width dependence and the shape of acoustic radiation induced static displacement pulses in solids. J. Appl. Phys. 2009, 105, 073506. [Google Scholar] [CrossRef]
- Qu, J.; Nagy, P.; Jacobs, L. On the acoustic-radiation-induced strain and stress in elastic solids with quadratic nonlinearity (L). J. Acoust. Soc. Am. 2011, 129, 3449–3452. [Google Scholar] [CrossRef]
- Qu, J.; Nagy, P.; Jacobs, L. Pulse propagation in an elastic medium with quadratic nonlinearity (L). J. Acoust. Soc. Am. 2012, 131, 1827. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Liu, Y.; Hu, N. Interaction of guided waves in isotropic elastic plates with weak material nonlinearity: Sum-frequency, difference-frequency, second harmonic and zero-frequency components. In Proceedings of the 9th International Symposium on NDT in Aerospace, Xiamen, China, 8–10 November 2017; Available online: http://www.ndt.net/?id=21993 (accessed on 5 February 2018).
- Wan, X.; Tse, P.; Zhang, X.; Xu, G.; Ma, H. Numerical study on static component generation from the primary Lamb waves propagating in a plate with nonlinearity. Smart Mater. Struct. 2018, 27, 045006. [Google Scholar] [CrossRef]
- Sun, X.; Ding, X.; Li, F.; Zhou, S.; Liu, Y.; Hu, N.; Zhao, Y.; Zhang, J. Interaction of Lamb wave modes with weak material nonlinearity: Generation of symmetric zero-frequency mode. Sensors 2018, 18, 2451. [Google Scholar] [CrossRef] [PubMed]
- Nagy, P.; Qu, J.; Jacobs, L. Finite-size effects on the quasistatic displacement pulse in a solid specimen with quadratic nonlinearity. J. Acoust. Soc. Am. 2013, 134, 1760–1774. [Google Scholar] [CrossRef]
- Sun, X.; Shui, G.; Zhao, Y.; Liu, W.; Deng, M.; Hu, N. Evaluation of early stage local plastic damage induced by bending using quasi-static component of Lamb waves. NDT E Int. 2020, 116, 102332. [Google Scholar] [CrossRef]
- Sun, X.; Liu, H.; Zhao, Y.; Qu, J.; Deng, M.; Hu, N. The zero-frequency component of bulk waves in solids with randomly distributed micro-cracks. Ultrasonics 2020, 107, 106172. [Google Scholar] [CrossRef] [PubMed]
- Deng, M. An experimental approach for detection of the acoustic radiation induced static component in solids. Chin. Phys. Lett. 2020, 37, 074301. [Google Scholar] [CrossRef]
- Gao, G.; Chen, H.; Hu, N.; Deng, M. Experimental observation of static component generation by Lamb wave propagation in an elastic plate. Ultrasonics 2021, 117, 106537. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Deng, M.; Gao, G.; Hu, N.; Xiang, Y. Modeling and simulation of static component generation of Lamb wave propagation in a layered plate. Ultrasonics 2021, 116, 106473. [Google Scholar] [CrossRef]
- Sun, X. Locating mutation damage based on the zero-frequency component of nonlinear Lamb waves. Mech. Sys. Signal Process. 2023, 197, 110384. [Google Scholar] [CrossRef]
- Hu, Z.; An, Z.; Kong, Y.; Lian, G.; Wang, X. The nonlinear S0 Lamb mode in a plate with a linearly-varying thickness. Ultrasonics 2018, 94, 102–108. [Google Scholar] [CrossRef]




| ρ (kg/m3) | A (GPa) | B (GPa) | C (GPa) | λ (GPa) | µ (GPa) | E (GPa) | ν |
|---|---|---|---|---|---|---|---|
| 2704 | −416 | −131 | −150.5 | 70.3 | 26.96 | 68.9 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Shui, G. Investigation of the Zero-Frequency Component of Nonlinear Lamb Waves in a Symmetrical Undulated Plate. Sensors 2024, 24, 4878. https://doi.org/10.3390/s24154878
Sun X, Shui G. Investigation of the Zero-Frequency Component of Nonlinear Lamb Waves in a Symmetrical Undulated Plate. Sensors. 2024; 24(15):4878. https://doi.org/10.3390/s24154878
Chicago/Turabian StyleSun, Xiaoqiang, and Guoshuang Shui. 2024. "Investigation of the Zero-Frequency Component of Nonlinear Lamb Waves in a Symmetrical Undulated Plate" Sensors 24, no. 15: 4878. https://doi.org/10.3390/s24154878






