GNSS Receiver Fingerprinting Based on Time Skew of Embedded CSAC Clock
Abstract
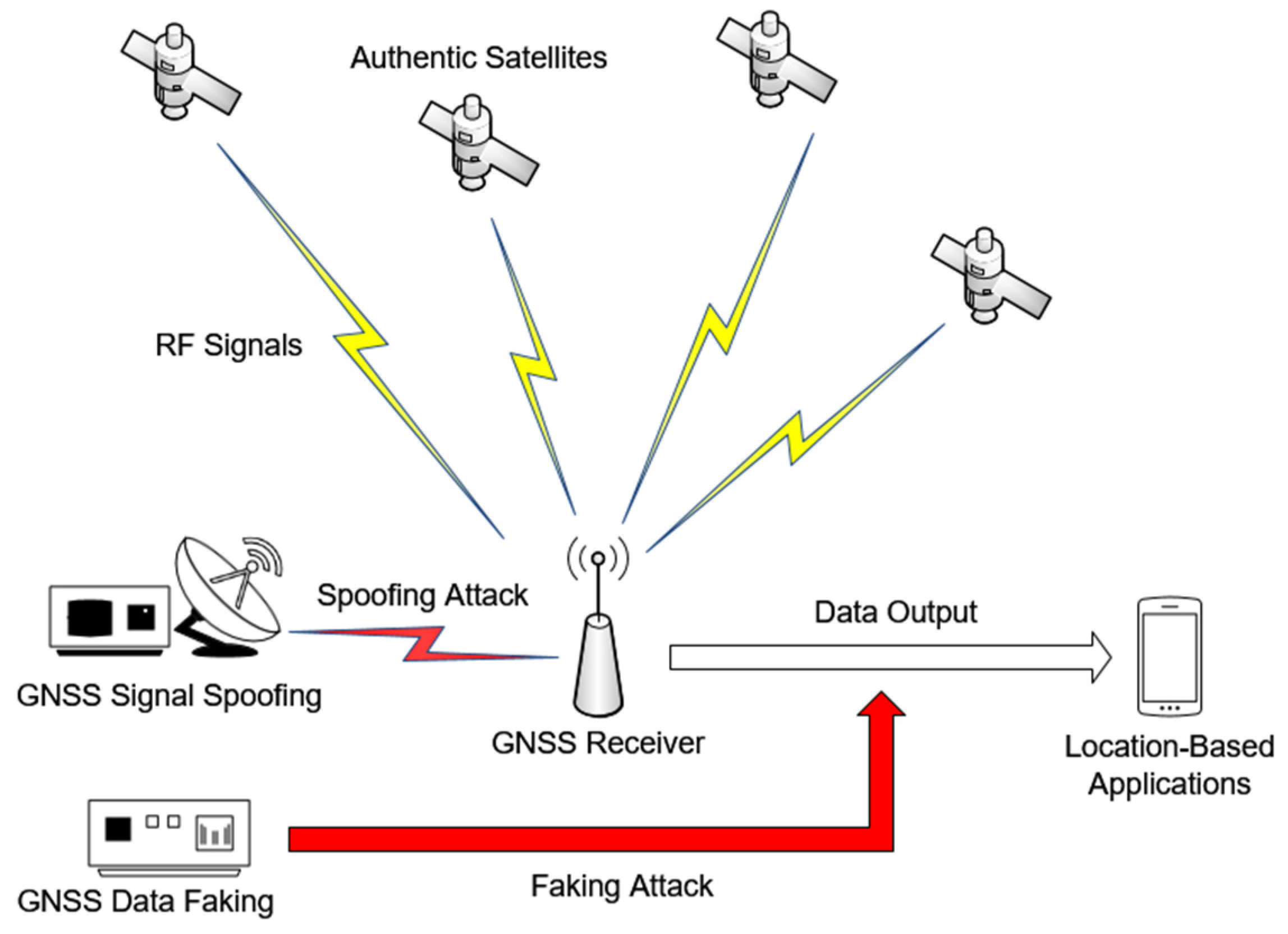
1. Introduction
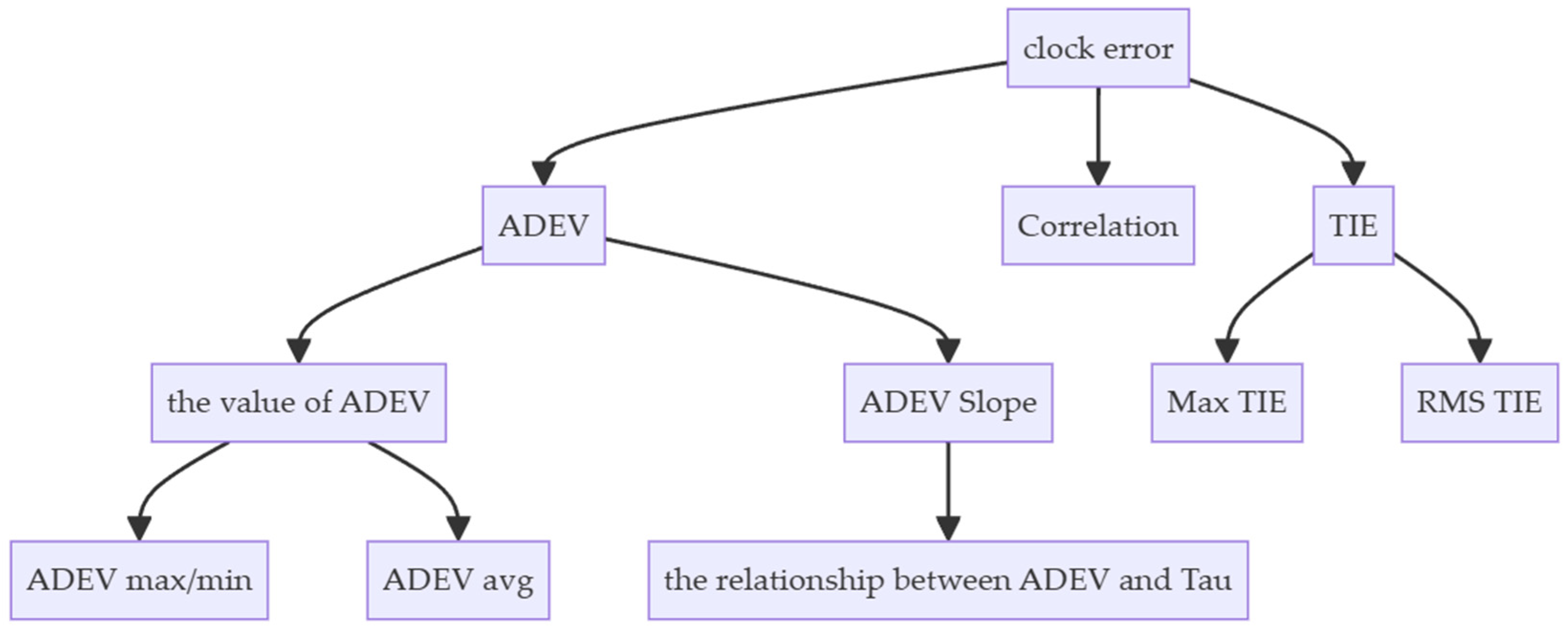
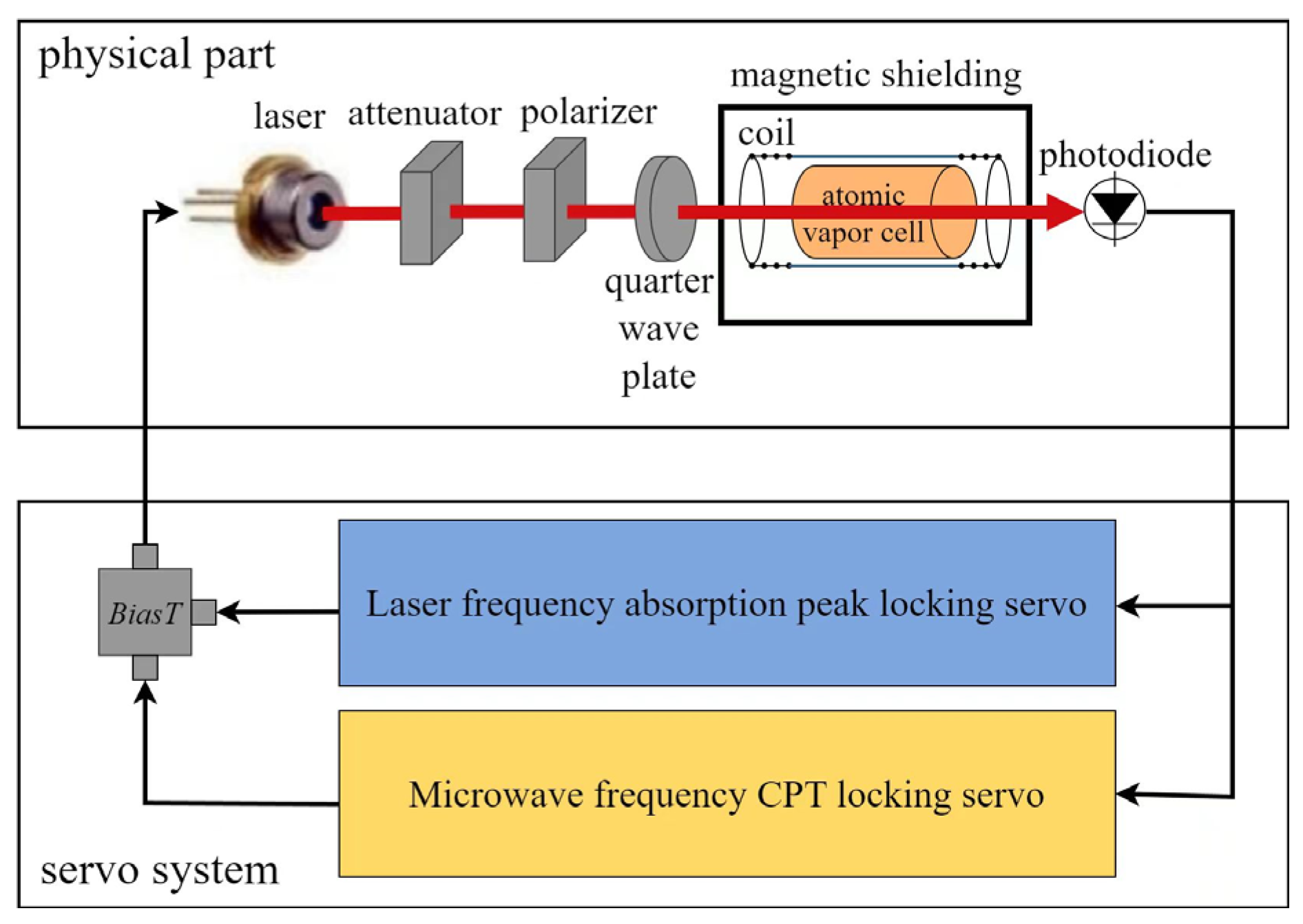
2. Theory
2.1. CSAC Time Skew Analysis
2.2. Fingerprinting Method
3. Results
3.1. Experiment Platform and Data Collecting
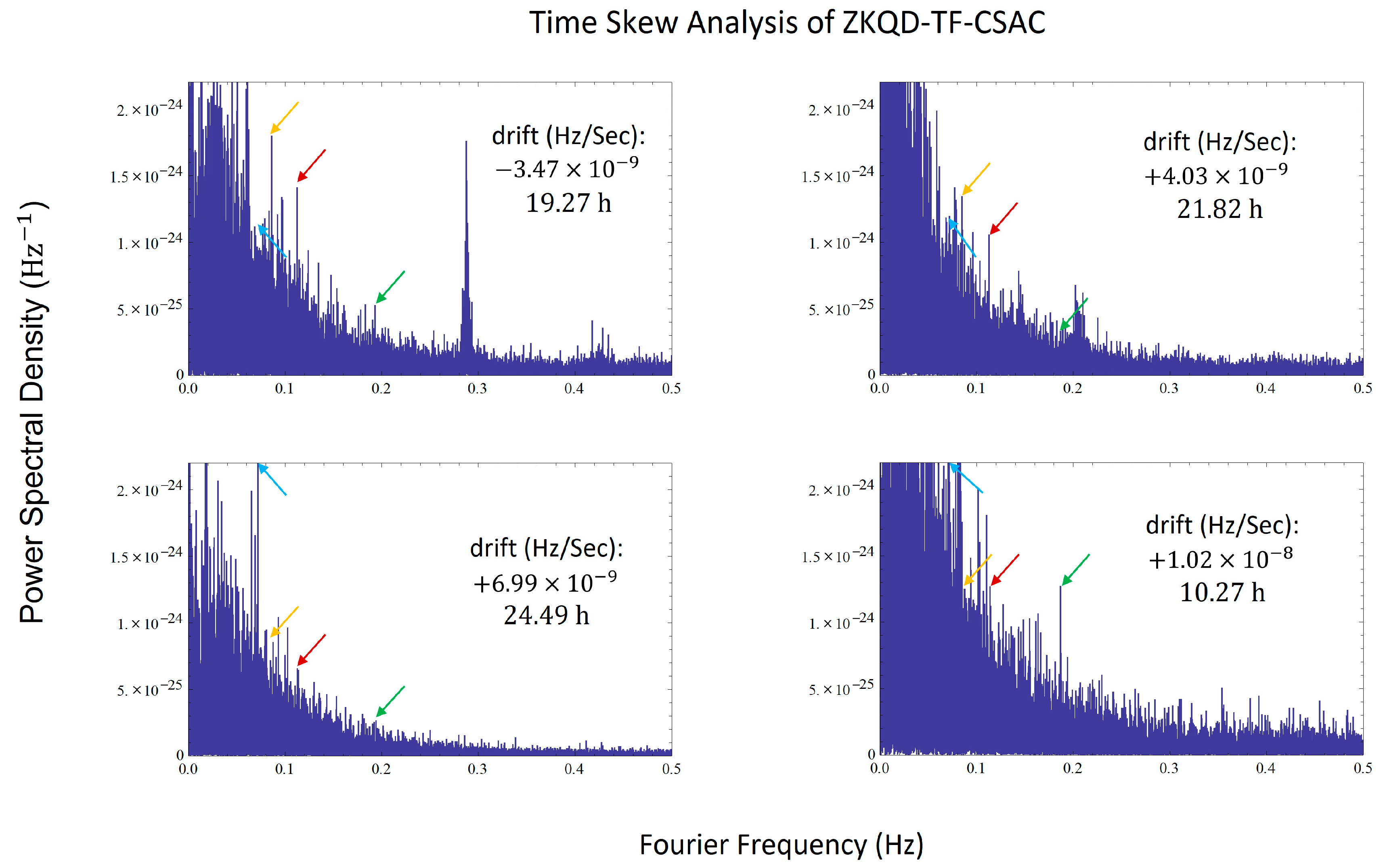
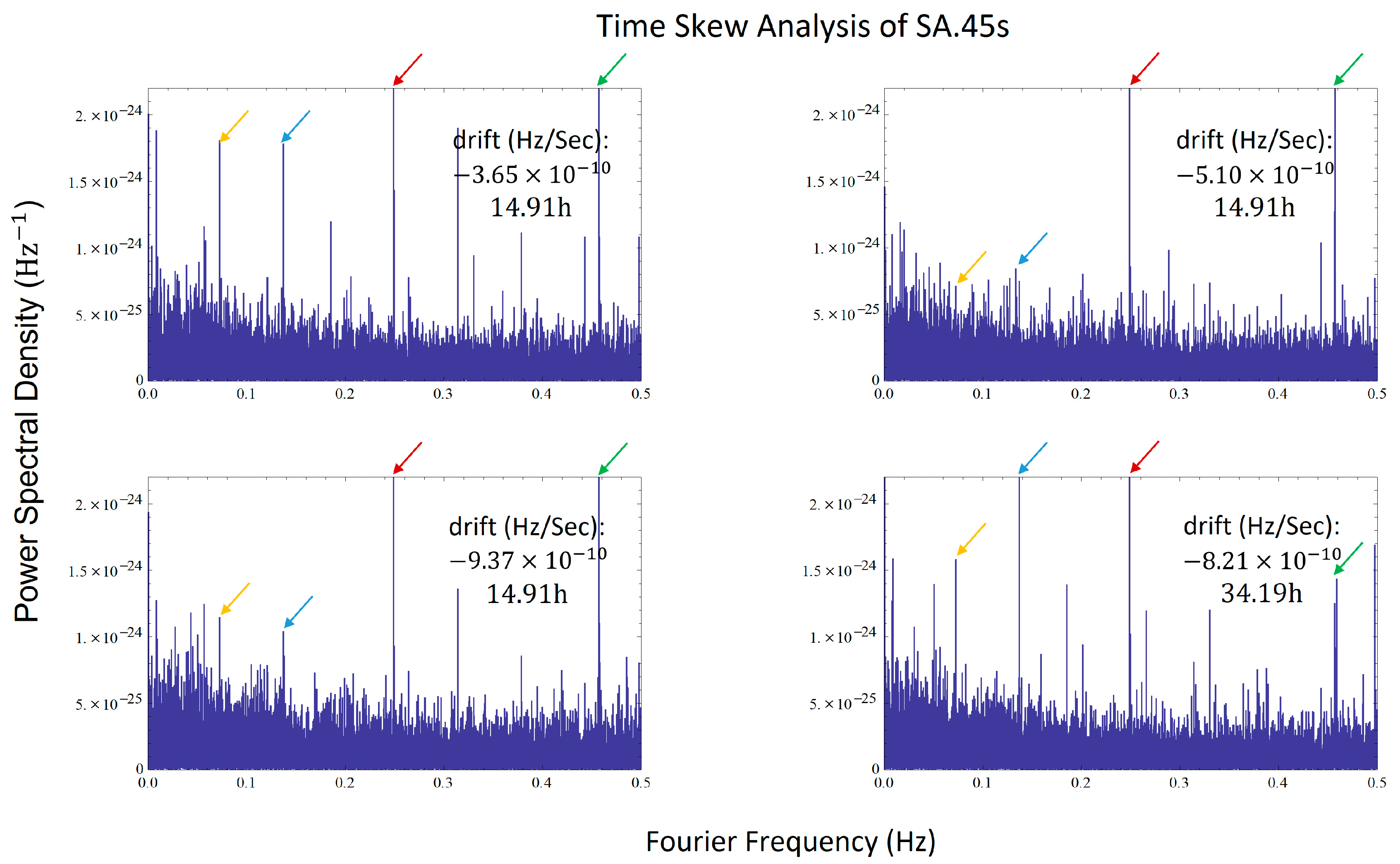
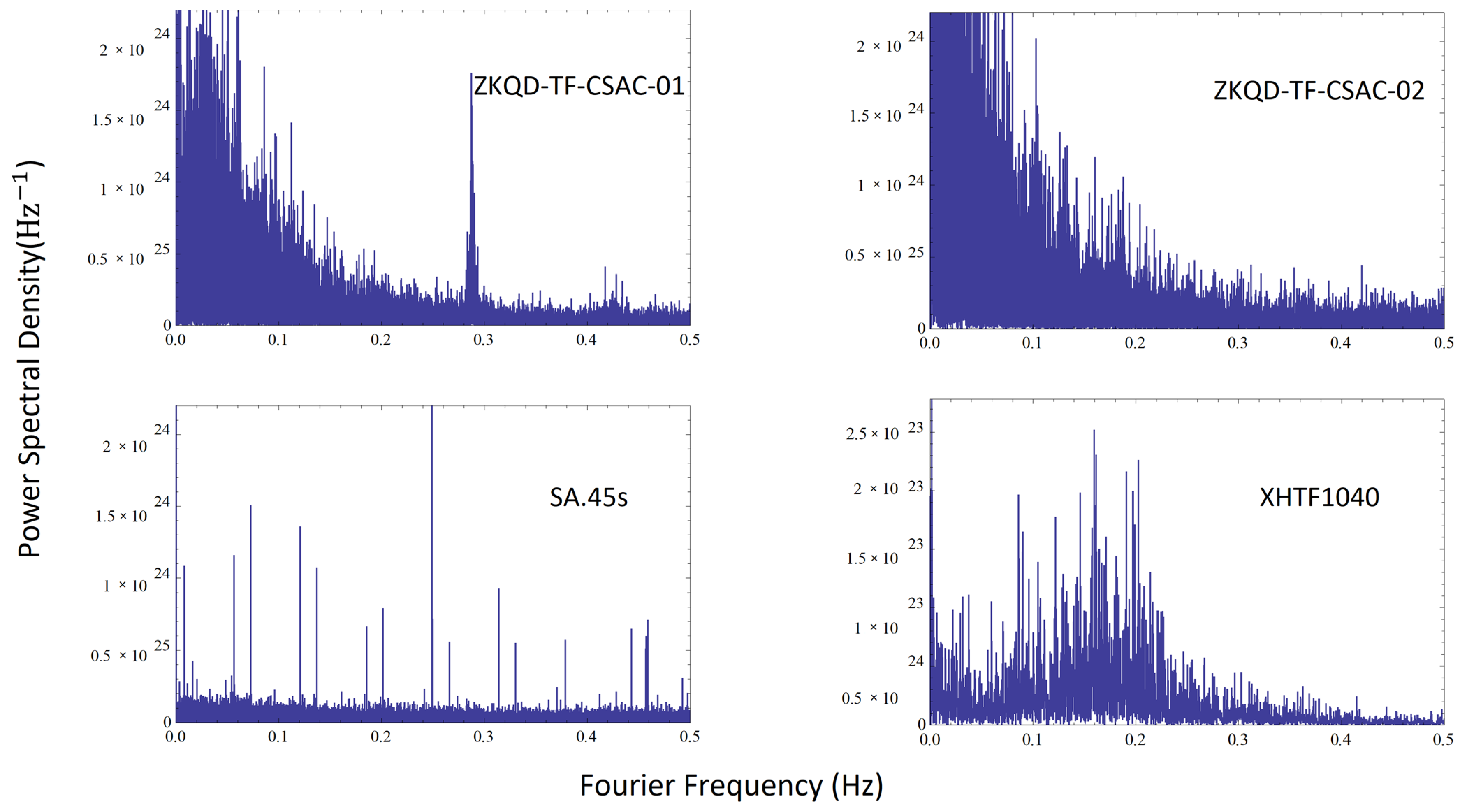
3.2. CSAC Time Skew Analysis
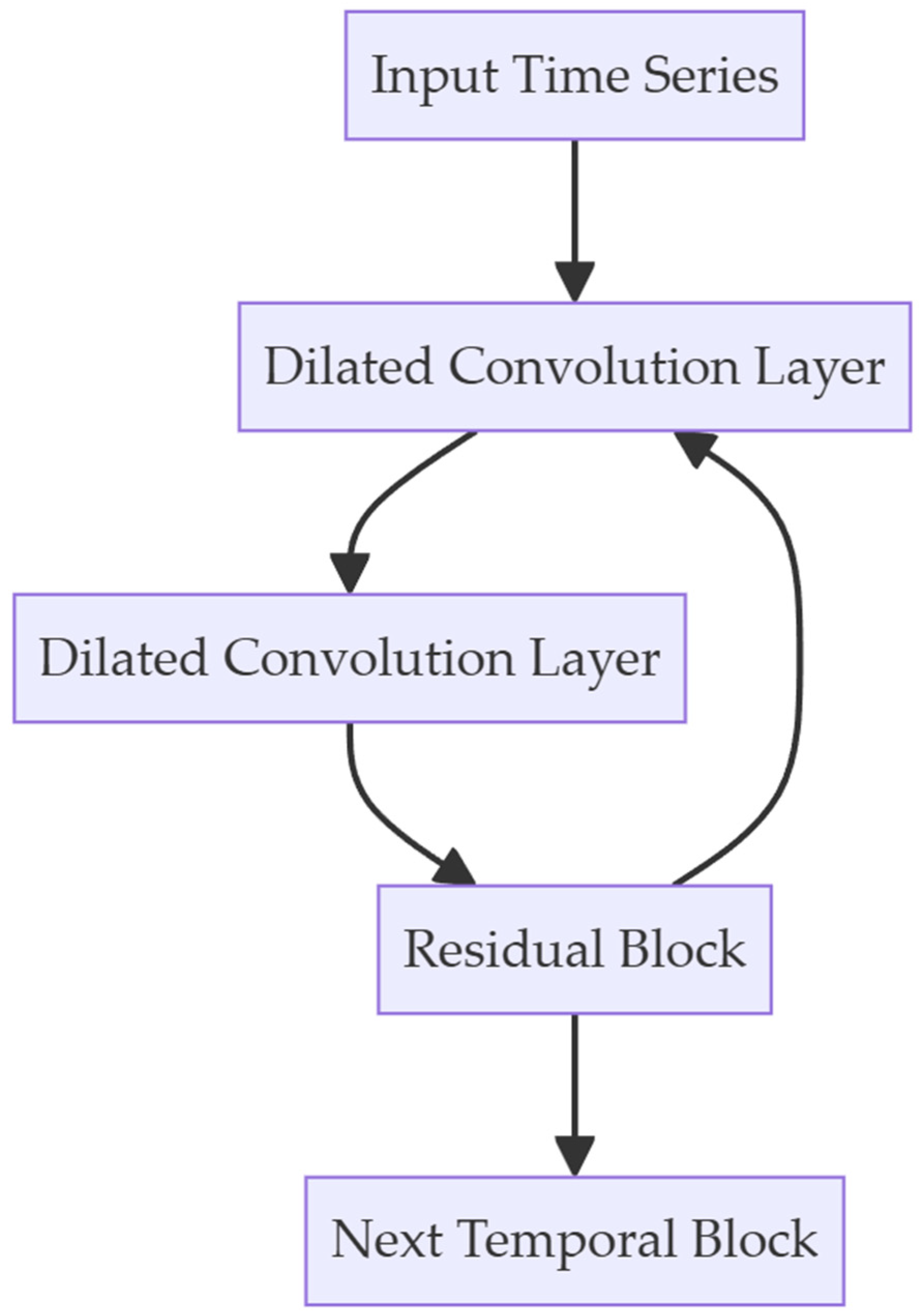
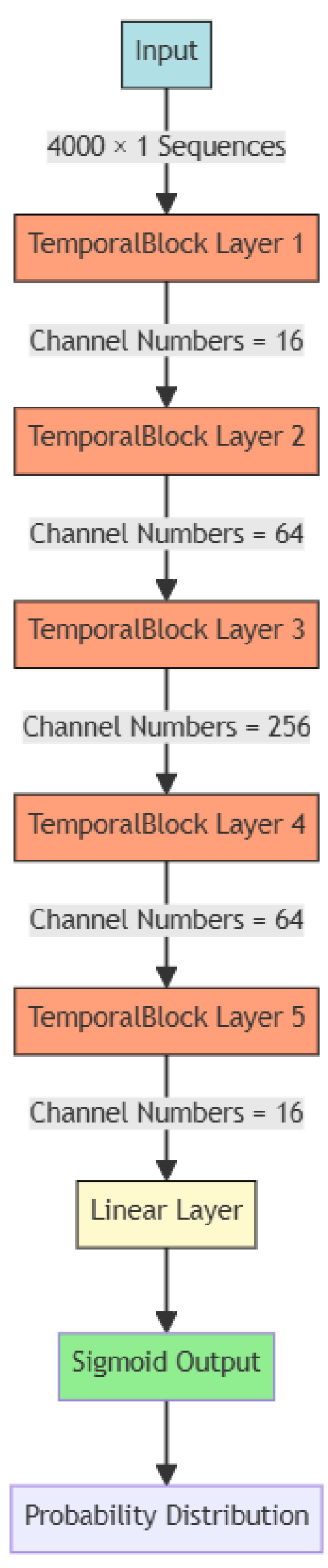
3.3. Fingerprint for Classification
4. Discussion
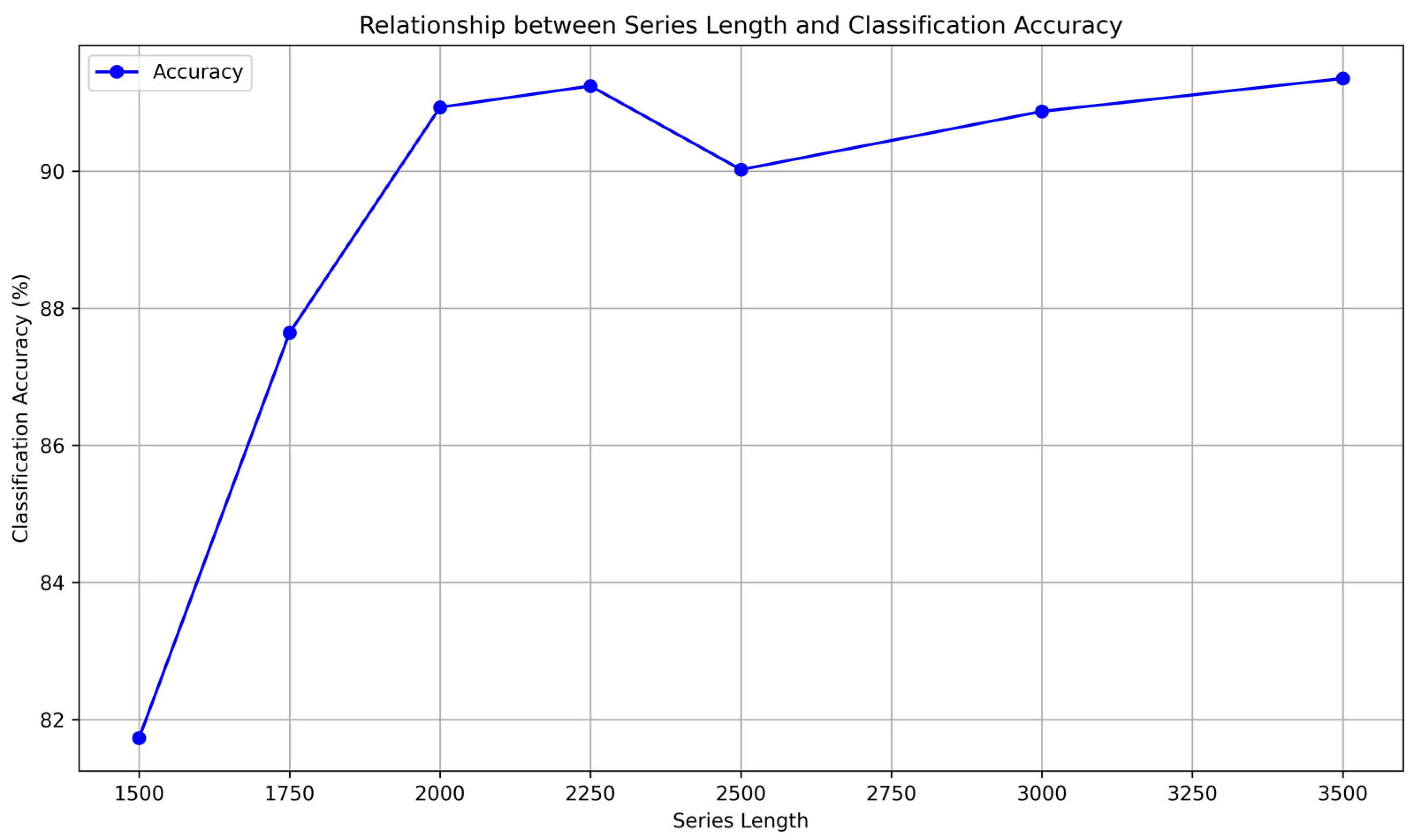
4.1. Impact of Time Skew Series Length
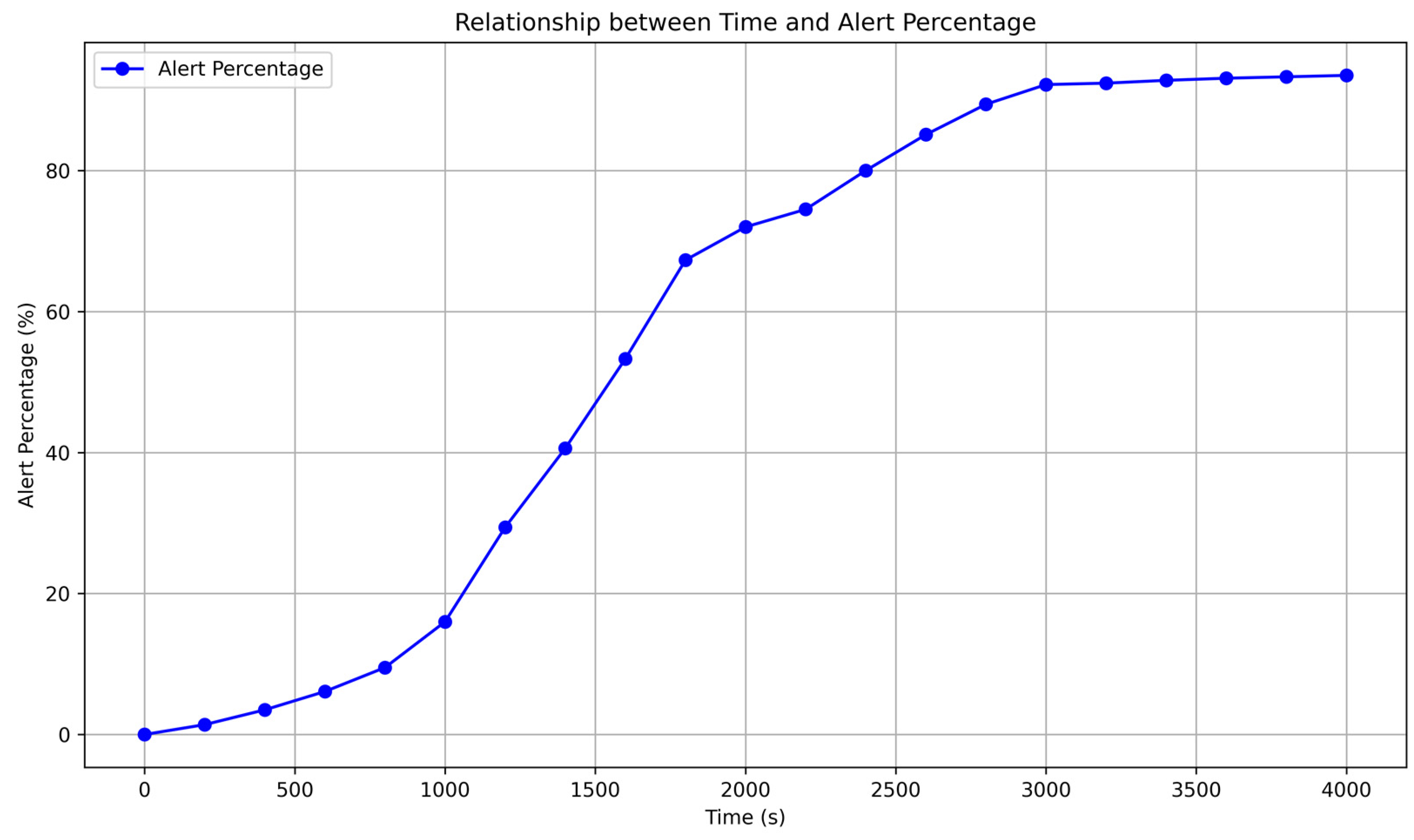
4.2. Impact of Unstable GNSS Timing Services
4.3. Feasibility for GNSS Spoofing Detection
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Kaplan, E.D.; Hegarty, C. Understanding GPS/GNSS: Principles and Applications; Artech House: Norwood, MA, USA, 2017. [Google Scholar]
- Rydlund, P.H.; Densmore, B.K. Methods of Practice and Guidelines for Using Survey-Grade Global Navigation Satellite Systems (GNSS) to Establish Vertical Datum in the United States Geological Survey; US Geological Survey: Reston, VA, USA, 2012. [Google Scholar]
- Regulation (EU) No 165/2014 of the European Parliament and of the Council of 4 February 2014 on Tachographs in Road Transport. Available online: http://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32014R0165from=EN (accessed on 11 September 2017).
- Grant, A.; Williams, P.; Shaw, G.; De Voy, M.; Ward, N. Understanding GNSS Availability and How it Impacts Maritime Safety. In Proceedings of the 2011 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 24–26 January 2011; pp. 687–695. [Google Scholar]
- Kerns, A.J.; Shepard, D.P.; Bhatti, J.A.; Humphreys, T.E. Unmanned aircraft capture and control via GPS spoofing. J. Field Robot. 2014, 31, 617–636. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Ledvina, B.M.; Psiaki, M.L.; O’Hanlon, B.W.; Kintner, P.M. Assessing the spoofing threat: Development of a portable GPS civilian spoofer. In Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 2314–2325. [Google Scholar]
- Harati-Mokhtari, A.; Wall, A.; Brooks, P.; Wang, J. Automatic Identification System (AIS): Data reliability and human error implications. J. Navig. 2007, 60, 373–389. [Google Scholar] [CrossRef]
- Xu, Q.; Zheng, R.; Saad, W.; Han, Z. Device Fingerprinting in Wireless Networks: Challenges and Opportunities. IEEE Commun. Surv. Tutor. 2016, 18, 94–104. [Google Scholar] [CrossRef]
- Kohno, T.; Broido, A.; Claffy, K.C. Remote physical device fingerprinting. IEEE Trans. Dependable Secur. Comput. 2005, 2, 93–108. [Google Scholar] [CrossRef]
- Choe, H.C.; Poole, C.E.; Andrea, M.Y.; Szu, H.H. Novel identification of intercepted signals from unknown radio transmitters. In Proceedings of the Wavelet Applications II, Orlando, FL, USA, 17–21 April 1995; pp. 504–517. [Google Scholar]
- Ureten, O.; Serinken, N. Wireless security through RF fingerprinting. Can. J. Electr. Comput. Eng. 2007, 32, 27–33. [Google Scholar] [CrossRef]
- Meng, W.; Xiao, W.; Ni, W.; Xie, L. Secure and robust Wi-Fi fingerprinting indoor localization. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011; pp. 1–7. [Google Scholar]
- Danev, B.; Heydt-Benjamin, T.S.; Capkun, S. Physical-layer Identification of RFID Devices. In Proceedings of the USENIX Security Symposium, Montreal, QC, Canada, 10–14 August 2009; pp. 199–214. [Google Scholar]
- Ellis, K.; Serinken, N. Characteristics of radio transmitter fingerprints. Radio Sci. 2001, 36, 585–597. [Google Scholar] [CrossRef]
- IEEE Std. 802.11-1997; Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. C/LAN/MAN-LAN/MAN Standards Committee: Washington, DC, USA, 1997.
- Arackaparambil, C.; Bratus, S.; Shubina, A.; Kotz, D. On the reliability of wireless fingerprinting using clock skews. In Proceedings of the Third ACM Conference on Wireless Network Security, Hoboken, NJ, USA, 22–24 March 2010; pp. 169–174. [Google Scholar]
- Sanchez-Rola, I.; Santos, I.; Balzarotti, D. Clock around the clock: Time-based device fingerprinting. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 1502–1514. [Google Scholar]
- Lanze, F.; Panchenko, A.; Braatz, B.; Zinnen, A. Clock skew based remote device fingerprinting demystified. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 813–819. [Google Scholar]
- Lu, X.; Pang, R.; Lio, P. Poster: CFMAP: A Robust CPU Clock Fingerprint Model for Device Authentication. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, CA, USA, 7–11 November 2022; pp. 3407–3409. [Google Scholar]
- Kikuchi, H.; Tominaga, Y.; Tanaka, Y. Remote host fingerprinting based on clock skew. In Proceedings of the 2008 International Symposium on Communications and Information Technologies, Vientiane, Laos, 21–23 October 2008; pp. 225–227. [Google Scholar]
- Shang, C.; Cao, J.; Zhu, T.; Zhang, Y.; Niu, B.; Li, H. CADFA: A Clock Skew-Based Active Device Fingerprint Authentication Scheme for Class-1 IoT Devices. IEEE Syst. J. 2024, 18, 590–599. [Google Scholar] [CrossRef]
- Borio, D.; Gioia, C.; Cano Pons, E.; Baldini, G. GNSS Receiver Identification Using Clock-Derived Metrics. Sensors 2017, 17, 2120. [Google Scholar] [CrossRef] [PubMed]
- Spanghero, M.; Papadimitratos, P. Detecting GNSS misbehaviour with high-precision clocks. In Proceedings of the 14th ACM Conference on Security and Privacy in Wireless and Mobile Networks, New York, NY, USA, 28 June–2 July 2021; pp. 389–391. [Google Scholar]
- Lin, Q.; Schön, S. Feasibility of CSAC-Assisted GNSS Receiver Fingerprinting; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Allan, D.W. Statistics of atomic frequency standards. Proc. IEEE 1966, 54, 221–230. [Google Scholar] [CrossRef]
- Jain, A.; Schön, S. Influence of receiver clock modeling in GNSS-based flight navigation: Concepts and experimental results. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 208–218. [Google Scholar]
- Knappe, S.; Schwindt, P.; Shah, V.; Hollberg, L.; Kitching, J.; Liew, L.; Moreland, J. A chip-scale atomic clock based on 87 Rb with improved frequency stability. Opt. Express 2005, 13, 1249–1253. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yang, W.; Zhang, S.; Zhao, J. Rubidium chip-scale atomic clock with improved long-term stability through light intensity optimization and compensation for laser frequency detuning. JOSA B 2016, 33, 1756–1763. [Google Scholar] [CrossRef]
- Ma, L.; You, Z.; Li, B.; Zhou, B.; Han, R. Deep coupled integration of CSAC and GNSS for robust PNT. Sensors 2015, 15, 23050–23070. [Google Scholar] [CrossRef] [PubMed]
- Fernández, E.; Calero, D.; Parés, M.E. CSAC characterization and its impact on GNSS clock augmentation performance. Sensors 2017, 17, 370. [Google Scholar] [CrossRef] [PubMed]
- Krawinkel, T.; Schön, S.; Bauch, A. Application of miniaturized atomic clocks in kinematic GNSS single point positioning. In Proceedings of the 2014 European Frequency and Time Forum (EFTF), Neuchâtel, Switzerland, 24–26 June 2014; pp. 97–100. [Google Scholar]
- Kunzi, F.; Montenbruck, O. Precise disciplining of a chip-scale atomic clock using PPP with broadcast ephemerides. GPS Solut. 2023, 27, 165. [Google Scholar] [CrossRef]
- Quessada, A.; Kovacich, R.P.; Courtillot, I.; Clairon, A.; Santarelli, G.; Lemonde, P. The Dick effect for an optical frequency standard. J. Opt. B Quantum Semiclas. Opt. 2003, 5, S150. [Google Scholar] [CrossRef]
- He, X.; Fang, S.; Yuan, Z.; Chen, J.; Qi, X.; Chen, X.; Wang, Q. Noise Sources Evaluation of Compact Optically Pumped Cesium Beam Atomic Clock. In Proceedings of the 2022 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS), Paris, France, 24–28 April 2022; pp. 1–2. [Google Scholar]
- Zhu, M.; Cutler, L. Theoretical and experimental study of light shift in a CPT-based Rb vapor cell frequency standard. In Proceedings of the 32th Annual Precise Time and Time Interval Systems and Applications Meeting, Reston, VA, USA, 28–30 November 2000; pp. 311–324. [Google Scholar]
- He, Y.; Zhao, J. Temporal convolutional networks for anomaly detection in time series. In Proceedings of the Journal of Physics: Conference Series, Guilin, China, 13 March 2019; p. 042050. [Google Scholar]
- Lea, C.; Flynn, M.D.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal convolutional networks for action segmentation and detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 156–165. [Google Scholar]
- Satelite PCIE Timing Board. Available online: https://qidigdz.com/products-dt?product_id=312 (accessed on 17 July 2024).
- Song, H.; Dong, S.; Wu, W.; Jiang, M.; Wang, W. Detecting an atomic clock frequency anomaly using an adaptive Kalman filter algorithm. Metrologia 2018, 55, 350. [Google Scholar] [CrossRef]
- Wang, X. Research on the Discipline of Secondary Frequency Sources Based on Time-to-Digital Converter (TDC). Master’s Thesis, Peking University, Beijing, China, 2019. [Google Scholar]




| TCXO (Freqtrol FCOX101) | CSAC (Microsemi sa.45s) | |
|---|---|---|
| Size | 21.0 mm × 13.6 mm × 8.5 mm | 40.6 mm × 35.5 mm × 11.4 mm |
| Frequency Accuracy | 3.0 × 10−7 | 5.0 × 10−11 |
| Frequency Stability (Allan Variation, 1 s) | 5.0 × 10−11 | 1.5 × 10−10 |
| Aging Rate (per year) | 5.0 × 10−8 | 1 × 10−9 |
| Atom Element | Chamber Technique | |
|---|---|---|
| ZKQD-TF-CSAC | Rb | Cell |
| XHTF1040 | Rb | MEMS |
| SA.45s | Cs | MEMS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, S.; Dai, L.; Shi, M.; Wang, J.; Tang, C.; Wu, H.; Zhao, J. GNSS Receiver Fingerprinting Based on Time Skew of Embedded CSAC Clock. Sensors 2024, 24, 4897. https://doi.org/10.3390/s24154897
Gui S, Dai L, Shi M, Wang J, Tang C, Wu H, Zhao J. GNSS Receiver Fingerprinting Based on Time Skew of Embedded CSAC Clock. Sensors. 2024; 24(15):4897. https://doi.org/10.3390/s24154897
Chicago/Turabian StyleGui, Sibo, Li Dai, Meng Shi, Junchao Wang, Chuwen Tang, Haitao Wu, and Jianye Zhao. 2024. "GNSS Receiver Fingerprinting Based on Time Skew of Embedded CSAC Clock" Sensors 24, no. 15: 4897. https://doi.org/10.3390/s24154897
APA StyleGui, S., Dai, L., Shi, M., Wang, J., Tang, C., Wu, H., & Zhao, J. (2024). GNSS Receiver Fingerprinting Based on Time Skew of Embedded CSAC Clock. Sensors, 24(15), 4897. https://doi.org/10.3390/s24154897





