An Experimental Study of the Acoustic Signal Characteristics of Locked-Segment Damage Evolution in a Landslide Model
Abstract
:1. Introduction
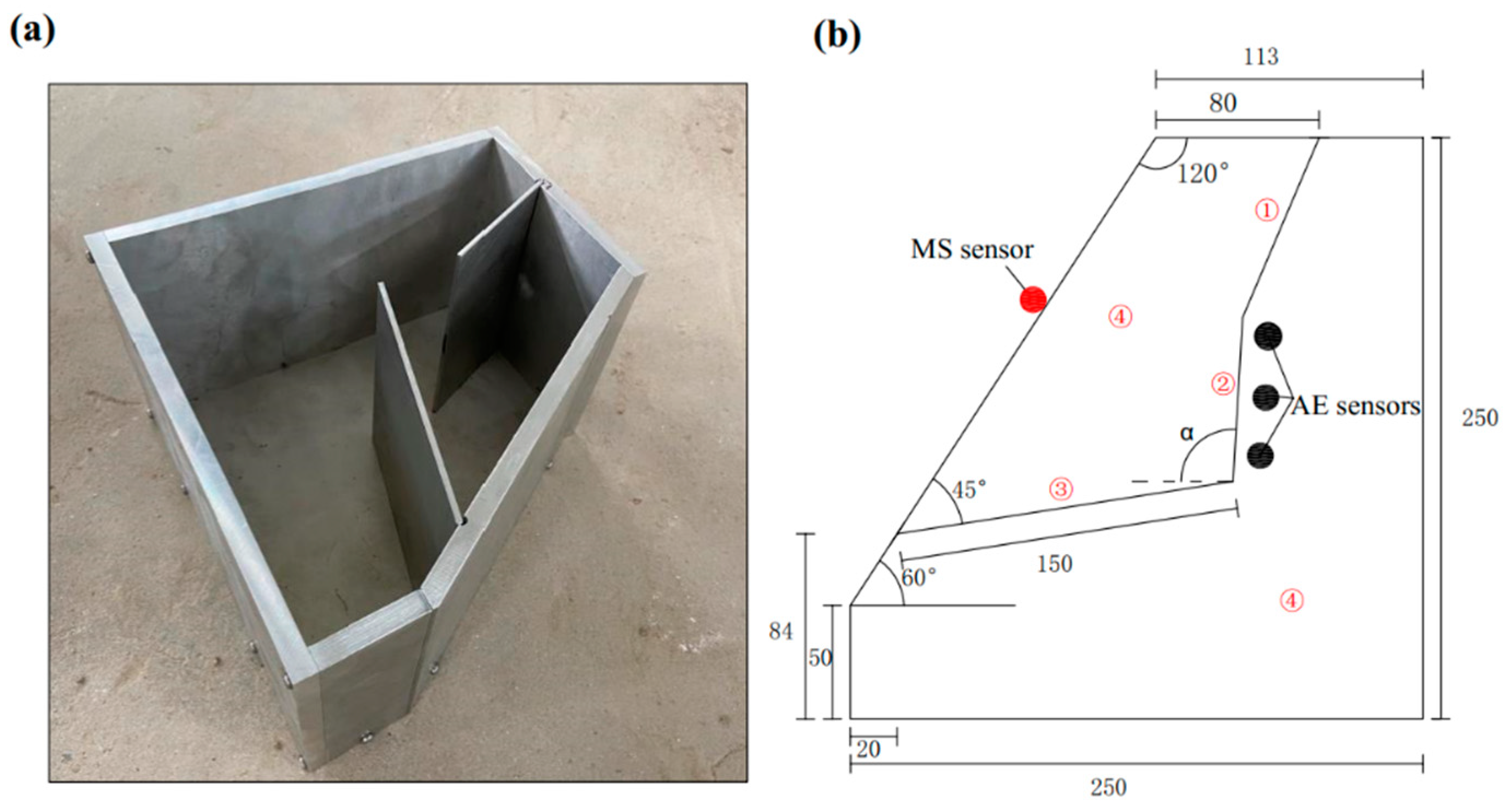
2. Experimental Methodology
2.1. Sample Preparation
2.2. Test Apparatus
2.3. Test Schemes
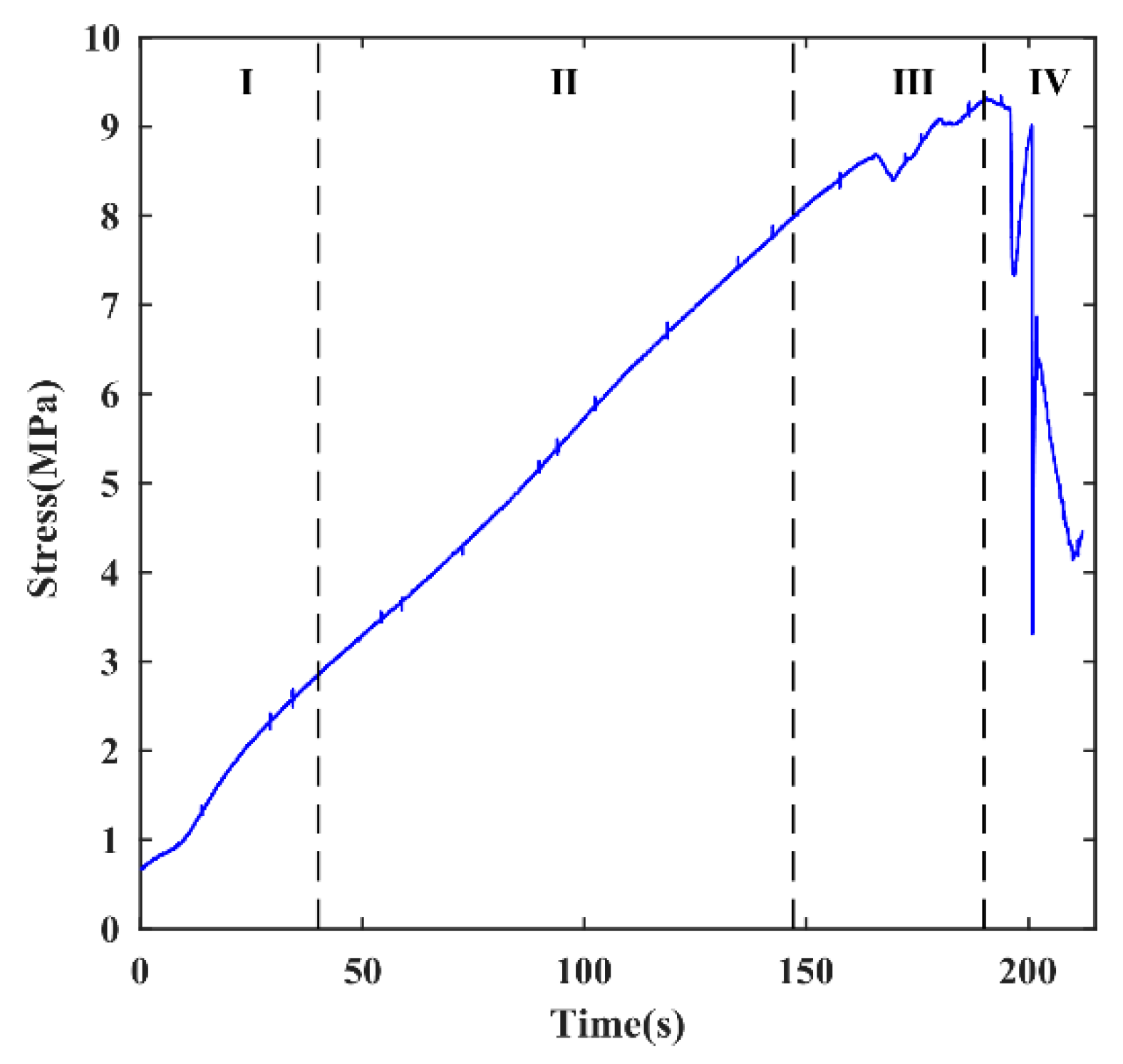
3. Results and Analysis
3.1. Analysis of Video Image
3.2. Analysis of MS Signal
3.2.1. Activity and Intensity
- (1)
- In the stage of compaction due to initial damage (stage I), the density and amplitude of the MS signal are small as the external pressure gradually compresses the pre-existing cracks, voids, and/or other defects.
- (2)
- During the elastic deformation stage (stage II), the density and amplitude of the MS signal are lower than those in the previous stage (stage I), indicating insufficient force to induce the formation of new microcracks in the locking section under the current load level. Notably, a significant locking effect and stress accumulation along the locking section are observed due to the creeping segment at the front and the tensile crack at the back of the slope.
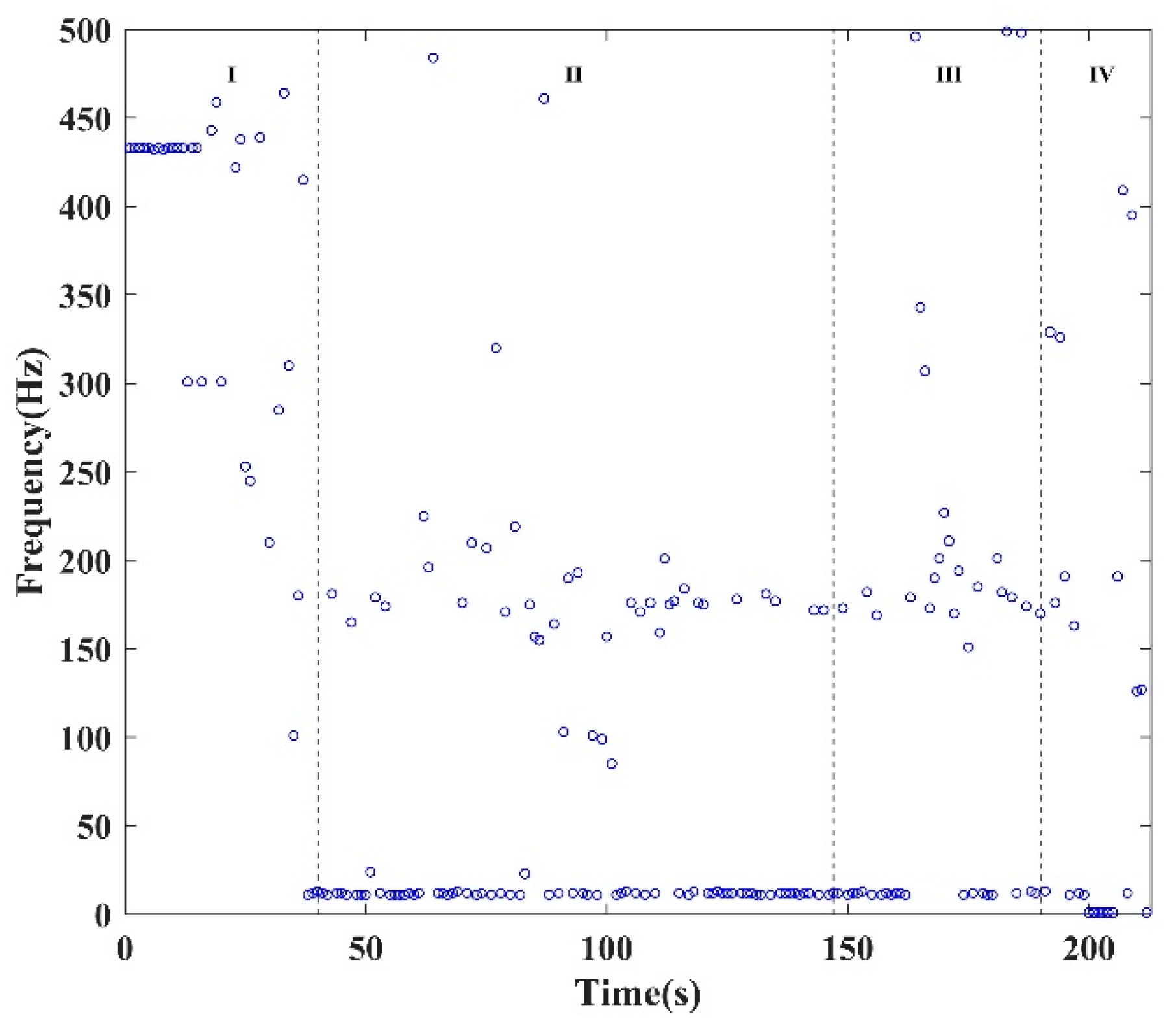
3.2.2. Frequency
- (1)
- In the compaction stage due to initial damage (stage I), the main frequencies ranged from 250 to 500 Hz, gradually transitioning towards the low-frequency band.
- (2)
- During the elastic deformation stage (stage II), the main frequencies of the intercepted MS signals were predominantly distributed below 250 Hz.
- (3)
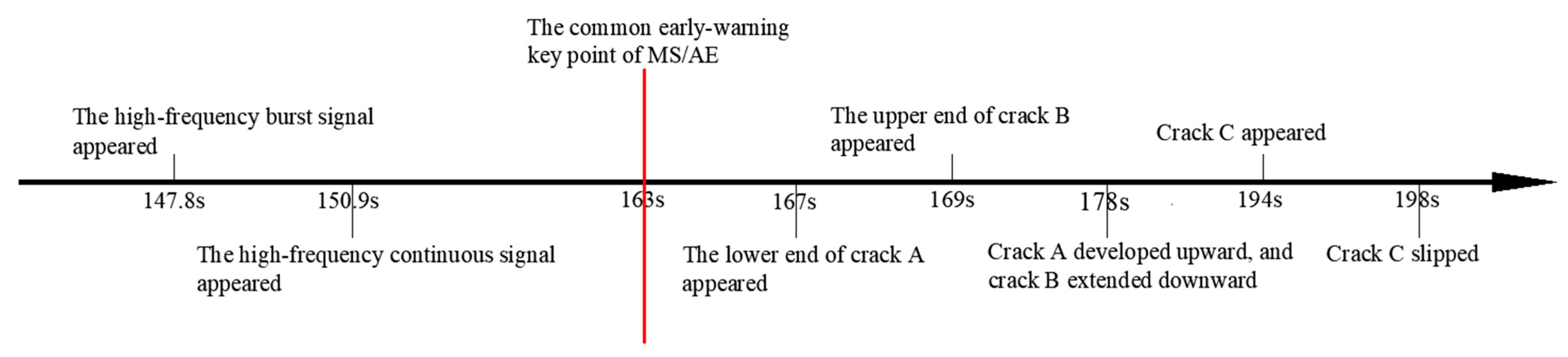
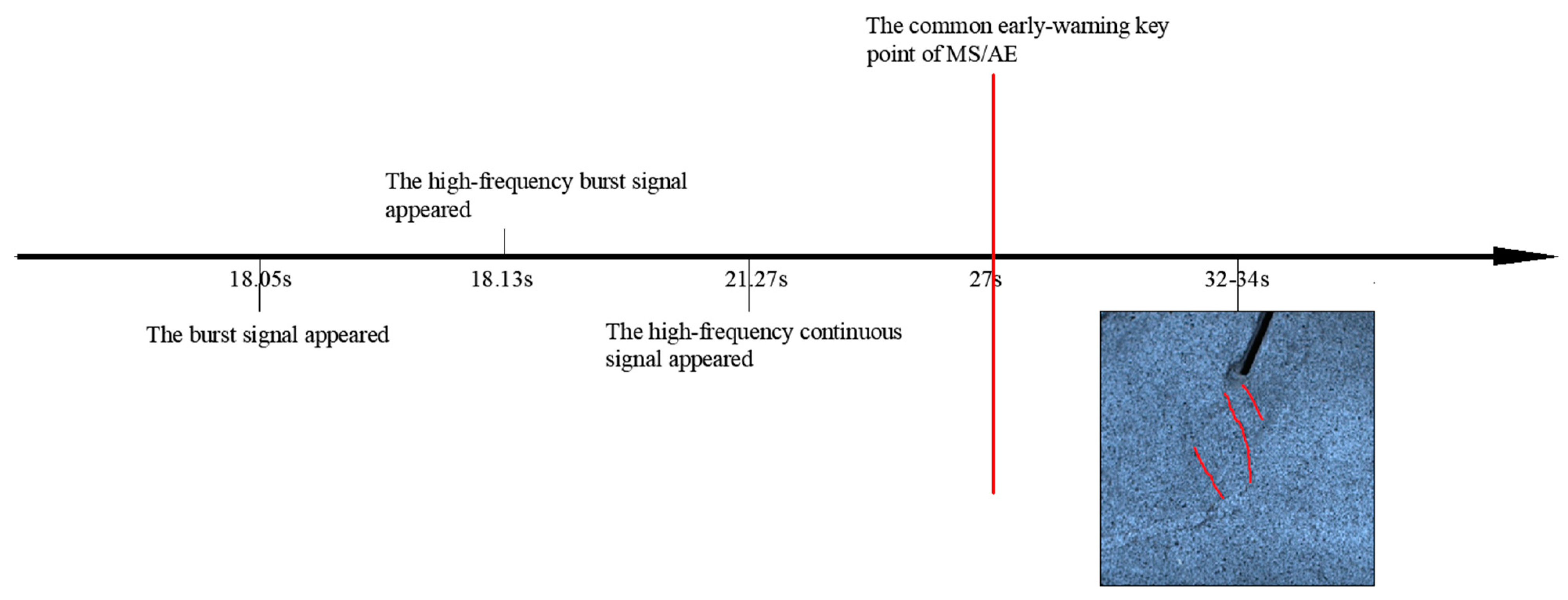
- In the crack propagation and failure stage (stages III and IV), high-frequency MS signals reappeared. At 163 s, the main frequency was 487.3 Hz. The resurgence of the high-frequency component signifies shear failure in the locking section and the emergence of microcracks appeared in the locking section. With increasing load, numerous microcracks in the locking section will expand and form macrocracks on the free face of the locking section. Thus, the reappearance of the high-frequency component serves as an early-warning point for rock instability. Notably, the first macrocrack appeared on the free face of the locking section under loading conditions at 167 s, while the time of the early-warning point of the MS signal was 163 s. Therefore, the time of the early-warning point of the MS signal precedes that of the video image.
3.3. Classification Method of AE Signals
4. Analysis of Classified AE Signals
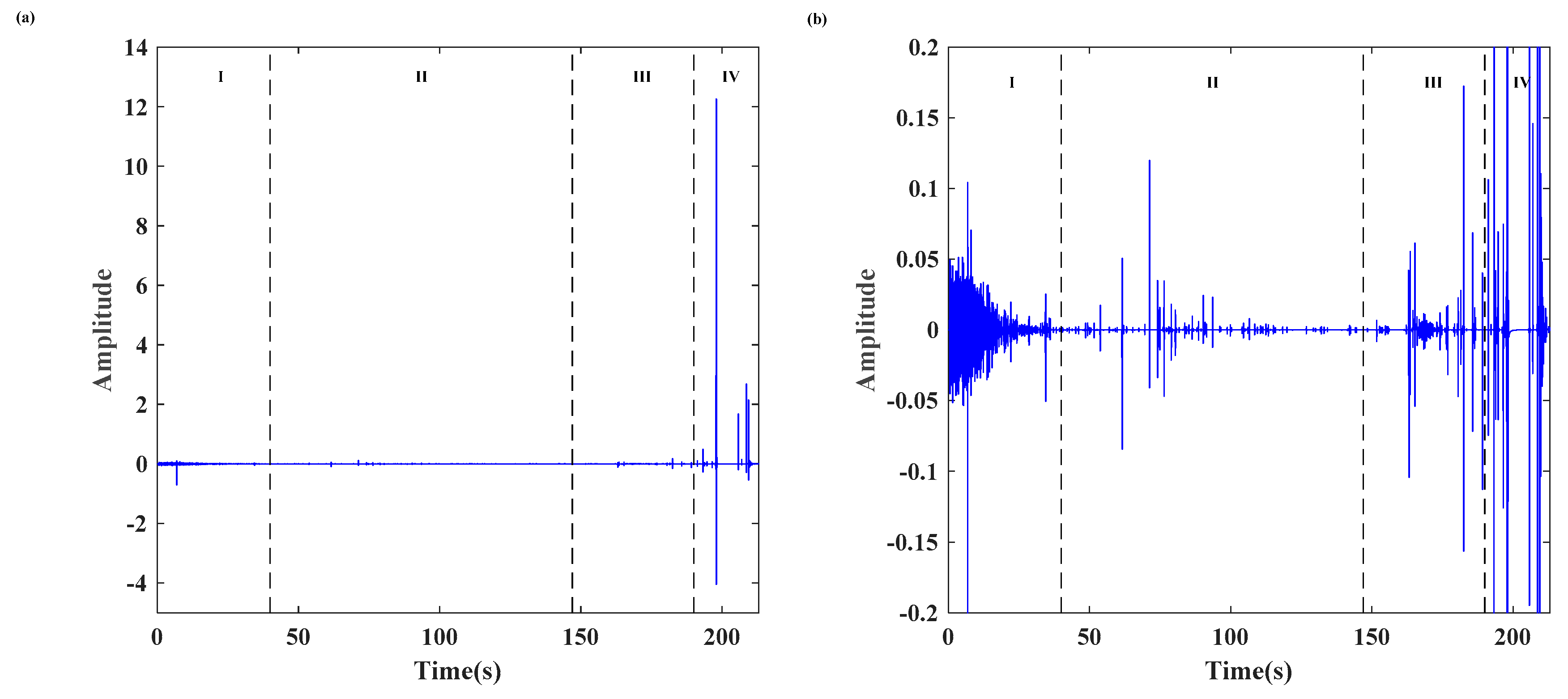
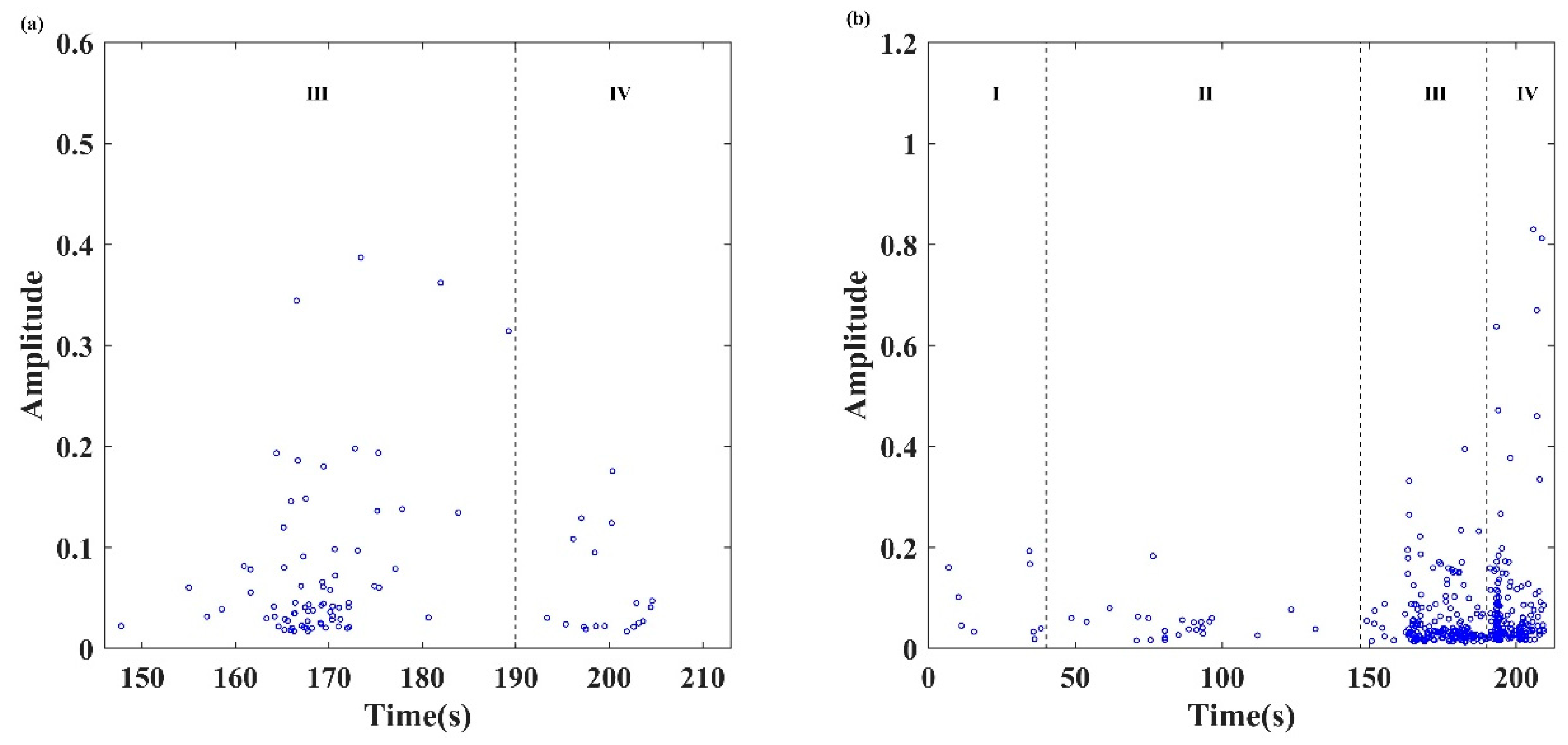
4.1. AE Hits (Activity)
- (1)
- In the stage of compaction by initial damage (stage I), the cumulative AE hits of the continuous signal gradually increased, reflecting the closure of pores and cracks in the rock caused by the stress.
- (2)
- In the elastic deformation stage (stage II), AE hits from the continuous signal remained at a low level, and the increase rate of the cumulative AE hits gradually stabilized. AE inactivity implies the rock grains reached a state of balance and associated with accumulating energy inside the locking section.
- (3)
- In the crack propagation and failure stages (stages III and IV), a burst signal first appeared at 147.8 s, indicating the formation of microcracks within the locking section. Therefore, in this study, the initial appearance of the burst signal was also used as the first early-warning point obtained from the AE hits. The emergence of the burst signal provides critical information obtained exclusively from the classification results. Accordingly, the time of the first early-warning point obtained from the AE hits (147.8 s) is 15.2 s earlier than that obtained from the MS signal (163 s). From 147.8 to 163 s, the AE hits increased slowly, indicating steady initiation and propagation of microcracks. Then, the cumulative AE hits of burst and continuous signals increased sharply induced by the shear failure of the locking section and microcracks were coalesced and propagated unstably. Therefore, the rapid increase in cumulative AE hits was regarded as the second early-warning point obtained from the AE hits, and the time of the second early-warning key point obtained from the AE hits is consistent with that of the MS signal, which is 163 s. After the shear failure occurred in the front and back of the locking segment alternately, the number of AE hits and cumulative AE hits increased again at 193 s, indicating that the main crack was forming as well as the sudden brittle shear failure of the locking section. It is worth noting that the number of AE hits of burst signal shows a decreasing trend, while the number of AE hits of continuous signal continues to remain at a high level.
4.2. Maximum Amplitude of Waveform (Intensity)
- (1)
- In the stage of compaction by initial damage (stage I), some continuous signals with low amplitude can be observed due to the compaction of internal pore.
- (2)
- In the elastic deformation stage (stage II), the load level is insufficient to induce new microcracks inside the locking section. AE events were caused by the occlusal failure of rough surfaces when cracks caused a relative slip. Therefore, a small number of continuous signals with low energy were observed.
- (3)
- In the stage of cracks propagation and failure (stages III and IV), the amplitude of the burst signals gradually increased and then decreased, while the amplitude of the continuous signals increased monotonously. The above phenomenon implies that several microcracks appeared with low energy after the main crack appeared, and continuous signals with higher energy were caused by the occlusal failure of rough surfaces when the cracks caused relative slippage.
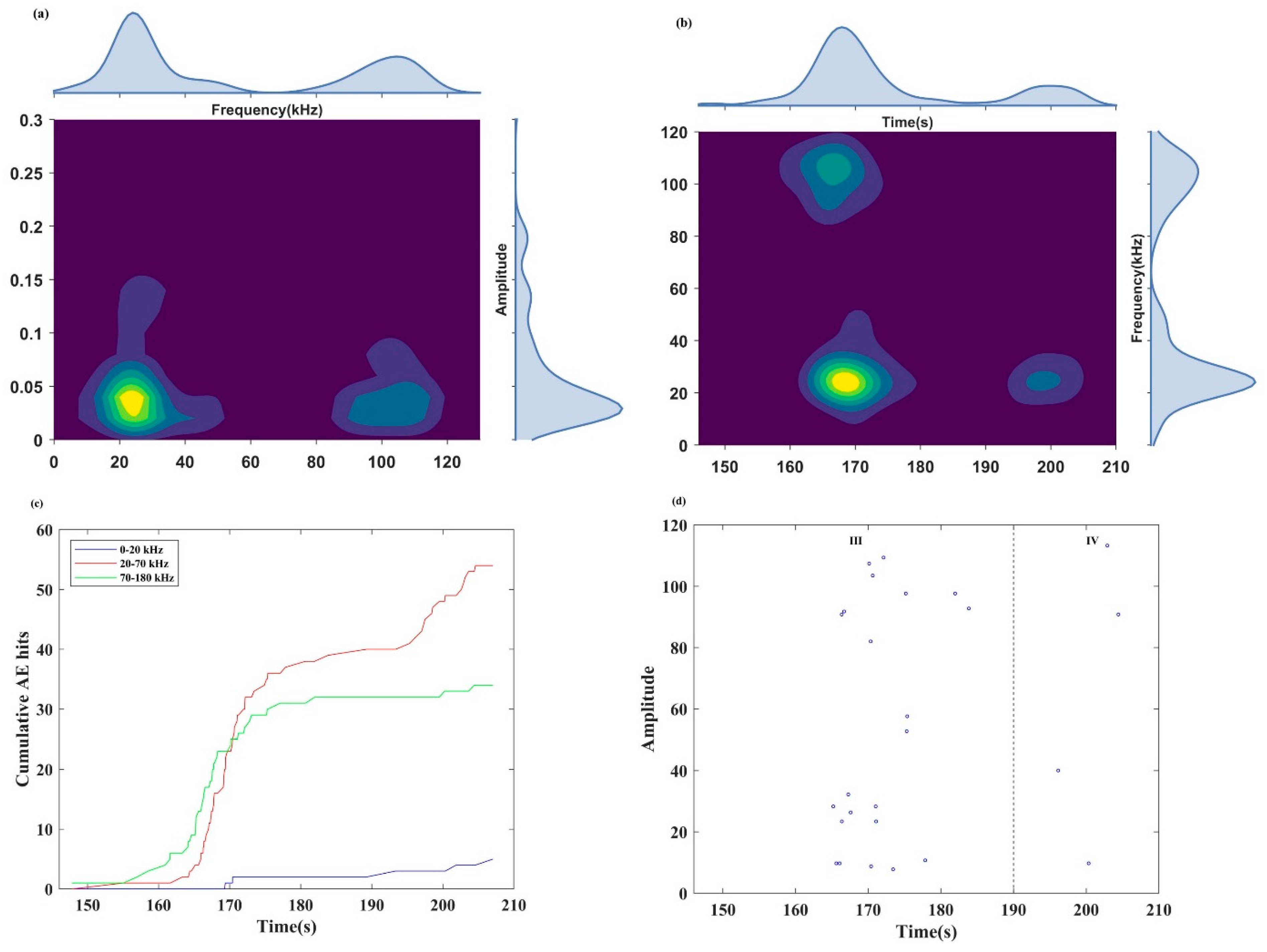
4.3. Frequency
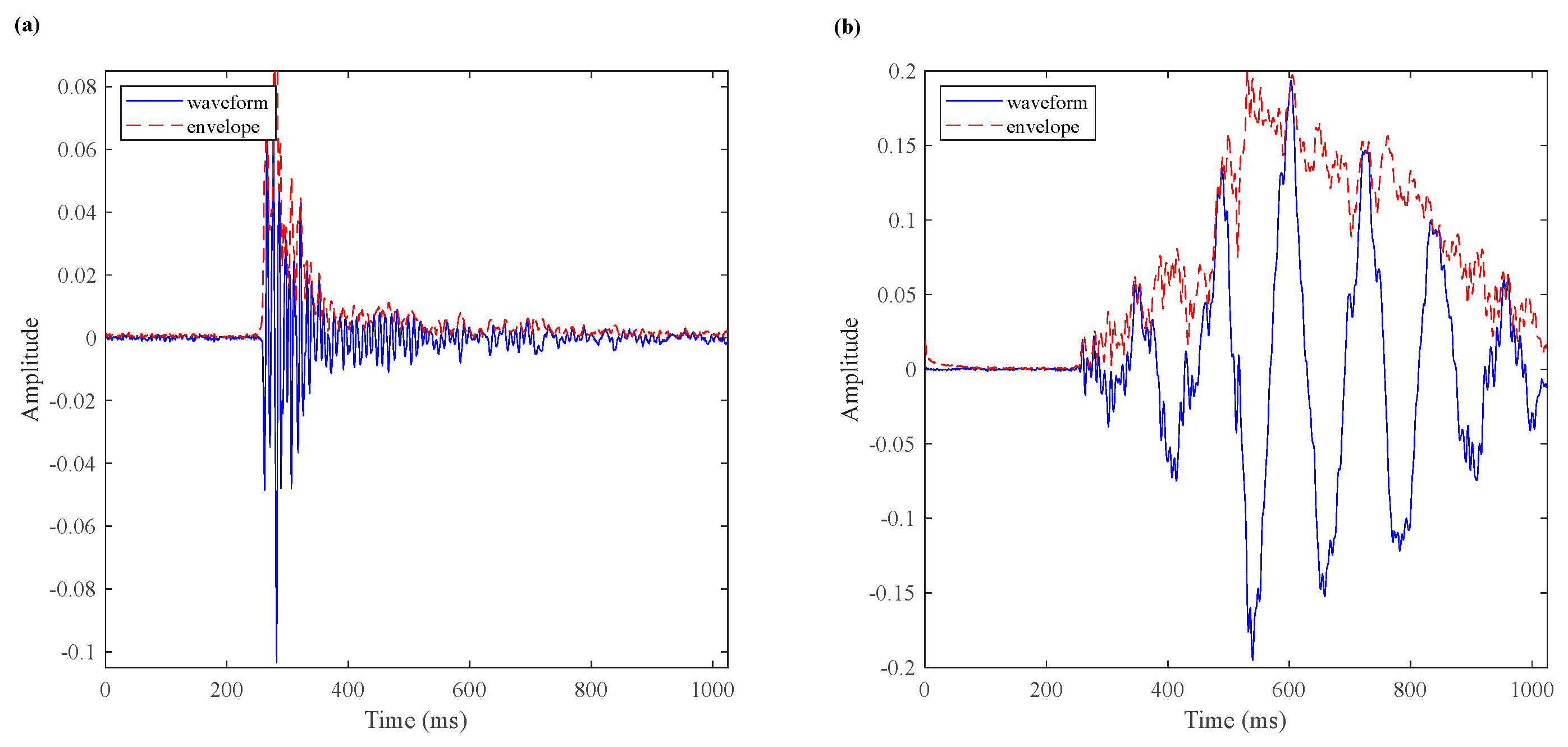
4.3.1. Frequency Characteristics of Burst Signals
4.3.2. Frequency Characteristics of Continuous Signals
5. Discussion
5.1. Evolution Characteristics of Sample #1
5.2. Evolution Characteristics of Other Samples
6. Conclusions
- (1)
- Pronounced distinctions are evident between burst signals and continuous signals concerning event frequency, intensity, and activity. Continuous signals exhibited significantly higher total AE hits compared to burst signals, which were exclusively observed during the crack propagation and failure stage. High-amplitude burst signals were predominantly distributed in the middle- and high-frequency bands, while high-amplitude continuous signals were primarily distributed in the low-frequency band. During the crack propagation stage, both burst signals and continuous signals with high amplitude occurred. In the stage of rock instability and failure, the AE hits of burst signals exhibited a decreasing trend, with their amplitude gradually declining, while the AE hits of the continuous signal remained at a high level, with further amplitude increases.
- (2)
- The emergence of a burst signal indicates the occurrence of microcracks in the rock mass, serving as an early-warning point of rock instability. Notably, this critical information is only obtained from the classification results. The generation of high-frequency AE signals indicates the presence of microcracks in the specimen, which can propagate and converge into macrofractures. Therefore, the occurrence of high-frequency AE signals is employed as an early-warning point for rock instability.
- (3)
- Comparison of the timing of the early-warning points derived from the video imaging, MS signals, and AE signals revealed that both MS signals and AE signals preceded video imaging, with AE signals leading MS signals. The occurrence of early-warning points was more frequent with AE signals compared to MS signals. Importantly, the timing of the early-warning point for burst signals preceded that of continuous signals, and the timing of the early-warning point for the classification results preceded that of the overall AE signals. The research findings indicate that AE and MS are more suitable as precursor warnings for sudden landslide disasters than deformation monitoring indicators.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, R.; Chen, G.; Guo, F.; Zhang, G.; Zhang, Y. Experimental Study on the Brittle Failure of the Locking Section in a Large-Scale Rock Slide. Landslides 2016, 13, 583–588. [Google Scholar] [CrossRef]
- Huang, R.Q. Mechanisms of Large-Scale Landslides in China. Bull. Eng. Geol. Environ. 2012, 71, 161–170. [Google Scholar] [CrossRef]
- Amare, K.; Mebrahtu, G.; Gebremiceal, A. Landslide Characterization and Distribution in Northern Ethiopia: A Case Study from the Adishu Area. Bull. Eng. Geol. Environ. 2018, 77, 581–593. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Coggan, J.S. Numerical Analysis of Initiation and Progressive Failure in Natural Rock Slopes—The 1991 Randa Rockslide. Int. J. Rock Mech. Min. Sci. 2004, 41, 69–87. [Google Scholar] [CrossRef]
- Elmo, D.; Donati, D.; Stead, D. Challenges in the Characterisation of Intact Rock Bridges in Rock Slopes. Eng. Geol. 2018, 245, 81–96. [Google Scholar] [CrossRef]
- Brideau, M.A.; Yan, M.; Stead, D. The Role of Tectonic Damage and Brittle Rock Fracture in the Development of Large Rock Slope Failures. Geomorphology 2009, 103, 30–49. [Google Scholar] [CrossRef]
- Romer, C.; Ferentinou, M. Numerical Investigations of Rock Bridge Effect on Open Pit Slope Stability. J. Rock Mech. Geotech. Eng. 2019, 11, 1184–1200. [Google Scholar] [CrossRef]
- Huang, R.Q.; Chen, G.Q.; Tang, P. Precursor Information of Locking Segment Landslides Based on Transient Characteristics. Chinese J. Rock Mech. Eng. 2017, 36, 521–533. [Google Scholar] [CrossRef]
- Pan, X.H.; Xue, L.; Qin, S.Q.; Li, G.L.; Li, P.; Wang, M.M. Types, formation Conditions and Pre-Decision Method for Large Landslides with Potential Locked Patches. J. Eng. Geol. 2014, 22, 1159–1167. [Google Scholar] [CrossRef]
- Gehle, C.; Kutter, H.K. Breakage and Shear Behaviour of Intermittent Rock Joints. Int. J. Rock Mech. Min. Sci. 2003, 40, 687–700. [Google Scholar] [CrossRef]
- Sarfarazi, V.; Ghazvinian, A.; Schubert, W.; Blumel, M.; Nejati, H.R. Numerical Simulation of the Process of Fracture of Echelon Rock Joints. Rock Mech. Rock Eng. 2014, 47, 1355–1371. [Google Scholar] [CrossRef]
- Ghazvinian, A.; Sarfarazi, V.; Schubert, W.; Blumel, M. A Study of the Failure Mechanism of Planar Non-Persistent Open Joints Using PFC2D. Rock Mech. Rock Eng. 2012, 45, 677–693. [Google Scholar] [CrossRef]
- Labuz, J.F.; Cattaneo, S.; Chen, L.H. Acoustic Emission at Failure in Quasi-Brittle Materials. Constr. Build. Mater. 2001, 15, 225–233. [Google Scholar] [CrossRef]
- Kasai, N.; Utatsu, K.; Park, S.; Kitsukawa, S.; Sekine, K. Correlation between Corrosion Rate and AE Signal in an Acidic Environment for Mild Steel. Corros. Sci. 2009, 51, 1679–1684. [Google Scholar] [CrossRef]
- Tan, C.K.; Mba, D. Identification of the Acoustic Emission Source during a Comparative Study on Diagnosis of a Spur Gearbox. Tribol. Int. 2005, 38, 469–480. [Google Scholar] [CrossRef]
- Pieri, M.; Burlini, L.; Kunze, K.; Stretton, I.; Olgaard, D.L. Rheological and Microstructural Evolution of Carrara Marble with High Shear Strain: Results from High Temperature Torsion Experiments. J. Struct. Geol. 2001, 23, 1393–1413. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y.; Asahina, D.; Wang, Z. Shear Behavior and Acoustic Emission Characteristics of En-Echelon Joints under Constant Normal Stiffness Conditions. Theor. Appl. Fract. Mech. 2020, 109, 102772. [Google Scholar] [CrossRef]
- Moradian, Z.A.; Ballivy, G.; Rivard, P.; Gravel, C.; Rousseau, B. Evaluating Damage during Shear Tests of Rock Joints Using Acoustic Emissions. Int. J. Rock Mech. Min. Sci. 2010, 47, 590–598. [Google Scholar] [CrossRef]
- Smith, A.; Dixon, N.; Meldrum, P.; Haslam, E.; Chambers, J. Acoustic Emission Monitoring of a Soil Slope: Comparisons with Continuous Deformation Measurements. Proc. Inst. Civ. Eng. Struct. Build. 2014, 4, 255–261. [Google Scholar] [CrossRef]
- Dixon, N.; Smith, A.; Flint, J.A.; Khanna, R.; Clark, B.; Andjelkovic, M. An Acoustic Emission Landslide Early Warning System for Communities in Low-Income and Middle-Income Countries. Landslides 2018, 15, 1631–1644. [Google Scholar] [CrossRef]
- Berg, N.; Smith, A.; Russell, S.; Dixon, N.; Proudfoot, D.; Andy Take, W. Correlation of Acoustic Emissions with Patterns of Movement in an Extremely Slow-Moving Landslide at Peace River, Alberta, Canada. Can. Geotech. J. 2018, 55, 1475–1488. [Google Scholar] [CrossRef]
- Kumar, D.; Mahapatro, A.K.; Singh, S.K. Active Waveguide Deformation Dynamics Using Acoustic Emission Technology for Landslide Early Warning System. Bull. Eng. Geol. Environ. 2024, 83, 1–13. [Google Scholar] [CrossRef]
- Deng, L.; Yuan, H.; Chen, J.; Zhang, M.; Su, G.; Zhou, Y.; Chen, Y. Experimental Investigation and Field Application of Acoustic Emission Array for Landslide Monitoring. Landslides 2024, 21, 71–81. [Google Scholar] [CrossRef]
- Moradian, Z.; Einstein, H.H.; Ballivy, G. Detection of Cracking Levels in Brittle Rocks by Parametric Analysis of the Acoustic Emission Signals. Rock Mech. Rock Eng. 2016, 49, 785–800. [Google Scholar] [CrossRef]
- Behnia, A.; Chai, H.K.; Shiotani, T. Advanced Structural Health Monitoring of Concrete Structures with the Aid of Acoustic Emission. Constr. Build. Mater. 2014, 65, 282–302. [Google Scholar] [CrossRef]
- Schiavi, A.; Niccolini, G.; Tarizzo, P.; Lacidogna, G.; Manuello, A.; Carpinteri, A. Analysis of Acoustic Emissions at Low Frequencies in Brittle Materials under Compression. In Proceedings of the Society for Experimental Mechanics—SEM Annual Conference and Exposition on Experimental and Applied Mechanics, Albuquerque, NM, USA, 1–4 June 2009. [Google Scholar]
- Rodríguez, P.; Celestino, T.B. Application of Acoustic Emission Monitoring and Signal Analysis to the Qualitative and Quantitative Characterization of the Fracturing Process in Rocks. Eng. Fract. Mech. 2019, 210, 54–69. [Google Scholar] [CrossRef]
- Wang, C.; Chang, X.; Liu, Y.; Chen, S. Mechanistic Characteristics of Double Dominant Frequencies of Acoustic Emission Signals in the Entire Fracture Process of Fine Sandstone. Energies 2019, 12, 3959. [Google Scholar] [CrossRef]
- Mei, F.; Hu, C.; Li, P.; Zhang, J. Study on Main Frequency Precursor Characteristics of Acoustic Emission from Deep Buried Dali Rock Explosion. Arab. J. Geosci. 2019, 12, 645. [Google Scholar] [CrossRef]
- Liu, G.H. The Research on the Key Technologies in Acoustic Emission’s Signal Processing; Zhejiang University: Hangzhou, China, 2008. [Google Scholar]
- Leśniak, A.; Isakow, Z. Space-Time Clustering of Seismic Events and Hazard Assessment in the Zabrze-Bielszowice Coal Mine, Poland. Int. J. Rock Mech. Min. Sci. 2009, 46, 918–928. [Google Scholar] [CrossRef]
- Pastén, D.; Estay, R.; Comte, D.; Vallejos, J. Multifractal Analysis in Mining Microseismicity and Its Application to Seismic Hazard in Mine. Int. J. Rock Mech. Min. Sci. 2015, 78, 74–78. [Google Scholar] [CrossRef]
- Calder, P.N.; Semadeni, T.J. High Frequency Microseismic Monitoring Trial near a Rapidly Changing Stress Field in a Hard Rock Mine. Gerlands Beitrage Geophys. 1990, 99, 21–34. [Google Scholar]
- Xiao, P.; Qian, B.; Jiang, P.; Xu, N.; Li, B. Deformation Forecasting of Surrounding Rock Mass Based on Correlation between Frequency and Fracture Scale of Microseismicity. Adv. Civ. Eng. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, Y.; Gao, Y.T.; Xu, C. Experimental and Numerical Study on Crack Development Characteristics between Two Cavities in Rock-like Material under Uniaxial Compression. Theor. Appl. Fract. Mech. 2020, 109, 102755. [Google Scholar] [CrossRef]
- Lotidis, M.A.; Nomikos, P.P.; Sofianos, A.I. Numerical Study of the Fracturing Process in Marble and Plaster Hollow Plate Specimens Subjected to Uniaxial Compression. Rock Mech. Rock Eng. 2019, 52, 4361–4386. [Google Scholar] [CrossRef]
- Zuo, J.; Wei, X.; Pei, J.; Zhao, X. Investigation of Meso-Failure Behaviors of Jinping Marble Using SEM with Bending Loading System. J. Rock Mech. Geotech. Eng. 2015, 7, 593–599. [Google Scholar] [CrossRef]
- Pappalardo, G.; Mineo, S.; Angrisani, A.C.; Di Martire, D.; Calcaterra, D. Combining Field Data with Infrared Thermography and DInSAR Surveys to Evaluate the Activity of Landslides: The Case Study of Randazzo Landslide (NE Sicily). Landslides 2018, 15, 2173–2193. [Google Scholar] [CrossRef]
- Gao, R.; Du, X.; Zeng, Y.; Li, Y.; Yan, J. A New Method to Simulate Irregular Particles by Discrete Element Method. J. Rock Mech. Geotech. Eng. 2012, 4, 276–281. [Google Scholar] [CrossRef]
- Kou, M.; Liu, X.; Tang, S.; Wang, Y. 3-D X-Ray Computed Tomography on Failure Characteristics of Rock-like Materials under Coupled Hydro-Mechanical Loading. Theor. Appl. Fract. Mech. 2019, 104, 102396. [Google Scholar] [CrossRef]
- Zhao, K.; Yang, D.; Gong, C.; Zhuo, Y.; Wang, X.; Zhong, W. Evaluation of Internal Microcrack Evolution in Red Sandstone Based on Time–Frequency Domain Characteristics of Acoustic Emission Signals. Constr. Build. Mater. 2020, 260, 120435. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, Q.; Zhou, J.; Tang, M. International Journal of Rock Mechanics & Mining Sciences Experimental Study of Infrasonic Signal Generation during Rock Fracture under Uniaxial Compression. Int. J. Rock Mech. Min. Sci. 2013, 60, 37–46. [Google Scholar] [CrossRef]
- Zhao, J.R. Acoustic Emission Signal Processing System and Source Recognition Methods; Jilin University: Changchun, China, 2010. [Google Scholar]
- Liu, H.D.; Zhang, Y.B.; Lu, L.P. Types of the Locked Section Landslide in the Western Henan Province. J. North China Univ. Water Resources Electr. Power 2018, 39, 2018. [Google Scholar] [CrossRef]
- Wang, C.Y.; Chang, X.K.; Liu, Y.L.; Guo, W. Bin Spectrum Evolution Characteristics of Acoustic Emission during the Rupture Process of Marble under Uniaxial Compression Condition. Rock Soil Mech. 2020, 41, 51–62. [Google Scholar] [CrossRef]
- Zhang, G.K.; Li, H.B.; Wang, M.Y.; Li, J.; Deng, S.X. Comparative Study on Damage Characterization and Damage Evolution of Rock under Uniaxial Compression. Chin. J. Geotech. Eng. 2019, 41, 1074–1082. [Google Scholar]
- Cai, M.; Kaiser, P.K.; Morioka, H.; Minami, M.; Maejima, T.; Tasaka, Y.; Kurose, H. FLAC/PFC Coupled Numerical Simulation of AE in Large-Scale Underground Excavations. Int. J. Rock Mech. Min. Sci. 2007, 44, 550–564. [Google Scholar] [CrossRef]





| Proportions (%) | Stage I | Stage II | Stage III | Stage IV | Whole Process |
|---|---|---|---|---|---|
| Burst signals | 0.00 | 0.00 | 15.32 | 3.93 | 19.25 |
| Continuous signals | 1.86 | 5.18 | 37.27 | 36.44 | 80.75 |
| AE signals | 1.86 | 5.18 | 52.59 | 40.37 | 100.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Chen, H.; Wu, Z.; Yang, S.; Li, X.; Li, T. An Experimental Study of the Acoustic Signal Characteristics of Locked-Segment Damage Evolution in a Landslide Model. Sensors 2024, 24, 4947. https://doi.org/10.3390/s24154947
Zhu X, Chen H, Wu Z, Yang S, Li X, Li T. An Experimental Study of the Acoustic Signal Characteristics of Locked-Segment Damage Evolution in a Landslide Model. Sensors. 2024; 24(15):4947. https://doi.org/10.3390/s24154947
Chicago/Turabian StyleZhu, Xing, Hui Chen, Zhanglei Wu, Shumei Yang, Xiaopeng Li, and Tiantao Li. 2024. "An Experimental Study of the Acoustic Signal Characteristics of Locked-Segment Damage Evolution in a Landslide Model" Sensors 24, no. 15: 4947. https://doi.org/10.3390/s24154947
APA StyleZhu, X., Chen, H., Wu, Z., Yang, S., Li, X., & Li, T. (2024). An Experimental Study of the Acoustic Signal Characteristics of Locked-Segment Damage Evolution in a Landslide Model. Sensors, 24(15), 4947. https://doi.org/10.3390/s24154947






