Between-Session Reliability of Field-Based Assessments of Isometric Neck Strength
Abstract
:1. Introduction
2. Materials and Methods
Statistical Analysis
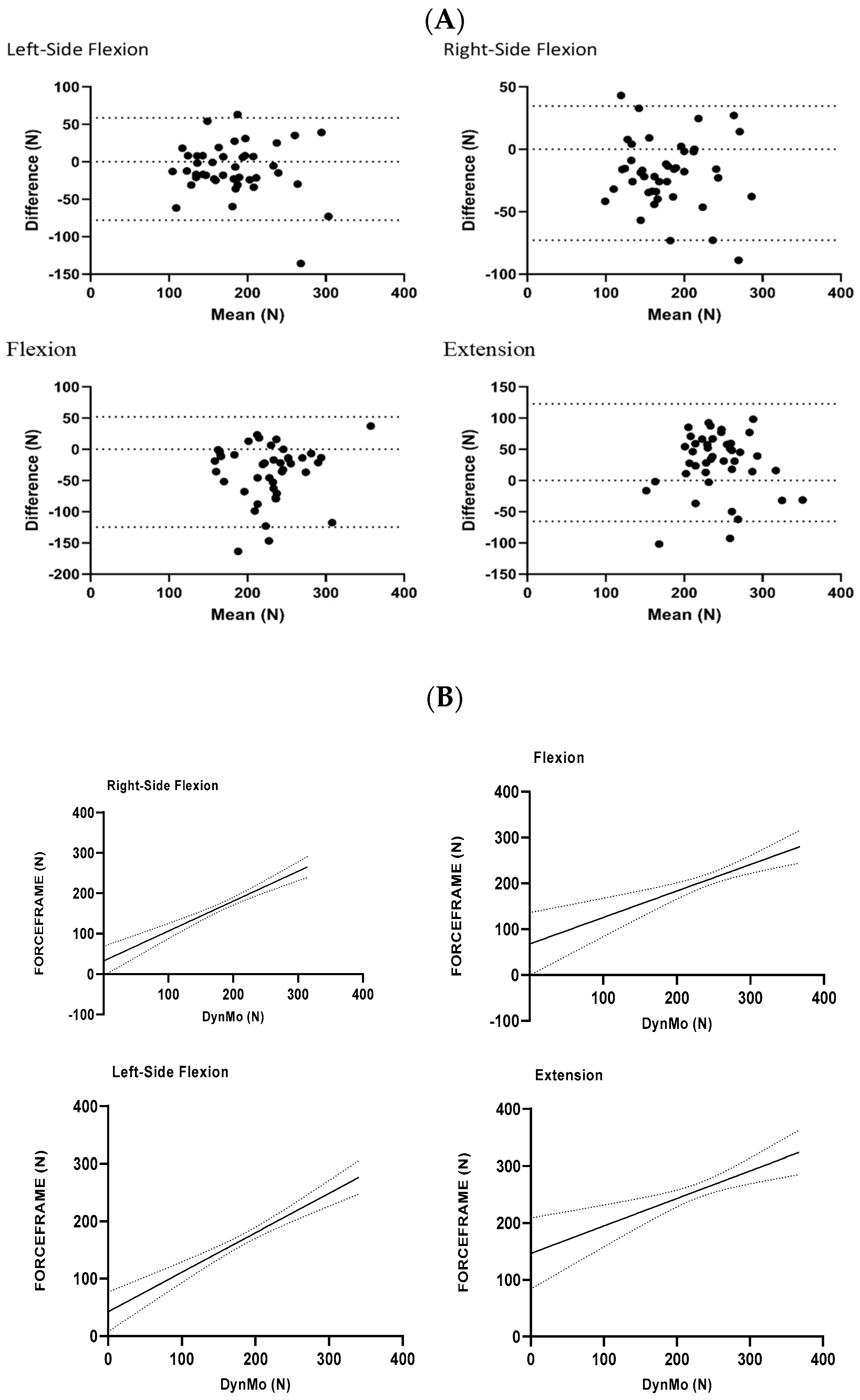
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Patricios, J.S.; Schneider, K.J.; Dvorak, J.; Ahmed, O.H.; Blauwet, C.; Cantu, R.C.; Davis, G.A.; Echemendia, R.J.; Makdissi, M.; McNamee, M. Consensus Statement on Concussion in Sport: The 6th International Conference on Concussion in Sport–Amsterdam, October 2022. Br. J. Sports Med. 2023, 57, 695–711. [Google Scholar] [CrossRef] [PubMed]
- McCrory, P.; Meeuwisse, W.; Dvorak, J.; Aubry, M.; Bailes, J.; Broglio, S.; Cantu, R.C.; Cassidy, D.; Echemendia, R.J.; Castellani, R.J.; et al. Consensus Statement on Concussion in Sport—The 5th International Conference on Concussion in Sport Held in Berlin, October 2016. Br. J. Sports Med. 2017, 51, 838–847. [Google Scholar] [CrossRef] [PubMed]
- Bailes, J.E.; Petraglia, A.L.; Omalu, B.I.; Nauman, E.; Talavage, T. Role of Subconcussion in Repetitive Mild Traumatic Brain Injury: A Review. J. Neurosurg. 2013, 119, 1235–1245. [Google Scholar] [CrossRef] [PubMed]
- Daly, E.; Pearce, A.J.; Ryan, L. A Systematic Review of Strength and Conditioning Protocols for Improving Neck Strength and Reducing Concussion Incidence and Impact Injury Risk in Collision Sports; Is There Evidence? J. Funct. Morphol. Kinesiol. 2021, 6, 8. [Google Scholar] [CrossRef] [PubMed]
- Farley, T.; Barry, E.; Sylvester, R.; De Medici, A.; Wilson, M.G. Poor Isometric Neck Extension Strength as a Risk Factor for Concussion in Male Professional Rugby Union Players. Br. J. Sports Med. 2022, 56, 616–621. [Google Scholar] [CrossRef] [PubMed]
- Hrysomallis, C. Neck Muscular Strength, Training, Performance and Sport Injury Risk: A Review. Sports Med. 2016, 46, 1111–1124. [Google Scholar] [CrossRef] [PubMed]
- Selistre, L.F.; de Sousa Melo, C.; de Noronha, M.A. Reliability and Validity of Clinical Tests for Measuring Strength or Endurance of Cervical Muscles: A Systematic Review and Meta-Analysis. Arch. Phys. Med. Rehabil. 2021, 102, 1210–1227. [Google Scholar] [CrossRef] [PubMed]
- Almosnino, S.; Pelland, L.; Stevenson, J.M. Retest Reliability of Force-Time Variables of Neck Muscles under Isometric Conditions. J. Athl. Train. 2010, 45, 453–458. [Google Scholar] [CrossRef]
- McDaniel, A.T.; Schroeder, L.H.; Freedman, J.A.; Wang, Y.; Heijnen, M.J.H. Evaluating the Intra-Rater and Inter-Rater Reliability of Fixed Tension Scale Instrumentation for Determining Isometric Neck Strength. Int. J. Exerc. Sci. 2021, 14, 563–577. [Google Scholar]
- Peek, K.; Andersen, J.; McKay, M.J.; Versteegh, T.; Gilchrist, I.A.; Meyer, T.; Gardner, A. The Effect of the FIFA 11 + with Added Neck Exercises on Maximal Isometric Neck Strength and Peak Head Impact Magnitude During Heading: A Pilot Study. Sports Med. 2022, 52, 655–668. [Google Scholar] [CrossRef]
- Konrath, J.; Appleby, B. An Investigation of Cervical Strength and Anthropometry in Professional Rugby Union Players. J. Aust. Strength Cond. 2013, 21, 12–18. [Google Scholar]
- McBride, L.; James, R.S.; Alsop, S.; Oxford, S.W. Intra and Inter-Rater Reliability of a Novel Isometric Test of Neck Strength. Sports 2023, 11, 2. [Google Scholar] [CrossRef] [PubMed]
- Mokkink, L.B.; Terwee, C.B.; Patrick, D.L.; Alonso, J.; Stratford, P.W.; Knol, D.L.; Bouter, L.M.; De Vet, H.C. The COSMIN Checklist for Assessing the Methodological Quality of Studies on Measurement Properties of Health Status Measurement Instruments: An International Delphi Study. Qual. Life Res. 2010, 19, 539–549. [Google Scholar] [CrossRef] [PubMed]
- Chavarro-Nieto, C.; Beaven, M.; Gill, N.; Hébert-Losier, K. Neck Strength in Rugby Union Players: A Systematic Review of the Literature. Physician Sportsmed. 2021, 49, 392–409. [Google Scholar] [CrossRef] [PubMed]
- de Koning, C.H.; van den Heuvel, S.P.; Staal, J.B.; Smits-Engelsman, B.C.; Hendriks, E.J. Clinimetric Evaluation of Methods to Measure Muscle Functioning in Patients with Non-Specific Neck Pain: A Systematic Review. BMC Musculoskelet. Disord. 2008, 9, 142. [Google Scholar] [CrossRef] [PubMed]
- Eckner, J.T.; Oh, Y.K.; Joshi, M.S.; Richardson, J.K.; Ashton-Miller, J.A. Effect of Neck Muscle Strength and Anticipatory Cervical Muscle Activation on the Kinematic Response of the Head to Impulsive Loads. Am. J. Sports Med. 2014, 42, 566–576. [Google Scholar] [CrossRef] [PubMed]
- Haff, G.G.; Ruben, R.P.; Lider, J.; Twine, C.; Cormie, P. A Comparison of Methods for Determining the Rate of Force Development during Isometric Midthigh Clean Pulls. J. Strength Cond. Res. 2015, 29, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Mcguigan, M.R.; Newton, M.J.; Winchester, J.B.; Nelson, A.G. Relationship between Isometric and Dynamic Strength in Recreationally Trained Men. J. Strength Cond. Res. 2010, 24, 2570–2573. [Google Scholar] [CrossRef] [PubMed]
- Thomas, C.; Jones, P.A.; Rothwell, J.; Chiang, C.Y.; Comfort, P. An Investigation into the Relationship between Maximum Isometric Strength and Vertical Jump Performance. J. Strength Cond. Res. 2015, 29, 2176–2185. [Google Scholar] [CrossRef]
- Comfort, P.; Jones, P.A.; McMahon, J.J.; Newton, R. Effect of Knee and Trunk Angle on Kinetic Variables during the Isometric Midthigh Pull: Test–Retest Reliability. Int. J. Sports Physiol. Perform. 2015, 10, 58–63. [Google Scholar] [CrossRef]
- Dos’ Santos, T.; Thomas, C.; Comfort, P.; McMahon, J.J.; Jones, P.A.; Oakley, N.P.; Young, A.L. Between-Session Reliability of Isometric Midthigh Pull Kinetics and Maximal Power Clean Performance in Male Youth Soccer Players. J. Strength Cond. Res. 2018, 32, 3364–3372. [Google Scholar] [CrossRef] [PubMed]
- Hughes, S.; Warmenhoven, J.; Haff, G.G.; Chapman, D.W.; Nimphius, S. Countermovement Jump and Squat Jump Force-Time Curve Analysis in Control and Fatigue Conditions. J. Strength Cond. Res. 2022, 36, 2752. [Google Scholar] [CrossRef]
- Borg, D.N.; Bach, A.J.E.; O’Brien, J.L.; Sainani, K.L. Calculating Sample Size for Reliability Studies. PMR 2022, 14, 1018–1025. [Google Scholar] [CrossRef] [PubMed]
- Streiner, D.L.; Norman, G.R.; Cairney, J. Health Measurement Scales: A Practical Guide to Their Development and Use; Oxford University Press: New York, NY, USA, 2015. [Google Scholar]
- Hopkins, W.G. A Spreadsheet to Compare Means of Two Groups. Sportscience 2007, 11, 22–24. [Google Scholar]
- Beckham, G.; Mizuguchi, S.; Carter, C.; Sato, K.; Ramsey, M.; Lamont, H.; Hornsby, G.; Haff, G.; Stone, M. Relationships of Isometric Mid-Thigh Pull Variables to Weightlifting Performance. J. Sports Med. Phys. Fit. 2013, 53, 573–581. [Google Scholar]
- Beckerman, H.; Roebroeck, M.E.; Lankhorst, G.J.; Becher, J.G.; Bezemer, P.D.; Verbeek, A. Smallest Real Difference, a Link between Reproducibility and Responsiveness. Qual. Life Res. 2001, 10, 571–578. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Bland, J.M.; Altman, D.G. Comparing Methods of Measurement: Why Plotting Difference against Standard Method Is Misleading. Lancet 1995, 346, 1085–1087. [Google Scholar] [CrossRef] [PubMed]
- Bilic-Zulle, L. Comparison of Methods: Passing and Bablok Regression. Biochem. Medica 2011, 21, 49–52. [Google Scholar] [CrossRef] [PubMed]
- Pataky, T.C. Generalized N-Dimensional Biomechanical Field Analysis Using Statistical Parametric Mapping. J. Biomech. 2010, 43, 1976–1982. [Google Scholar] [CrossRef]
- Sinclair, J.; Brooks, D.; Stainton, P. Biomechanical Effects of a Lightweight, Sock-Style Minimalist Footwear Design during Running: A Musculoskeletal Simulation and Statistical Parametric Mapping Approach. Footwear Sci. 2019, 11, 71–83. [Google Scholar] [CrossRef]
- Pataky, T.C.; Robinson, M.A.; Vanrenterghem, J. Vector Field Statistical Analysis of Kinematic and Force Trajectories. J. Biomech. 2013, 46, 2394–2401. [Google Scholar] [CrossRef] [PubMed]
- Salmon, D.M.; Handcock, P.J.; Sullivan, S.J.; Rehrer, N.J.; Niven, B.E. Reliability of Repeated Isometric Neck Strength and Endurance Testing in a Simulated Contact Posture. J. Strength Cond. Res. 2015, 29, 637–646. [Google Scholar] [CrossRef] [PubMed]
- Hall, T.; Morissette, M.P.; Cordingley, D.; Leiter, J. Reliability of a Novel Technique for the Measurement of Neck Strength. Int. J. Athl. Ther. Train. 2017, 22, 43–50. [Google Scholar] [CrossRef]
- Peolsson, A.; Kjellman, G. Neck Muscle Endurance in Nonspecific Patients with Neck Pain and in Patients after Anterior Cervical Decompression and Fusion. J. Manip. Physiol. Ther. 2007, 30, 343–350. [Google Scholar] [CrossRef] [PubMed]
- Merrigan, J.J.; Stone, J.D.; Hornsby, W.G.; Hagen, J.A. Identifying Reliable and Relatable Force–Time Metrics in Athletes—Considerations for the Isometric Mid-Thigh Pull and Countermovement Jump. Sports 2021, 9, 4. [Google Scholar] [CrossRef] [PubMed]
- Haff, G.G.; Nimphius, S. Training Principles for Power. Strength Cond. J. 2012, 34, 2–12. [Google Scholar] [CrossRef]
- Newton, R.U.; Kraemer, W.J. Developing Explosive Muscular Power: Implications for a Mixed Methods Training Strategy. Strength Cond. J. 1994, 16, 20–31. [Google Scholar] [CrossRef]


| Dynamo | ForceFrame | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Direction | ||||||||||
| Variable | EXT | FLEX | LSF | RSF | EXT | FLEX | LSF | RSF | ||
| Intra Session (Session 1) | Rep 1 | Peak F (N) | 216 ± 36 | 241 ± 44 | 180 ± 54 | 178 ± 50 | 248 ± 52 | 198 ± 51 | 159 ± 51 | 161 ± 46 |
| Rep 2 | Peak F (N) | 215 ± 41 | 246 ± 46 | 183 ± 52 | 182 ± 51 | 241 ± 53 | 194 ± 55 | 161 ± 52 | 162 ± 45 | |
| Rep 3 | Peak F (N) | 221 ± 49 | 246 ± 42 | 186 ± 54 | 182 ± 50 | 241 ± 49 | 186 ± 60 | 156 ± 51 | 165 ± 51 | |
| Rep 1–2 | ICC | 0.86 | 0.96 | 0.94 | 0.95 | 0.94 | 0.93 | 0.98 | 0.95 | |
| Rep 1–2 | 95% CI | 0.72–0.94 | 0.91–0.98 | 0.87–0.97 | 0.89–0.98 | 0.86–0.97 | 0.86–0.97 | 0.96–0.99 | 0.9–0.98 | |
| Rep 1–2 | SEm | 14 | 9 | 13 | 11 | 13 | 14 | 7 | 10 | |
| Rep 1–2 | MDC | 40 | 25 | 36 | 31 | 35 | 38 | 20 | 28 | |
| Rep 1–2 | CV % | 7.2 | 4.1 | 7.5 | 6.9 | 6.8 | 7.8 | 4.6 | 7.1 | |
| Rep 1–2 | CV 95% CI | 5.6–10.1 | 3.2–5.7 | 5.8–10.5 | 5.3–9.6 | 5.3–9.5 | 6.1–10.9 | 3.6–6.4 | 5.6–9.9 | |
| Rep 2–3 | ICC | 0.83 | 0.96 | 0.97 | 0.93 | 0.96 | 0.87 | 0.97 | 0.95 | |
| Rep 2–3 | 95% CI | 0.66–0.92 | 0.92–0.98 | 0.93–0.99 | 0.86–0.97 | 0.91–0.97 | 0.74–0.94 | 0.93 –0.99 | 0.90–0.98 | |
| Rep 2–3 | SEm | 18 | 9 | 9 | 13 | 10 | 57 | 51 | 11 | |
| Rep 2–3 | MDC | 51 | 24 | 25 | 37 | 28 | 158 | 141 | 29 | |
| Rep 2–3 | CV % | 8.9 | 3.8 | 5.1 | 7.9 | 5.5 | 11.6 | 5.9 | 7.1 | |
| Rep 2–3 | CV 95% CI | 6.9–12.5 | 3.0–5.3 | 4–7.1 | 6.2–11.1 | 4.3–7.6 | 9.0–16.2 | 4.6 –8.2 | 5.6–9.9 | |
| Rep 1–3 | ICC | 0.76 | 0.87 | 0.93 | 0.8 | 0.88 | 0.86 | 0.92 | 0.9 | |
| Rep 1–3 | 95% CI | 0.59–0.88 | 0.76–0.94 | 0.69–0.92 | 0.65–0.90 | 0.78–0.94 | 0.74–0.93 | 0.84 –0.96 | 0.81–0.95 | |
| Rep 1–3 | SEm | 21 | 15 | 14 | 22 | 17 | 21 | 14 | 15 | |
| Rep 1–3 | MDC | 58 | 43 | 40 | 61 | 48 | 57 | 40 | 42 | |
| Rep 1–3 | CV % | 8.7 | 5.3 | 9.2 | 10.8 | 6.6 | 9.9 | 7.7 | 8 | |
| Rep 1–3 | CV 95% CI | 6.7–12.2 | 4.1–7.3 | 7.1–12.9 | 8.4–15.2 | 5.2–9.2 | 7.7–13.8 | 6.0–10.8 | 6.2–11.1 | |
| Intra Session (Session 2) | Rep 1 | Peak F (N) | 207 ± 38 | 233 ± 39 | 170 ± 46 | 172 ±49 | 244 ± 46 | 208 ± 42 | 141 ± 39 | 158 ± 52 |
| Rep 2 | Peak F (N) | 208 ± 53 | 235 ± 42 | 173 ± 49 | 173 ± 51 | 237 ± 46 | 194 ± 42 | 138 ± 45 | 153 ± 47 | |
| Rep 3 | Peak F (N) | 206 ± 50 | 238 ± 47 | 172 ± 50 | 173 ± 52 | 233 ± 45 | 193 ± 40 | 137 ± 43 | 153 ± 46 | |
| Rep 1–2 | ICC | 0.78 | 0.98 | 0.97 | 0.96 | 0.94 | 0.9 | 0.94 | 0.95 | |
| Rep 1–2 | 95% CI | 0.52–0.91 | 0.92–0.99 | 0.92–0.99 | 0.89–0.98 | 0.84–0.97 | 0.76–0.96 | 0.85–0.97 | 0.88–0.98 | |
| Rep 1–2 | SEm | 21 | 10 | 8 | 10 | 10 | 13 | 10 | 11 | |
| Rep 1–2 | MDC | 59 | 27 | 23 | 29 | 27 | 35 | 27 | 30 | |
| Rep 1–2 | CV % | 11.8 | 2.9 | 5.5 | 6.8 | 5.8 | 7.5 | 8.6 | 7.6 | |
| Rep 1–2 | CV 95% CI | 8.7–18.1 | 2.2–4.4 | 4.1–8.1 | 5.1–10.1 | 4.4–8.5 | 5.6–11.1 | 6.5–12.8 | 5.8–11.4 | |
| Rep 2–3 | ICC | 0.91 | 0.94 | 0.97 | 0.97 | 0.93 | 0.95 | 0.97 | 0.95 | |
| Rep 2–3 | 95% CI | 0.77–0.96 | 0.85–0.98 | 0.92–0.99 | 0.91–0.99 | 0.84–0.97 | 0.87–0.98 | 0.92–0.99 | 0.88–0.98 | |
| Rep 2–3 | SEm | 15 | 11 | 9 | 9 | 11 | 37 | 43 | 10 | |
| Rep 2–3 | MDC | 42 | 30 | 24 | 26 | 29 | 103 | 118 | 28 | |
| Rep 2–3 | CV % | 7.9 | 5.2 | 5.7 | 6 | 6.2 | 5.5 | 6.5 | 7.4 | |
| Rep 2–3 | CV 95% CI | 5.9–12.1 | 3.9–8.0 | 4.3–8.4 | 4.5–8.9 | 4.7–9.2 | 4.2–8.2 | 4.9–9.6 | 5.6–10.9 | |
| Rep 1–3 | ICC | 0.69 | 0.87 | 0.92 | 0.91 | 0.83 | 0.91 | 0.89 | 0.93 | |
| Rep 1–3 | 95% CI | 0.47–0.86 | 0.72–0.95 | 0.81–0.96 | 0.80–0.96 | 0.66–0.92 | 0.81–0.96 | 0.76–0.95 | 0.83–0.97 | |
| Rep 1–3 | SEm | 24 | 15 | 14 | 16 | 16 | 12 | 13 | 13 | |
| Rep 1–3 | MDC | 68 | 43 | 38 | 44 | 45 | 32 | 37 | 36 | |
| Rep 1–3 | CV % | 10.8 | 6.2 | 6.6 | 7 | 7.2 | 5.2 | 8.5 | 6.4 | |
| Rep 1–3 | CV 95% CI | 8.0–16.6 | 4.6–9.4 | 5.0–9.8 | 5.3–10.5 | 5.4–10.7 | 3.9–7.7 | 6.4–12.7 | 4.8–9.4 | |
| Inter Session | Session 1 | Peak F (N) | 226 ± 49 | 248 ± 47 a | 190 ± 47 a | 187 ± 53 a | 263 ± 44 b | 210 ± 41 bc | 170 ± 49 bc | 160 ± 50 bc |
| Session 2 | Peak F (N) | 217 ± 48 | 241 ± 43 a | 181 ± 51 a | 179 ± 48 a | 250 ± 48 b | 210 ± 42 bc | 163 ± 9.4 bc | 148 ± 45 bc | |
| Session 1–2 | ICC | 0.76 | 0.84 | 0.78 | 0.8 | 0.8 | 0.83 | 0.84 | 0.85 | |
| Session 1–2 | 95% CI | 0.48–0.90 | 0.65–0.94 | 0.53–0.91 | 0.55–0.91 | 0.57–0.92 | 0.62–0.93 | 0.64–0.93 | 0.65–0.94 | |
| Session 1–2 | SEm | 24 | 18 | 43 | 23 | 21 | 17 | 19 | 18 | |
| Session 1–2 | MDC | 65 | 50 | 119 | 63 | 57 | 47 | 54 | 51 | |
| Session 1–2 | CV % | 10.9 | 8.3 | 13.8 | 13.6 | 9.7 | 9.4 | 13.2 | 13.8 | |
| Session 1–2 | CV 95% CI | 8.1–16.2 | 6.2–12.3 | 10.3–20.8 | 10.2–20.4 | 7.3–14.4 | 7.0–14 | 9.9–19.9 | 10.3–20.8 | |
| ICC | CV | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable | Session 1 | Session 2 | ICC | 95% CI | SEm | MDC | % | 95% CI | |
| Extension | Time to peak force (s) | 1.4 ± 0.7 | 1.4 ± 0.5 | 0.63 | 0.18–0.87 | 0.36 | 1.66 | 34.7 | 24.1–61.6 |
| Force at 50 ms (N) | 94 ± 30 | 80 ± 25 | 0.58 | 0.10–0.84 | 18.20 | 11.82 | 22.7 | 16.0–39.0 | |
| Force at 100 ms (N) | 138 ± 47 | 121 ± 41 | 0.64 | 0.19–0.87 | 26.47 | 14.26 | 24.7 | 17.3–42.6 | |
| Force at 150 ms (N) | 169 ± 51 | 156 ± 54 | 0.70 | 0.30–0.89 | 28.62 | 14.83 | 21.8 | 15.4–37.4 | |
| Force at 200 ms (N) | 190 ± 53 | 180 ± 61 | 0.65 | 0.20–0.87 | 33.16 | 15.96 | 22.7 | 16.0–39.0 | |
| Flexion | Time to peak force (s) | 1.5 ± 0.7 | 1.5 ± 0.5 | 0.60 | 0.13–0.85 | 0.39 | 1.72 | 36.2 | 25.1–64.4 |
| Force at 50 ms (N) | 67 ± 15 | 70 ± 14 | 0.78 | 0.45–0.92 | 6.68 | 7.16 | 10.7 | 7.6–17.7 | |
| Force at 100 ms (N) | 96 ± 26 | 101 ± 25 | 0.75 | 0.37–0.91 | 12.48 | 9.79 | 15.5 | 11.0–26.1 | |
| Force at 150 ms (N) | 116 ± 34 | 126 ± 33 | 0.78 | 0.44–0.92 | 24.51 | 13.72 | 16.1 | 11.4–27.2 | |
| Force at 200 ms (N) | 129 ± 39 | 142 ± 37 | 0.78 | 0.44–0.92 | 17.78 | 11.69 | 16.1 | 11.4–27.2 | |
| LSF | Time to peak force (s) | 1.7 ± 0.6 | 1.5 ± 0.5 | 0.66 | 0.22–0.88 | 0.34 | 1.62 | 27.2 | 19.1–47.4 |
| Force at 50 ms (N) | 65 ± 12 | 60 ± 12 | 0.83 | 0.54–0.94 | 5.02 | 6.21 | 8.6 | 6.2–14.2 | |
| Force at 100 ms (N) | 87 ± 15 | 79 ± 25 | 0.79 | 0.46–0.93 | 11.39 | 9.35 | 14.4 | 10.2–24.2 | |
| Force at 150 ms (N) | 104 ± 36 | 94 ± 35 | 0.84 | 0.58–0.95 | 14.06 | 10.39 | 14.6 | 10.4–24.5 | |
| Force at 200 ms (N) | 113 ± 41 | 104 ± 42 | 0.87 | 0.65–0.96 | 14.66 | 10.61 | 13.9 | 9.9–23.3 | |
| RSF | Time to peak force (s) | 1.6 ± 0.6 | 1.5 ± 0.6 | 0.45 | −0.08–0.78 | 0.44 | 1.85 | 44.8 | 30.8–81.5 |
| Force at 50 ms (N) | 67 ± 11 | 67 ± 11 | 0.78 | 0.43–0.92 | 5.14 | 6.29 | 8.7 | 6.3–14.5 | |
| Force at 100 ms (N) | 88 ± 20 | 91 ± 23 | 0.76 | 0.40–0.92 | 10.42 | 8.95 | 13.7 | 9.7–22.9 | |
| Force at 150 ms (N) | 102 ± 28 | 109 ± 33 | 0.85 | 0.59–0.95 | 11.83 | 9.54 | 13.3 | 9.5–22.2 | |
| Force at 200 ms (N) | 115 ± 33 | 121 ± 40 | 0.88 | 0.68–0.96 | 12.43 | 9.77 | 12.1 | 8.6–20.2 | |
| Bland–Altman Bias ± SD (Lower LOA, Upper LOA) | Passing–Bablok Regression | ||||||
|---|---|---|---|---|---|---|---|
| Slope (95% CI) | Proportional Bias | Intercept (95% CI) | Systematic Bias | Cohen d (95% CI) | Paired t-test (p-Value) | ||
| LSF | −9.64 ± 34.85 (−77.96, 58.67) | 0.9 (0.5, 1.3) | No | 8.4 (−53.9, 70.7) | No | 0.27 (−0.29, 0.58) | 0.38 |
| RSF | −19.22 ± 27.43 (−72.99, 34.55) | 0.9 (0.7, 1.2) | No | −6.6 (−52.8, 39.7) | No | 0.7 (0.36, 1.03) | <0.001 |
| FLEX | −36.59 ± 45.08 (−124.9, 51.76) | 1.1 (0.5, 1.7) | No | −64.5 (−217.3, 88.3) | No | 0.81 (0.46, 1.15) | <0.001 |
| EXT | 28.44 ± 48.04 (−65.72, 122.6) | 1.0 (0.2, 1.8) | No | 29.4 (−144.4, 203.1) | No | −0.59 (−0.91, −0.26) | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oxford, S.W.; Clarke, N.D.; Tallis, J. Between-Session Reliability of Field-Based Assessments of Isometric Neck Strength. Sensors 2024, 24, 5015. https://doi.org/10.3390/s24155015
Oxford SW, Clarke ND, Tallis J. Between-Session Reliability of Field-Based Assessments of Isometric Neck Strength. Sensors. 2024; 24(15):5015. https://doi.org/10.3390/s24155015
Chicago/Turabian StyleOxford, Samuel W., Neil D. Clarke, and Jason Tallis. 2024. "Between-Session Reliability of Field-Based Assessments of Isometric Neck Strength" Sensors 24, no. 15: 5015. https://doi.org/10.3390/s24155015
APA StyleOxford, S. W., Clarke, N. D., & Tallis, J. (2024). Between-Session Reliability of Field-Based Assessments of Isometric Neck Strength. Sensors, 24(15), 5015. https://doi.org/10.3390/s24155015






