The Prediction and Evaluation of Surface Quality during the Milling of Blade-Root Grooves Based on a Long Short-Term Memory Network and Signal Fusion
Abstract
:1. Introduction
2. Experimental Design
2.1. Experimental Platform Construction Scheme
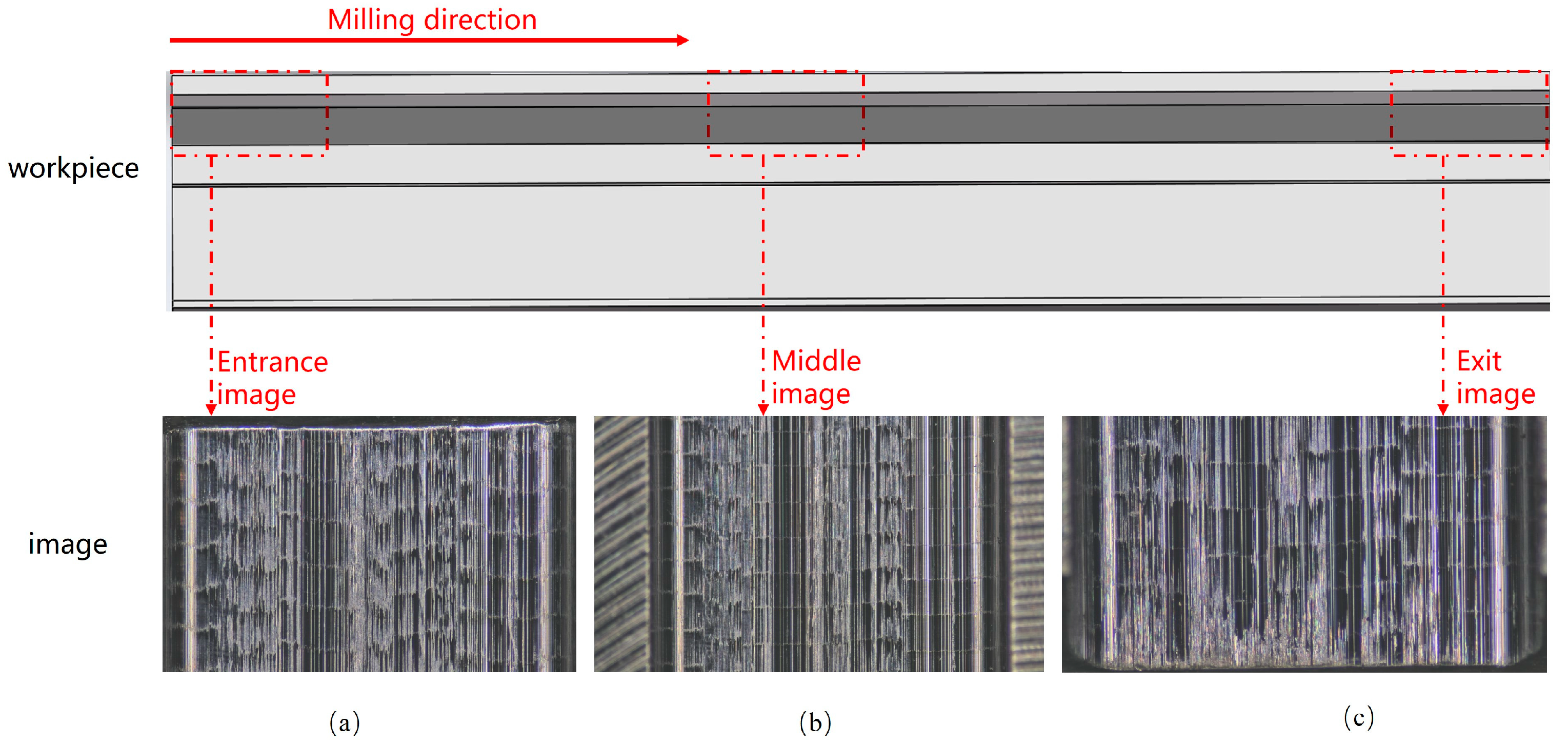
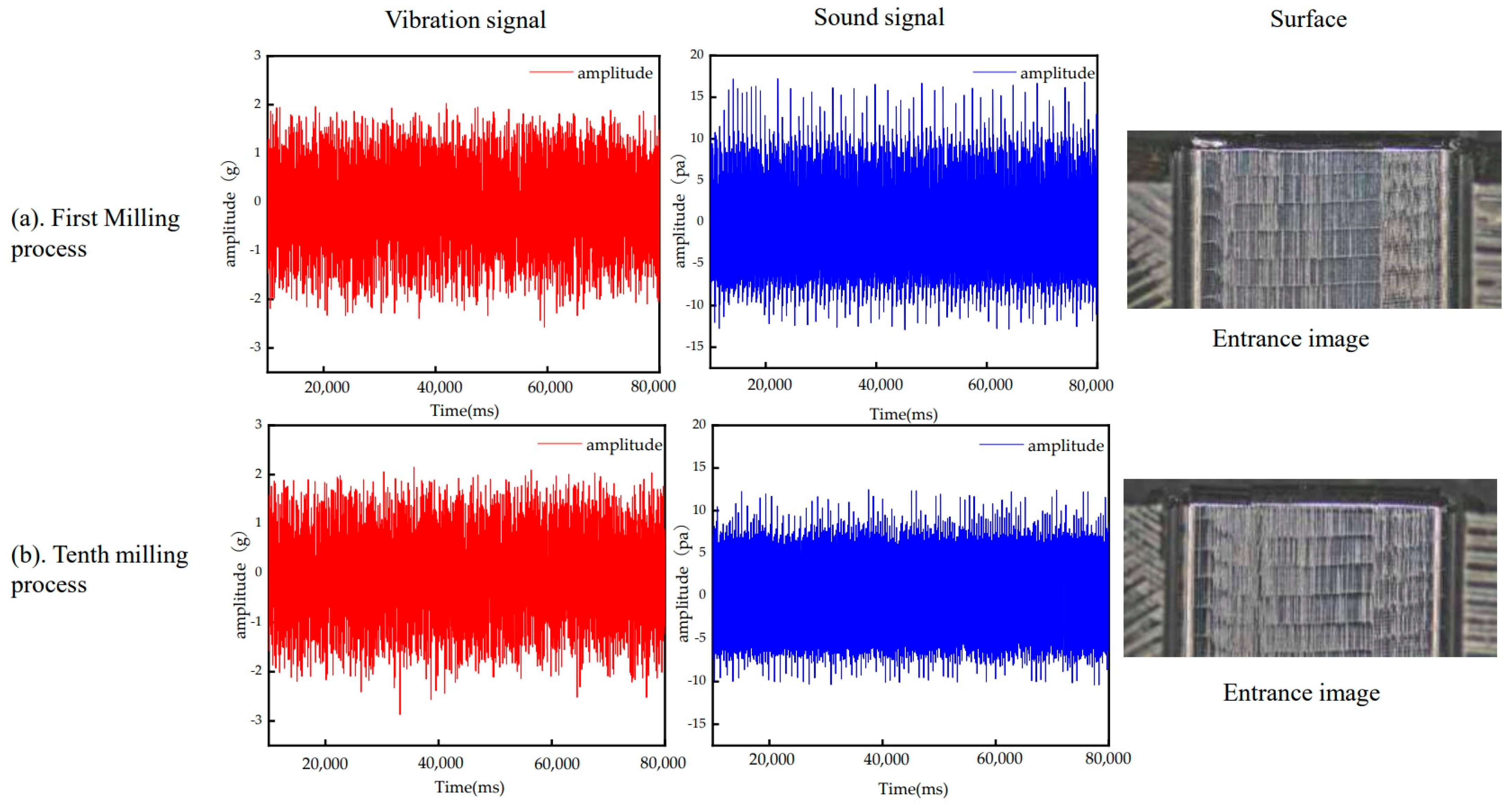
2.2. Experimental Data Acquisition
3. Feature Extraction and Correlation Analysis
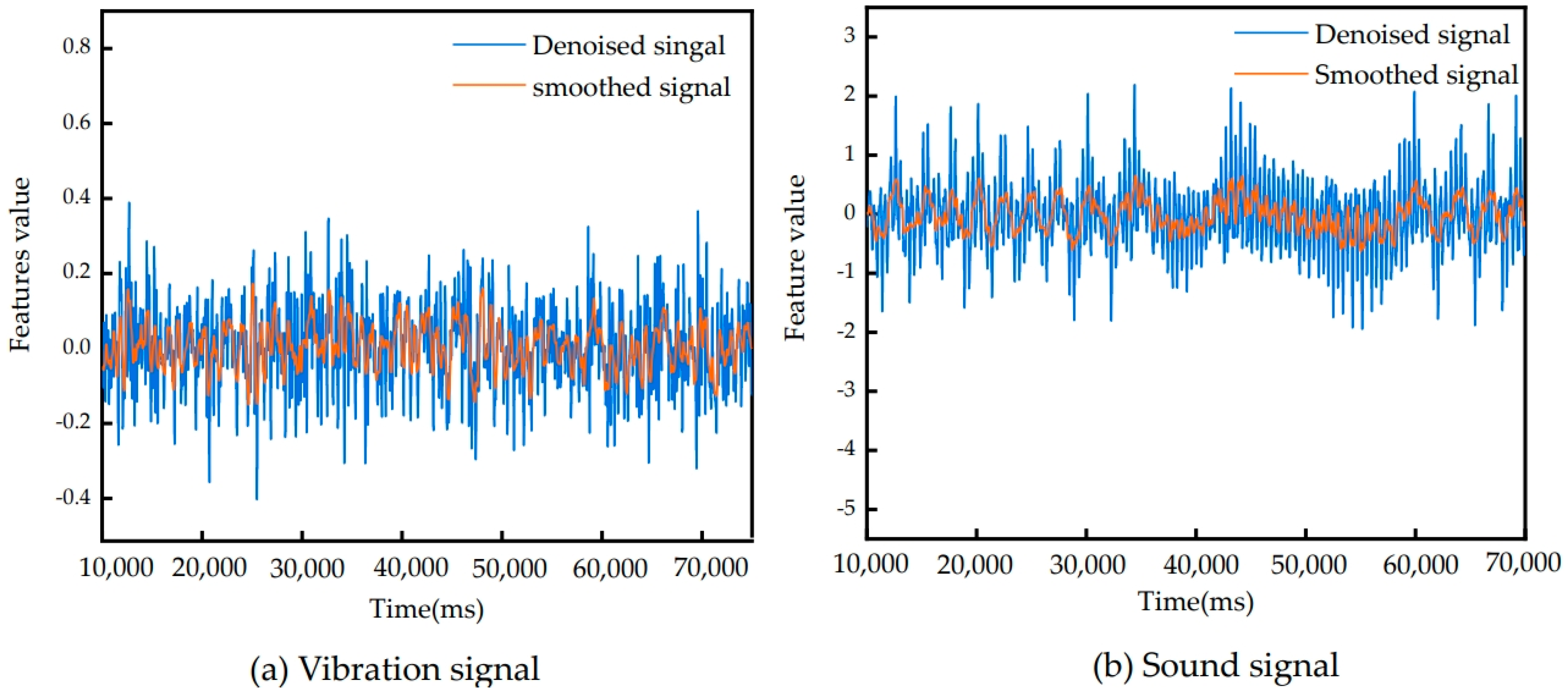
3.1. Signal Feature Extraction
3.2. Surface Texture Image Feature Extraction
3.3. Correlation Analysis
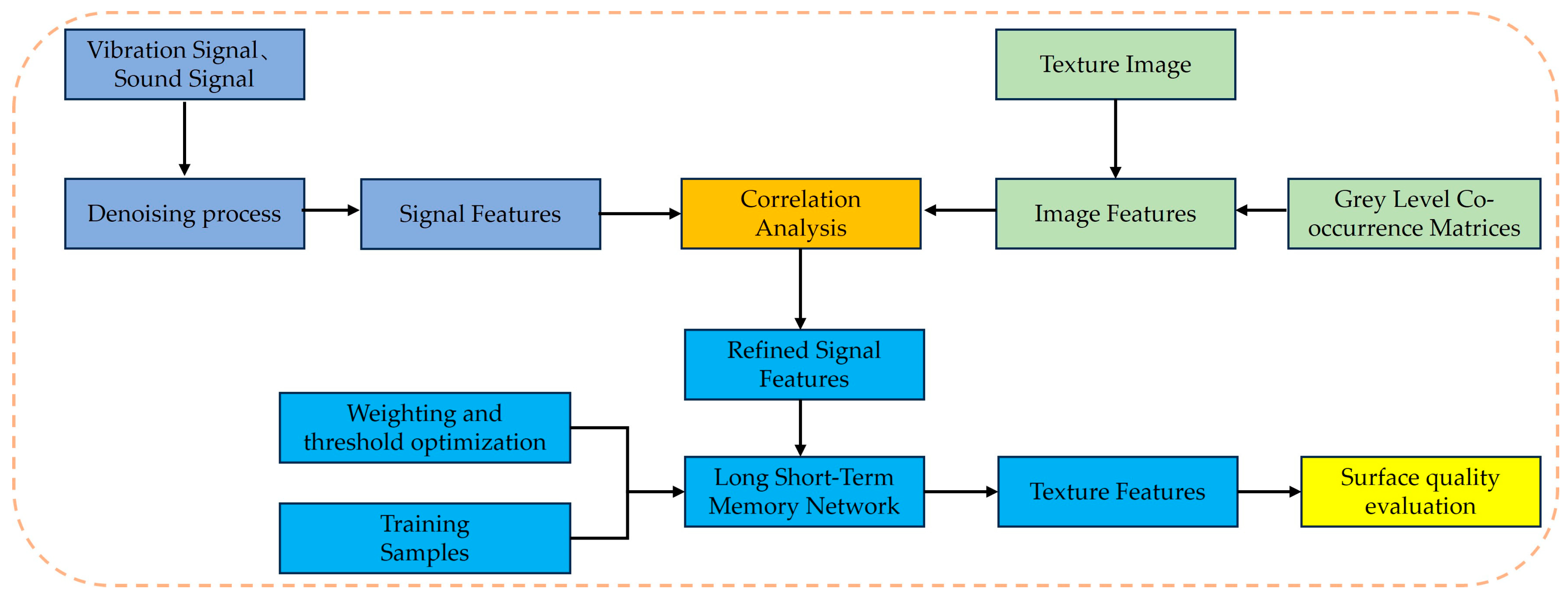
4. The Evaluation of Surface Quality Based on LSTM and Signal Fusion
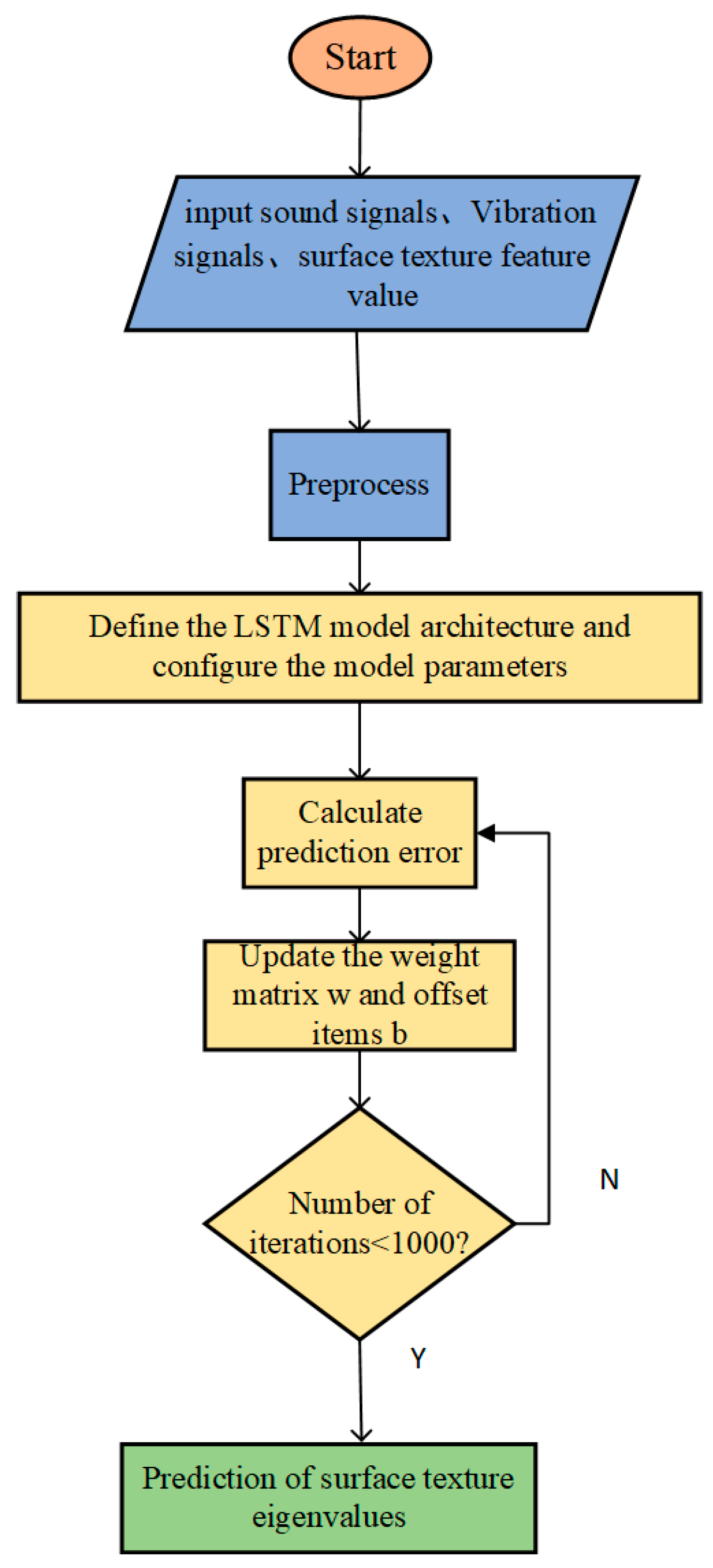
4.1. Model Building
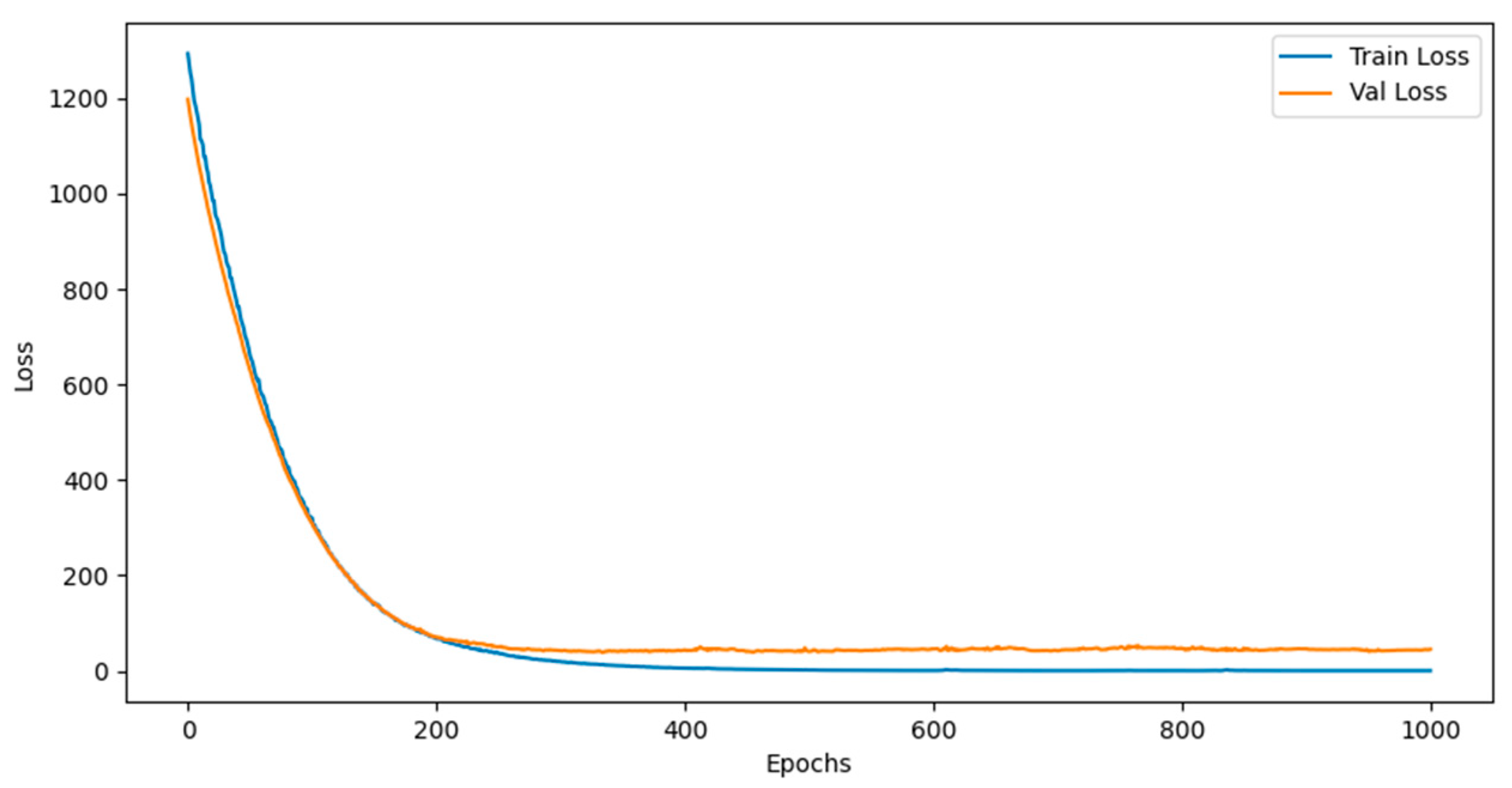
4.2. Network Structure and Parameter Setting
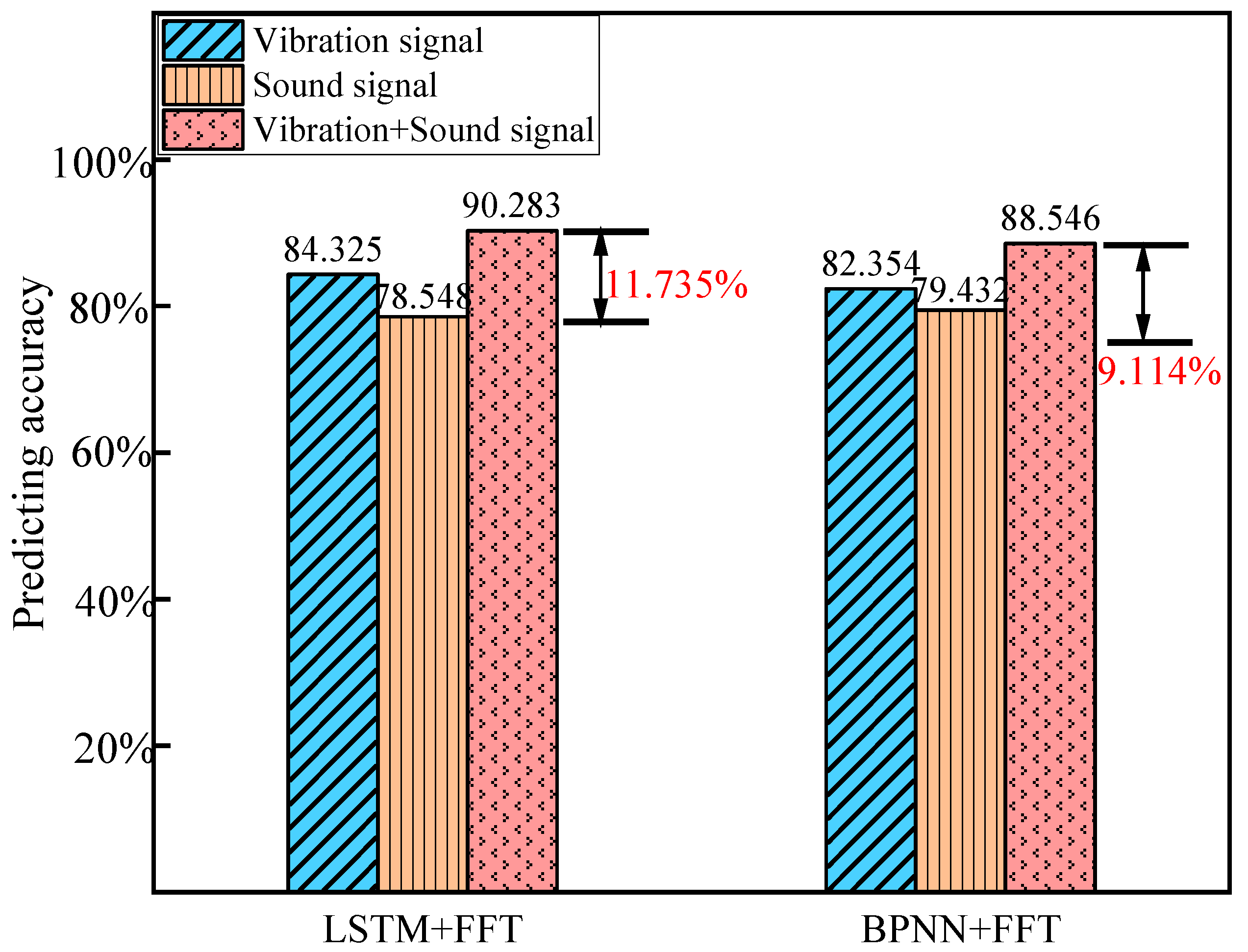
4.3. Surface Quality Evaluation and Result Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Puspitasari, P.; Andoko, A.; Kurniawan, P. Failure analysis of a gas turbine blade: A review. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1034, 012156. [Google Scholar] [CrossRef]
- Podsiadlo, P.; Wolski, M.; Stachowiak, G.W. Directional Signatures of Surface Texture. Tribol. Lett. 2019, 67, 109. [Google Scholar] [CrossRef]
- Otsuki, T.; Okita, K.; Sasahara, H. Evaluating surface quality by luminance and surface roughness. Precis. Eng. 2022, 74, 147–162. [Google Scholar] [CrossRef]
- Deng, Y.; Tan, Y.; Wu, X.; Zhu, J. Local tolerance and quality evaluation for optical surfaces. Optica 2022, 9, 1039–1049. [Google Scholar] [CrossRef]
- Yu, S.; Zhao, G.; Li, C.; Xu, S.; Zheng, Z. Prediction models for energy consumption and surface quality in stainless steel milling. Int. J. Adv. Manuf. Technol. 2021, 117, 3777–3792. [Google Scholar] [CrossRef]
- Zhao, B.; Chen, F.; Jia, X.-F.; Zhao, C.-Y.; Wang, X.-B. Surface quality prediction model of nano-composite ceramics in ultrasonic vibration-assisted ELID mirror grinding. J. Mech. Sci. Technol. 2017, 31, 1877–1884. [Google Scholar] [CrossRef]
- Dutta, S.; Pal, S.; Mukhopadhyay, S.; Sen, R. Application of digital image processing in tool condition monitoring: A review. CIRP J. Manuf. Sci. Technol. 2013, 6, 212–232. [Google Scholar] [CrossRef]
- Gadelmawla, E.S.; Al-Mufadi, F.A.; Al-Aboodi, A.S. Calculation of the machining time of cutting tools from captured images of machined parts using image texture features. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 228, 203–214. [Google Scholar] [CrossRef]
- Grzesik, W.; Rech, J.; Żak, K. Characterization of surface textures generated on hardened steel parts in high-precision machining operations. Int. J. Adv. Manuf. Technol. 2015, 78, 2049–2056. [Google Scholar] [CrossRef]
- Grigoriev, A.Y.; Myshkin, N. Comparing surface roughness and texture concepts. In Proceedings of the 8th International Conference BALTTRIB’2015, Kaunas, Lithuania, 26–27 November 2015; Volume 6, pp. 6–69. [Google Scholar]
- Kim, D.-S.; Chang, I.-C.; Kim, S.-W. Microscopic topographical analysis of tool vibration effects on diamond turned optical surfaces. Precis. Eng. 2002, 26, 168–174. [Google Scholar] [CrossRef]
- Sun, H.; Gao, D.; Zhao, Z.; Tang, X. An approach to in-process surface texture condition monitoring. Robot. Comput. Manuf. 2017, 48, 254–262. [Google Scholar] [CrossRef]
- Lu, X.; Zeng, F.; Xv, K.; Zhang, Y.; Liang, S.Y. Prediction of tool wear during micro-milling Inconel 718 based on long short-term memory network. Precis. Eng. 2024, 86, 195–202. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Bustillo, A.; Wojciechowski, S.; Sharma, V.S.; Gupta, M.K.; Kuntoğlu, M. Artificial intelligence systems for tool condition monitoring in machining: Analysis and critical review. J. Intell. Manuf. 2023, 34, 2079–2121. [Google Scholar] [CrossRef]
- Liu, X.; Liu, S.; Li, X.; Zhang, B.; Yue, C.; Liang, S.Y. Intelligent tool wear monitoring based on parallel residual and stacked bidirectional long short-term memory network. J. Manuf. Syst. 2021, 60, 608–619. [Google Scholar] [CrossRef]
- Gao, K.; Zhou, Z.; Qin, Y. Gas concentration prediction by LSTM network combined with wavelet thresholding denoising and phase space reconstruction. Heliyon 2024, 10, e28112. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Li, C.; Liu, C.; Wang, C.; Zhang, X.; Sun, W. Machined surface prediction and reliability analysis in peripheral milling operations. Int. J. Mech. Sci. 2024, 272, 109193. [Google Scholar] [CrossRef]
- Andrews, A.; Manisekar, K.; Rex, F.M.T.; Sivakumar, G.; Narayanan, M. An expert system for vibration-based surface roughness prediction using firefly algorithm and LSTM network. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 414. [Google Scholar] [CrossRef]
- Tang, K.-E.; Weng, C.-Y.; Cheng, Y.-C.; Liu, C.-W. Typical signal anomaly monitoring and support vector regression-based surface roughness prediction with acoustic emission signals in single-point diamond turning. J. Manuf. Process. 2024, 112, 126–135. [Google Scholar] [CrossRef]
- Manjunath, K.; Tewary, S.; Khatri, N. Surface roughness prediction in milling using long-short term memory modelling. Mater. Today Proc. 2022, 64, 1300–1304. [Google Scholar] [CrossRef]
- Sajjady, S.; Abadi, H.N.H.; Amini, S.; Nosouhi, R. Analytical and experimental study of topography of surface texture in ultrasonic vibration assisted turning. Mater. Des. 2016, 93, 311–323. [Google Scholar] [CrossRef]
- Bi, G.; Liu, S.; Su, S.; Wang, Z. Diamond Grinding Wheel Condition Monitoring Based on Acoustic Emission Signals. Sensors 2021, 21, 105. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Shi, T.; Xuan, J. Milling tool wear prediction using multi-sensor feature fusion based on stacked sparse autoencoders. Measurement 2022, 190, 110719. [Google Scholar] [CrossRef]
- Jansen, M. Multiscale local polynomial smoothing in a lifted pyramid for non-equispaced data. IEEE Trans. Signal Process. 2012, 61, 545–555. [Google Scholar] [CrossRef]
- Li, J.; Cao, X.; Chen, R.; Zhao, C.; Li, Y.; Huang, X. Prediction of remaining fatigue life of metal specimens using data-driven method based on acoustic emission signal. Appl. Acoust. 2023, 211, 109571. [Google Scholar] [CrossRef]
- Browne, M.; Mayer, N.; Cutmore, T. A multiscale polynomial filter for adaptive smoothing. Digit. Signal Process. 2007, 17, 69–75. [Google Scholar] [CrossRef]
- Dutta, S.; Pal, S.K.; Sen, R. On-machine tool prediction of flank wear from machined surface images using texture analyses and support vector regression. Precis. Eng. 2016, 43, 34–42. [Google Scholar] [CrossRef]
- Su, H.; Chen, J.; Li, Z.; Meng, H.; Wang, X. The fusion feature wavelet pyramid based on FCIS and GLCM for texture classification. Int. J. Mach. Learn. Cybern. 2023, 15, 1907–1926. [Google Scholar] [CrossRef]
- Sonka, M.; Hlavac, V.; Boyle, R. Image Processing, Analysis and Machine Vision; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zhang, X.; Li, M.; Huang, D. Surface quality and burr characterization during drilling CFRP/Al stacks with acoustic emission monitoring. J. Manuf. Process. 2023, 98, 138–148. [Google Scholar] [CrossRef]
- Bhat, N.N.; Dutta, S.; Pal, S.K.; Pal, S. Tool condition classification in turning process using hidden Markov model based on texture analysis of machined surface images. Measurement 2016, 90, 500–509. [Google Scholar] [CrossRef]
- Dutta, S.; Pal, S.K.; Sen, R. Progressive tool flank wear monitoring by applying discrete wavelet transform on turned surface images. Measurement 2016, 77, 388–401. [Google Scholar] [CrossRef]
- Menezes, P.L. Surface texturing to control friction and wear for energy efficiency and sustainability. Int. J. Adv. Manuf. Technol. 2016, 85, 1385–1394. [Google Scholar] [CrossRef]
- Kulisz, M.; Kłosowski, G.; Rymarczyk, T.; Hoła, A.; Niderla, K.; Sikora, J. The use of the multi-sequential LSTM in electrical tomography for masonry wall moisture detection. Measurement 2024, 234, 114860. [Google Scholar] [CrossRef]
- Huang, F.; Li, X.; Yuan, C.; Zhang, S.; Zhang, J.; Qiao, S. Attention-Emotion-Enhanced Convolutional LSTM for Sentiment Analysis. IEEE Trans. Neural Networks Learn. Syst. 2021, 33, 4332–4345. [Google Scholar] [CrossRef] [PubMed]
- Filzasavitra, P.; Purboyo, T.; Saputra, R. Analysis of Steganography on PNG hnage using Least Significant Bit (LSB), Peak Signal to Noise Ratio (PSNR) and Mean Square Error (MSE). J. Eng. Appl. Sci. 2019, 14, 7821–7827. [Google Scholar]
- Plaza, E.G.; López, P.N.; González, E.B. Efficiency of vibration signal feature extraction for surface finish monitoring in CNC machining. J. Manuf. Process. 2019, 44, 145–157. [Google Scholar] [CrossRef]
- Liu, M.-K.; Tseng, Y.-H.; Tran, M.-Q. Tool wear monitoring and prediction based on sound signal. Int. J. Adv. Manuf. Technol. 2019, 103, 3361–3373. [Google Scholar] [CrossRef]



| Tensile Strength (MPa) | Yield Strength (MP) | Elongation (%) | (%) | Work of Impact (AKV/j) | Anneal HB |
|---|---|---|---|---|---|
| ≥635 |
| Workpiece Materials | Spindle Speed | Cutting Speed | Feed | Milling Cutter Diameter | Milling Cutter Materials |
|---|---|---|---|---|---|
| 21Cr13 | 350 rpm | 137.7 mm/min | 0.078 mm | 125 mm | Cemented carbide |
| Texture Image Features | Most Correlate Vibration Signal Features | Most Correlate Sound Signal Features | Correlation Coefficient with Vibration Signal | Correlation Coefficient with Sound Signal |
|---|---|---|---|---|
| 0.882 | 0.904 | |||
| 0.924 | 0.950 | |||
| 0.884 | 0.898 | |||
| 0.893 | 0.896 | |||
| 0.948 | 0.932 |
| No | Name | ASM | CON | ENT | IDM | COR | Surface Quality |
|---|---|---|---|---|---|---|---|
| 1 | Predictive Value | 0.2781 | 4.7901 | 12.8995 | 3.8747 | 69.6736 | 1 |
| Experimental Value | 0.2511 | 4.6264 | 12.8026 | 3.6728 | 70.62 | ||
| 2 | Predictive Value | 0.2398 | 4.5409 | 13.0305 | 3.6454 | 67.3391 | 1 |
| Experimental Value | 0.2606 | 4.5345 | 12.7417 | 3.6533 | 68.6107 | ||
| 3 | Predictive Value | 0.2583 | 3.9633 | 13.4303 | 3.5864 | 66.9725 | 1 |
| Experimental Value | 0.2573 | 4.0201 | 13.1948 | 3.5708 | 67.9129 | ||
| 4 | Predictive Value | 0.2406 | 3.7427 | 12.9331 | 3.4863 | 67.0368 | 1 |
| Experimental Value | 0.2565 | 3.9882 | 13.4364 | 3.438 | 68.1714 | ||
| 5 | Predictive Value | 0.3218 | 2.5488 | 11.9048 | 3.2482 | 58.4772 | 0 |
| Experimental Value | 0.3234 | 2.7415 | 11.9697 | 3.2739 | 58.6743 | ||
| 6 | Predictive Value | 0.2751 | 3.7142 | 13.9174 | 3.2117 | 67.0527 | 1 |
| Experimental Value | 0.2875 | 3.8327 | 14.0919 | 3.2144 | 67.3678 | ||
| 7 | Predictive Value | 0.3119 | 3.7786 | 14.2259 | 3.1109 | 66.4437 | 1 |
| Experimental Value | 0.2992 | 3.8315 | 14.1941 | 3.1029 | 66.8836 | ||
| 8 | Predictive Value | 0.3025 | 3.6839 | 14.1422 | 3.1737 | 67.4613 | 1 |
| Experimental Value | 0.2992 | 3.8315 | 14.1941 | 3.1029 | 66.8836 | ||
| 9 | Predictive Value | 0.2997 | 3.7508 | 14.6923 | 3.0815 | 66.9251 | 0 |
| Experimental Value | 0.323 | 3.7122 | 14.3677 | 3.1175 | 66.2705 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, J.; Chen, K.; Meng, Z.; Li, Z.; Li, R.; Liu, W. The Prediction and Evaluation of Surface Quality during the Milling of Blade-Root Grooves Based on a Long Short-Term Memory Network and Signal Fusion. Sensors 2024, 24, 5055. https://doi.org/10.3390/s24155055
Ni J, Chen K, Meng Z, Li Z, Li R, Liu W. The Prediction and Evaluation of Surface Quality during the Milling of Blade-Root Grooves Based on a Long Short-Term Memory Network and Signal Fusion. Sensors. 2024; 24(15):5055. https://doi.org/10.3390/s24155055
Chicago/Turabian StyleNi, Jing, Kai Chen, Zhen Meng, Zuji Li, Ruizhi Li, and Weiguang Liu. 2024. "The Prediction and Evaluation of Surface Quality during the Milling of Blade-Root Grooves Based on a Long Short-Term Memory Network and Signal Fusion" Sensors 24, no. 15: 5055. https://doi.org/10.3390/s24155055
APA StyleNi, J., Chen, K., Meng, Z., Li, Z., Li, R., & Liu, W. (2024). The Prediction and Evaluation of Surface Quality during the Milling of Blade-Root Grooves Based on a Long Short-Term Memory Network and Signal Fusion. Sensors, 24(15), 5055. https://doi.org/10.3390/s24155055






