Adaptive Control for a Two-Axis Semi-Strapdown Stabilized Platform Based on Disturbance Transformation and LWOA-PID
Abstract
1. Introduction
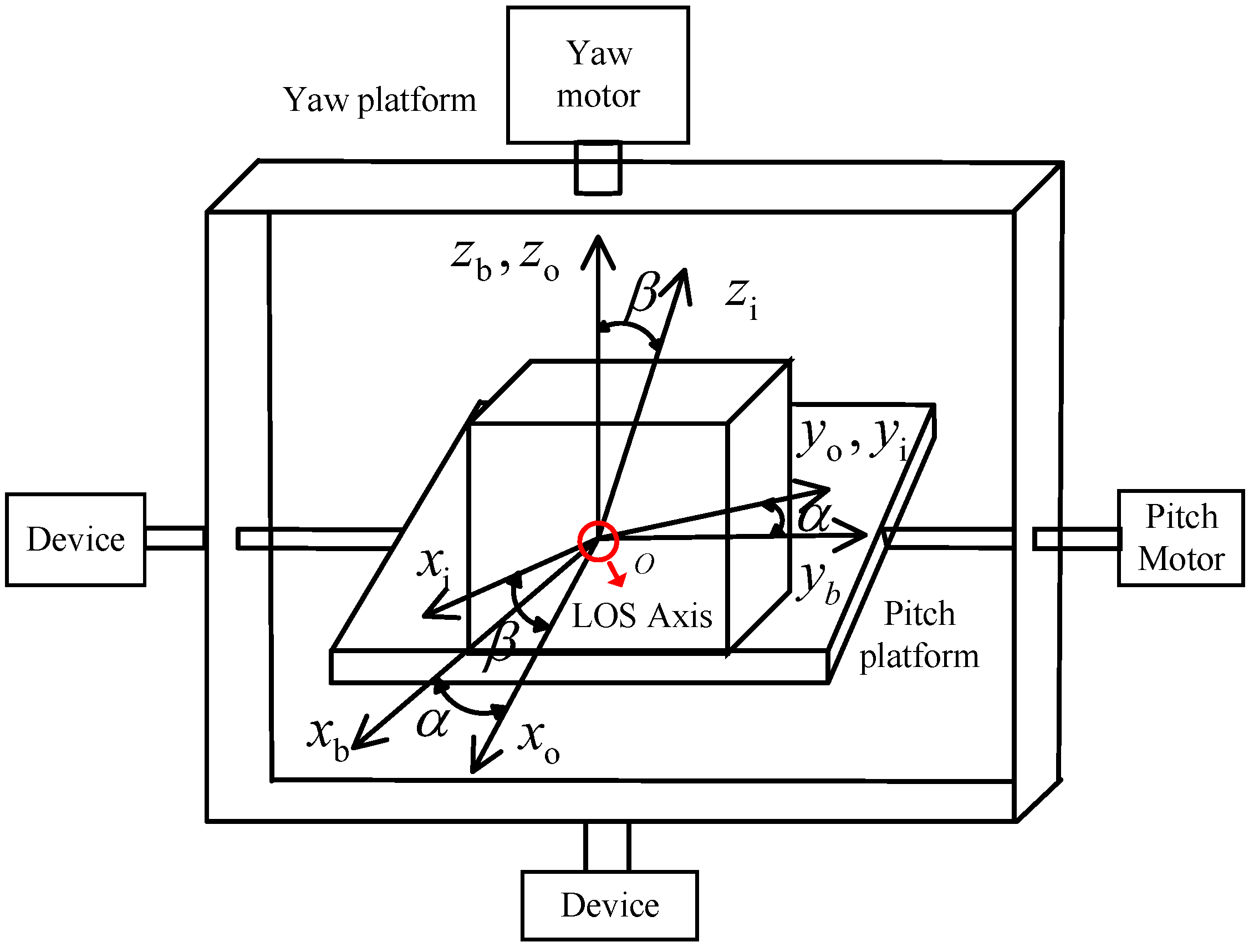
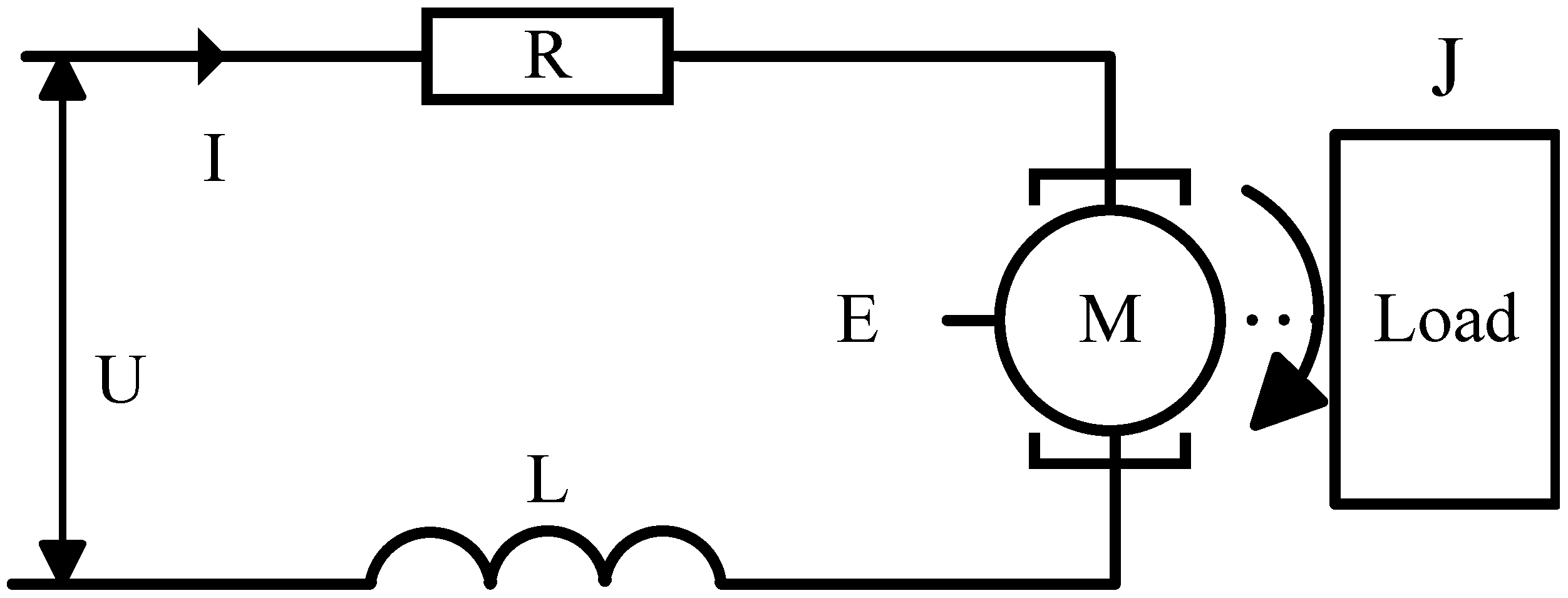
2. Coordinate System Definition and Model Analysis
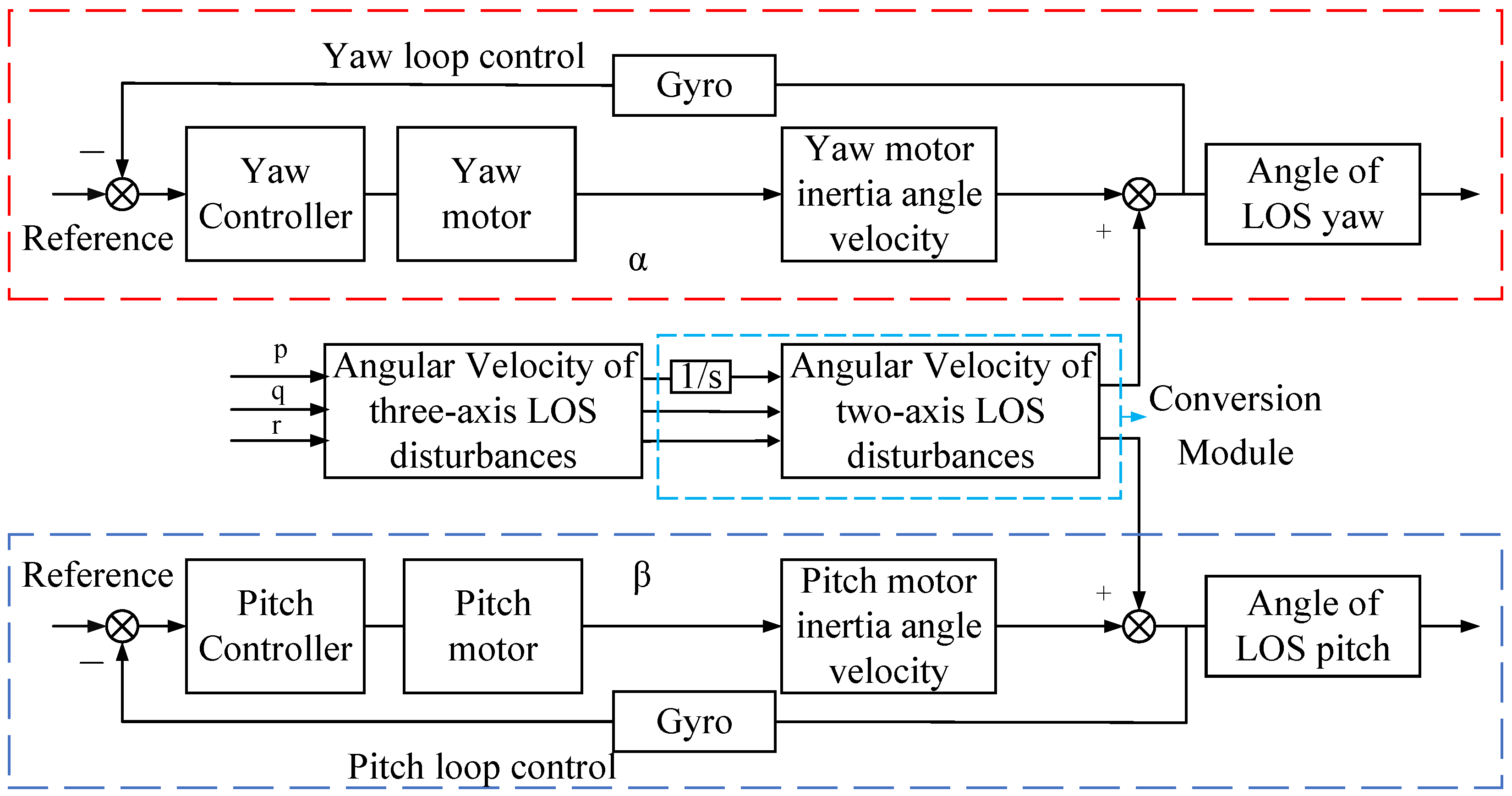
3. Conversion Module and LWOA-PID Design
3.1. Conversion Module
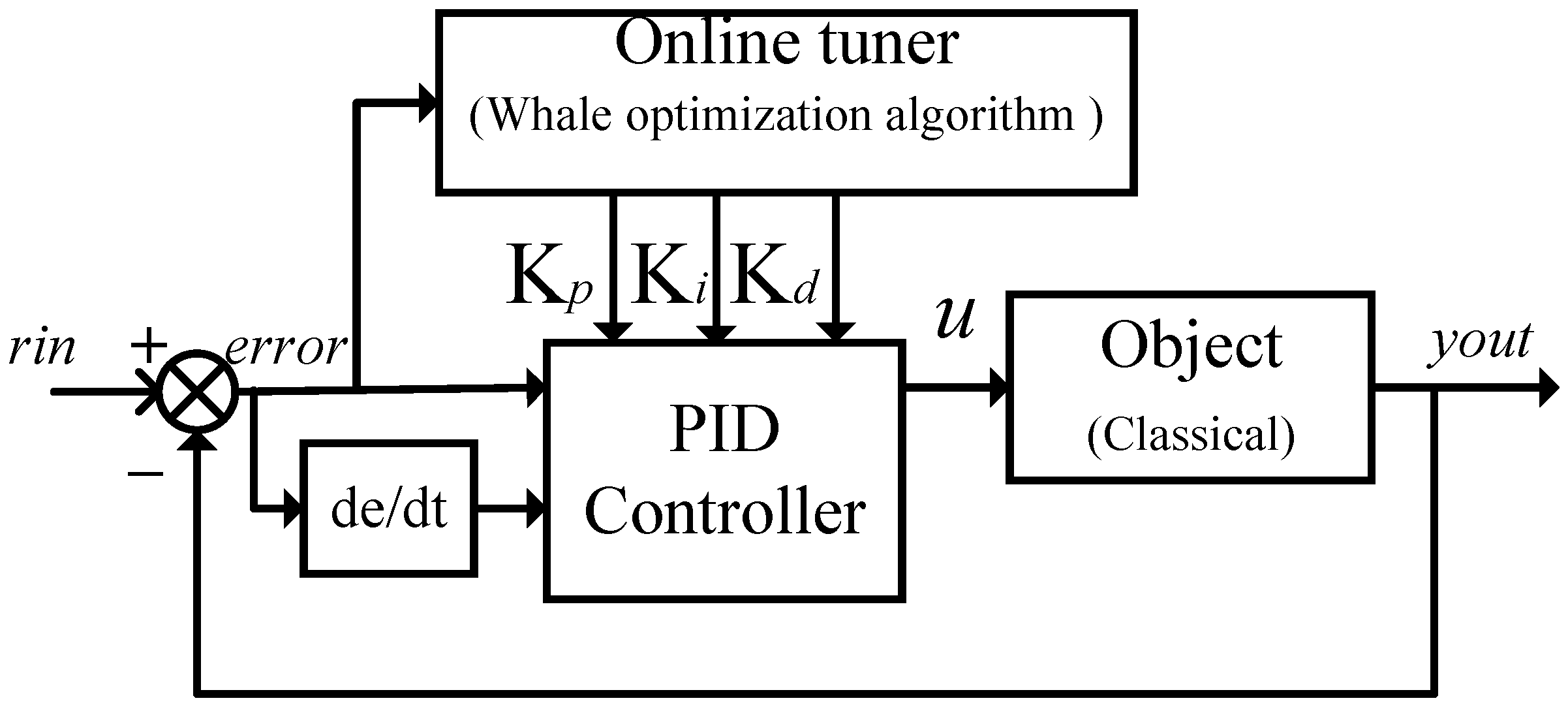
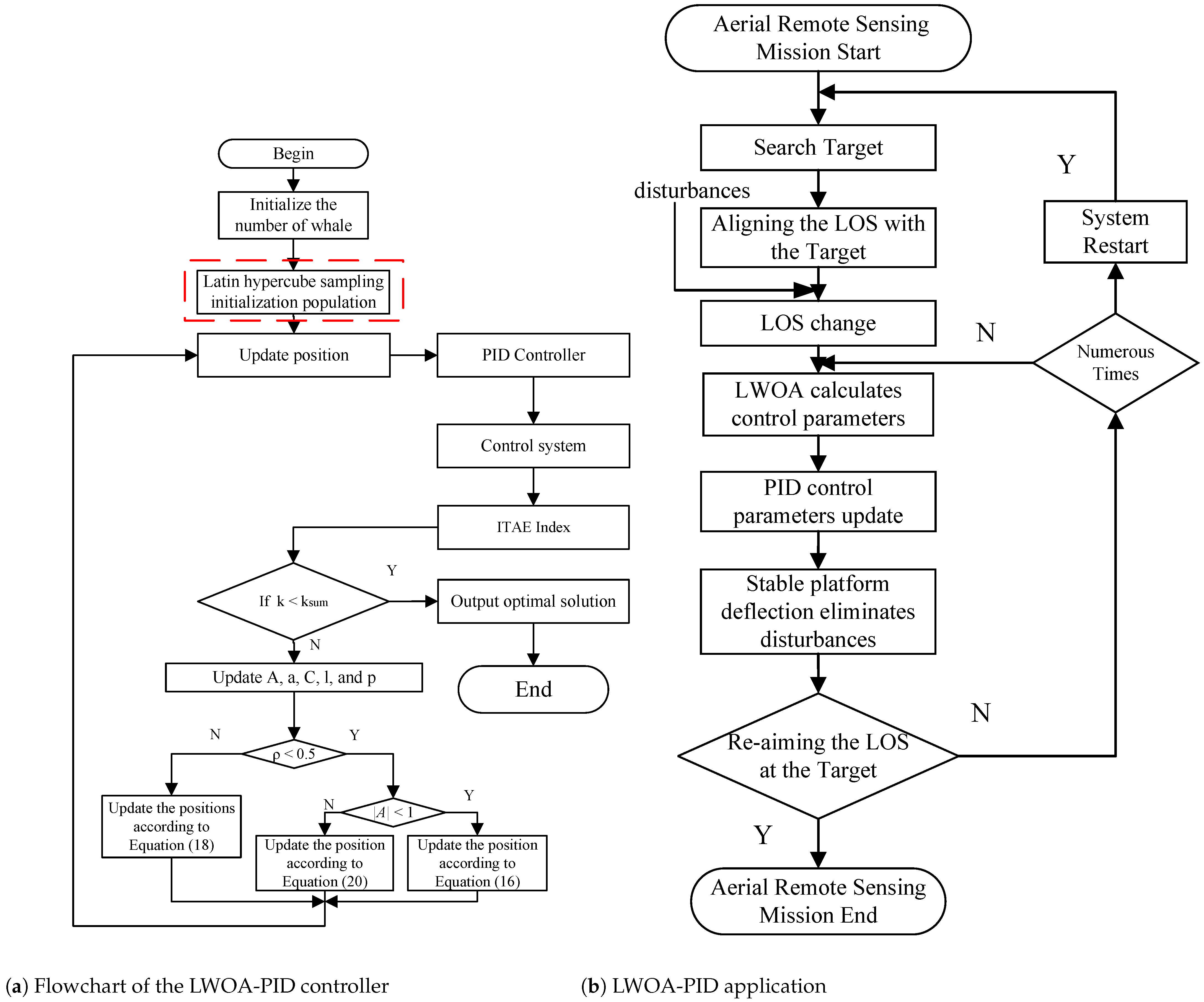
3.2. LWOA-PID Controller
4. Simulink Results and Analysis
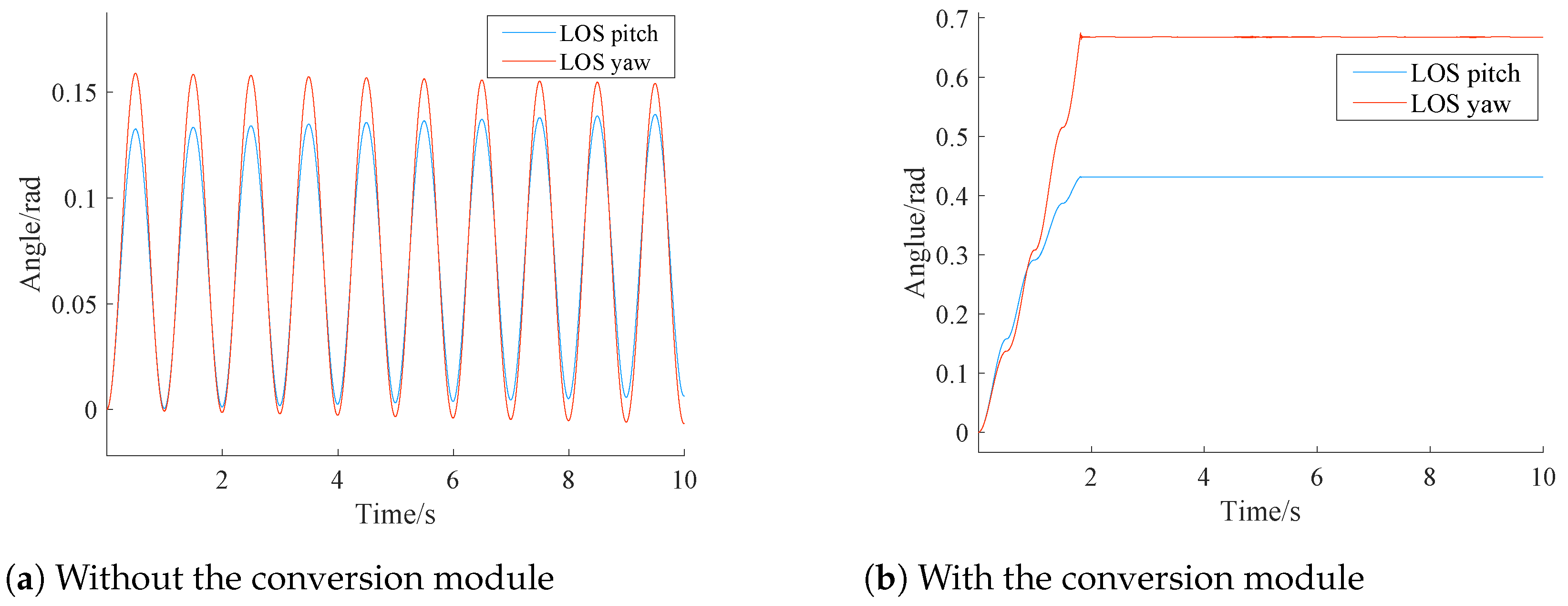
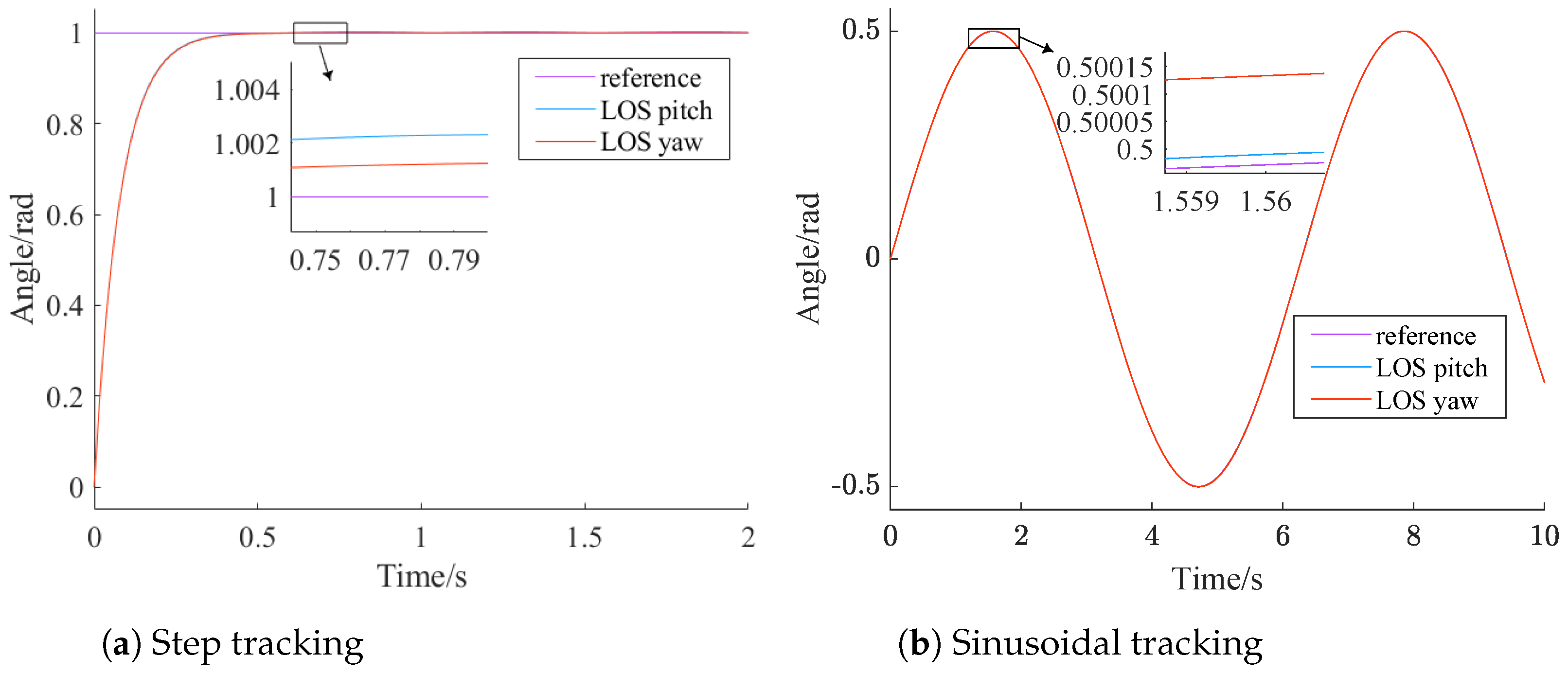
4.1. Conversion Module Validation
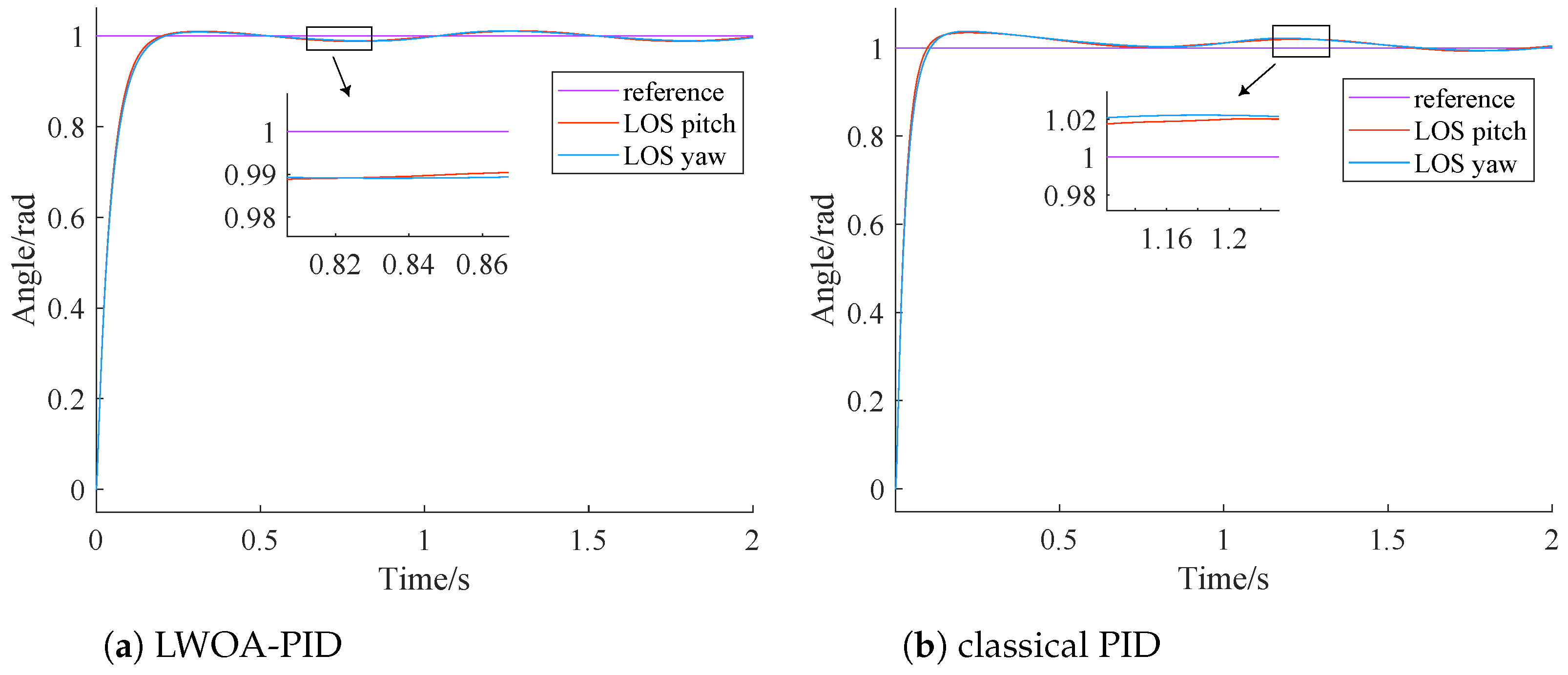
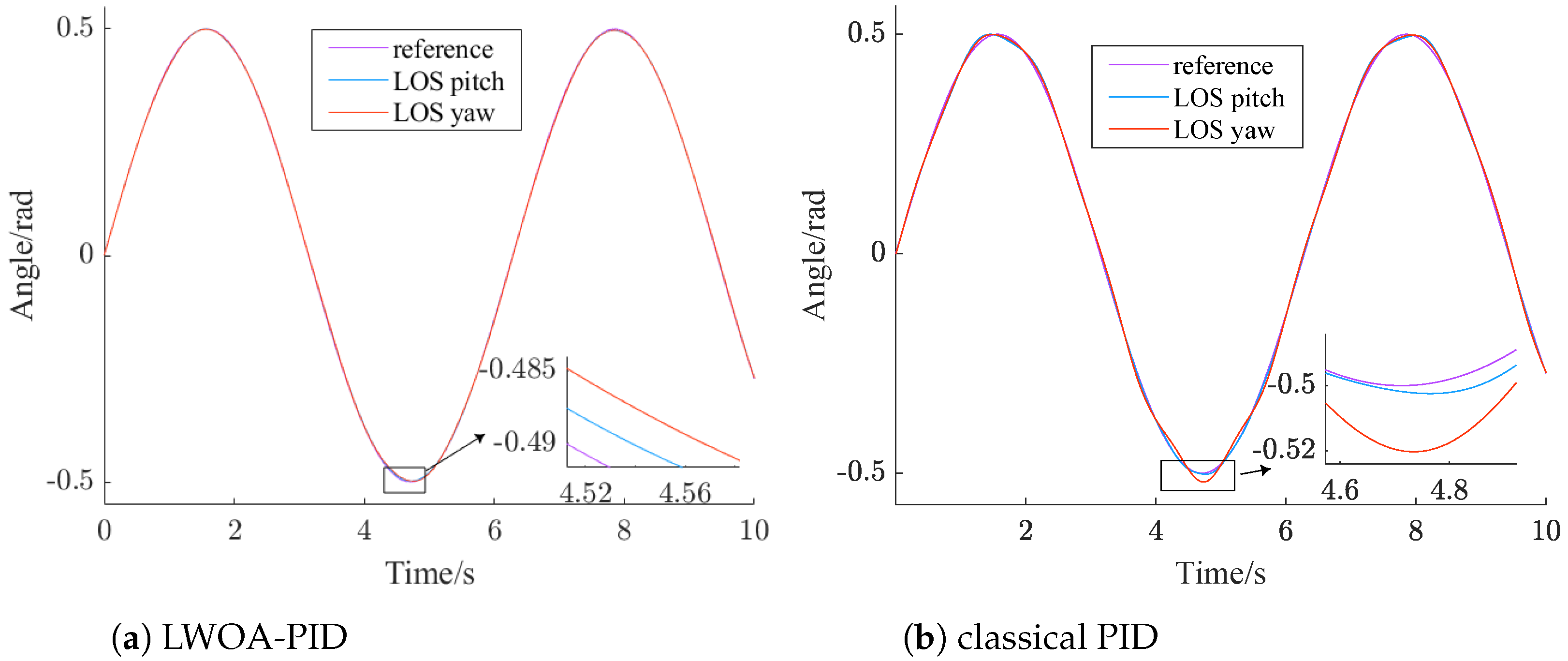
4.2. Comparison between LWOA-PID and Classical PID
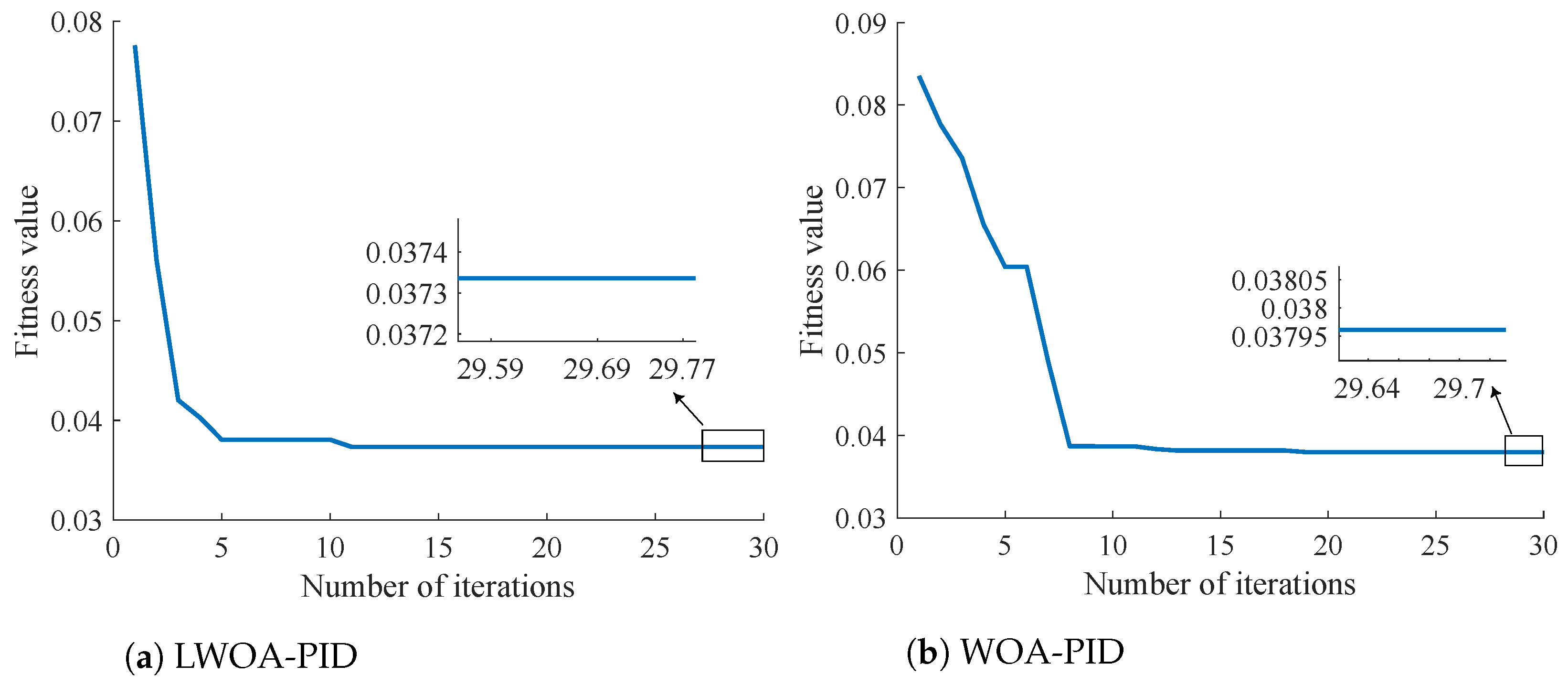
4.3. Comparison between LWOA-PID and WOA-PID
4.4. Combined Control
4.5. Sensitivity Analysis of the Conversion Module
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Laššák, M.; Draganova, K.; Blišťanová, M.; Kalapoš, G.; Mikloš, J. Small UAV Camera Gimbal Stabilization Using Digital Filters and Enhanced Control Algorithms for Aerial Survey and Monitoring. Acta Montan. Slovaca 2020, 25, 127. [Google Scholar]
- Liu, Z.Y. Research on Error Analysis and Structural Optimization of Semi-Strapdown Inertial Stabilized Platform for Aerial Remote Sensing; Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences: Changchun, China, 2017. [Google Scholar]
- Wang, Y.; Lei, H.; Ye, J.; Bu, X. Backstepping sliding mode control for radar seeker servo system considering guidance and control system. Sensors 2018, 18, 2927. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.Y. The Research of Nonlinear Hyperchaos System Synchronization; Northeast Petroleum University: Daqing, China, 2015. [Google Scholar]
- Bai, E.W.; Lonngren, K.E. Sequential synchronization of two Lorenz systems using active control. Chaos Solitons Fractals 2000, 11, 1041–1044. [Google Scholar] [CrossRef]
- Almatroud, O.A.; Shukur, A.A.; Pham, V.-T.; Grassi, G. Oscillator with Line of Equilibiria and Nonlinear Function Terms: Stability Analysis, Chaos, and Application for Secure Communications. Mathematics 2024, 12, 1874. [Google Scholar] [CrossRef]
- Sui, S.; Zhao, T. Active disturbance rejection control for optoelectronic stabilized platform based on adaptive fuzzy sliding mode control. ISA Trans. 2022, 125, 85–98. [Google Scholar] [CrossRef] [PubMed]
- Battistel, A.; Oliveira, T.R.; Rodrigues, V.H.P.; Fridman, L. Multivariable binary adaptive control using higher-order sliding modes applied to inertially stabilized platforms. Eur. J. Control 2022, 68, 28–39. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.; Qiao, P. Gain Function-Based Visual Tracking Control for Inertial Stabilized Platform with Output Con-straints and Disturbances. Electronics 2022, 11, 1137. [Google Scholar] [CrossRef]
- Guo, B.; Ke, F.; Yu, X.; Gao, X.; Sun, A. Control Strategy for Photoelectric Stabilized Platform Based on Sliding Mode Variable Structure Control. Acta Armamentarii 2022, 43, 1874. [Google Scholar]
- Ren, Y. Advanced Motion Control for Optoelectronic Tracking Systems; Beijing, Science Press: Beijing, China, 2017. [Google Scholar]
- Melo, A.G.; Andrade, F.A.A.; Guedes, I.P.; Carvalho, G.F.; Zachi, A.R.L.; Pinto, M.F. Fuzzy gain-scheduling PID for UAV position and altitude controllers. Sensors 2022, 22, 2173. [Google Scholar] [CrossRef]
- Tan, K.K.; Lee, T.H.; Khoh, C.J. PID-Augmented Adaptive Control of a Gyro Mirror Los System. Asian J. Control 2002, 4, 240–245. [Google Scholar] [CrossRef]
- Wei, J.; Qi, L. Application of adaptive fuzzy PID controller to tracker line of sight stabilized system. Control Theory Appl. 2008, 25, 278–282. [Google Scholar]
- Sabir, M.M.; Ali, T. Optimal PID controller design through swarm intelligence algorithms for sun tracking system. Appl. Math. Comput. 2016, 274, 690–699. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, J.C.; Wang, W. Self-tuning of PID parameters based on particle swarm optimization. Control Decis. 2005, 20, 5. [Google Scholar]
- Yamamoto, T.; Shah, S.L. Design and experimental evaluation of a multivariable self-tuning PID controller. IEEE Proc.-Control Theory Appl. 2004, 151, 645–652. [Google Scholar] [CrossRef]
- Kownacki, C.; Ambroziak, L. Asymmetrical artificial potential field as framework of nonlinear PID loop to control position tracking by nonholonomic UAVs. Sensors 2022, 22, 5474. [Google Scholar] [CrossRef] [PubMed]
- Jin, G.G.; Son, Y.D. Design of a nonlinear PID controller and tuning rules for first-order plus time delay models. Stud. Inform. Control 2019, 28, 157–166. [Google Scholar] [CrossRef]
- Şahin, M. Stabilization of Two Axis Gimbal System with Self Tuning PID Control. Politeknik Dergisi 2023. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Feng, X.; Donghai, L.; Yali, X. Comparing and optimum seeking of PID tuning methods base on ITAE index. Proc.-Chin. Soc. Electr. Eng. 2003, 23, 206–210. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Wang, G.Y.; Yu, H.; Yang, D.C. Decision Table Reduction based on Conditional Information Entropy. Chin. J. Comput. 2002, 25, 759–766. [Google Scholar]
- Deng, F.Y.; Zou, Y. Simulation of stable tracking control for gimbal of phase array seeker. Syst. Eng. Electron. 2013, 35, 402–407. [Google Scholar]
- Peng, F. Research on Parameter Self Tuning of Permanent Magnet Synchronous Motor Control Systems; Guangdong University of Technology: Guangzhou, China, 2016. [Google Scholar]
- Ji, T.; Ji, M.; Xu, Q.Q.; Wu, Y.J.; Xue, F. Modeling and dynamic characteristics analysis of airborne photoelectric stabilization platform. Laser Infrared 2021, 51, 206–211. [Google Scholar]




| Conversion Algorithm Table |
|---|
| Input: , , and |
| Output: and |
| 1. Begin |
| 2. Initialize Conversion Module |
| 3. While () do: |
| 4. The combined disturbance at the current time is calculated using Equations (11) to (14). |
| 5. Roll disturbances are compensated using Equation (15). |
| 6. Return to Step 4. |
| 7. End while |
| 8. End |
| Latin Hypercube Sampling Algorithm |
|---|
| Input: Population size and dimensionality. |
| Out: Population randomly distributed in the dimension. |
| 1. Determine the population size N and the population dimension D. |
| 2. Set the interval for variable x as [xmin, xmax], where xmin and |
| xmax are the lower and upper bounds of the quantity. |
| 3. Divide the interval [xmin, xmax] into N equal subintervals. |
| 4. Randomly select a point within each subinterval in every dimension. |
| 5. Combine the points from each dimension to form the initial population. |
| LWOA-PID Calculation Process |
|---|
| Input: The number of whale, the values of Ksum and the range of kp, ki, kd |
| Output: The optimal control parameters |
| 1. Latin hypercube sampling to initialize the whales population |
| 2. Calculate the fitness of each search agent according to Equation (25), |
| X* = the optimal control parameters |
| 3. while () |
| 4. for Update a, A, C, l, and p |
| 5. if1 (p < 0.5) |
| 6. If2 (|A| < 1) |
| 7. Update the position of the current search agent by the Equation (16) |
| 8. Else if2 (|A| >= 1) |
| 9. Update the position of the current search agent by the Equation (20). |
| 10. End if2 |
| 11. else if1 (p >= 0.5) |
| 12. Update the position of the current search by the Equation (18). |
| 13. end if1 |
| 14. End for |
| 15. Check if any search agent goes beyond the search space and amend it |
| 16. Calculate the fitness of each search agent. Update X* if there is a better solution |
| 17. K = k + 1 |
| 18. End while |
| Parameter | Value |
|---|---|
| Input sinusoidal disturbance | 1 rad/s, 1 Hz |
| Number of whales | 30 |
| Number of iterate | 30 |
| Optimization parameter range | 0–100 |
| Initial LOS axis pitch | 0 rad |
| Initial LOS axis yaw | 0 rad |
| J | |
| R | |
| 0 |
| Optical Yaw | Optical Pitch | |||
|---|---|---|---|---|
| Stable Time | Max Optical Error | Stable Time | Max Optical Error | |
| setp PID | 0.82 | 0.02 | 075 | 0.02 |
| setp NPSO-PID | 0.54 | 0.01 | 0.53 | 0.01 |
| sinusoidal PID | - | 0.02 | - | 0.002 |
| sinusoidal NPSO-PID | - | 0.005 | - | 0.0025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Zhou, J.; Chen, X.; Li, Q.; Chen, R. Adaptive Control for a Two-Axis Semi-Strapdown Stabilized Platform Based on Disturbance Transformation and LWOA-PID. Sensors 2024, 24, 5198. https://doi.org/10.3390/s24165198
Huang Q, Zhou J, Chen X, Li Q, Chen R. Adaptive Control for a Two-Axis Semi-Strapdown Stabilized Platform Based on Disturbance Transformation and LWOA-PID. Sensors. 2024; 24(16):5198. https://doi.org/10.3390/s24165198
Chicago/Turabian StyleHuang, Qixuan, Jiaxing Zhou, Xiang Chen, Qing Li, and Runjing Chen. 2024. "Adaptive Control for a Two-Axis Semi-Strapdown Stabilized Platform Based on Disturbance Transformation and LWOA-PID" Sensors 24, no. 16: 5198. https://doi.org/10.3390/s24165198
APA StyleHuang, Q., Zhou, J., Chen, X., Li, Q., & Chen, R. (2024). Adaptive Control for a Two-Axis Semi-Strapdown Stabilized Platform Based on Disturbance Transformation and LWOA-PID. Sensors, 24(16), 5198. https://doi.org/10.3390/s24165198




