A Magneto-Electric Device for Fluid Pipelines with Vibration Damping and Vibration Energy Harvesting
Abstract
1. Introduction
2. Theoretical Model
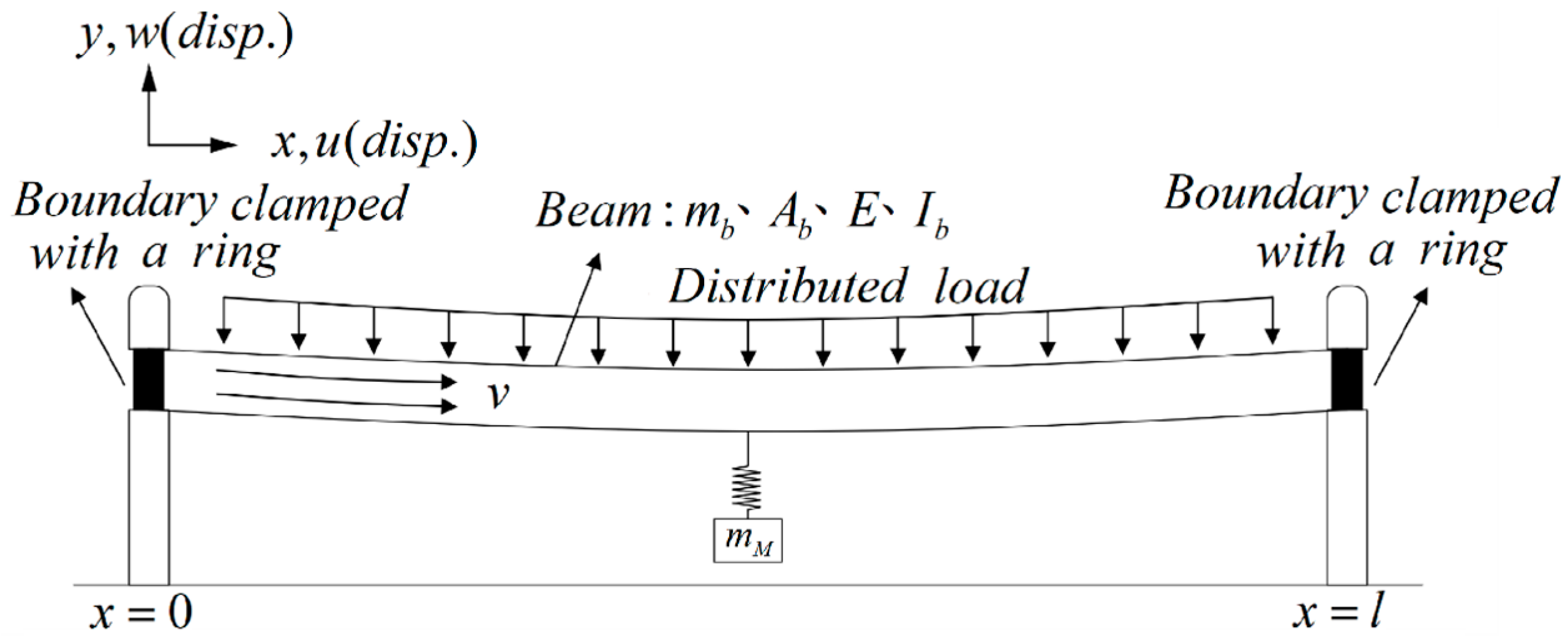
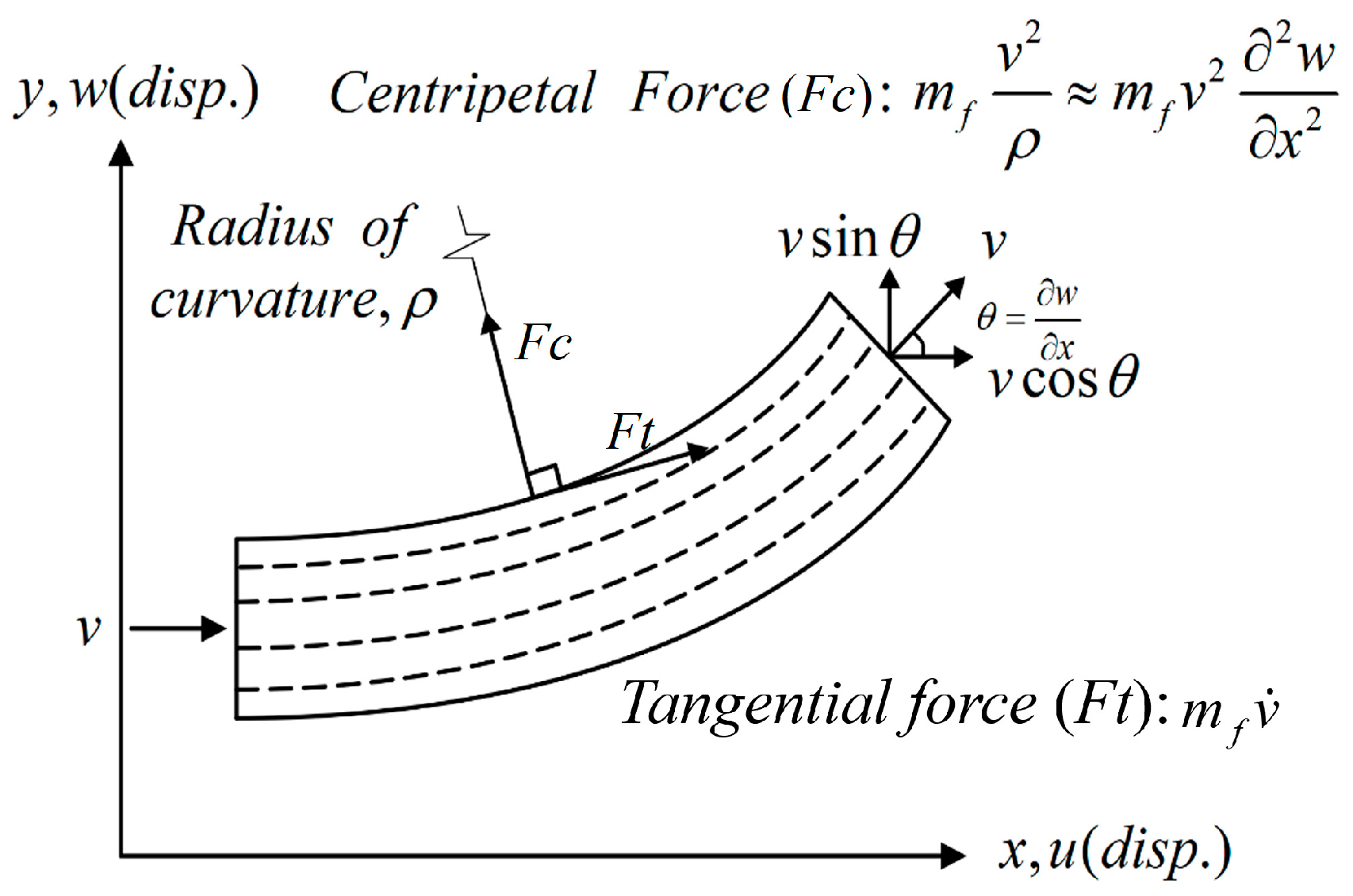
2.1. Derivation of Nonlinear Fluid–Structure Coupling Equations of Motion
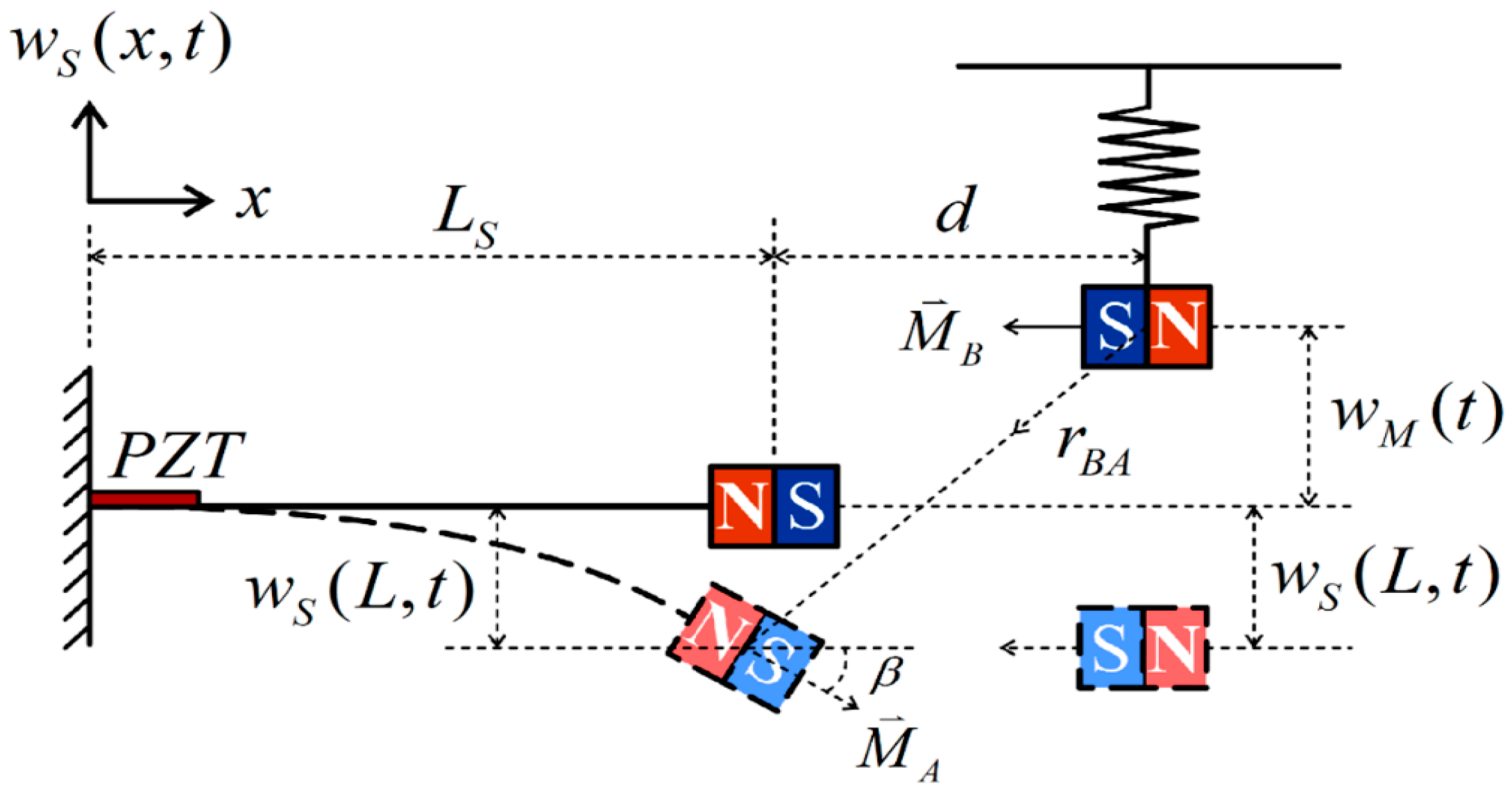
2.2. Simulation and Analysis of Magnet Repulsion Force
2.3. Derivation of the Nonlinear Cantilever Beam Equation
2.4. Establishment of Theoretical Model of Piezoelectric Equation
3. Theoretical Analysis
3.1. Method of Multiple Scales (MOMS)
3.2. Analysis of Fluid–Solid Coupling Elastic Beam
3.3. System Frequency Analysis
3.4. Numerical Analysis of Time Response and Voltage Generation Efficiency
4. Experimental Analysis
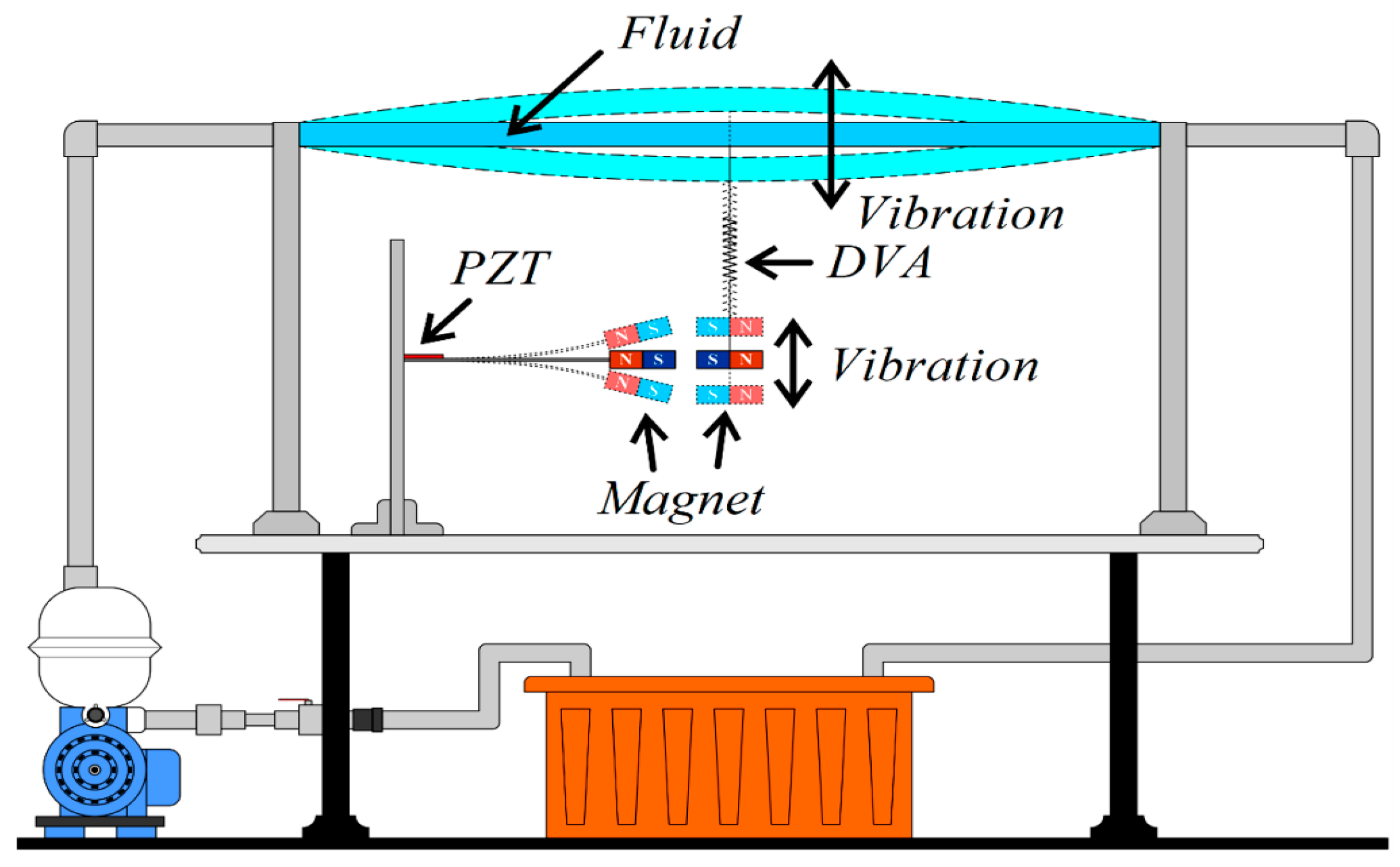
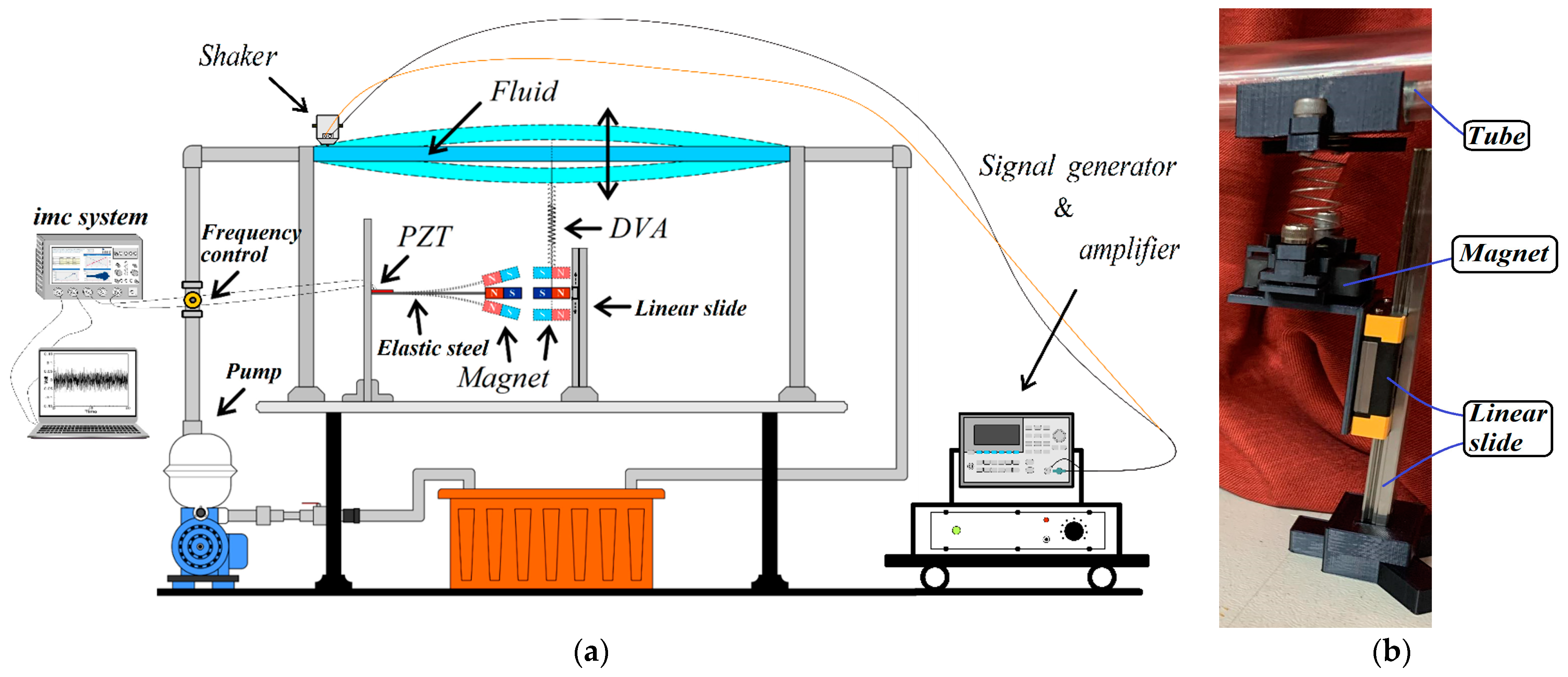
4.1. Experimental Set Up
4.2. Measurement of the Natural Frequencies
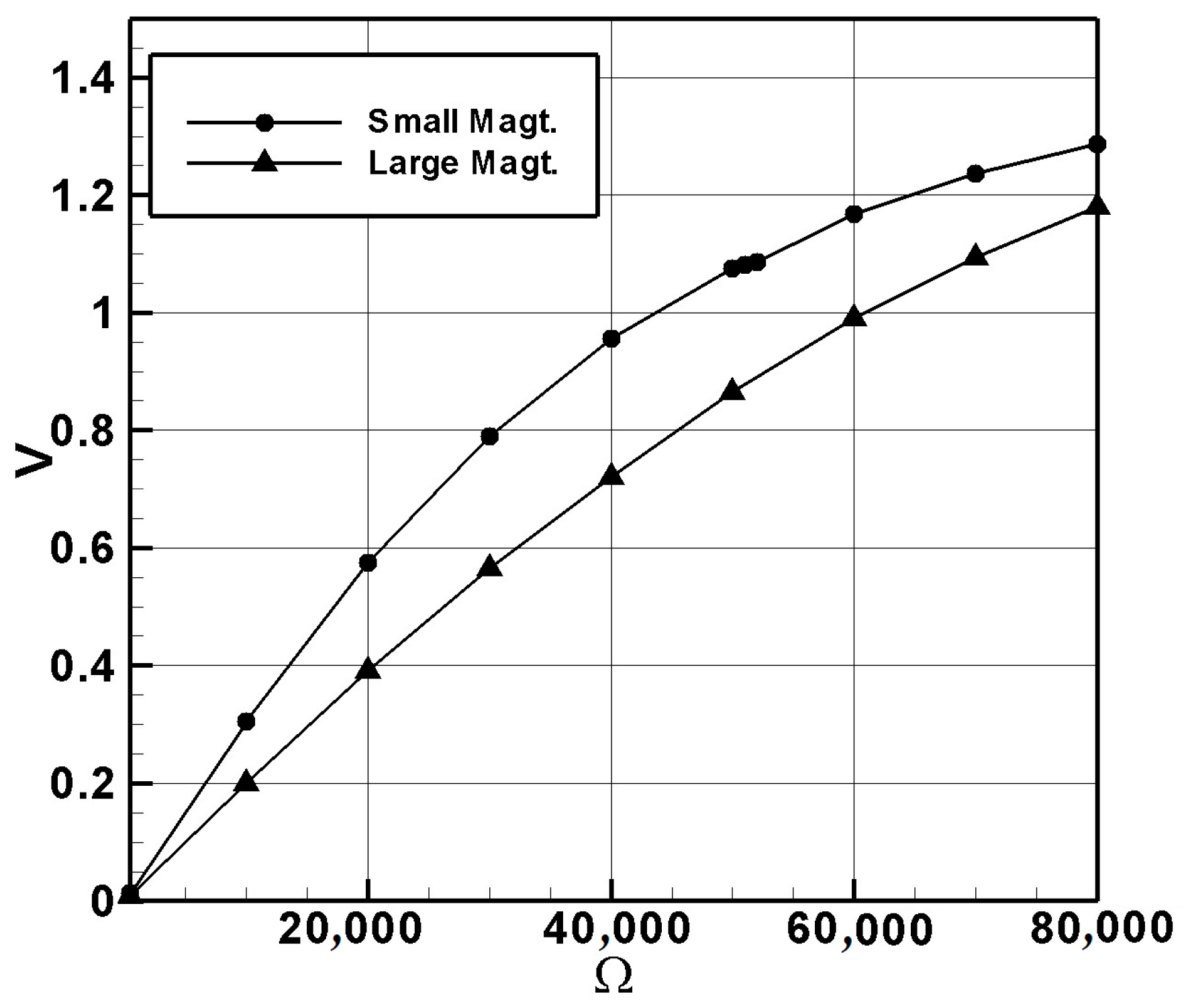
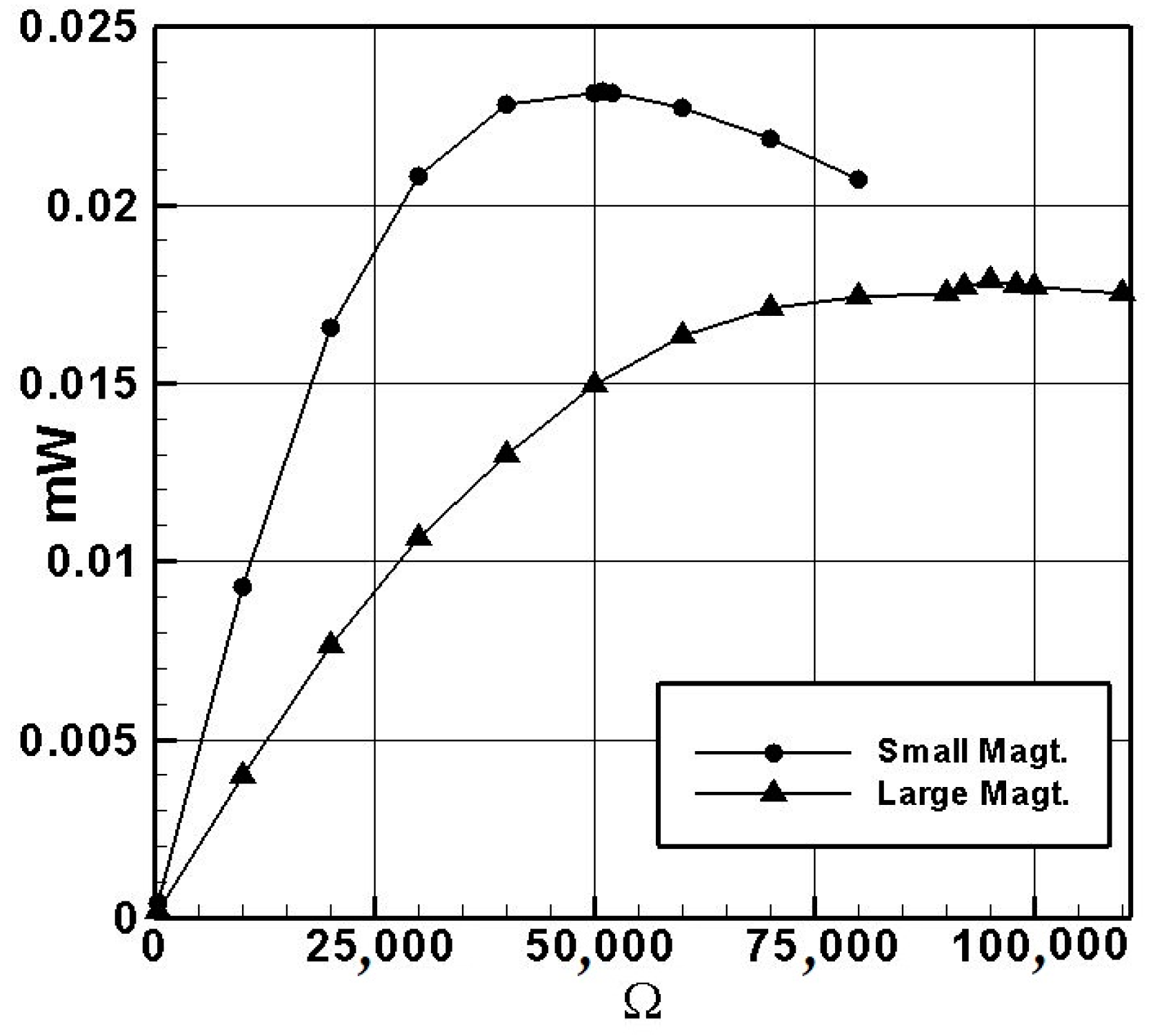
4.3. Internal Resistance Measurement
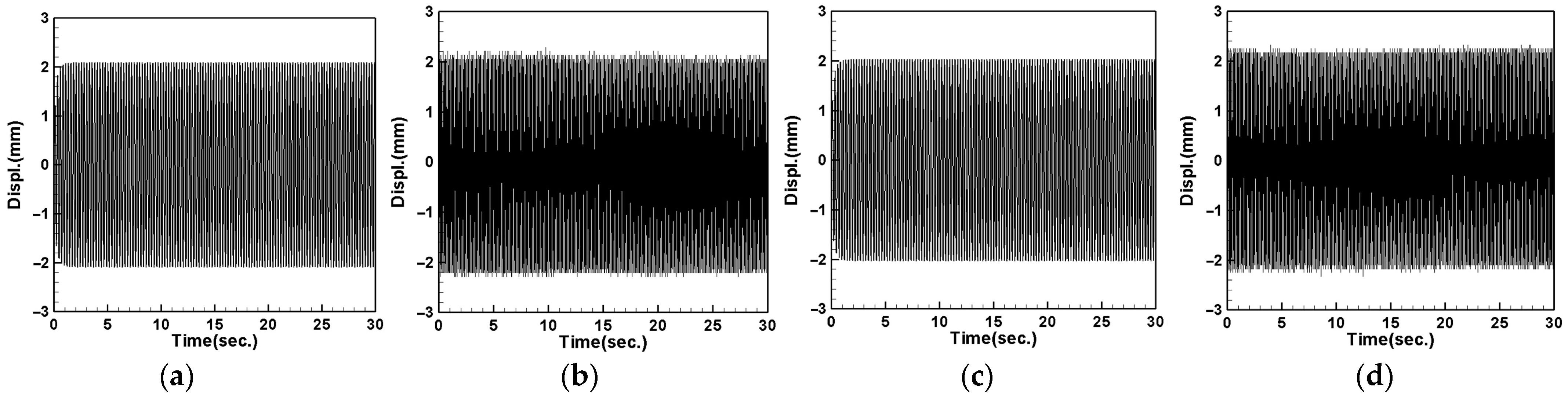
4.4. System Displacement Measurement and Theoretical Verification
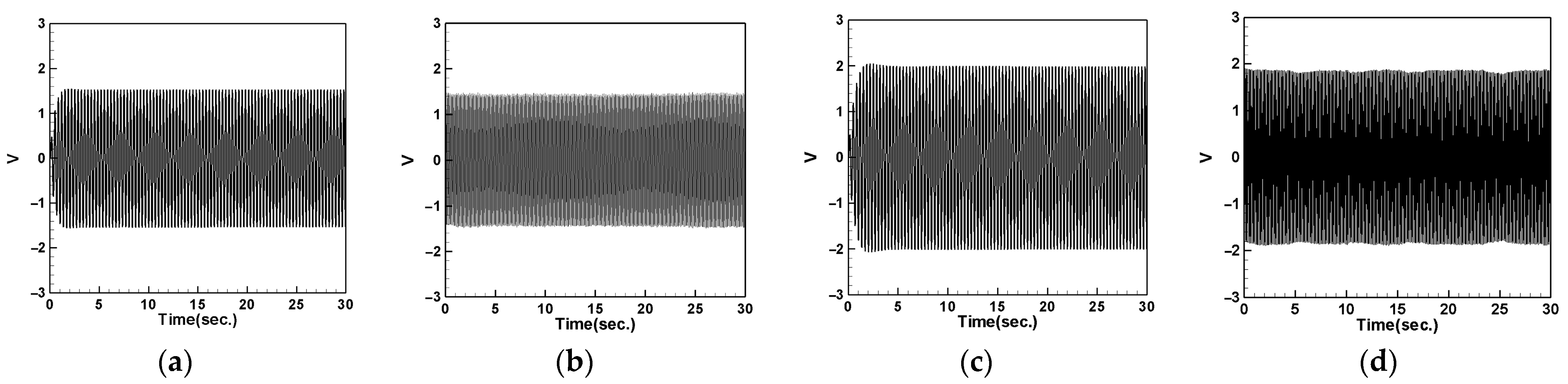
4.4.1. Tube Vibration with DVA at Midpoint
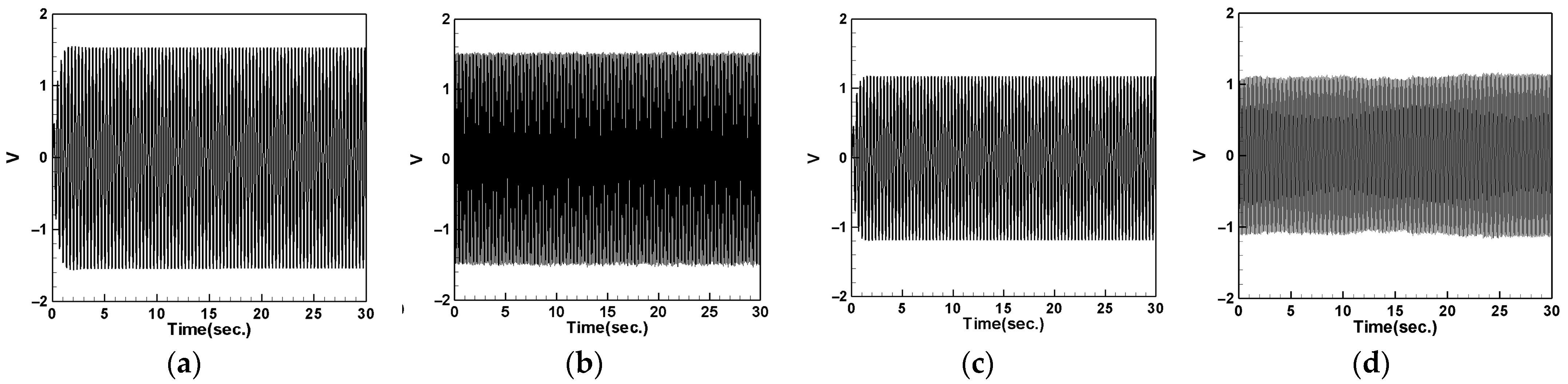
4.4.2. Tube Vibration with DVA at 1/4 Tube Length
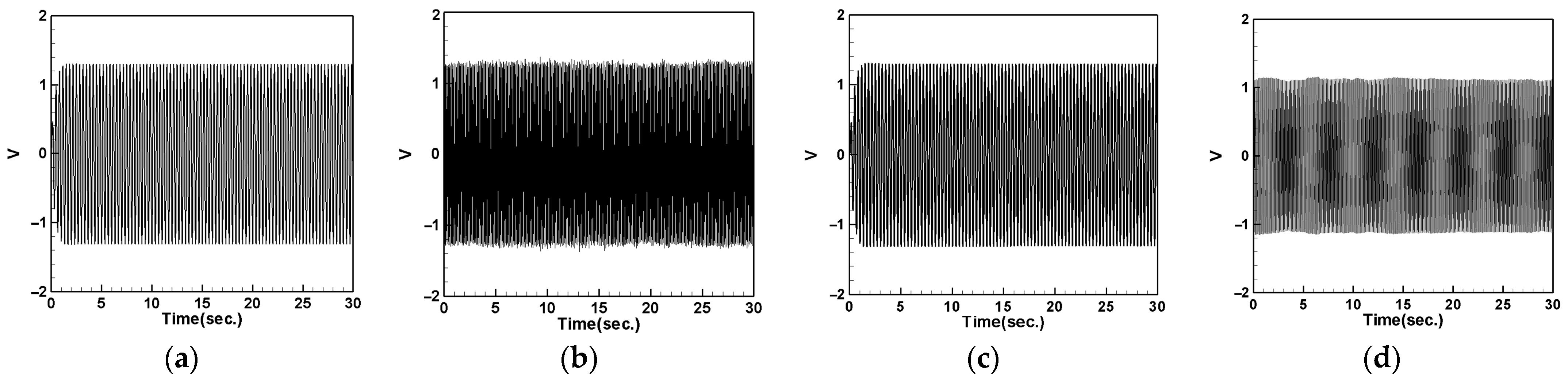
4.4.3. Tube Displacement with Different DVA Spring Constants
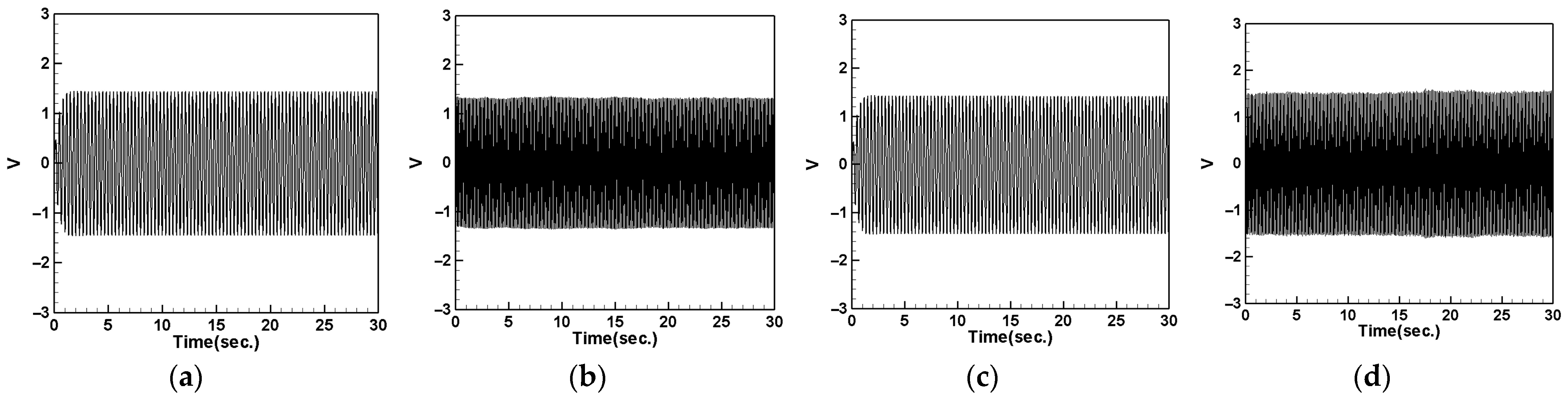
4.5. Voltage Measurement and Theoretical Verification of the System
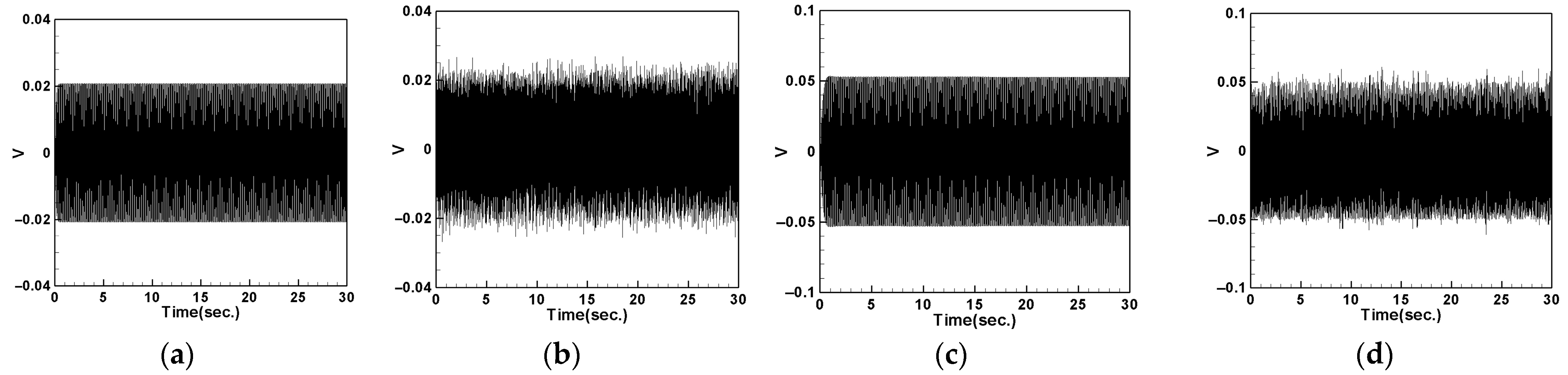
4.5.1. Voltage with DVA Positioned at 1/2 of the Tube Length
4.5.2. Voltage with DVA Positioned at 1/4 of the Tube Length
4.5.3. System Output Voltage with Different DVA Spring Constants
5. Conclusions
- Using Hamilton’s Principle to derive the equations of motion for a nonlinear fixed-free beam coupled with unsteady fluid flow and the DVA. The Biot–Savart Law is employed to develop an integrated model of this fluid–structure coupled DVA magnetic excitation MDDI energy harvesting system. The beam’s significant structural deformation and the tangential and normal forces on the pipe wall are considered as nonlinear fixed-free beams may experience large vibrations and deformations due to fluid excitation, which should be analyzed before executing vibration energy conversion.
- Analyzing the system’s frequency response using the method of multiple scales (MOMS). The second part of the study involves determining the frequency response and amplitude of the system by exciting the flow tube’s vibration frequency to define the efficiency of this energy harvesting system. The integrated model of this fluid–structure coupled DVA magnetic excitation MDDI energy harvesting system is established and its electrical energy conversion efficiency is analyzed. The impact of different DVA parameters, including external excitation frequency, DVA mass, spring constant, and DVA position, on the system’s electrical energy conversion efficiency is examined as these are the key factors determining the system’s efficiency.
- Conducting a simple experiment to verify the accuracy and feasibility of the theoretical model of this fluid–structure coupled DVA magnetic excitation energy harvesting system. The experiment involves fixing both ends of a flow tube at the water inlet and outlet, pressurizing the water flow with a variable-frequency pump at the inlet, and connecting the outlet to a storage tank via a conduit. The flow pipe is supported by a 3D-printed model. The experiment uses imc© to measure the damping effect and output voltage of the energy conversion for different DVA magnet masses and positions in the flow tube. The experimental and theoretical system output voltages for different DVA masses, positions, and spring constants are compared to verify the proposed model’s feasibility.
- When the DVA is installed at the vibration source, it significantly absorbs the vibration energy generated by the source, with the midpoint (1/2) of the tube performing better than the 1/4 position. Since the tube’s vibration energy is transmitted to the DVA, the tube experiences reduced vibration, while the DVA undergoes more intense vibrations.
- The first-mode damping amplitude of the small-magnet system is about 18%, superior to the large-magnet system’s 12%. The second-mode damping amplitude is about 48% for the small-magnet system compared to 27% for the large-magnet system, indicating that the small-magnet system is more suitable as a damper for the flow tube.
- For the current flow tube model, a spring constant of k = 20 is more suitable. Both the theoretical and experimental results show that the spring with k = 20 has significantly better damping effects across various modes compared to the springs with k = 13.3 and 12.5.
- Measuring the internal resistance of the system reveals that the small-magnet system achieves the maximum power output when connected in series with a 50.45 K ohm resistor and the large-magnet system with a 95 K ohm resistor. Under these conditions, the small-magnet system has a higher power output than the large-magnet system, making it more suitable for use as a high-power damper.
- The experiments changing three sets of springs and two different magnet masses show that larger magnets result in smaller spring vibrations regardless of the spring constant, while smaller magnets lead to more intense DVA vibrations. Thus, small magnets appear to be more capable of absorbing tube vibration amplitudes, leading to better damping effects and higher power output due to lower internal resistance, despite the larger magnetic repulsive force of large magnets causing greater elastic steel deformation and higher PZT output voltage.
- The experimental results verify the feasibility of the proposed theoretical model. However, further research is needed to determine the optimal magnet size and spring constant for the best damping and power generation effects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Dimensionless Parameters
Appendix B. Coefficients Definitions
References
- Jia, Y. Review of nonlinear vibration energy harvesting: Duffing, bistability, parametric, stochastic and others. J. Intell. Mater. Syst. Struct. 2020, 31, 921–944. [Google Scholar] [CrossRef]
- Lan, C.; Hu, G.; Liao, Y.; Qin, W. A wind-induced negative damping method to achieve high-energy orbit of a nonlinear vibration energy harvester. Smart Mater. Struct. 2021, 30, 02LT02. [Google Scholar] [CrossRef]
- Yang, T.; Zhou, S.; Cao, Q.; Zhang, W.; Chen, L. Some advancews in nonlinear vibration energy harvesting technology. Chin. J. Theor. Appl. Mech. 2021, 53, 550–564. [Google Scholar] [CrossRef]
- Bastien, C.; Cyrille, S.; Adrien, R.; Guilhem, M. Damping adjustment of a nonlinear vibration absorber using an electro-magneto mechanical coupling. J. Sound Vib. 2022, 518, 116508. [Google Scholar]
- Parseh, M.; Dardel, M.; Ghasemi, M.H. Performance comparison of nonlinear energy sink and linear tuned mass damper in steady-state dynamics of a linear beam. Nonlinear Dyn. 2015, 81, 1981–2002. [Google Scholar] [CrossRef]
- Jin, J.; Yang, W.; Koh, H.I.; Park, J. Development of tuned particle impact damper for reduction of transient railway vibrations. Appl. Acoust. 2020, 169, 107487. [Google Scholar] [CrossRef]
- Gupta, S.K.; Malla, A.L.; Barry, O.R. Nonlinear vibration analysis of vortex-induced vibrations in overhead power lines with nonlinear vibration absorbers. Nonlinear Dyn. 2021, 103, 27–47. [Google Scholar] [CrossRef]
- Forsat, M. Investigating nonlinear vibrations of higher-order hyper-elastic beams using the Hamiltonian method. Acta Mech. 2019, 231, 125–138. [Google Scholar] [CrossRef]
- Liu, M.; Cao, D.; Zhang, X.; Wei, J.; Zhu, D. Nonlinear dynamic responses of beamlike truss based on the equivalent nonlinear beam model. Int. J. Mech. Sci. 2021, 194, 106197. [Google Scholar] [CrossRef]
- Jiang, H.; Gong, X.; Wang, J.; Wu, R.; Huang, B. An analysis of nonlinear beam vibrations with the extended Rayleigh-Ritz Method. J. Appl. Comput. Mech. 2022, 8, 1299–1306. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Pai, P.F. Linear and Nonlinear Structural Mechanics; John Wiley & Sons: New York, NY, USA, 2004; pp. 171–225. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: New York, NY, USA, 1995; pp. 50–62. [Google Scholar]
- Czerwiński, A.; Łuczko, J. Nonlinear vibrations of planar curved pipes conveying fluid. J. Sound Vib. 2021, 501, 116054. [Google Scholar] [CrossRef]
- Wang, Y.R.; Wei, Y. Internal resonance analysis of a fluid-conveying tube resting on a nonlinear elastic foundation. Eur. Phys. J. Plus 2020, 135, 1–38. [Google Scholar] [CrossRef]
- Syuhri, S.N.H.; Zare-Behtash, H.; Cammarano, A. Investigating the Influence of Fluid-Structure Interactions on Nonlinear System Identification. Vibration 2020, 3, 521–544. [Google Scholar] [CrossRef]
- Malazi, M.T.; Eren, E.T.; Luo, J.; Mi, S.; Temir, G. Three-Dimensional Fluid–Structure Interaction Case Study on Elastic Beam. J. Mar. Sci. Eng. 2020, 8, 714. [Google Scholar] [CrossRef]
- Wang, Y.R.; Chen, P.T. Energy harvesting analysis of the magneto-electric and fluid-structure interaction parametric excited system. J. Sound Vib. 2024, 569, 118087. [Google Scholar] [CrossRef]
- Pennisi, G.; Mann, B.P.; Naclerio, N.; Stephan, C.; Michon, G. Design and experimental study of a Nonlinear Energy Sink coupled to an electromagnetic energy harvester. J. Sound Vib. 2018, 437, 340–357. [Google Scholar] [CrossRef]
- Wang, J.; Geng, L.; Yang, K.; Zhao, L.; Wang, F.; Yurchenko, D. Dynamics of the double-beam piezo–magneto–elastic nonlinear wind energy harvester exhibiting galloping-based vibration. Nonlinear Dyn. 2020, 100, 1963–1983. [Google Scholar] [CrossRef]
- Zang, J.; Cao, R.Q.; Fang, B.; Zhang, Y.W. A vibratory energy harvesting absorber using integration of a lever-enhanced nonlinear energy sink and a levitation magnetoelectric energy harvester. J. Sound Vib. 2020, 484, 115534. [Google Scholar] [CrossRef]
- Kecik, K. Simultaneous vibration mitigation and energy harvesting from a pendulum-type absorber. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105479. [Google Scholar] [CrossRef]
- Chen, H.; Zeng, Y.; Zeng, Y.; Ding, H.; Chen, L.-Q. Dynamics and vibration reduction performance of asymmetric tristable nonlinear energy sink. Appl. Math. Mech. 2024, 45, 389–406. [Google Scholar] [CrossRef]
- Rezaei, M.; Talebitooti, R.; Liao, W.-H. Investigations on magnetic bistable PZT-based absorber for concurrent energy harvesting and vibration mitigation: Numerical and analytical approaches. Energy 2022, 239 Pt E, 122376. [Google Scholar] [CrossRef]
- Guo, M.; Tang, L.; Wang, H.; Liu, H.; Gao, S. A comparative study on transient vibration suppression of magnetic nonlinear vibration absorbers with different arrangements. Nonlinear Dyn. 2023, 111, 16729–16776. [Google Scholar] [CrossRef]
- Rezaei, M.; Talebitooti, R.; Liao, W.-H.; Friswell, M.I. A comparative study on vibration suppression and energy harvesting via mono-, bi-, and tri-stable piezoelectric nonlinear energy sinks. Nonlinear Dyn. 2024, 112, 10871–10910. [Google Scholar] [CrossRef]
- Rezaei, M.; Talebitooti, R.; Liao, W.H. Exploiting bi-stable magneto-piezoelastic absorber for simultaneous energy harvesting and vibration mitigation. Int. J. Mech. Sci. 2021, 207, 106618. [Google Scholar] [CrossRef]
- Yang, T.; Zhou, S.; Fang, S.; Qin, W.; Inman, D.J. Nonlinear vibration energy harvesting and vibration suppression technologies: Designs, analysis, and applications. Appl. Phys. Rev. 2021, 8, 031317. [Google Scholar] [CrossRef]
- Qian, F.; Zuo, L. Tuned nonlinear spring-inerter-damper vibration absorber for beam vibration reduction based on the exact nonlinear dynamics model. J. Sound Vib. 2021, 509, 116246. [Google Scholar] [CrossRef]
- Liao, B.; Zhao, R.; Yu, K.; Liu, C.; Lian, Y.; Liu, S. Theoretical and experimental investigation of a bi-stable piezoelectric energy harvester incorporating fluid-induced vibration. Energy Convers. Manag. 2022, 255, 115307. [Google Scholar] [CrossRef]
- Lu, Z.-Q.; Chen, J.; Ding, H.; Chen, L.-Q. Energy harvesting of a fluid-conveying piezoelectric pipe. Appl. Math. Model. 2022, 107, 165–181. [Google Scholar] [CrossRef]
- Rezaei, M.; Talebitooti, R. Investigating the performance of tri-stable magneto-piezoelastic absorber in simultaneous energy harvesting and vibration isolation. Appl. Math. Model. 2021, 102, 661–693. [Google Scholar] [CrossRef]
- Pai, P.F. Nonlinear Flexural-Flexural-Torsional Dynamics of Metallic and Composite Beams. Ph.D. Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1990. Chapter 2. [Google Scholar]
- Fang, S.; Chen, K.; Xing, J.; Zhou, S.; Liao, W.-H. Tuned bistable nonlinear energy sink for simultaneously improved vibration suppression and energy harvesting. Int. J. Mech. Sci. 2021, 212, 106838. [Google Scholar] [CrossRef]
- Fan, Y.; Niu, M.-Q.; Ghayesh, M.H.; Amabili, M.; Chen, L.-Q. Nonlinear vibration energy harvesting via parametric excitation: Snap-through with time-varying potential wells. Mech. Syst. Signal Process. 2024, 220, 111625. [Google Scholar] [CrossRef]
- Mei, X.; Nan, H.; Dong, R.; Zhou, R.; Jin, J.; Sun, F.; Zhou, S. Magnetic-linkage nonlinear piezoelectric energy harvester with time-varying potential wells: Theoretical and experimental investigations. Mech. Syst. Signal Process. 2024, 208, 110998. [Google Scholar] [CrossRef]
- Fan, Y.; Ghayesh, M.H.; Lu, T.-F. A broadband magnetically coupled bistable energy harvester via parametric excitation. Energy Convers. Manag. 2021, 244, 114505. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Z.-Y.; Wang, T.; Fu, G.-Q.; Lu, C.-J.; Wang, D.-D. Dynamic and energetic characteristics comparison of tri-stable vibration absorber and energy harvester using different permanent magnet arrays. Int. J. Struct. Stab. Dyn. 2022, 22, 2250062. [Google Scholar] [CrossRef]
- Leng, Y.-G.; Gao, Y.-J.; Tan, D.; Fan, S.-B.; Lai, Z.-H. An elastic-support model for enhanced bistable piezoelectric en-ergy harvesting from random vibrations. J. Appl. Phys. 2015, 17, 64901. [Google Scholar] [CrossRef]
- Wang, Y.R.; Chu, M.C. Analysis of double elastic steel wind driven magneto-electric vibration energy harvesting system. Sensors 2021, 21, 7364. [Google Scholar] [CrossRef]
- Rajora, A.; Dwivedi, A.; Vyas, A.; Gupta, S.; Tyagi, A. Energy harvesting estimation from the vibration of a simply supported beam. Int. J. Acoust. Vib. 2017, 22, 186–193. [Google Scholar] [CrossRef]

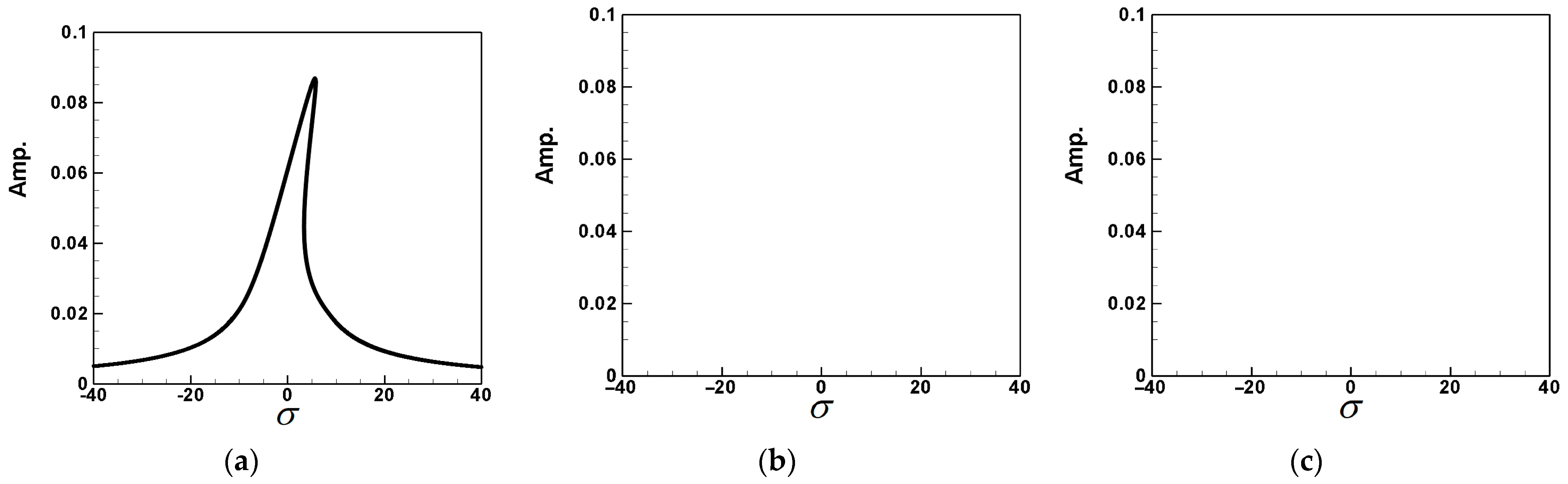
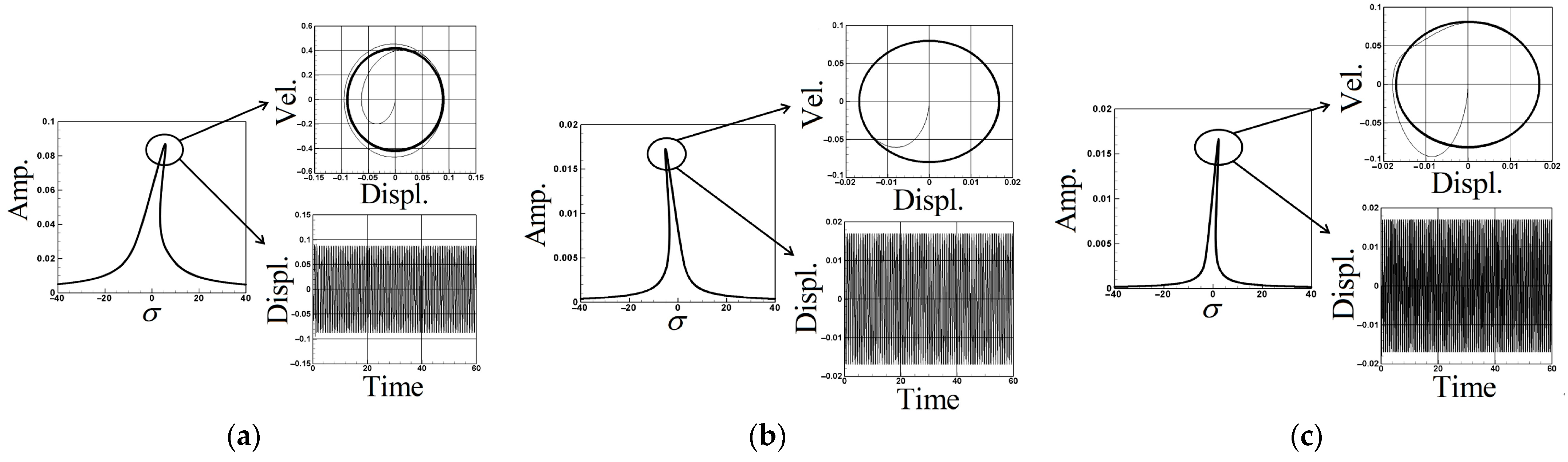
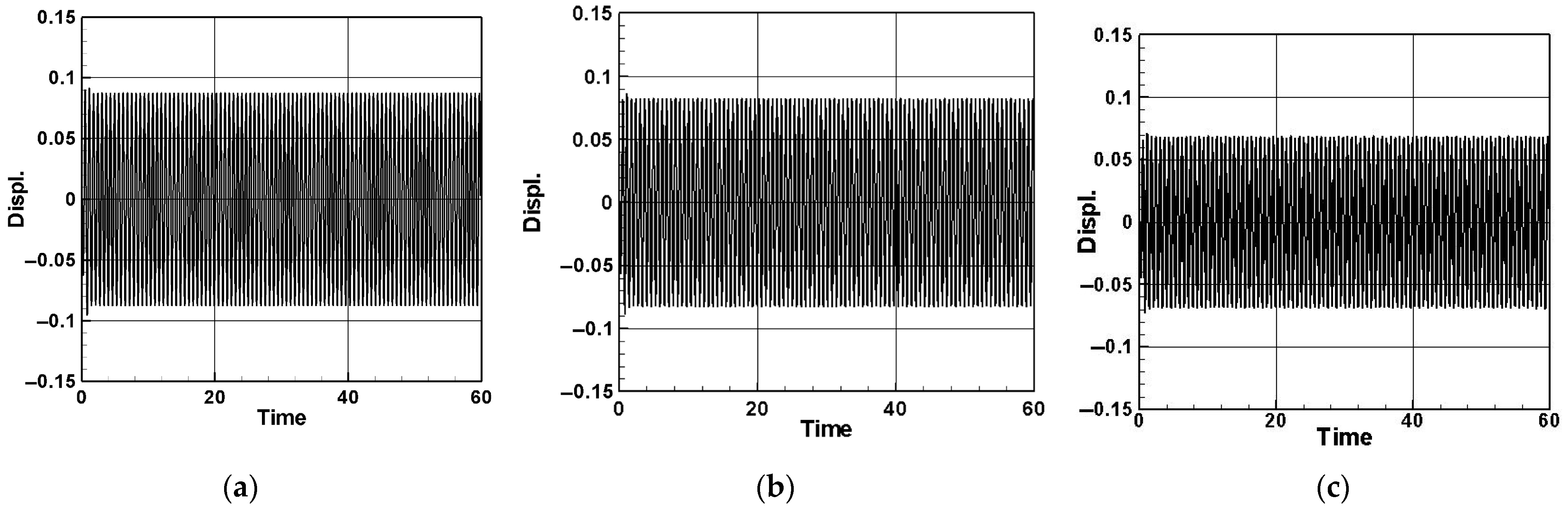
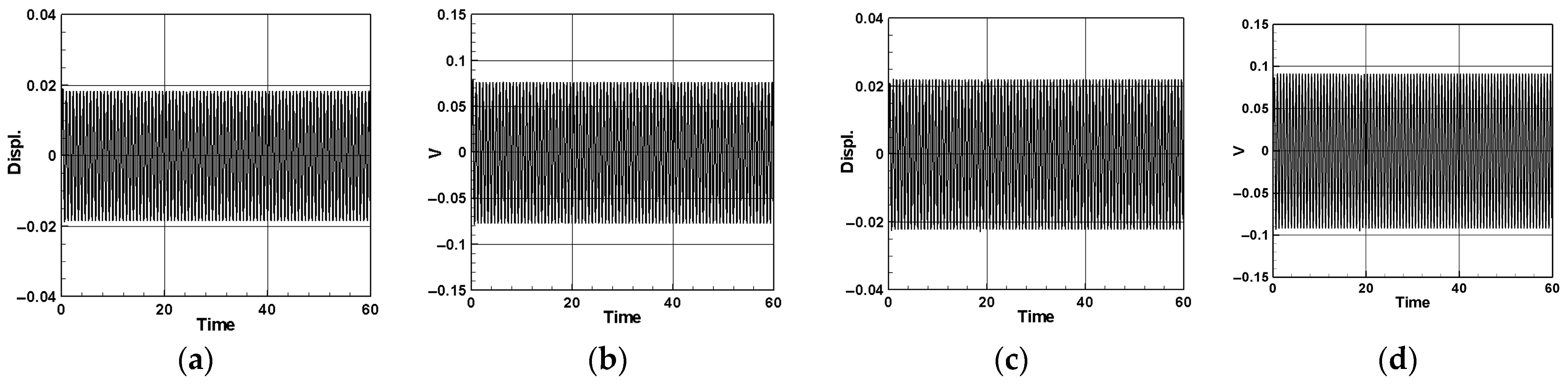





| Excited Mode | 1st Mode Amp. | 2nd Mode Amp. | 3rd Mode Amp. |
|---|---|---|---|
| 1st mode | 0.0878 | 5.8138 × 10−12 | 3.4677 × 10−12 |
| 2nd mode | 4.9683 × 10−13 | 0.01725 | 3.2079 × 10−16 |
| 3rd mode | 4.7497 × 10−13 | 2.5870 × 10−14 | 0.01694 |
| Fixed Points Plot | Time Response | |
|---|---|---|
| 1st mode | 0.0878 | 0.0878 |
| 2nd mode | 0.0173 | 0.0172 |
| 3rd mode | 0.0169 | 0.0170 |
| 1st Mode | 2nd Mode | 3rd Mode | |
|---|---|---|---|
| No TMD | 0.0878 | 0.0172 | 0.0170 |
| TMD (x = 0.25) | 0.0825 | 0.0056 | 0.0034 |
| TMD (x = 0.5) | 0.0692 | 0.0043 | 0.0022 |
| 1st Mode | 2nd Mode | 3rd Mode | |
|---|---|---|---|
| TMD (x = 0.25) | 0.0185 | 0.0009 | 0.0003 |
| TMD (x = 0.5) | 0.0222 | 0.0022 | 0.0004 |
| 1st Mode | 2nd Mode | 3rd Mode | |
|---|---|---|---|
| TMD (x = 0.25) | 0.0769 | 0.0152 | 0.0127 |
| TMD (x = 0.5) | 0.0922 | 0.0378 | 0.0153 |
| 1st Mode | 2nd Mode | 3rd Mode | |
|---|---|---|---|
| Theo. (Hz) | 12.886 | 30.652 | 57.471 |
| Exp. (Hz) | 12.210 | 29.291 | 56.641 |
| Error (%) | 5.246 | 4.444 | 1.444 |
| Voltage (V) | |||||||
|---|---|---|---|---|---|---|---|
| Ω | A | B | C | D | E | Average | Power (mW) |
| 430 | 0.01341 | 0.01306 | 0.01313 | 0.01326 | 0.01340 | 0.01325 | 0.00041 |
| 10,000 | 0.28531 | 0.31143 | 0.31204 | 0.30489 | 0.30909 | 0.30455 | 0.00928 |
| 20,000 | 0.57152 | 0.57020 | 0.57633 | 0.57733 | 0.57935 | 0.57495 | 0.01653 |
| 30,000 | 0.78125 | 0.78260 | 0.77936 | 0.80679 | 0.79866 | 0.78973 | 0.02079 |
| 40,000 | 0.95133 | 0.94998 | 0.94172 | 0.97054 | 0.96278 | 0.95527 | 0.02281 |
| 50,000 | 1.08257 | 1.06119 | 1.06150 | 1.07731 | 1.09487 | 1.07549 | 0.02313 |
| 50,450 | 1.11676 | 1.11314 | 1.11645 | 1.11855 | 1.11524 | 1.11603 | 0.02469 |
| 51,000 | 1.08310 | 1.09361 | 1.08583 | 1.08459 | 1.08304 | 1.08603 | 0.02313 |
| 60,000 | 1.13522 | 1.14919 | 1.16478 | 1.16756 | 1.18949 | 1.16725 | 0.02271 |
| 70,000 | 1.23184 | 1.22401 | 1.23502 | 1.23554 | 1.25942 | 1.23717 | 0.02187 |
| 80,000 | 1.28294 | 1.27579 | 1.28429 | 1.28749 | 1.30656 | 1.28741 | 0.02072 |
| Open-circuit voltage | 1.58124 | 1.55870 | 1.56093 | 1.57052 | 1.57095 | 1.56847 | |
| Voltage (V) | |||||||
|---|---|---|---|---|---|---|---|
| Ω | A | B | C | D | E | Average | Power (mW) |
| 430 | 0.00843 | 0.00849 | 0.00850 | 0.00842 | 0.00843 | 0.00846 | 0.00016 |
| 10,000 | 0.19845 | 0.19960 | 0.19994 | 0.19847 | 0.19962 | 0.19922 | 0.00397 |
| 20,000 | 0.38930 | 0.39306 | 0.39310 | 0.39345 | 0.38736 | 0.39125 | 0.00765 |
| 30,000 | 0.56633 | 0.56085 | 0.56699 | 0.56688 | 0.56765 | 0.56574 | 0.01067 |
| 40,000 | 0.72011 | 0.71781 | 0.72070 | 0.72212 | 0.72133 | 0.72022 | 0.01230 |
| 50,000 | 0.86169 | 0.86612 | 0.86223 | 0.86687 | 0.86335 | 0.86405 | 0.01493 |
| 60,000 | 0.98776 | 0.99144 | 0.99149 | 0.98860 | 0.98833 | 0.98952 | 0.01632 |
| 70,000 | 1.09244 | 1.08930 | 1.10459 | 1.09134 | 1.09356 | 1.09425 | 0.01711 |
| 80,000 | 1.18010 | 1.17803 | 1.18155 | 1.18086 | 1.17990 | 1.18009 | 0.01741 |
| 90,000 | 1.24568 | 1.25064 | 1.2575 | 1.26221 | 1.26023 | 1.25525 | 0.01751 |
| 92,000 | 1.27862 | 1.25892 | 1.27078 | 1.28101 | 1.28771 | 1.27541 | 0.01768 |
| 95,000 | 1.31192 | 1.30146 | 1.30254 | 1.30213 | 1.29894 | 1.30340 | 0.01788 |
| 98,000 | 1.30630 | 1.32030 | 1.32304 | 1.32119 | 1.31843 | 1.31785 | 0.01772 |
| 100,000 | 1.33391 | 1.33339 | 1.33102 | 1.32391 | 1.32874 | 1.33030 | 0.01770 |
| 110,000 | 1.38694 | 1.38147 | 1.38903 | 1.39027 | 1.38948 | 1.38744 | 0.01750 |
| Open-circuit voltage | 1.91610 | 1.89146 | 1.89380 | 1.88344 | 1.86312 | 1.88958 | |
| 1st Mode | 2nd Mode | |||||
|---|---|---|---|---|---|---|
| Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | |
| Theo. (mm) | 1.59414 | 1.68435 | 1.59414 | 0.38618 | 0.40259 | 0.38618 |
| Exp. (mm) | 1.58068 | 1.68142 | 1.58507 | 0.37235 | 0.39631 | 0.39893 |
| Error (%) | 0.844 | 0.174 | 0.569 | 3.581 | 1.560 | 3.302 |
| Theoretical/ Experimental | 1st Mode | 2nd Mode | ||||
|---|---|---|---|---|---|---|
| Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | |
| Theo.Displ. (mm) | 1.50635 | 1.46144 | 1.50635 | 0.28776 | 0.28587 | 0.28776 |
| Redu.Amp. (mm) | 0.08779 | 0.22291 | 0.08779 | 0.09842 | 0.11672 | 0.09842 |
| % | 5.507 | 13.234 | 5.507 | 25.486 | 28.992 | 25.486 |
| Exp.Displ. (mm) | 1.50979 | 1.46813 | 1.51705 | 0.29039 | 0.28972 | 0.30913 |
| Redu.Amp. (mm) | 0.07089 | 0.21329 | 0.06802 | 0.08196 | 0.10659 | 0.08980 |
| % | 4.485 | 12.685 | 4.291 | 22.012 | 26.896 | 22.510 |
| Theoretical/ Experimental | 1st Mode | 2nd Mode | ||||
|---|---|---|---|---|---|---|
| Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | |
| Theo.Displ. (mm) | 1.34984 | 1.36352 | 1.34984 | 0.21997 | 0.20084 | 0.21997 |
| Redu.Amp. (mm) | 0.24430 | 0.32083 | 0.24430 | 0.16621 | 0.20175 | 0.16621 |
| % | 15.325 | 19.048 | 15.325 | 43.040 | 50.113 | 43.040 |
| Exp.Displ. (mm) | 1.35158 | 1.37467 | 1.35949 | 0.23603 | 0.20660 | 0.22002 |
| Redu.Amp. (mm) | 0.22910 | 0.30675 | 0.22558 | 0.13632 | 0.18971 | 0.17891 |
| % | 14.494 | 18.244 | 14.232 | 36.611 | 47.869 | 44.847 |
| Theoretical/ Experimental | 1st Mode | 2nd Mode | ||||
|---|---|---|---|---|---|---|
| Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | |
| Theo.Displ. (mm) | 1.48762 | 1.59968 | 1.53637 | 0.32963 | 0.38724 | 0.39292 |
| Redu.Amp. (mm) | 0.10652 | 0.08467 | 0.05777 | 0.05655 | 0.01535 | 0.00674 |
| % | 6.682 | 5.027 | 3.624 | 14.643 | 3.813 | 1.745 |
| Exp.Displ. (mm) | 1.49135 | 1.60842 | 1.54401 | 0.33059 | 0.39078 | 0.39544 |
| Redu.Amp. (mm) | 0.08933 | 0.07300 | 0.04106 | 0.04176 | 0.00553 | 0.00349 |
| % | 5.651 | 4.342 | 2.590 | 11.215 | 1.395 | 0.875 |
| Theoretical/ Experimental | 1st Mode | 2nd Mode | ||||
|---|---|---|---|---|---|---|
| Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | |
| Theo.Displ. (mm) | 1.47156 | 1.58327 | 1.50552 | 0.30944 | 0.36278 | 0.37949 |
| Redu.Amp. (mm) | 0.12258 | 0.10108 | 0.08862 | 0.07674 | 0.03981 | 0.00669 |
| % | 7.689 | 6.001 | 5.559 | 19.872 | 9.888 | 1.732 |
| Exp.Displ. (mm) | 1.47671 | 1.58718 | 1.51026 | 0.31087 | 0.36360 | 0.38196 |
| Redu.Amp. (mm) | 0.10397 | 0.09424 | 0.07481 | 0.06148 | 0.03271 | 0.01697 |
| % | 6.578 | 5.605 | 4.720 | 16.511 | 8.254 | 4.255 |
| Theoretical/ Experimental | 1st Mode | 2nd Mode | ||||
|---|---|---|---|---|---|---|
| k = 20 | k = 13.3 | k = 12.5 | k = 20 | k = 13.3 | k = 12.5 | |
| Theo.Displ. (mm) | 1.46144 | 1.49801 | 1.50527 | 0.28587 | 0.33996 | 0.35027 |
| Redu.Amp. (mm) | 0.22291 | 0.18634 | 0.17908 | 0.11672 | 0.06263 | 0.05232 |
| % | 13.234 | 11.063 | 10.632 | 28.992 | 15.557 | 12.996 |
| Exp.Displ. (mm) | 1.46813 | 1.50355 | 1.51061 | 0.28972 | 0.34182 | 0.35245 |
| Redu.Amp. (mm) | 0.21329 | 0.17787 | 0.17081 | 0.10659 | 0.05449 | 0.04386 |
| % | 12.685 | 10.579 | 10.159 | 26.896 | 13.749 | 11.067 |
| Theoretical/ Experimental | 1st Mode | 2nd Mode | ||||
|---|---|---|---|---|---|---|
| k = 20 | k = 13.3 | k = 12.5 | k = 20 | k = 13.3 | k = 12.5 | |
| Theo.Displ. (mm) | 1.36352 | 1.44757 | 1.45817 | 0.20084 | 0.27551 | 0.28839 |
| Redu.Amp. (mm) | 0.32083 | 0.23678 | 0.22618 | 0.20175 | 0.12708 | 0.11420 |
| % | 19.048 | 14.058 | 13.428 | 50.113 | 31.566 | 28.366 |
| Exp.Displ. (mm) | 1.37467 | 1.45469 | 1.46360 | 0.20660 | 0.27983 | 0.29278 |
| Redu.Amp. (mm) | 0.30675 | 0.22673 | 0.21782 | 0.18971 | 0.11648 | 0.10353 |
| % | 18.244 | 13.484 | 12.955 | 47.869 | 29.391 | 26.123 |
| Large Magnet | 1st Mode | 2nd Mode | ||||
|---|---|---|---|---|---|---|
| Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | |
| Theo. (V) | 1.04574 | 1.35580 | 1.04574 | 0.01460 | 0.03681 | 0.01460 |
| Exp. (V) | 1.01995 | 1.30340 | 1.00110 | 0.01341 | 0.03381 | 0.01324 |
| Error (%) | 2.466 | 3.865 | 4.269 | 8.151 | 8.150 | 9.315 |
| Small Magnet | 1st Mode | 2nd Mode | ||||
| Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | |
| Theo. (V) | 0.91366 | 1.12608 | 0.91366 | 0.03844 | 0.05065 | 0.03844 |
| Exp. (V) | 0.88341 | 1.08188 | 0.87720 | 0.03549 | 0.04642 | 0.03521 |
| Error (%) | 3.311 | 3.925 | 3.991 | 7.674 | 8.351 | 8.403 |
| Large Magnet | 1st Mode | 2nd Mode | ||||
|---|---|---|---|---|---|---|
| Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | |
| Theo. (V) | 1.04574 | 0.80998 | 0.50129 | 0.01275 | 0.01037 | 0.00861 |
| Exp. (V) | 1.01007 | 0.78325 | 0.48673 | 0.01172 | 0.00957 | 0.00788 |
| Error (%) | 3.411 | 3.300 | 2.905 | 8.078 | 7.715 | 8.479 |
| Small Magnet | 1st Mode | 2nd Mode | ||||
| Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | Shaker 1/4 | Shaker 1/2 | Shaker 3/4 | |
| Theo. (V) | 0.89235 | 0.79300 | 0.69102 | 0.02596 | 0.02066 | 0.01935 |
| Exp. (V) | 0.86239 | 0.76335 | 0.66700 | 0.02386 | 0.01910 | 0.01768 |
| Error (%) | 3.357 | 3.739 | 3.476 | 8.089 | 7.551 | 8.630 |
| Large Magnet (1/2) | 1st Mode | 2nd Mode | ||||
|---|---|---|---|---|---|---|
| k = 20 | k = 13.3 | k = 12.5 | k = 20 | k = 13.3 | k = 12.5 | |
| Theo. (V) | 1.35580 | 0.98379 | 0.97550 | 0.03681 | 0.01560 | 0.01521 |
| Exp. (V) | 1.30340 | 0.94948 | 0.94088 | 0.03381 | 0.01428 | 0.01400 |
| Error (%) | 3.865 | 3.488 | 3.549 | 9.150 | 8.462 | 7.955 |
| Small Magnet (1/2) | 1st Mode | 2nd Mode | ||||
| k = 20 | k = 13.3 | k = 12.5 | k = 20 | k = 13.3 | k = 12.5 | |
| Theo. (V) | 1.12608 | 0.48588 | 0.24249 | 0.05065 | 0.02335 | 0.02302 |
| Exp. (V) | 1.08188 | 0.46942 | 0.23299 | 0.04642 | 0.02140 | 0.02111 |
| Error (%) | 3.925 | 3.387 | 3.918 | 8.351 | 8.351 | 8.297 |
| 1st Mode | 2nd Mode | |||
|---|---|---|---|---|
| Large Magnet | Small Magnet | Large Magnet | Small Magnet | |
| Theo. (V) | 1.35580 | 1.12608 | 0.03681 | 0.050655 |
| Power (mV) | 0.01935 | 0.02513 | 0.000014 | 0.000051 |
| Exp. (V) | 1.30340 | 1.08188 | 0.03381 | 0.04642 |
| Power (mV) | 0.01788 | 0.02320 | 0.000012 | 0.000043 |
| Magnet Weight | 45 g | 35 g | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k | 20 | 13.3 | 12.5 | 20 | 13.3 | 12.5 | ||||||
| Mode | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| Redu. Amp. (%) | 12.685 | 26.896 | 10.579 | 13.749 | 10.159 | 11.067 | 18.244 | 47.869 | 13.484 | 29.391 | 12.955 | 26.123 |
| Exp. (V) | 1.3034 | 0.03381 | 0.94948 | 0.01428 | 0.94088 | 0.014 | 1.08188 | 0.04642 | 0.46942 | 0.0214 | 0.23299 | 0.02111 |
| Power (mW) | 0.01788 | 0.000012 | 0.00949 | 0.000002 | 0.00932 | 0.000002 | 0.0232 | 0.000043 | 0.00437 | 0.000009 | 0.00108 | 0.000009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-R.; Huang, P.-C. A Magneto-Electric Device for Fluid Pipelines with Vibration Damping and Vibration Energy Harvesting. Sensors 2024, 24, 5334. https://doi.org/10.3390/s24165334
Wang Y-R, Huang P-C. A Magneto-Electric Device for Fluid Pipelines with Vibration Damping and Vibration Energy Harvesting. Sensors. 2024; 24(16):5334. https://doi.org/10.3390/s24165334
Chicago/Turabian StyleWang, Yi-Ren, and Po-Chuan Huang. 2024. "A Magneto-Electric Device for Fluid Pipelines with Vibration Damping and Vibration Energy Harvesting" Sensors 24, no. 16: 5334. https://doi.org/10.3390/s24165334
APA StyleWang, Y.-R., & Huang, P.-C. (2024). A Magneto-Electric Device for Fluid Pipelines with Vibration Damping and Vibration Energy Harvesting. Sensors, 24(16), 5334. https://doi.org/10.3390/s24165334







