A Multi-Strategy Hybrid Sparse Reconstruction Method Based on Spatial–Temporal Sparse Wave Number Analysis for Enhancing Pipe Ultrasonic-Guided Wave Anomaly Imaging
Abstract
:1. Introduction
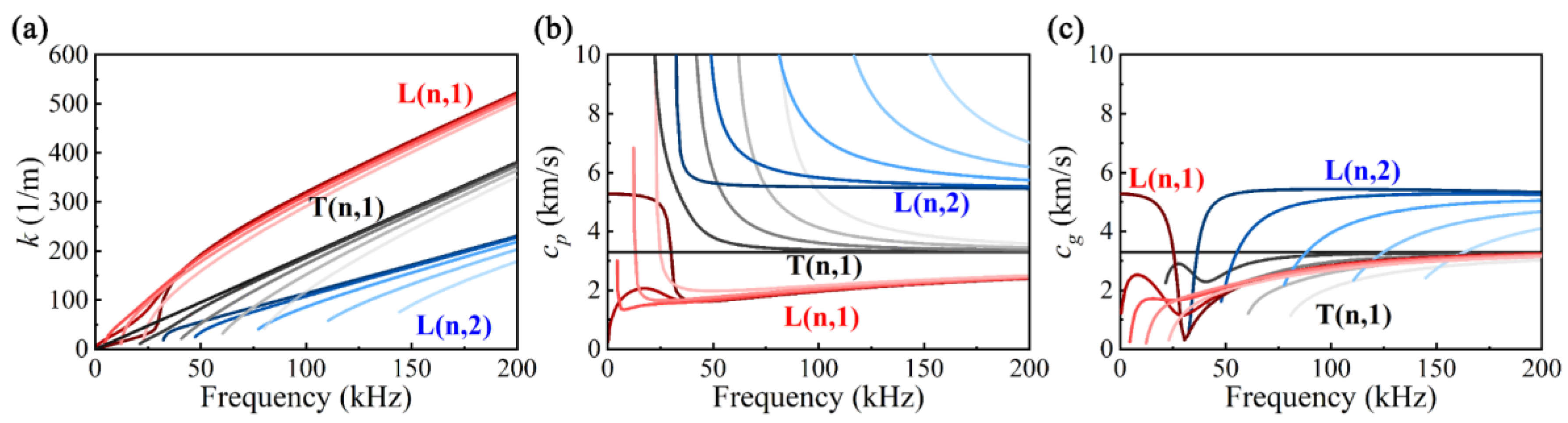
2. Pipe UGW Characteristics
3. Pipe UGW Propagation Model
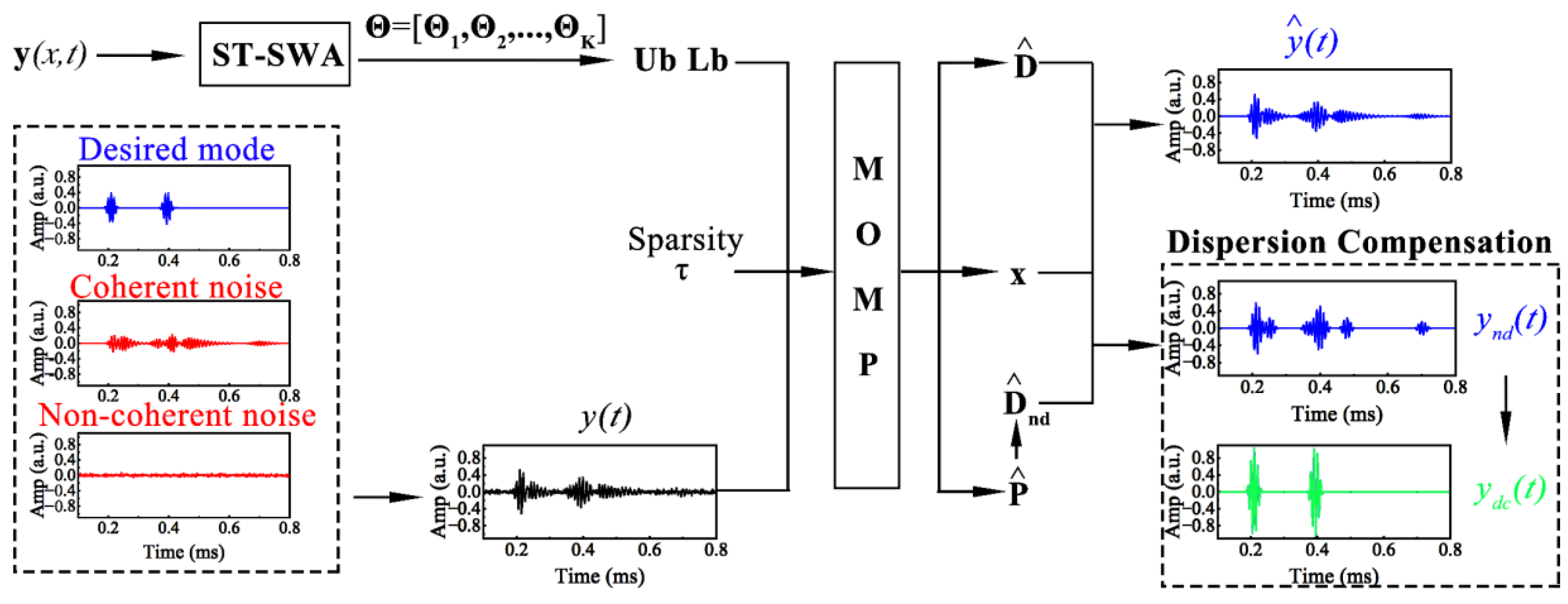
4. Proposed Methodology
4.1. Spatial–Temporal Sparse Wavenumber Analysis
| Algorithm 1 ST-SWA |
| Input: y, DL, DR, τ Initialize: , , , Output: x fori = 1: τ do , , , , end for return X |
4.2. Multi-Strategy Hybrid Sparse Reconstruction
| Algorithm 2 MOMP |
| Input: N, I, τ, Ub, Lb Output: , , , for k ← 1 to τ do while (i ≤ I) do for j ← 1 to N do if j == ball-rolling dung beetle then δ = rand(1); if δ < 0.9 then by ball-rolling way; else by dancing way; end if ; end if if j == brood ball then by breeding way, ; end if if j == small dung beetle then by foraging way, ; end if if j == thief then by stealing way, ; end if end for then Update Para(i); end if I = i + 1; end while , , , , end for |
4.3. Sparse Reconstruction Imaging
5. Validation of Synthetic UGW Signals
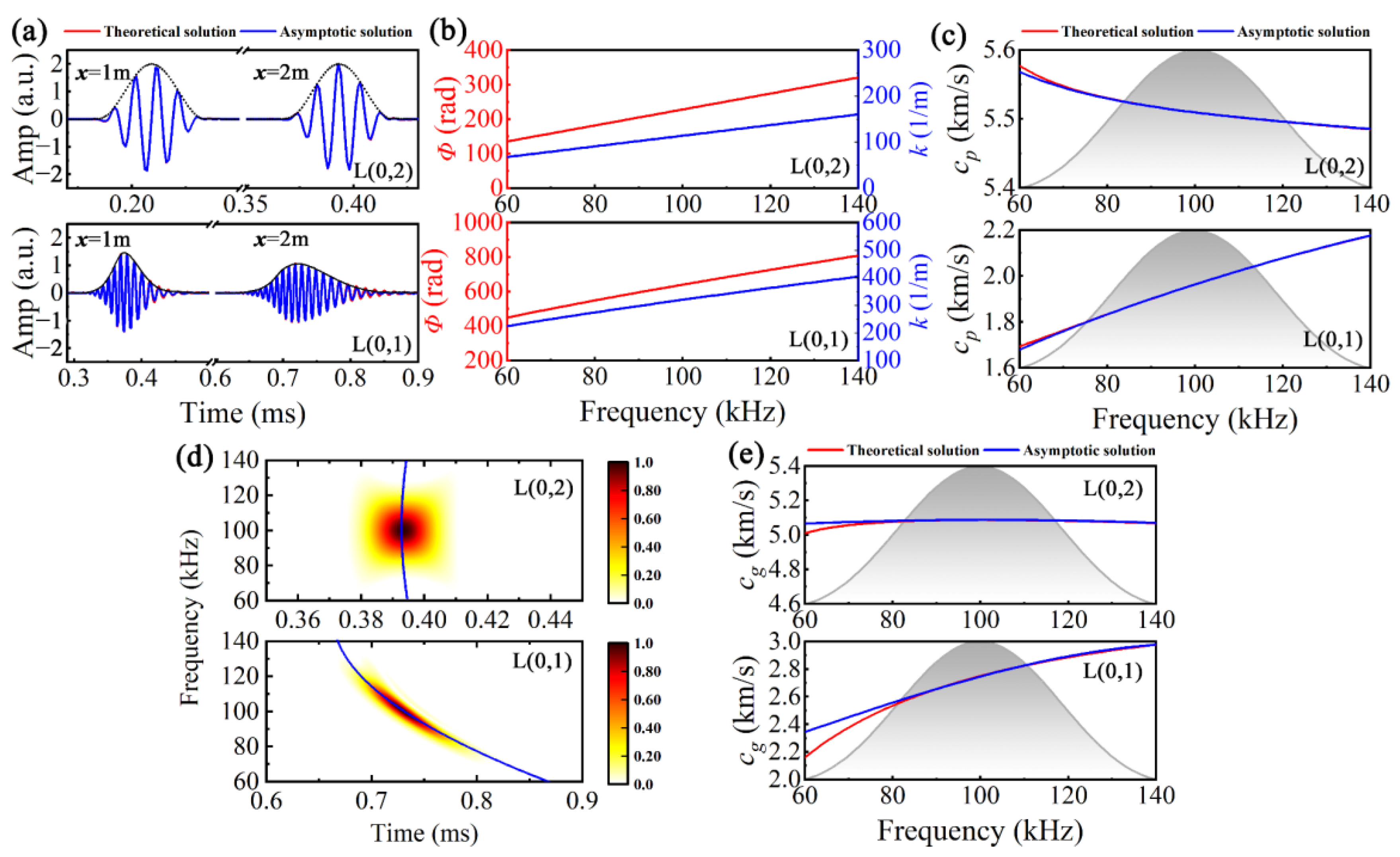
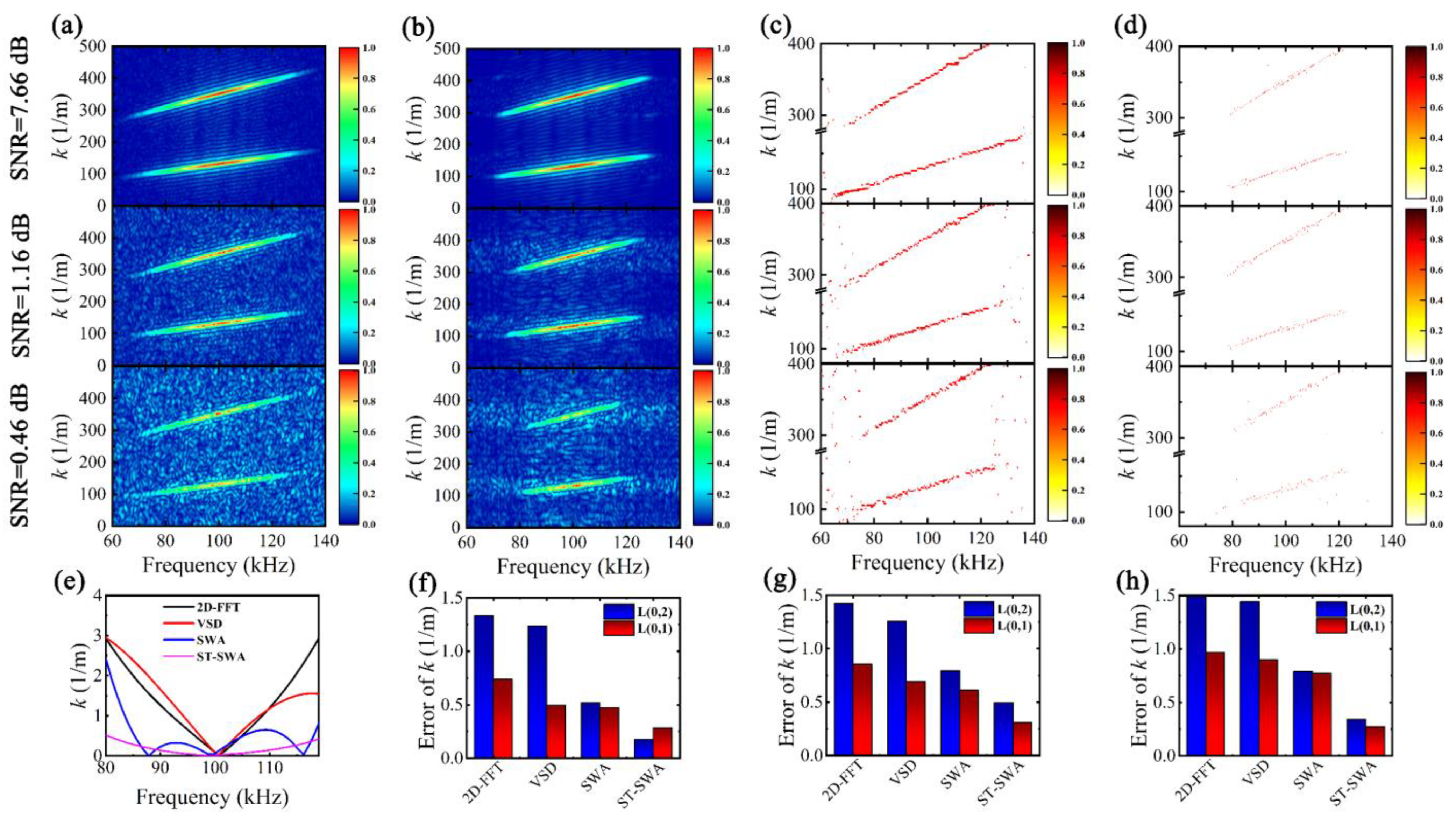
5.1. Estimation of Wavenumber Dispersion Curves
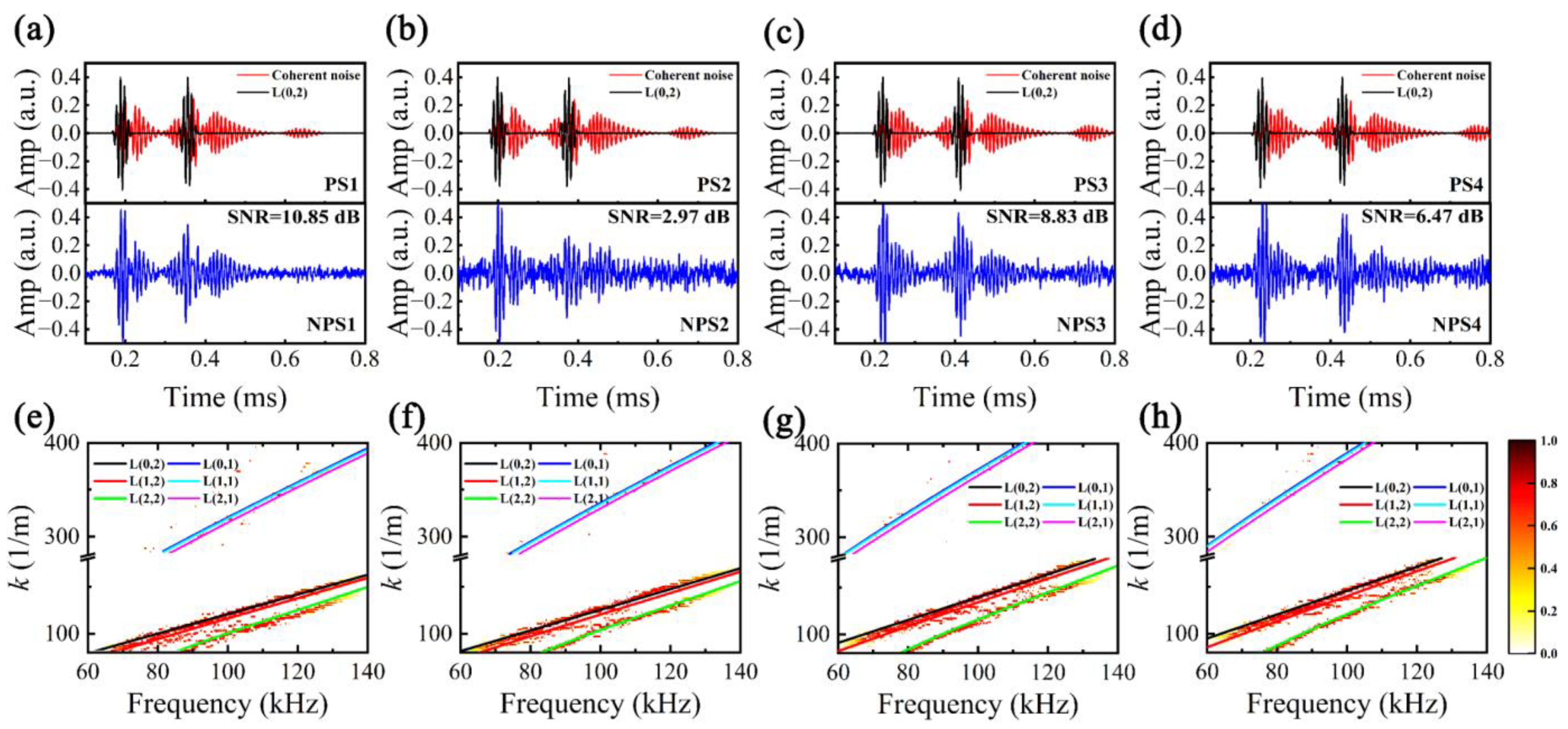
5.2. Sparse Reconstruction of Dispersive Perturbated Signals
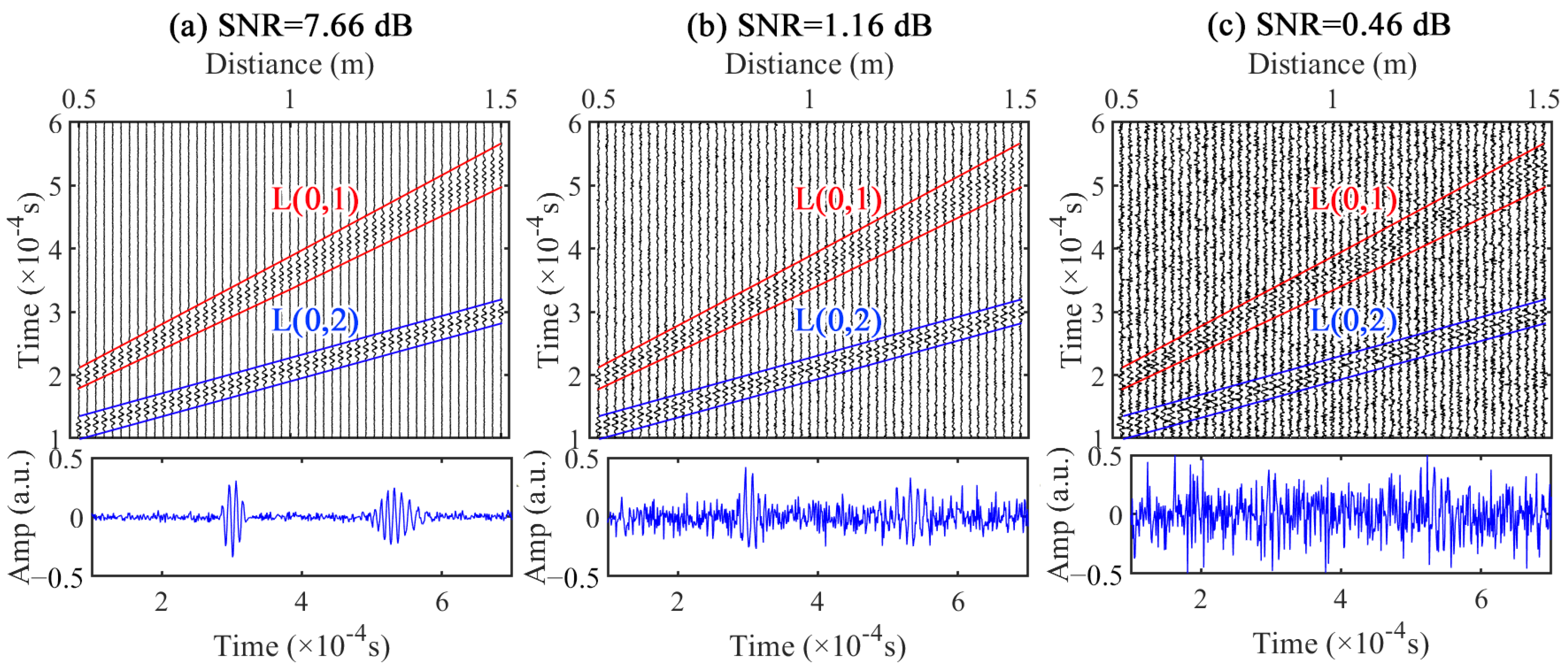
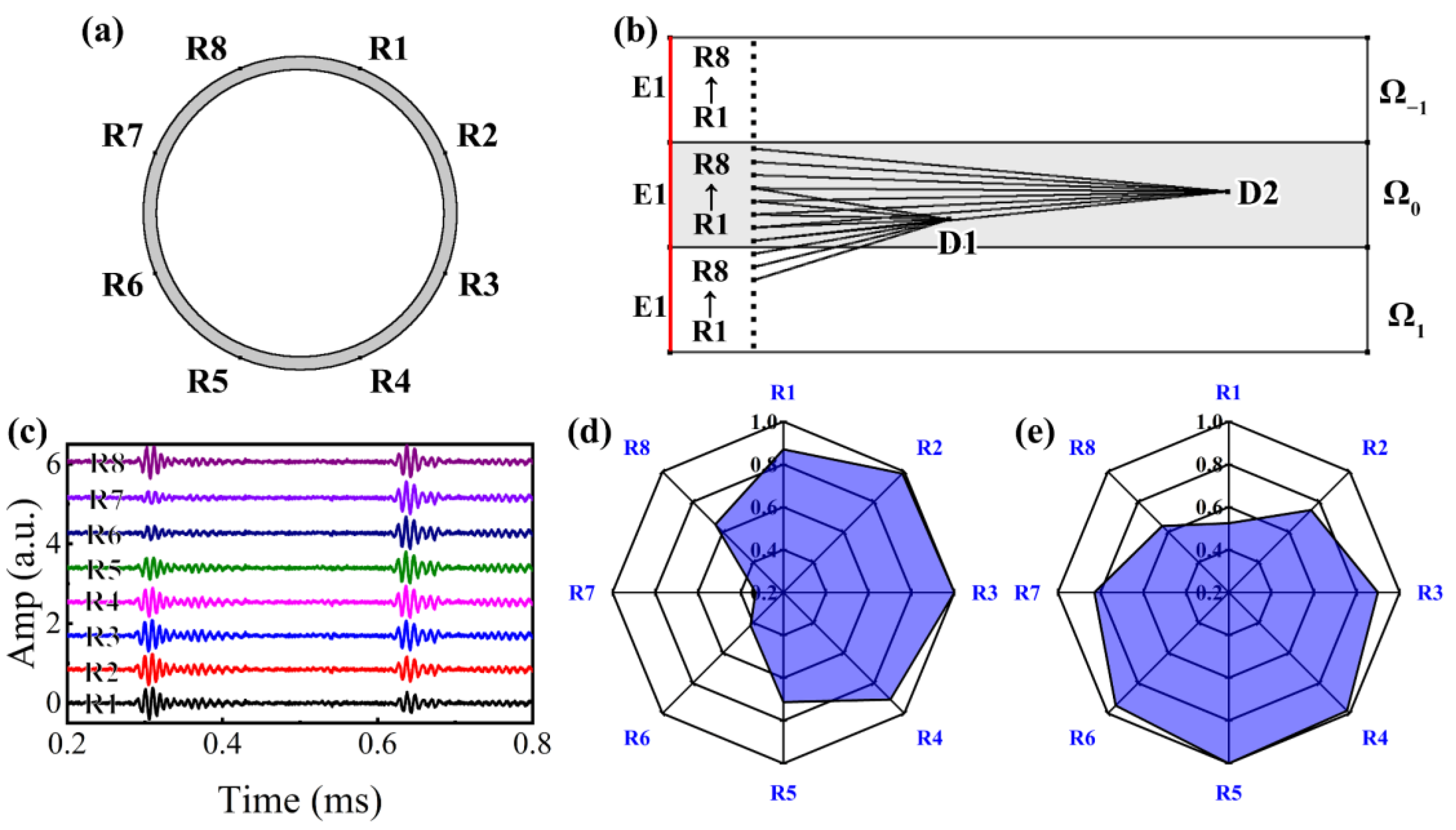
5.3. Pipe Sparse Reconstruction Imaging
- (1)
- Delay and sum (DAS) [26]
- (2)
- Eigenvalue decomposition (EVD) [44]
- (3)
- Reconstruction algorithm for probabilistic inspection of damage (RAPID) [28]
- (4)
- Multiple signal classification (MUSIC) [31]
6. Validation of Experimental UGW Signals
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zang, X.; Xu, Z.D.; Zhu, C.; Zhang, Z. Ultrasonic guided wave techniques and applications in pipeline defect detection: A review. Int. J. Press. Vessel. Pip. 2023, 206, 105033. [Google Scholar] [CrossRef]
- Diogo, A.R.; Moreira, B.; Gouveia, C.A.; Tavares, J.M.R. A review of signal processing techniques for ultrasonic guided wave testing. Metals 2022, 12, 936. [Google Scholar] [CrossRef]
- Olisa, S.C.; Khan, M.A.; Starr, A. Review of current guided wave ultrasonic testing (GWUT) limitations and future directions. Sensors 2021, 21, 811. [Google Scholar] [CrossRef] [PubMed]
- Capineri, L.; Bulletti, A. Ultrasonic guided-waves sensors and integrated structural health monitoring systems for impact detection and localization: A review. Sensors 2021, 21, 2929. [Google Scholar] [CrossRef]
- Draudvilienė, L.; Meškuotienė, A.; Raišutis, R.; Griškevičius, P.; Stasiškienė, Ž.; Žukauskas, E. The usefulness and limitations of ultrasonic lamb waves in preventing the failure of the wind turbine blades. Appl. Sci. 2022, 12, 1773. [Google Scholar] [CrossRef]
- Shah, J.; El-Hawwat, S.; Wang, H. Guided Wave Ultrasonic Testing for Crack Detection in Polyethylene Pipes: Laboratory Experiments and Numerical Modeling. Sensors 2023, 23, 5131. [Google Scholar] [CrossRef]
- Narayanan, M.M.; Arjun, V.; Kumar, A.; Mukhopadhyay, C.K. Development of in-bore magnetostrictive transducer for ultrasonic guided wave based-inspection of steam generator tubes of PFBR. Ultrasonics 2020, 106, 106148. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Li, Z.; Zhang, Z.; Wang, S. A new design to Rayleigh wave EMAT based on spatial pulse compression. Sensors 2023, 23, 3943. [Google Scholar] [CrossRef]
- Liao, W.; Sun, H.; Wang, Y.; Qing, X. A novel damage index integrating piezoelectric impedance and ultrasonic guided wave for damage monitoring of bolted joints. Struct. Health Monit. 2023, 22, 3514–3533. [Google Scholar] [CrossRef]
- Wang, W.; Sun, Q.; Zhao, Z.; Sun, X.; Qin, F.; Kho, K.; Zheng, Y. Laser-induced ultrasonic guided waves based corrosion diagnosis of rail foot. IEEE Trans. Instrum. Meas. 2023, 72, 1–9. [Google Scholar] [CrossRef]
- Yang, Y.; Zhong, J.; Qin, A.; Mao, H.; Mao, H.; Huang, Z.; Lin, Y. Feature extraction of ultrasonic guided wave weld detection based on group sparse wavelet transform with tunable Q-factor. Measurement 2023, 206, 112314. [Google Scholar] [CrossRef]
- Mohammed, M.S.; Ki-Seong, K. Chirplet Transform in Ultrasonic Non-Destructive Testing and Structural Health Monitoring: A Review. Eng. Technol. Appl. Sci. Res. 2019, 9, 3778–3781. [Google Scholar] [CrossRef]
- Sun, H.; Peng, L.; Huang, S.; Wang, S.; Wang, Q.; Zhao, W. Mode identification of denoised SH guided waves using variational mode decomposition method. In Proceedings of the IEEE SENSORS, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–3. [Google Scholar]
- Levine, R.M.; Michaels, J.E. Block-sparse reconstruction and imaging for lamb wave structural health monitoring. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1006–1015. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Wang, D.; Huang, X.; Liang, L.; Tang, Z.; Liu, Y. Sparse ultrasonic guided wave imaging with compressive sensing and deep learning. Mech. Syst. Signal Process. 2022, 178, 109346. [Google Scholar] [CrossRef]
- Zheng, S.; Chen, H.; Ling, F.; Minonzio, J.G.; Ta, D.; Xu, K. Orthogonal Matching Pursuit based Sparse Dispersive Radon Transform for Ultrasonic Guided Mode Extraction. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022; pp. 1–4. [Google Scholar]
- Fan, W.; Wan, D.; Xu, Z.; Wang, Y.; Du, H. Feature extraction of echo signal of weld defect guided waves based on sparse representation. IEEE Sens. J. 2019, 20, 2692–2700. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Boßmann, F.; Plonka, G.; Peter, T.; Nemitz, O.; Schmitte, T. Sparse deconvolution methods for ultrasonic NDT: Application on TOFD and wall thickness measurements. J. Nondestruct. Eval. 2012, 31, 225–244. [Google Scholar] [CrossRef]
- Qian, Z.; Zhang, C.; Li, P.; Wang, B.; Qian, Z.; Kuznetsova, I.; Li, X. A dictionary-reconstruction approach for separating helical-guided waves in cylindrical pipes. J. Phys. D Appl. Phys. 2023, 56, 305301. [Google Scholar] [CrossRef]
- Gholami, A.; Honarvar, F.; Moghaddam, H.A. Modeling the ultrasonic testing echoes by a combination of particle swarm optimization and Levenberg–Marquardt algorithms. Meas. Sci. Technol. 2017, 28, 065001. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Z.; Wu, B.; He, C. A technique based on nonlinear Hanning-windowed chirplet model and genetic algorithm for parameter estimation of Lamb wave signals. Ultrasonics 2021, 111, 106333. [Google Scholar] [CrossRef] [PubMed]
- Pei, J.; Yousuf, M.I.; Degertekin, F.L.; Honein, B.V.; Khuri-Yakub, B.T. Lamb wave tomography and its application in pipe erosion/corrosion monitoring. J. Res. Nondestruct. Eval. 1996, 8, 189–197. [Google Scholar] [CrossRef]
- Huthwaite, P.; Simonetti, F. High-resolution guided wave tomography. Wave Motion 2013, 50, 979–993. [Google Scholar] [CrossRef]
- Willey, C.L.; Simonetti, F.; Nagy, P.B.; Instanes, G. Guided wave tomography of pipes with high-order helical modes. Ndt E Int. 2014, 65, 8–21. [Google Scholar] [CrossRef]
- Levine, R.M.; Michaels, J.E. Model-based imaging of damage with Lamb waves via sparse reconstruction. J. Acoust. Soc. Am. 2013, 133, 1525–1534. [Google Scholar] [CrossRef]
- Kim, H.; Yuan, F.G. Adaptive signal decomposition and dispersion removal based on the matching pursuit algorithm using dispersion-based dictionary for enhancing damage imaging. Ultrasonics 2020, 103, 106087. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Sikdar, S.; Wandowski, T.; Malinowski, P.H. Ultrasonic guided wave-based debond identification in a GFRP plate with L-stiffener. Smart Mater. Struct. 2021, 31, 015023. [Google Scholar] [CrossRef]
- Zhang, H.; Teng, F.; Wei, J.; Lv, S.; Zhang, L.; Zhang, F.; Jiang, M. Damage Location Method of Pipeline Structure by Ultrasonic Guided Wave Based on Probability Fusion. IEEE Trans. Instrum. Meas. 2024, 73, 1–14. [Google Scholar] [CrossRef]
- Vergallo, P.; Lay-Ekuakille, A. Brain source localization: A new method based on MUltiple SIgnal Classification algorithm and spatial sparsity of the field signal for electroencephalogram measurements. Rev. Sci. Instrum. 2013, 84, 085117. [Google Scholar] [CrossRef]
- Zuo, H.; Yang, Z.; Xu, C.; Tian, S.; Chen, X. Damage identification for plate-like structures using ultrasonic guided wave based on improved MUSIC method. Compos. Struct. 2018, 203, 164–171. [Google Scholar] [CrossRef]
- Cai, J.; Yuan, S.; Qing, X.P.; Chang, F.K.; Shi, L.; Qiu, L. Linearly dispersive signal construction of Lamb waves with measured relative wavenumber curves. Sens. Actuators A Phys. 2015, 221, 41–52. [Google Scholar] [CrossRef]
- Barzegar, M.; Pasadas, D.J.; Ribeiro, A.L.; Ramos, H.G. Experimental estimation of Lamb wave dispersion curves for adhesively bonded aluminum plates, using two adjacent signals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2143–2151. [Google Scholar] [CrossRef]
- Zeng, L.; Huang, L.; Cao, X.; Gao, F. Determination of Lamb wave phase velocity dispersion using time–frequency analysis. Smart Mater. Struct. 2019, 28, 115029. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, K.; Ta, D. High-resolution Lamb waves dispersion curves estimation and elastic property inversion. Ultrasonics 2021, 115, 106427. [Google Scholar] [CrossRef] [PubMed]
- Kalkowski, M.K.; Muggleton, J.M.; Rustighi, E. Axisymmetric semi-analytical finite elements for modelling waves in buried/submerged fluid-filled waveguides. Comput. Struct. 2018, 196, 327–340. [Google Scholar] [CrossRef]
- Tang, B.; Wang, Y.; Gong, R.; Zhou, F. Sparse reconstruction of ultrasonic guided wave signals of fluid-filled pipes by multistrategy hybrid DBO-OMP using dispersive Hanning-windowed chirplet model. Measurement 2024, 231, 114648. [Google Scholar] [CrossRef]
- Hu, Y.; Cui, F.; Li, F.; Tu, X.; Zeng, L. Sparse wavenumber analysis of guided wave based on hybrid lasso regression in composite laminates. Struct. Health Monit. 2022, 21, 1367–1378. [Google Scholar] [CrossRef]
- Sabeti, S.; Harley, J.B. Guided wave retrieval from temporally undersampled data. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017; pp. 1–4. [Google Scholar]
- Sabeti, S.; Harley, J.B. Two-dimensional sparse wavenumber recovery for guided wavefields. AIP Conf. Proc. 2018, 1949, 230003. [Google Scholar]
- Sabeti, S.; Harley, J.B. Polar sparse wavenumber analysis for guided wave reconstruction. AIP Conf. Proc. 2019, 2102, 050012. [Google Scholar]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Xu, C.B.; Yang, Z.B.; Zhai, Z.; Qiao, B.J.; Tian, S.H.; Chen, X.F. A weighted sparse reconstruction-based ultrasonic guided wave anomaly imaging method for composite laminates. Compos. Struct. 2019, 209, 233–241. [Google Scholar] [CrossRef]
- Wang, P.; Zhou, W.; Li, H. A singular value decomposition-based guided wave array signal processing approach for weak signals with low signal-to-noise ratios. Mech. Syst. Signal Process. 2020, 141, 106450. [Google Scholar] [CrossRef]
- Si, D.; Gao, B.; Guo, W.; Yan, Y.; Tian, G.Y.; Yin, Y. Variational mode decomposition linked wavelet method for EMAT denoise with large lift-off effect. Ndt E Int. 2019, 107, 102149. [Google Scholar] [CrossRef]


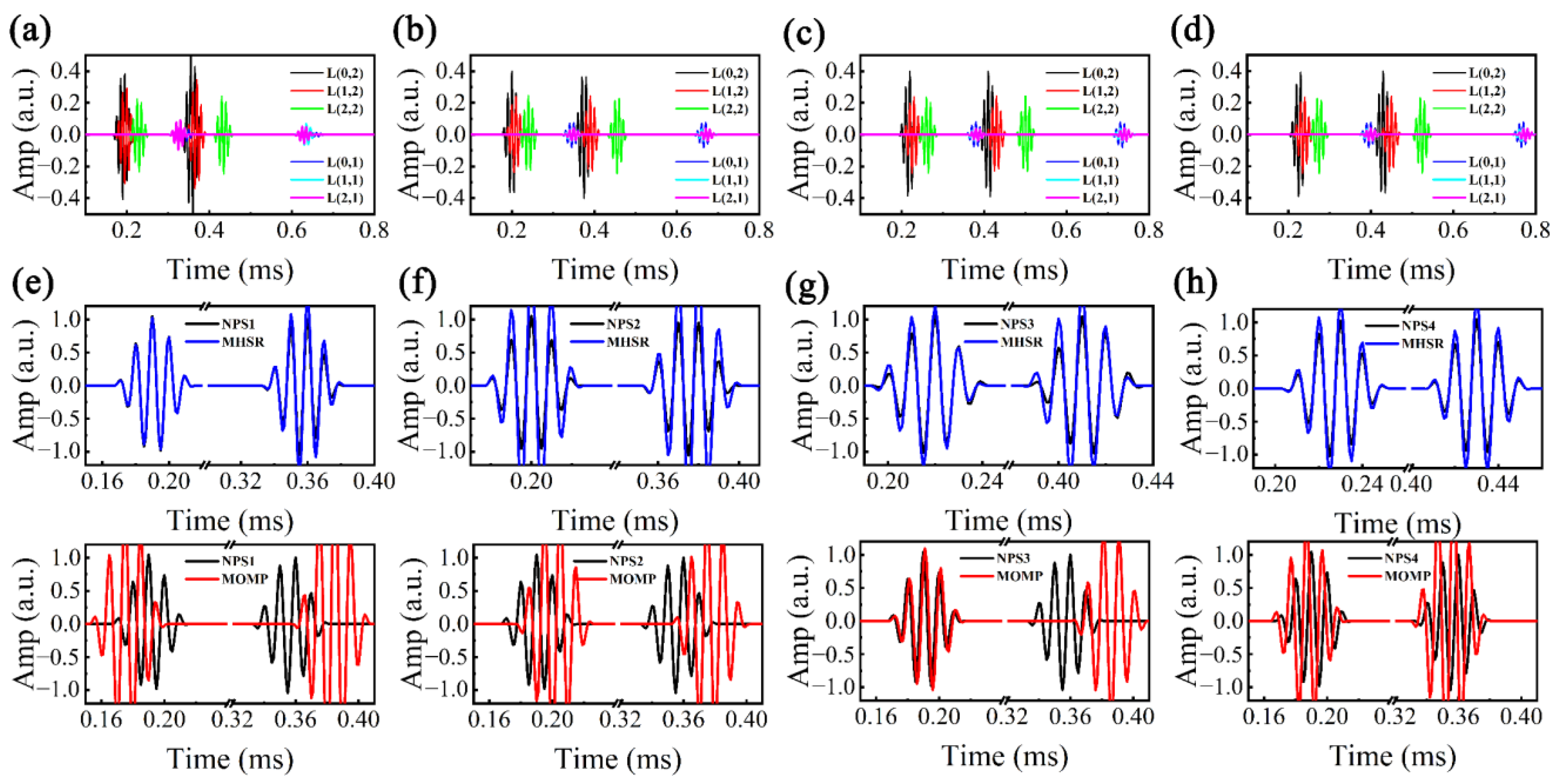
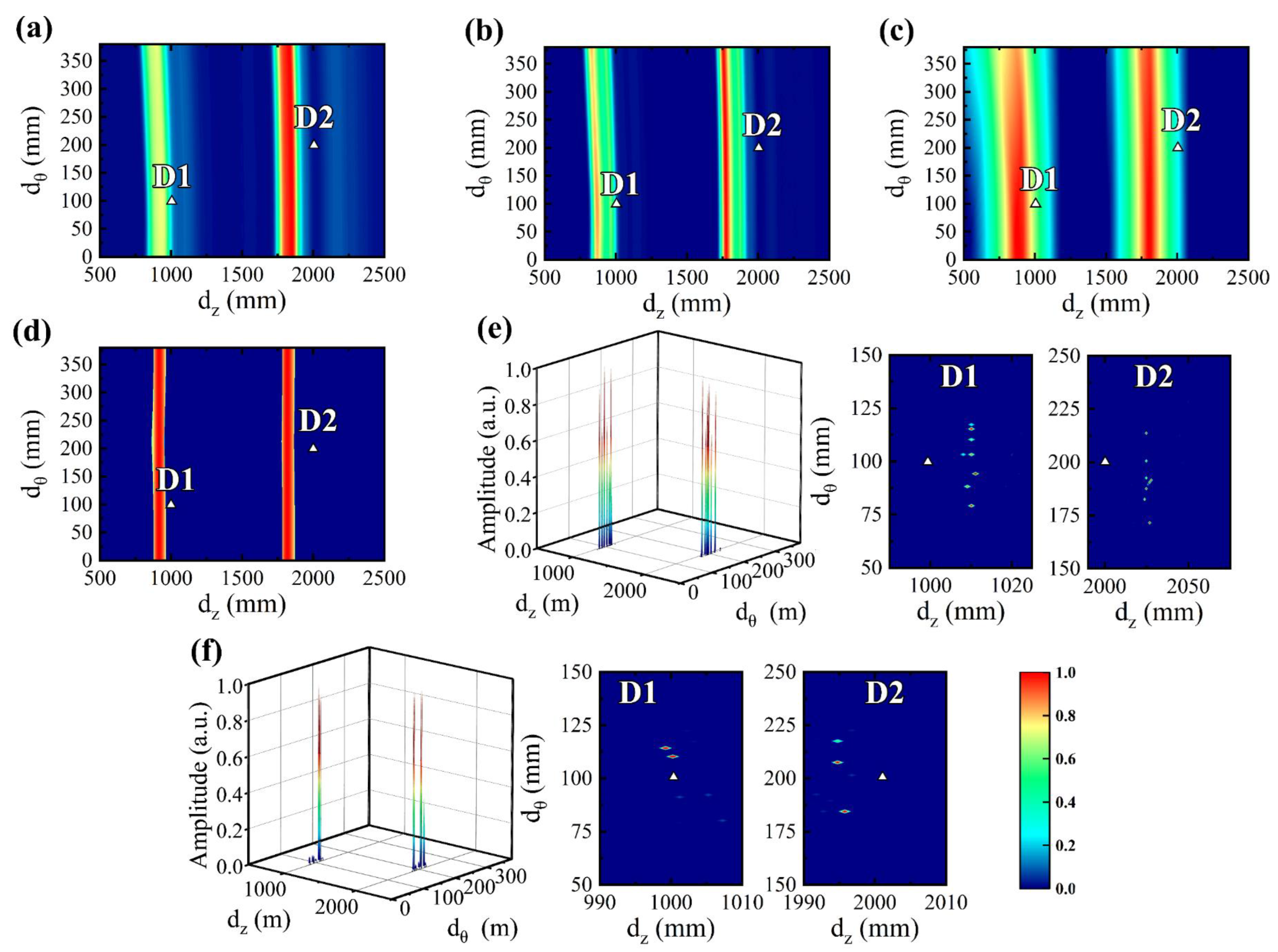
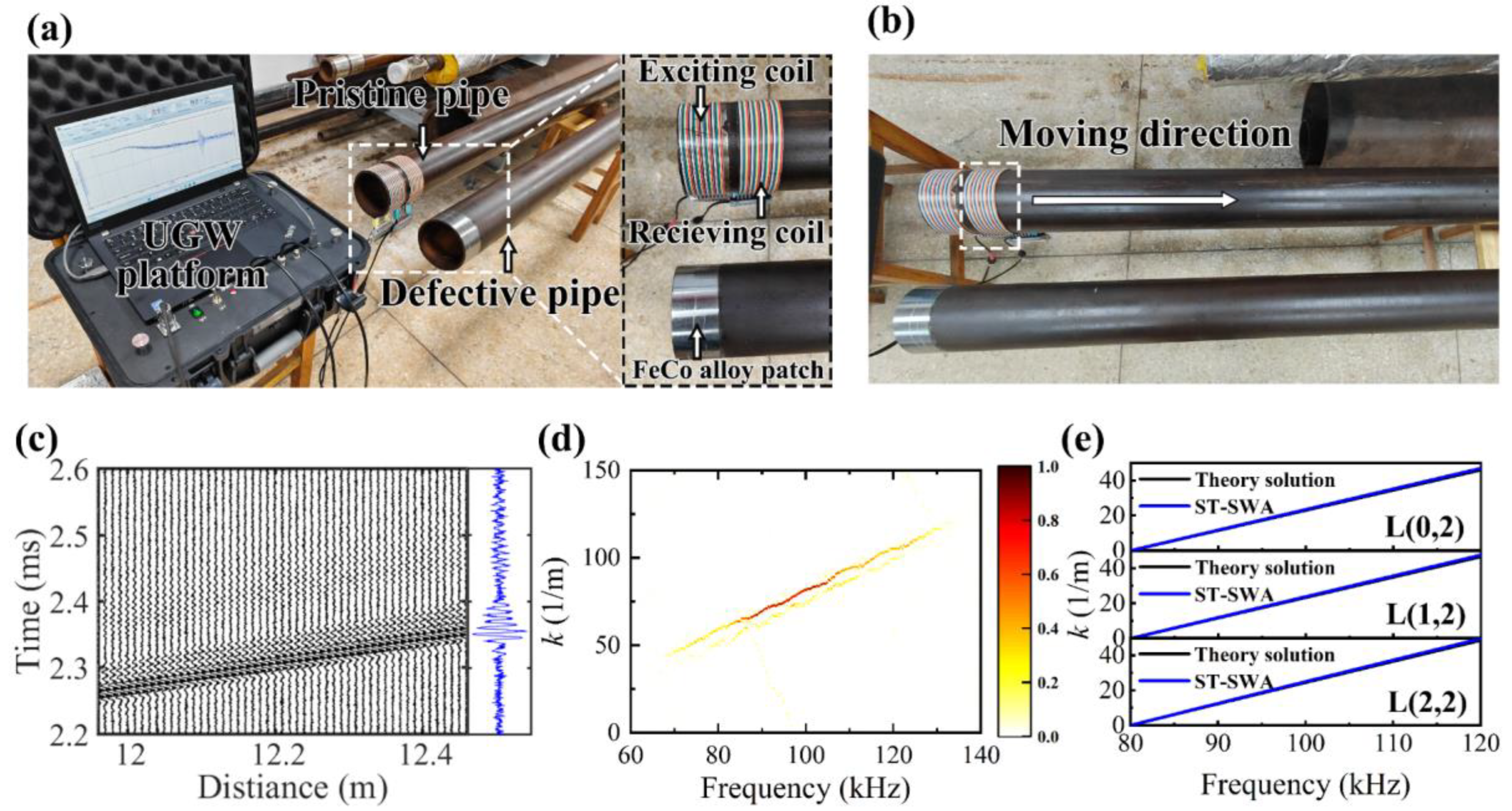


| NPS1 | NPS2 | NPS3 | NPS4 | |||||
|---|---|---|---|---|---|---|---|---|
| d1 (mm) | d2 (mm) | d1 (mm) | d2 (mm) | d1 (mm) | d2 (mm) | d1 (mm) | d2 (mm) | |
| MHSR | 4.24 | 11.79 | 4.26 | 7.05 | 0.96 | 1.44 | 5.15 | 8.63 |
| MOMP | 10.82 | 24.48 | 9.81 | 28.31 | 3.63 | 17.28 | 6.29 | 16.73 |
| Error | DAS | EVD | RAPID | MUSIC | MOMPI | MHSRI |
|---|---|---|---|---|---|---|
| D1 | (66, 6) | (132, 0) | (130, 11) | (85, 0) | (22, 6) | (1, 5) |
| D2 | (157, 40) | (229, 68) | (182, 45) | (183, 2) | (29, 11) | (5, 7) |
| Average | (111.5, 23) | (180.5, 34) | (156, 28) | (134, 1) | (25.5, 8.5) | (3, 6.5) |
| Error | DAS | EVD | RAPID | MUSIC | MOMPI | MHSRI |
|---|---|---|---|---|---|---|
| D1 | (76, 92) | (4, 91) | (38, 27) | (70, 86) | (21, 6) | (13, 16) |
| D2 | (153, 10) | (38, 131) | (97, 125) | (83, 24) | (19, 24) | (10, 4) |
| Average | (114.5, 51) | (21, 111) | (67.5, 101) | (76.5, 55) | (20, 15) | (11.5, 11) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, B.; Wang, Y.; Gong, R.; Zhou, F. A Multi-Strategy Hybrid Sparse Reconstruction Method Based on Spatial–Temporal Sparse Wave Number Analysis for Enhancing Pipe Ultrasonic-Guided Wave Anomaly Imaging. Sensors 2024, 24, 5374. https://doi.org/10.3390/s24165374
Tang B, Wang Y, Gong R, Zhou F. A Multi-Strategy Hybrid Sparse Reconstruction Method Based on Spatial–Temporal Sparse Wave Number Analysis for Enhancing Pipe Ultrasonic-Guided Wave Anomaly Imaging. Sensors. 2024; 24(16):5374. https://doi.org/10.3390/s24165374
Chicago/Turabian StyleTang, Binghui, Yuemin Wang, Ruqing Gong, and Fan Zhou. 2024. "A Multi-Strategy Hybrid Sparse Reconstruction Method Based on Spatial–Temporal Sparse Wave Number Analysis for Enhancing Pipe Ultrasonic-Guided Wave Anomaly Imaging" Sensors 24, no. 16: 5374. https://doi.org/10.3390/s24165374




