Shape Classification Using a Single Seal-Whisker-Style Sensor Based on the Neural Network Method
Abstract
:1. Introduction
2. Materials and Methods
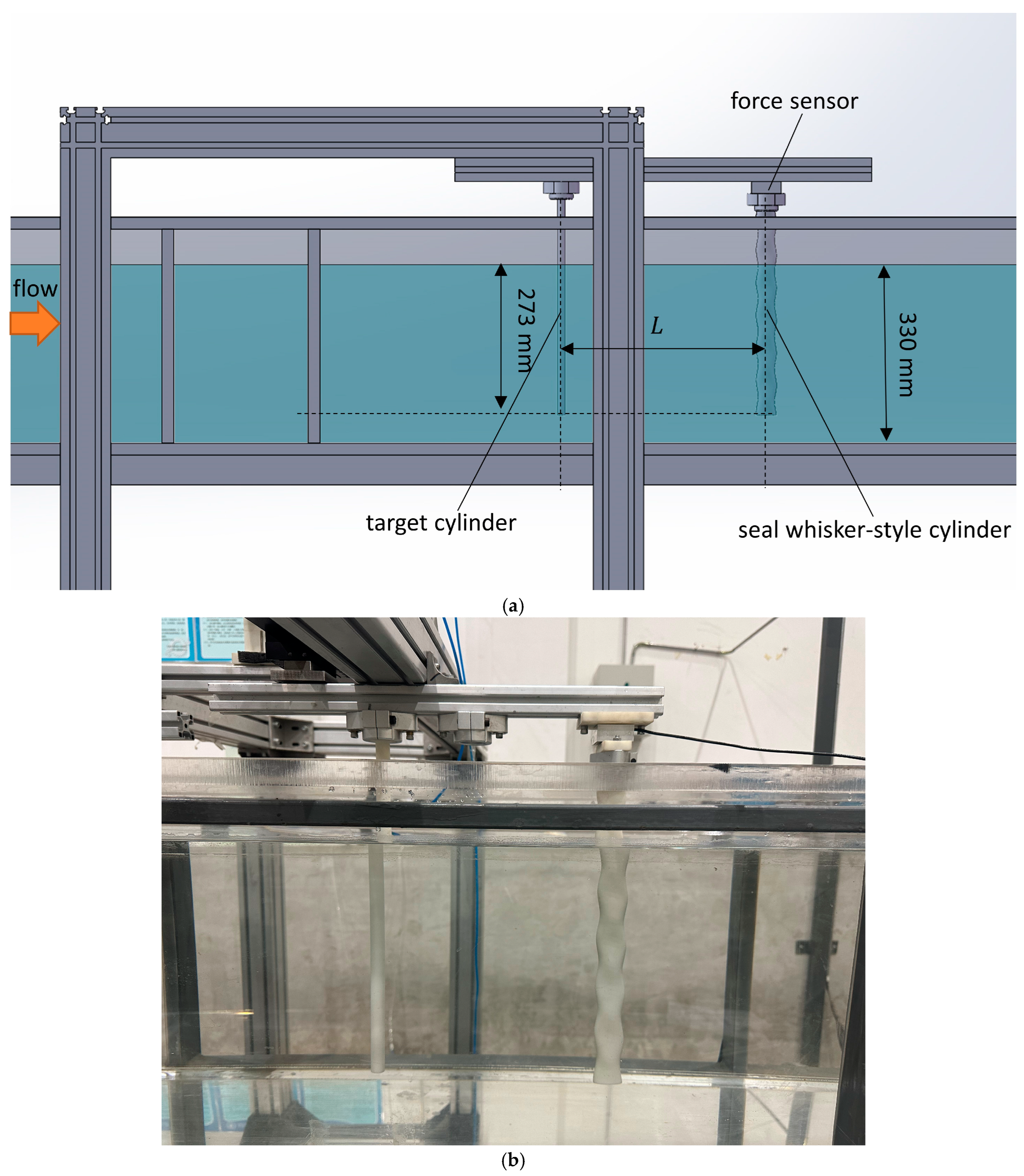
2.1. Experimental Setup and Procedure
2.2. CNN Structure and Settings
3. Results
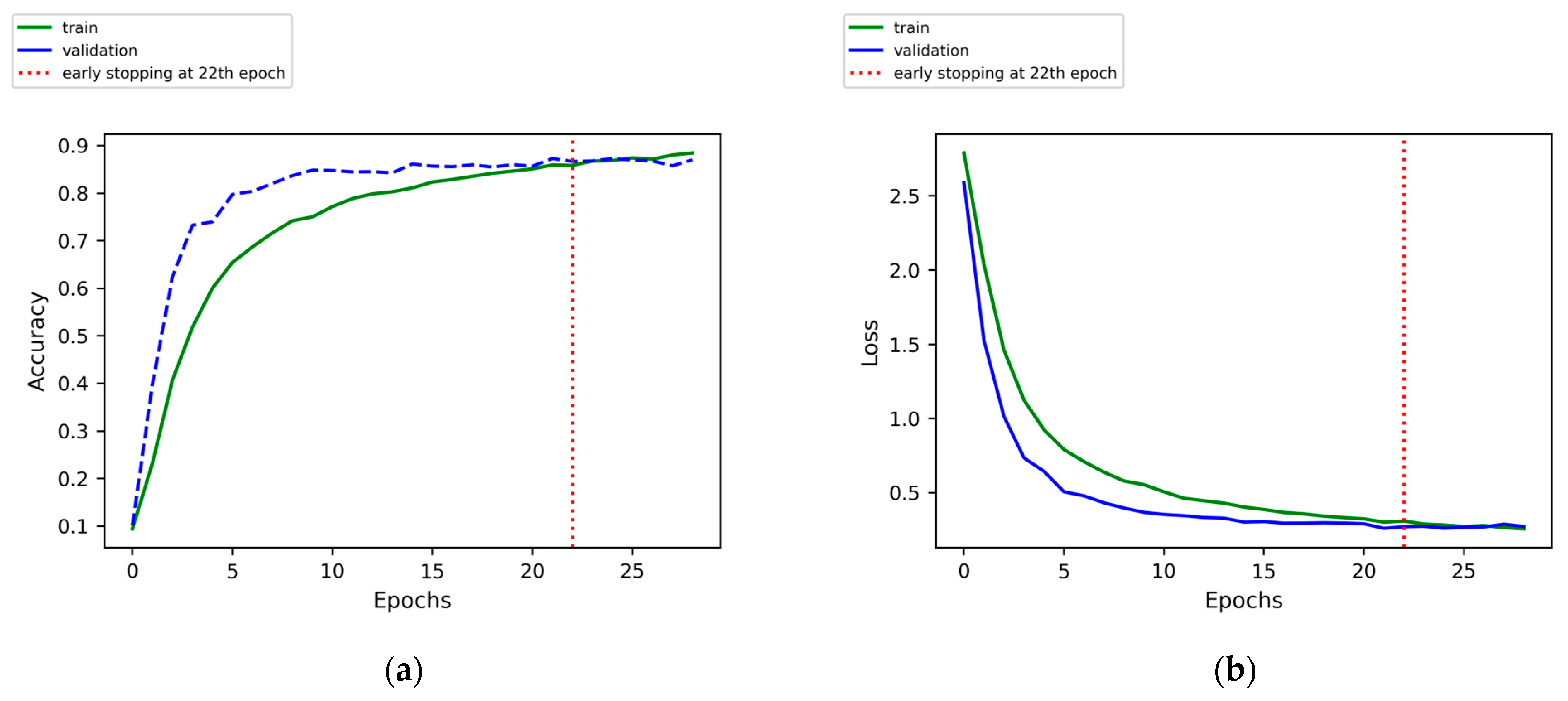
3.1. Validation of the CNN Model
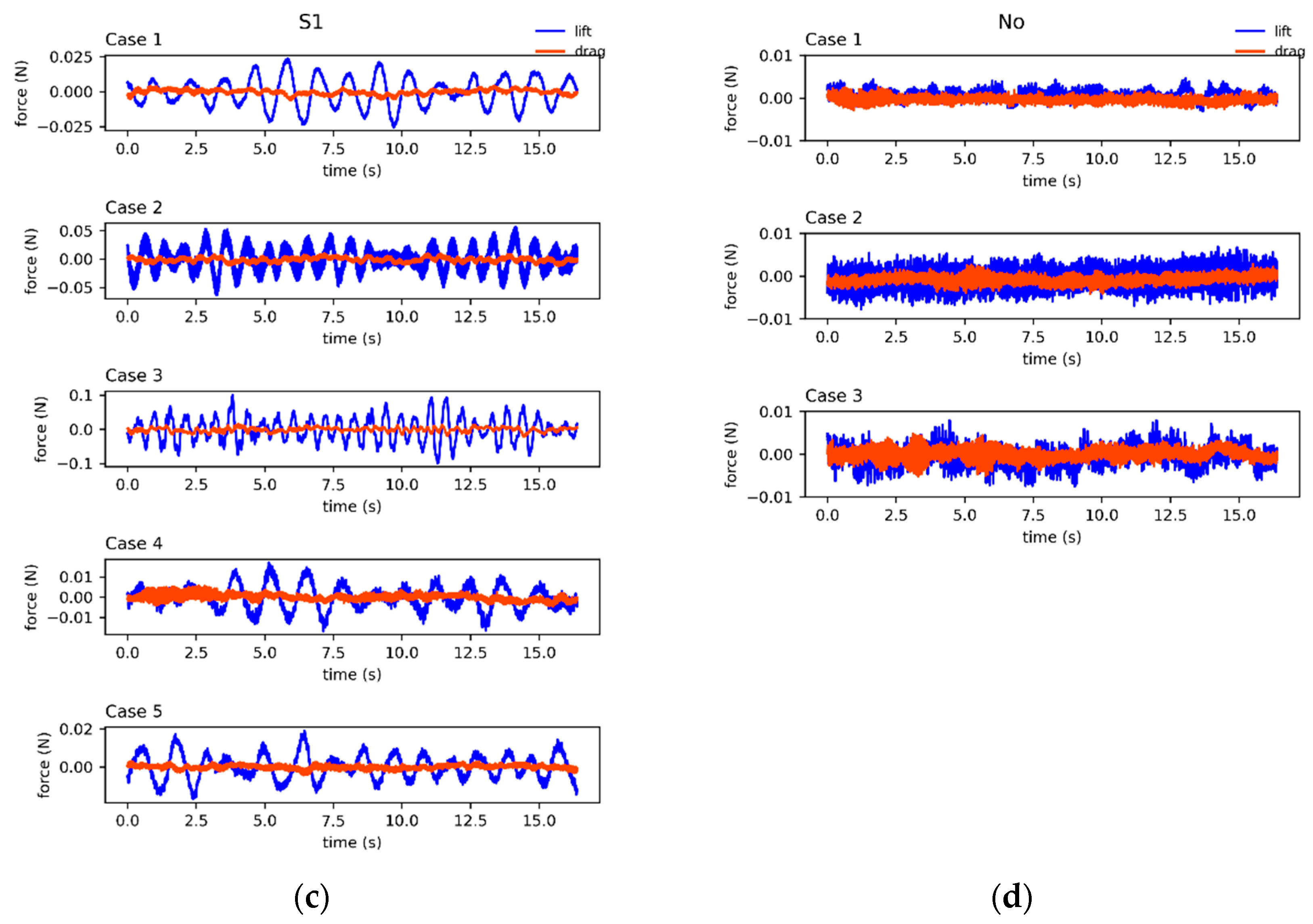
3.2. Experimental Results of Seal-Whisker-Style Sensor Force Signals
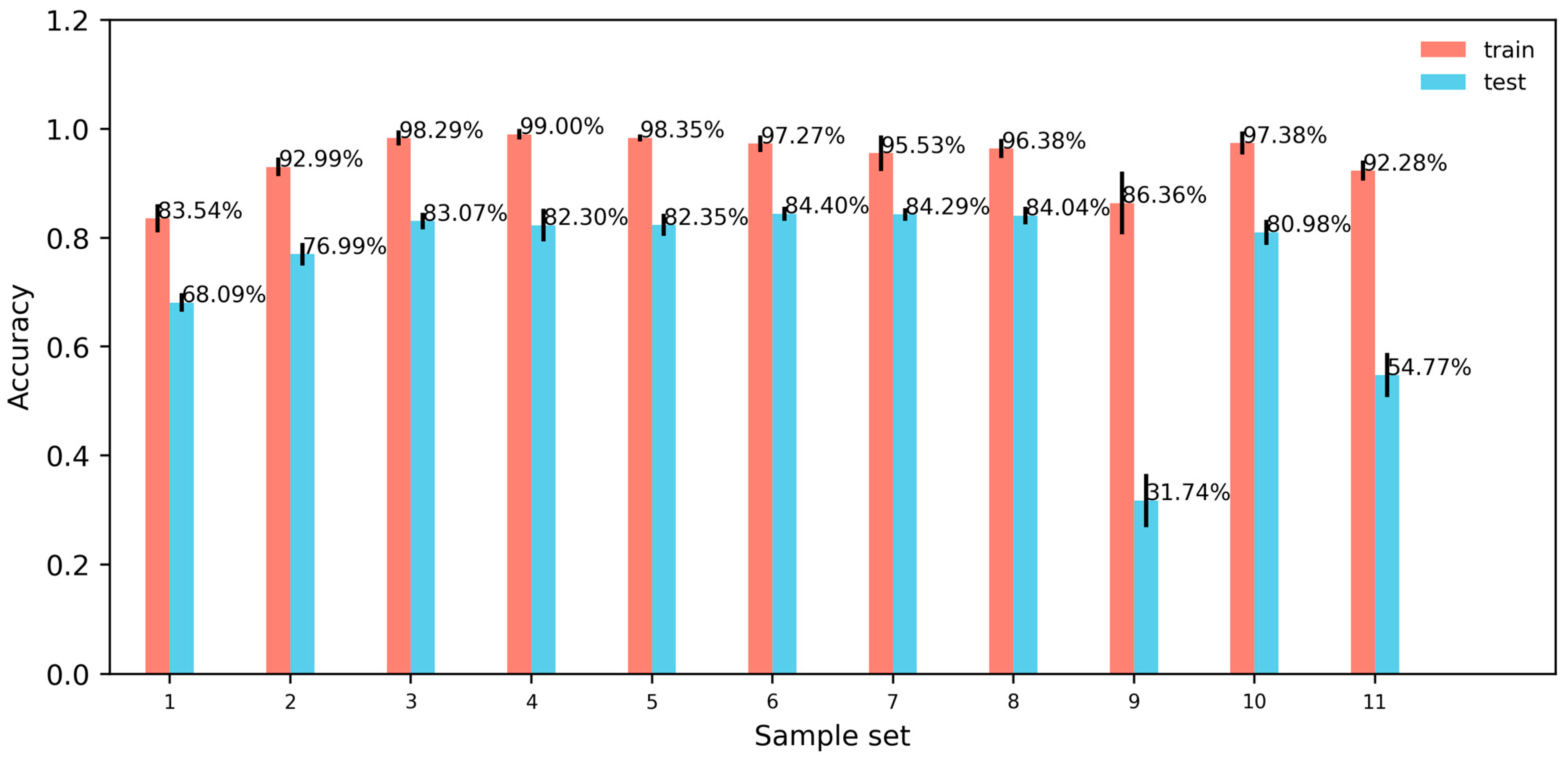
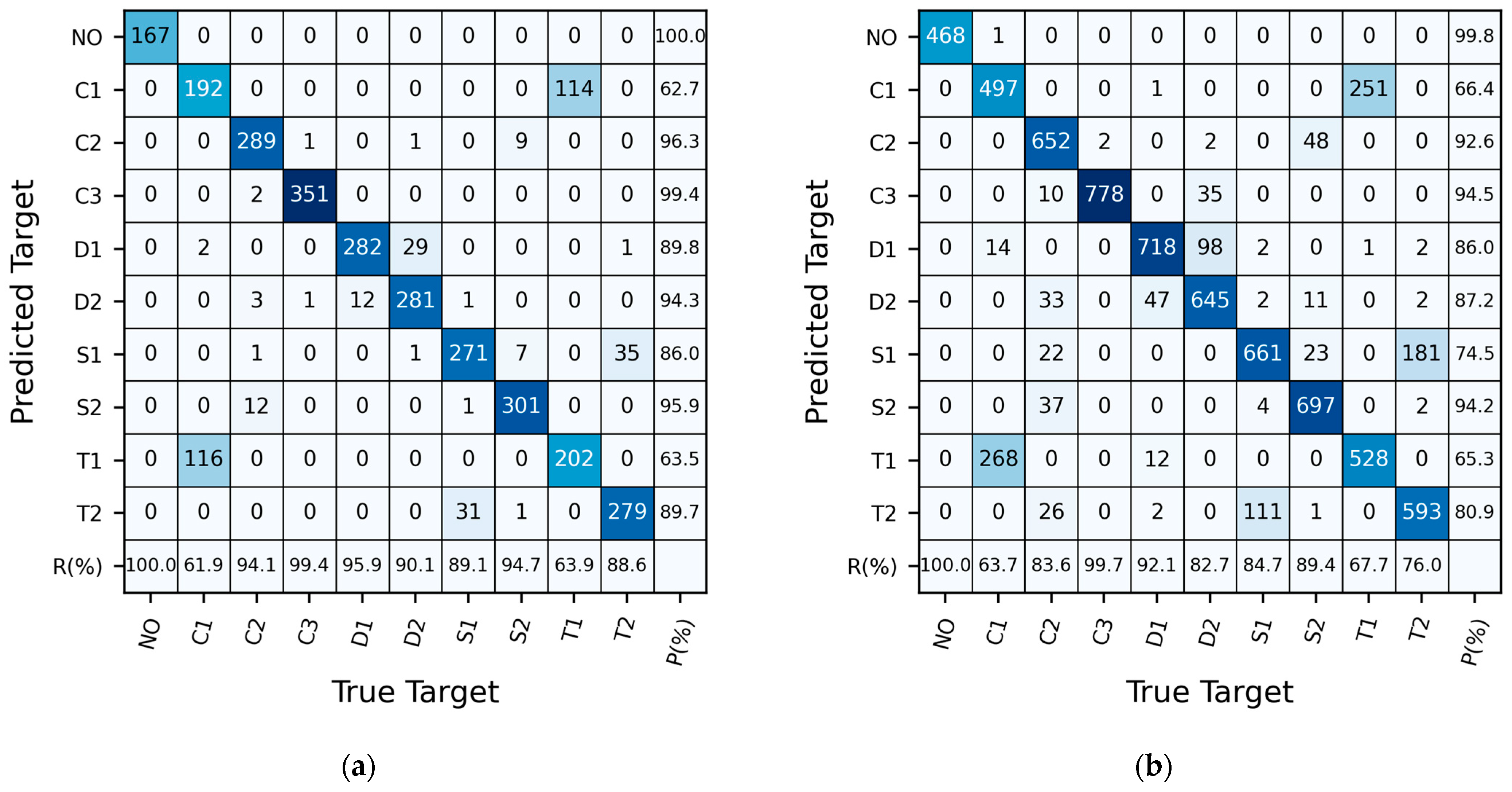
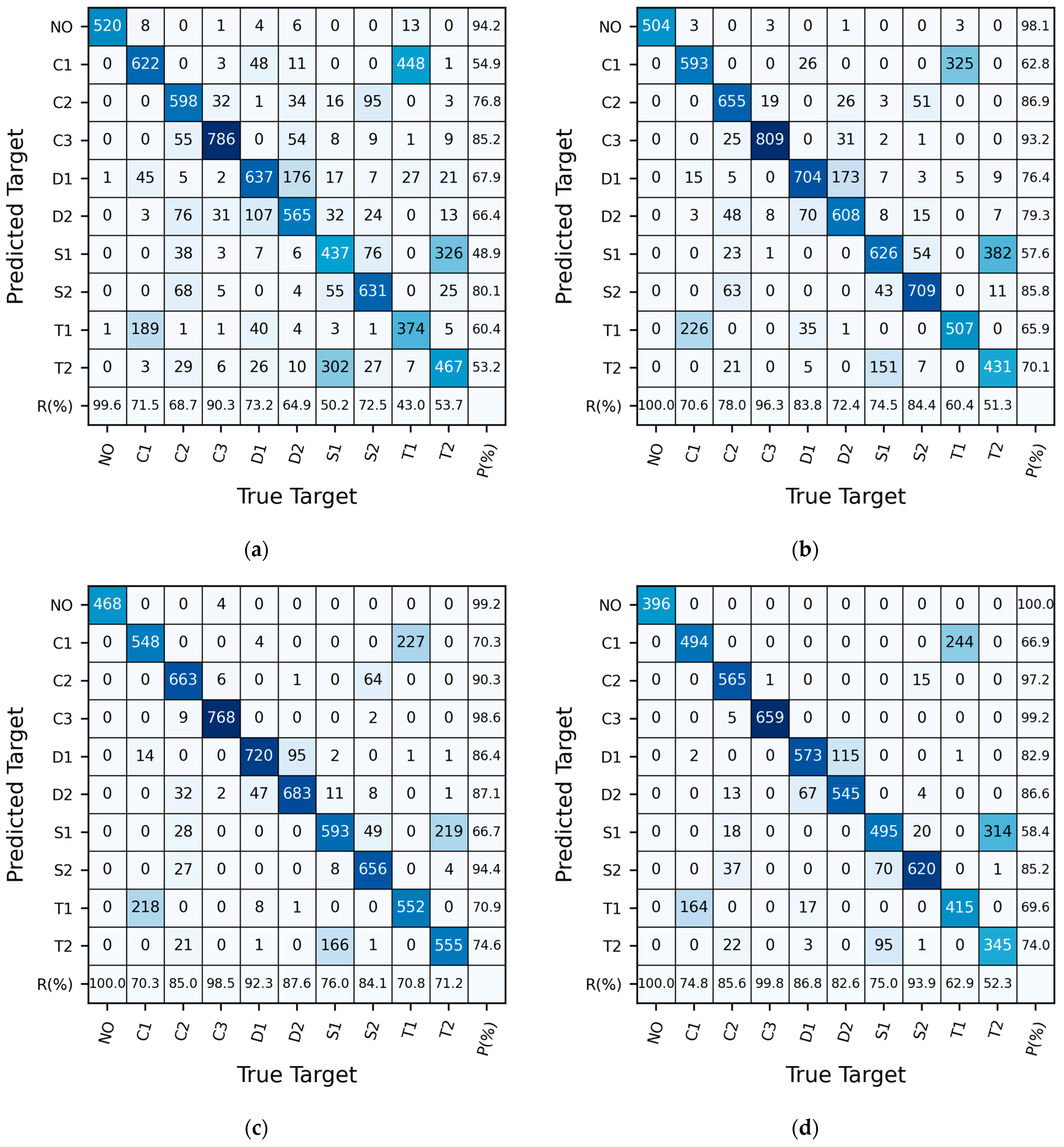
3.3. Results of the CNN Model
4. Discussion
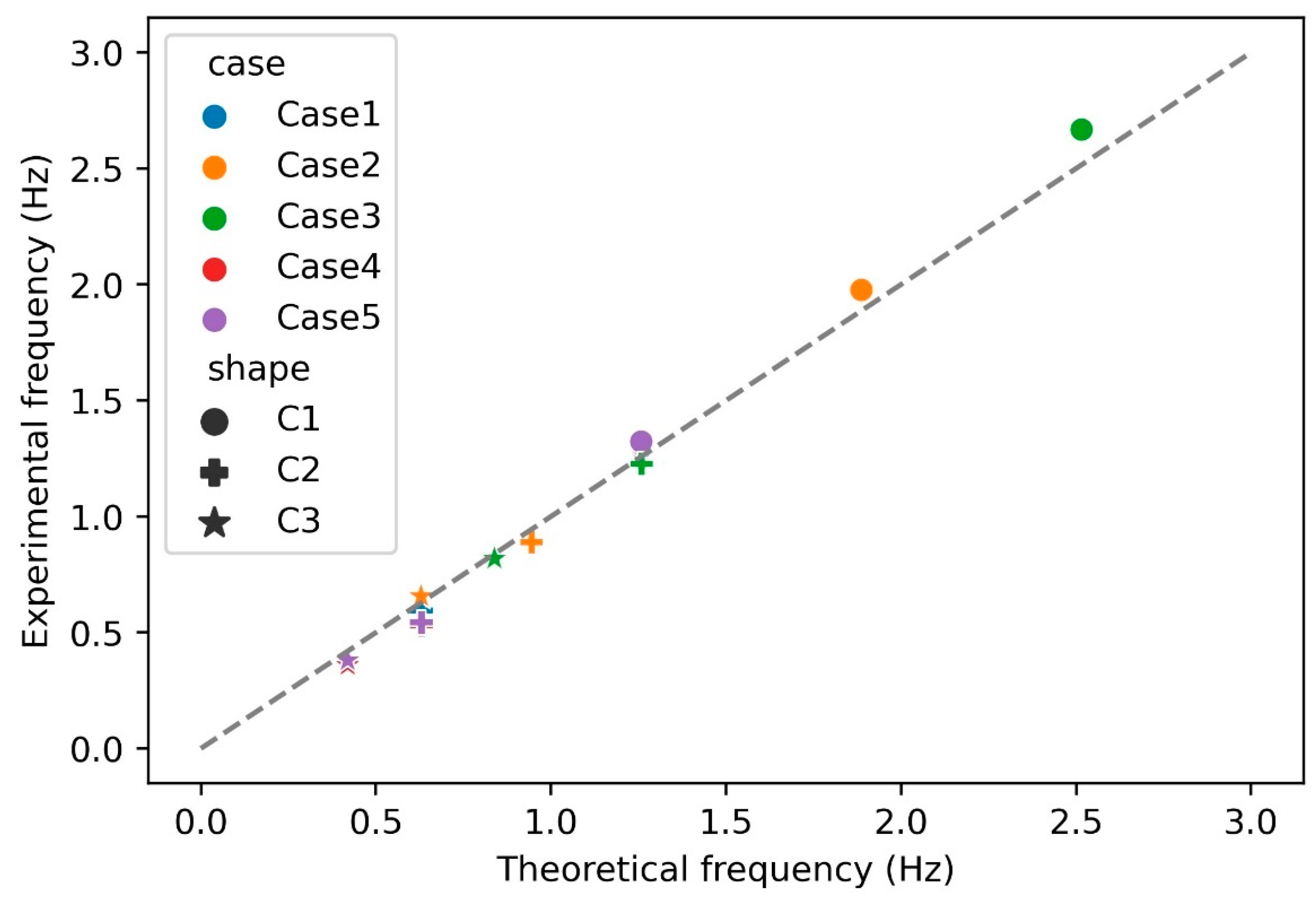
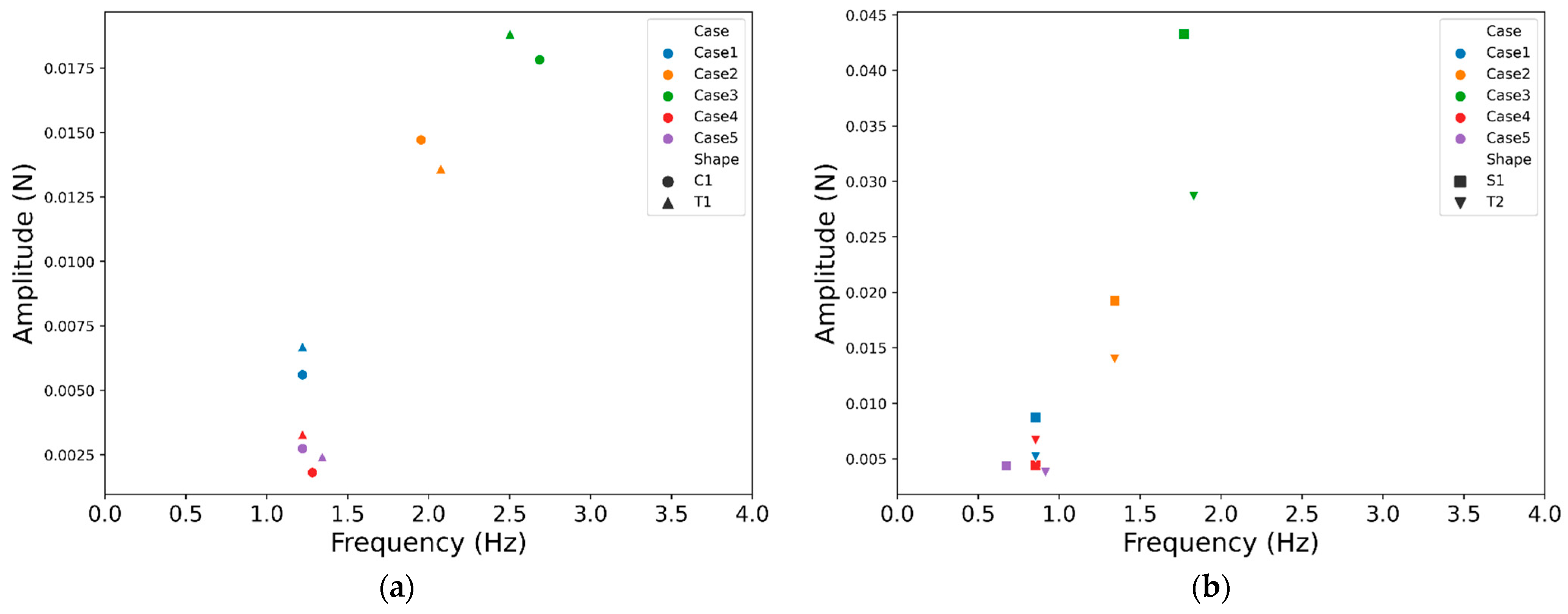
4.1. The Impact of Vortex Shedding Frequency on Force Signals
4.2. The Influence of Sample Length and Filtering on the CNN Model
4.3. Lift Signal Spectra and Their Impact on Target Recognition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beem, H.; Hildner, M.; Triantafyllou, M. Calibration and Validation of a Harbor Seal Whisker-Inspired Flow Sensor. Smart Mater. Struct. 2013, 22, 014012. [Google Scholar] [CrossRef]
- Kottapalli, A.G.; Asadnia, M.; Miao, J.M.; Barbastathis, G.; Triantafyllou, M.S. A Flexible Liquid Crystal Polymer MEMS Pressure Sensor Array for Fish-like Underwater Sensing. Smart Mater. Struct. 2012, 21, 115030. [Google Scholar] [CrossRef]
- Schrope, M. Whale Deaths Caused by US Navy’s Sonar. Nature 2002, 415, 106. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, J.; Engel, J.; Pandya, S.; Chen, N.; Tucker, C.; Coombs, S.; Jones, D.L.; Liu, C. Distant Touch Hydrodynamic Imaging with an Artificial Lateral Line. Proc. Natl. Acad. Sci. USA 2006, 103, 18891–18895. [Google Scholar] [CrossRef] [PubMed]
- Dehnhardt, G.; Mauck, B.; Bleckmann, H. Seal Whiskers Detect Water Movements. Nature 1998, 394, 235–236. [Google Scholar] [CrossRef]
- Dehnhardt, G.; Mauck, B.; Hanke, W.; Bleckmann, H. Hydrodynamic Trail-Following in Harbor Seals (Phoca vitulina). Science 2001, 293, 102–104. [Google Scholar] [CrossRef]
- Miersch, L.; Hanke, W.; Wieskotten, S.; Hanke, F.D.; Oeffner, J.; Leder, A.; Brede, M.; Witte, M.; Dehnhardt, G. Flow Sensing by Pinniped Whiskers. Philos. Trans. R. Soc. B Biol. Sci. 2011, 366, 3077–3084. [Google Scholar] [CrossRef]
- Hanke, W.; Witte, M.; Miersch, L.; Brede, M.; Oeffner, J.; Michael, M.; Hanke, F.; Leder, A.; Dehnhardt, G. Harbor Seal Vibrissa Morphology Suppresses Vortex-Induced Vibrations. J. Exp. Biol. 2010, 213, 2665–2672. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Lu, Y.; Jia, Q.; Xia, C.; Chu, S. Investigation on the Behavior of Flow and Aerodynamic Noise Generated around the Tandem Seal-Vibrissa-Shaped Cylinder. Phys. Fluids 2023, 35, 117124. [Google Scholar] [CrossRef]
- Morrison, H.E.; Brede, M.; Dehnhardt, G.; Leder, A. Simulating the Flow and Trail Following Capabilities of Harbour Seal Vibrissae with the Lattice Boltzmann Method. J. Comput. Sci. 2016, 17, 394–402. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Y. Wake Dynamics behind a Seal-Vibrissa-Shaped Cylinder: A Comparative Study by Time-Resolved Particle Velocimetry Measurements. Exp. Fluids 2016, 57, 32. [Google Scholar] [CrossRef]
- Teixeira, I.A.V.C.M. Experimental Investigation on Vortex Induced Vibrations of Bio-Cylinders Based on a Harbor Seal Vibrissa. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]
- Gong, Z.; Cao, Y.; Cao, H.; Wan, B.; Yang, Z.; Ke, X.; Zhang, D.; Chen, H.; Wang, K.; Jiang, Y. Morphological Intelligence Mechanisms in Biological and Biomimetic Flow Sensing. Adv. Intell. Syst. 2023, 5, 2300154. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, Z.; Ji, C.; Zhao, Y.; Li, X.; Du, M. Dynamics of Harbor Seal Whiskers at Different Angles of Attack in Wake Flow. Phys. Fluids 2024, 36, 071914. [Google Scholar] [CrossRef]
- Kottapalli, A.G.P.; Asadnia, M.; Hans, H.; Miao, J.M.; Triantafyllou, M.S. Harbor Seal Inspired MEMS Artificial Micro-Whisker Sensor. In Proceedings of the 2014 IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS), San Francisco, CA, USA, 26–30 January 2014; pp. 741–744. [Google Scholar]
- Eberhardt, W.C.; Wakefield, B.F.; Murphy, C.T.; Casey, C.; Shakhsheer, Y.; Calhoun, B.H.; Reichmuth, C. Development of an Artificial Sensor for Hydrodynamic Detection Inspired by a Seal’s Whisker Array. Bioinspir. Biomim. 2016, 11, 056011. [Google Scholar] [CrossRef]
- Chu, S.; Xia, C.; Wang, H.; Fan, Y.; Yang, Z. Three-Dimensional Spectral Proper Orthogonal Decomposition Analyses of the Turbulent Flow around a Seal-Vibrissa-Shaped Cylinder. Phys. Fluids 2021, 33, 025106. [Google Scholar] [CrossRef]
- Verma, S.; Papadimitriou, C.; Lüthen, N.; Arampatzis, G.; Koumoutsakos, P. Optimal Sensor Placement for Artificial Swimmers. J. Fluid Mech. 2020, 884, A24. [Google Scholar] [CrossRef]
- Zheng, X.; Kamat, A.M.; Harish, V.S.; Cao, M.; Kottapalli, A.G.P. Optimizing Harbor Seal Whisker Morphology for Developing 3D-Printed Flow Sensor. In Proceedings of the 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 20–24 June 2021; pp. 1271–1274. [Google Scholar]
- Carrillo, M.; Que, U.; González, J.A.; López, C. Recognition of an Obstacle in a Flow Using Artificial Neural Networks. Phys. Rev. E 2017, 96, 023306. [Google Scholar] [CrossRef]
- Lakkam, S.; Balamurali, B.T.; Bouffanais, R. Hydrodynamic Object Identification with Artificial Neural Models. Sci. Rep. 2019, 9, 11242. [Google Scholar] [CrossRef]
- Du, P.; Zhao, S.; Xing, C.; Chen, X.; Hu, H.; Ren, F.; Zhang, M.; Xie, L.; Huang, X.; Wen, J. Hydrodynamic Detection Based on Multilayer Perceptron and Optimization Using Dynamic Mode Decomposition. Ocean Eng. 2023, 278, 114258. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, Y.; Ji, M.; Liu, Y.; Lin, X.; Qiu, J.; Liu, G. Underwater Positioning Based on an Artificial Lateral Line and a Generalized Regression Neural Network. J. Bionic Eng. 2018, 15, 883–893. [Google Scholar] [CrossRef]
- Wolf, B.J.; Pirih, P.; Kruusmaa, M.; Van Netten, S.M. Shape Classification Using Hydrodynamic Detection via a Sparse Large-Scale 2D-Sensitive Artificial Lateral Line. IEEE Access 2020, 8, 11393–11404. [Google Scholar] [CrossRef]
- Pu, Y.; Hang, Z.; Wang, G.; Hu, H. Bionic Artificial Lateral Line Underwater Localization Based on the Neural Network Method. Appl. Sci. 2022, 12, 7241. [Google Scholar] [CrossRef]
- Bodaghi, D.; Wang, Y.; Liu, G.; Liu, D.; Xue, Q.; Zheng, X. Deciphering the Connection between Upstream Obstacles, Wake Structures, and Root Signals in Seal Whisker Array Sensing Using Interpretable Neural Networks. Front. Robot. AI 2023, 10, 1231715. [Google Scholar] [CrossRef]
- Li, Y.; Pang, Y.; Wang, J.; Li, X. Patient-Specific ECG Classification by Deeper CNN from Generic to Dedicated. Neurocomputing 2018, 314, 336–346. [Google Scholar] [CrossRef]
- Eren, L.; Ince, T.; Kiranyaz, S. A Generic Intelligent Bearing Fault Diagnosis System Using Compact Adaptive 1D CNN Classifier. J. Signal Process. Syst. 2019, 91, 179–189. [Google Scholar] [CrossRef]
- Loparo, K. Case Western Reserve University Bearing Data Center. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 31 July 2024).
- Blevins, R.D. Flow-Induced Vibration; Van Nostrand Reinhold: New York, NY, USA, 1977; ISBN 978-0-442-20651-2. [Google Scholar]
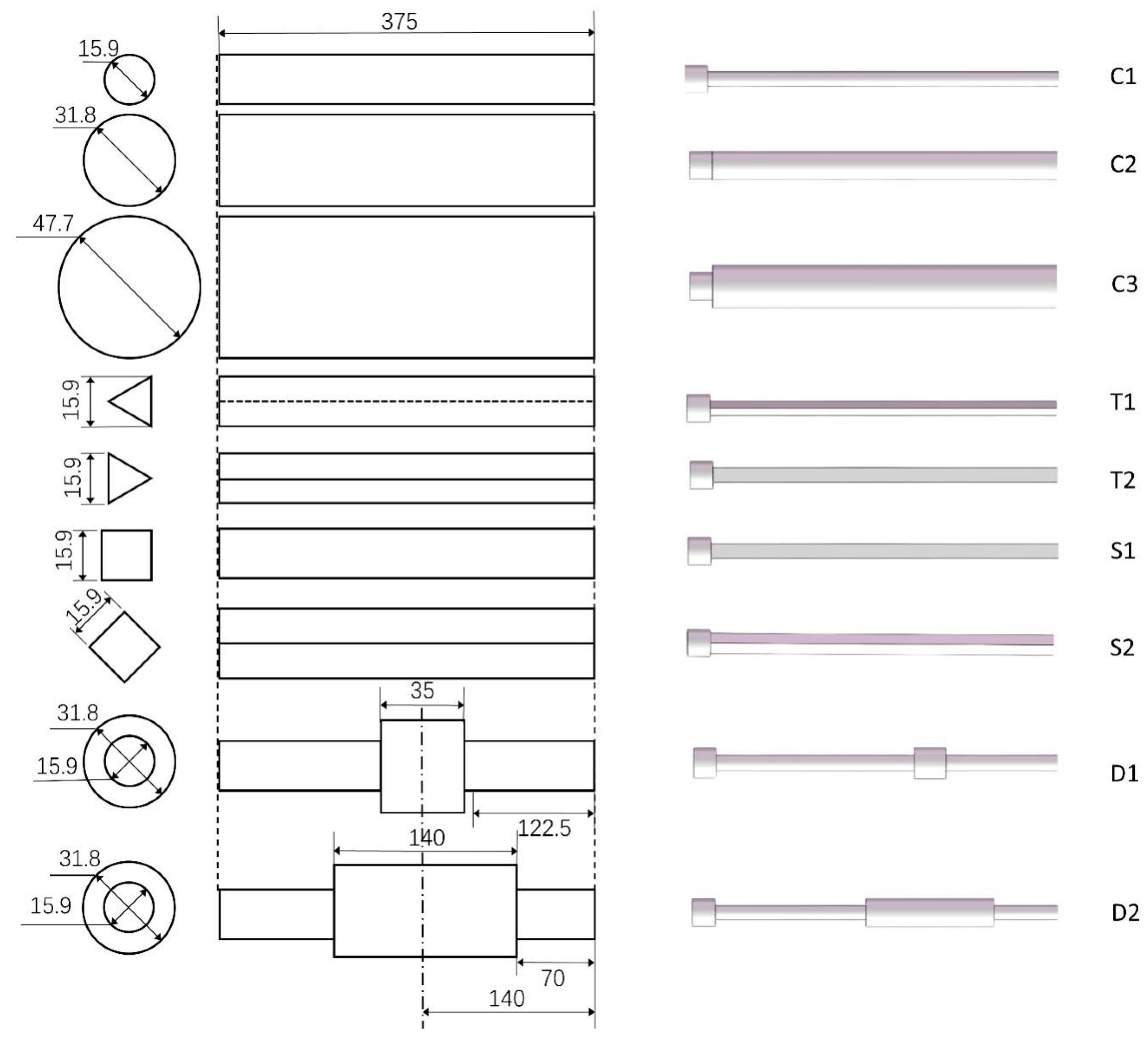



| C1 | C2 | C3 | T1 | T2 | S1 | S2 | D1 | D2 | No | |
|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 , | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Case 2 , | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Case 3 , | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Case 4 , | √ | √ | √ | √ | √ | √ | √ | √ | √ | - |
| Case 5 , | √ | √ | √ | √ | √ | √ | √ | √ | √ | - |
| Network Structure | Parameters | |
|---|---|---|
| Convolution Block 1 | Conv1d + Leaky ReLU | filter size: 256; stride: 64; channel: 64; padding: no padding; negative slope: 0.01 |
| Batch Normalization | - | |
| Max Pooling | pooling size: 4; stride: 1; padding: no padding | |
| Convolution Block 2 | Conv1d + Leaky ReLU | filter size: 7; stride: 1; channel: 64; padding: no padding; negative slope: 0.01 |
| Batch Normalization | - | |
| Max Pooling | pooling size: 4; stride: 1; padding: no padding | |
| Convolution Block 3 | Conv1d + Leaky ReLU | filter size: 7; stride: 1; channel: 64; padding: no padding; negative slope: 0.01 |
| Batch Normalization | - | |
| Max Pooling | pooling size: 4; stride: 1; padding: no padding | |
| Flatten | - | |
| Full Connect + Leaky ReLU | node number: 120; dropout: 0.2; negative slope: 0.01 | |
| Full Connect + Leaky ReLU | node number: 80; dropout: 0.2; negative slope: 0.01 | |
| Full Connect + Softmax | node number = number of classes | |
| Sample Sets | Length | Time Step | Filtering | Channel | Train Set | Validation Set | Test Set |
|---|---|---|---|---|---|---|---|
| Sample Set 1 | 2048 | unfiltered | lift and drag | 13,363 | 3341 | 8352 | |
| Sample Set 2 | 2048 | unfiltered | lift and drag | 12,902 | 3226 | 8064 | |
| Sample Set 3 | 2048 | unfiltered | lift and drag | 11,981 | 2995 | 7488 | |
| Sample Set 4 | 2048 | unfiltered | lift and drag | 10,138 | 2534 | 6336 | |
| Sample Set 5 | 2048 | 50 Hz low-pass | lift and drag | 11,981 | 2995 | 7488 | |
| Sample Set 6 | 2048 | 30 Hz low-pass | lift and drag | 11,981 | 2995 | 7488 | |
| Sample Set 7 | 2048 | 10 Hz low-pass | lift and drag | 11,981 | 2995 | 7488 | |
| Sample Set 8 | 2048 | 5 Hz low-pass | lift and drag | 11,981 | 2995 | 7488 | |
| Sample Set 9 | 2048 | 5 Hz high-pass | lift and drag | 11,981 | 2995 | 7488 | |
| Sample Set 10 | 2048 | unfiltered | lift only | 11,981 | 2995 | 7488 | |
| Sample Set 11 | 2048 | unfiltered | drag only | 11,981 | 2995 | 7488 |
| Learning Settings | |
|---|---|
| Optimizer | Adam |
| Loss function | Categorical cross-entropy function |
| Learning rate | 0.0001 |
| Batch size | 32 |
| Maximum number of training epochs | 75 |
| Patience of early stopping | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Y.; Lv, Y.; Wang, Y.; Yuan, D.; Liu, L.; Song, Z.; Ji, C. Shape Classification Using a Single Seal-Whisker-Style Sensor Based on the Neural Network Method. Sensors 2024, 24, 5418. https://doi.org/10.3390/s24165418
Mao Y, Lv Y, Wang Y, Yuan D, Liu L, Song Z, Ji C. Shape Classification Using a Single Seal-Whisker-Style Sensor Based on the Neural Network Method. Sensors. 2024; 24(16):5418. https://doi.org/10.3390/s24165418
Chicago/Turabian StyleMao, Yitian, Yingxue Lv, Yaohong Wang, Dekui Yuan, Luyao Liu, Ziyu Song, and Chunning Ji. 2024. "Shape Classification Using a Single Seal-Whisker-Style Sensor Based on the Neural Network Method" Sensors 24, no. 16: 5418. https://doi.org/10.3390/s24165418
APA StyleMao, Y., Lv, Y., Wang, Y., Yuan, D., Liu, L., Song, Z., & Ji, C. (2024). Shape Classification Using a Single Seal-Whisker-Style Sensor Based on the Neural Network Method. Sensors, 24(16), 5418. https://doi.org/10.3390/s24165418







