DIO-SLAM: A Dynamic RGB-D SLAM Method Combining Instance Segmentation and Optical Flow
Abstract
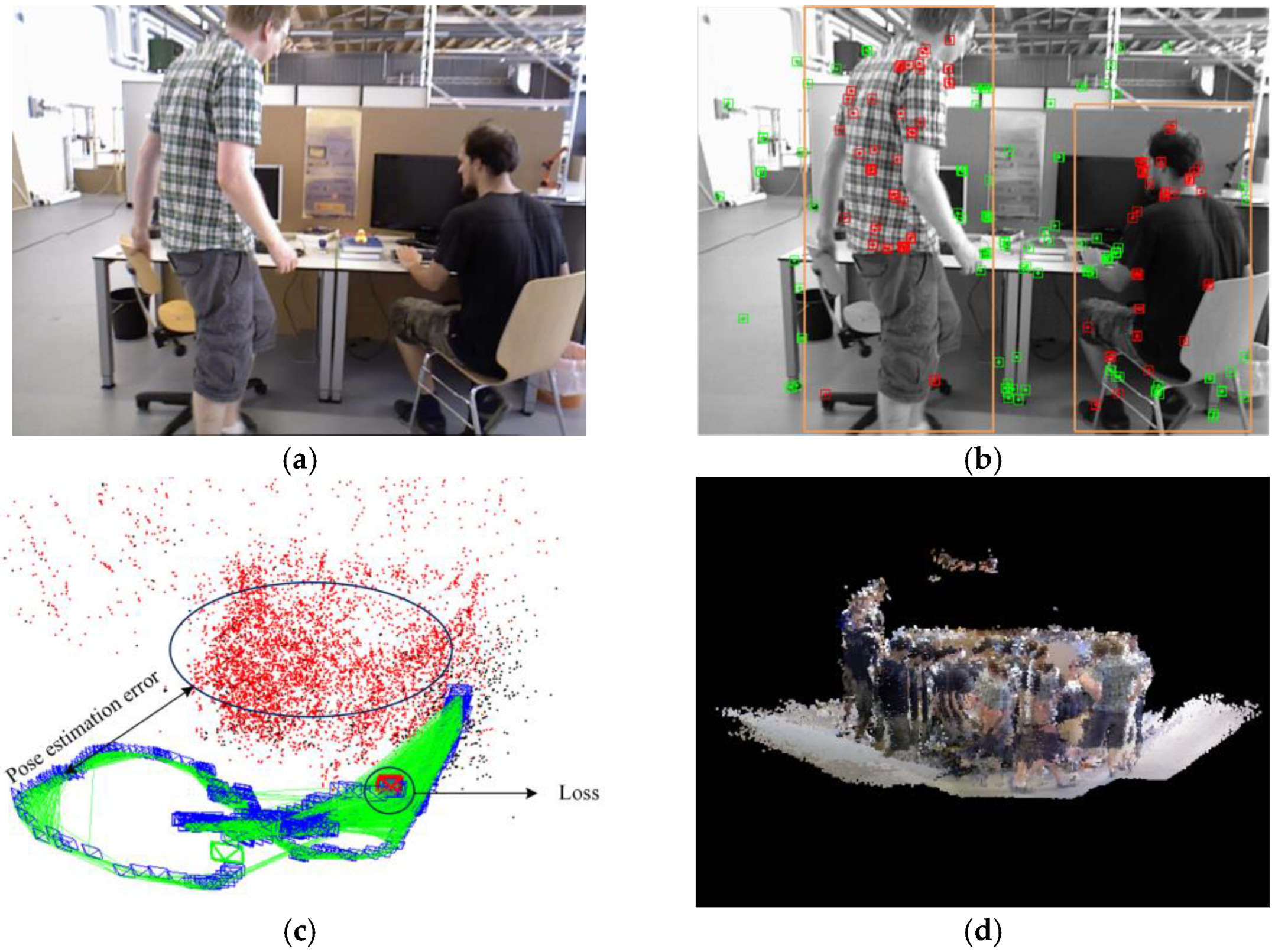
:1. Introduction
- To deal with the issue of excessive noise in existing dense optical flow algorithms, which makes it difficult to accurately identify moving objects, this paper proposes an optical flow consistency method based on optical flow residuals. This method effectively removes optical flow noise caused by camera movement, providing a solid foundation for the tight coupling of dense optical flow and instance segmentation algorithms.
- A motion frame propagation method is proposed, which transfers dynamic information from dynamic frames to subsequent frames and estimates the location of dynamic masks based on the camera’s motion matrix. By compensating for missed detections or blurring caused by significant object or camera movements, this approach reduces the likelihood of detection thread failure, thereby enhancing the accuracy and robustness of the system.
2. Related Work
2.1. Algorithms Based on Geometric Constraints and Detection Segmentation
2.2. Algorithms Based on Optical Flow and Detection Segmentation
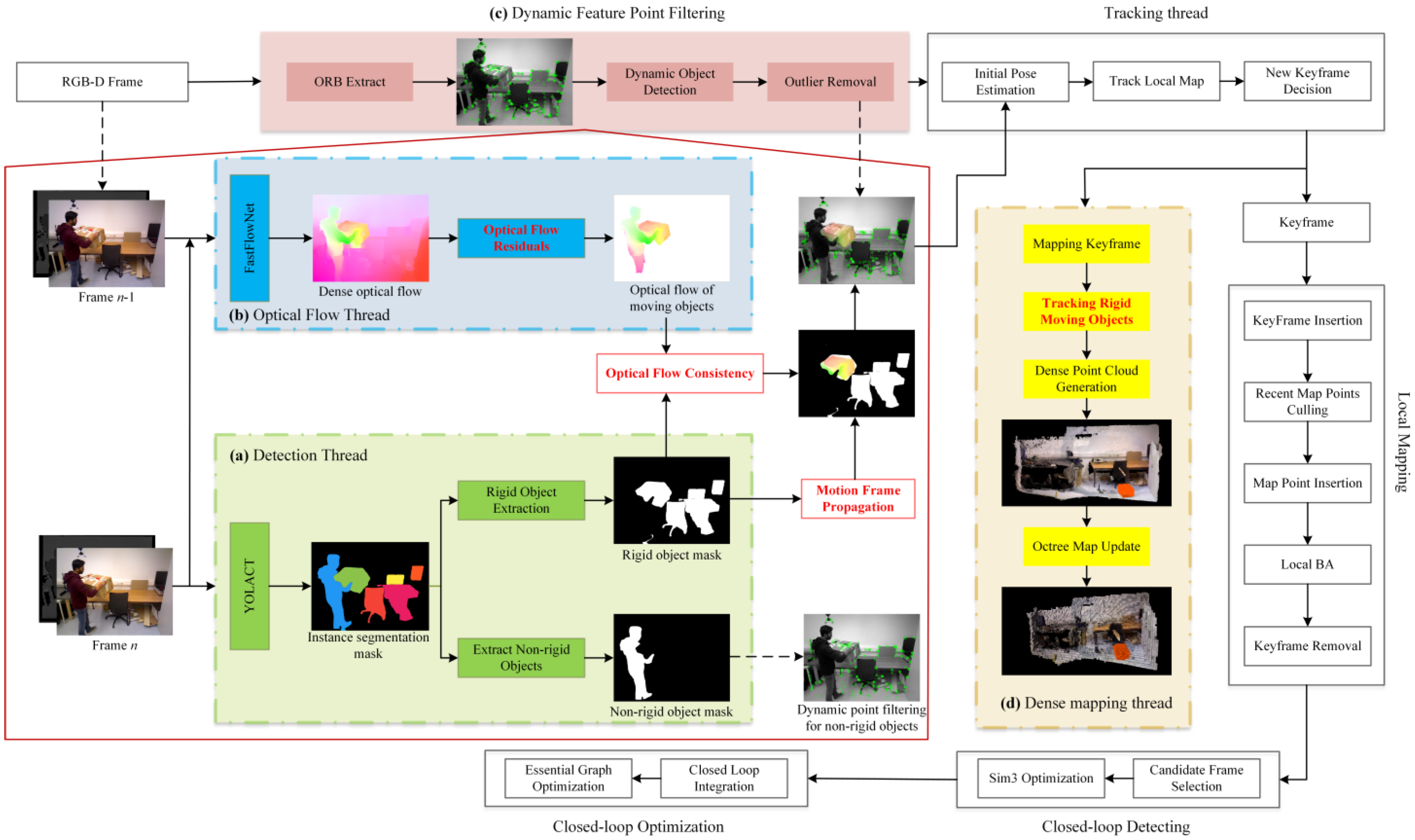
3. Overall System Framework
4. Methodology Overview
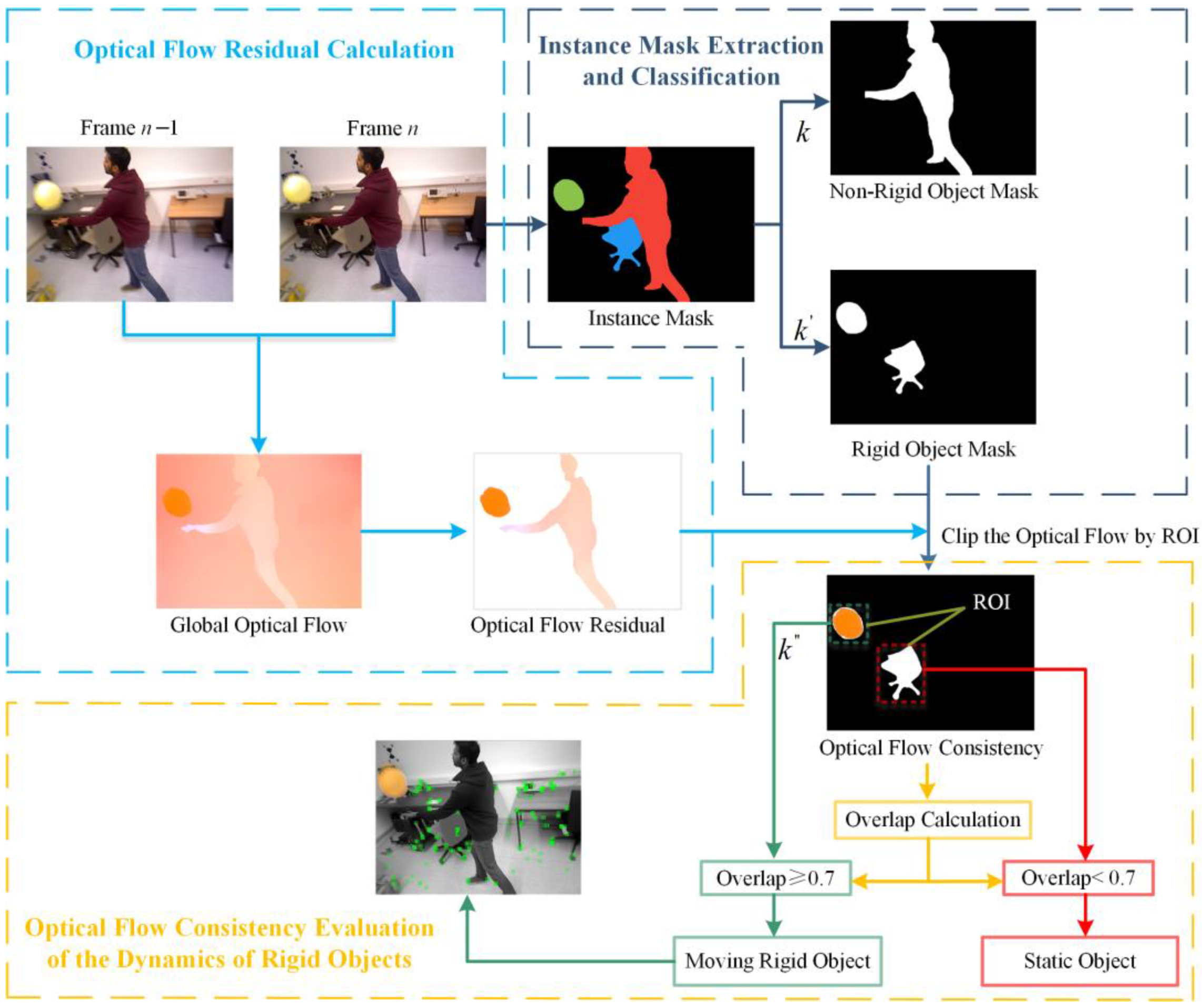
4.1. Mask Extraction in the Detection Thread
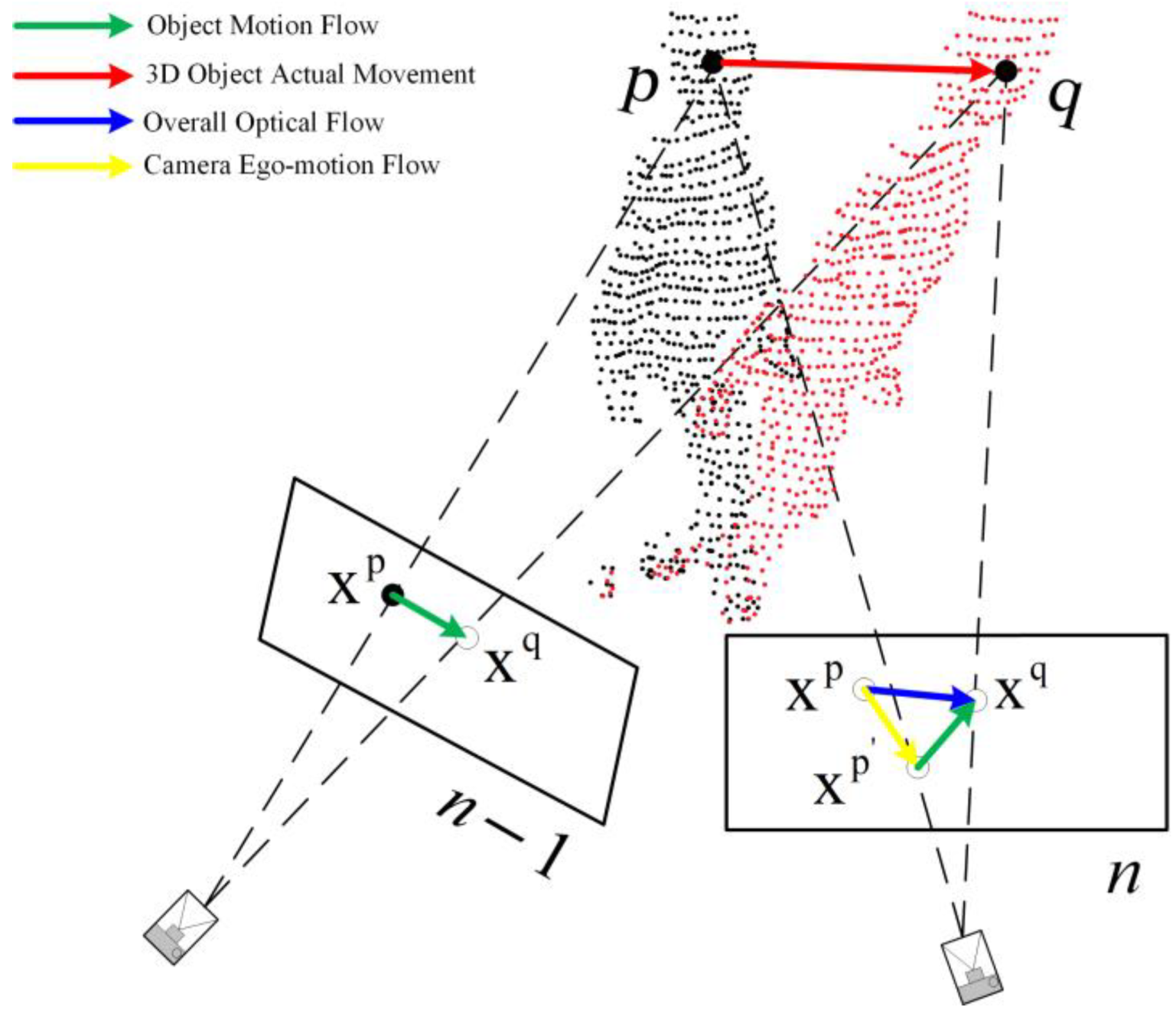
4.2. Determining Object Motion State in the Optical Flow Thread
4.3. Optical Flow Consistency
| Algorithm 1 Optical flow consistency calculation |
| # Set the rigid object mask region as the ROI region. #Set the optical flow region as the processing image region. ) # Ensure the mask is binary # Get the pixels from the instance mask region GetInstanceMaskRegionPixels) # Get the pixels from the optical flow region GetOpticalFlowRegionPixels) # Multiply the two sets of pixels element-wise ) GetOpticalFlowConsistencyImage Return extract_roi 4. is the number of intersecting pixels. then GetMovingRigidObjectMask) End If |
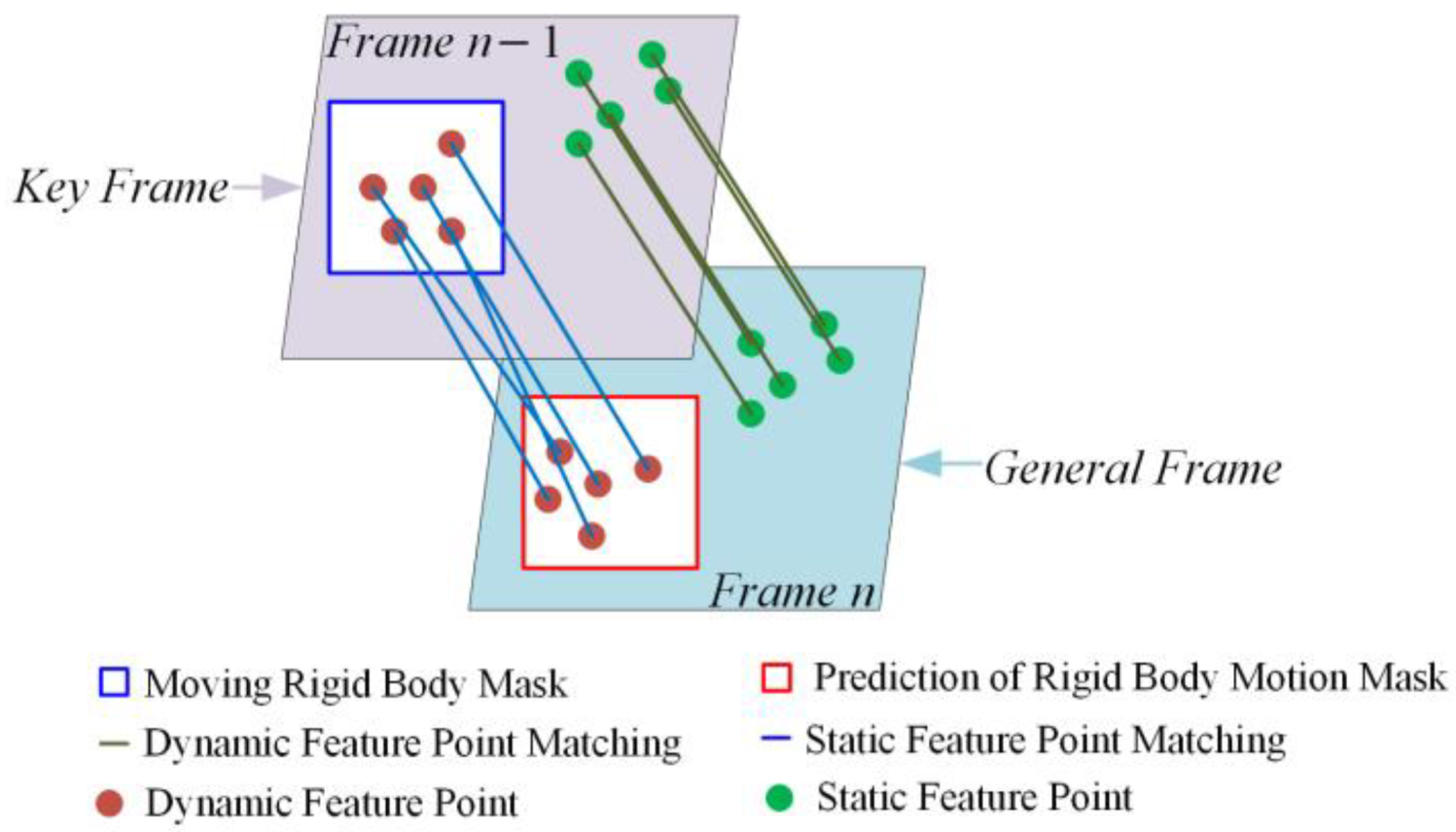
4.4. Motion Frame Propagation
4.5. Dense Mapping Thread
5. Experiments and Results Analysis
5.1. Hardware and Software Platform
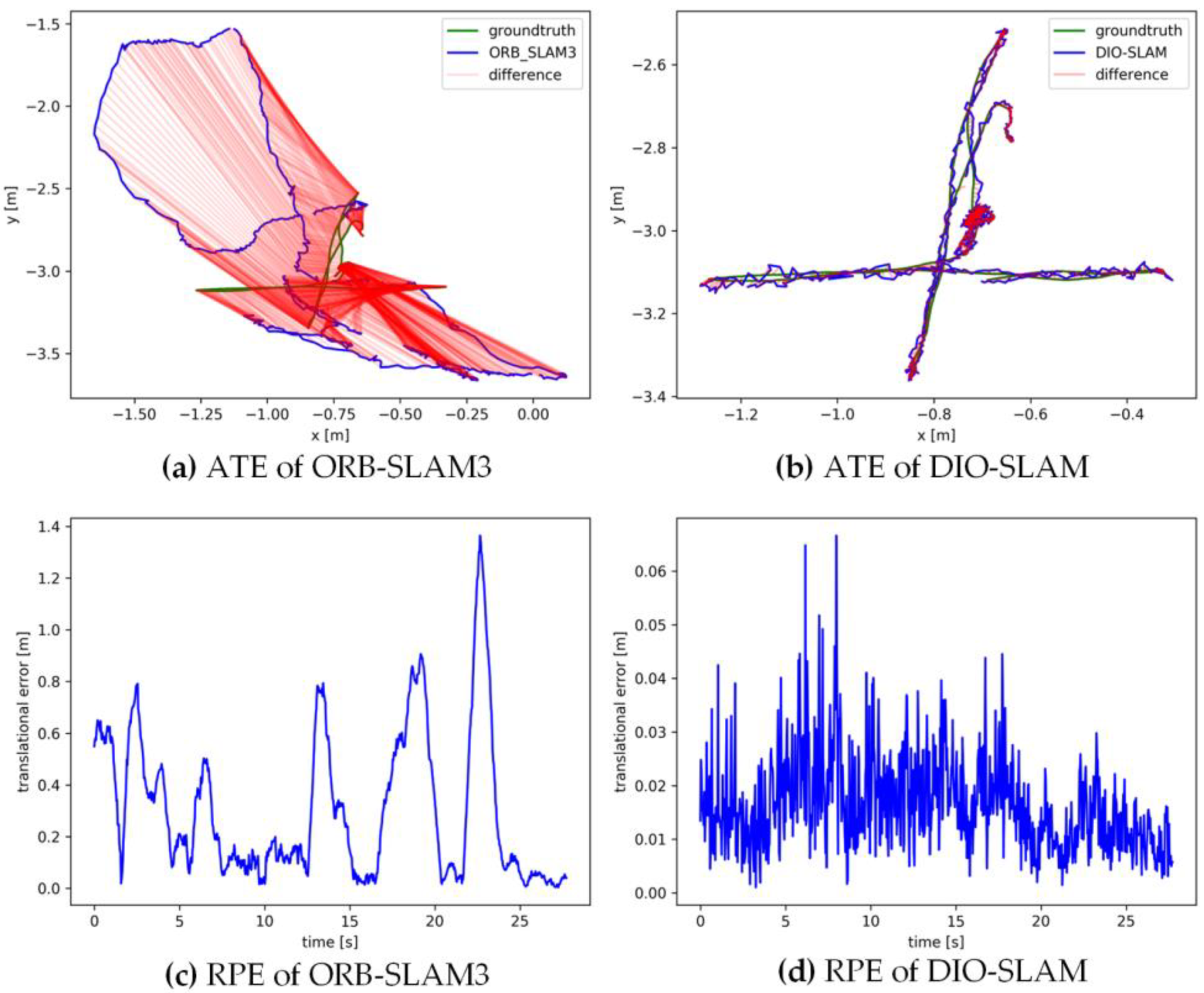
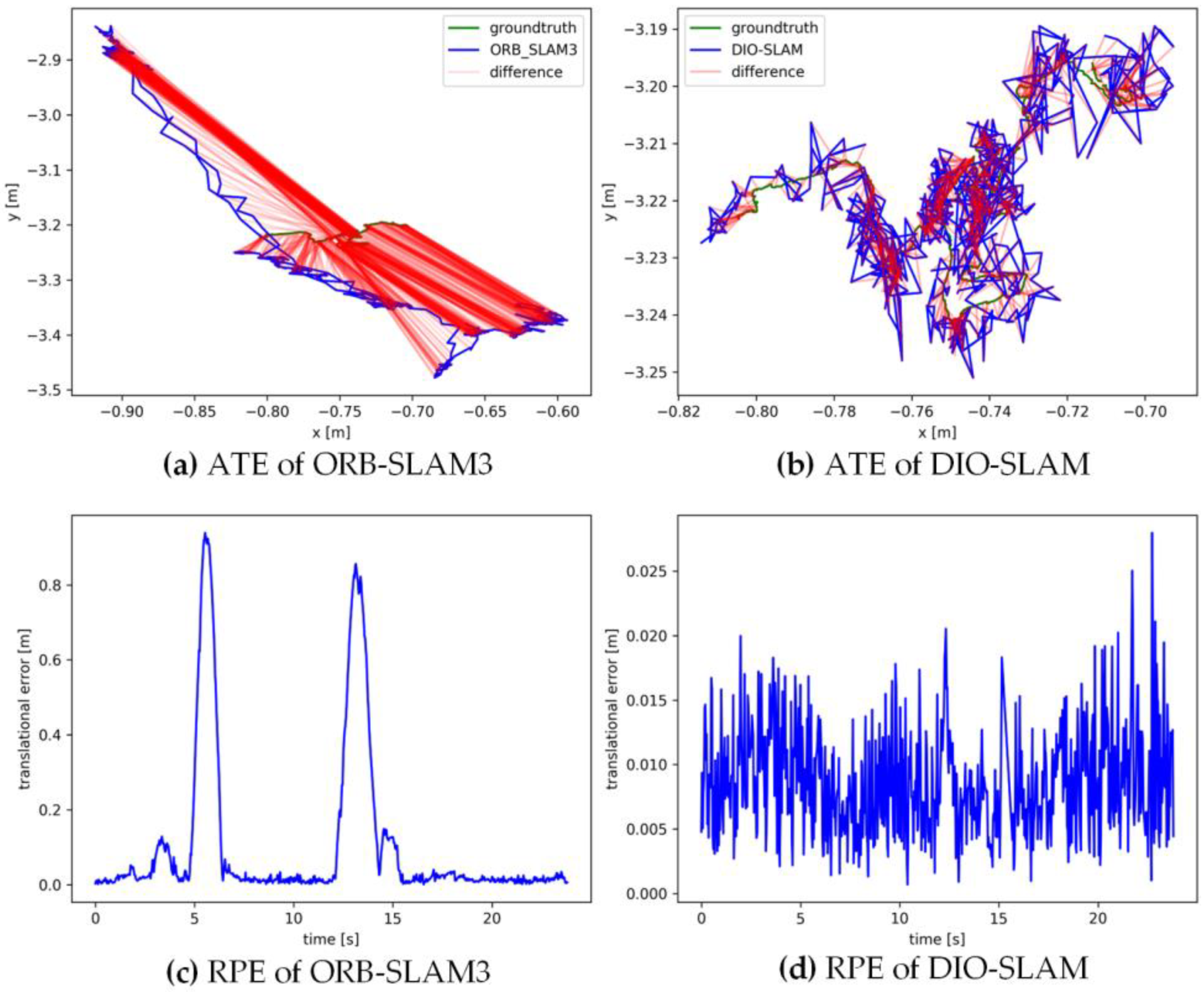
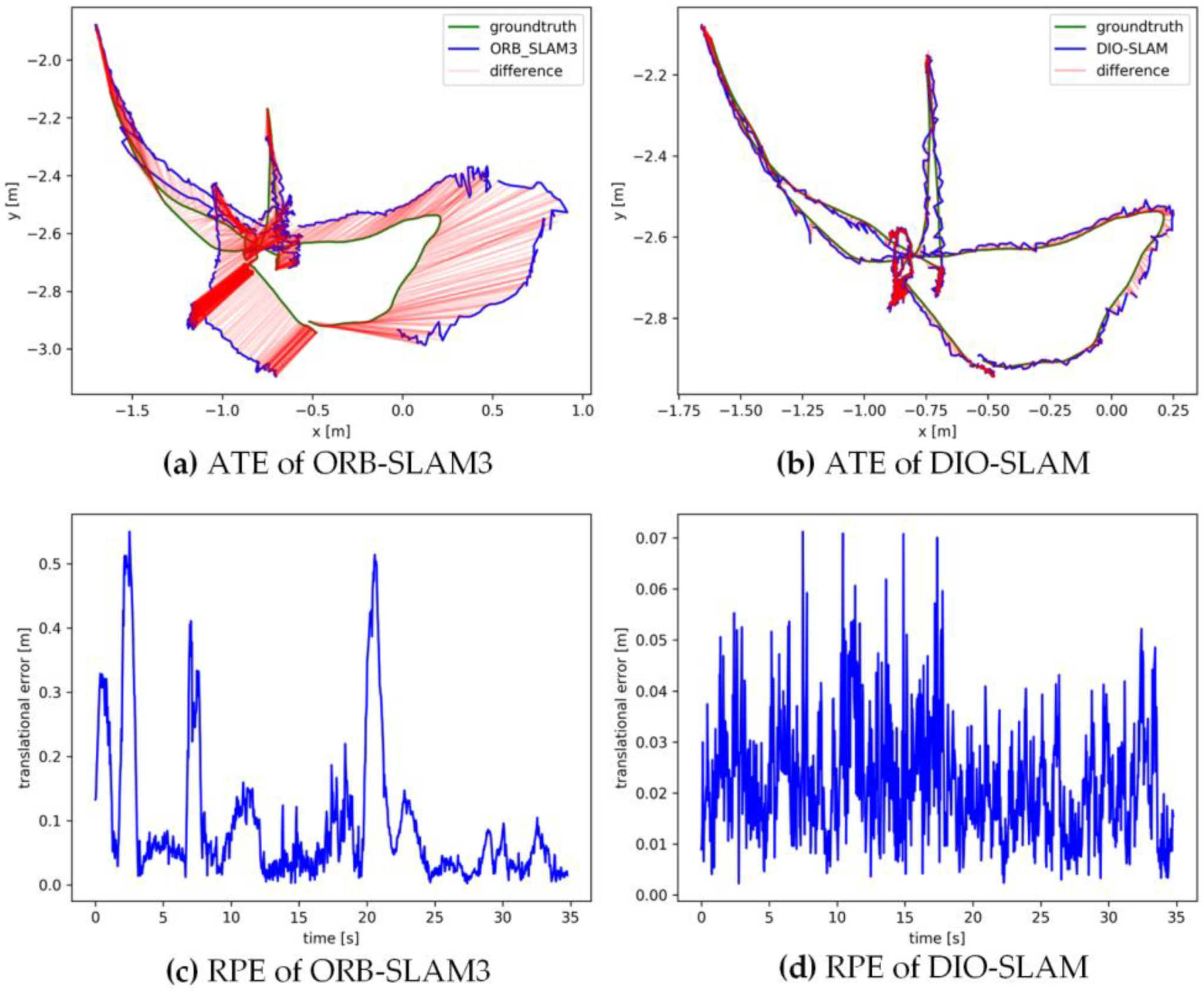
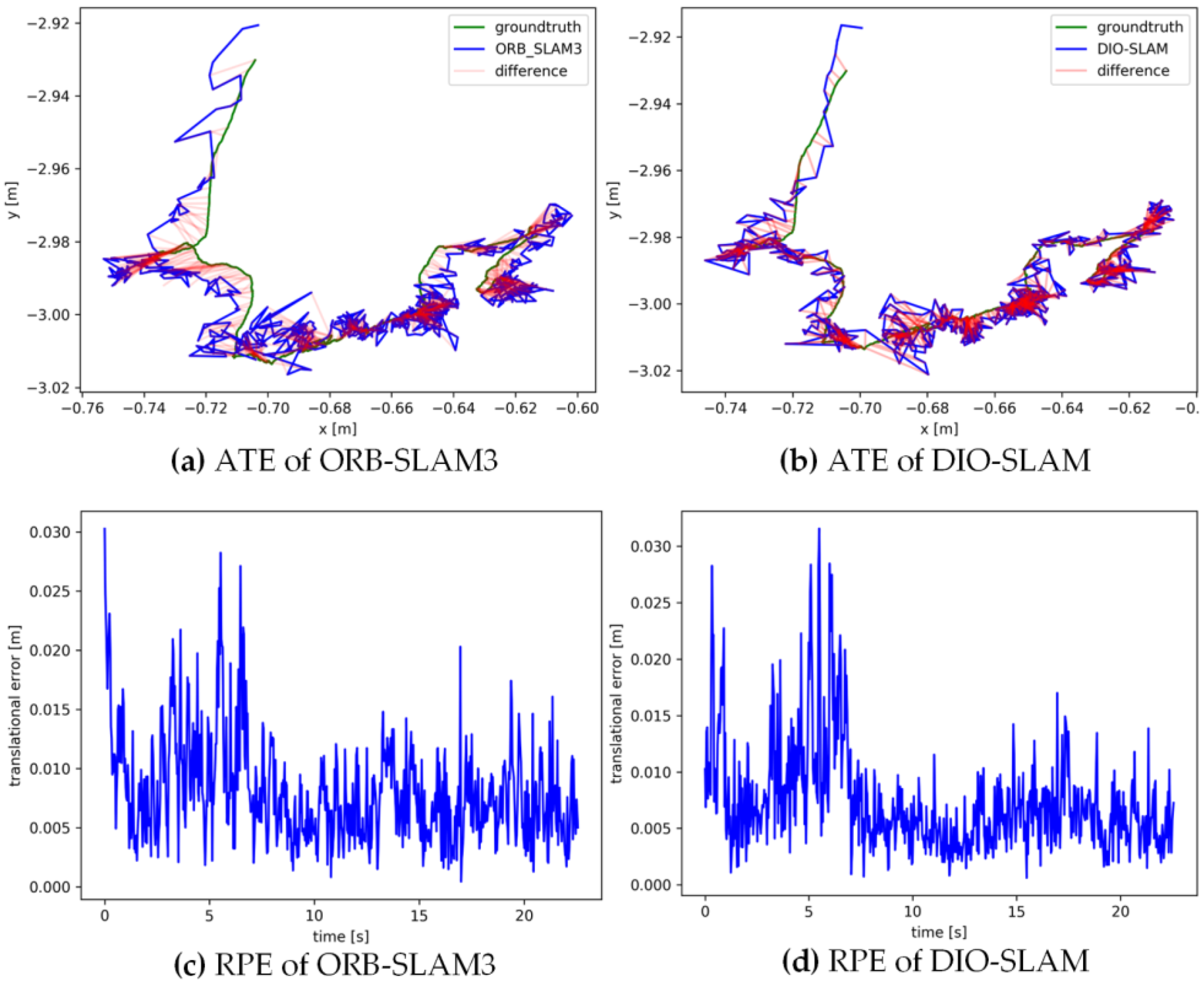
5.2. Comparative Experiment on Camera Pose Accuracy with ORB-SLAM3
5.3. Comparative Experiment on Pose Accuracy with Cutting-Edge Dynamic VSLAM Algorithms
5.4. Ablation Experiment
5.5. Dense Mapping Experiment
5.6. Real-World Scenario Testing
5.7. Time Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, Z.; Lin, S.; Yang, C. RLD-SLAM: A Robust Lightweight VI-SLAM for Dynamic Environments Leveraging Semantics and Motion Information. IEEE Trans. Ind. Electron. 2024, 71, 14328–14338. [Google Scholar] [CrossRef]
- Jia, G.; Li, X.; Zhang, D.; Xu, W.; Lv, H.; Shi, Y.; Cai, M. Visual-SLAM Classical Framework and Key Techniques: A Review. Sensors 2022, 22, 4582. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Shang, G.; Ji, A.; Zhou, C.; Wang, X.; Xu, C.; Li, Z.; Hu, K. An Overview on Visual SLAM: From Tradition to Semantic. Remote Sens. 2022, 14, 3010. [Google Scholar] [CrossRef]
- Macario Barros, A.; Michel, M.; Moline, Y.; Corre, G.; Carrel, F. A Comprehensive Survey of Visual SLAM Algorithms. Robotics 2022, 11, 24. [Google Scholar] [CrossRef]
- Tourani, A.; Bavle, H.; Sanchez-Lopez, J.L.; Voos, H. Visual SLAM: What Are the Current Trends and What to Expect? Sensors 2022, 22, 9297. [Google Scholar] [CrossRef]
- Zhang, F.; Rui, T.; Yang, C.; Shi, J. LAP-SLAM: A Line-Assisted Point-Based Monocular VSLAM. Electronics 2019, 8, 243. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Aad, G.; Anduaga, X.S.; Antonelli, S.; Bendel, M.; Breiler, B.; Castrovillari, F.; Civera, J.V.; Del Prete, T.; Dova, M.T.; Duffin, S.; et al. The ATLAS Experiment at the CERN Large Hadron Collider. J. Instrum. 2008, 3, S08003. [Google Scholar] [CrossRef]
- Zhong, F.; Wang, S.; Zhang, Z.; Chen, C.; Wang, Y. Detect-SLAM: Making Object Detection and SLAM Mutually Beneficial. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1001–1010. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Runz, M.; Buffier, M.; Agapito, L. MaskFusion: Real-Time Recognition, Tracking and Reconstruction of Multiple Moving Objects. In Proceedings of the 2018 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Munich, Germany, 16–20 October 2018; pp. 10–20. [Google Scholar]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Whelan, T.; Leutenegger, S.; Salas Moreno, R.; Glocker, B.; Davison, A. ElasticFusion: Dense SLAM Without A Pose Graph. In Proceedings of the Robotics: Science and Systems XI, Rome, Italy, 13–17 July 2015. [Google Scholar]
- Yu, C.; Liu, Z.; Liu, X.-J.; Xie, F.; Yang, Y.; Wei, Q.; Fei, Q. DS-SLAM: A Semantic Visual SLAM towards Dynamic Environments. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1168–1174. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Wei, J.; Su, S.; Wu, P. SOLO-SLAM: A Parallel Semantic SLAM Algorithm for Dynamic Scenes. Sensors 2022, 22, 6977. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, R.; Kong, T.; Li, L.; Shen, C. SOLOv2: Dynamic and Fast Instance Segmentation. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 17721–17732. [Google Scholar]
- Bescos, B.; Fácil, J.M.; Civera, J.; Neira, J. DynaSLAM: Tracking, Mapping, and Inpainting in Dynamic Scenes. IEEE Robot. Autom. Lett. 2018, 3, 4076–4083. [Google Scholar] [CrossRef]
- Bescos, B.; Campos, C.; Tardós, J.D.; Neira, J. DynaSLAM II: Tightly-Coupled Multi-Object Tracking and SLAM. IEEE Robot. Autom. Lett. 2021, 6, 5191–5198. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, S.; Lin, X.; Zhu, F. Improving RGB-D SLAM Accuracy in Dynamic Environments Based on Semantic and Geometric Constraints. Measurement 2023, 217, 113084. [Google Scholar] [CrossRef]
- Islam, Q.U.; Ibrahim, H.; Chin, P.K.; Lim, K.; Abdullah, M.Z. MVS-SLAM: Enhanced Multiview Geometry for Improved Semantic RGBD SLAM in Dynamic Environment. J. Field Robot. 2024, 41, 109–130. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, H.; Li, Y.; Nakamura, Y.; Zhang, L. FlowFusion: Dynamic Dense RGB-D SLAM Based on Optical Flow. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 7322–7328. [Google Scholar]
- Sun, D.; Yang, X.; Liu, M.-Y.; Kautz, J. PWC-Net: CNNs for Optical Flow Using Pyramid, Warping, and Cost Volume. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 8934–8943. [Google Scholar]
- Chang, Z.; Wu, H.; Sun, Y.; Li, C. RGB-D Visual SLAM Based on Yolov4-Tiny in Indoor Dynamic Environment. Micromachines 2022, 13, 230. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, R.; Wang, X. Visual SLAM Mapping Based on YOLOv5 in Dynamic Scenes. Appl. Sci. 2022, 12, 11548. [Google Scholar] [CrossRef]
- Theodorou, C.; Velisavljevic, V.; Dyo, V. Visual SLAM for Dynamic Environments Based on Object Detection and Optical Flow for Dynamic Object Removal. Sensors 2022, 22, 7553. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the IJCAI’81: 7th international joint conference on Artificial intelligence, Vancouver, BC, Canada, 24–28 August 1981; Volume 2, pp. 674–679. [Google Scholar]
- Cheng, J.; Wang, Z.; Zhou, H.; Li, L.; Yao, J. DM-SLAM: A Feature-Based SLAM System for Rigid Dynamic Scenes. ISPRS Int. J. Geo-Inf. 2020, 9, 202. [Google Scholar] [CrossRef]
- Bujanca, M.; Lennox, B.; Luján, M. ACEFusion—Accelerated and Energy-Efficient Semantic 3D Reconstruction of Dynamic Scenes. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 11063–11070. [Google Scholar]
- Qin, L.; Wu, C.; Chen, Z.; Kong, X.; Lv, Z.; Zhao, Z. RSO-SLAM: A Robust Semantic Visual SLAM With Optical Flow in Complex Dynamic Environments. IEEE Trans. Intell. Transp. Syst. 2024, 1–16. [Google Scholar] [CrossRef]
- Zhang, J.; Henein, M.; Mahony, R.; Ila, V. VDO-SLAM: A Visual Dynamic Object-Aware SLAM System. arXiv 2021, arXiv:2005.11052. [Google Scholar]
- Bolya, D.; Zhou, C.; Xiao, F.; Lee, Y.J. YOLACT: Real-Time Instance Segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9157–9166. [Google Scholar]
- Kong, L.; Shen, C.; Yang, J. FastFlowNet: A Lightweight Network for Fast Optical Flow Estimation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 10310–10316. [Google Scholar]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar]
- Xu, H.; Zhang, J.; Cai, J.; Rezatofighi, H.; Tao, D. GMFlow: Learning Optical Flow via Global Matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Wang, C.; Luo, B.; Zhang, Y.; Zhao, Q.; Yin, L.; Wang, W.; Su, X.; Wang, Y.; Li, C. DymSLAM: 4D Dynamic Scene Reconstruction Based on Geometrical Motion Segmentation. IEEE Robot. Autom. Lett. 2021, 6, 550–557. [Google Scholar] [CrossRef]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A Benchmark for the Evaluation of RGB-D SLAM Systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Liu, Y.; Miura, J. RDMO-SLAM: Real-Time Visual SLAM for Dynamic Environments Using Semantic Label Prediction With Optical Flow. IEEE Access 2021, 9, 106981–106997. [Google Scholar] [CrossRef]
- Liu, Y.; Miura, J. RDS-SLAM: Real-Time Dynamic SLAM Using Semantic Segmentation Methods. IEEE Access 2021, 9, 23772–23785. [Google Scholar] [CrossRef]
- Cheng, S.; Sun, C.; Zhang, S.; Zhang, D. SG-SLAM: A Real-Time RGB-D Visual SLAM Toward Dynamic Scenes With Semantic and Geometric Information. IEEE Trans. Instrum. Meas. 2023, 72, 7501012. [Google Scholar] [CrossRef]
- Palazzolo, E.; Behley, J.; Lottes, P.; Giguère, P.; Stachniss, C. ReFusion: 3D Reconstruction in Dynamic Environments for RGB-D Cameras Exploiting Residuals. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 7855–7862. [Google Scholar]
- Handa, A.; Whelan, T.; McDonald, J.; Davison, A.J. A Benchmark for RGB-D Visual Odometry, 3D Reconstruction and SLAM. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1524–1531. [Google Scholar]
- Hui, T.-W.; Tang, X.; Loy, C.C. LiteFlowNet: A Lightweight Convolutional Neural Network for Optical Flow Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 8981–8989. [Google Scholar]










| Name | Configuration |
|---|---|
| CPU | Intel Core i9-13900HX (Intel, Santa Clara, CA, USA) |
| GPU | NVIDIA GeForce RTX 4060 8G (NVIDIA, Santa Clara, CA, USA) |
| Memory | 32GB |
| Operating system | Ubuntu 20.04 64-bit |
| Python, CUDA, PyTorch versions | python3.8, CUDA = 11.8, pytorch = 2.0.0 |
| OpenCV, PCL versions | OPENCV = 4.8.0, PCL = 1.10 |
| TensorRT version | TensorRT = 8.6.1.6 |
| Seq. | ORB-SLAM3 | DIO-SLAM (Ours) | Improvements | |||
|---|---|---|---|---|---|---|
| RMSE | S.D. | RMSE | RMSE | RMSE (%) | S.D. (%) | |
| w_xyz | 0.8336 | 0.4761 | 0.0145 | 0.0145 | 98.26 | 98.53 |
| w_static | 0.4078 | 0.1831 | 0.0072 | 0.0072 | 98.23 | 98.31 |
| w_rpy | 1.1665 | 0.6294 | 0.0306 | 0.0306 | 97.38 | 97.47 |
| w_half | 0.3178 | 0.1557 | 0.0259 | 0.0259 | 91.85 | 91.91 |
| s_static | 0.0099 | 0.0044 | 0.0062 | 0.0062 | 37.37 | 34.09 |
| Seq. | ORB-SLAM3 | DIO-SLAM (Ours) | Improvements | |||
|---|---|---|---|---|---|---|
| RMSE | S.D. | RMSE | RMSE | RMSE (%) | S.D. (%) | |
| w_xyz | 0.4154 | 0.2841 | 0.0186 | 0.0089 | 95.52 | 96.87 |
| w_static | 0.2355 | 0.2123 | 0.0096 | 0.0041 | 95.92 | 98.07 |
| w_rpy | 0.3974 | 0.2836 | 0.0426 | 0.0228 | 89.28 | 91.96 |
| w_half | 0.1424 | 0.1075 | 0.0250 | 0.0110 | 82.44 | 89.77 |
| s_static | 0.0092 | 0.0045 | 0.0087 | 0.0047 | 5.43 | −4.44 |
| Seq. | ORB-SLAM3 | DIO-SLAM (Ours) | Improvements | |||
|---|---|---|---|---|---|---|
| RMSE | S.D. | RMSE | RMSE | RMSE (%) | S.D. (%) | |
| w_xyz | 8.0130 | 5.5450 | 0.5020 | 0.2455 | 93.74 | 95.57 |
| w_static | 4.1851 | 3.7462 | 0.2708 | 0.1106 | 93.53 | 97.05 |
| w_rpy | 7.7448 | 5.5218 | 0.8731 | 0.4221 | 88.73 | 92.36 |
| w_half | 2.3482 | 1.6014 | 0.7321 | 0.3435 | 68.82 | 78.55 |
| s_static | 0.2872 | 0.1265 | 0.2802 | 0.1287 | 2.44 | −1.74 |
| Seq. | w_xyz | w_static | w_rpy | w_half | s_static | |
|---|---|---|---|---|---|---|
| Dyna-SLAM * (N + G) | RMSE | 0.0161 | 0.0067 | 0.0345 | 0.0293 | 0.0108 |
| S.D. | 0.0083 | 0.0038 | 0.0195 | 0.0149 | 0.0056 | |
| DS-SLAM * | RMSE | 0.0247 | 0.0081 | 0.4442 | 0.0303 | 0.0065 |
| S.D. | 0.0161 | 0.0067 | 0.2350 | 0.0159 | 0.0033 | |
| RDMO-SLAM | RMSE | 0.0226 | 0.0126 | 0.1283 | 0.0304 | 0.0066 |
| S.D. | 0.0137 | 0.0071 | 0.1047 | 0.0141 | 0.0033 | |
| DM-SLAM | RMSE | 0.0148 | 0.0079 | 0.0328 | 0.0274 | 0.0063 |
| S.D. | 0.0072 | 0.0040 | 0.0194 | 0.0137 | 0.0032 | |
| RDS-SLAM * | RMSE | 0.0571 | 0.0206 | 0.1604 | 0.0807 | 0.0084 |
| S.D. | 0.0229 | 0.0120 | 0.0873 | 0.0454 | 0.0043 | |
| ACE-Fusion | RMSE | 0.0146 | 0.0067 | 0.1869 | 0.0425 | 0.0066 |
| S.D. | 0.0074 | 0.0032 | 0.1467 | 0.0264 | 0.0032 | |
| SG-SLAM * | RMSE | 0.0152 | 0.0073 | 0.0324 | 0.0268 | 0.0060 |
| S.D. | 0.0075 | 0.0034 | 0.0187 | 0.0203 | 0.0047 | |
| DIO-SLAM(Ours) | RMSE | 0.0145 | 0.0072 | 0.0306 | 0.0259 | 0.0062 |
| S.D. | 0.0070 | 0.0031 | 0.0159 | 0.0126 | 0.0029 |
| Seq. | w_xyz | w_static | w_rpy | w_half | s_static | |
|---|---|---|---|---|---|---|
| Dyna-SLAM * (N + G) | RMSE | 0.0217 | 0.0089 | 0.0448 | 0.0284 | 0.0126 |
| S.D. | 0.0119 | 0.0040 | 0.0262 | 0.0149 | 0.0067 | |
| DS-SLAM * | RMSE | 0.0333 | 0.0102 | 0.1503 | 0.0297 | 0.0078 |
| S.D. | 0.0229 | 0.0038 | 0.1168 | 0.0152 | 0.0038 | |
| RDMO-SLAM | RMSE | 0.0299 | 0.0160 | 0.1396 | 0.0294 | 0.0090 |
| S.D. | 0.0188 | 0.0090 | 0.1176 | 0.0130 | 0.0040 | |
| DM-SLAM | RMSE | - | - | - | - | - |
| S.D. | - | - | - | - | - | |
| RDS-SLAM * | RMSE | 0.0426 | 0.0221 | 0.1320 | 0.0482 | 0.0123 |
| S.D. | 0.0317 | 0.0149 | 0.1067 | 0.0036 | 0.0070 | |
| ACE-Fusion | RMSE | - | - | - | - | - |
| S.D. | - | - | - | - | - | |
| SG-SLAM * | RMSE | 0.0194 | 0.0100 | 0.0450 | 0.0279 | 0.0075 |
| S.D. | 0.0100 | 0.0051 | 0.0262 | 0.0146 | 0.0035 | |
| DIO-SLAM(Ours) | RMSE | 0.0186 | 0.0096 | 0.0426 | 0.0250 | 0.0087 |
| S.D. | 0.0089 | 0.0041 | 0.0228 | 0.0110 | 0.0047 |
| Seq. | w_xyz | w_static | w_rpy | w_half | s_static | |
|---|---|---|---|---|---|---|
| Dyna-SLAM * (N + G) | RMSE | 0.6284 | 0.2612 | 0.9894 | 0.7842 | 0.3416 |
| S.D. | 0.3848 | 0.1259 | 0.5701 | 0.4012 | 0.1642 | |
| DS-SLAM * | RMSE | 0.8266 | 0.2690 | 3.0042 | 0.8142 | 0.2735 |
| S.D. | 0.2826 | 0.1215 | 2.3065 | 0.4101 | 0.1215 | |
| RDMO-SLAM | RMSE | 0.7990 | 0.3385 | 2.5472 | 0.7915 | 0.2910 |
| S.D. | 0.5502 | 0.1612 | 2.0607 | 0.3782 | 0.1330 | |
| DM-SLAM | RMSE | - | - | - | - | - |
| S.D. | - | - | - | - | - | |
| RDS-SLAM * | RMSE | 0.9222 | 0.4944 | 13.1693 | 1.8828 | 0.3338 |
| S.D. | 0.6509 | 0.3112 | 12.0103 | 1.5250 | 0.1706 | |
| ACE-Fusion | RMSE | - | - | - | - | - |
| S.D. | - | - | - | - | - | |
| SG-SLAM* | RMSE | 0.5040 | 0.2679 | 0.9565 | 0.8119 | 0.2657 |
| S.D. | 0.2469 | 0.1144 | 0.5487 | 0.3878 | 0.1163 | |
| DIO-SLAM(Ours) | RMSE | 0.5020 | 0.2708 | 0.8731 | 0.7321 | 0.2802 |
| S.D. | 0.2455 | 0.1106 | 0.4221 | 0.3435 | 0.1287 |
| Seq. | ORB-SLAM3 | DIO-SLAM (Y) | DIO-SLAM (Y + O) | DIO-SLAM (Y + O+M) | |||
|---|---|---|---|---|---|---|---|
| RMSE | RMSE | RMSE | Im(%) | RMSE | Im(%) | ||
| 1 | balloon | 0.1762 | 0.0309 | 0.0307 | 0.6 | 0.0291 | 5.2 |
| 2 | balloon2 | 0.2898 | 0.0312 | 0.0296 | 5.1 | 0.0284 | 4.1 |
| 3 | balloon_tracking | 0.0284 | 0.0280 | 0.0272 | 2.9 | 0.0259 | 4.8 |
| 4 | balloon_tracking2 | 0.1400 | 0.0992 | 0.0589 | 40.6 | 0.0568 | 3.6 |
| 5 | crowd | 0.6262 | 0.0289 | 0.0289 | - | 0.0292 | −1.0 |
| 6 | crowd2 | 1.5959 | 0.0297 | 0.0297 | - | 0.0303 | −2.0 |
| 7 | crowd3 | 0.9958 | 0.0281 | 0.0280 | 0.3 | 0.0274 | 2.1 |
| 8 | moving_no_box | 0.2634 | 0.0294 | 0.0196 | 33.3 | 0.0173 | 11.7 |
| 9 | moving_no_box2 | 0.0379 | 0.0477 | 0.0314 | 34.2 | 0.0286 | 8.9 |
| 10 | placing_no_box | 0.7875 | 0.0486 | 0.0201 | 58.6 | 0.0189 | 6.0 |
| 11 | placing_no_box2 | 0.0283 | 0.0290 | 0.0182 | 37.2 | 0.0167 | 8.2 |
| 12 | placing_no_box3 | 0.2076 | 0.0656 | 0.0433 | 34.0 | 0.0388 | 10.3 |
| 13 | removing_no_box | 0.0167 | 0.0161 | 0.0155 | 3.7 | 0.0140 | 9.7 |
| 14 | removing_no_box2 | 0.0225 | 0.0227 | 0.0224 | 1.3 | 0.0211 | 5.8 |
| 15 | moving_o_box | 0.6476 | 0.2628 | 0.2628 | - | 0.2633 | −0.2 |
| 16 | moving_o_box2 | 0.7903 | 0.1344 | 0.1241 | 7.7 | 0.1248 | −0.6 |
| Seq. | Mean Distance | Std Deviation |
|---|---|---|
| kt0 | 0.0253 | 0.0193 |
| kt1 | 0.0203 | 0.0142 |
| kt2 | 0.0378 | 0.0296 |
| kt3 | 0.0193 | 0.0159 |
| Average | 0.0257 | 0.0198 |
| Algorithm | Average Processing Time per Frame (ms) | Hardware Platform |
|---|---|---|
| ORB-SLAM3 | 25.46 | Intel Core i9-13900HX Without GPU |
| Dyna-SLAM # | 192.00 (at least) | Nvidia Tesla M40 GPU |
| DS-SLAM # | 59.40 | Intel i7 CPU, P4000 GPU |
| RDS-SLAM # | 57.50 | Nvidia RTX 2080Ti GPU |
| SG-SLAM # | 65.71 | Nvidia Jetson AGX Xavier Developer Kit |
| SG-SLAM # | 39.51 | AMD Ryzen 7 4800H (AMD, Santa Clara, CA, USA), Nvidia GTX 1650 |
| DIO-SLAM (Before TensorRT acceleration) | 124.80 | Intel Core i9-13900HX NVIDIA GeForce RTX 4060 8G |
| DIO-SLAM (TensorRT acceleration) | 43.10 | Intel Core i9-13900HX NVIDIA GeForce RTX 4060 8G |
| Method | ORB Extraction | FastFlowNet (TensorRT Acceleration) | YOLACT (TensorRT Acceleration) | OFC | MFP | Each Frame |
|---|---|---|---|---|---|---|
| Time Cost | 3.89 | 18.39 | 25.20 | 5.01 | 14.01 | 43.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Li, S.; Qiu, J.; Zhang, C. DIO-SLAM: A Dynamic RGB-D SLAM Method Combining Instance Segmentation and Optical Flow. Sensors 2024, 24, 5929. https://doi.org/10.3390/s24185929
He L, Li S, Qiu J, Zhang C. DIO-SLAM: A Dynamic RGB-D SLAM Method Combining Instance Segmentation and Optical Flow. Sensors. 2024; 24(18):5929. https://doi.org/10.3390/s24185929
Chicago/Turabian StyleHe, Lang, Shiyun Li, Junting Qiu, and Chenhaomin Zhang. 2024. "DIO-SLAM: A Dynamic RGB-D SLAM Method Combining Instance Segmentation and Optical Flow" Sensors 24, no. 18: 5929. https://doi.org/10.3390/s24185929
APA StyleHe, L., Li, S., Qiu, J., & Zhang, C. (2024). DIO-SLAM: A Dynamic RGB-D SLAM Method Combining Instance Segmentation and Optical Flow. Sensors, 24(18), 5929. https://doi.org/10.3390/s24185929






